Ilya Selyuzhenkov
Strong Parity Violation
Global polarization
Anisotropic Flow
Acceptance effects
Systematics Study
Down Scaled DST files
2004
year 2004 posts:
2005
year 2005 posts
2006
year 2006 posts
2007
year 2007 posts
2008
year 2008 posts
2009
2009.09.26 parity estimates for BES Run 10 from Au+Au9.2 GeV
See this BES-hyper-new thread for more discussions
Fig. 1 Parity error estimates for 5M events of 9.2 GeV collisions.
- Upper left: reference multiplicity distribution for Au+Au@200GeV
- Lower left: reference multiplicity distribution for Au+Au@9.2GeV
- Upper right: actual errors for v2-scaled 3-particle correlations (same charge)
vs. reference multiplicity for Au+Au@200GeV - Lower right: error estimates for v2-scaled 3-particle correlations (same charge)
vs. reference multiplicity for Au+Au@9.2GeV
Au+Au@20GeV points with the same RefMult value are converted
(based on equation shown in the legend)
to the error estimates for 9.2GeV collisions
Fig. 2 Parity error estimates are shown together with possible singal
for 1M events of 9.2 GeV collisions
(assuming the same values for 3-particle correlator as in 200GeV collisions)
Charged particle and strange hadron elliptic flow from Cu+Cu collisions
Charged particle and strange hadron elliptic flow from sNN = 62.4 and 200 GeV Cu+Cu collisions
DPF 2009 presentation (Ilya Selyuzhenkov)
DPF 2009 presentation (Ilya Selyuzhenkov)
DPF 2009 proceedings (Ilya Selyuzhenkov)
DPF 2009 proceedings
Ilya Selyuzhenkov
"Azimuthal charged particle correlations
as a probe for local strong parity violation
in heavy-ion collisions"
Joint CATHIE/TECHQM Workshop, December 14-18, 2009
Ilya Selyuzhenkov for the STAR Collaboration
Plenary talk at Joint CATHIE/TECHQM Workshop (December 14-18, 2009) on
"STAR probes of local strong parity violation in heavy ion collisions"
QM2009 poster abstracts on Parity violation
QM2009 poster abstracts on Parity violation at STAR
-
Poster 1
"Strong parity violation at STAR:
Quantifying background effects with Monte-Carlo event generators
and detector effects study" -
Poster 2
"Strong parity violation at STAR:
Evaluating experimental measurement technique
and estimating background contributions from multi-particle production processesParity group recommended
Evan Finch (Yale) and Ilya Selyuzhenkov (Indiana)
as a possible candidates to present these posters at QM2009.
2010
2010.06.07 RHIC & AGS Users' Meeting: Workshop on Local strong parity violation
LPV workshop website:
http://www.bnl.gov/rhic_ags/users_meeting/Workshops/3.asp
Presentation:
Ilya Selyuzhenkov for the STAR Collaboration
"Probes of local strong parity violation: Experimental results from STAR"
Slides: see attached pdf(s)
Charge flow
Charged particle anisotropic flow
Directed flow measurement in AuAu@62GeV
Two methods were used to calculate directed flow:
- three particle correlations (mixed harmonic method). FTPC and TPC data were used.
- two particle correlations with spectator nucleons. Data from newly installed in 2004 ZDC SMD detector were used.
Talks and Publications
- Results are presented at QM2005 conference (nucl-ex/0510034)
- Paper on "Directed flow in Au+Au collisions at sqrt(s_NN)= 62GeV"submitted for publication to PRC Rapid Communication (nucl-ex/0510053).
Charged particle elliptic flow in AuAu@62GeV and AuAu200GeV data (RUN IV)
The measurement of elliptic flow in AuAu at 62 and 200 GeV data were performed using TPC and FTPC data. The non-flow contribution to two particle correlations at different pseudorapidity regions was discussed.
Supporting materials:
- Charged particles flow in FTPC’s
- Update on acceptance corrections for directed flow in Au+Au at 62GeV
- Getting directed flow: standard way and X and Y direction separately
- Update on acceptance corrections for directed flow
- Acceptance corrections for directed flow
- Charged particle directed flow: two particle correlations and mixed harmonic method with X and Y taken separately
- Charged particles directed flow: event plane from East/West FTPC's asymmetry
- Charged particles directed flow in Au+Au@62GeV calculated with event plane from ZDC SMD
- Calculating directed flow in the case of different resolution in the different transverse direction
- Calculating directed flow in the case of different resolution in the different transverse direction
- Directed and elliptic flows of charged particles in Au+Au at 62 GeV
- Directed and elliptic flows of charged particles in Au+Au at 62 and 200 GeV
- Directed flow of charged particles from mixed harmonics in Au+Au at 62 GeV
Down-scaled DST
DownScaleDst file format description
Here is the brief list of what are in the Down Scale DST files:
- Basic event information, like Event Id, refMult, etc.
- Calculated event plane components X and Y from TPC and FTPCs (not corrected)
- Information to get event plane from ZDC SMD.
- V0 tracks with applied cuts to select Lambda / Anti-Lambda / K0Short
- Primary tracks information.
For p_t < 1.8 GeV each 50th track from FTPCs and each 100th from TPC are taken.
For p_t > 1.8 GeV all tracks are taken.
NOTE: There is no event cuts - all events are taken.
Why we need DownScaleDst file?
The main advantage of DownScaleDst files is smaller size compared to STAR MuDst files. It is about 50 times smaller than those of MuDst files. The smaller size results in faster data analysis.
Down Scale files could be used in flow analysis of charged or strange particles, high pt correlations.
The list of DownScaleDst TTree leaves (with some comments on "non-standard" variables)
DownScaleDst TTree
mZdcAdcAttentuatedSumWest
mZdcAdcAttentuatedSumEast
mZdcSmdWest[16]
mZdcSmdEast[16]
mCtbMultiplicity
mPrimaryVertexX
mPrimaryVertexY
mPrimaryVertexZ
mX[2][3][2][31] // X component of the event plane vector
mY[2][3][2][31] // Y component of the event planevector
// Q[charge][harmonic][subEvent][etaBin]; harmonic = 0 => multiplicity;
//ETA BINS: FTPCE -4.1 < eta < -2.5 (8 bins); FTPCW 2.5 < eta < 4.1 (8 bins); TPC -1.5 < eta < 1.5 (15 bins)
mEventId
mRunId
mNumberOfGoodPrimaryTracks
mNumberOfV0Tracks
mNumberOfPrimaryTracks
mNominalTriggerId[32]
mCentrality // centrality calculated according to the standard STAR refMult regions
mRefMult
mRefMultEtaWide // refMult calculated from tracks with wide eta cut |eta|<0.8
V0 branch
V0.mTypeOfStrangeParticle // 0 Lambda; 1 Anti-Lambda; 2 K0Short
V0.mMomPos.fX
V0.mMomPos.fY
V0.mMomPos.fZ
V0.mMomNeg.fX
V0.mMomNeg.fY
V0.mMomNeg.fZ
V0.mPtV0
V0.mPtPos
V0.mPtNeg
V0.mIsPosPrimary // need to remove auto correlations if the pos V0 track is in Event Plane
V0.mIsNegPrimary // if the neg V0 track is in Event Plane v0IsPrimary = etaBin+1-(nEtaTotal+1)*(1-subEvent)
V0.mPseudoRapV0
V0.mPseudoRapPos
V0.mPseudoRapNeg
V0.mMassLambda
V0.mMassAntiLambda
V0.mMassK0Short
Primary branch
Primary.mId
Primary.mCharge
Primary.mMaxPoints
Primary.mFitPoints
Primary.mTrackInEventPlaneFlag // need to remove auto correlations if track is in Event Plane TrackInEventPlane = etaBin+1-(nEtaTotal+1)*(1-subEvent)
Primary.mDEdx
Primary.mPt
Primary.mPhi
Primary.mEta
Primary.mDcaGlobal.mX1
Primary.mDcaGlobal.mX2
Primary.mDcaGlobal.mX3
Flow acceptance
Effects of non-uniform acceptance in anisotropic flow measurement
Authors
Ilya Selyuzhenkov and Sergei Voloshin
Journal
Abstract
The applicability of anisotropic flow measurement techniques and their extension for detectors with nonuniform azimuthal acceptance are discussed. Considering anisotropic flow measurements with two and three (mixed harmonic) azimuthal correlations we introduce a set of observables based on the x and y components of the event flow vector. These observables provide independent measures of anisotropic flow and can be used to test the self-consistency of the analysis. Based on these observables we propose a technique that explicitly takes into account the effects of nonuniform detector acceptance. Within this approach the acceptance corrections, as well as parameters that define the method applicability, can be determined directly from experimental data. For practical purposes a brief summary of the method is provided at the end.
Download latest version
Full text from SLAC data-base
Comments and reports on the paper
Referee report and Reply
Old paper draft versions
01 02 03 04 05 06 07 08 09
10 11 12 13 14 15 16 17 18 19
20 21 22 23 24 25 26 27 28 29
30 31 32 33 34 35 36
Supporting documents
Flow systematics
FTPC multiplicity study for AuAu@200GeV
The strange "File Id" dependence in both FTPC East and FTPC West were found in AuAu@200GeV data. It was fould that for the same production library there was files produced with different library setup, and large part of the files was with broken FTPC data.
Supporting materials:
- Charged particle flow in FTPC's with File ID cuts
- FTPC's File ID dependence in RUN IV data
- Update on FTPC's multiplicity study in Au+Au@200GeV
- FTPC multiplicity FileId dependence in Au+Au@200GeV
- FTPC multiplicity studies
- FTPCs systematic studies
Anisotropic flow in the case of azimuthally asymmetric detector
The method for acceptance correction in the case of azimuthally asymmetric detector (for example ZDC SMD in STAR) was suggested. The method was successfully applied in the anisotropic flow analysis of AuAu@62GeV ZDC SMD data
Supporting materials:
- Update on acceptance corrections for directed flow in Au+Au at 62GeV
- Getting directed flow: standard way and X and Y direction separately
- Update on acceptance corrections for directed flow
- Acceptance corrections for directed flow
- Charged particle directed flow: two particle correlations and mixed harmonic method with X and Y taken separately
- Charged particles directed flow: event plane from East/West FTPC's asymmetry
- Charged particles directed flow in Au+Au@62GeV calculated with event plane from ZDC SMD
- Calculating directed flow in the case of different resolution in the different transverse direction
- Calculating directed flow in the case of different resolution in the different transverse direction
Global polarization
Global polarization measurement in Au+Au collisions (paper proposal)
Principal Authors
Ilya Selyuzhenkov and Sergei Voloshin (for the STAR collaboration)
Target Journal
Abstract
The system created in non-central relativistic nucleus-nucleus collisions possesses large orbital angular momentum. Due to spin-orbit coupling, particles produced in such a system could become globally polarized along the direction of the system angular momentum. We present the results of Lambda and Anti-Lambda hyperon global polarization measurements in Au+Au collisions at sqrt{s_NN}=62 GeV and 200 GeV performed with the STAR detector at RHIC.
The observed global polarization of Lambda and Anti-Lambda hyperons in the STAR acceptance is consistent with zero within the precision of the measurements. The obtained upper limit, |P_{Lambda,Anti-Lambda}| < 0.02, is compared to the theoretical values discussed recently in the literature.
Paper draft
GPC: 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0
Collaboration: 11.0 12.0 13.0 14.0
Referee: 15.0 16.0
As sumbitted to PRC: 01 02
Comments and reports on the paper
God Parent Committee (GPC) comments
comments by the STAR Collaboration
Referee reports
Note: Separate page for the Anti-Lambda hyperon global polarization
Figures
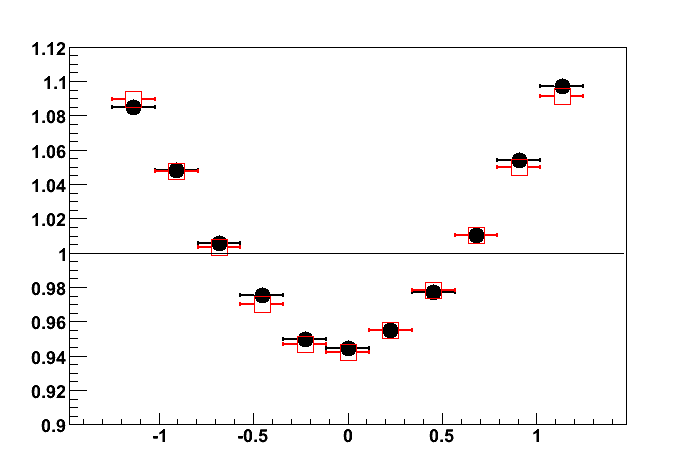
Fig.1 Global polarization of Lambda hyperons as a function of Lambda transverse momentum.
Filled circles show the results for Au+Au collisions at sqrt{s_NN}=200 GeV (centrality region 20-70%) and open squares indicate the results for Au+Au collisions at sqrt{s_NN}=62 GeV (centrality region 0-80%).
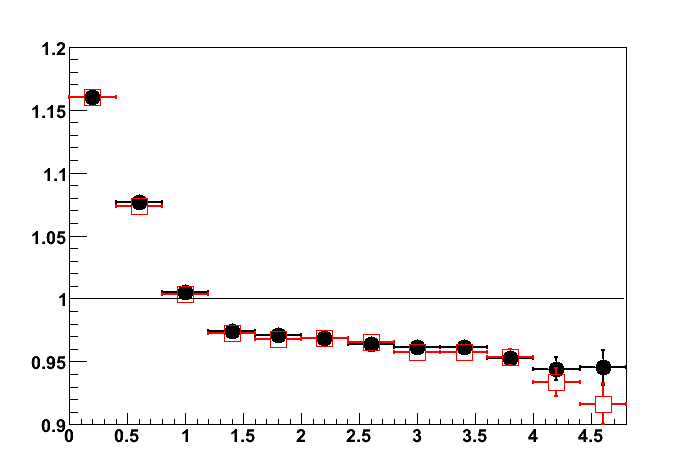
Fig.2 Global polarization of Lambda hyperons as a function of Lambda pseudorapidity.
Filled circles show the results for Au+Au collisions at sqrt{s_NN}=200 GeV (centrality region 20-70%). A constant line fit to these data points yields P_Lambda = (2.8 +- 9.6)x10^{-3} with chi^2/ndf = 6.5/10. Open squares show the results for Au+Au collisions at sqrt{s_NN}=62 GeV (centrality region 0-80%). A constant line fit gives P_Lambda = (1.9 +- 8.0)x10^{-3} with chi^2/ndf = 14.3/10.
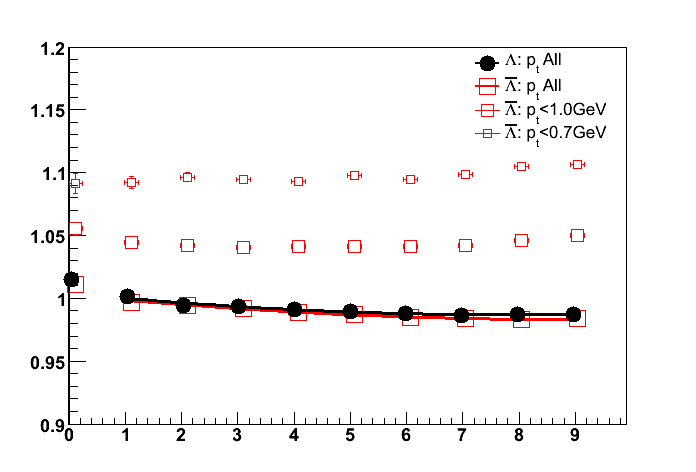
Fig.3 Global polarization of Lambda hyperons as a function of centrality given as fraction of the total inelastic hadronic cross section.
Filled circles show the results for Au+Au collisions at sqrt{s_NN}=200 GeV (centrality region 20-70%) and open squares indicate the results for Au+Au collisions at sqrt{s_NN}=62 GeV (centrality region 0-80%).
Conclusion
The Lambda and Anti-Lambda hyperon global polarization has been measured in Au+Au collisions at center of mass energies sqrt{s_NN}=62 and 200 GeV with the STAR detector at RHIC.
An upper limit of |P_{Lambda,Anti-Lambda}| < 0.02 for the global polarization of Lambda and Anti-Lambda hyperons within the STAR acceptance is obtained. This upper limit is far below the few tens of percent values discussed in Phys. Rev. Lett. 94, 102301 (2005), but it falls within the predicted region from the more realistic calculations Liang:Xian Workshop (2006) based on the HTL (Hard Thermal Loop) model.
Bibliography
- Globally Polarized Quark-Gluon Plasma in Noncentral A + A Collisions
Z.-T. Liang and X.-N. Wang
Phys. Rev. Lett. 94, 102301 (2005) [ erratum:Phys. Rev. Lett. 96, 039901 (2006)] - Polarized secondary particles in unpolarized high energy hadron-hadron collisions?
Sergei A. Voloshin
nucl-th/0410089 - Spin Alignment of Vector Mesons in Non-central A + A Collisions
Z.-T. Liang and X.-N. Wang
Phys.Lett.B629:20-26 (2005) [nucl-th/0411101] - Global quark polarization in QGP in non-central AA collisions
Gao Jian-hua and Z. T. Liang
Talk on November 24, 2006 (power point file) at Xi'an Workshop (Xi'an, China)
Talks and Publications on the subject
- Anti-Lambda hyperon global polarization in Au+Au collisions at RHIC
Ilya Selyuzhenkov [for the STAR Collaboration]
International Workshop on "Hadron Physics and Property of High Baryon Density Matter", Xi'an, China (2006)
arXiv:nucl-ex/0702001 (2007) - Centrality dependence of hyperon global polarization in Au + Au collisions at RHIC
Ilya Selyuzhenkov [for the STAR Collaboration]
19th International Conference on "Ultra-Relativistic Nucleus-Nucleus Collisions" (Quark Matter 2006) Shanghai, China, 2006
arXiv:nucl-ex/0701034 (2007) - Acceptance effects in the hyperons global polarization measurement
Ilya Selyuzhenkov [for the STAR Collaboration]
9th Conference on the Intersections of Particle and Nuclear Physics ( CIPANP 2006), Westin Rio Mar Beach, Puerto Rico, 2006
AIP Conf. Proc. 870, 712 (2006) [arXiv:nucl-ex/0608034] - Global polarization measurement in Au+Au collisions
Ilya Selyuzhenkov [for the STAR Collaboration]
International Conference on Strangeness in Quark Matter (SQM 2006), Los Angeles, CA, USA, 2006
J. Phys. G: Nucl. Part. Phys. 32, S557 (2006) [arXiv:nucl-ex/0605035] - Global polarization and parity violation in Au+Au collisions
Ilya Selyuzhenkov [for the STAR Collaboration]
Midwest Critical Mass Workshop (MCM), Toledo OH, USA, 2005
Download slides - Global polarization and parity violation study in Au+Au collisions
Ilya Selyuzhenkov [for the STAR Collaboration]
18th International Conference on "Ultra-Relativistic Nucleus-Nucleus Collisions" (Quark Matter 2005), Budapest, Hungary, 2005
Rom.Rep.Phys. 58, 049 (2006) [arXiv:nucl-ex/0510069]
Supporting materials
- Acceptance corrections in the global polarization measurement
- Monte-Carlo simulation for the global polarization measurement
- Presentations on the subject
- Global polarization of Lambda hyperons in Au+Au collisions at RHIC
Quark Matter 2006 talk - Global polarization: more on acceptance & Anti-Lambda results
STAR EbyE PWG Phone Meeting, 2006 - Global polarization measurement: systematics study
STAR Collaboration Meeting, 2006 - Global polarization measurements in Au+Au at 200 GeV: results from ProductionLow
STAR EbyE PWG Phone Meeting, 2006 - Global polarization measurements in Au+Au collisions
STAR Collaboration Meeting, 2006 - Global polarization measurements in Au+Au collisions (PWG Conveners Preview)
STAR PWG Conveners phone meeting, 2006 - Lambda global polarization p_t dependence
Plot "global polarization p_t dependence" added to the proposal, EbyE phone meeting, 2006 - Global polarization measurements in Au+Au collisions
Initial paper proposal, EbyE phone meeting, 2006 - Global polarization and parity violation in Au+Au collisions
Quark Matter 2005 poster - Global polarization and parity violation in Au+Au collisions
WSU RHIG group meeting, 2005 - Global polarization and parity violation in Au+Au collisions
materials for Quark Matter 2005 abstract - Polarization and directed flow of Lambda/Anti-Lambda hyperons in Au+Au@62GeV
WSU RHIG group meeting, 2005 - Polarization and directed flow of Lambda/Anti-Lambda hyperons in Au+Au@62GeV
STAR analysis Meeting, 2005 - Lambda and Anti-Lambda polarization and directed flow in Au+Au collisions at 62 GeV
STAR Analysis Meeting, 2004 - Lambda and Anti-Lambda production in Au+Au collisions at 62GeV
WSU RHIG group meeting, 2004
- Global polarization of Lambda hyperons in Au+Au collisions at RHIC
Acceptance corrections
Acceptance corrections in global polarization measurement
Figures for the A_0 function
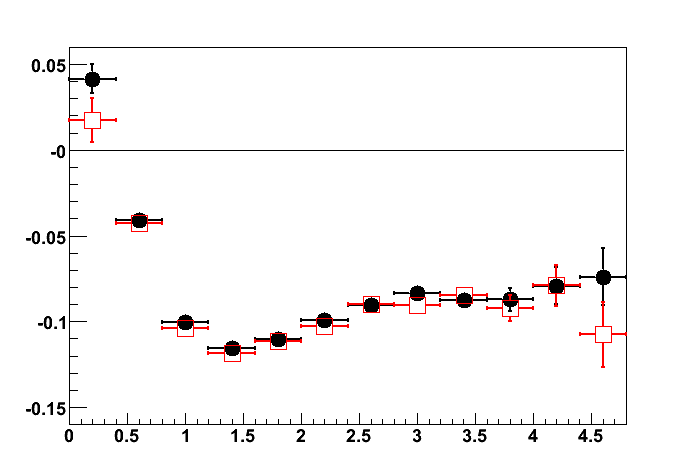
Fig.1 A_0 for Lambda (Filled circles) and Anti-Lambda (open squares) hyperons as a function of hyperon pseudorapidity.
Fig.2 A_0 for Lambda (Filled circles) and Anti-Lambda (open squares) hyperons as a function of hyperon transverse momentum.
Fig.3 A_0 for Lambda (Filled circles) and Anti-Lambda (open squares) hyperons as a function of centrality.
Figures for the A_2 function
Fig.4 A_2 for Lambda (Filled circles) and Anti-Lambda (open squares) hyperons as a function of hyperon pseudorapidity.
Fig.5 A_2 for Lambda (Filled circles) and Anti-Lambda (open squares) hyperons as a function of hyperon transverse momentum.
Collaboration comments
Collaboration comments on "Global polarization measurement in Au+Au collisions"
Comments by Bedanga Mohanty
- Acceptance effect - results presented without acceptance correction
The reason why we present uncorrected data is that due to detector effects the higher harmonic terms of the global polarization expansion (6) can contribute. To measure higher harmonic terms one needs to use different observable than (3), and such measurement requires an independent analysis.
This question is discussed on page 8 of the paper draft (left column at the bottom):
"Since the values of P_H^(2) (p_t^H, eta^H) are not measured in this analysis we present uncorrected data in Figs.3-8 providing only an estimate of the non-uniform detector acceptance effects." - Usually the Equation 1 in traditional polarization measurements (say for example transverse polarization) is written as
dN/dcos(theta) = A(cos(theta))( 1 + alpha P cos(theta))
Where A(cos(theta)) represents the detector/acceptance effects.
I find we do not have an "equality" in the Eqn. 1 in the paper, is it because we do not want to write "A" or is it because we do not know how dN/dcos(theta) should be ?We do not want to obstruct the first equation with acceptance function and we introduce it only when discussing detector acceptance effect in section IIC (see equation (5)).
- Further we arrive at Eqn 2 which has a "equality" directly from Eqn 1 which is an approximate relation as per our paper. How is it possible to arrive at an exact relation as in Eqn. 2 from a relation we do not know exactly as in Eqn. 1 may be some things get canceled out or may be I am missing something ....
There is a proportionality sign in equation (1). In the average the proportionality coefficient cancels out and we get the equality sign in (2). Equation (2) assumes the perfect detector acceptance. The effects of non uniform acceptance and modification of this equation are discussed later in section IIC.
- I understand a two body differential cross sections may be expressed in terms of Legendre Polynomial expansion
dSigma/dOmega = B X Sum(from 0 to n=N) An Pn(cos(theta)) Where Pn = Legendre Polynomial of order "n"
But is it also valid to expand the Polarization P_H as shown in Eqn. 6 ? Are we trying to say the Polarization we are trying to measure in heavy ion collisions is similar to what we studied in electrodynamics - linearly polarized, circular polarization and elliptic polarization ?We are measuring polarization with respect to the system orbital momentum (perpendicular to the reaction plane) which is defined in transverse plane of the collision (two dimensions). This is the reason why we transform from equation (2) to (3). In two dimensions the appropriate orthogonal set of function in the range of (0,2pi) are cos and sin functions, not the Legendre polynomials.
- Motivation for presenting Polarization results as a function of various kinematic variables.
We present the results of acceptance uncorrected polarization for lambda hyperons as a function of transverse momentum, pseudorapidity (why not rapidity ?) and centrality. But we do not say why we need to study the polarization as a function of these observables ?We are studying the polarization as a function of kinematics variables of hyperon (such as p_t and eta) and collision parameters (energy and centrality). This is a complete set of variables on which polarization can depends in heavy ion collisions. Although none of results are significantly deviates from zero, we report them for completeness.
- From our paper, I could not find what I should expect (even if naive) of polarization variation with respect to these variables.
We are comparing the results with available theory predictions, which are limited so far to those in reference [1-4]. For the moment we have only an estimate of the integrated value for the global polarization, and no expectations on p_t, or centrality dependence. The only expectation is that at mid rapidity the polarization should not change much. Thus we fit the results with constant line.
- Need for results from p+p and/or d+Au collisions
In principle, based on particle azimuthal distribution in pp or dAu collisions, we can define the quantity similar to the reaction plane in non central AuAu collisions, but physics of such phenomena is different from those of global polarization in heavy ion collisions.
- "Based on the results in [30], the contribution of feed-downs from multiply strange hyperons (...) is estimated to be less than 15%. This can dilute the measured polarization and introduce a similar systematic uncertainty (~ 15%) to the global polarization measurement.
Does that mean error on Polarization is directly equal to percentage feed down ?We estimate the feed down effects assuming the same polarization for hyperons and multi-strange hyperons. Thus the uncertainty in polarization is proportional to feed-down from multiply strange hyperons.
- "Thus, the effect of the spin precession on the global polarization measurements is found to be negligible (<0:1%)."
What is gamma_lambda,lambdabar in the experssion. We need to have a relation between Polarisation and the delta_phi_lambda to understand how the error comes out to be 0.1%.The gamma_lambda,lambdabar is a Lorenz factor: gamma = 1/sqrt(1-v**2). For p = 3 GeV it is about 2.87. The effect on polarization is defined by cos(delta_phi), what is approximately 1-delta_phi^2/2, since angle delta_phi is small. This leads to the estimate of <0.1%.
- "In any case, the corresponding corrections to the absolute value of the global polarization are esti- mated to be less than 20% of the extracted polarization values."
The acceptance correction can be 20% as we see from the figures. Does that mean uncertainty due to non uniform acceptance is 20% ?There are two different contribution from acceptance effects, A_0 and A_2. As it can be seen from equation (9) the term (10) and (11) affect the global polarization in a different way and we have a separate estimate of 20% for each of them.
- Finally we get 125% uncertainty. With this unceratinty how was the upper limit obtained is not clearly described. What is the confidence level of this upper limit ?
With that many sources of systematic uncertainties it is very difficult to calculate the confidence level, and we feel that it is not needed. If you have any specific idea how to do it, we can try it.
- I think it is important to atleast have a few lines of discussion regarding what is the difference between this polarisation measurements and the traditional polarisation measurements which usually has been carried out in pp and pA collisions and by E896 in heavy ion collisions.
Since we basically have null results with huge 125% uncertainty, it may be good to provide an outlook for such measurements, will choice of other particles helpThe obtained upper limit of 0.01 (or 0.02 together with systematic uncertainties), is very small compared to the first, naive, predictions of 0.3 for the polarization discussed in [1]. At this point the large magnitude of 125% for the relative uncertainty is not change the significance of the results, which gives an order of magnitude smaller value. More work from the theory side has to be done to understand the reason why the polarization is so small.
- In introduction we mention one of the observable consequence is "polarization of thermal photons" - Just for my information - how can we measure this in heavy ion collisions ?
We can not measure this in STAR, as far as we know.
- We need to give the reference for STAR detector when it gets mentioned in the Introduction.
We are reffering to the STAR detector in section IIA when discussing the analysis technique. We think it is not necessary to give such a reference in the introduction.
- Alpha_h is called as a "decay parameter" - it is not clear. Some paper we refer in the current manuscript call it ias "asymmetry parameter" - Why not give a brief description that it is a s-p wave interference term factor ....Or may be say that they are from measurements. or may be say that alpha charecterizes the degree of mixing of parity in the hyperon decay as Lee and Yang found out.
In the PDG book, which we are referring to, there is an introduction to what decay parameter is and how it is defined from the amplitude.
- Beam energy is given as 62 GeV shouldn't it be 62.4 GeV
Corrected in the paper draft Version 11.
- Reference ordering is all mixed up. Ref. 12,13,14,15 come after Ref. 16. ref. 21 after Ref. 26 ...etc etc ...
Fixed in the paper draft Version 11.
- Spell check is needed - for example : multiply strange hyperons --> multiple strange hyperons
Replaced it by "multistrange hyperons" in the paper draft Version 11.
- Reference to alpha_lambda = 0.642 is PDG in Page # 1 It is actually given in Page # 924!
(answer by Spencer Klein) Ref. 15 is OK as written. The article begins on pg. 1; and we give the first page of journal article references, not the page where the result appears.
- It is not clear why we need a 3rd order polynomial function in the fitting of Minv. May be we should mention that is for background. Even for background - looking at Fig. 2, it does not seem we need 3rd order polynomial.
This is how it was done. We do not think it needs further explanations.
- I am not sure if ref. 28 is an experimental paper which measures direct hyperons to be 27% for Lambda. Please let me know how that number is obtained.
This is a theory paper. These numbers can be found in the Tables at the end of this paper.
- We discuss quite a bit about ZDC SMD finally to say we will use FTPC. May be I missed some of the points for the need to go into detail discussion about ZDC SMD when we do not use their information in the analysis.
We use ZDC SMD to define the sign of directed flow in the FTPC region and consequently reconstruct the system orbital momentum direction as it is explained in the paragraph just after equation (4).
- It may be better to mention that Eqn.4 is finally used to get all the results figure from 3 to 8
Fixed in the paper draft Version 11.
- It is not clear what is mean't by "saturation effects in FTPC" it will be nice to see the multiplicity correlation plot for FTPC Vs. TPC.
Just to note : dnch/dy for 10-20% 200 GeV AuAu ~ 484 5 - 10% 200 GeV AuAu ~ 648 For 0-5% AuAu 62.4 GeV it is about 588. So we should be able to get couple of more points in Fig. 5 and 8.For the FTPC event plane resolution study please have a look at the following slides (in particular page 4):
20060202_ChargedFlowWithFileIdCuts_FlowPhoneMeeting.pdf - Did we try fitting 62.4 GeV data in Fig. 4 by first order polynomial and see the results - if yes, can you please let us know the values.
We expect global polarization to be a symmetric function of pseudorapidity, but the first order polynomial is anti-symmetric.
- We discuss in Page 9 how protons and pions losses can be different and how it affects A0 and A2. In the expresions in Eqn 10 and 11, it seems only protons are relevant. So it is not clear why we discuss the pion acceptance effect on A0.
These functions are calculated in the hyperons rest frame, which is defined both by pion and proton momenta. Thus the acceptance effects both from pion and proton are important.
- It is not clear why we give Ref. 13 - it was for d+Au collisions.
In this reference the hyperon reconstruction procedure (for dAu) is discussed.
- It is also not clear why we give so many reference to directed flow measurements, specially when ref. 11 does not have even the relation we are refering to.
Removed in the paper draft Version 11.
- The author names are written in different way for Ref. 26.
Fixed in the paper draft Version 11.
- May be make it more clear in the paper by saying
"We do not observe any transfer of global angular momentum of the system to its consitutent particles that leads to particle having a preferential spin orientation"In the conclusion we are stating that we set an upper limit for the global polarization, what is more than just saying "We do not observe any transfer ...". We think that in the current form the conclusion is more appropriate for the obtained results.
- From the link you have given regarding what is mean't by "saturation effect in FTPC", shows the v1-FTPC has a difference in value for Fullfield and ReverseFullField configuration for central events. Not sure how that leads to conclusion we make. Because for the reverse and actual field configuration the multiplicity should be same.
So still not clear when we write -
"With higher multiplicity at sNN=200 GeV, saturation effects in the Forward TPC's for the most central collisions become evident, and the estimated reaction plane angle is unreliable."Please, have a look at the following link:
20050922_FTPCmultiplicity_FlowPhoneMeeting.pdf
On page 3 you can see the correlation between multiplicity in TPC and FTPC. Together with plot for v1 in FTPC pseudorapidity region (what is essentially defines the resolution of the first order event plane from FTPC) this should clarify this question. Note, that we expect RFF and FF results to be consistent. The discrepancy between them for most central collisions is an additional indication on detector effects at higher multiplicities in AuAu@200GeV.
You can also check the links at the FTPC event plane study web page:
"FTPC Systematics" - You also mentioned "we have no expectations on pT or centrality"
This is what I read from one of the papers we quote in the paper :
We can also provide other qualitative predictions of the global hyperon polarization PH in non-central heavyion collisions: (1) Hyperons and their anti-particles are similarly polarized along the same direction perpendicular to the reaction plane in non-central heavy-ion collisions.We check this by measuring both Lambda and anti-Lambda global polarization
- The global hyperon polarization PH vanishes in central collisions and increases almost linearly with b in semi-central collisions.
The centrality region 0-5% corresponds to a wide range of impact parameters and it is not clear how we can interpret results and compare them with the expected zero polarization at b=0. Together with observed zero signal we afraid that such discussions can be misleading and will potentially confuse the reader.
- It should have a finite value at small pT and in the central rapidity region. It should increase with rapidity and eventually decreases and vanishes at large rapidities.
We essentially measuring the polarization at mid rapidity and the results are dominated by small p_t region. Again, it is not clear how to compare the obtained zero result in this region with theoretical predictions your are referring to.
- Since hyperon's production planes are randomly oriented with respect to the reaction plane of heavy-ion collisions, the observed hyperon polarization in p + A collisions should not contribute to the global polarization as we have defined here, except at large rapidity region where directed flow is observed [13].
We have checked this from the measurement. See reference [21] in the paper draft and corresponding text on page 9 (right column, last paragraph):
"The hyperon directed flow is defined as the first order coefficient in the Fourier expansion of the hyperon azimuthal angular distribution with respect to the reaction plane. Due to non-uniform detector acceptance it will interfere with the hyperon global polarization measurement and this can dilute the measured polarization [21]." - In future may be we should just look at Eqn 1 from data (dN/dcos(theta) Vs. cos(theta)) as is done in usual polarization measurements. That would have reduced quite a bit of uncertainty from flow related issues. Did we attempt it ?
This method requires to introduce additional bins in theta* and further fits dN/dcos(theta*) distribution assuming the polarization dependence according to equation (1). Reconstructed dN/dcos(theta*) distribution can contains other contributions together with those from global polarization (i.e. directed flow, or higher harmonics from expansion (6)). This requires to make additional assumptions regarding the fitting function, what will complicates the interpretation of the final result.
In the current analysis we are averaging other theta* angle (equations (2) and (3)) and cuts only the particular harmonic in the dN/dcos(theta*) distribution, which corresponds to the polarization contribution. We think is is more straightforward and not biased by assumptions regarding the fitting function. We also have a good control on anisotropic flow contribution in this case.
Comments by Huan Z. Huang
- page 5, left column paragraph 2 on the Sigma0/Lambda ratio. A ratio of 15% without errors was quoted as from reference [29], which is a conference proceeding from Gene Van Buren for the STAR collaboration. I do not think this ratio should be quoted as an official STAR result. The number is smaller than string-fragmentation model calculation (~30%) and the thermal statistical model, which has been used to describe RHIC Au+Au data well, would predict the ratio to be ~65% or so. The systematic error estimate should cover this range of variation in the ratio.
Yes, we estimate systematic errors from Sigma^0 feed-down based on results for dAu collisions. This is the only known measurement by STAR so far. Since we do not have such a measurement for AuAu collisions, we only mention that according to theoretical calculations it is possible for this uncertainty to be larger for AuAu collisions. See page 5, left column, second paragraph from top:
"The Sigma0/Lambda production ratio value (15%) is measured [29] for d+Au and it can be 2-3 times higher for Au+Au collisions (this can affect the estimated uncertainty)." - in sections B and C, you presented results without acceptance correction and attribute all acceptance effect in uncertainties. That is an unusual way to present experimental results. I still do not understand fully how the errors were included.
The reason why we present uncorrected data is that due to detector effects the higher harmonic terms of the global polarization expansion (6) can contribute. To measure higher harmonic terms one needs to use different observable than (3), and such measurement requires the independent analysis.
This question is discussed on page 8 of the paper draft (left column at the bottom):
"Since the values of P_H^(2) (p_t^H, eta^H) are not measured in this analysis we present uncorrected data in Figs.3-8 providing only an estimate of the non-uniform detector acceptance effects." - For example in figure 9, the value one (unity) corresponds to no polarization (null measurement).
Figure 9 presents the function A_0, which is independent of the global polarization and it is unity in case of perfect acceptance.
- You seem to attribute the difference from the unity as a relative error on the polarization measurement.
According to equation (9) the deviation of this function from unity affects the overall scale of the measured global polarization. Thus we consider it as a relative uncertainty.
- in anisotropic flow measurement a phi-weight function is used to calculate the event-plane angle and the resulting event-plane angle is very flat only after the weighting. Did you use the weighting in your PHI_RP calculation? How is this weighting on the event-plane included in the phi angle integration in section C?
We use the same technique as for anisotropic flow measurement. We do the recentering (or shifting) of the event plane vector.
The integration over reaction plane angle is independent from integration over the angles of hyperon and its decay products. Thus effects from event plane determination are separate from acceptance effects due to hyperon's reconstruction procedure. This allows us to integrate over psi_RP in equation (5) and further introduce function A_0 and A_2 in equation (9). The residual effects from event plane determination procedure (after the event plane vector recentering) are taken into account when the results are corrected by the event plane resolution. - Is this 15% used for the estimate of the uncertainty? I argued that this range should be increased to include the variation either based on model prediction or errors from Gene Van Buren's measurement if STAR agrees to use the number. I believe STAR's existing publication policy does not favor using Gene's preliminary number.
To our understanding, it is better to base estimates on experimental results (although the preliminary one) rather that completely rely on theoretical assumptions. Note, that Gene mentioned that systematic errors in his measurement are also strongly model dependent. As a compromise, we provide an estimate based on Gene's results and state in the paper draft, that depends on model predictions for Au+Au the systematic uncertainty can be larger.
- This sounds like because in our analysis we did not measure these quantities, therefore we present the data without the acceptance correction. That does not work well to convince the community about the validity of the analysis IMHO.
The acceptance effects can not be completely taken into account since they affects not only the magnitude of the measured polarization (A_0 term) but due to these effects the higher harmonics of the global polarization expansion (A_2 term) or the hyperon directed flow can contribute. We believe that, providing a partially corrected points will be misleading since it can be understood that we completely correct our results on acceptance. Thus we estimate the acceptance effects from the data and put them together with other systematic uncertainty.
- If the global polarization value is ZERO, what DOES this relative uncertainty mean? I am not convinced of this relative uncertainty interpretation or derivation.
The relative uncertainty means that if polarization is decreasing in its absolute value (goes to zero) the uncertainty of the measurement is also decreasing (in its value).
- I think it is necessary to show a coverage of sin(theta*_p) (equation 10) distribution in the paper. Imagine you are not dealing with STAR TPC, you only have a small detector with acceptance centered around the mean value of sin(theta*_p). From equation (3) and equation (10), you may still get a polarization measurement and acceptance A_0 near unity. But this could be misleading because a small acceptance detector may not have the sensitivity to the polarization measurement at all. I think there could be biases in the analysis here which may not be adequately reflected in the numbers shown in the figures.
In your example it is assumed that hyperons theta*_p angle is correlated with the reaction plane angle due to narrow detector acceptance (measured with the same detector). In our measurement these angles are independent, since we are using two different detectors (TPC for hyperons and FTPC to reconstruct the event plane). This validates our derivation in section IIC and equations (8)-(11) where it is assumed that acceptance effects originates from hyperon reconstruction procedure and due to reaction plane angle determination are independent. This also makes possible to measure polarization even with a narrow detector acceptance for the hyperons.
Note, that this is true only for global polarization measurement and the acceptance effects in case of narrow detector you discussed will be a real problem when measuring polarization (or spin alignment) with respect to production plane, where polarization axis and particle angle theta* are affected by the same detector effects.
Comments by Carl Gagliardi
- I admit that I am completely baffled by the choice not to acceptance correct your physics results as presented in Figs. 3-8. If I take Fig 9 at face value, you know the acceptance corrections very well. Thus, I see no reason not to apply them. Furthermore, this appears to require only a very straightforward modification to the flow of the paper. Specifically, you could split the current Sect. II.C into two separate sections. The first half, "Acceptance effects", would be placed before the current "Results" section. That would then allow you to end it with a remark that, "All of the results in the following section have been corrected for the non-uniform detector acceptance." This would have the added benefit of letting you reduce the systematic uncertainty due to "Non uniform acceptance" from 20% to <~1%. The other half of the current Sect. II.C, "Systematic uncertainties", would appear after "Results" as it does now.
Obviously, the systematic uncertainty due to P_H(phi_H-psi_RP) dependence would remain. But that arises from incomplete knowledge of the physics, not from incomplete knowledge of (or corrections for) the acceptance.The systematic uncertainty from P_H(phi_H-psi_RP) dependence are defined not only by values of term with P_H^(2) in the expansion (6), but they also ruled by the deviation from zero (the perfect detector case) of function A_2. Only non zero values of A_2 due to non-uniform acceptance leads to the contribution from higher harmonic term in the observable (9). It happens that in this case detector effects and physics contribution are linked with each other. This is the reason why we can not take into account all detector effects, although functions A_0 and A_2 are well defined from the data. In this view, providing a partially corrected points will be misleading since it can be understood that we completely correct our results on acceptance.
Comments by Jim Sowinski
- Crucial to the measurement is determining the direction of the normal to the reaction plane, L in the paper, and not just the reaction plane itself. There is a lot of discussion of systematic errors from the resolution of the reaction plane but little about a 180 deg direction ambiguity.
If I understand the paragraphs in the second column of pg 5 the reaction plane is determined from the FTPCs but the ambiguity in the direction is determined from the ZDCs. Ref. 10 to the STAR directed flow measurements is given to justify this. However the neither the reference nor the present paper have any results indicating the efficiency for determining the direction of L. Clearly the presence of a v1 defines the vector on average but it is not clear that every event has the direction of L clearly defined. Ref. 10 refers to a correlation between east and west event plane determinations. Do they always agree in the sign of L? Ref. 10 states that this does not work for the 0-10% bin. This would lead me to believe for the next bin it is less than 100% efficient. Correlations event by event could also be checked in different regions of eta.
My first thought would have been that one would not be able to resolve the ambiguity as to which direction the matter is spinning. A v1 clearly shows you do on average determine the direction. But unless you can determine it for every event one would need to define an efficiency for determining the direction that divides the lambda polarization results. It seems likely that this efficiency depends on centrality at least and maybe other kinematic variables.Indeed we can not determine the exact direction in each event, and we do it only on statistical basis. What you call the efficiency for determining the direction we call event plane resolution. It is determined from correlations of two event plane defined in different FTPCs. According to a convention, the directed flow of neurons in the ZDC SMD is taken to be positive. From correlations between FTPC and ZDC SMD we find that directed flow in FTPC is negative for a positive pseudorapidity values. This fixes the direction of the orbital momentum.
We do not expect that the relative sign of directed flow in ZDC SMD and Forward TPC region depends on centrality.
In reference 10 it is only stated that results for directed flow measured with ZDC SMD event plane failed for most central collisions, this does not mean that it is not possible to measure directed flow and to define the event plane angle for charge particles measured with FTPCs in these region (see for example this slides, page 2: FTPCmultiplicity) The only uncertainty is in the "resolution" of the event plane angle, which is defined by the denominator in equation (4). This uncertainty depends on centrality and it increases towards most central collisions. This is discussed in Section IIC of the paper draft, page 10, right column, first paragraph).
Comments by Steve Vidgor
- I am confused by the phrase "(this can affect the estimated uncertainty)". My understanding all along had been that this higher possible feeddown in Au+Au was, indeed, included in the 30% systematic uncertainty on the extracted P_Lambda. The following calculation shows that, under the stated assumptions in the manuscript, a 30% feeddown would give rise to a 30% error in the polarization:
yield(Lambda from Sigma^0)/yield(direct Lambda) = 0.30
=> P_observed = (10/13) P_direct Lambda + (3/13)(-1/3) P_Sigma^0
under stated assumption P_Sigma^0 = P_direct Lambda, one gets
P_observed = (9/13) P_direct Lambda = 0.69 P_direct Lambda.
Thus, I thought the feeddown error estimate on measured polarization had been made allowing for ~30% Sigma^0 feeddown, twice the value measured in d+Au.It looks like we calculate feed down uncertainty in a different way. Your estimate is obtained from this relation:
P_observed = alpha * P_lambda (in you case for 30% of feed down alpha = 0.69)
and in our calculations we get it from:
P_lambda = (1/alpha) P_observed (for 17% [Gene's proceedings: nucl-ex/0512018] feed down I get for 1/alpha = 1.29)
From these different numbers (0.69 and 1.2) we both occasionally conclude the same, i.e. the uncertainty of 30%. I think this is the source of our confusion.
Comments by Spencer Klein
- It would be useful to clearly define what global polarization is early on (perhaps the first paragraph of the introduction). It's defined in Section II, but only after it is used quite a few times.
The global polarization is already defined in the first paragraph of the introduction as a transformation of the system orbital momentum L into the particles spin which leads to the polarization of secondary produced particles along the direction of L. We think that this definition is enough for the introduction section. We gave mathematical definition with equation (1) shortly in the beginning of section II.
- I had a question about Eq. (4). Using a trig identity, this can be rewritten
P_Lambda = 8/(pi alpha) <[sin(phi_p)cos(Psi_EP) - cos(phi_p)sin(Psi_EP)]/R_EP >
I'm wondering about the application of a single R_EP to the entire ensemble of sin(phi_p)s. Is a single dilution factor adequate in the denominator here. If one were considering the errors on an event-by-event basis, one should plug Psi_EP+1sigma of R_EP, and psi_EP-1sigma of R_EP; this will occasionally change the sign of P_\Lambda determined for that event. Is there a mathematical relationship (or other argument) that a simple division of the result of the ensemble averaging is OK here.We do not define resolution for each particular event and we do not correct on it for each event separately. In other words the correct equation we use is:
P_Lambda = 8/(pi alpha) <[sin(phi_p)cos(Psi_EP) - cos(phi_p)sin(Psi_EP)]> / < R_EP >
This equation assumes the symmetry between these two terms and the results for each terms can be used to check the consistency of the measurements. In fact this is one of the systematics and consistency checks done in the analysis.The above expression for P_Lambda can be obtained as follows. We start from the equation:
< sin(psi-Psi_RP)> = < sin(phi- Psi_EP) cos(Psi_EP-Psi-RP) + cos(...) sin(...)>
We assume that there is no correlation between arguments of sin and cos in this expression and do average separately. Then the second term vanishes due to < sin(Psi_EP-Psi_RP) > = 0 and the first term gives < sin(phi-Psi_EP) > < cos(Psi_EP-Psi_RP >. the second term we call resolution: R_EP = < cos(Psi_EP-Psi_RP >. Dividing everything by this resolution we obtain equation for the polarization. - Also, it would be helpful to the reader if you gave a typical value for R_EP.
We are using scalar product technique, the resolution is the same order as the directed flow in FTPC pseudorapidity region. Such results can be found in reference [10].
- I don't understand why there is a long discussion about the neutron detection in the ZDC, when it is only used to determine the sign of the polarization. It would be better to focus on the FTPC event plane determination (perhaps giving some representative numbers), and then have a brief discussion of the ZDC/SMD combo, focusing on what they are actually used for.
Please, see the detailed answer above to Jim Sowinski's comment.
- Figs. 3-8 might be more accessible if you combined the 2 p_T histograms (lambda + Lambda bar), 2 rapidity histograms, and two centrality histograms. It would simplify particle/antiparticle comparisons, and lead to shorter figure captions, with less repetition. Also, the fit results & chi^2/DOF would be more accessible if they were all put in a single table.
It is not clear if you propose to put lambda and anti-lambda results in one plot or you propose to combine statistics?
In general Lambda and anti-Lambda global polarization can be defined by different spin orbital transformation mechanisms and they can have a different magnitude, thus we do not like to combine these results in a single plot.
We are also reluctant to create a new table as it is not obvious it would clarify the presentation. - We need to explain exactly where the 0.02 limit given in the conclusions comes from. I couldn't figure out how the results were combined with the systematic errors to give a limit; this needs to be clearly laid out.
We modify the very end of the text before Conclusions in the paper draft Version 11:
"Taking all these possible correction factors into account, and that our measurements are consistent with zero with statistical error of about 0.01, our results suggest that the global Lambda and anti-Lambda polarizations are |P_{Lambda, anti-Lambda}| < 0:02 in magnitude." - Is it possible to expand the conclusions, to discuss what we really learn from this? We've ruled out one theory paper; what physics do we learn from this?
We did not just ruled out one of the theory paper. We are trying to set an upper limit for the global polarization, which appears to has an order of magnitude smaller value than those from the first estimate. It is hard to make any further physics conclusions.
- Minor comments:
write '30\%' instead of 'thirty percent'
Remove the excess "note that's and 'It was found in...' s
gamma_lambda needs to be defined.Fixed in the paper draft Version 11.
Comments by Qinghua Xu and LBL journal club
- You might consider to specify in the title of the paper that you study lambda and anti-lambda since there may be other global polarization effect as mentioned in the introduction.
This is the first measurement of the effect of global polarization. The orbital momentum transformation into the particles spin can reveals itself in other effects, such as spin alignment of vector mesons. This is the first measurement of the global polarization and, although we present only Lambda and anti-Lambda results, the measurement technique discussed in the paper is applicable not only for these particular particles but can be used to measure polarization of other hyperons, for example multistrange one. We think that in the current form the title of the paper is more appropriate in this case.
- In Eq.1 you introduce the decay parameter but only on page 2 in the second column you give its value. - you can consider to move it closer to Eq.1.
In the beginning of Section II we discuss the hyperon global polarization, and this discussion is applicable not only for Lambda and anti-Lambda particles, but for other hyperons (for example multistrange hyperons). We provide the particular numbers for Lambda and anti-Lambda decay parameter later, when discussing the measurement details.
- Might be good to mention the value of the event plane resolution used in Eq.4.
See answer to Spencer Klein comment #3 above.
- You show global polarization versus pt, centrality and eta for lambda and anti-lambda as separate plots. Might be good to try to make one panel consists of six plots ( two columns one for lambda and other one for anti-lambda and three rows to show centrality, pt, eta dependence). You might want to add legend in plots for different energy and shorten the text in the captions.
In the current style of PRL with two columns it will be difficult to put these plots side by side because the scale of the plots will be too small. We also do not like to put legends in the figures, since it will clutter the plots, in particular Fig. 4 and 7.
- You might consider removing the fit values from the caption since they are already in the text.
It was requested by GPC, but we do not mind to remove them from the captions.
- You might consider moving the two paragraphs on feed down and spin precession effects on page 5 to the results section when you discuss systematics (close to the table).
We think it's better to discuss feed down effects together with the Lambda/anti-Lambda hyperon reconstruction technique. To indicate that these effects are contribute to systematic uncertainties of the measurement we refer here to section IIC (Acceptance effects and systematic uncertainties) and also provide our estimates in the summary Table I.
- On page 10 you give the systematic error estimate on the direct flow contribution <=1% together with the reference [21]. In reference [21] below Fig.2 you say "...the flow contribution (8) appears to be less than 2x10-3. This is an order of magnitude smaller than the upper limit for the Lambda global polarization ..." indicating 10% effect. Could you explain how you get the 1% estimate?
From Figure 2 of the reference [21] you can see that 2x10^3 value is at maximum (essentially one point at low p_t). For most points the values are much smaller (of the order of 5*10^-4) what decrease the estimate of 10% by 75 per cent. Furthermore directed flow is also p_t dependant (unfortunately our STAR results for Lambda/anti-Lambda are consistent with zero so far). For charge particles it goes to zero at low p_t and saturates at about 2 GeV (see figure 4 in the reference [10]). The value of 10% for directed flow is also can be over estimated by a factor of 2. In this case it is difficult to get an exact estimate from just Figure 2 of the reference [21], and taking into account the written above we estimate it to be <1%.
GPC comments
God Parent Committee for the paper on "Global polarization measurement in Au+Au collisions"
GPC members:
- Hal Spinka (Chair)
- Aihong Tang (PWG representative)
- Ilya Selyuzhenkov (PA representative)
- Evan Finch
- Mark Heinz
- Ernst Sichtermann
- Steve Vigdor (English/grammar QA)
Main GPC comments
- (Ernst Sichtermann) The uncertainty in polarization caused by feed-down contribution should presumably be presented as a possible offset instead of a percentage.
We report the systematic errors on feed down from multi strange hyperon assuming the same polarization as for direct lambdas. Therefore we report the relative systematic error in percents.
- (Evan Finch) The systematic error from acceptance is not naturally a relative error, right?
Second line in equation (9) of the paper draft shows that both acceptance function A^(0,2) contribute together with polarization expansion coefficients P_H^(0,2). If polarization is zero (all P_H^(n) = 0), the acceptance effects in A^(0,2) are not contribute. This allows us to treat the deviation in A^(0,2) of 20% from perfect acceptance case as a relative uncertainty.
- (Hal Spinka) In Figs. 5 and 8, there are points with centrality 0-5%. I would have naively thought that you couldn't define a reaction plane for these events (or maybe have a reaction plane with such large uncertainty as to be meaningless). In any case, I suspect that the polarization should vanish as the centrality (and p_T) goes to zero.
We do expect the polarization and anisotropic flow (which defines the event plane) are goes to zero only for b=0. Centrality region 0-5% corresponds to a relatively large range of impact parameters. Although the systematic uncertainties are larger, we still are able to reconstruct reaction plane angle and measure the polarization in this centrality region.
- (Mark Heinz) The lowest p_T point on the figures 3 and 6. The efficiency for reconstructing the lowest p_T point - was this ever resolved?
Large error bars for lowest p_t points are showing the increase in uncertainty to reconstruct hyperons in this p_t region and we left these points in figures to indicate this effect.
- (Evan Finch) The 0.15 sigma0/lambda ratio referred to is Gene's d+Au; for Au+Au the predictions are (as he notes) 2-3 times this big.
We estimate systematic errors from Sigma^0 feed-down based on results for dAu collisions and exactly this estimate is given in the paper draft. Since we do not have such a measurement for AuAu collisions, we only mention that it is possible for this uncertainty to be larger for AuAu collisions.
-
(Ernst Sichtermann) I do agree with Evan's comment that the repeated "Data points are not acceptance corrected" in the figure captions is not (longer) needed - it is clear enough from the text and can be viewed as just one source of systematic uncertainty. If you want to keep the message in the caption, I would probably phrase it as "The indicated uncertainties are statistical only. The systematic uncertainties include acceptance and other effects, and are estimated to be smaller as discussed in sec IIC."
Replaced in the paper draft Version 11
-
(Ernst Sichtermann) Reference [28], Y.J. Pei hep-ph/9703243 - have you considered F. Becattini and U. Heinz, ZPC 76 (1997) 269?
Added with corresponding discussions in the paper draft Version 11
-
(Ernst Sichtermann) Last, I would like to suggest some (other) minor rewording:
On page 5, "This estimate takes into account ... Au+Au collisions (this can affect the estimated uncertainty)." How about: This estimate takes into account the average polarization transfer from Σ0 to Λ, which we estimate to be -1/3 [26, 27], neglecting the possible effect from non-uniform acceptance of the daughter Λ. The production ratio of Σ0/Λ is measured to be 0.15 for d+Au collisions [29]. Our uncertainty estimate takes into account that it can be 2-3 times higher for Au+Au collisions.There is a confusion here. Please see corresponding comment by Steve Vidgor at this page.
Recent GPC comments
- (Hal Spinka)
PACS - you only have the PACS for collective flow. Perhaps include 24.70.+s for polarization, or maybe others for hyperon production? Sorry I didn't notice this before.
page 8, left col., line 7 and beyond paragraph. I make a suggestion for this paragraph, but think some improvement is still needed. -> "To check the reconstruction code, Monte Carlo simulations with sizable linear ... spectra have been performed. Both the sign and magnitude of the reconstructed polarization agreed with the input values (within statistical uncertainties?)."Added PACS numbers:
23.20.En Angular distribution and correlation measurements 24.70.+s Polarization phenomena in reactions 25.75.-q Relativistic heavy-ion collisions 25.75.Ld Collective flow 14.20.Jn Hyperons 25.75.Gz Particle correlations 25.75.Dw Particle and resonance production
Paragraph discussing simulation results is replaced by what Hal suggested: "To check the reconstruction code, Monte Carlo simulations with sizable linear transverse momentum dependence of hyperon global polarization and hydrodynamic p_t^H spectra have been performed. Both the sign and magnitude of the reconstructed polarization agreed with the input values within statistical uncertainties." - (Steve Vidgor)
1) In a number of places the text refers to colors (red vs. black, etc.) in describing figures. Since the colors will likely not appear in the journal, choose different descriptions (e.g., darker vs. lighter shading in Fig. 2; open circles vs. filled squares in Figs. 3-8), and modify the text accordingly.
2) Since the discussion of feed-down comes quite a bit before the discussion of systematic errors, the reader is left hanging a bit at the end of the feed-down discussion, as to what will be made of these estimates. So I would suggest adding a sentence in the 2nd paragraph, left column on page 5:
"...decaying via strong interactions. THE EFFECT OF THESE FEED-DOWNS, ESTIMATED AS DESCRIBED BELOW, IS INCORPORATED IN OUR SYSTEMATIC ERRORS IN SEC. II C. Under the assumption..." 3) Under eq. (4), the sentence that begins "The direction of the system..." will be clearer if the final parenthetical "(event plane)" is removed, and the earlier description in that sentence modified to say: "...defined to be along the normal to the EVENT plane spanned by..."
4) I find the addition of the average values of trigonometric functions in eqs. (9-11) helps quite a bit in thinking about the acceptance non- uniformities. However, I find the added sentence "The stronger deviation from unity of A_0 at smaller p_t^H..." still not very illuminating. I would suggest a slightly longer description along the following lines -- I don't know if my explanation is correct, but it sounds plausible. If you have a better understanding of the behavior, please describe that in somewhat more detail than the present version.
"The deviation of this function from unity is small and it reflects losses of the daughter protons or pions from the STAR detector acceptance, primarily at small angles with respect to the beam direction. Proton losses and pion losses dominate in different regions of phase space, since in the detector frame the protons follow the parent Lambda direction much more closely than do the pions. When the Lambda momentum is itself near the acceptance edges ($|\eta| \approx 1$), then the primary losses come from protons falling even closer to the beam direction. This disfavoring of small $\theta_p*$ tends to increase $\overline{\sin \theta_p*}$, hence $A_0$, with respect to uniform acceptance. In contrast, when the Lambda is near mid- rapidity or at high $p_t^H$, the daughter protons are constrained to stay within the detector acceptance. Then the primary losses arise from forward-going daughter pions, preferentially correlated with large $\sin \theta_p*$, tending to reduce $A_0$ from unity. In any case, the corresponding corrections to the absolute value of the global polarization are estimated to be less than 20\% of the extracted polarization values."
5) Some grammatical corrections in the last paragraph on page 9: "The hyperon directed flow is defined as THE first-order coefficient in THE Fourier expansion of THE hyperon azimuthal..." Later: "...of the same order of magnitude as FOR charged particles ($\leq 10\%$), the effects of such interference HAVE been found...due to both the hyperon reconstruction procedure and IMPERFECTION of the reaction plane determination..."
6) The 0.02 limit appears for the first time in the conclusions. I would suggest foreshadowing this appearance at the very end of section IIC: "...less than a factor of 2--2.5. TAKING ALL THESE POSSIBLE CORRECTION FACTORS INTO ACCOUNT, OUR RESULTS SUGGEST THAT THE GLOBAL LAMBDA AND LABMDA-BAR POLARIZATIONS ARE <= 0.02 IN MAGNITUDE."All figures are modified and only filled circles and oped squares symbols are used
sentences added
This para added. The only changes were made are (see page 9, left column): protons -> protons (anti-protons) Lambda -> Lambda (Anti-Lambda)
"factor of 2" replaced by "factor of 2-2.5" - (Evan Finch)
I would take the statement "Data points are not acceptance corrected" out of the figure captions, It's clear now in the text and I think it will just confuse people who skim the text and look at the figures.
Left as is. This sentence was added as the result of previous GPC comments. We are ready to remove it if other GPC members agreed on this too.The statement on strong feed down/string fragmentation model would benefit from mentioning what fraction of the indirect lambdas come from strong feed down (in the model) as opposed to sources you've already accounted for.
Left as is. This fraction of indirect hyperons from strong decay depends on both, our estimate of weak decay feed-downs and on the fraction of direct hyperons. Since the latter one is not measured with STAR, providing such a model dependent number without detailed explanation can potentially confuse the reader.Is it possible to replace 'negligible' with a real number for the effect of spin precession? If you have a number at hand, it would be better to include it.
The relative uncertainty from this effect is < 0.1%. This number is added to the text and the Table 1.In the acceptance section, I might replace "A() is a function to account for detector acceptance" with "A() is the fraction of lambdas which are accepted as a function of hyperon and daughter momentum".
Left as is. This statement will be difficult to understand together with the normalization of this function to unity. We can modified it as follows: "A() is a function to account for detector acceptance which is proportional to the fraction of accepted hyperons." In this form it is just a repetition of what we understand under detector acceptance.And some minor grammar points... From the first line in page 3, I would remove "the". Also, take out the last occurence of "the" in that same paragraph.
RemovedRemove "in distance" from "at least 6cm in distance" on page 4. In that same paragraph, replace "choose" with "chose" to stay in the past tense.
Removed and replacedPage 5, first column, I would add "in" to "Based on the results in [30].
Added
Global polarization of Anti-Lambda hyperon
Figures for the Anti-Lambda hyperon global polarization
Fig.1 Global polarization of Anti-Lambda hyperons as a function of Anti-Lambda transverse momentum.
Filled circles show the results for Au+Au collisions at sqrt{s_NN}=200 GeV (centrality region 20-70%) and open squares indicate the results for Au+Au collisions at sqrt{s_NN}=62 GeV (centrality region 0-80%).
Fig.2 Global polarization of Anti-Lambda hyperons as a function of Anti-Lambda pseudorapidity.
Filled circles show the results for Au+Au collisions at sqrt{s_NN}=200 GeV (centrality region 20-70%). A constant line fit to these data points yields P_Anti-Lambda = (1.8 +- 10.8)x10^{-3} with chi^2/ndf = 5.5/10. Open squares show the results for Au+Au collisions at sqrt{s_NN}=62 GeV (centrality region 0-80%). A constant line fit gives P_Anti-Lambda = (-17.6 +- 11.1)x10^{-3} with chi^2/ndf = 8.0/10.
Fig.3 Global polarization of Ant-Lambda hyperons as a function of centrality.
Filled circles show the results for Au+Au collisions at sqrt{s_NN}=200 GeV (centrality region 20-70%) and open squares indicate the results for Au+Au collisions at sqrt{s_NN}=62 GeV (centrality region 0-80%).
Parity violation
Ilya Selyuzhenkov for the STAR Collaboration
Strong local parity violation studies and presentations
- 2010
- 2010/06/07: Probes of local strong parity violation: Experimental results from STAR
(talk at RHIC & AGS Users' Meeting workshop on LPV)
- 2010/06/07: Probes of local strong parity violation: Experimental results from STAR
- 2009
- 2009/12/16: plenary talk at CATHIE/TECHQM Workshop on local parity violation at STAR
- 2009/07/28: DPF 2009 proceedings on STAR probes of parity violation
- 2009/07/28: DPF 2009 presentation on STAR probes of parity violation
- 2009/03/25: QM2009 poster on "Strong parity violation at STAR"
- 2009/02/13: QM2009 poster abstract
- 2008
- 2008/12/25: Au+Au@200GeV Run4 data vs. AMPT results
- 2008/12/22: AMPT model: delta eta and pt sum centrality dependence
- 2008/12/15: AMPT model: correlations vs. delta pt/eta and pt/eta sum
- 2007
- 2007/11/21: Fit points cut study (with and without TPC eta sub-events)
- 2007/11/20: DCA cut study
- 2007/11/19: Eta and pt subevents (eta subs: particles from different TPC half barrels; p_t subs: pt<1 and low pt>1 particles)
- 2007/11/19: Fit points cut study
- 2007/11/13: p_t and eta dependence: event plane from TPC vs FTPCs
- 2007/11/07: p_t and eta dependence: TPC fit points cut study, pt and eta weights (WSU RHIG group meeting)
- 2007/10/16: Search for the strong parity violation in HIC (BNL STAR Analysis Meeting)
- 2007/10/07: Update: bug fixed results (plus: comparison with Vasily's Dzhordzhadze results)
- 2007/03/01: Searching for novel phenomena in heavy ion collisions (BNL Particle Physics Seminar)
- 2006
- 2006/03/03: Status of the STAR parity violation measurement in Au+Au collisions (STAR Collaboration Meeting)
- 2006/02/28: Status of the STAR parity violation measurement in Au+Au collisions (EbyE Preview at STAR Collaboration Meeting)
- 2006/02/23: Status of the STAR parity violation measurement in Au+Au collisions (WSU RHIG group preview)
- 2005
- 2005/12/05: Strong parity violation study in Au+Au collisions at 62 and 200 GeV (Plenary at STAR Analysis Meeting)
- 2005/12/03: Strong parity violation study in Au+Au collisions at 62 and 200 GeV (EbyE parallel at STAR Analysis Meeting)
- 2005/11/15: Strong parity violation in Au+Au collisions: systematics study (WSU group Meeting)
- 2005/10/21: Global polarization and parity violation in Au+Au collisions (Midwest Critical Mass Meeting, Toledo)
- 2005/07/05: Global polarization and parity violation in Au-Au collisions (materials for QM 2005 plenary talk, EbyE phone)
- 2005/04/26: Global polarization and parity violation in Au+Au collisions (WSU group Meeting)
- 2005/04/21: Global polarization and parity violation in Au+Au collisions (materials for QM 2005 abstract)
Spin alignment
Global spin alignment in HIC
Main paper's web page
Some supporting material (see also files attached):
Strange flow
V0 directed flow study in AuAu@62GeV
Lambda, Anti-Lambda, K0Short directed flow in AuAu@62GeV data was measured by two and three particle correlations (FTPC, ZDCSMD and TPC data were used). In the error range the obtained results are consistent with zero.
Elliptic flow study in AuAu@62GeV
Non-flow contribution
By using the different charged sub-events the significant non-flow contribution from KSI decays were found, both in Lambda and Anti-Lambda elliptic flows. By correlating with event planes from different pseudo-rapidity region (TPC and FTPC event planes) the non-flow contribution to V0 elliptic flow has been estimate.
Barion to anti-barion asymmetry
The barion/anti-barion asymmetry investigated by studying the Lambda to anti-Lambda elliptic flow ratio. The barion to anti-barion elliptic flow ratio is found systematically different from 1 by few percents.
Talks and Publications
- The paper on "PID v2 in AuAu@62GeV" are currently in preparation.
It will include the results on V0 nonflow study and barion to anti-barion elliptic flow ratio results.
Supporting materials:
- V0's elliptic flow from Au+Au@62GeV, Au+Au@200GeV and Cu+Cu@200GeV
- V0's elliptic flow: dependence on charge of the particles in the event plane
- Comparing results for K0short elliptic flow
- V0's flows in Au+Au@62GeV
- V0's directed flow in Au+Au@62GeV
- Lambda, Anti-Lambda and K0Short directed and elliptic flows in Au+Au collision at 62 GeV
- Lambda and Anti-Lambda production in Au+Au collisions at 62GeV
Talks and posters
Talks and posters given at various conferences and workshops
2005 MCM
2005 Mindwest Critical Mass workshop, Toledo OH
Global polarization and parity violation in Au+Au collisions:
Slides: pdf or Open Office format
2005 QM
Quark Matter 2005 conference
Poster presentation on "Global polarization and parity violation study in Au+Au collisions:
- Abstract
- Proceedings at SCAL data base
- Poster and poster source files
2006 CIPANP
CIPANP2006 conference
Talk on "Acceptance effects in the hyperons global polarization measurement"
- Abstract
- Slides
- Proceedings at SLAC data-base
2006 QM
Quark Matter 2006 conference
Talk on "Centrality dependence of hyperon global polarization in Au+Au collisions at RHIC"
- Abstract
- Proceedings at SCAL data base
- Slides
2006 SQM
Strangeness in Quark Matter (SQM2006) conference
Talk on "Global polarization measurement in Au + Au collisions":
- Abstract
- Slides
- Proceedings at SCAL data base
- Referee reports:
- 1st report and reply
- 2nd report and reply
- 3rd report
2006 Xian
2006 Xian (China) workshop
Talk on "Anti-Lambda hyperon global polarization in Au+Au collisions at RHIC".
- Slides
- Proceedings at SLAC data base