Upsilon Analysis
Links related to Upsilon Analysis.
- Upsilon paper page from Pibero.
- Technical Note is located in Attachments to this page.
- TeX source (saved as .txt so drupal doesn't complain) for Technical Note is also in Attachments.
- Upsilon paper drafts are found below.
Combinatorial background subtraction for e+e- signals
It is common to use the formula 2*sqrt(N++ N--) to model the combinatorial background when studying e+e- signals, e.g. for J/psi and Upsilon analyses. We can obtain this formula in the following way.
Assume we have an event in which there are Nsig particles that decay into e+e- pairs. Since each decay generates one + and one - particle, the total number of unlike sign combinations we can make is N+- = Nsig2. To obtain the total number of pairs that are just random combinations, we subtract the number of pairs that came from a real decay. So we have
N+-comb=Nsig2-Nsig=Nsig(Nsig-1)
For the number of like-sign combinations, for example for the ++ combinations, there will be a total of (Nsig-1) pairs that can be made by the first positron, then (Nsig-2) that can be made by the second positron, and so on. So the total number of ++ combinations will be
N++ = (Nsig-1) + (Nsig - 2) + ... + (Nsig - (Nsig-1)) + (Nsig-Nsig)
Where there are Nsig terms. Factoring, we get:
N++ = Nsig2 - (1+2+...+Nsig) = Nsig2 - (Nsig(Nsig+1))/2 = (Nsig2 - Nsig)/2=Nsig(Nsig-1)/2
Similarly,
N-- = Nsig(Nsig-1)/2
If there are no acceptance effects, either the N++ or the N-- combinations can be used to model the combinatorial background by simply multiplying them by 2. The geometric average also works:
2*sqrt(N++ N--) = 2*Nsig(Nsig-1)/sqrt(4) = Nsig(Nsig-1) = N+-comb.
The geometric average can also work for cases where there are acceptance differences, with the addition of a multiplicative correction factor R to take the relative acceptance of ++ and -- pairs into account. So the geometric average is for the case R=1 (similar acceptance for ++ and --).
Estimating Acceptance Uncertainty due to unknown Upsilon Polarization
The acceptance of Upsilon decays depends on the polarization of the Upsilon. We do not have enough statistics to measure the polarization. It is also not clear even at higher energies if there is a definite pattern: there are discrepancies between CDF and D0 about the polarization of the 1S. The 2S and 3S show different polarizations trends than the 1S. So for the purposes of the paper, we will estimate the uncertainty due to the unknown Upsilon polarization using two extremes: fully transverse and fully longitudinal polarization. This is likely an overestimate, but the effect is not the dominant source of uncertainty, so for the paper it is good enough.
There are simulations of the expected acceptance for the unpolarized, longitudinal and transverse cases done by Thomas:
http://www.star.bnl.gov/protected/heavy/ullrich/ups-pol.pdf
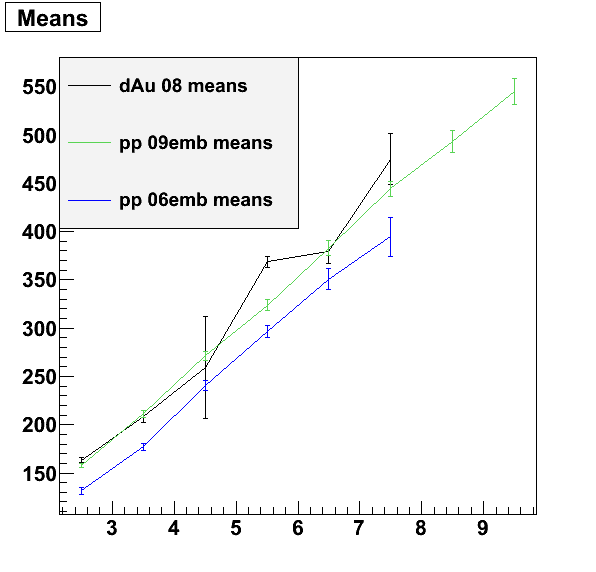
Using the pT dependence of the acceptance for the three cases (see page 9 of the PDF) we must then apply it to our measured upsilons. We do this by obtaining the pT distribution of the unlike sign pairs (after subtracting the like-sign combinatorial background) in the Upsilon mass region and with |y|<0.5. This is shown below as the black data points.
.gif)
The data points are fit with a function of the form A pT2 exp(-pT/T), shown as the solid black line (fit result: A=18.0 +/- 8.3, T = 1.36 +/- 0.16 GeV/c). We then apply the correction for the three cases, shown in the histograms (with narrow line width). The black is the correction for the unpolarized case (default), the red is for the longitudinal and the blue is for the transverse case. The raw yield can be obtained by integrating the histogram or the function. These give 89.7 (histo) and 89.9 (fit), which given the size of the errors is a reasonable fit. We can obtain the acceptance corrected yield (we ignore all other corrections here) by integrating the histograms, which give:
- Unpol: 158.9 counts
- Trans: 156.4 counts
- Longi: 163.6 counts
We estimate from this that fully transverse Upsilons should have a yield lower by -1.6% and fully longitudinal Upsilons should have a higher yield by 2.9%. We use this as a systematic uncertainty in the acceptance correction.
In addition, the geometrical acceptance can vary in the real data due to masked towers which are not accounted for in the simulation. We estimate that this variation is of order 25 towers (which is used in the 2007 and 2008 runs as the number of towers allowed to be dynamically masked). This adds 25/4800 = 0.5% to the uncertainty in the geometrical acceptance.
Estimating Drell-Yan contribution from NLO calculation.
Ramona calculated the cross section for DY at NLO and sent the data points to us. These were first shown in the RHIC II Science Workshop, April 2005, in her Quarkonium talk and her Drell-Yan (and Open heavy flavor) talk.
The total cross section (integral of all mass points in the region |y|<5) is 19.6 nb (Need to check if there is an additional normalization with Ramona, but the cross section found by PHENIX using Pythia is 42 nb with 100% error bar, so a 19.6 nb cross section is certainly consistent with this). She also gave us the data in the region |y|<1, where the cross section is 5.24 nb. The cross section as a function of invariant mass in the region |y|<1 is shown below.
.gif)
The black curve includes a multiplication with an error function (as we did for the b-bbar case) and normalized such that the ratio between the blue and the black line is 8.5% at 10 GeV/c to account for the efficiency and acceptance found in embedding for the Upsilon 1s. The expected counts in the region 8-11 are 20 +/- 3, where the error is given by varying the parameters of the error function within its uncertainty. The actual uncertainty is likely bigger than this if we take into account the overall normalization uncertainty in the calculation.
I asked Ramona for the numbers in the region |y|<0.5, since that is what we use in STAR. The corresponding plot is below.
.gif)
The integral of the data points gives 2.5 nb. The integral of the data between 7.875 and 11.125 GeV/c2 is 42.30 pb. The data is parameterized by the function shown in blue. The integral of the function in the same region gives 42.25 pb, so it is quite close to the calculation. In the region 8<m<11 GeV/c2, the integral of the funciton is 38.6 pb. The expected counts with this calculation are 25 for both triggers.
Response to PRD referee comments on Upsilon Paper
First Round of Referee Responses
Click here for second round.
-------------------------------------------------------------------------
Report of Referee A:
-------------------------------------------------------------------------
This is really a well-written paper. It was a pleasure to read, and I
have only relatively minor comments.
We thank the reviewer for careful reading of our paper and for providing
useful feedback. We are pleased to know that the reviewer finds the
paper to be well written. We have incorporated all the comments into a
new version of the draft.
Page 3: Although there aren't published pp upsilon cross sections there
is a published R_AA and an ee mass spectrum shown in E. Atomssa's QM09
proceedings. This should be referenced.
We are aware of the PHENIX results from
E. Atomssa, Nucl.Phys.A830:331C-334C,2009
and three other relevant QM proceedings:
P. Djawotho, J.Phys.G34:S947-950,2007
D. Das, J.Phys.G35:104153,2008
H. Liu, Nucl.Phys.A830:235C-238C,2009
However, it is STAR's policy to not reference our own preliminary data on the manuscript we submit for publication on a given topic, and by extension not to reference other preliminary experimental data on the same topic either.
Page 4, end of section A: Quote trigger efficiency.
The end of Section A now reads:
"We find that 25% of the Upsilons produced at
midrapidity have both daughters in the BEMC acceptance and at least one
of them can fire the L0 trigger. The details of the HTTP
trigger efficiency and acceptance are discussed in Sec. IV"
Figure 1: You should either quote L0 threshold in terms of pt, or plot
vs. Et. Caption should say L0 HT Trigger II threshold.
We changed the figure to plot vs. E_T, which is the quantity that is
measured by the calorimeter. For the electrons in the analysis, the
difference between p_T and E_T is negligible, so the histograms in
Figure 1 are essentially unchanged. We changed the caption as suggested.
Figures 3-6 would benefit from inclusion of a scaled minimum bias spectrum
to demonstrate the rejection factor of the trigger.
We agree that it is useful to quote the rejection factor of the trigger.
We prefer to do so in the text. We added to the description of Figure
3 the following sentence: "The rejection factor achieved with Trigger
II, defined as the number of minimum bias events counted by the trigger scalers
divided by the number events where the upsilon trigger was issued, was
found to be 1.8 x 105."
Figure 9: There should be some explanation of the peak at E/p = 2.7
We investigated this peak, and we traced it to a double counting error.
The problem arose due to the fact that the figure was generated from
a pairwise Ntuple, i.e. one in which each row represented a pair of
electrons (both like-sign and unlike-sign pairs included), each with a
value of E and p, instead of a single electron Ntuple. We had plotted
the value of E/p for the electron candidate which matched all possible
high-towers in the event. The majority of events have only one candidate
pair, so there were relatively few cases where there was double
counting. We note that for pairwise quantities such as opening angle and
invariant mass, each entry in the Ntuple is still different. However,
the case that generated the peak at E/p = 2.7 in the figure was traced
to one event that had one candidate positron track, with its
corresponding high-tower, which was paired with several other electron
and positron candidates. Each of these entries has a different invariant
mass, but the same E/p for the first element of the pair. So its entry
in Figure 9, which happened to be at E/p=2.7, was repeated several times
in the histogram. The code to generate the data histogram in Figure 9
has now been corrected to guarantee that the E/p distribution is made
out of unique track-cluster positron candidates. The figure in the paper
has been updated. The new histogram shows about 5 counts in that
region. As a way to gauge the effect the double counting had on the
E/p=1 area of the figure, there were about 130 counts in the figure at
the E/p=1 peak position in the case with the double-counting error, and
there are about 120 counts in the peak after removing the
double-counting. The fix leads to an improved match between the data
histogram and the Monte Carlo simulations. We therefore leave the
efficiency calculation, which is based on the Monte Carlo Upsilon
events, unchanged. The pairwise invariant mass distribution from which
the main results of the paper are obtained is unaffected by this. We
thank the reviewer for calling our attention to this peak, which allowed
us to find and correct this error.
-------------------------------------------------------------------------
Report of Referee B:
-------------------------------------------------------------------------
The paper reports the first measurement of the upsilon (Y) cross-section
in pp collisions at 200 GeV. This is a key piece of information, both
in the context of the RHIC nucleus-nucleus research program and in its
own right. The paper is rather well organized, the figures are well
prepared and explained, and the introduction and conclusion are clearly
written. However, in my opinion the paper is not publishable in its
present form: some issues, which I enumerate below, should be addressed
by the authors before that.
The main problems I found with the paper have to do with the estimate
of the errors. There are two issues:
The first: the main result is obtained by integrating the counts above
the like-sign background between 8 and 11 GeV in figure 10, quoted to
give 75+-20 (bottom part of table III). This corresponds the sum Y +
continuum. Now to get the Y yield, one needs to subtract an estimated
contribution from the continuum. Independent of how this has been
estimated, the subtraction can only introduce an additional absolute
error. Starting from the systematic error on the counts above background,
the error on the estimated Y yield should therefore increase, whereas
in the table it goes down from 20 to 18.
Thanks for bringing this issue to our attention. It is true that when
subtracting two independently measured numbers, the statistical
uncertainty in the result of the subtraction can only be larger than the
absolute errors of the two numbers, i.e. if C = A - B, and error(A) and
error(B) are the corresponding errors, then the statistical error on C
would be sqrt(error(B)2+error(A)2) which would yield a larger absolute
error than either error(A) or error(B). However, the extraction of the
Upsilon yield in the analysis needs an estimate of the continuum
contribution, but the key difference is that it is not obtained by an
independent measurement. The two quantities, namely the Upsilon yield
and the continuum yield, are obtained ultimately from the same source:
the unlike sign dielectron distribution, after the subtraction of the
like-sign combinatorial background. This fact causes an
anti-correlation between the two yields, the larger the continuum yield,
the smaller the Upsilon yield. So one cannot treat the subtraction of
the continuum yield and the Upsilon yield as the case for independent
measurements. This is why in the paper we discuss that an advantage of
using the fit includes taking automatically into account the correlation
between the continuum and the Upsilon yield. So the error that is
quoted in Table III for all the "Upsilon counts", i.e. the Fitting
Results, the Bin-by-bin Counting, and the Single bin counting, is quoted
by applying the percent error on the Upsilon yield obtained from the
fitting method, which is the best way to take the anti-correlation
between the continuum yield and the Upsilon yield into account. We will
expand on this in section VI.C, to help clarify this point. We thank the referee for
alerting us.
The second issue is somewhat related: the error on the counts (18/54, or
33%) is propagated to the cross section (38/114) as statistical error,
and a systematic error obtained as quadratic sum of the systematic
uncertainties listed in Table IV is quoted separately. The uncertainty on
the subtraction of the continuum contribution (not present in Table IV),
has completely disappeared, in spite of being identified in the text as
"the major contribution to the systematic uncertainty" (page 14, 4 lines
from the bottom).
This is particularly puzzling, since the contribution of the continuum
is even evaluated in the paper itself (and with an error). This whole
part needs to be either fixed or, in case I have misunderstood what the
authors did, substantially clarified.
We agree that this can be clarified. The error on the counts (18/54, or
33%) includes two contributions:
1) The (purely statistical) error on the unlike-sign minus like sign
subtraction, which is 20/75 or 26%, as per Table III.
2) The additional error from the continuum contribution, which we
discuss in the previous comment, and is not just a statistical sum of
the 26% statistical error and the error on the continuum, rather it must
include the anti-correlation of the continuum yield and the Upsilon
yield. The fit procedure takes this into account, and we arrive at the
combined 33% error.
The question then arises how to quote the statistical and systematic
uncertainties. One difficulty we faced is that the subtraction of the
continuum contribution is not cleanly separated between statistical and
systematic uncertainties. On the one hand, the continuum yield of 22
counts can be varied within the 1-sigma contours to be as low as 14 and
as large as 60 counts (taking the range of the DY variation from Fig.
12). This uncertainty is dominated by the statistical errors of the
dielectron invariant mass distribution from Fig. 11. Therefore, the
dominant uncertainty in the continuum subtraction procedure is
statistical, not systematic. To put it another way, if we had much
larger statistics, the uncertainty in the fit would be much reduced
also. On the other hand, there is certainly a model-dependent component
in the subtraction of the continuum, which is traditionally a systematic
uncertainty. We chose to represent the combined 33% percent error as a
statistical uncertainty because a systematic variation in the results
would have if we were to choose, say, a different model for the continuum
contribution, is smaller compared to the variation allowed by the
statistical errors in the invariant mass distribution. In other words,
the reason we included the continuum subtraction uncertainty together in
the quote of the statistical error was that its size in the current
analysis ultimately comes from the statistical precision of our
invariant mass spectrum. We agree that this is not clear in the text,
given that we list this uncertainty among all the other systematic
uncertainties, and we have modified the text to clarify this. Perhaps a
more appropriate way to characterize the 33% error is that it includes
the "statistical and fitting error", to highlight the fact that in
addition to the purely statistical errors that can be calculated from
the N++, N-- and N+- counting statistics, this error includes the
continuum subtraction error, which is based on a fit that takes into
account the statistical error on the invariant mass spectrum, and the
important anti-correlation between the continuum yield and the Upsilon
yield. We have added an explanation of these items in the updated draft of
the paper, in Sec VI.C.
There are a few other issues which in my opinion should be dealt with
before the paper is fit for publication:
- in the abstract, it is stated that the Color Singlet Model (CSM)
calculations underestimate the Y cross-section. Given that the discrepancy
is only 2 sigma or so, such a statement is not warranted. "Seems to
disfavour", could perhaps be used, if the authors really insist in making
such a point (which, however, would be rather lame). The statement that
CSM calculations underestimate the cross-section is also made in the
conclusion. There, it is even commented, immediately after, that the
discrepancy is only a 2 sigma effect, resulting in two contradicting
statements back-to-back.
Our aim was mainly to be descriptive. To clarify our intent, the use of
"underestimate" is in the sense that if we move our datum point lower by the
1-sigma error of our measurement and this value is higher than the top
end of the CSM calculation. We quantify this by saying that the
size of the effect is about 2-sigma. We think that the concise statement
"understimate by 2sigma" objectively summarizes the observation, without
need to use more subjective statements, and we modified
the text in the abstract and conclusion accordingly.
- on page 6 it is stated that the Trigger II cuts were calculated offline
for Trigger I data. However, it is not clear if exactly the same trigger
condition was applied offline on the recorded values of the original
trigger input data or the selection was recalculated based on offline
information. This point should be clarified.
Agreed. We have added the sentence: "The exact same trigger condition was
applied offline on the recorded values of the original trigger input data."
- on page 7 it is said that PYTHIA + Y events were embedded in zero-bias
events with a realistic distribution of vertex position. Given that
zero-bias events are triggered on the bunch crossing, and do not
necessarily contain a collision (and even less a reconstructed vertex),
it is not clear what the authors mean.
We do not know if the statement that was unclear is how the realsitic
vertex distribution was obtained or if the issue pertained to where the analyzed collision comes from.
We will try to clarify both instances. The referee has correctly understood
that the zero-bias events do not necessarily contain a collision.
That is why the PYTHIA simulated event is needed. The zero-bias events
will contain additional effects such as out of time pile-up in the Time
Projection Chamber, etc. In other words, they will contain aspects of
the data-taking environment which are not captured by the PYTHIA events.
That is what is mentioned in the text:
"These zero-bias events do not always have a collision in the given
bunch crossing, but they include all the detec-
tor effects and pileup from out-of-time collisions. When
combined with simulated events, they provide the most
realistic environment to study the detector e±ciency and
acceptance."
The simulated events referred to in this text are the PYTHIA events, and
it is the simulated PYTHIA event, together with the Upsilon, that
provides the collision event to be studied for purposes of acceptance
and efficiency. In order to help clarify our meaning, we have also added
statements to point out that the dominant contribution to the TPC occupancy
is from out of time pileup.
Regarding the realistic distribution of vertices,
this is obtained from the upsilon triggered events (not from the zero-bias events, which
have no collision and typically do not have a found vertex, as the referee correctly
interpreted). We have added a statement to point this out and hopefully this will make
the meaning clear.
- on page 13 the authors state that they have parametrized the
contribution of the bbar contribution to the continuum based on a PYTHIA
simulation. PYTHIA performs a leading order + parton shower calculation,
while the di-electon invariant mass distribution, is sensitive to
next-to-leading order effects via the angular correlation of the the two
produced b quarks. Has the maginuted of this been evaluated by comparing
PYTHIA results with those of a NLO calculation?
We did not do so for this paper. This is one source of systematic
uncertainty in the continuum contribution, as discussed in the previous
remarks. For this paper, the statistics in the dielectron invariant
mass distribution are such that the variation in the shape of the b-bbar
continuum between LO and NLO would not contribute a significant
variation to the Upsilon yield. This can be seen in Fig. 12, where the
fit of the continuum allows for a removal of the b-bbar yield entirely,
as long as the Drell-Yan contribution is kept. We expect to make such
comparisons with the increased statistics available in the run 2009
data, and look forward to including NLO results in the next analysis.
- on page 13 the trigger response is emulated using a turn-on function
parametrised from the like-sign data. Has this been cross-checked with a
simulation? If yes, what was the result? If not, why?
We did not cross check the trigger response on the continuum with a
simulation, because a variation of the turn-on function parameters gave
a negligible variation on the extracted yields, so it was not deemed
necessary. We did use a simulation of the trigger response on simulated
Upsilons (see Fig. 6, dashed histogram).
Finally, I would like to draw the attention of the authors on a few less
important points:
- on page 6 the authors repeat twice, practically with the same words,
that the trigger rate is dominated by di-jet events with two back-to-back
pi0 (once at the top and once near the bottom of the right-side column).
We have changed the second occurrence to avoid repetitiveness.
- all the information of Table I is also contained in Table 4; why is
Table I needed?
We agree that all the information in Table I is contained in Table 4
(except for the last row, which shows the combined efficiency for the
1S+2S+3S), so it could be removed. We have included it for convenience
only: Table I helps in the discussion of the acceptance and
efficiencies, and gives the combined overall correction factors, whereas
the Table IV helps in the discussion of the systematic uncertainties of
each item.
- in table IV, the second column says "%", which is true for the
individual values of various contributions to the systematic uncertainty,
but not for the combined value at the bottom, which instead is given
in picobarn.
Agreed. We have added the pb units for the Combined error at the bottom of the
table.
- in the introduction (firts column, 6 lines from the bottom) the authors
write that the observation of suppression of Y would "strongly imply"
deconfinement. This is a funny expression: admitting that such an
observation would imply deconfinement (which some people may not be
prepared to do), what's the use of the adverb "strongly"? Something
either does or does not imply something else, without degrees.
We agree that the use of "imply" does not need degrees, and we also
agree that some people might not be prepared to admit that such an
observation would imply deconfinement. We do think that such an
observation would carry substantial weight, so we have rephrased that
part to "An observation of suppression of Upsilon
production in heavy-ions relative to p+p would be a strong argument
in support of Debye screening and therefore of
deconfinement"
We thank the referee for the care in reading the manuscript and for all
the suggestions.
Second Round of Referee Responses
> I think the paper is now much improved. However,
> there is still one point (# 2) on which I would like to hear an
> explanation from the authors before approving the paper, and a
> couple of points (# 6 and 7) that I suggest the authors should
> still address.
> Main issues:
> 1) (errors on subtraction of continuum contribution)
> I think the way this is now treated in the paper is adequate
> 2) (where did the subtraction error go?)
> I also agree that the best way to estimate the error is
> to perform the fit, as is now explicitly discussed in the paper.
> Still, I am surprised, that the additional error introduced by
> the subtraction of the continuum appears to be negligible
> (the error is still 20). In the first version of the paper there
> was a sentence – now removed – stating that the uncertainty
> on the subtraction of the continuum contribution was one
> of the main sources of systematic uncertainty!
> -> I would at least like to hear an explanation about
> what that sentence
> meant (four lines from the bottom of page 14)
Response:
Regarding the size of the error:
The referee is correct in observing that the error before
and after subtraction is 20, but it is important to note
that the percentage error is different. Using the numbers
from the single bin counting, we get
75.3 +/- 19.7 for the N+- - 2*sqrt(N++ * N--),
i.e. the like-sign subtracted unlike-sign signal. The purely
statistical uncertainty is 19.7/75.3 = 26%. When we perform
the fit, we obtain the component of this signal that is due
to Upsilons and the component that is due to the Drell-Yan and
b-bbar continuum, but as we discussed in our previous response,
the yields have an anti-correlation, and therefore there is no
reason why the error in the Upsilon yield should be larger in
magnitude than the error of the like-sign subtracted unlike-sign
signal. However, one must note that the _percent_ error does,
in fact, increase. The fit result for the upsilon yield alone
is 59.2 +\- 19.8, so the error is indeed the same as for the
like-sign subtracted unlike-sign signal, but the percent error
is now larger: 33%. In other words, the continuum subtraction
increases the percent error in the measurement, as it should.
Note that if we one had done the (incorrect) procedure of adding
errors in quadrature, using an error of 14.3 counts for the
continuum yield and an error of 19.7 counts for the
background-subtracted unlike-sign signal, the error on the
Upsilon yield would be 24 counts. This is a relative error of 40%, which
is larger than the 33% we quote. This illustrates the effect
of the anti-correlation.
Regarding the removal of the sentence about the continuum
subtraction contribution to the systematic uncertainty:
During this discussion of the continuum subtraction and
the estimation of the errors, we decided to remove the
sentence because, as we now state in the paper, the continuum
subtraction uncertainty done via the fit is currently
dominated by the statistical error bars of the data in Fig. 11,
and is therefore not a systematic uncertainty. A systematic
uncertainty in the continuum subtraction would be estimated,
for example, by studying the effect on the Upsilon yield that
a change from the Leading-Order PYTHIA b-bbar spectrum we use
to a NLO b-bbar spectrum, or to a different Drell-Yan parameterization.
As discussed in the response to point 6), a complete
removal of the b-bbar spectrum, a situation allowed by the fit provided
the Drell-Yan yield is increased, produces a negligible
change in the Upsilon yield. Hence, systematic variations
in the continuum do not currently produce observable changes
in the Upsilon yield. Varying the continuum yield
of a given model within the statistical error bars does, and
this uncertainty is therefore statisitcal. Therefore, we removed the
sentence stating that the continuum subtraction is one
of the dominant sources of systematic uncertainty because
in the reexamination of that uncertainty triggered by the
referee's comments, we concluded that it is more appropriate
to consider it as statistical, not systematic, in nature.
We have thus replaced that sentence, and in its stead
describe the uncertainty in the cross
section as "stat. + fit", to draw attention to the fact that
this uncertainty includes the continuum subtraction uncertainty
obtained from the fit to the data. The statements in the paper
in this respect read (page 14, left column):
It should be noted that
with the statistics of the present analysis, we find that the
allowed range of variation of the continuum yield in the fit is
still dominated by the statistical error bars of the invariant mass
distribution, and so the size of the 33% uncertainty is mainly
statistical in nature. However, we prefer to denote
the uncertainty as “stat. + fit” to clarify that it includes the estimate of the anticorrelation
between the Upsilon and continuum yields obtained
by the fitting method. A systematic uncertainty due to
the continuum subtraction can be estimated by varying
the model used to produce the continuum contribution
from b-¯b. These variations produce a negligible change in
the extracted yield with the current statistics.
We have added our response to point 6) (b-bbar correlation systematics)
to this part of the paper, as it pertains to this point.
> Other issues:
> 3) (two sigma effect)
> OK
> 4) (Trigger II cuts)
> OK
> 5) (embedding)
> OK
> 6) (b-bbar correlation)
> I suggest adding in the paper a comment along the lines of what
> you say in your reply
> 7) (trigger response simulation)
> I suggest saying so explicitly in the paper
Both responses have been added to the text of the paper.
See page 13, end of col. 1, (point 7) and page 14, second column (point 6).
> Less important points:
> 8) (repetition)
> OK
> 9) (Table I vs Table IV)
> OK…
> 10) (% in last line of Table IV)
> OK
> 11) (“strongly imply”)
> OK
We thank the referee for the care in reading the manuscript, and look forward to
converging on these last items.
Upsilon Analysis in d+Au 2008
Upsilon yield and nuclear modification factor in d+Au collisions at sqrt(s)=200 GeV.
PAs: Anthony Kesich, and Manuel Calderon de la Barca Sanchez.
- Dataset QA
- Trigger ID, runs
- Trigger ID = 210601
- ZDC East signal + BEMC HT at 18 (Et>4.3 GeV) + L2 Upsilon
- Total Sampled Luminosity: 32.66 nb^-1; 1.216 Mevents
- http://www.star.bnl.gov/protected/common/common2008/trigger2008/lum_pertriggerid_dau2008.txt
- Trigger ID = 210601
- Run by Run QA
- Integrated Luminosity estimate
- Systematic Uncertainty
- Trigger ID, runs
- Acceptance (Check with Kurt Hill)
- Raw pT, y distribution of Upsilon
- Accepted pT, y distribution of Upsilons
- Acceptance
- Raw pT, eta distribution of e+,e- daughters
- Accepted pT, eta distribution of e+,e- daughters
- Comparison plots between single-electron embedding, Upsilon embedding
- L0 Trigger
- DSM-ADC Distribution (data, i.e. mainly background)
- DSM-ADC Distribution (Embedding) For accepted Upsilons, before and after L0 trigger selection
- Systematic Uncertainty (Estimate of possible calibration and resolution systematic offsets).
- "highest electron/positron Et" distribution from embedding (Accepted Upsilons, before and after L0 trigger selection)
- L2 Trigger
- E1 Cluster Et distribution (data, i.e. mainly background)
- E1 Cluster Et distribution (embedding, L0 triggered, before and after all L2 trigger cuts)
- L2 pair opening angle (cos theta) data (i.e. mainly background)
- L2 pair opening angle (cos theta) embedding. Needs map of (phi,eta)_MC to (phi,eta)_L2 from single electron embedding. Then a map from r1=(phi,eta, R_emc) to r1=(x,y,z) so that one can do cos(theta^L2) = r1.dot(r2)/(r1.mag()*r2.mag()). Plot cos theta distribution for L0 triggered events, before and after all L2 trigger cuts. (Kurt)
- L2 pair invariant mass from data (i.e. mainly background)
- L2 pair invariant mass from embedding. Needs simulation as for cos(theta), so that one can do m^2 = 2 * E1 * E2 * (1 - cos(theta)) where E1 and E2 are the L2 cluster energies. Plot the invariant mass distribution fro L0 triggered events, before and after all L2 trigger cuts. (Check with Kurt)
- PID
- dE/dx
- dE/dx vs p for the Upsilon triggered data
- nsigma_dE/dx calibration of means and sigmas (done by C. Powell for his J/Psi work)
- Cut optimization (Maximization of electron effective signal)
- Final cuts for use in data analysis
- E/p
- E/p distributions for various p bins
- Study of E calibration and resolution between data and embedding (for L0 Trigger systematic uncertainty)
- Resolution and comparison with embedding (for cut efficiency estimation)
- dE/dx
- Yield extraction
- Invariant mass distributions
- Unlike-sign and Like-sign inv. mass
- Like-sign subtracted inv. mass
- Crystal-Ball shapes from embedding/simulation. Crystal-ball parameters to be used in fit
- Fit to Like-sign subtracted inv. mass, using CB, DY, b-bbar
- Contour plot (1sigma and 2sigma) of b-bbar cross section vs. DY cross section
- Upsilon yield estimation and stat. + fit error
- Invariant mass distributions
- Cross section calculation.
- Yield, dN/dy
- Integrated luminosity (for 1/N_events, where N_events were the total events sampled by the L0 trigger)
- Efficiency (Numbers for each state, and cross-section-branching-ratio-weighted average)
- Uncertainty
- pt Distribution (invariant, i.e. 1/N_event 1/2pi, 1/pt dN/dpt dy) in |y|<0.5 vs pt) This might need one to do the CB, DY, bbbar fit in pt bins.
- Nuclear Modification Factor
- Estimation of <Npart> for the dataset, and uncertainty.
- Putting it all together: dN/dy in dAu, Npart, Luminosity (N_events), divided by the pp numbers (dsigma/dy, sigma_pp)
- Plot of R_dAu vs y, comparison with theory
- Plot of R_dAu vs Npart, together with Au+Au
- Plot of R_dAu vs pt. Try to do together with Au+Au (minbias, maybe in centrality bins, but maybe not enough stats)
Upsilon Analysis in p+p 2009
Upsilon cross-section in p+p collisions at sqrt(sNN) = 200 GeV, 2009 data.
PAs: Kurt Hill, Andrew Peterson, Gregory Wimsatt, Anthony Kesich, Rosi Reed, Manuel Calderon de la Barca Sanchez.
- Dataset QA (Andrew Peterson)
- Trigger ID, runs
- Run by Run QA
- Integrated Luminosity estimate
- Systematic Uncertainty
- Acceptance (Kurt Hill)
- Raw pT, y distribution of Upsilon
- Accepted pT, y distribution of Upsilons
- Acceptance
- Raw pT, eta distribution of e+,e- daughters
- Accepted pT, eta distribution of e+,e- daughters
- Comparison plots between single-electron embedding, Upsilon embedding
- L0 Trigger
- DSM-ADC Distribution (data, i.e. mainly background) (Drew)
- DSM-ADC Distribution (Embedding) For accepted Upsilons, before and after L0 trigger selection
- Systematic Uncertainty (Estimate of possible calibration and resolution systematic offsets).
- "highest electron/positron Et" distribution from embedding (Accepted Upsilons, before and after L0 trigger selection)
- L2 Trigger
- E1 Cluster Et distribution (data, i.e. mainly background)
- E1 Cluster Et distribution (embedding, L0 triggered, before and after all L2 trigger cuts)
- L2 pair opening angle (cos theta) data (i.e. mainly background)
- L2 pair opening angle (cos theta) embedding. Needs map of (phi,eta)_MC to (phi,eta)_L2 from single electron embedding. Then a map from r1=(phi,eta, R_emc) to r1=(x,y,z) so that one can do cos(theta^L2) = r1.dot(r2)/(r1.mag()*r2.mag()). Plot cos theta distribution for L0 triggered events, before and after all L2 trigger cuts. (Kurt)
- L2 pair invariant mass from data (i.e. mainly background)
- L2 pair invariant mass from embedding. Needs simulation as for cos(theta), so that one can do m^2 = 2 * E1 * E2 * (1 - cos(theta)) where E1 and E2 are the L2 cluster energies. Plot the invariant mass distribution fro L0 triggered events, before and after all L2 trigger cuts. (Kurt)
- PID (Greg)
- dE/dx
- dE/dx vs p for the Upsilon triggered data
- nsigma_dE/dx calibration of means and sigmas
- Cut optimization (Maximization of electron effective signal)
- Final cuts for use in data analysis
- E/p
- E/p distributions for various p bins
- Study of E calibration and resolution between data and embedding (for L0 Trigger systematic uncertainty)
- Resolution and comparison with embedding (for cut efficiency estimation) (Kurt and Greg)
- dE/dx
- Yield extraction
- Invariant mass distributions
- Unlike-sign and Like-sign inv. mass (Drew)
- Like-sign subtracted inv. mass (Drew)
- Crystal-Ball shapes from embedding/simulation. (Kurt) Crystal-ball parameters to be used in fit (Drew)
- Fit to Like-sign subtracted inv. mass, using CB, DY, b-bbar.
- Contour plot (1sigma and 2sigma) of b-bbar cross section vs. DY cross section. (Drew)
- Upsilon yield estimation and stat. + fit error. (Drew)
- (2S+3S)/1S (Drew)
- Invariant mass distributions
- pT Spectra (Drew)
- Cross section calculation.
- Yield
- Integrated luminosity
- Efficiency (Numbers for each state, and cross-section-branching-ratio-weighted average)
- Uncertainty
- h+/h- Corrections
Upsilon Analysis in p+p 2009 data - Acceptance
- Acceptance (Kurt Hill) - Upsilon acceptance aproximated using a simulation that constructs Upsilons (flat in pT and y), lets them decay to e+e- pairs in the Upsilon's rest frame, and uses detector response functions generated from a single electron embedding to model detector effects. An in depth study of this method will also be included.
- Raw pT, y distribution of Upsilon
- Accepted pT, y distribution of Upsilons
- Acceptance
- Raw pT, eta distribution of e+,e- daughters
- Accepted pT, eta distribution of e+,e- daughters
- Comparison plots between single-electron embedding, Upsilon embedding
Upsilon Analysis in p+p 2009 data - Acceptance
- Acceptance (Kurt Hill)
- Raw pT, y distribution of Upsilon
- Accepted pT, y distribution of Upsilons
- Acceptance
- Raw pT, eta distribution of e+,e- daughters
- Accepted pT, eta distribution of e+,e- daughters
- Comparison plots between single-electron embedding, Upsilon embedding
Upsilon Paper: pp, d+Au, Au+Au
Page to collect the information for the Upsilon paper based on the analysis of
Anthony (4/24):
in data, the electrons were selected via 0<nSigE<3, R<0.02. For pt<5, we fit to 0<adc<303. For pt>5, 303<adc<1000.
In embedding, the only selections are the p range, R<0.02, and eleAcceptTrack. The embedding pt distro was reweighted to match the data.
Anthony (4/5): Added new Raa plot with comparison to strickland's supression models
Anthony (4/4): I attached some dAu cross section plots on this page. The eps versions are on nuclear. The cross sections are as follows:
all: 25.9±4.0 nb
0-2: 1.8±1.7 nb
2-4: 10.9±2.9 nb
4-6. 5.2±5.3 nb
6-8: 0.57±0.59 nb
I expect the cross sections to change once I get new efficiences from embedding, but not by a whole lot.
Drew (4/6): Got Kurt's new lineshapes, efficiencies, and double-ERF parameters today. Uploading the fits to them. I'm not sure I believe the fits...
Bin-by-Bin Counting Cross Section by pT (GeV/c):
|y|<1.0 all: 134.6 ± 10.6 pb
0-2: 27.6 ± 6.3 pb
2-4: 39.1 ± 5.8 pb
4-6: 19.9 ± 3.8 pb
6-8: 13.6 ± 5.1 pb
|y|<0.5 all: 119.2 ± 12.4 pb
0-2: 23.8 ± 6.8 pb
2-4: 35.9 ± 7.4 pb
4-6: 19.0 ± 4.5 pb
6-8: 14.2 ± 4.6 pb
The double ERF is a turn-off from the L2 trigger's mass cut. Kurt used the form: ( {erf*[(m-p1)/p2]+1}*{erf*[(p3-m)/p4]+1} )/2, but I used /4 in the actual fit because each ERF can be at most 2. By fits are also half a bin shifted from Tony's, we'll need to agree on it at some point. The |y|<1 are divided by 2 units in rapidity, and the |y|<0.5 by 1 unit.
Upsilon pp, dAu, AuAu Paper Documents
This page is for collecting the following documents related to the Upsilon pp (2009), dAu (2008) and AuAu (2010) paper:
- Paper Proposal (Most Recent: Version 3)
- New in v3: Now says we're going for PLB and has the E772 and MC plots included. Also has |y|<1.0 results
- Technical Note (Most Recent: Version 6)
- New in v3: AuAu consistency analysis and expanded summary table
- New in v4: Added JPsi study of linewidth and 1S numbers
- New in v6 : Final version for paper as resubmitted to PLB
- Paper Draft (Latest: Version 25)
- New in v26: Updated with changes made in PLB proof
- v25-resub: Version as re-submitted to PLB (no line numbers).
- New in v25: Updated acknowledgements.
- New in v24: Minor changes to discussion or TPC misalignment
- New in v23.1: Added systematics to Fig. 3
- New in v23: Updated with comments from Lanny and Thomas. Changes are in red.
- New in v22: Made changed based on GPC responses to our responses to the referees. Also, all Tables are now correct. Changes are in blue.
- New in v21: Changed in response to PLB referee comments. Changed results to likelihood fits. Added binding energy plot. Tabs. II and III are NOT correct.
- New in v20: ???
- New in v19: Updated with minor comments from Thomas on Nov 25.
- New in v18: Incorporated lost changes from v16. Added 3 UC Davis undergrads to the author list.
- New in v17: A few more changes from GPC comments and addition of AuAu cross sections
- New in v16: Changes from GPC comments after collaboration review
- New in v15: Collaboration review changes
- New in v14: English QA changes
- New in v13: Mostly minor edits suggested by Lanny and Thomas
- New in v12: Updated the MC section to addredd |y|<0.5. Also did some other, minor graphwork on fig 3b
- New in v11: Updated with latest comments from the GPC. Official version before the first GPC meeting
- New in v10: Updated from PWG discussion. Cleaned and enchanced plots
- New in v9: Cleaned up v8
- New in v8: Added analysis of 1S state and discussion of E772
- New in v7: Made many changes based on first round of GPC e-mails. Summaries of changes and responses can be found on the responses sub-page.
- New in v6: Cleaned up most plots. Reworded end of intro. Cleaned up triggering threshold discussion. Added labels for subfigures.
- New in v5.1: Made stylistic clarifications and fixed a few typos. Updated dAu mass spectrum legend to explain grey curve.
- New in v5: PLB formatting and some plot clean-up
- New in v4: E772 results and |y|<1.0 and |y|<0.5 both included for AuAu
Responses to Collaboration comments
- Comments from JINR
- Comments from Tsinghua
- Comments from UCLA
- Comments from Creighton
- Comments from WUT
- Comments from BNL
Thanks to all the people who submitted comments. These have helped to improve the draft. Please find the responses to the comments below.
Comments from JINR (Stanislav Vokal)
1) Page 3, line 40, „The cross section for bottomonium production is smaller than that of charmonium [8-10]...“, check it, is there any cross section for bottomonium production in these papers?
Answer: Both papers report a quarkonium result. The PHENIX papers quote a J/psi cross section of ~178 nb. Our paper from the 2006 data quotes the Upsilon cross section at 114 pb.
2) Page 3, lines 51-52, „compared to s_ccbar approx 550 - 1400 mb [13, 14]). ...“. It should be checked, in [13] s is about 0.30 mb and in [14], Tab.VII, s is about 0.551 – 0.633 mb.“.
Answer: In Ref. 13, the 0.3 mb is for dsigma/dy, not for sigma_cc. To obtain sigma_cc, one has to use a multiplicative factor of 4.7 that was obtained from simulations (Pythia), as stated in that reference. This gives a cross section of ~ 1.4 mb, which is the upper value we quote (1400 \mu b). In reference 14, in Table VIII the low value of 550 \mu b is the lower value we use in the paper. So both numbers we quote are consistent with the numbers from those two references.
3) Page 3, line 78, „...2009 (p+p)...“ and line 80 „20.0 pb-1... “, In Ref. [10] the pp data taken during 2006 were used, 7.9 pb-1, it seems that this data sample was not included in the present analysis. Am I true? If yes – please explain, why? If the data from 2006 are included in the present draft, then add such information in the text, please.
Answer: That is correct: the data from 2006 was not included in the present analysis. There were two major differences. The first difference is the amount of inner material. In 2006 (and 2007), the SVT was still in STAR. In 2008, 2009, and 2010, which are the runs we are discussing in this paper, there was no SVT. This makes the inner material different in 2006 compared to 2009, but it is kept the same in the entire paper. This is the major difference. The inner material has a huge effect on electrons because of bremsstrahlung, and this distorts the line shape of the Upsilons. The second difference is that the trigger in 2006 was different than in 2009. This difference in triggers is not insurmountable, but given the difference in the amount of inner material, it was not worth to try to join the two datasets. We have added a comment to the text about this:
4) Page 4, Fig.1, numbers on the y-axe should be checked, because in [10], Fig.10, are practically the same acounts, but the statistic is 3 times smaller;
Answer: The number that matters is the counts in the Upsilon signal. In Fig. 10 of Ref. 10, there is a lot more combinatorial background (because of the aforementioned issue with the inner material), so when looking at the total counts one sees a similar number than in the present paper. However, in the case of the 2006 data, most of the counts are from background. The actual signal counts in the highest bin of the 2006 data are ~55-30 = 25, whereas the signal counts in the present paper are ~ 50 - 5 = 45 in the highest bin. When you also notice that the 2006 plot had bins that were 0.5 GeV/c^2 wide, compared to the narrower bins of 0.2 GeV/c^2 we are using in Figure 1 (a), it should now be clear that the 2009 data has indeed more statistics.
5) Page 5, line 31, „114 ± 38+23-14 pb [10]“, value 14 should 24;
Answer: Correct. We have fixed this typo. Thank you.
6) Page 5, Fig.2, yee and yY should be identical;
Answer: We will fix the figures to use one symbol for the rapidity of the upsilons throughout the paper.
7) Page 5, Fig.2 – description, „Results obtained by PHENIX are shown as filled tri-angles.“ à diamond;
Answer: Fixed.
8) Page 6, Fig.3a, here should be hollow star for STAR 1S (dAu) as it is in Fig.3b;
Answer: Fixed.
9) Page 8, line 7, „we find RAA(1S) = 0.44 ± ...“ à should be 0.54;
Answer: Fixed.
10) Page 8, lines 9-12, „The ratio of RAA(1S) to RAA(1S+2S+3S) is consistent with an RAA(2S+3S) approximately equal to zero, as can be seen by examining the mass range 10-11 GeV/c2 in Fig. 4.“, it is not clear, check this phrase, please;
Answer: We have modified this phrase to the following: "If 2S+3S states were completely dissociated in Au+Au collisions, then R_AA(1S+2S+3S) would be approximately equal to $R_AA(1S) \times 0.69$. This is consistent with our observed R_AA values, and can also be inferred
11) Page 8, line 26, „CNM“, it means Cold Nuclear Matter suppression? – should be explained in text;
Answer: The explanation of the CNM acronym is now done in the Introduction.
12) Page 9, line 30-31, „The cross section in d+Au collisions is found to be = 22 ± 3(stat. + fit)+4- 3(syst.) nb.“, but there is no such results in the draft before;
Answer: This result is now given in the same paragraph where the corresponding pp cross section is first
stated, right after the description of Figure 1.
13) Page 9, line 34, „0.08(p+p syst.).“ à „0.07(p+p syst.).“, see p.7;
Answer: Fixed. It was 0.08
14) Page 10, Ref [22], should be added: Eur. Phys. J C73, 2427 (2013);
Answer: We added the published bibliography information to Ref [22].
15) Page 10,, Ref [33] is missing in the draft.
Answer: We have now removed it. It was left over from a previous version of the draft which included text that has since been deleted.
Comments from Tsinghua
1) Replace 'Upsilon' in the title and text with the Greek symbol.
Answer: Done.
2) use the hyphen consistently across the whole paper, for example, sometimes you use 'cold-nulcear matter', and at another place 'cold-nuclear-matter'. Another example is 'mid-rapidity', 'mid rapidity', 'midrapidity'...
Answer: On the hyphenation, if the words are used as an adjectivial phrase, then those need to be hyphenated. In the phrase "the cold-nuclear-matter effects were observed", the words "cold-nuclear-matter" are modifying
the word "effects", so they are hyphenated. However, from a previous comment we decided to use the acronym "CNM" for "cold-nuclear matter", which avoids the hyphenation. We now use "mid-rapidity" throughout the paper.
3) For all references, remove the 'arxiv' information if the paper has been published.
Answer: We saw that published papers in PLB do include the arxiv information in their list of references. For the moment, we prefer to keep it there since not all papers are freely available online, but arxiv manuscripts are. We will leave the final word to the journal, if the editors ask us to remove it, then we will do so.
4) Ref. [33] is not cited in the text. For CMS, the latest paper could be added, PRL 109, 222301 (2012).
Answer: Ref [33] was removed. Added the Ref. to the latest CMS paper on Upsilon suppression.
5) For the model comparisons, you may also compare with another QGP suppression model, Y. Liu, et al., PLB 697, 32-36 (2011)
Answer: This model is now included in the draft too, and plotted for comparison to our data in Fig. 5c.
6) page 3, line 15, you may add a reference to lattice calculations for Tc ~ 175 MeV.
Answer: Added a reference to hep-lat/0305025.
7) Fig 1a, \sqrt{s_{NN}} -> \sqrt{s}. In the caption, |y| -> |y_{ee}|
Answer: Fixed.
8) For the dAu rapidity, the directions of Au-going and p-going should be explicitly defined.
Answer: We also realized that this was important to do. This is now done by adding the sentence: "Throughout this paper, the positive rapidity region is the deuteron-going direction, and the
negative rapidity region is the Au-going direction. "
9) Fig.2a, the label of x-axis, 'y_{ee}' -> 'y_{\Upsilon}'. In the caption for Fig. 2a, Ref. [21] should be cited after 'EPS09 nPDF'.
Answer: We moved the citation to the first part of the caption.
10) page 5, around line 28-29, please mention explicitly this result is for p+p 200 GeV.
Answer: Done. The text now reads "we calculate a production cross section in p+p collisions..."
11) page 7, line 33, add space after N_{part}
Answer: Fixed.
12) page 7, line 36, Fig. 5c -> Figure 5c
Answer: Done.
13) page 7, line 46, remove 'bin from'
Answer: Done.
14) page 7, line 55, 'the latter' -> 'the former' ?
Answer: Split the sentence into two, and explicitly stated "The level of suppression we observe for
|y|<0.5 stays approximately constant from dAu up to central AuAu collisions. " to make it clear.
15) Fig. 4 a, b, and c, '30%-60%' -> 30-60%, '10%-30%' -> '10-30%', '0%-10%' -> '0-10%' In the caption, |y| -> |y_{ee}|
Answer: Fixed.
16) Fig. 5, the label of the y axis better to be the same style as Fig. 2
Answer: Fixed.
17) Page 9, line 33, line 45, when quoting the RdAu and RAA, why omit the p+p stat. errors? Also the p+p syst. err. in line 34 is not the same as that in page 7, line 41, please check.
Answer: The p+p stat. errors are combined together with the Au+Au stat. errors because it is straightforward to combine stat. errors, and we just quote the combined stat. error. Syst errors are fixed.
Comments from UCLA
1. In the legends of Fig 1 and Fig 4, the line color for the like-sign and unlike-sign should be blue and red, instead of black.
Answer: Fixed.
2. On page 5, line 29, it is not specified whether this is for p+p or dAu.
Answer: Done. The text now reads "we calculate a production cross section in p+p collisions..."
3. The directions of the d and Au beams were not defined: which goes forward and which backward in y? It will be good to specifiy the direction, and briefly discuss the different physics we expect from the forward and backward regions.
Answer: We also realized that this was important to do. This is now done by adding the sentence: "Throughout this paper, the positive rapidity region is the deuteron-going direction, and the
negative rapidity region is the Au-going direction. "
4. Page 7, line 50, "Pb+Pb" should be upright.
Answer: Done.
5. Page 7, line 55-56, "the latter" should be the model, which doesn't look constant. It seems you are talking about the measurements. Then it should be "the former".
Answer: Split the sentence into two, and explicitly stated "The level of suppression we observe for
|y|<0.5 stays approximately constant from dAu up to central AuAu collisions. " to make it clear.
6. Page 8, line 13-14, "in d+Au to be $2\sigma$ from unity and consistent with unity in peripheral" -> "to be $2\sigma$ from unity in d+Au and consistent with unity in peripheral"
Answer: Done.
7. Page 8, line 22, "modeling"
Answer: There are two aims: to incorporate... and to model ... Since we use the infinitive form in the description of the first aim ("to incorporate") we also use the infinitive form ("to model") in the second aim.
8. Page 3, line 82, "pQCD" -> "perturbative QCD (pQCD)"
9. Page 5, line 6, "perturbative QCD" -> "pQCD"
Answer: Both are now fixed.
10. Page 5, Fig 2, the caption says "Results obtained by PHENIX are shown as filled triangles", but they are "diamonds", not triangles in figure.
Answer: Fixed.
11. Pg 4 Line 1 : Barrel Electro-Magnetic Calorimeter (EMC) - Barrel Electro-Magnetic Calorimeter (BEMC) and replace EMC with BEMC throughout.
Answer: Done.
12. Pg 4 Line 65 : |y_{\upsilon}| - |y|. In the following Figure 1, its |y_{ee}| < 0.5 in figure panels and |y| < 0.5 in caption. Inconsistency, if all of them are same.
Answer: Fixed.
13. Pg 5 Line 1 : The data are fit .. - The data are fitted ..
Answer: Both forms are grammatically correct. The past participle can be either "fit" or "fitted".
http://en.wiktionary.org/wiki/fit#Verb
We kept the text as is.
14. Pg 5 Line 6 : via a perturbative (pQCD) next to leading order (NLO) - via a next to leading order (NLO) pQCD
Answer: Done.
15. Pg 5 Line 41 : ... with respect to ... - ... with respect to the ...
Answer: It is correct as written, usage: with respect to (something). One could also use "with respect to the" but then we would need to add another noun, for example as in, "with respect to the binary-collision-scaling expectation". We felt the original form was ok.
16. Pg 5 Line 46 : ... yield ... - ... yields ...
Answer: Done.
17. Pg 6 Line 25 : The present data ... - The present data in which figure ?
Answer: It is now made clear in the text that this refers to Figure 2b.
18. Pg 6 Caption for Fig. 3 : Use a) and b) instead of top and bottom
Answer: Done.
19. Pg 6 Caption for Fig. 3 : x_{F} in caption and X_{F} in figure
Answer: Fixed.
20. Pg 8 Line 26 : when CNM first appears, it needs to be spelled out.
Answer: Done, it is now given in the Introduction.
21. Pg 9 Line 28 & 31 : The term B_{ee} \times is missing in front of d\sigma/dy
Answer: Done.
Comments from Creighton
Page 3, Line 71. Why only p+p and d+Au? Why is the Au+Au cross-section not extracted?
Answer: We typically extract the yield per event in AA. This can be transformed into a cross section if we use the integrated luminosity. To get from a total number of minimum-bias events to an integrated luminosity all that is needed is the hadronic cross section for AuAu collisions, which is typically obtained using a Glauber model. We typically don't quote it mainly because what the community wants to know is R_AA itself. That is the quantity that the theorists typically calculate, and so we had received guidance to not include a cross section. (It was actually included in earlier versions of the draft.) Given this call for including it, we have now brought it back to the draft.
Figure 2. It might be more appropriate to include the description of the symbols in the figure caption rather than in the text. The legend might be reformatted so the description of symbols has the same structure for STAR, PHENIX, and Ramona Vogt. Why not use a consistent label for what we understand to be the same quantity expressed on the horizontal axis? (Figure 2a uses the rapidity for e+e- while Figure 2b uses rapidity for the upsilon.)
Answer: The caption now describes the symbols too. We left the description in the text also, to help the reader.
Page 5, Line 4. The wording in the text makes it sound like the red line in Figure 2 could refer exclusively to the upsilon production.
Answer: We have reworded this part to:
"The data are fit with a parameterization consisting of the sum of various contributions to the
Page 6, Line 18. It might be more appropriate to discuss here why the mid-rapidity point is lower than the prediction (rather than later in the text).
Answer: In a sense, the next paragraphs and figures are meant to discuss this point being low. We use R_dAu to have more discussion of the model predictions (and show their uncertainties). We next compare our result to previous measurements, which show a similar suppression. We added the sentence "To study this observation for \dAu\ further, we make a closer comparison to models and to previous measurements of \upsi\ production in p+A collisions. " to highlight this.
Page 7, Line 11/Figure 3b. It is unclear how the plot in terms of Feynman-x improves the comparison of rapidity coverage.
Answer: We added the x_F plot because the E772 data were given in x_F. We can massage our data to get x_F from rapidity making some estimates about the pT, which we can do because we have all the information on the Upsilon 4-momenta for our data, but we do not have this information for E772. So in order to compare to their result, it was best to not touch their data and massage ours, with intimate knowledge of ours, than to keep everything in y_Upsilon but having to massage their data without knowledge of their pT distribution so that we would only be guessing as to the correct y_Upsilon that would correspond to a particular x_F range.
Page 9, Line 30. This result in the conclusions does not seem to have been presented in the body of the paper.
Answer: This result is now given in the same paragraph where the corresponding pp cross section is first
stated, right after the description of Figure 1.
Comments from WUT
Reader 1:
1. legend of Fig. 1b
--------------------
I would rather put R_{dA}=1 (not R_{AA}) to be consistent with the figure caption and the main text
Answer: Fixed.
2. Fig 2a and discussion in the text
of the results for pp at positive and negative rapidities.
----------------------------------------------------------
I found it a bit awkward that we are presenting results just after folding in data at positive and negative y.
Of course the physics for pp is symmetric wrt y=0,
but it would be better to present separately results
for -1 < y < -0.5 and 0.5 < y < 1.0 to show that indeed the results are consistent.
(Also as a cross check of correctness of including all experimental corrections, and nothing to hide)
Answer: We did check that the results were consistent for pp, but we wanted to maximize the statistical power of the data, given that we are still somewhat statistics limited. Note that the acceptance and efficiency is lower for the 0.5 < |y|< 1.0 region, so that is why we wanted to add the two in pp, thanks to the symmetry, to show our best results. For the d+Au case, as we say in the paper, we did leave the analysis in distinct rapidity regions because the system is not symmetric.
3. legend of Fig. 2a
--------------------
For STAR and PHENIX points it would be more transparent,
if the legend would have similar layout as for NLO pQCD CEM.
I.e. 'STAR' in a single line followed by two lines
'pp' and 'dAu/1000' and analogously for
PHENIX/
Answer: Fixed.
4. line 2 on page 7
------------------
"their deuterium result" => "their pd result"
would be more straightward statement
(I assume E772 had a liquid deuterium target to study pd collisions)
Answer: Done. And yes, we say in the text that they had a liquid deuterium target.
5. Fig. 4
---------
The curves for combinatorial background should be made smooth
like for all other curves, not going in steps.
Answer: Fixed.
Reader 2:
page 4, line 1 and in further occurences: shouldn't it be BEMC instead of EMC ?
--------------------
Answer: Done.
page 5, line 1: shouldn't it be "The data are fitted"
---------------------------------------
Answer: Both forms are grammatically correct. The past participle can be either "fit" or "fitted".
http://en.wiktionary.org/wiki/fit#Verb
We kept the text as is.
Reader 3:
Overall it is a very well written paper and important results.
1. Acronyms in the introduction should be defined there (RHIC, LHC, pQCD or even QCD)
--------------------
Answer: Done.
p. 3, l. 60: you use "cold-nuclear-matter effects" without defining what "cold" and "hot" nuclear matter is. It would be good to introduce these terms when you talk about QGP and then other possible sources of suppression (line 52-63)
--------------------
Answer: Added short phrases to better define these terms.
p.8 l.26 - CNM should be defined
--------------------
Answer: It is now defined in the Introduction.
p.8 l.44-48 - it is not clear from the text how exactly CNM and QGP effects were combined for the scenario 4.
--------------------
Answer: We now state "For scenario 4), the expected suppression is simply taken to be the product of the suppression from scenario 2) and scenario 3)."
p.9 l.29 "with NLO" -> with "pQCD NLO"
--------------------
Answer: In the rest of the paper, we have used NLO pQCD, so at this point, it should be clear that when we are talking about
a Next-to-Leading Order calculation, we are implicitly talking about a perturbative QCD calculation (the fact that we are talking
about "orders" in a calculation implies
that we are talking about perturbation theory,
and this entire paper deals with QCD), so it should be clear from the context.
Figures: Caption of Fig 2: " from EPS09 with shadowing" - "EPS09" is nPDF which includes shadowing already, maybe write "due to shadowing using EPS09"?
--------------------
Answer: Changed the caption so it reads: "The dAu
Fig 2 and Fig 6 - the contrast of the figures could be improved - for instance lines for models in Fig. 2 are barely visible when printed in black and white
Answer: Fixed.
Reader 4: Fig. 1 and Fig 4 - The information on pT range,
in which the signal is presented, can be added.
-------------------------------------
Answer: We added a sentence at the end of the "Experimental Methods" section to state: "For all results we quote, the Upsilon data are integrated over all transverse momenta."
Comments from BNL
The new p+p result is significant, why is it not in title?
Answer: We already have one paper that is all about the pp cross section. Our result in this paper is an improvement, but the new results on suppression are the highlight of the paper, and we felt they deserved to be emphasized in the title. If we change the title to something like "Upsilon production in pp, d+Au, and Au+Au collisions at sqrt(s_NN) = 200 GeV" would include the pp result in the title, but it will not mention suppression. We prefer to emphasize the suppression, as that is the new, important result. Since we are attempting to publish in Physics Letters B, we felt it was more appropriate.
The paper is not clear in many places, and would be helped from a re-write keeping the audience in mind, i.e. not nesc. an expert in HI. It was commented that in particular the introduction on page 2 line 56 to 66 has much expert knowledge assumed, but does cover the field. Some examples are given below in the individual comments.
Answer: We tried to make the introduction section a short review of the field so that a non-expert could follow. We don't understand which expert knowledge is assumed in the introduction in lines 56-66. We certainly have strived to make the paper clear, and we will look for the specific comments and suggestions below.
The different RAA values appears multiple places in text. We think it is important to present these in tabular form, particular since so many numbers are presented RAA |y| <0.5, 1 centrality and collision system. Noted by several readers. Page 7,30-‐50 Page 8, 4-‐20
Answer: A table with all the values has now been added to the paper.
The definition of RAA seems a bit colloquial, normally this is defined vs. e.g pt, but in the case of the Upsilon it is our understanding this is an integral of the cross section over all (or some) pt-‐range divided by the pp . The paper should define this clearly.
Answer: We specifically wrote in the paper the equation used for R_AA. This is as clear a definition as we can make. We also now specify that our measurements are integrated over all pt.
The abstract should reflect the conclusion of the paper, this does not at present.
Our results are consistent with complete suppression of excited-state Υ mesons in Au+Au collisions. The additional suppression in Au+Au is consistent with the level expected in model calculations that include the presence of a hot, deconfined Quark-Gluon Plasma. However, understanding the effects seen in d+Au is still needed before fully interpreting the Au+Au results.
The most important observation, which is the unexpected observation that R_dAu is the same as R_AA for central events in the |y|<0.5 region, is the reason why we wrote the last sentence in the abstract.
Answer: We have discussed the differences in the |y|<1 and |y|<0.5 in the PWG, precisely to try to make sure that the results we are observing in |y|<1 and in |y|<0.5 are statistically consistent. One of the results is a subset of the other, so one must be careful to take into account the correlations. This study is in the technical note, in section 6A (page 33). We concluded that the results are self consistent. As to whether the result is statistical fluctuation, this is a possibility, but that is the case for any result, and the only way to remedy that situation is to run more dAu. As to whether it could be a systematic effect, we have done the analysis in |y|<0.5, in |y|<1, and in 0.5<|y|<1 where for each we use the same methods for extracting the signal, for applying efficiency and acceptance corrections, for estimating the backgrounds, etc. So if there is a systematic effect, it would affect the |y|<0.5 and the 0.5<|y|<1 region in the same way, and therefore it would not lead to differences between these two regions. We do not think that this "takes away" from the final conclusions, because it is an observation that is not expected if there should be binary scaling in dAu, and it makes the result more interesting. The reason why we included the E772 data was precisely because we observed such a striking suppression in dAu. So indeed, the fact that the data in Fig. 5b do not show a significant centrality dependence vs. Npart is one of the most important observations of the paper. And with the E772 data, we can point to a previous result that shows a similar level of suppression in pA. Therefore, this paper will serve to exhort the community to take a closer look at Upsilon suppression in pA or dA. We do not understand the comment about conclusions being "iffy". If there is a specific conclusion that does not seem to be supported by the data, then we can address that.
The last sentence in conclusion seem exaggerated, and not documented from text just remove.
Answer: One of the main points of the paper is that in Fig. 5b, as we explain in the previous answer, there is no evidence for a significant centrality dependence of Upsilon suppression in dAu. The models predict the level of suppression we see in AuAu, but one of the key results of the paper is the suppression seen in dAu. The GPC strongly advocated to include a sentence in the conclusions of the paper that cautions readers that one must understand the dAu suppression before any strong claims can be made. The last sentence was rephrased slighly to better reflect this.
In abstract suggest the remove the sentence “Our measurements p+p…” and add to the text where relevant in the introduction. Not really relevant.
Answer: Done.
Individual comments:
Page 3 line 34: it is not at all obvious how the 2 statements (deconfinement and high temperature phase of lattice QCD where color is an active degree of freedom) in this sentence are scientifically connected.
Answer: The connection is that color Debye screening, which is the original effect proposed by Matsui and Satz,
requires a quark-gluon plasma where the color charges of the high-temperature plasma screen the heavy-quark potential that binds the bottomonium (or charmonium) states. This is one of the key ideas in QGP physics.
Page 3 line 59 for a non HI guru this argumentation is basically impossible to follow. Also ccbar and bbar pairs are produced the same way through gg fusion so why should there be a difference.
Answer: It seems that the question arises because the inquirer did not follow that the arguments presented are about final state effects, since the comment about ccbar and b-bbar pairs being produced through gluon fusion is about their production in the inital state, not about the possible ways that they can be broken up in the final state. The comment about
the interaction cross section of the Upsilon with hadrons applies to the final state, once the hadrons are produced. The size of the upsilon meson is much smaller than the J/psi meson, and the corresponding cross section of an Upsilon to interact with a final state pion (and then break up into a pair of B mesons) is much smaller than the cross section for a J/psi to be broken up by a pion into a pair of D mesons. We will add a comment that the effects discussed in this section are final state effects.
Page 3 line 46. There is no reference to statistical recombination.
Answer: Added a reference to Thews et al.
Page 3 line 78 there is no issues using the 2008 dAu data even so other analysis claim they cannot publish because of the non perfect tpc alignment?
Answer: We put a lot of work to take into account the effect of the TPC misalignment. This is discussed in the Technical Note in Section V.F, page 29. In particular, the 2009 pp data was originally processed with the same misalignment that the 2008 dAu data and the 2010 AuAu data both have. The 2009 pp data was subsequently reprocessed with fixed calibrations, and we studied the effect that the distortions had on our invariant mass reconstruction on an event-by-event basis, i.e. comparing the mass obtained in the production with the misalignment and then with the misalignment fixed on the exact same event. This allowed us to characterize the effect of the misalignment and to take it into account in embedding for the line-shapes and then in the extraction of the Upsilon yield via the fits using those line-shapes. This was studied extensively in the PWG in large part because we wanted to make sure that any issues regarding the misalignment would be dealt with appropriately. We cannot comment on other analyses, but if they can also study the differences in the two pp 2009 productions, that could help them to account for the TPC misalignment in their own analyses.
Fig 1 caption – comment to fit: the chi^2 of the pp fit must be horrible, any reason why the fit does not describe the data better.
Answer: The chi^2/NDF is 1.37 in the pp fit. This is not something we would characterize as "horrible". Given the statistics, there is not a strong reason to change the fit from using components we expect to have, namely the Upsilon states, the Drell-Yan and b-bbar continuum, and the combinatorial background.
2nd question: was the setup of STAR, especially the material budget, the same? If not, which I assume, how different are they?
Answer: The material budget was the same. The TPC misalignment in dAu, and AuAu increases the width compared to pp. The higher occupancy in AuAu also contributes to a broadening compared to pp. As noted above, we now explicitly state
in the paper that the material budget in all three datasets is the same.
page 5 line 6 (fig caption) ‘band’ -> box/square
Answer: The NLO calculations are shown as a band, and that is what is mentioned in the caption.
page 6 line 48: the effect at mid rapidity taking the systematic uncertainty into account is 2 sigma max. I think this is a number which needs to be stated.
Answer: We state the value of R_dAu with statistic and systematic uncertainties. We will also provide a table with all the R_AA and R_dAu values. The sentence we use in page 6 line 48 says that the suppresion is "indicative" of effects beyond shadowing, initial-state parton energy loss, or absorption by spectator nucleons.
Using "indicative" is usually warranted for effects that are of ~2 to 3 sigma significance, we certainly not claim a "discovery" (5sigma).
Itʼs a bit hard to follow the various R_AA and R_dAu quoted in the paper. A table listing the R_{AB} for the various combinations might be more useful than scattering the values through the text.
Answer: A table is now provided.
Abstract: I realize that in the abstract you donʼt want to get too technical, but omitting the rapidity range and whether it is 1S or 1S+2S+3S makes the numbers not useful.
Answer: We added a short clarification in the abstract as to the result quoted being 1S+2S+3S, and in the rapidity range |y|<1.
p. 4: Lines 55-57: the tracking and electron identification efficiencies would be the same across the three datasets, but in the previous paragraph there was discussion about differences in efficiency. Needs to be made clearer.
Answer: The text is now clear that the main thing that was chosen to be the same was the electron identification efficiency.
Fig1 The N_{--} is unclear the – runs together with the N
Answer: Fixed
Fig. 2: Vogt band does not print well.
Answer: Increased the line weights and changed the colors to darken them so that they print better.
fig 2a needs ""Phenix"" in dAu/1000 (open diamonds)
Answer: Fixed
Fig 2: “are shown as triangles There are no triangles,
Answer: Done. It should be diamonds.
c) Fig 3a The label A^0.96 is not the actual black curve which is (A/2)^{-0.04) according" "to the text in pg 7. Maybe writting the A^{alpha} scaling of cross section in the figure may help.
Answer: Fixed
in Fig 4 where the CB in all three panels is not a smooth curve nor a histogram; it has an unusual "mexican pyramid" shape
Answer: What's wrong with Mexican pyramids? :-) The plot will now be a smooth curve.
The A to the 0.96 does not match the text in line 5 page 7
Answer: As noted above, the Figure will now display A^0.96 scaling to make clear that the line shown is not A^0.9, but
rather derived from a cross section that scales as A^0.96.
Fig. 5: Are the shaded boxes systematics in the AB system? If so, needs to be in the caption.
Answer: Fixed
Fig. 6: "Our data is shown as a red vertical line with systematics shown by the pink box. There are two systematics (pp and AB). What was done with these? The pp is common to d+Au and Au+Au, so not clear, actually, what should be done.
Answer: The two systematics were added in quadrature for Fig. 6, we now state that in the paper. (Agree that it is debatable how to best combine them, but we should state what was done.)
.p. 6, lines 43-44: Do you mean y<~-1.2, rather than 1.2? Otherwise the argument doesnʼt make sense. And, where is the 1.2 from (citation)?
Answer: Correct, it should be -1.2. We do give the reference (23) for this statement in the previous sentence.
p. 8, line 11: consistent with an RAA(2S+3S) approximately equal to zero. Would be better to quantify this as an upper limit.
Answer: This section was reworded based on suggestions from another reader. The argument now starts with the hypothesis of an approximately zero yield of the 2S+3S, states what that would imply for the R_AA(1S) and R_AA(1S+2S+3S) values, and
then notes that this is consistent with our data.
p. 9, line 1: at how many sigma was the exclusion? At 4.2 sigma, as quoted later?
Answer: The exclusion the "no-suppression" scenario had a p-value of less than 1 in 10^7 (better than 5 sigma) for all R_AA cases in AuAu. The R_dAu had a different p-value of 1.8 * 10^-5 (~4.2 sigma).
Line 18: result rather than effect reads better.
Answer: Done.
How were systematics taken into account in the quoting of “sigma”?"
Answer: The only time we quote "sigma" are for the exclusion of the "no-suppression" scenarios. For R_AA, they would still
be excluded at better than ~5 sigma even including systematics. For the dAu case, if the p-value is calculated with the systematic uncertainty shift we get 1.5 x 10^-3, which is about 3sigma.
a) The style of the paper is too colloquial for my taste, but I'm told that journals have relaxed their style requirements.
Answer: This is a style issue, we are certainly willing to discuss this with the editors of the journal if need be.
d) Reference [10] explains that the Combinatorial background is obtained by fitting the same charge sign pair distribution and that appears to be the case in this paper except in Fig 4 where the CB in all three panels is not a smooth curve nor a histogram; it has an unusual ""mexican pyramid"" shape.
Answer: The plots will all have a smooth curve.
Page 7 top (line)9 From the figs its not obvious there is 4.2 deviation, more like 3, can you cross check.
Answer: See previous comments on the deviations and statistical significance.
Clearly the difference between y 0.5 and 1.0 make the conclusion a bit waffly.
Answer: For dAu, in both scenarios we are excluding the no-suppression scenario. Both datasets are supporting this conclusion. Furthermore, the comment we make in about a 4.2sigma exclusion of the no-suppression scenario comes
from the |y|<1 measurement, which is the weaker exclusion of the two. The |y|<0.5 only serves to make this conclusion stronger.
The notation and fonts for RAA and Upsilon(1S+2S+3s) not not consistent across paper.
Answer: plots are now consistent (For Anthony).
Page 8 line 48 “ assumed a flat prior..” This reference to statistics may or may not come across well to the general reader,
Possible expand on this.
Answer: We have followed other papers in the Physics Letters B which use these same statistical techniques, and this usage was accepted.
One minor comment:" "In Fig.6, “CMN effects” should be “CNM effects”
Answer: Fixed.
Page 4 line 28&57, the three datasets” clarify to indicate “between the datasets from the three collisions systems”"
Answer: Done.
"line 57" "‘be the same” Really, should it not be “approximately the same".
Answer: Done.
Responses to GPC, April 2014
Thomas:
1. General: with the new text (in red) there's no a wild mix
of Au in roman and italic in normal text and in super/sub-scripts. Since Au is a chemical symbol I would put it all in roman
consistently.
This sentence doesn't say a lot and as I already mentioned that
I do not think the feed-down pattern is any more complex
than that in the charmomium sector. I attached a schematic
diagram. Replace Y with Psi and chi_b with chi_c and h_b with h_c
and that's it.
Why not simply saying here that the amount of feed-down into
the Y(states) is not measured at RHIC energies and then give
numbers of the next closest energy (which is Tevatron I guess).
3. Fig 1,: I already mentioned that I suggest to turn this
into a table. The plot doesn't really provide any new insight.
4. Page 9, line 13.
"*" -> "\times" or just leave it out
5. Page 11, Line 18.
I wonder if one should add one sentence mentioning the Y suppression
in high multiplicity pp events seen by CMS. Fits in the context.
6. Page 11, line 50.
Delete "However".
7. Fig. 6. The font size of the legend is a bit on the small side.
There's enough room to make it a tic bigger.
8. Table II.
Can we really say that d-Au is 0-100%? That would be zero bias.
Wasn't there a min-bias mixed with the Y trigger. To my knowledge
we never quoted anything above 80/90%. What about simply saying
min. bias instead of 0-100%.
Lanny:
P3 L30 -- remove "complex" (it is an unnecessary adjective here)
P4 (new) Fig.1 and red text lines 50-51, 65-69: The efficiencies are
about the same for the 30-60, 10-30 and 0-60 at each rapidity bin.
This information probably should be in the text since HF reco. eff.
are useful to know by others in the business. I recommend putting
this information in the text in place of the above Figure 1 and lines, e.g.
"The $\Upsilon$ acceptance $\times$ efficiency for three centrality
bins (30-60%, 10-30%, 0-60%) are XX, XX and XX for respective
rapidity bins |y|<0.5, |y|<1.0 and 0.5<|y|<1.0. For the 0-10% centrality
the corresponding total efficiencies are reduced by approximately XX%."
Please check that the various uses of "total efficiency", "reconstruction
efficiency", "acceptance times efficiency" etc are used consistently and
avoid extra such terms if possible.
P5 Fig2b -- The legend "p+p x <Ncoll>" is misleading and may be what ref.2
is asking about. The grey band in 2b is not simply the red curve in 2a
multiplied by a constant (Ncoll). There are resolution effects as discussed
on P6. The caption should say, "The grey band shows the expected yield if
RDAu = 1 including resolution effects (see text)."
P5 L8 -- Are b-bbar pair backgrounds NPE from open HF meson
decays (B-mesons)? Just curious.
P5 Tabel I -- I assume momentum resolution effects are included in
the line shape entries. Ref.1 is concerned about p-resolution and in
addition to the response, this table caption should note that p-resol.
is included in the line shape errors if that is true.
P5 L17-28 -- I did not find any discussion in the paper about the
use of max likelihood fitting. This turned out to be a big deal and
will be discussed in the response. This parag. would be the place
to say, briefly how the fits were done.
P6 L6 -- "miscalibration" sounds scary. Can this issue be explained
in the text, and more so in the responses, so that neither referee nor
the readers are put-off by the statement and dismiss the paper's results?
P6 L26 -- I recommend against arguing with the referee over simple
wording changes that have equivalent meanings. Is there a subtlety
here that I don't recognize?
P6 Fig.3a -- The referee is asking that the legend "Upsilon -> e+e-"
say explicitly "Upsilon(1S+2S+3S) -> e+e-". But also change to l+l-.
She/he wants the states listed explicitly.
P8 Fig 5c caption - same issue as above with the grey band. The
last sentence in the caption should read: "The grey band ... number
of binary collisions including resolution effects (see text)."
P9 L8 -- Referring to Fig. 6c, the 10-30% RAA is consistent with unity
also. This sentence should say, "..consistent with unity in peripheral
to more-central Au+Au collisions..." BTW, "events" is jargon which we
all use, but I think it is better to say "collisions" here and throughout
the paper unless we are specifically discussing a triggered event in
DAQ.
Also, I changed event to collision where approriate in the text. Those changes are unhighlighted.
P10 L8 -- "With two possibilities.." implies that CNM and QGP are
the only possibilities for reducing yields. There is at least the
possibility of modified fragmentation of HF quarks in a
dense system. I recommend saying "Considering two possible
sources..." which more accurately reflects what was done; we
considered these two effects and not others.
P10 L37-39 -- Isn't the "QGP only" preferred in Fig. 8b? Why
mention the other as "consistent" and not also mention the
Thorsten: - p3, l31-l32: I don't like the formulation too much, maybe "...there exists a feed-down pattern in the bottomonium sector, and thus melting of the higher states affects also the measured yield of the lower states."
- fig 1 take a lot of space for basically not much information, maybe a table would be sufficient?
- p6, l6: TPC miscalibration sounds scary, maybe non-perfect TPC calibration?
- p11, l5: I'm not too happy with the A^alpha discussion: after all it is a just a fit to the data. Have you used for this statement the alpha value from our own measurement, e.g. fig 4 bottom or the integrated one from fig 4 top? The integrated one is significantly above the midrapidity one, also for E772
Responses to PLB Referees
Responses to Reviewers' comments:
We would like to thank the referees for the insightful and constructive comments. We discuss below our detailed replies to your questions and the corresponding explanation of changes to the manuscript. But before we go into the replies to the comments, we want to make the referees aware of changes to the results that were prompted via our studies of the systematic effects on the yield extraction. Since this paper deals with cross sections and with nuclear-modification factors, both of which involve obtaining the yields of the Upsilon states, this change affects all the results in the paper. We therefore wanted to discuss this change first. Please note that the magnitude of these effects do not change the overall message of the paper.
We wanted to alert the referees up-front about this important change before we proceeded into the detailed responses. This study was indirectly prompted by one of the questions from Referee 2 regarding systematic effects from yield extraction.
In the process of investigating the systematic difference between extracting the upsilon yield through simultaneous fitting compared to background subtraction as requested by the referee, we also studied the effects of chi^2 fits (specifically of Modified Least-Squares fits) compared to maximum-likelihood fits. We used chi^2 fits in our original submission. We were aware that extracting yields using a chi^2 fit introduces a bias (e.g see Glen Cowan's "Statistical Data Analysis", Sec. 7.4). The size of the bias is proportional to the value of the chi^2 of the fit. In the case of the Modified Least-squares fit, when fitting a histogram including the total yield as a fit parameter, the yield will on average be lower than the true yield by an amount equal to chi^2. The relative bias, i.e. the size of the bias divided by the extracted yield, goes to zero in the large yield limit, which is why for cases with large statistics this effect can be negligible. We had attempted to mitigate the effects of this bias by using the integral of the data, since this removes the bias completely in the signal-only case. But a bias remains in the case where there are both signal and background present. For our case, the yield extracted from the fit for the background is also biased toward lower values, and since we used this background estimate to subtract from the integral of the data in the extraction of the Upsilon yields, these biased the Upsilon yields towards higher values. Through simulation studies, where we include signal and 3 background components as in our analysis, we were able to quantify these effects. Given that in some cases the biases could be of order 10-20%, the fits needed to be redone in order to remove the bias. The solution is straightforward since the extraction of yields using a maximum-likelihood fit is unbiased. We have studied the difference of a modified-least squares fit and a maximum-likelihood fit and confirmed that the yield extraction in the latter method is essentially unbiased. We therefore have redone all the fits to extract the Upsilon yields via maximum-likelihood fits. The revised results are now quoted in the paper. The overall message of the paper is not affected by these changes.
We proceed next to answer the specific points raised by the reviewers.
Reviewer #1: This paper reports results on Y production in pp, dAu, and AuAu
collisions at top RHIC energy. It contains original and important
results and clearly qualifies for publication in PLB. However, there
are many aspects of the paper which need attention and/or improvement
prior to publication. They are detailed below:
1. the introduction is carelessly written. For example, the value
quoted for the pseudo-critical temperature near mu = 0 of 173 MeV is
taken from an old publication in 2003. Recent lattice results from the
Wuppertal-Budapest group (PoS LATTICE2013 (2013) 155) and the Hot QCD
Collaboration (Phys.Rev. D81 (2010) 054504) imply much lower T values
near 150 MeV and are far superior in terms of lattice sizes and spacing.
the results from the Hot QCD collaboration (Phys.Rev. D81 (2010) 054504) do not imply
much lower T values. In that paper, in section IV "Deconfinement and Chiral aspects of the QCD transition", when discussing the deconfinement transition temperature range the authors write:
"...we have seen that the energy density shows a rapid rise in the temperature interval T = 170–200. MeV. This is usually interpreted to be due to deconfinement, i.e., liberation of many new degrees of freedom".
Therefore, this does not indicate T values near 150 MeV. In addition, they also mention this range when discussing their results for the renormalized Polyakov loop, which
is the parameter most closely related to the deconfiment transition, being that it is the exact order parameter in the pure
gauge case:
"The renormalized Polyakov loop rises in the temperature interval T = 170–200 MeV where we also see the rapid increase of the energy density."
Therefore, the results from the Hot QCD collaboration do not imply T values near 150 MeV.
In addition, in reference 9 of the Wuppertal-Budapest group (JHEP 1009 (2010) 073 arXv:1005.3508), which is a paper comparing the various results for Tc between the Wuppertal-Budapest and HotQCD groups, again the results for the renormalized Polyakov loop (figure 7, right) indicate a broad transition region in the region T=160-200 MeV. They do have a table discussing values of Tc of about 147 MeV, but that is for the chiral transition, which is not the most relevant one for quarkonium suppression.
When they look at the trace anomaly (e-3p)/T^4, they see 154 MeV for the Tc value. They in addtion make the point that the transition is a broad crossover, which is something we also say in our paper. The fact that the transition is a broad crossover leads to differences in the estimates of the pseudo-critical temperatures depending on which observable is used. As an example, in the caption of Table 2, where they give the values of Tc for many observables, they mention that the Bielefeld-Brookhaven-Columbia-Riken Collaboration obtained Tc=192. They also note "It is more informative to look at the complete T dependence of observables, than
just at the definition-dependent characteristic poins of them." So given the above, we will modify the paper to give a range of temperatures, 150-190, and cite the papers from the
Wuppertal-Budapest and HotQCD collaborations.
probe..' does not get to any of the real issues, such as the complex
feeding pattern in the Y sector and the crucial question of whether Y
mesons reach equilibrium in the hot fireball as required to interpret
the apparent sequential melting pattern in terms of 'break-up'
temperatures.
The reviewer also mentions that there is a crucial question as to whether the Upsilon mesons reach equilibrium with the fireball as a requirement to interpret the sequential melting pattern. We respectfully disagree with the referee in this matter. The Upsilon is by definition not in equilibrium. The only requirement of course is that the medium is deconfined. In lattice QCD studies only the medium is thermalized; the potential between the heavy quarks is screened independent of whether the Upsilon is in equilibrium or not. We discussed this issue with lattice expert Peter Petreczky who confirmed our view.
furthermore, statistical recombination is not a 'complication' but a
direct measure of deconfinement. And the smallness of off-diagonal
terms in the recombination matrix does not imply absence of
recombination as the diagonal terms can be substantial.
Also the newest results on p-Pb collisions from the LHC are entirely
ignored, see, e.g., arXiv:1308.6726.
2. section on experimental methods
no detail is given concerning the crucial momentum resolution but it
is stated at the end of this section that cuts were adjusted for
different systems such that 'tracking and electron id would be the
same across the 3 data sets'. On the other hand, already in Fig. 1 we
see a strong dependence of the mass resolution on the system even for
low multiplicities as in pp and p-Pb. The effect must be much stronger
in Pb-Pb as is indeed visible in Fig. 4. Especially in view of the
importance of resolution for the separation of excited Y states this
referee has to be convinced that the systematic errors are under
control for momentum and pid measurements as a function of
multiplicity. Also how the systematic errors for the separation of Y'
and Y'' from Y are determined as a function of multiplicity needs to
be demonstrated explicitely.
3. Fig. 2b
even at y = 0 the difference between data and models is less than 2
sigma, taking uncertainties due to the pp reference into account and I
don't believe it makes sense to argue about effects beyond shadowing
and initial state parton energy loss in these data.
4. in Fig. 3 the size of the systematic errors should be indicated.
5. in Fig. 5 it is demonstrated that the observed suppression near
midrapidity is independent of system size (N_part). This could imply
that the higher Y states are already disappeared in dAu
collisions. This is mentioned briefly in the conclusion, but could be
stressed more.
6. At LHC energy, the anisotropic model of Strickland reproduces well
the centrality dependence of R_AA but not the rapidity dependence,
see, e.g. the final session of the recent hard probes meeting in South
Africa.
7. The presentation in Fig. 6 on the quantitative evaluation of
different model assumptions compared to data depends again strongly on
the size of the systematic errors, see the comment in section 2.
----------------------------------------------------------------------------------------------------------------------------------------------------------------------
Reviewer #2: I have read the manuscript PLB-D-13-01645 submitted to me for review.
The authors present a detail analysis on the suppression of Y production in d+Au and Au+Au collisions at sqrt(s_NN)=200 GeV using the STAR detector at RHIC. The article is very well written and deserves publication. However, I would like to suggest considering the following remarks to improve the understandability of the article:
1. Page 1, column 1, paragraph 1: The now accepted value for the critical temperature (chiral transition) is Tc = 150 - 160 MeV (depending on the exact definition of the observables). Reference 3 is outdated and should be replaced by more recent publications, i.e. arXiv:1005.3508 [hep-lat]
2. Page 2, column 2, paragraph 1: Please quantify the corrections due to the trigger bias w.r.t. the event centrality. Same for the tracking efficiency as a function of N_part. How does acceptance times efficiency for detecting Y as a function of rapidity and N_part looks like?
3. Page 3, column 1, paragraph 1: statement "some information will be lost" is too general! What are the systematic uncertainties arising from the different methods (same-event like-sign CB, fit to the CB) of the combinatorial background subtraction? What is the signal significance, in particular in the d+Au measurement? How does the signal looks like after CB and physical background subtraction? Systematic errors should be clearly mentioned.
We have studied these effects through various MC simulations in order to extract the biases. The likelihood fits have negligible biases. Furthermore, and to get back to the original question posed by the referee, in these simulations we obtained the variance of our results when doing simultaneous fits when compared to background-subtracted fits. We found a reduction in the variance when using simultaneous fits which was our original impetus. We also found no systematic effect in the expectation values of the yields obtained by the two different fitting methods. However, given the reduction in the variance of the extracted yield (i.e. in their error) in the simultaneous fit, we favor this method since it introduces a smaller uncertainty. We have redone all of our fits using the likelihood method and we corrected for any extraction biases seen through simulation.
Regarding signal significance, in all cases we see significant signals in d+Au. This can be infered by examining Fig. 3a and comparing the size of the statistical+fit error bars to the measured value of the cross section. This ratio is a good indicator of the statistical significance of our signal. For example, the dAu signal at |y|<0.5 has a significance of 11.7/3.2 = 3.7 sigma.
Since the referee also asked about systematic uncertainties, we have added a full table covering all measured sources of systematic uncertainty and added additional comments about the main sources in the text.
4. Fig 1: It would be easier for reader if the range of the y axis would be the same in Fig 1a and Fig 1b. Why is the explanation of the grey curves in the figure discussed in this complicated way, to my understanding the gray band simply shows the pp yield scaled by the number of binary collisions? If so, the label could read simply pp*<N_coll>.
5. Fig 1a: From where the line shape for pp comes from? It seems NOT to fit experimental data, i.e. all data points around 9 GeV/c^2 and below. Is it then evident to take as a cross section the integral of the data points?
6. Page 3, column 2, paragraph 1: How was the measured Y(1S+2S+3S) yield transformed to cross section?
7. Page 3, column 2, paragraph 3 (wording): "Hence, averaging between forward and reverse rapidities is not warranted as it is in
p+p." --> "Hence, averaging between forward and backward rapidities is not justified as it is in p+p." sounds more understandable.
8. Page 4: Try to arrange the placement of Figs such that there will not be a single line of the text within one column.
9. Fig 2: also here Fig a and Fig b could be presented with the same range on the Y axis, e.g. from -3 to 3.
10. Fig 2a : what is shown here is Y(1S+2S+3S), moreover PHENIX results on Y -> mu+mu- are shown in the same plot, that is why the figure label should be changed, i.e. Y->e+e- should be replaced by Y(1S+2S+3S)
11. Page 4, column 2, paragraph 2: <N_coll> (not <N_bin>) is commonly used as notation for the number of binary collisions. Sigma_AA is sigma^tot_AA (same for pp). It is important to indicate in the text the values for the total inelastic cross sections in pp, dA and AA and <N_coll> used to calculate R_AA.
12. Page 4, column 2, paragraph 3: In view of the discussion would it be helpful to also show R_AuAu vs. Rapidity?
13. Page 6, column 1, paragraph 1: Which function has been used to fit the CB - exponential? Again, what are the systematic uncertainty arising from the different methods (same-event like-sign CB, fit to the CB) of the combinatorial background subtraction. See also comment 4. concerning the label.
The function used to model the CB is now discussed in the text. Systematics from the fit methods are summarized in Tab. I.
14. Page 6, column 1, paragraph 2: The statement "Similar suppression is found by CMS in PbPb collisions (37)" should be moved to the paragraph 4 where the authors discuss Y(1S) suppression. Actually, for the same value of N_part=325 R_AuAu=0.54+-0.09 as for R_PbPb=0.45
Done.
15. Page 6, column 1, paragraph 4: How did the authors derived: R_AA(1S+2S+3S) = R_AA(1S)*0.69?
We had aimed to keep the text brief, since we were mindful of the space constraints, but given this question, we have added a few more sentences and references to clarify the R_AA(1S+2S+3S)=R_AA(1S)*0.7 statement, and also reduced our significant figures, quoting only a factor of 0.7.
16. Page 6, column 2, paragraph 2: What are the uncertainties on Drell-Yan and bbbar cross sections and how does it influence the significance of the signal.
Various normalizations are used in the fit. This is accounted for in the correllation
17. http://arxiv.org/pdf/1109.3891.pdf reports on the first measurement of the Y nuclear modification factor with STAR. It is probably worth to mention this work in the ms.
18. The R_AA of J/psi (p_T > 5 GeV), Y(1S) and an upper limit on the R_AA (2S+3S) was obtained in STAR. I would like to suggest to add a plot showing R_AA as a function of binding energy as a summary figure (also as a key figure to the long discussion on the extraction of the upper limit on R_AA(2S+3S)).
In summary, this ms. contains very interesting results and I propose publication in Phys. Letter B after the authors have taken care of the remarks above.
We thank the referee for her/his comments and remarks, which have helped improve the paper. We hope that we have addressed the issues raised, and adequately answered the questions posed, and look forward to the publication of the paper.
Upsilon pp, dAu, AuAu GPC E-mail Responses
This is a page to house long e-mail responses.
Using Pythia 8 to get b-bbar -> e+e-
We used Pythia 8 to produce b-bbar events. First we used the default Pythia 8. Macro for running with default parameters is here. We then used the STAR Heavy Flavor tune v1.1 for Pythia 8. The macro for running with the STAR HF tune is here.
The cross-sections reported by Pythia (numbers after 5M events) using the default parameters:
*------- PYTHIA Event and Cross Section Statistics -------------------------------------------------------------*
| |
| Subprocess Code | Number of events | sigma +- delta |
| | Tried Selected Accepted | (estimated) (mb) |
| | | |
|-----------------------------------------------------------------------------------------------------------------|
| | | |
| g g -> b bbar 123 | 19262606 4198826 4198275 | 6.971e-04 1.854e-07 |
| q qbar -> b bbar 124 | 3126270 801174 800981 | 1.331e-04 8.216e-08 |
| | | |
| sum | 22388876 5000000 4999256 | 8.303e-04 2.028e-07 |
| |
*------- End PYTHIA Event and Cross Section Statistics ----------------------------------------------------------*
So gg initiated subprocess has a 0.697 ub cross section and the q-qbar initiated subprocess has a 0.133 ub cross section. The sum for both subprocesses pp -> b bbar is 0.830 ub.
Using the STAR HF Tune, the cross section statistics reported by Pythia change to the following:
*------- PYTHIA Event and Cross Section Statistics -------------------------------------------------------------*
| |
| Subprocess Code | Number of events | sigma +- delta |
| | Tried Selected Accepted | (estimated) (mb) |
| | | |
|-----------------------------------------------------------------------------------------------------------------|
| | | |
| g g -> b bbar 123 | 31956918 4520459 4520459 | 9.247e-04 2.542e-07 |
| q qbar -> b bbar 124 | 2259563 479541 479541 | 9.817e-05 8.544e-08 |
| | | |
| sum | 34216481 5000000 5000000 | 1.023e-03 2.682e-07 |
| |
*------- End PYTHIA Event and Cross Section Statistics ----------------------------------------------------------*
The cross section increases to 1.023 ub with the STAR HF Tune v1.1. The main changes to the default parameters are the reduction of the bottom quark mass from 4.8 (default) to 4.3 GeV/c2, the change of PDF from CTEQ5L (default) to the LHAPDF set MRSTMCal.LHgrid, and the choice of renormalization and factorization scales.
The selection of e+e- in the final state is done by following the fragmentation of the b or bbar quark into a B meson or baryon, and then looking at its decay products to find an electron or positron. The pT distribution of the genrated b quarks is shown below.
Fig. 1: Generated b quarks.
.gif)
The <pT> of the b quarks is 3.3 GeV. These then fragment into B mesons and baryons. As an example, we plot here the B0 and B0-bar pT distribution, below.
Fig. 2:Pt distribution of B0 and B0-bar mesons.
.gif)
The <pT> of the B mesons is 3.055 GeV/c, one can estimate the peak of the Z distribution (most of the momentum of the b quark is carried by the meson, so it should be close to 1) as 3.055/3.331=0.92.
After the beauty hadrons are produced, they can decay producing electrons and positrons. We search for the e+e- daughters of the beauty hadrons, their pT distribution is shown below.
Fig. 3: pT distribution of the e+ e- daughters of the b quarks.
.gif)
When an event has both an electron and positron from the b-bbar pair this can generate a trigger. However, these are generated in all of phase space, and we mainly have acceptance at mid-rapidity. The full rapidity distribution of the e+e- pairs is shown below:
Fig. 4: Rapidity distribution of the e+e- pairs from b decay.
.gif)
The distribution is well approximated by a Gaussian with mean ~ 0 and width close to 1 (off by 4.3%).
We calculate the invariant mass. This is shown below:
Fig 6. Invariant mass spectrum of e-e+ pairs originating from b-bbar pairs.
.gif)
The red histogram is for all e+e- pairs generated by Pythia. The blue histogram is for pairs with |y_pair|<0.5, which is the region of interest. The distributions are fit to a function to parameterize the shape, shown in the black lines. This is inspired by using a QCD tree-level power-law distribution multiplied with a phase-space factor in the numerator. The fit parameters for the blue line are:
- b = 1.59 +/- 0.06
- c = 27.6 +/- 5.8
- m0 = 29.7 +/- 7.8
Using the STAR HF Tune, the parameters are:
- b = 1.45 +/- 0.05
- c = 64.2 +/- 26.1
- m0 = 49.7 +/- 18.0
With the default parameters, in mass region 8 < m < 11 GeV/c2 and for |y|<0.5 the Pythia prediction is for a cross section of 29.5 pb.
With the STAR HF Tune, in the same phase space region the Pythia prediciton is for a cross section of 46.9 pb.
One can calculate from the Pythia cross section, the STAR efficiency*acceptance and the integrated luminosity the expected yield in the region 8< m < 11 GeV/c2. This gives 12 expected counts for trigger 137603, assuming the trigger doesn't affect the invariant mass shape.
However, tince the trigger has a turn-on region, we need to take this into account. The turn on can be obtained by looking at the background counts in the real data. By modeling the background with an error function of the form (erf((m-m0)/sigma)+1)/2 and multiplying by an exponential, we obtain the parameters m0=8.07 +/- 0.74 GeV/c2 and sigma = 1.75 +/- 0.45 GeV/c2. The fit to obtain the error function is shown below (it is one of the figures in the paper):
Fig. 7 Unlike-sign and like-sign invariant mass distributions from data. The like-sign is fit with and exponential multiplied by an erf.
We then need to apply this function to parameterize the turn-on region of the trigger to the b-bbar e+e- invariant mass spectrum. We have one additional piece of information from the efficiency estimation: the overall acceptance * trigger efficiency * tracking efficiency and including additional PID cuts for the Upsilon(12) is 5.4%, we can use this to normalize the function after including the trigger turn-on so that at M=10 GeV/c2 it gives 5.4% of the yield before applying the trigger turn-on. This way we take care of the trigger turn-on shape and the overall normalization given by the acceptance, efficiency, etc. obtained from the upsilon embedding. This assumes that an e+e- pair with invariant mass identical to the upsilon will have identical efficiency and acceptance. Using this, we estimate the yield in the region 8<m<11 including the trigger turn-on and acceptance and efficiency to be 19 counts from b-bbar in the Upsilon mass region in the entire dataset.
For the STAR HF Tune, the cross section is larger and the expected counts are larger:
Code to run Pythia and produce b-bbar -> e+ e- events
// main00.cc
// Modified from the main01.cc
// which is a part of the PYTHIA event generator.
// Copyright (C) 2008 Torbjorn Sjostrand.
// PYTHIA is licenced under the GNU GPL version 2, see COPYING for details.
// Please respect the MCnet Guidelines, see GUIDELINES for details.
// This is a simple test program.
#include "Pythia.h"
#include "TROOT.h"
#include "TFile.h"
#include "TH1.h"
bool isBHadron(int id) {
// This snippet is meant to capture all B hadrons
// as given in the PDG.
if (id<0) id*=-1;
if (id<500) return false;
return (fmod(id/100,5.)==0.0 || id/1000==5);
}
using namespace Pythia8;
int main() {
// Initialize root
TROOT root("Manuel's ROOT Session","PYTHIA Histograms");
// Generator. Process selection. LHC initialization. Histogram.
Pythia pythia;
// Uncomment line below to turns on all HardQCD processses
// These are 111-116 and 121-124
//pythia.readString("HardQCD:all = on");
// Turn on only bbar production:
// g g -> b bbar (subprocess 123)
// q qbar -> b bbar (subprocess 124)
pythia.readString("HardQCD:gg2bbbar = on");
pythia.readString("HardQCD:qqbar2bbbar = on");
pythia.readString("PhaseSpace:pTHatMin = 20.");
// Random number Generator Should be Set Here if needed (before pythia.init())
// On seeds:
// seed = -1 : default (any number < 0 will revert to the default). seed = 19780503
// seed = 0 : calls Stdlib time(0) to provide a seed based on the unix time
// seed = 1 through 900 000 000: various numbers that can be used as seeds
//pythia.readString("Random.setSeed = on");// doesn't work needs fixing
//pythia.readString("Random.seed = 3000000");
pythia.init( 2212, 2212, 200.);
Hist mult("charged multiplicity", 100, -0.5, 799.5);
TH1D* multHist = new TH1D("multHist","Multiplicity",100,-0.5,99.5);
TH1D* bquarkPt = new TH1D("bquarkPt","bquarkPt",100,0,50);
TH1D* bbarquarkPt = new TH1D("bbarquarkPt","bbar quark Pt",100,0,50);
TH1D* B0mesonPt = new TH1D("BOmesonPt","B0mesonPt",100,0,50);
TH1D* B0barmesonPt = new TH1D("BObarmesonPt","B0bar meson Pt",100,0,50);
TH1D* electronFrombPt = new TH1D("electronFrombPt","electrons from b",100,0,30);
TH1D* positronFrombPt = new TH1D("positronFrombPt","positrons from b",100,0,30);
TH1D* epluseminusMinv = new TH1D("epluseminusMinv","e+ e- Inv. Mass",100,0,30);
// Begin event loop. Generate event. Skip if error. List first one.
for (int iEvent = 0; iEvent < 10000; ++iEvent) {
if (!pythia.next()) continue;
if (iEvent < 1) {pythia.info.list(); pythia.event.list();}
// Find number of all final charged particles and fill histogram.
// Find the b (id = 5) and bbar (id = -5), find their daughters,
// if daughters include electron (id = 11) and positron (id=-11), calculate their
// invariant mass
// Status flags:
// 21 incoming particles of hardest subprocess
// 23 outgoing particles of hardest subprocess
// 81-89 primary hadrons produced by hadronization process (B mesons, e.g.)
// 91-99 particles produced in decay process or by B-E effects (e.g. the electrons)
int nCharged = 0;
int indexBQuark(0), indexBbarQuark(0);
for (int i = 0; i < pythia.event.size(); ++i) {
if (pythia.event[i].isFinal() && pythia.event[i].isCharged()) {
++nCharged;
}
Particle& theParticle = pythia.event[i];
if (theParticle.id() == 5 ) {
indexBQuark = i;
//cout << "Mother 1, Mother 2 = " << theParticle.mother1() << ", " << theParticle.mother2() << endl;
}
if (theParticle.id() == -5) {
indexBbarQuark = i;
//cout << "Mother 1, Mother 2 = " << theParticle.mother1() << ", " << theParticle.mother2() << endl;
}
} // particle loop
cout << "Found b quark at index " << indexBQuark << endl;
cout << "Found bbar quark at index " << indexBbarQuark << endl;
bquarkPt->Fill(pythia.event[indexBQuark].pT());
bbarquarkPt->Fill(pythia.event[indexBbarQuark].pT());
mult.fill( nCharged );
multHist->Fill(nCharged);
//cout << "Event " << iEvent << ", Nch= " << nCharged << endl;
//Find hadronization products of b and bbar.
int bQuarkDaughter1 = pythia.event[indexBQuark].daughter1();
int bQuarkDaughter2 = pythia.event[indexBQuark].daughter2();
int bbarQuarkDaughter1 = pythia.event[indexBbarQuark].daughter1();
int bbarQuarkDaughter2 = pythia.event[indexBbarQuark].daughter2();
// Obtain the two hadrons from the fragmentation process
// Use the PDG id's for this. All B mesons id's are of the form xx5xx, and
// all B baryons are of the form 5xxx.
// So we obtain the id, (make it positive if needed) and then test
// to see if it is a meson with fmod(currId/100,5)==0.0
// to see if it is a baryon with currId/1000==5
int HadronFromBQuark(0), HadronFromBbarQuark(0);
if (bQuarkDaughter1<bQuarkDaughter2) {
cout << "Daughters of b Quark" << endl;
for (int j=bQuarkDaughter1; j<=bQuarkDaughter2; ++j) {
if (isBHadron(pythia.event[j].id())) {
cout << "Fragmentation: b -> " << pythia.event[j].name() << endl;
cout << " id " << pythia.event[j].id() << " at index " << j << endl;
HadronFromBQuark = j;
}
}
}
if (bbarQuarkDaughter1<bbarQuarkDaughter2) {
cout << "Daughters of bbar Quark" << endl;
for (int k=bbarQuarkDaughter1; k<=bbarQuarkDaughter2; ++k) {
if (isBHadron(pythia.event[k].id())) {
cout << "Fragmentation : bbar -> " << pythia.event[k].name() << endl;
cout << " id " << pythia.event[k].id() << " at index " << k << endl;
HadronFromBbarQuark = k;
}
}
}
// Search the daughters of the hadrons until electrons and positrons are found
// if there are any from a semileptonic decay of a beauty hadron
// Start with the b quark
int Daughter(HadronFromBQuark), electronIndex(0), positronIndex(0);
while (Daughter!=0) {
cout << "Checking " << pythia.event[Daughter].name() << " for e+/e- daughters" << endl;
if (pythia.event[Daughter].id()==-511) {
// This is a Bbar0, enter its pT
cout << "Filling Bbar0 pT" << endl;
B0barmesonPt->Fill(pythia.event[Daughter].pT());
}
if (pythia.event[Daughter].id()==511) {
// This is a B0, enter its pT
cout << "Filling Bbar0 pT" << endl;
B0mesonPt->Fill(pythia.event[Daughter].pT());
}
int nextDaughter1 = pythia.event[Daughter].daughter1();
int nextDaughter2 = pythia.event[Daughter].daughter2();
// search for electron or positron
for (int iDaughter = nextDaughter1; iDaughter<=nextDaughter2; ++iDaughter) {
if (pythia.event[iDaughter].id()==11) {
cout << "Found electron" << endl;
cout << pythia.event[iDaughter].name() << endl;
electronIndex=iDaughter;
electronFrombPt->Fill(pythia.event[electronIndex].pT());
break;
}
if (pythia.event[iDaughter].id()==-11) {
cout << "Found positron" << endl;
cout << pythia.event[iDaughter].name() << endl;
positronIndex=iDaughter;
positronFrombPt->Fill(pythia.event[positronIndex].pT());
break;
}
}// loop over daughters to check for e+e-
// If we get here, that means there were no electrons nor positrons.
// Set the Daughter index to zero now.
Daughter = 0;
// If any of the daughters is still a beauty-hadron, we can try again
// and reset the Daughter index, but only if one of the daughters contains a
// b quark.
for (int jDaughter = nextDaughter1; jDaughter<=nextDaughter2; ++jDaughter) {
if (isBHadron(pythia.event[jDaughter].id())) {
//One of the daughters is a beauty hadron.
Daughter = jDaughter;
}
}// loop over daughters to check for another b hadron
}// end of search for electrons in all the daughters of the b quark
// Now search among the daughters of the bbar quark
Daughter=HadronFromBbarQuark;
while (Daughter!=0) {
cout << "Checking " << pythia.event[Daughter].name() << " for e+/e- daughters" << endl;
if (pythia.event[Daughter].id()==-511) {
// This is a Bbar0, enter its pT
cout << "Filling Bbar0 pT" << endl;
B0barmesonPt->Fill(pythia.event[Daughter].pT());
}
if (pythia.event[Daughter].id()==511) {
// This is a B0, enter its pT
cout << "Filling B0 pT" << endl;
B0mesonPt->Fill(pythia.event[Daughter].pT());
}
int nextDaughter1 = pythia.event[Daughter].daughter1();
int nextDaughter2 = pythia.event[Daughter].daughter2();
// search for electron or positron
for (int iDaughter = nextDaughter1; iDaughter<=nextDaughter2; ++iDaughter) {
//cout << "daughter is a " << pythia.event[iDaughter].name() << endl;
if (pythia.event[iDaughter].id()==11) {
cout << "Found electron" << endl;
cout << pythia.event[iDaughter].name() << endl;
electronIndex=iDaughter;
electronFrombPt->Fill(pythia.event[electronIndex].pT());
break;
}
if (pythia.event[iDaughter].id()==-11) {
cout << "Found positron" << endl;
cout << pythia.event[iDaughter].name() << endl;
positronIndex=iDaughter;
positronFrombPt->Fill(pythia.event[positronIndex].pT());
break;
}
}// loop over daughters to check for e+e-
// If we get here, that means there were no electrons nor positrons.
// Set the Daughter index to zero now.
Daughter = 0;
// If any of the daughters is still a beauty-hadron, we can try again
// and reset the Daughter index, but only if one of the daughters contains a
// b quark.
for (int jDaughter = nextDaughter1; jDaughter<=nextDaughter2; ++jDaughter) {
if (isBHadron(pythia.event[jDaughter].id())) {
//One of the daughters is a beauty hadron.
Daughter = jDaughter;
}
}// loop over daughters to check for another b hadron
}//end of search for electron among daughters of bbar quark
if (electronIndex!=0 && positronIndex!=0) {
cout << "Found an e+e- pair from bbar" << endl;
cout << "Ele 4-mom = " << pythia.event[electronIndex].p() << endl;
cout << "Pos 4-mom = " << pythia.event[positronIndex].p() << endl;
Vec4 epluseminus(pythia.event[electronIndex].p()+pythia.event[positronIndex].p());
epluseminusMinv->Fill(epluseminus.mCalc());
}
else {
cout << "No e+e- pair in event" << endl;
}
// End of event loop. Statistics. Histogram. Done.
}// event loop
pythia.statistics();
//cout << mult << endl;
//Write Output ROOT hisotgram into ROOT file
TFile* outFile = new TFile("pythiaOutputHistos1M.root","RECREATE");
multHist->Write();
bquarkPt->Write();
bbarquarkPt->Write();
B0mesonPt->Write();
B0barmesonPt->Write();
electronFrombPt->Write();
positronFrombPt->Write();
epluseminusMinv->Write();
outFile->Close();
return 0;
}
Code to run with STAR HF Tune
// main00.cc
// Modified from the main01.cc
// which is a part of the PYTHIA event generator.
// Copyright (C) 2008 Torbjorn Sjostrand.
// PYTHIA is licenced under the GNU GPL version 2, see COPYING for details.
// Please respect the MCnet Guidelines, see GUIDELINES for details.
// This is a simple test program.
#include "Pythia.h"
#include "Basics.h"
#include "TROOT.h"
#include "TFile.h"
#include "TH1.h"
bool isBHadron(int id) {
// This snippet is meant to capture all B hadrons
// as given in the PDG.
if (id<0) id*=-1;
if (id<500) return false;
return (fmod(id/100,5.)==0.0 || id/1000==5);
}
using namespace Pythia8;
double myRapidity(Vec4& p) {
return 0.5*log(p.pPlus()/p.pMinus());
}
int main() {
// Initialize root
TROOT root("Manuel's ROOT Session","PYTHIA Histograms");
// Generator. Process selection. LHC initialization. Histogram.
Pythia pythia;
// Shorthand for some public members of pythia (also static ones).
//Event& event = pythia.event;
ParticleDataTable& pdt = pythia.particleData;
// The cmnd file below contains
// the Pythia Tune parameters
// the processes that are turned on
// and the PDFs used
// for the pythia run.
pythia.readFile("main00.cmnd");
UserHooks *oniumUserHook = new SuppressSmallPT();
pythia.setUserHooksPtr(oniumUserHook);
cout << "Mass of b quark " << ParticleDataTable::mass(5) << endl;
cout << "Mass of b bar " << ParticleDataTable::mass(-5) << endl;
// Extract settings to be used in the main program.
int nEvent = pythia.mode("Main:numberOfEvents");
int nList = pythia.mode("Main:numberToList");
int nShow = pythia.mode("Main:timesToShow");
int nAllowErr = pythia.mode("Main:timesAllowErrors");
bool showCS = pythia.flag("Main:showChangedSettings");
bool showSett = pythia.flag("Main:showAllSettings");
bool showStat = pythia.flag("Main:showAllStatistics");
bool showCPD = pythia.flag("Main:showChangedParticleData");
pythia.init();
if (showSett) pythia.settings.listAll();
if (showCS) pythia.settings.listChanged();
if (showCPD) pdt.listChanged();
Hist mult("charged multiplicity", 100, -0.5, 799.5);
TH1D* multHist = new TH1D("multHist","Multiplicity",100,-0.5,99.5);
TH1D* bquarkPt = new TH1D("bquarkPt","bquarkPt",100,0,50);
TH1D* bbarquarkPt = new TH1D("bbarquarkPt","bbar quark Pt",100,0,50);
TH1D* B0mesonPt = new TH1D("BOmesonPt","B0mesonPt",100,0,50);
TH1D* B0barmesonPt = new TH1D("BObarmesonPt","B0bar meson Pt",100,0,50);
TH1D* BplusmesonPt = new TH1D("BplusmesonPt","BplusmesonPt",100,0,50);
TH1D* BminusmesonPt = new TH1D("BminusmesonPt","Bminus meson Pt",100,0,50);
TH1D* BplusmesonPtCDFrap = new TH1D("BplusmesonPtCDFrap","BplusmesonPt |y|<1",100,0,50);
TH1D* BminusmesonPtCDFrap = new TH1D("BminusmesonPtCDFrap","Bminus meson Pt |y|<1",100,0,50);
TH1D* electronFrombPt = new TH1D("electronFrombPt","electrons from b",100,0,30);
TH1D* positronFrombPt = new TH1D("positronFrombPt","positrons from b",100,0,30);
TH1D* epluseminusMinv = new TH1D("epluseminusMinv","e+ e- Inv. Mass",300,0,30);
TH1D* epluseminusRapidity = new TH1D("epluseminusRapidity","e+ e- y",80,-4,4);
TH1D* epluseminusMinvMidRap = new TH1D("epluseminusMinvMidRap","e+ e- Inv. Mass |y|<0.5",300,0,30);
// Begin event loop. Generate event. Skip if error. List first one.
int nPace = max(1,nEvent/nShow);
int nErrors(0);
for (int iEvent = 0; iEvent < nEvent; ++iEvent) {
if (!pythia.next()) {
++nErrors;
if (nErrors>=nAllowErr) {
cout << "Reached error limit : " << nErrors << endl;
cout << "Bailing out! " << endl;
break;
}
continue;
}
if (iEvent%nPace == 0) cout << " Now begin event " << iEvent << endl;
if (iEvent < nList) {pythia.info.list(); pythia.event.list();}
// Find number of all final charged particles and fill histogram.
// Find the b (id = 5) and bbar (id = -5), find their daughters,
// if daughters include electron (id = 11) and positron (id=-11), calculate their
// invariant mass
// Status flags:
// 21 incoming particles of hardest subprocess
// 23 outgoing particles of hardest subprocess
// 81-89 primary hadrons produced by hadronization process (B mesons, e.g.)
// 91-99 particles produced in decay process or by B-E effects (e.g. the electrons)
int nCharged = 0;
int indexBQuark(0), indexBbarQuark(0);
for (int i = 0; i < pythia.event.size(); ++i) {
if (pythia.event[i].isFinal() && pythia.event[i].isCharged()) {
++nCharged;
}
Particle& theParticle = pythia.event[i];
if (theParticle.id() == 5 ) {
indexBQuark = i;
//cout << "Mother 1, Mother 2 = " << theParticle.mother1() << ", " << theParticle.mother2() << endl;
}
if (theParticle.id() == -5) {
indexBbarQuark = i;
//cout << "Mother 1, Mother 2 = " << theParticle.mother1() << ", " << theParticle.mother2() << endl;
}
} // particle loop
cout << "Found b quark at index " << indexBQuark << endl;
cout << "Found bbar quark at index " << indexBbarQuark << endl;
bquarkPt->Fill(pythia.event[indexBQuark].pT());
bbarquarkPt->Fill(pythia.event[indexBbarQuark].pT());
mult.fill( nCharged );
multHist->Fill(nCharged);
//cout << "Event " << iEvent << ", Nch= " << nCharged << endl;
//Find hadronization products of b and bbar.
int bQuarkDaughter1 = pythia.event[indexBQuark].daughter1();//first daughter index
int bQuarkDaughter2 = pythia.event[indexBQuark].daughter2();//last daughter index
int bbarQuarkDaughter1 = pythia.event[indexBbarQuark].daughter1();
int bbarQuarkDaughter2 = pythia.event[indexBbarQuark].daughter2();
// Obtain the two hadrons from the fragmentation process
// Use the PDG id's for this. All B mesons id's are of the form xx5xx, and
// all B baryons are of the form 5xxx.
// So we obtain the id, (make it positive if needed) and then test
// to see if it is a meson with fmod(currId/100,5)==0.0
// to see if it is a baryon with currId/1000==5
int HadronFromBQuark(0), HadronFromBbarQuark(0);
if (bQuarkDaughter1<bQuarkDaughter2) {
cout << "Daughters of b Quark" << endl;
for (int j=bQuarkDaughter1; j<=bQuarkDaughter2; ++j) {
if (isBHadron(pythia.event[j].id())) {
cout << "Fragmentation: b -> " << pythia.event[j].name() << endl;
cout << " id " << pythia.event[j].id() << " at index " << j << endl;
HadronFromBQuark = j;
}
}
}
if (bbarQuarkDaughter1<bbarQuarkDaughter2) {
cout << "Daughters of bbar Quark" << endl;
for (int k=bbarQuarkDaughter1; k<=bbarQuarkDaughter2; ++k) {
if (isBHadron(pythia.event[k].id())) {
cout << "Fragmentation : bbar -> " << pythia.event[k].name() << endl;
cout << " id " << pythia.event[k].id() << " at index " << k << endl;
HadronFromBbarQuark = k;
}
}
}
// Search the daughters of the hadrons until electrons and positrons are found
// if there are any from a semileptonic decay of a beauty hadron
// Start with the b quark, the b-bar quark loop comes after this
int Daughter(HadronFromBQuark), electronIndex(0), positronIndex(0);
while (Daughter!=0) {
cout << "Checking " << pythia.event[Daughter].name() << " for e+/e- daughters" << endl;
if (pythia.event[Daughter].id()==-511) {
// This is a Bbar0, enter its pT
cout << "Filling Bbar0 pT" << endl;
B0barmesonPt->Fill(pythia.event[Daughter].pT());
}
if (pythia.event[Daughter].id()==511) {
// This is a B0, enter its pT
cout << "Filling Bbar0 pT" << endl;
B0mesonPt->Fill(pythia.event[Daughter].pT());
}
Vec4 daughterVec4 = pythia.event[Daughter].p();
double daughterRap = myRapidity(daughterVec4);
if (pythia.event[Daughter].id()==-521) {
// This is a Bminus, enter its pT
cout << "Filling Bminus pT" << endl;
BminusmesonPt->Fill(pythia.event[Daughter].pT());
if (fabs(daughterRap)<1.0) {
BminusmesonPtCDFrap->Fill(pythia.event[Daughter].pT());
}
}
if (pythia.event[Daughter].id()==521) {
// This is a Bplus, enter its pT
cout << "Filling Bplus pT" << endl;
BplusmesonPt->Fill(pythia.event[Daughter].pT());
if (fabs(daughterRap)<1.0) {
BplusmesonPtCDFrap->Fill(pythia.event[Daughter].pT());
}
}
int nextDaughter1 = pythia.event[Daughter].daughter1();
int nextDaughter2 = pythia.event[Daughter].daughter2();
// search for electron or positron
for (int iDaughter = nextDaughter1; iDaughter<=nextDaughter2; ++iDaughter) {
if (pythia.event[iDaughter].id()==11) {
cout << "Found electron" << endl;
cout << pythia.event[iDaughter].name() << endl;
electronIndex=iDaughter;
electronFrombPt->Fill(pythia.event[electronIndex].pT());
break;
}
if (pythia.event[iDaughter].id()==-11) {
cout << "Found positron" << endl;
cout << pythia.event[iDaughter].name() << endl;
positronIndex=iDaughter;
positronFrombPt->Fill(pythia.event[positronIndex].pT());
break;
}
}// loop over daughters to check for e+e-
// If we get here, that means there were no electrons nor positrons.
// Set the Daughter index to zero now.
Daughter = 0;
// If any of the daughters is still a beauty-hadron, we can try again
// and reset the Daughter index, but only if one of the daughters contains a
// b quark.
for (int jDaughter = nextDaughter1; jDaughter<=nextDaughter2; ++jDaughter) {
if (isBHadron(pythia.event[jDaughter].id())) {
//One of the daughters is a beauty hadron.
Daughter = jDaughter;
}
}// loop over daughters to check for another b hadron
}// end of search for electrons in all the daughters of the b quark
// Now search among the daughters of the bbar quark
Daughter=HadronFromBbarQuark;
while (Daughter!=0) {
cout << "Checking " << pythia.event[Daughter].name() << " for e+/e- daughters" << endl;
if (pythia.event[Daughter].id()==-511) {
// This is a Bbar0, enter its pT
cout << "Filling Bbar0 pT" << endl;
B0barmesonPt->Fill(pythia.event[Daughter].pT());
}
if (pythia.event[Daughter].id()==511) {
// This is a B0, enter its pT
cout << "Filling B0 pT" << endl;
B0mesonPt->Fill(pythia.event[Daughter].pT());
}
Vec4 daughterVec4 = pythia.event[Daughter].p();
double daughterRap = myRapidity(daughterVec4);
if (pythia.event[Daughter].id()==-521) {
// This is a Bminus, enter its pT
cout << "Filling Bminus pT" << endl;
BminusmesonPt->Fill(pythia.event[Daughter].pT());
if (fabs(daughterRap)<1.0) {
BminusmesonPtCDFrap->Fill(pythia.event[Daughter].pT());
}
}
if (pythia.event[Daughter].id()==521) {
// This is a Bplus, enter its pT
cout << "Filling Bplus pT" << endl;
BplusmesonPt->Fill(pythia.event[Daughter].pT());
if (fabs(daughterRap)<1.0) {
BplusmesonPtCDFrap->Fill(pythia.event[Daughter].pT());
}
}
int nextDaughter1 = pythia.event[Daughter].daughter1();
int nextDaughter2 = pythia.event[Daughter].daughter2();
// search for electron or positron
for (int iDaughter = nextDaughter1; iDaughter<=nextDaughter2; ++iDaughter) {
//cout << "daughter is a " << pythia.event[iDaughter].name() << endl;
if (pythia.event[iDaughter].id()==11) {
cout << "Found electron" << endl;
cout << pythia.event[iDaughter].name() << endl;
electronIndex=iDaughter;
electronFrombPt->Fill(pythia.event[electronIndex].pT());
break;
}
if (pythia.event[iDaughter].id()==-11) {
cout << "Found positron" << endl;
cout << pythia.event[iDaughter].name() << endl;
positronIndex=iDaughter;
positronFrombPt->Fill(pythia.event[positronIndex].pT());
break;
}
}// loop over daughters to check for e+e-
// If we get here, that means there were no electrons nor positrons.
// Set the Daughter index to zero now.
Daughter = 0;
// If any of the daughters is still a beauty-hadron, we can try again
// and reset the Daughter index, but only if one of the daughters contains a
// b quark.
for (int jDaughter = nextDaughter1; jDaughter<=nextDaughter2; ++jDaughter) {
if (isBHadron(pythia.event[jDaughter].id())) {
//One of the daughters is a beauty hadron.
Daughter = jDaughter;
}
}// loop over daughters to check for another b hadron
}//end of search for electron among daughters of bbar quark
if (electronIndex!=0 && positronIndex!=0) {
cout << "Found an e+e- pair from bbar" << endl;
cout << "Ele 4-mom = " << pythia.event[electronIndex].p() << endl;
cout << "Pos 4-mom = " << pythia.event[positronIndex].p() << endl;
Vec4 epluseminus(pythia.event[electronIndex].p()+pythia.event[positronIndex].p());
epluseminusMinv->Fill(epluseminus.mCalc());
double epluseminusRap = 0.5*log((epluseminus.e()+epluseminus.pz())/(epluseminus.e()-epluseminus.pz()));
epluseminusRapidity->Fill(epluseminusRap);
if (fabs(epluseminusRap)<0.5) epluseminusMinvMidRap->Fill(epluseminus.mCalc());
}
else {
cout << "No e+e- pair in event" << endl;
}
// End of event loop. Statistics. Histogram. Done.
}// event loop
if (showStat) pythia.statistics();
//cout << mult << endl;
//Write Output ROOT hisotgram into ROOT file
TFile* outFile = new TFile("pythiaOutputHistosTest.root","RECREATE");
multHist->Write();
bquarkPt->Write();
bbarquarkPt->Write();
B0mesonPt->Write();
B0barmesonPt->Write();
BplusmesonPt->Write();
BminusmesonPt->Write();
BplusmesonPtCDFrap->Write();
BminusmesonPtCDFrap->Write();
electronFrombPt->Write();
positronFrombPt->Write();
epluseminusMinv->Write();
epluseminusRapidity->Write();
epluseminusMinvMidRap->Write();
outFile->Close();
return 0;
}
Varying the Continuum Contribution to the Dielectron Mass Spectrum
Initial Normalization
The normalization to the Drell-Yan and b-bbar cross sections are given by the calculation from Ramona in the Drell-Yan case and by Pythia in the b-bbar case. There is an uncertainty in the overall normalization of the contribution from these two sources to the dielectron continuum under the Upsilon peak. We can do a fit to obtain the Upsilon yield with the normalization fixed. This is shown below.
Fig. 1: Fit to the invariant mass spectrum. The data points are in blue. The Drell-Yan curve is the dot-dashed line and the b-bbar is the dashed line. The Red line is the sum of the Upsilon line shape (obtained from embedding for the 1S+2S+3S keeping their ratios according to the PDG values) plus the continuum contribution from DY+b-bbar. The red histogram is the integral of the red line, which is what is used to compare to the data in the fit (we fit using the "i" option to use the integral of the function in each bin).
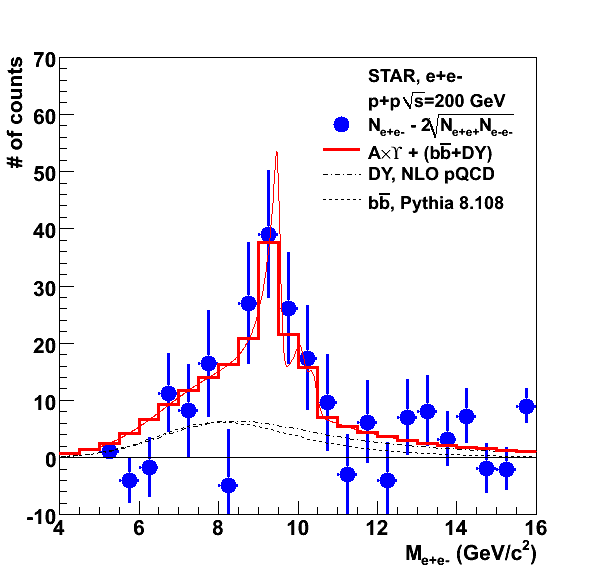
With the above fit, we obtain 64.3 counts after integrating the upsilon part (the yield of DY is 32.3 and the yield of b-bbar is 26.8, both are held fixed for the fit). This gives a cross section of 63.4/(1*0.054*9.6 pb-1) = 124 pb. The efficiency estimate of 5.4% for the overall efficiency is still being checked though, given the E/p shape not being gaussian due to the trigger bias near the L0 threshold, so this can still change.
It is also possible to let the yield of the continuum vary and study if the chisquare/dof of the fit improves. That way, we can not just assume a continuum yield, but actually measure it. Since the yields of the DY and the b-bbar are very similar and given our statistics we can't really discriminate one from the other, we are mainly sensitive to the sum. One way to study this is to keep their ratios fixed as in the plot above, but vary the overall yield of both of them This adds one extra parameter to the fit to account for the total sum of the continuum yield. We perform the fit in the region 5< m < 16 GeV/c2.
One issue is that the Crystal-Ball fit is a user defined function, and we use the integral of the function to fit, which seems to push ROOT to its limit in an interactive session with a macro interpreted on the fly. This is alleviated somewhat by cleaning up the code to do the one-parameter fit in a compiled macro. However, trying out the two-parameter fit directly seems to be too much for ROOT even in compiled mode and the code runs out of memory and seg-faults. A (rather inelegant) way around this is to scale the continuum yield by hand, compile the macro each time and do the one-parameter fit. For each of those fits, one can obtain the chisquare/deg. of freedom. This is shown in the plot below:
Fig. 2. Chisquare per degree of freedom as a function of the continuum yield (Drell-Yan + b-bbar).
We find a clear minimum, indicating that our data do have some sensitivity to the continuum yield. The Rightmost point with 59.1 counts is the yield obtained directly from Pythia 8.108 and from Ramona's calculation. Our data indicate that the yield is likely smaller by about a factor of 2, we obtain at the minimum a yield of 26.6 counts. Since the yield of Upsilons is obtained from the same fit, our fitted Upsilon yield will increase with decreasing counts from the continuum. This is shown below.
Fig. 3: Fitted yield of Upsilons for a given continuum yield. The minimum found above is illustrated by the vertical line.
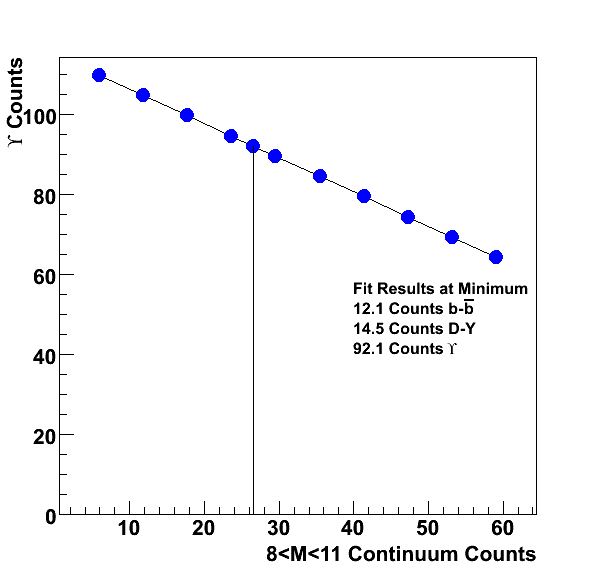
The corresponding plot with the fit at the minimum is shown below.
Fig. 4: Dielectron data with the curves for the DY and b-bbar at the yield which minimizes the chi-square. In other words, the result of a (poor man's) two-parameter fit to find both the Upsilon yield and the Continuum yield.
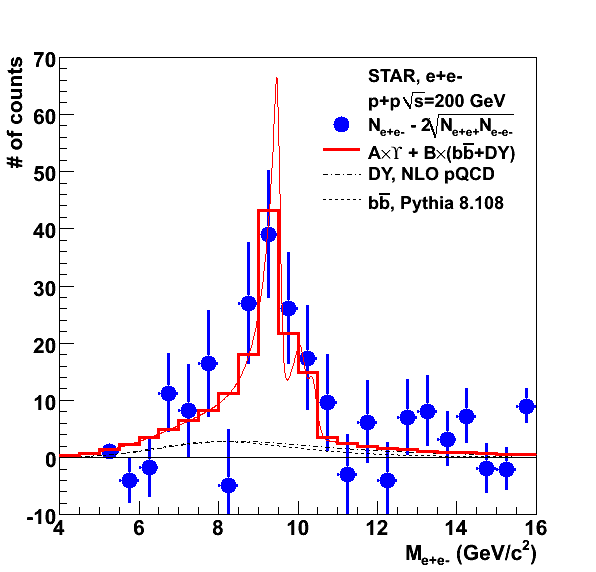
The results of this fit give 14.5 counts for DY and 12.1 counts for b-bbar, i.e a factor 0.45 lower than the 32.3 counts for DY and the 26.8 counts for b-bbar is 26.8 obtained before. Ramona's calculation for dsigma/dm |y|<1 gave 5.25 nb and the Pythia cross section b-bbar cross section times the BR into e+e- gives 6.5 nb, so our data indicate that we can decrease these by a factor 0.45 (or decrease one by essentially 100% and leave the other one unchanged). The Upsilon yield in this case increases to 92.1 counts, which gives a cross section of 92.1/(1*0.054*9.6) = 178 pb. So this has a large effect on the yield (92.1-64.338)/92.1 = 0.3, i.e. a 30% change in the yield (and hence in the cross section). Note also that 178 pb is quite larger than our first estimate for the cross section. This highlights the importance of getting the efficiency estimates right.