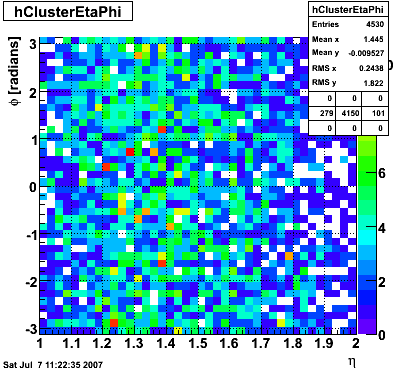
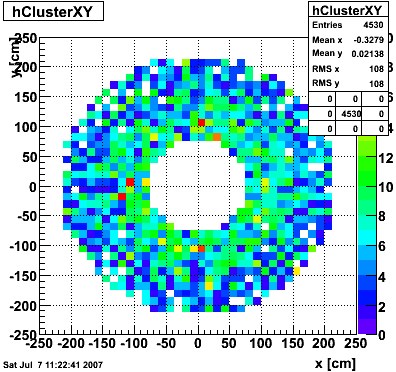
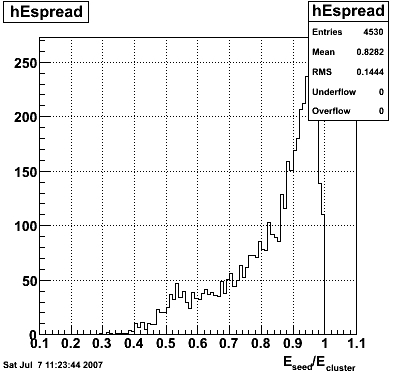
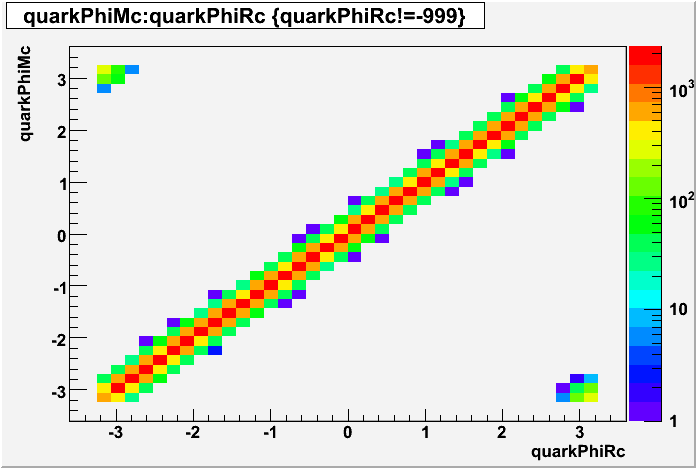
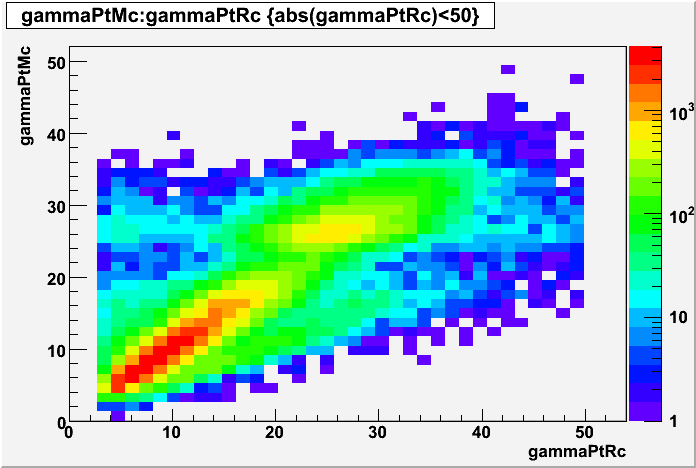
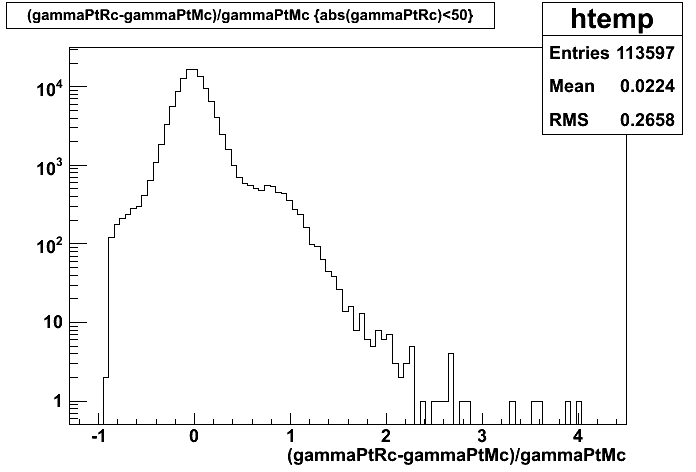
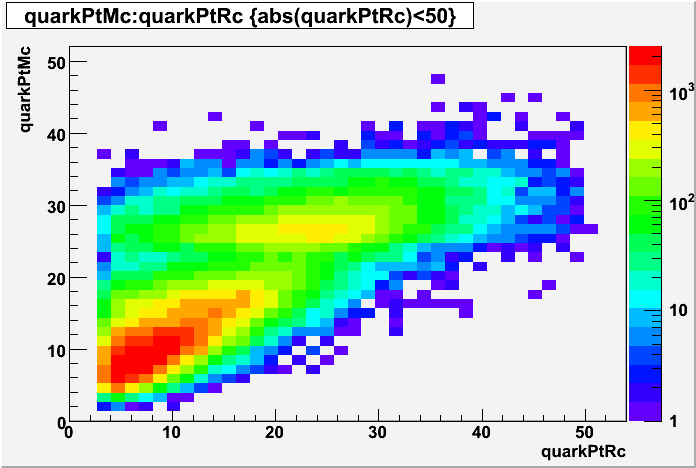
EEMC Direct Photon Studies (Pibero Djawotho, 2006-2008)
Everything as a single pdf file (341 pages, 8.2Mb)
2006.07.31 First Look at SMD gamma/pi0 Discrimination
Pibero Djawotho
Indiana University
July 31, 2006
Simulation
Simulation were done by Jason for the SVT review.
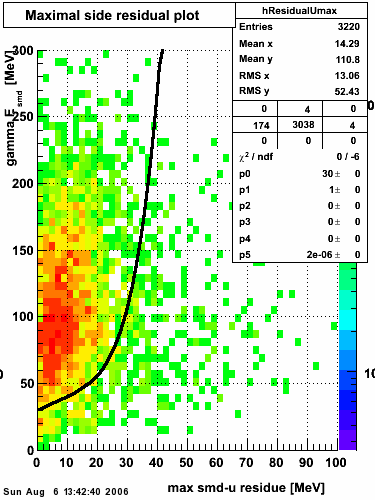
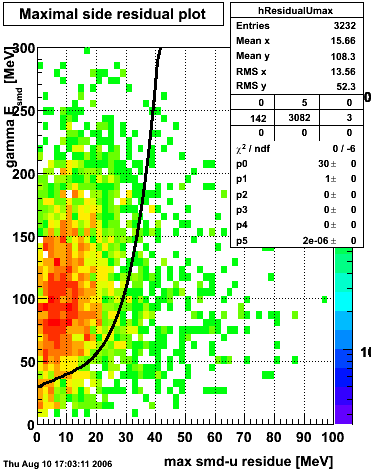
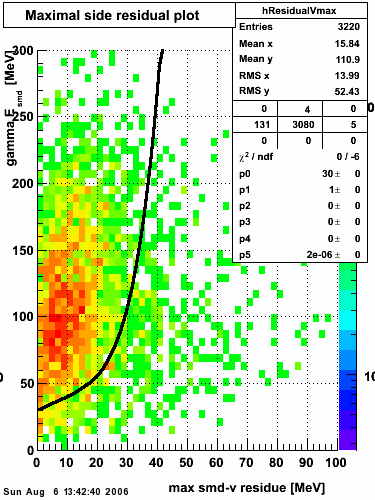
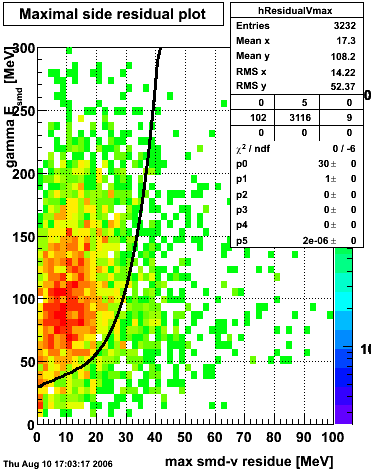
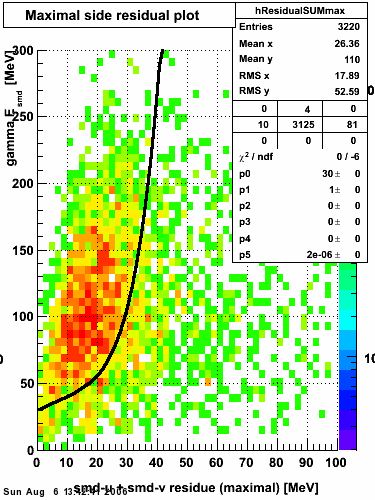
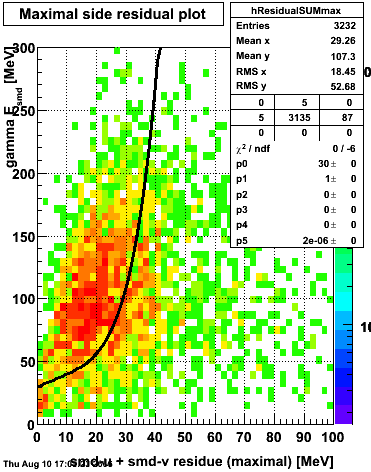
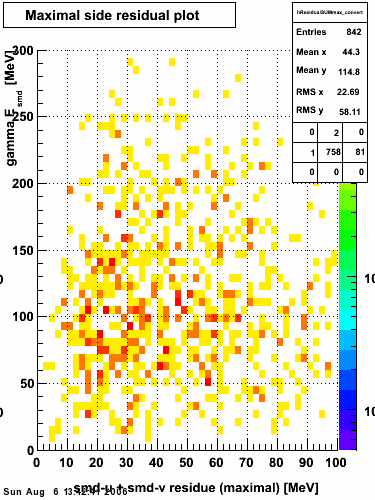
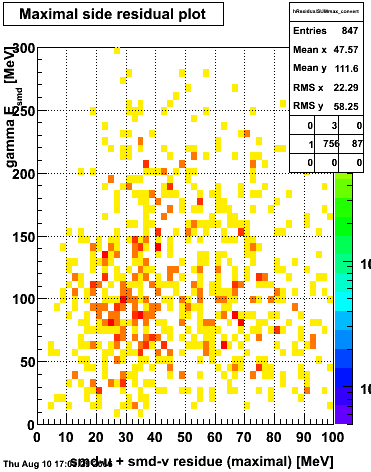
Maximal side residual
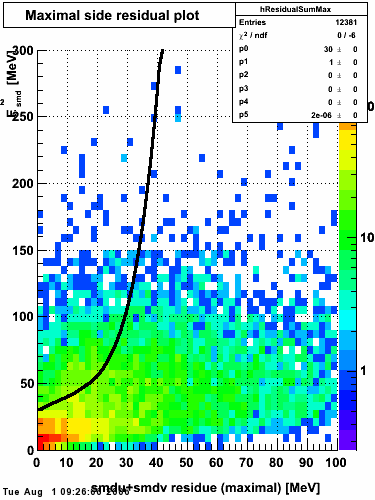 |
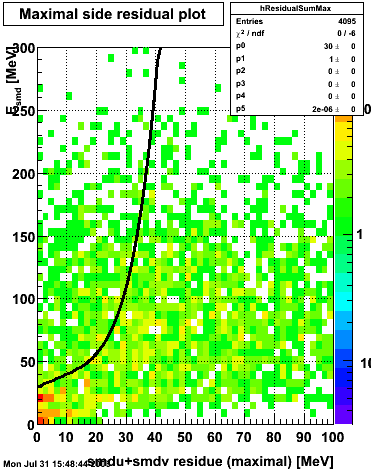 |
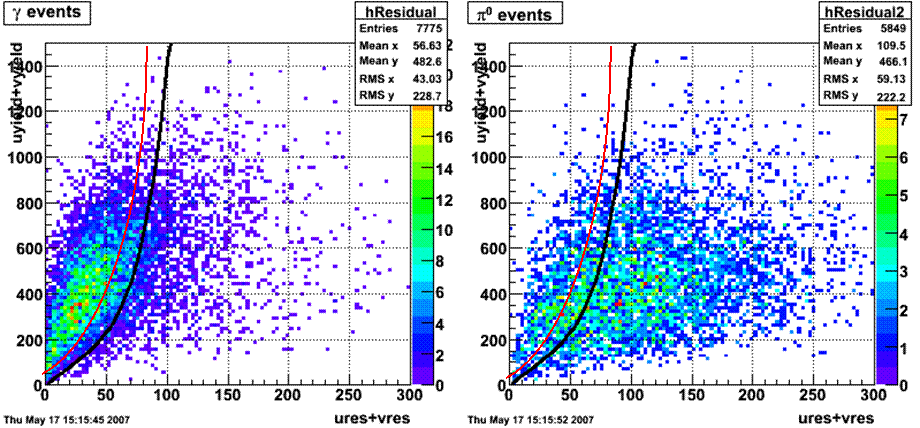
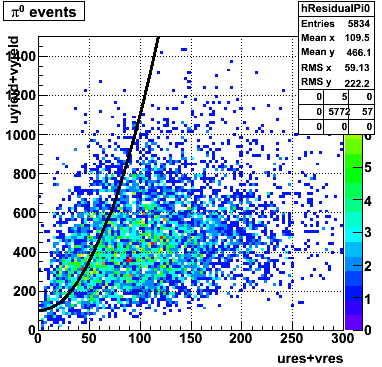
| Figure 1: Fitted peak integral vs. fit residual sum (U+V) from st_jpsi input stream (J/psi trigger only). | Figure 2: Fitted peak integral vs. fit residual sum (U+V) from st_physics input stream (all triggers except express stream triggers). |
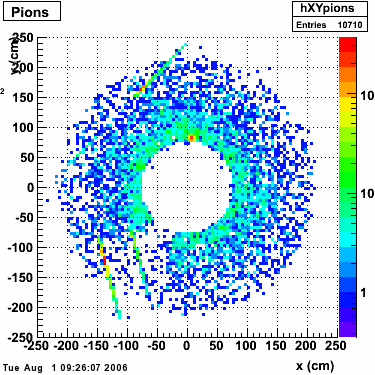
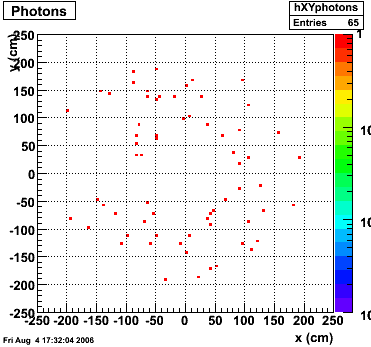
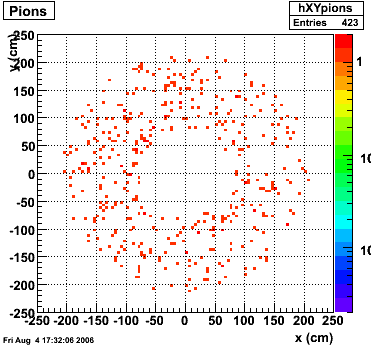
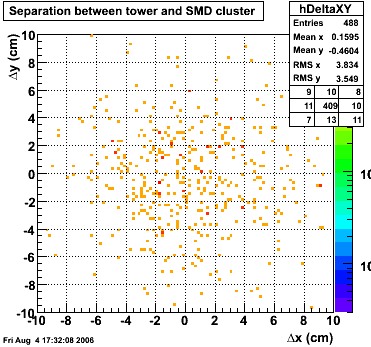
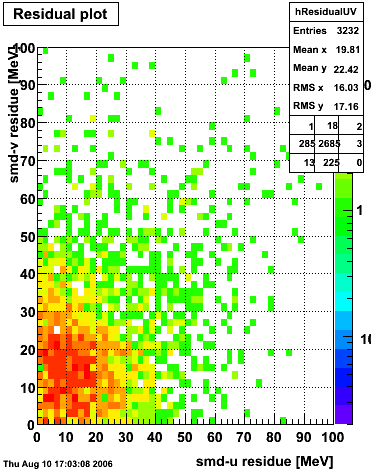
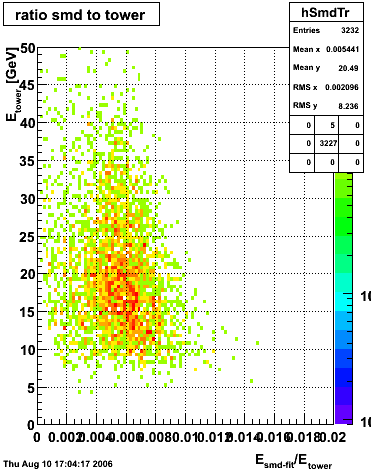
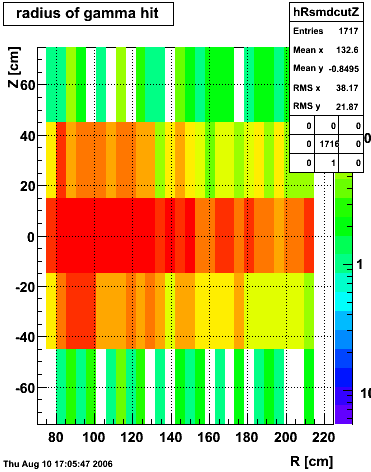
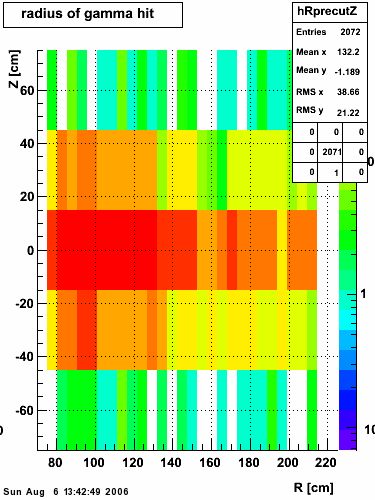
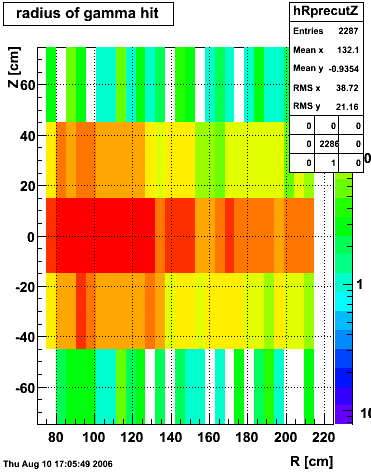
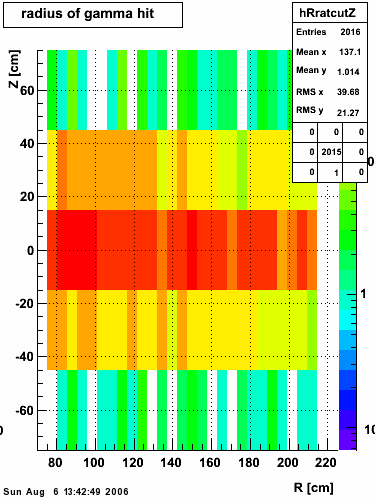
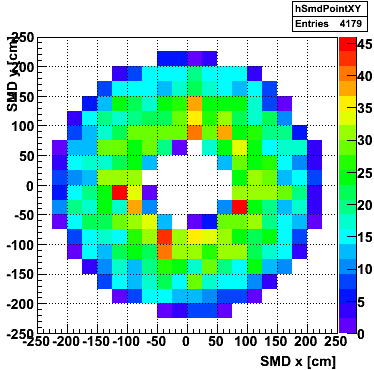
xy distribution of SMD hits
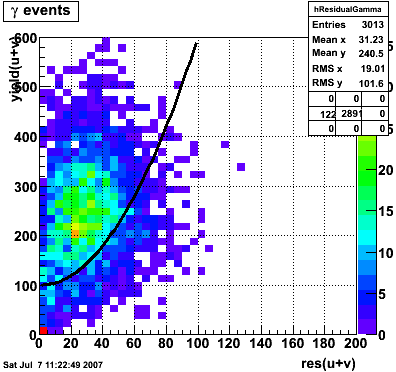
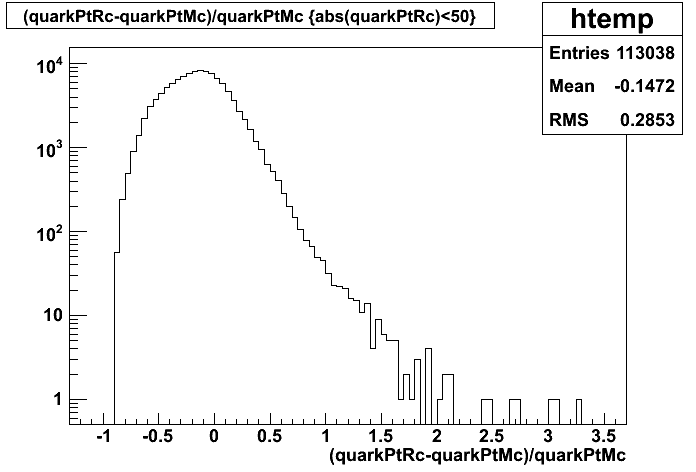
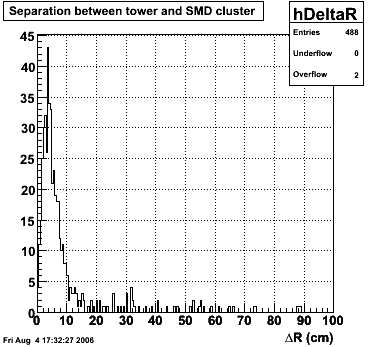
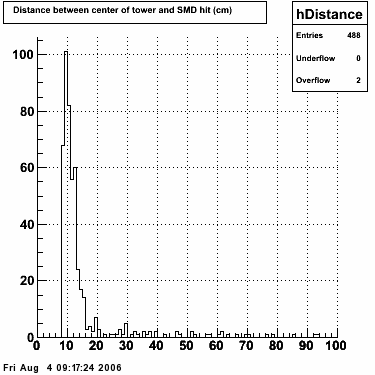
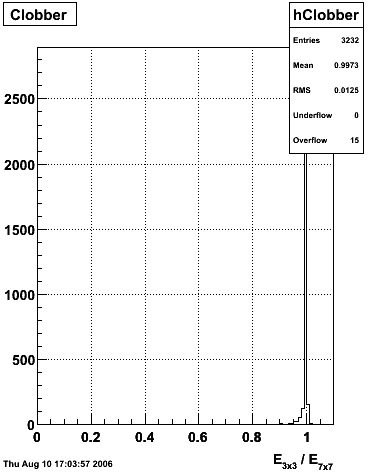
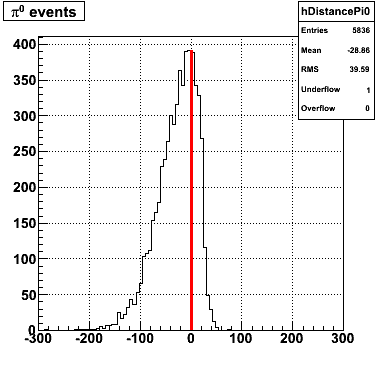
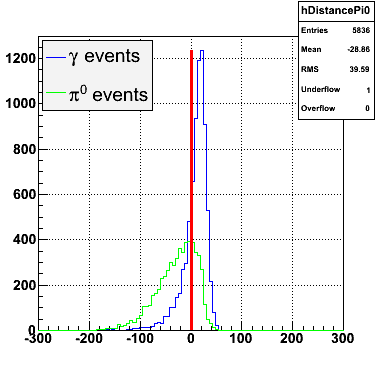
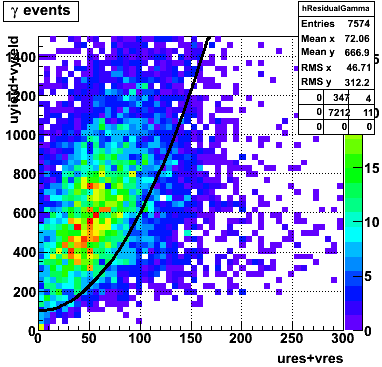
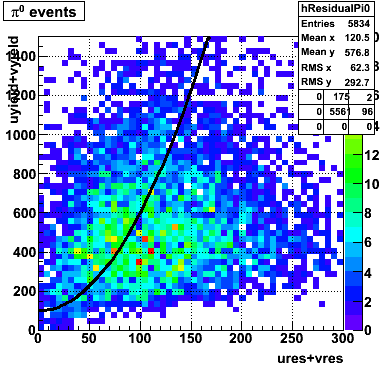
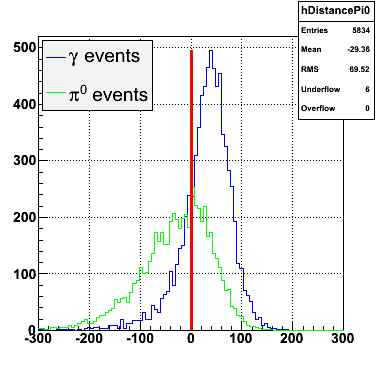
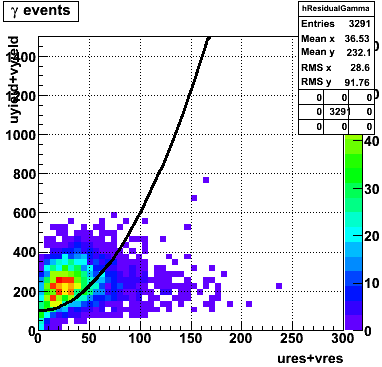
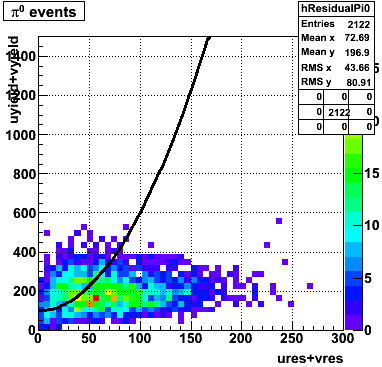
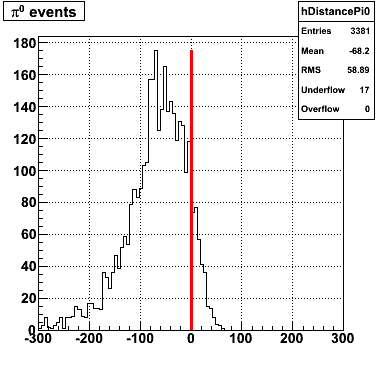
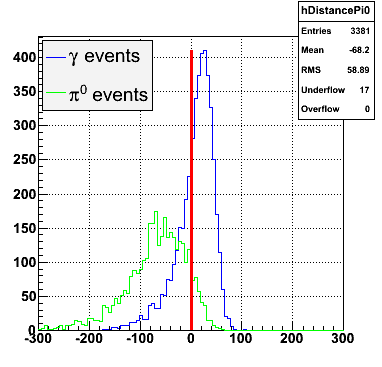
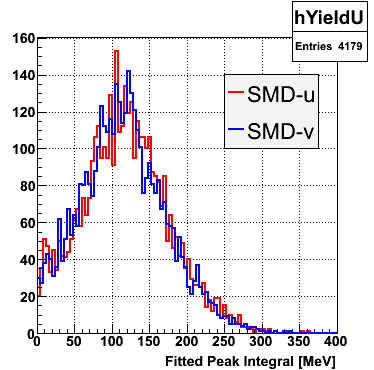
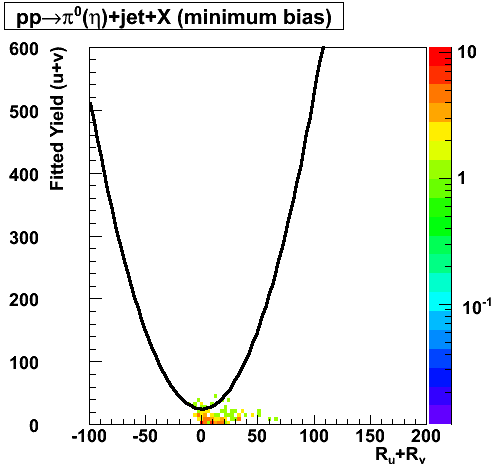
The separation between photons and pions was achieved by using Les cut in the above figures where photons reside above the curve and pions below. The data set used is the st_jpsi express stream.
 |
 |
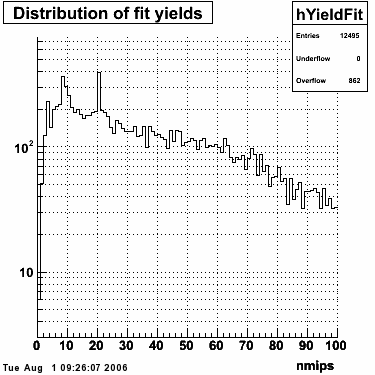
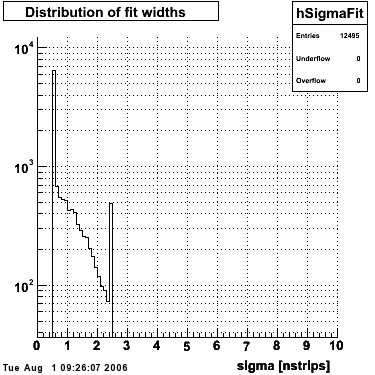
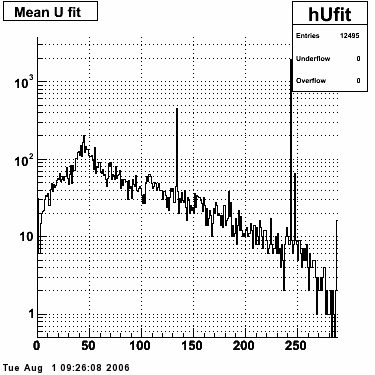
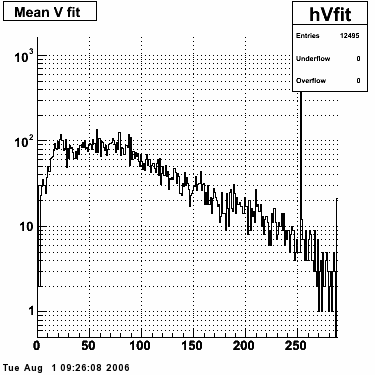
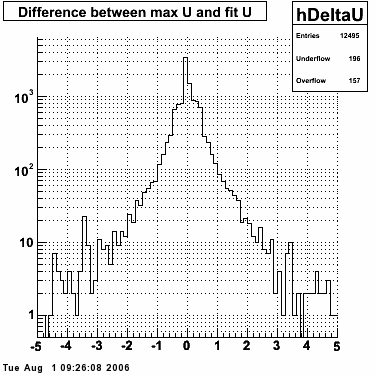
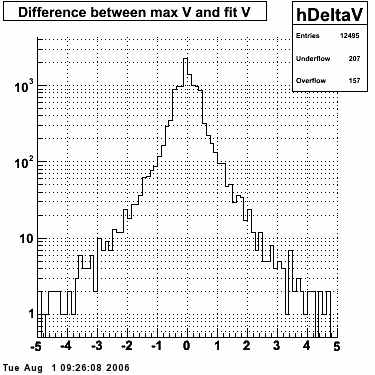
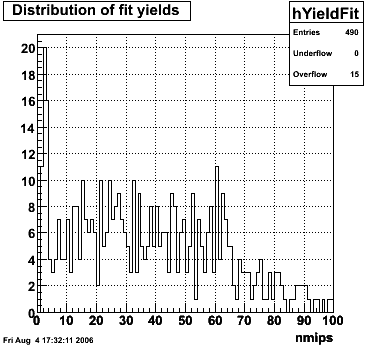
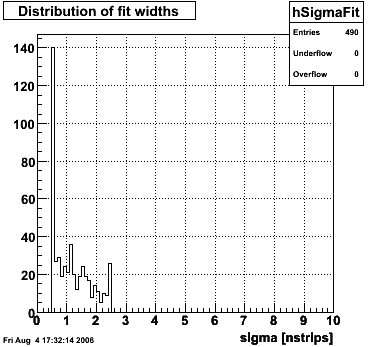
Single peak characteristics
 |
 |
 |
 |
 |
 |
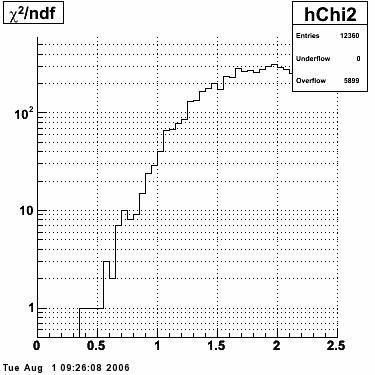 |
Fit function
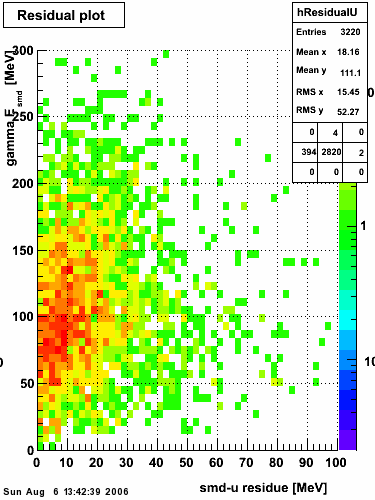
The transverse profile of an electromagnetic shower in the SMD can be parametrized by the equation below in each SMD plane:
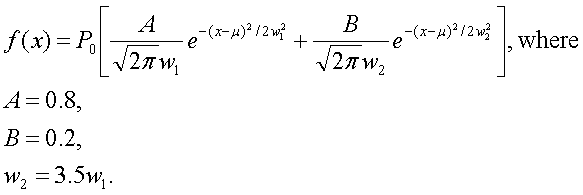
f(x) is the energy in MeV as a function of SMD strip x. The algorithm performs a simultaneous fit in both the U and V plane. The maximal residual (data - fit) is then calculated. A single photon in the SMD should be well descibed by the equation above and therefore will have a smaller maximal residual. A neutral pion, which decays into two photons, should exhibit a larger maximal residual. Typically, the response would be a double peak, possibly a larger peak and a smaller peak corresponding to a softer photon.
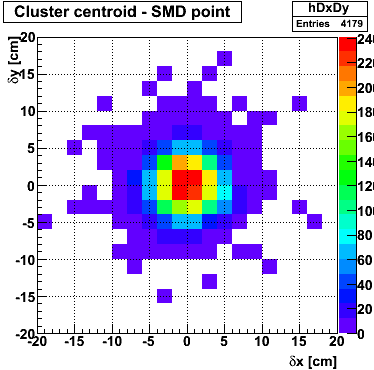
Single event SMD response
This directory contains images of single event SMD responses in both U and V plane. The file name convention is SMD_RUN_EVENT.png. The fit function for a single peak is the one described in the section above with 5 parameters:
- p0 = yield (P0), area under the peak in MeV
- p1 = mean (μ), center of peak in strips
- p2 = sigma of the first Gaussian (w1)
- p3 = fraction of the amplitude of the second Gaussian with respect to the first one (B), fixed to 0.2
- p4 = ratio of the width of the second Gaussian to the width of the first one (w2/w1), fixed to 3.5
Code
Documents
- Proposal to Contstruct an Endcap Calorimeter for Spin Physics at STAR
- Appendix Simulation Studies of Direct Photon Production at STAR
- An Endcap Calorimeter for STAR Conceptual Design Report
- The STAR Endcap Electromagnetic Calorimeter (EEMC NIM)
- An Endcap Calorimeter for STAR Technical Design Update #1
- Jan's gamma/pi0 algorithm
- Endcap Calorimeter Proposal (HTML @ IUCF)
- STAR Note 401: An Endcap Electromagnetic Calorimeter for STAR--Conceptual Design Report
- Spin Effects at Suppercollider Energies
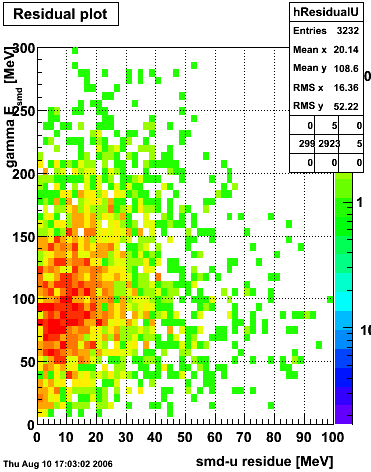
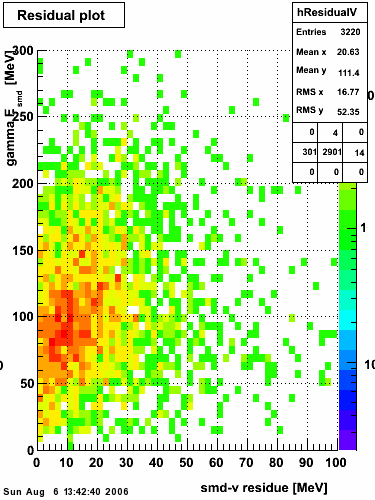
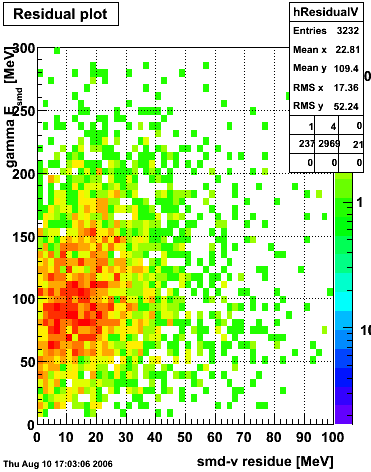
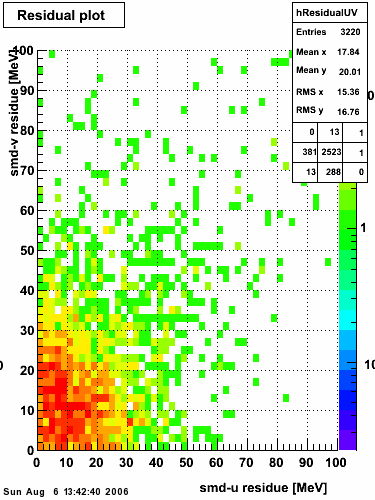
2006.08.04 Second Look at SMD gamma/pi0 Discrimination
Second Look at SMD gamma/pi0 Discrimination
Pibero Djawotho
Indiana University
August 4, 2006
Dataset
The dataset used in this analysis is the 2005 p+p collision at √s=200 GeV with the endcap calorimeter high-tower-1 (eemc-ht1-mb = 96251) and high-tower-2 (eemc-ht2-mb = 96261) triggers.
The file catalog query used to locate the relevant files is:
get_file_list.pl -keys 'path,filename' -delim / -cond 'production=P05if, trgsetupname=ppProduction,filetype=daq_reco_MuDst,filename~st_physics, tpc=1,eemc=1,sanity=1' -delim 0
Results
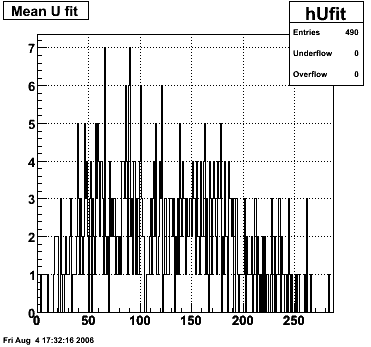
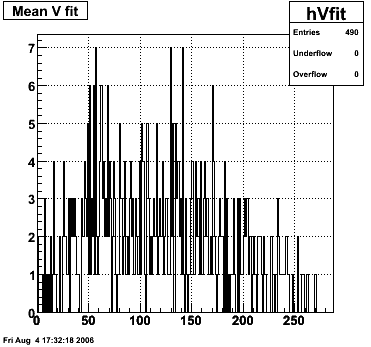
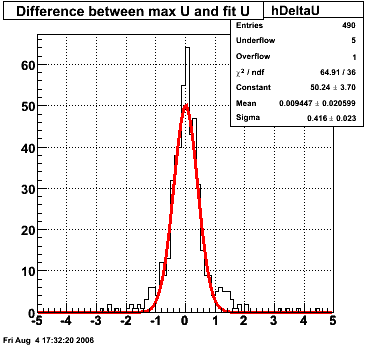
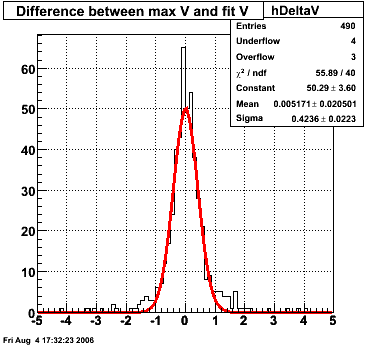
SMD U and V Fits
Code
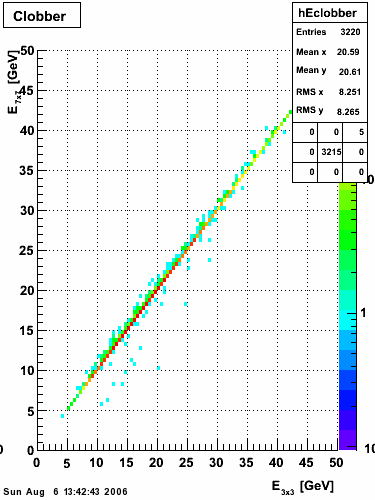
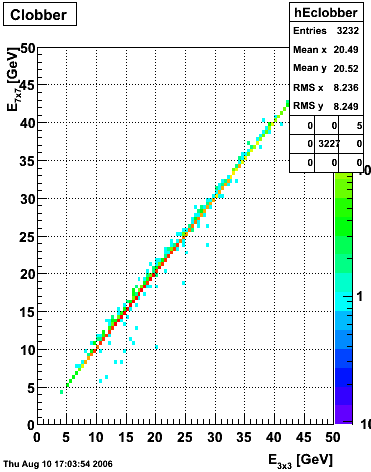
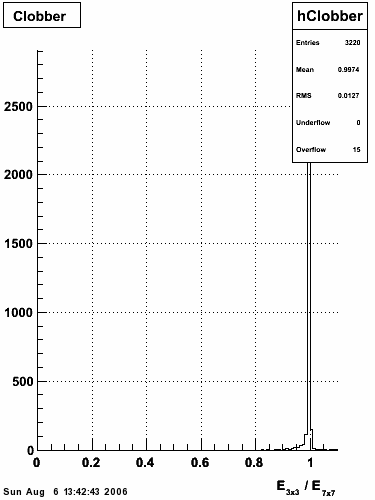
2006.08.06 Comparison between EEMC fast and slow simulator
Comparison between EEMC fast and slow simulator
Pibero Djawotho
Indiana University
August 6, 2006
A detailed description of the EEMC slow simulator is presented at the STAR EEMC Web site.
The following settings were used in running the slow simulator:
//--
//-- Initialize slow simulator
//--
StEEmcSlowMaker *slowSim = new StEEmcSlowMaker("slowSim");
slowSim->setDropBad(1); // 0=no action, 1=drop chn marked bad in db
slowSim->setAddPed(1); // 0=no action, 1=ped offset from db
slowSim->setSmearPed(1); // 0=no action, 1=gaussian ped, width from db
slowSim->setOverwrite(1); // 0=no action, 1=overwrite muDst values
slowSim->setSource("StEvent");
slowSim->setSinglePeResolution(0.1);
slowSim->setNpePerMipSmd(2.0);
slowSim->setNpePerMipPre(3.9);
slowSim->setMipElossSmd(1.00/1000);
slowSim->setMipElossPre(1.33/1000);
EEMC Fast Simulator |
EEMC Slow Simulator |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
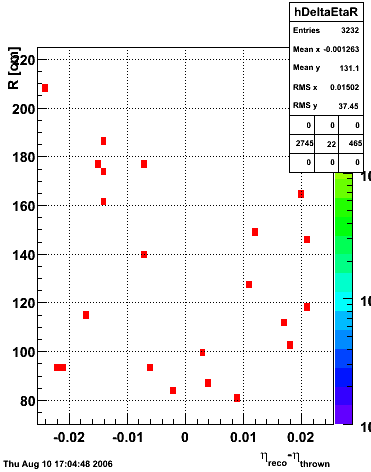 |
 |
 |
 |
 |
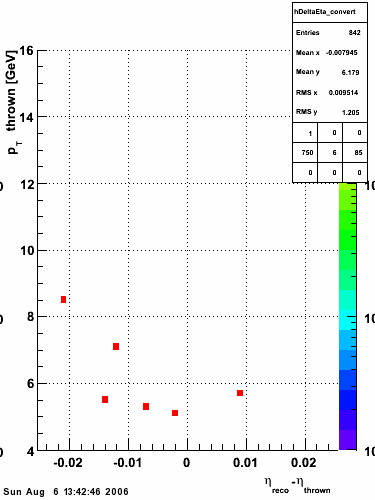 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
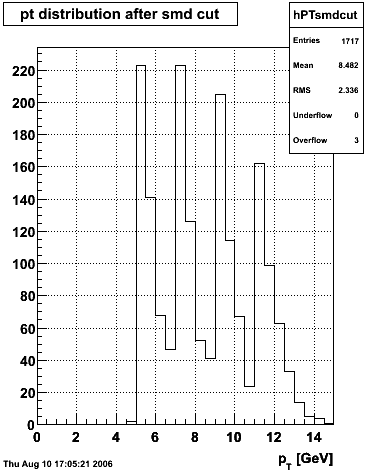 |
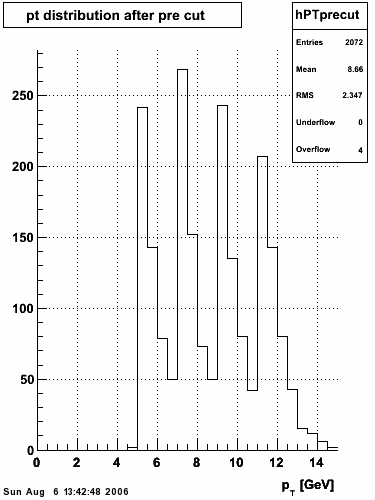 |
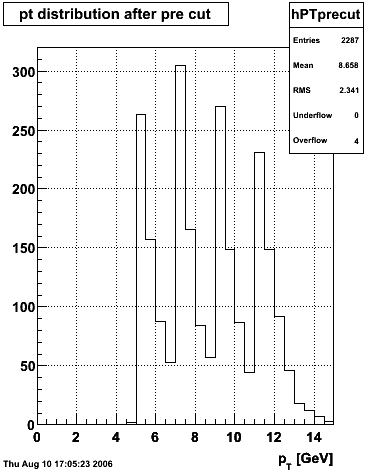 |
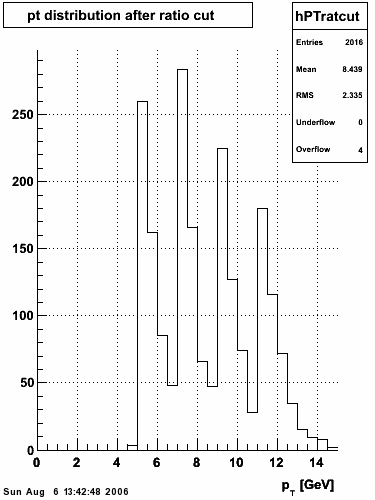 |
 |
 |
 |
 |
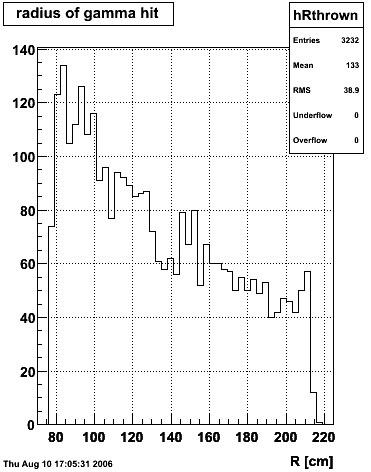 |
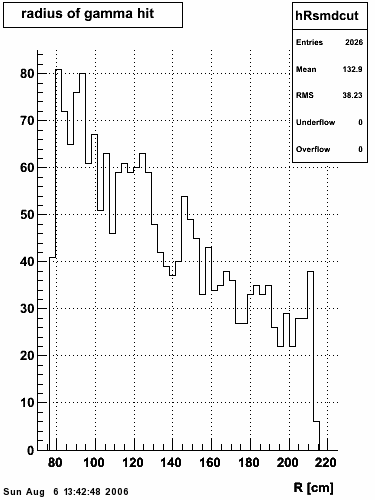 |
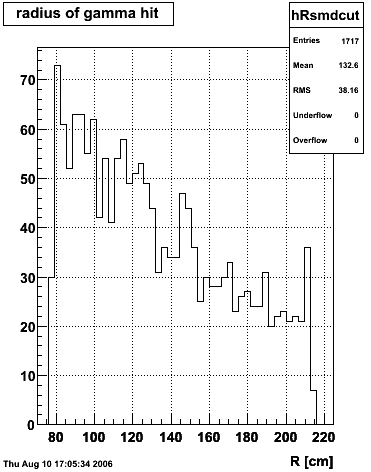 |
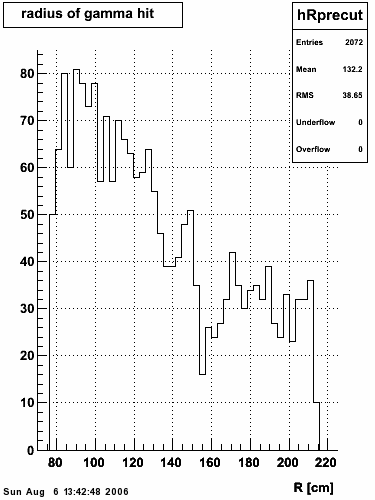 |
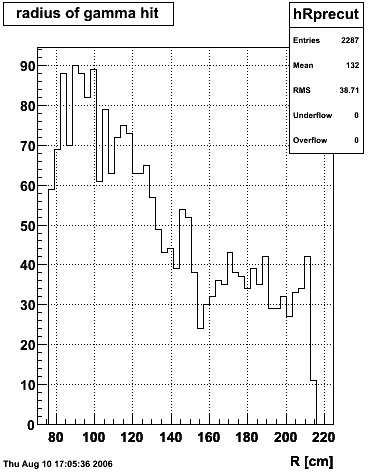 |
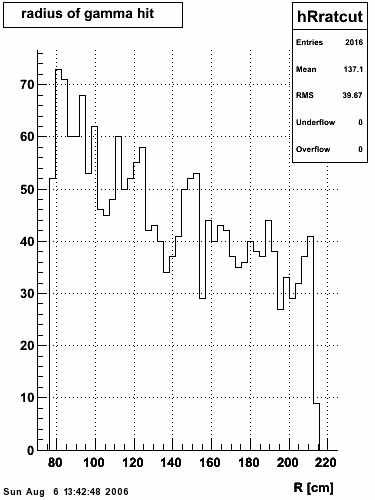 |
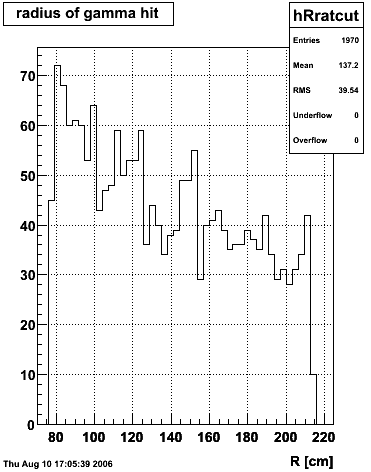 |
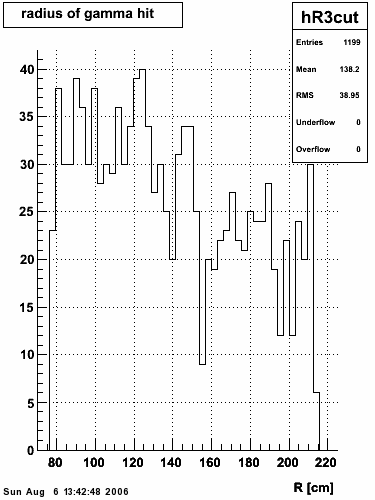 |
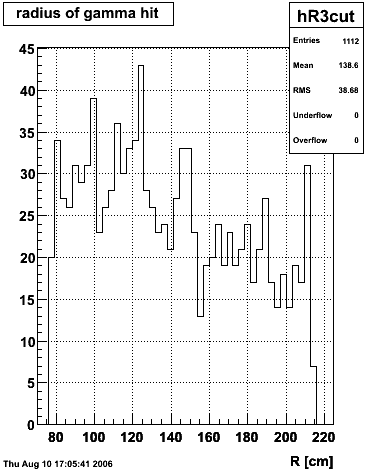 |
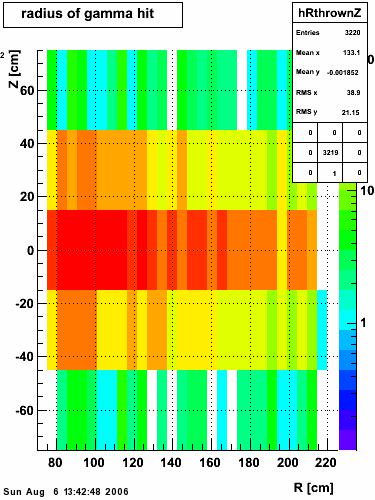 |
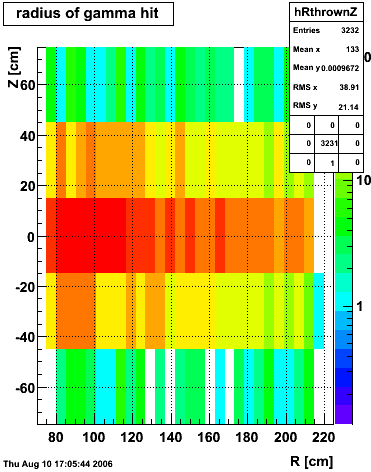 |
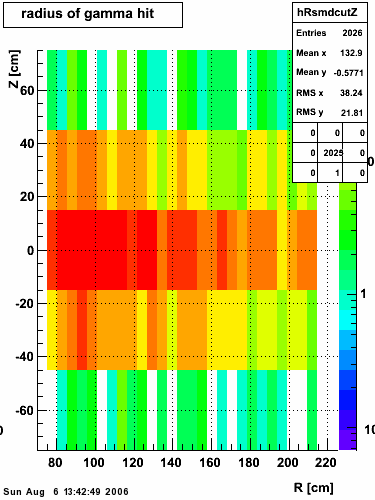 |
 |
 |
 |
 |
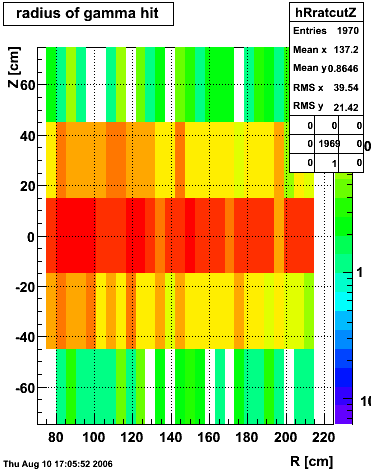 |
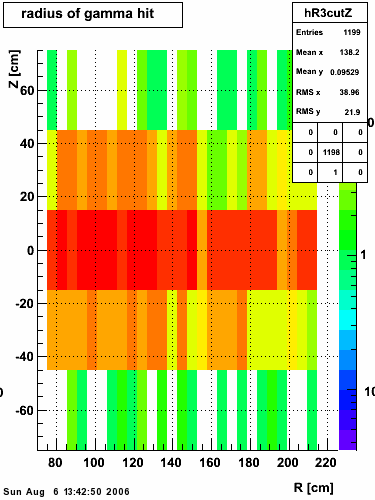 |
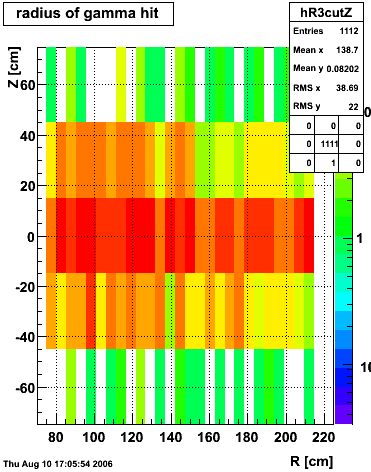 |
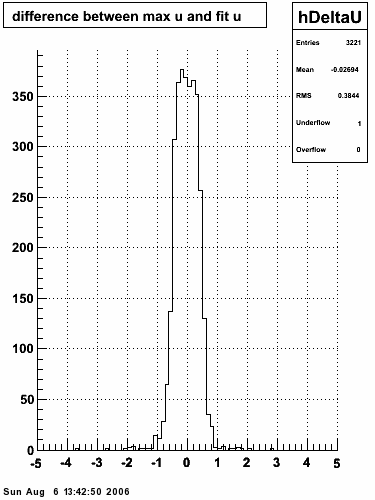 |
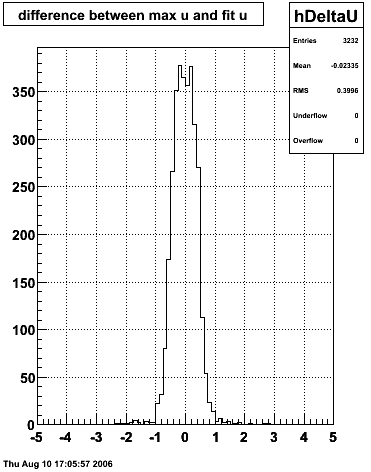 |
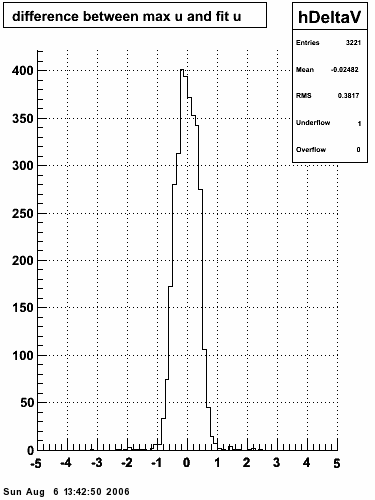 |
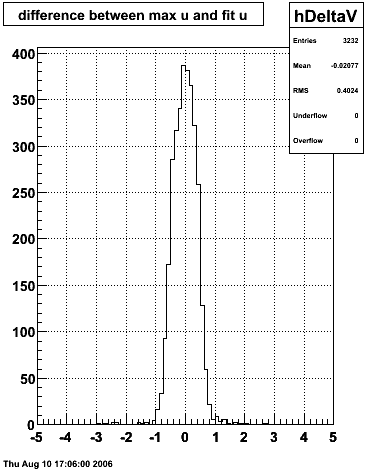 |
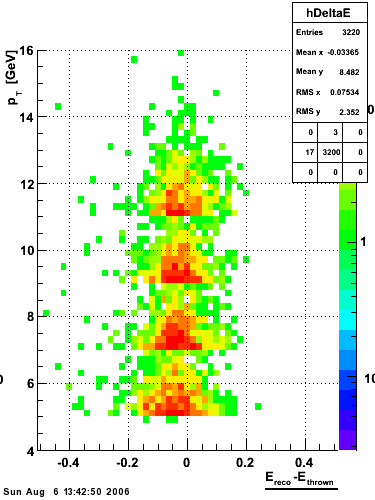 |
 |
 |
 |
 |
 |
 |
 |
 |
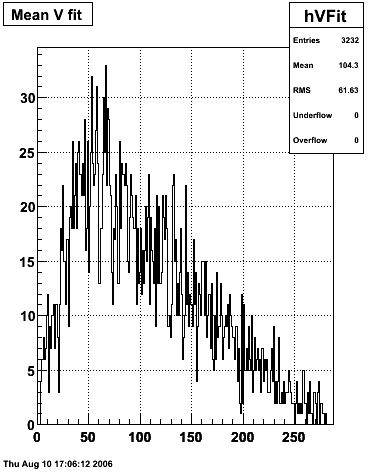 |
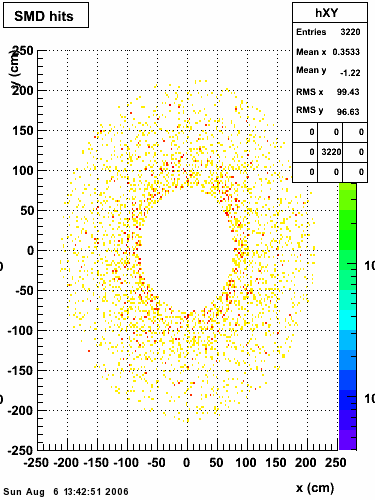 |
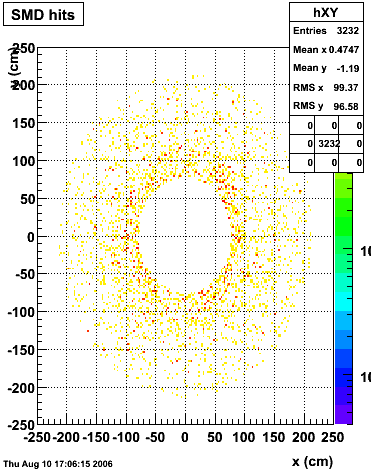 |
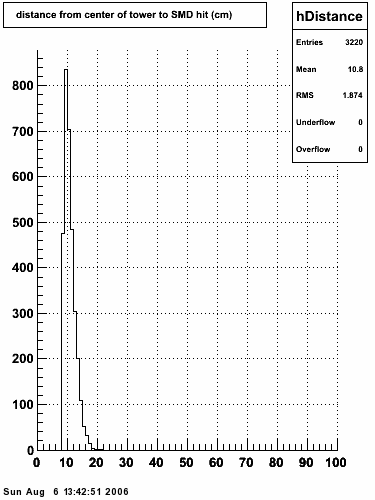 |
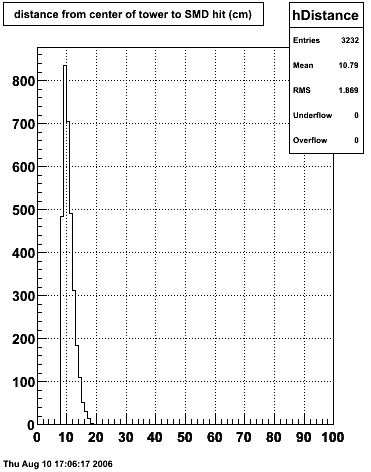 |
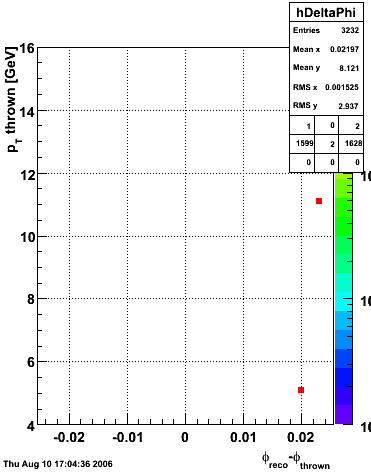
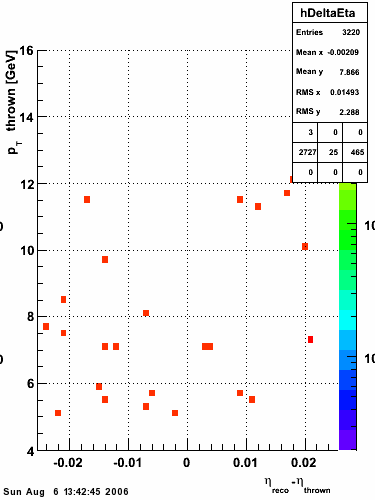
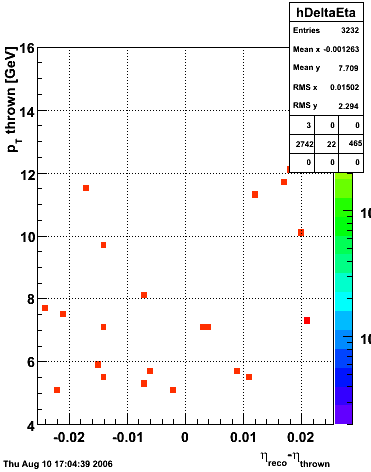
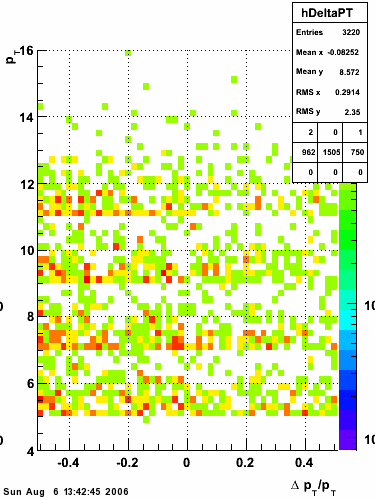
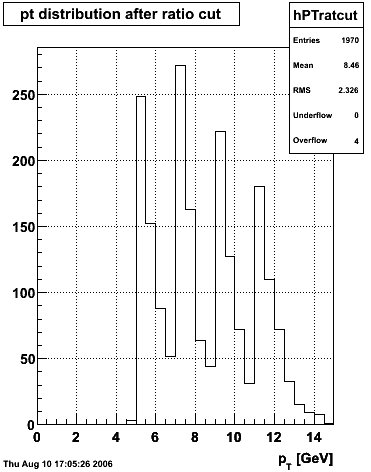
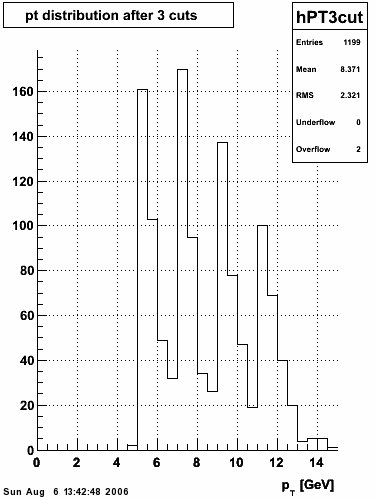
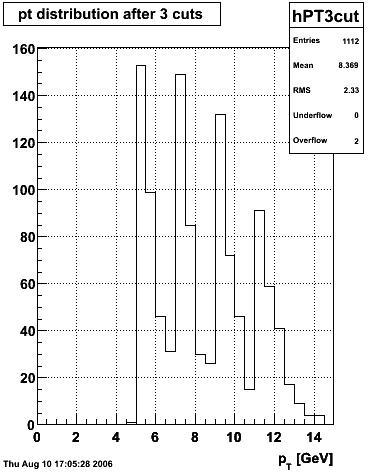
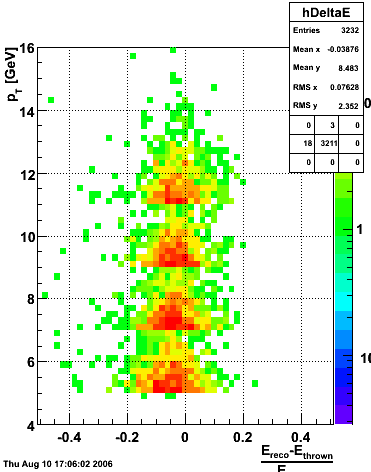
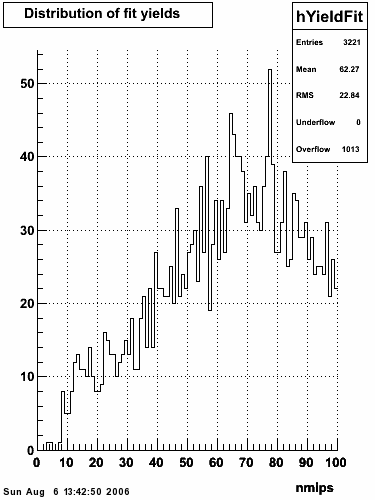
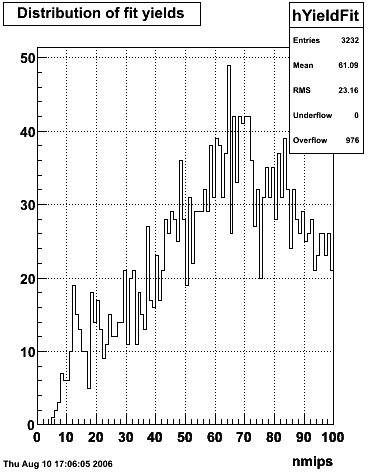
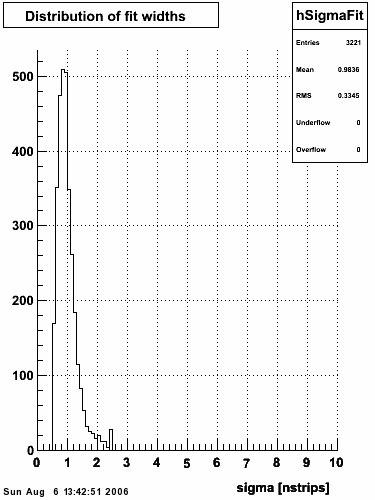
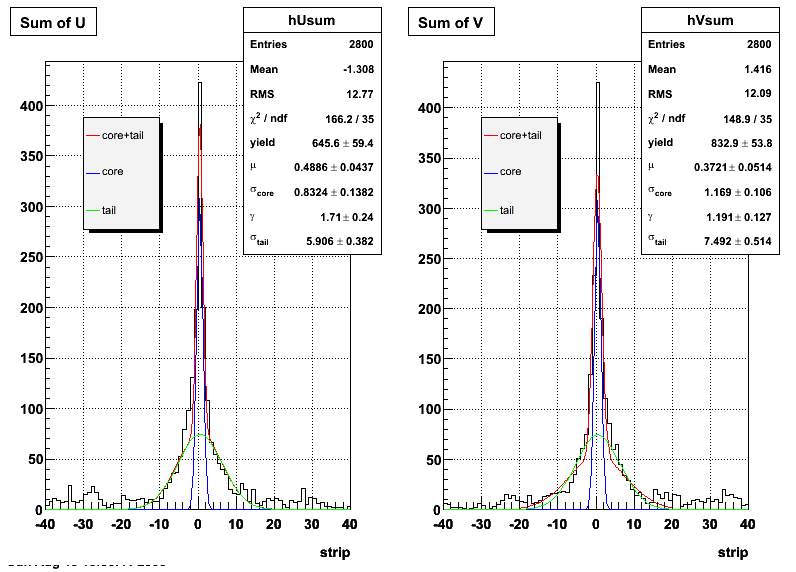
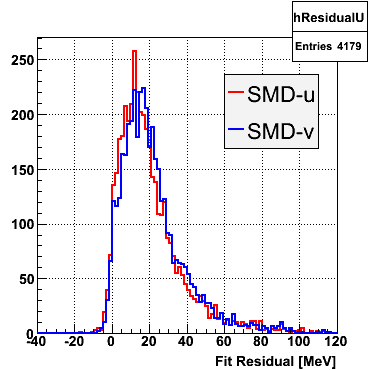
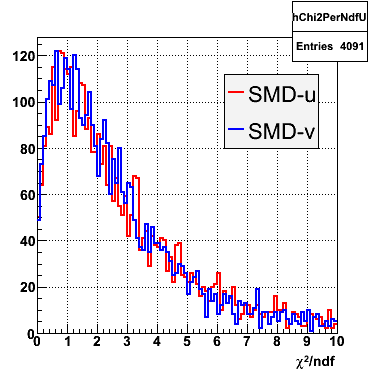
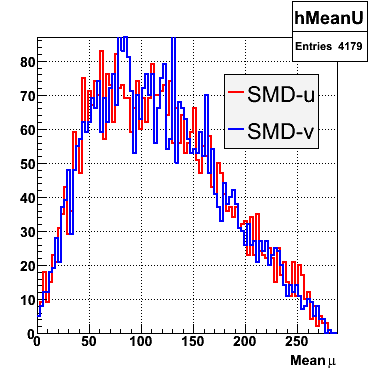
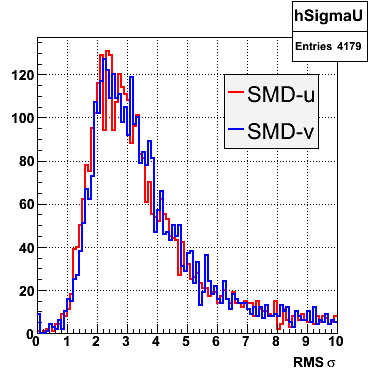
2006.09.15 Fit Parameters
Fit Parameters
Fit Function
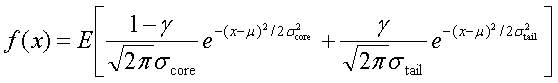
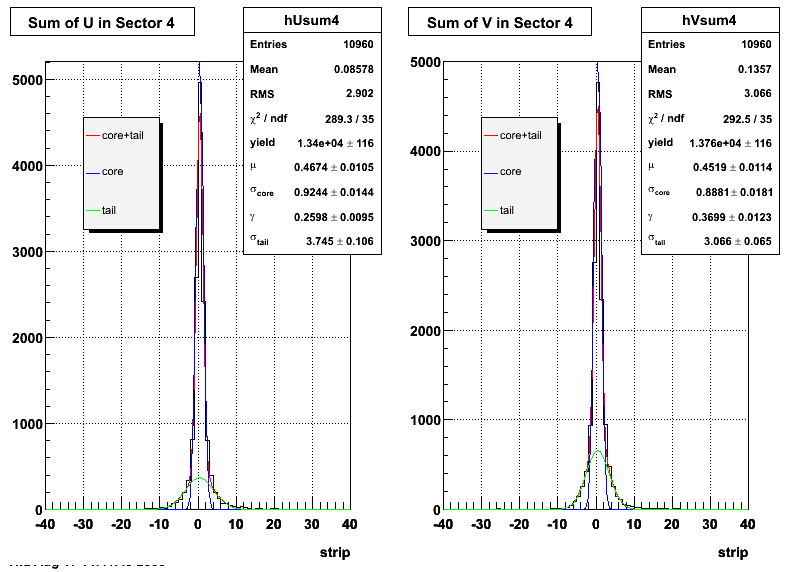
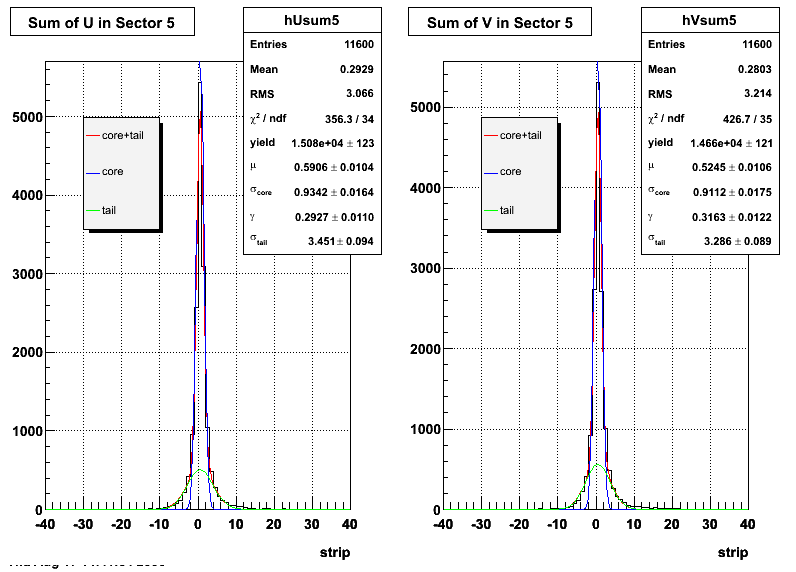
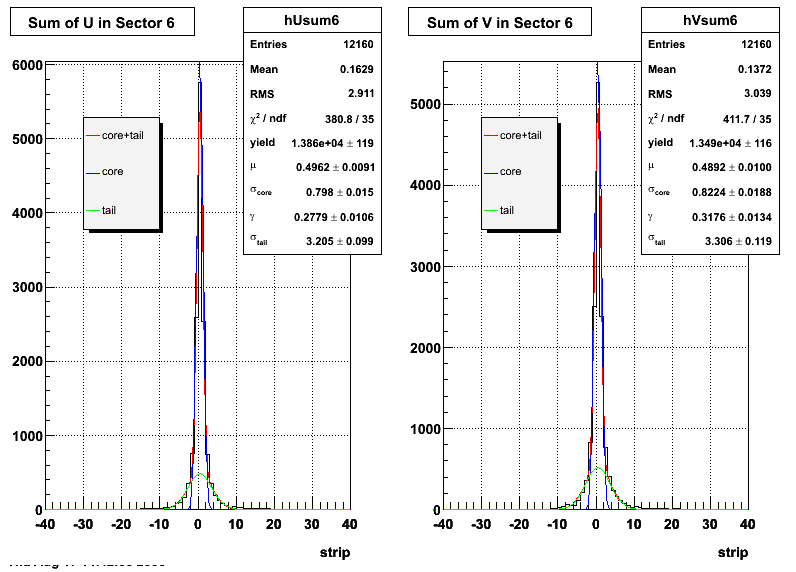
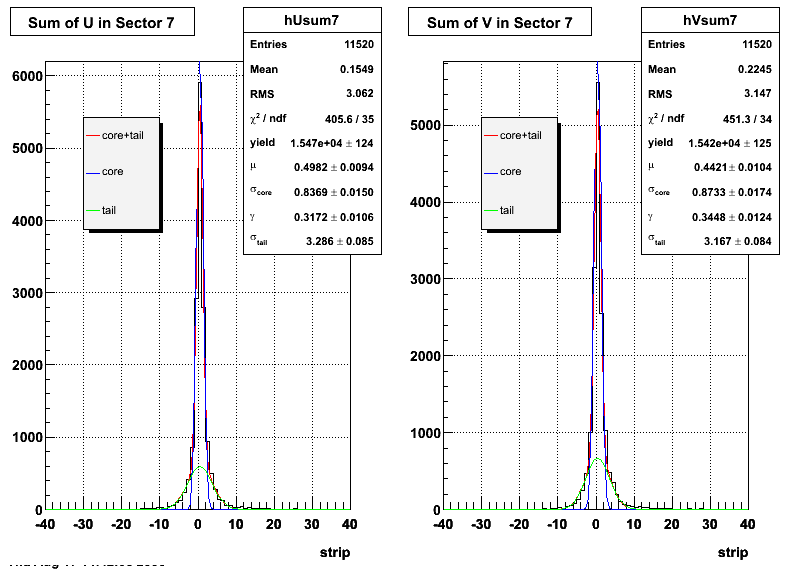
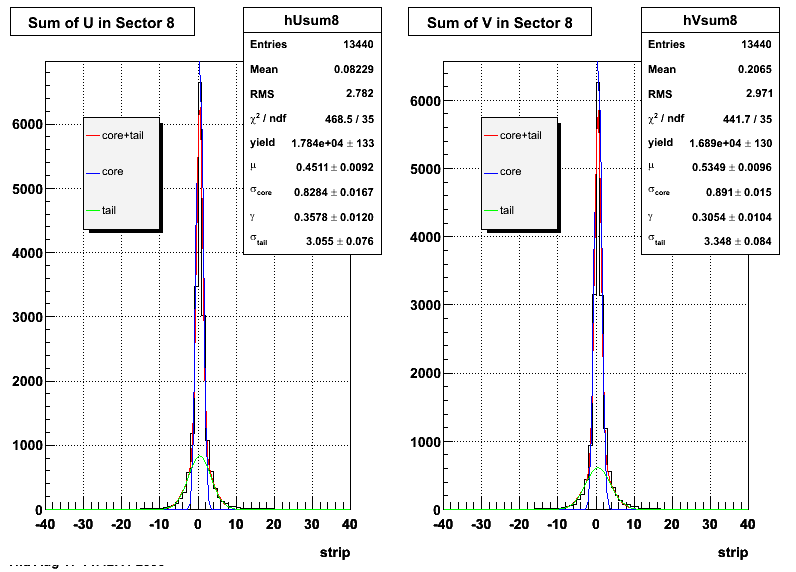
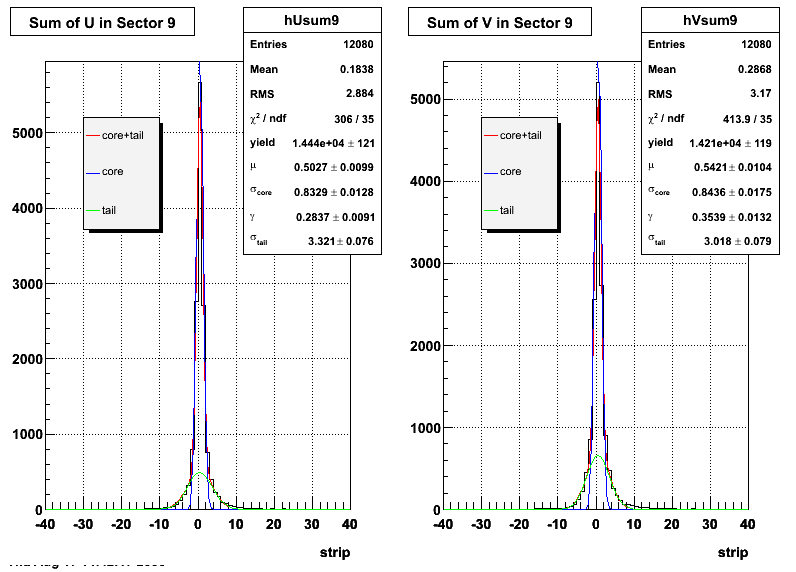
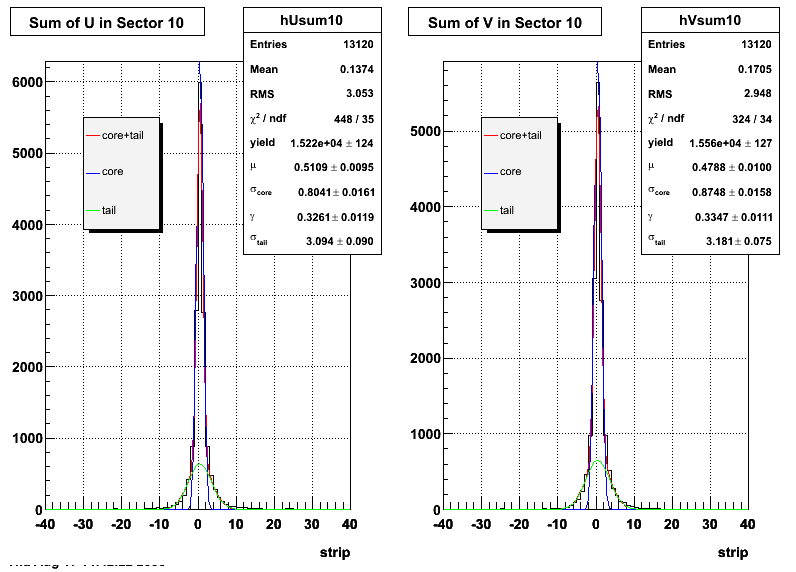
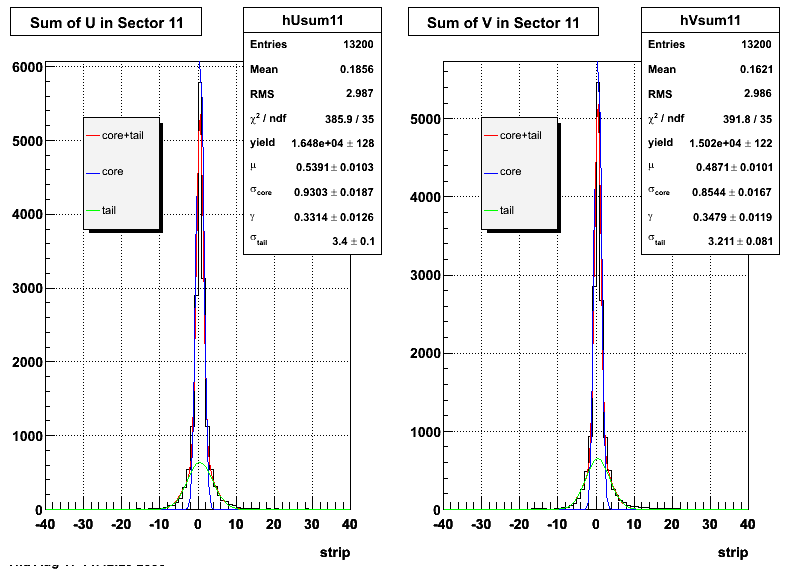
The plots that follow are sums of individual SMD responses in each plane centered around a common mean (here 0), over a +/-40 strips range. The convention for the parameters in the fits below is:
- p0=E -- area under the curve which represents energy in MeV
- p1=μ -- mean
- p2=σcore -- width of the narrow Gaussian
- p3=γ -- relative contribution of the wide Gaussian to the area/height
- p4=σtail -- width of the wide Gaussian
Simulation
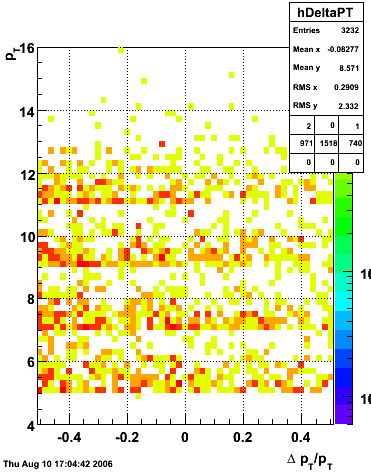
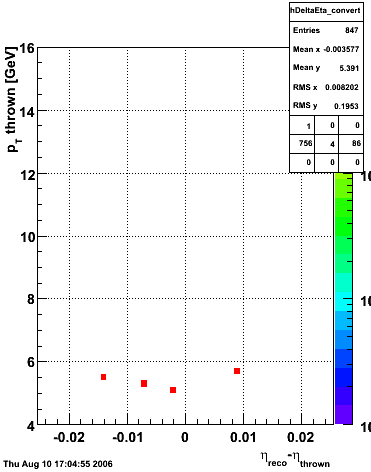
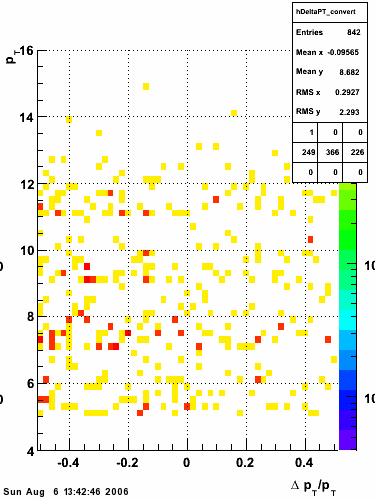
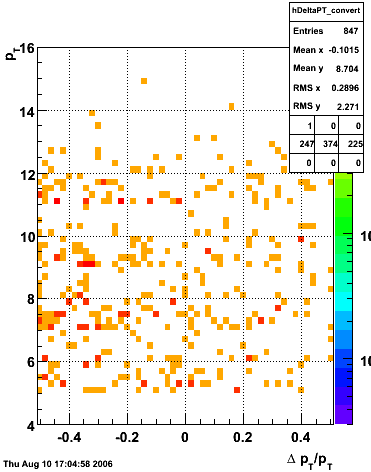
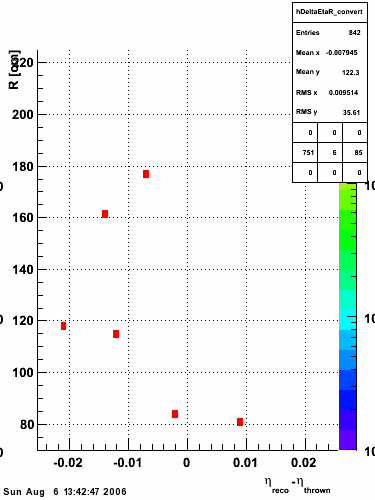
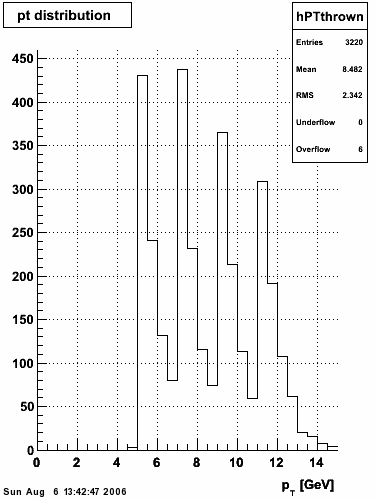
The simulation is from single photons thrown at the EEMC with the following pT distribution:
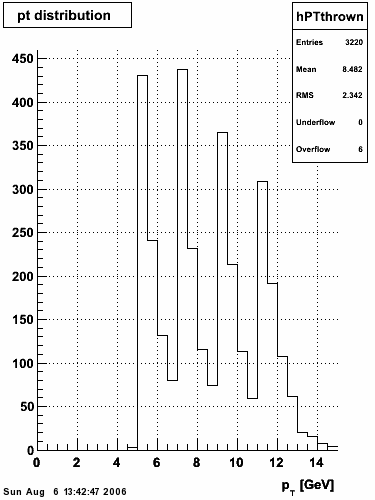
The highest tower above 4 GeV in total energy is selected and the corresponding SMD sector fitted for peaks in both planes, where the area of the peaks in the U plane is constrained to be identical to that of the peak in the V plane. The peak is shifted to be centered at 0 where peaks from other events are then summed. The summed SMD response in each plane is displayed below:
Ditto in log scale.
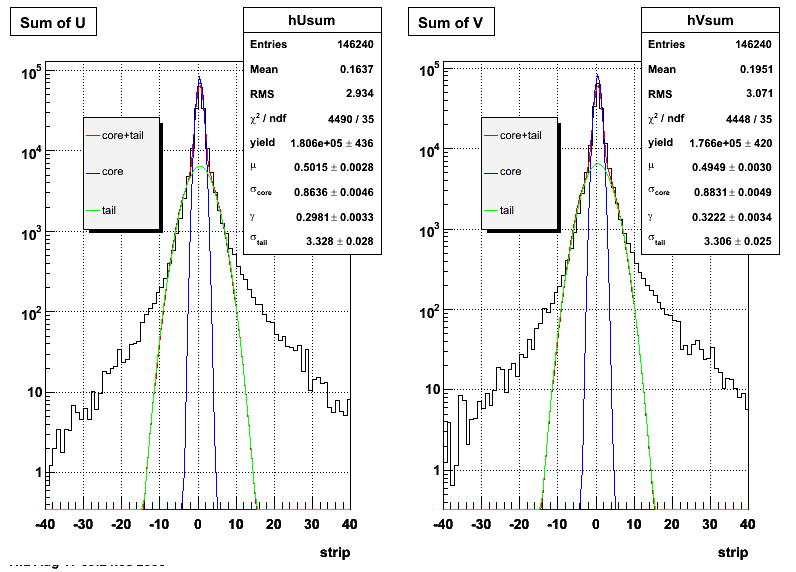
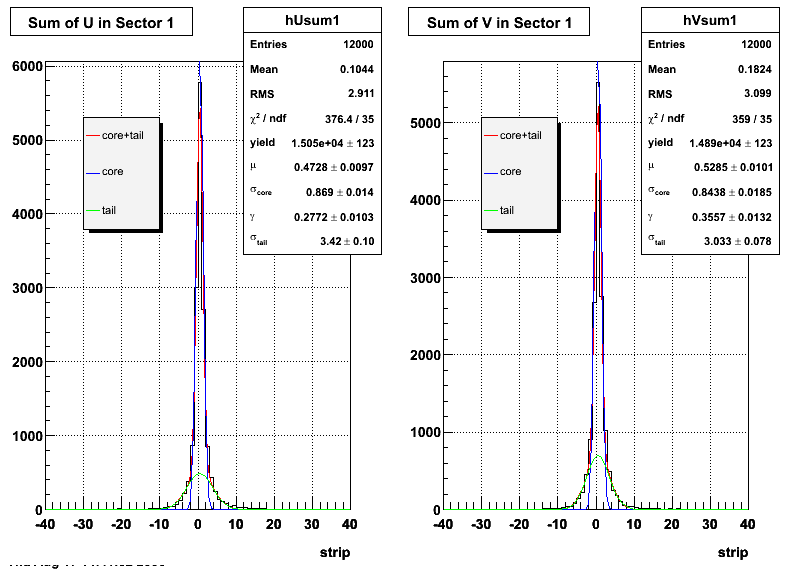
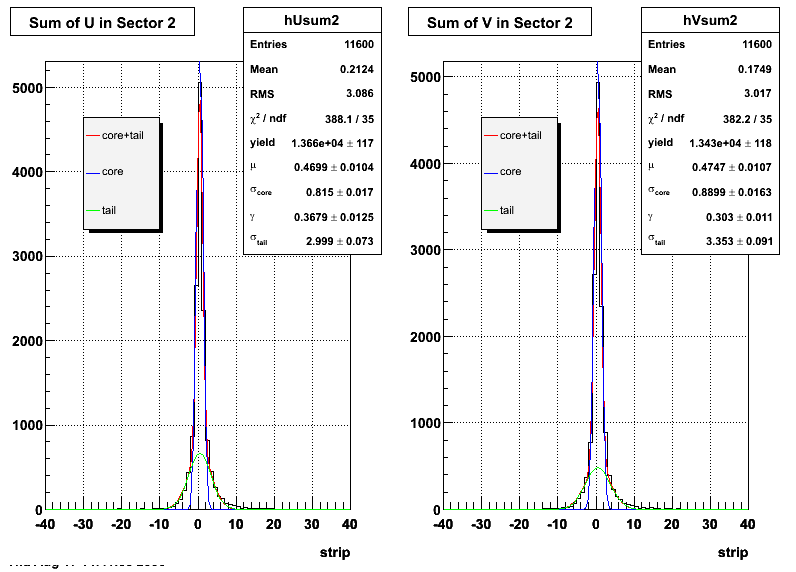
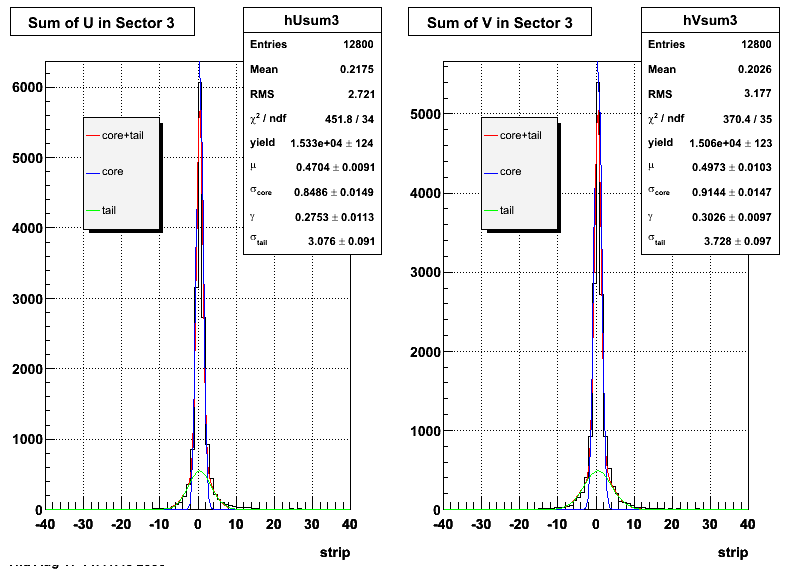
Ditto by sector.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
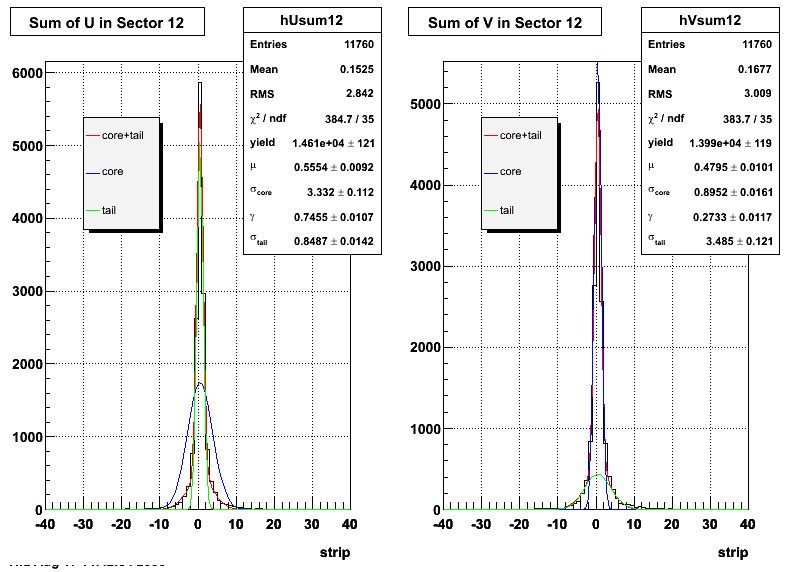 |
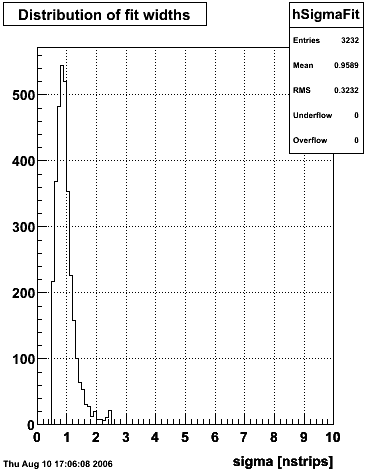
Fit Widths
| Sector # | SMD-u σcore | SMD-u σtail | SMD-v σcore | SMD-v σtail |
| Sector 1 | 0.869033 ± 0.0142868 | 3.42031 ± 0.10226 | 0.84379 ± 0.0185107 | 3.03287 ± 0.0775009 |
| Sector 2 | 0.814959 ± 0.0169271 | 2.99941 ± 0.0730426 | 0.889892 ± 0.0163065 | 3.35288 ± 0.0911979 |
| Sector 3 | 0.84862 ± 0.0148706 | 3.07648 ± 0.0909689 | 0.914377 ± 0.014706 | 3.72821 ± 0.0966915 |
| Sector 4 | 0.924398 ± 0.0144207 | 3.74458 ± 0.10611 | 0.888146 ± 0.0180771 | 3.06618 ± 0.0647075 |
| Sector 5 | 0.934218 ± 0.0163887 | 3.45149 ± 0.0944309 | 0.911209 ± 0.0175273 | 3.28633 ± 0.0890581 |
| Sector 6 | 0.797976 ± 0.0148133 | 3.20464 ± 0.0986085 | 0.822437 ± 0.018835 | 3.30595 ± 0.118813 |
| Sector 7 | 0.836936 ± 0.0150085 | 3.28589 ± 0.0853598 | 0.873338 ± 0.0173883 | 3.16654 ± 0.0838938 |
| Sector 8 | 0.828403 ± 0.0167005 | 3.05517 ± 0.075584 | 0.891045 ± 0.0152102 | 3.34806 ± 0.0836394 |
| Sector 9 | 0.832881 ± 0.0127855 | 3.3214 ± 0.0762928 | 0.8436 ± 0.0175466 | 3.0183 ± 0.079444 |
| Sector 10 | 0.804059 ± 0.0160906 | 3.0943 ± 0.0897946 | 0.874845 ± 0.015788 | 3.18113 ± 0.0748357 |
| Sector 11 | 0.930286 ± 0.0187086 | 3.40024 ± 0.0951671 | 0.854395 ± 0.0167265 | 3.21076 ± 0.0812402 |
| Sector 12 | 3.33227 ± 0.111911 | 0.848668 ± 0.0142344 | 0.895174 ± 0.0160939 | 3.48527 ± 0.12061 |
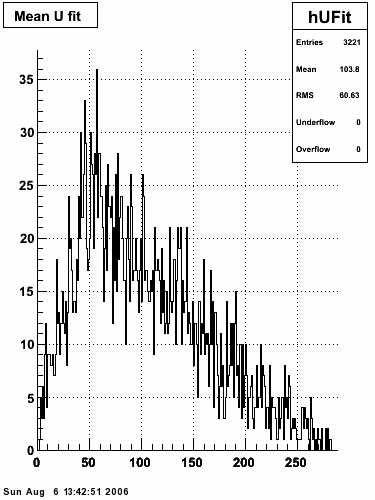
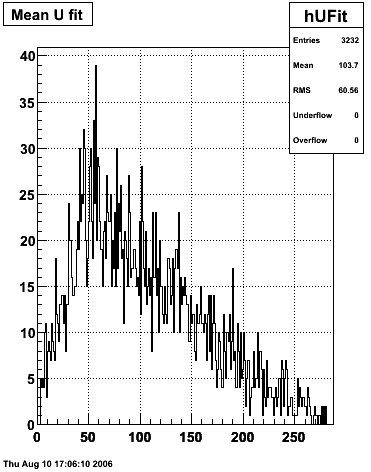
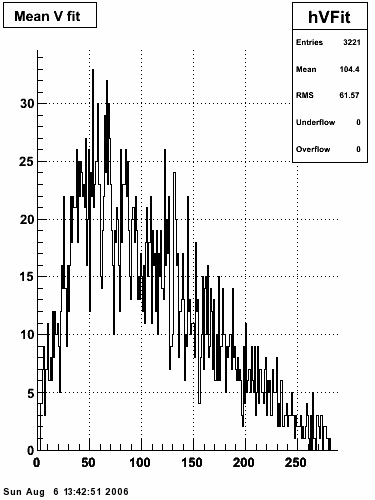
Data from 2005 pp200 EEMC HT 1 and 2 triggers
In this sample, high tower triggers, eemc-ht1-mb (96251) and eemc-ht2-mb (96261), from the 2005 p+p at √s=200 GeV ppProduction are selected. The highest tower above 4 GeV is chosen and the corresponding SMD sector is searched for peaks in both planes. Peaks from several events are summed together taking care of shifting them around to have a common mean.
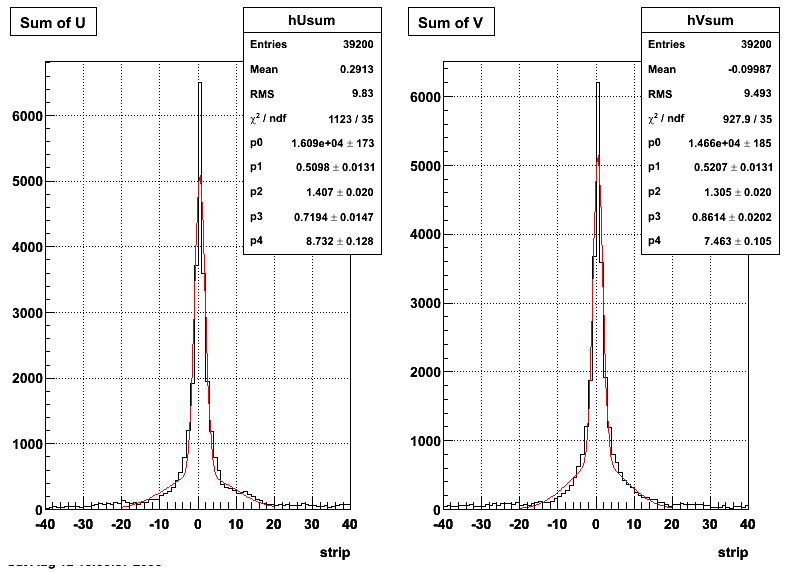
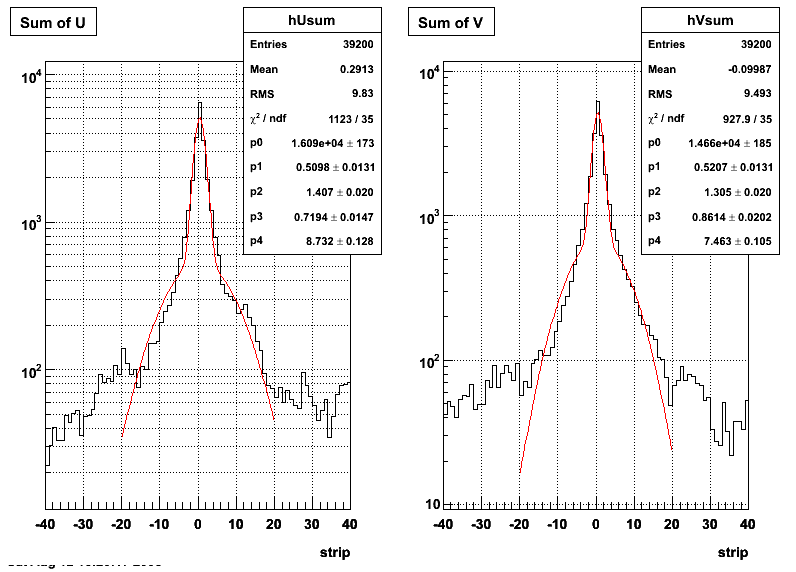
Ditto in log scale.
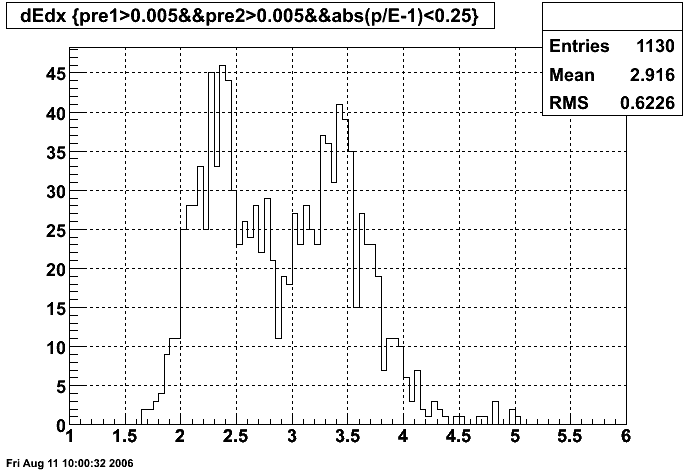
Data from 2005 pp200 electrons
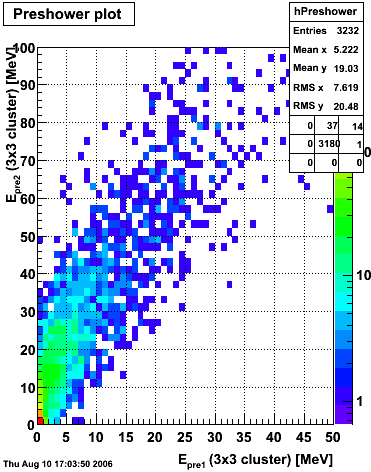
Here, I try to pick a representative sample of electrons from the 2005 pp200 dataset. The cuts used to pick out electrons are:
- Epreshower1 > 5 MeV
- Epreshower2 > 5 MeV
- 0.75 < p/Etower < 1.25
- 3 < dE/dx < 4 keV/cm
The selection for electrons is illustrated in the dE/dx plot below, where the pions should be on the left and the electrons on the right.
Pibero Djawotho Last modified Tue Aug 15 10:41:19 EDT 2006
2007.02.05 Reconstructed/Monte Carlo Photon Energy
Reconstructed/Monte Carlo Photon Energy
This study is motivated by Weihong's photon energy loss study where an eta-dependence of reconstructed photon energy to generated photon energy in EEMC simulation was observed.
In this study, the eta-dependence is investigated by running the EEMC slow simulator with the new readjusted weights for the preshower and postshower layers of the EEMC. Details on this are here.
- Fit to a constant
- Fit to a line
- Fit to a quadratic
- Comparison between Weihong's and Pibero's results
- Constant
- Linear
- Quadratic
- Conclusion
- References
- M. Albrow et al., NIM A 480 (2002) 524-546.
- R. Blair et al. (CDF Collaboration), CDF II Technical Design Report, FERMILAB-PUB-96-390-E, 1996.



The parameters from the fits are used to plot the fit functions for comparison between Weihong's and Pibero's results.


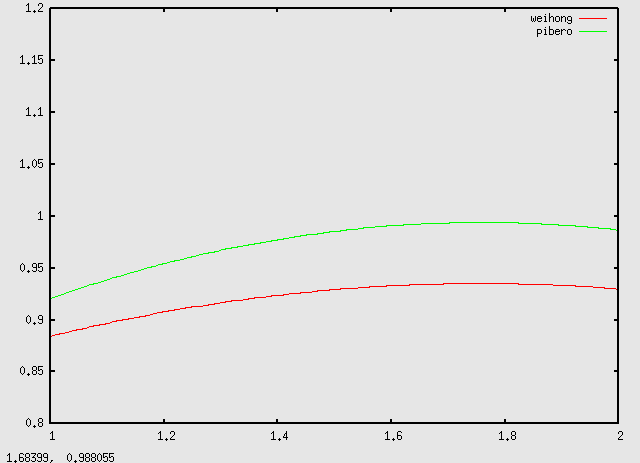
While the adjusted weights for the different EEMC layers contribute to bringing the ratio of reconstructed energy to generated energy closer to unity, they do not remove the eta-dependence.
Pibero Djawotho Last updated Mon Feb 5 10:10:42 EST 2007
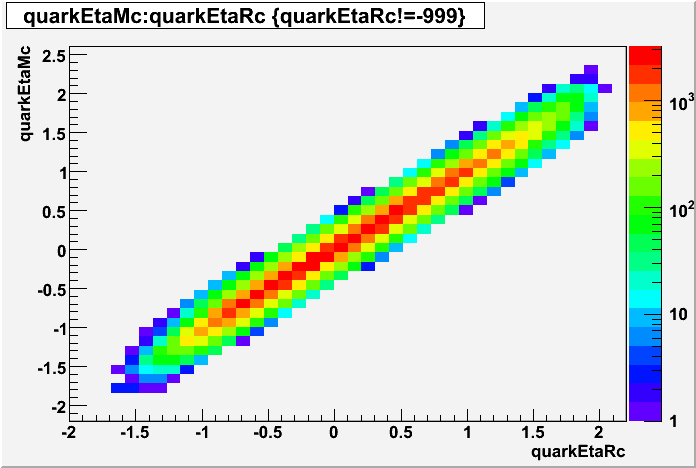
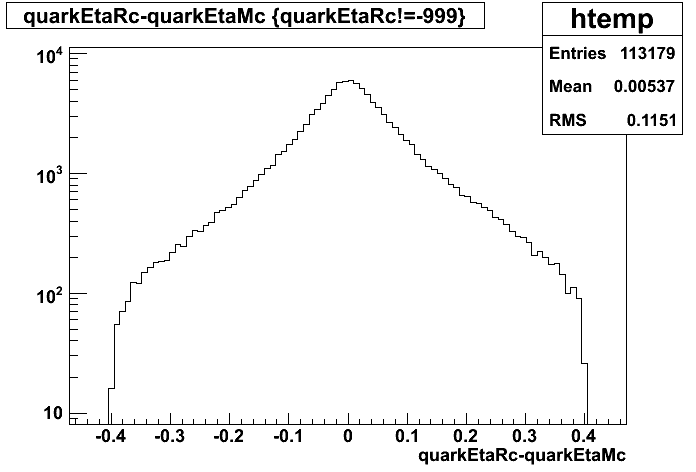
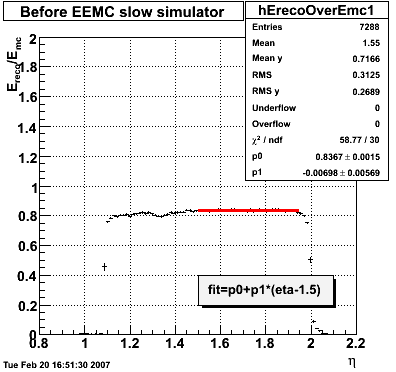
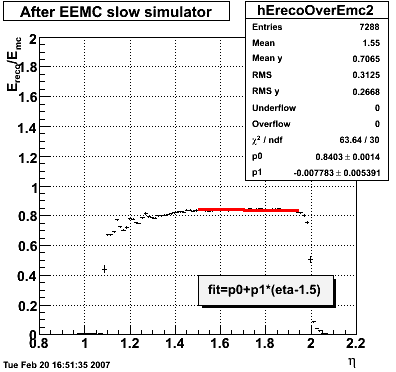
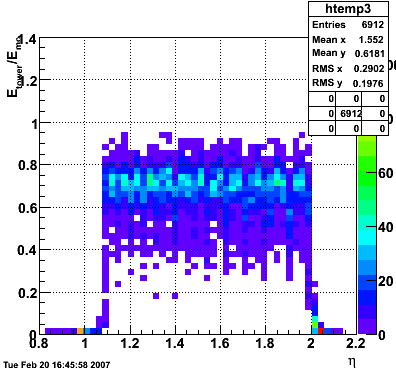
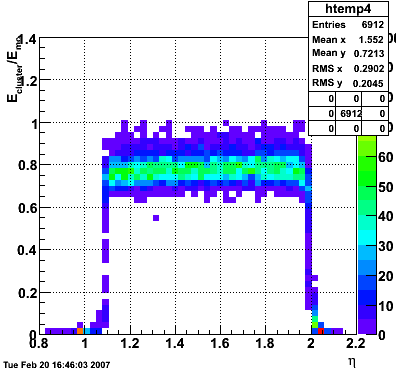
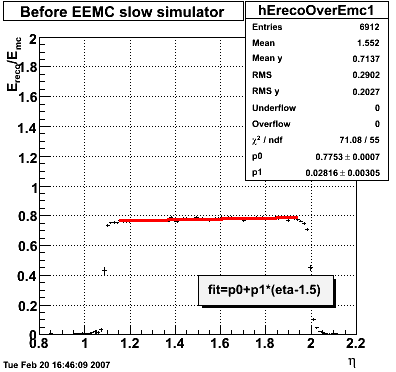
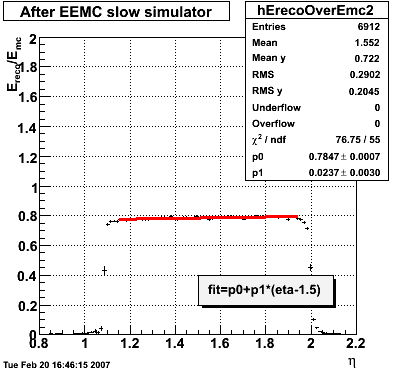
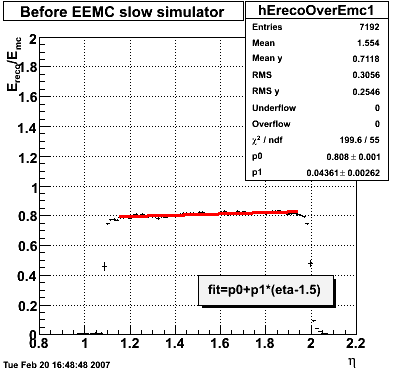
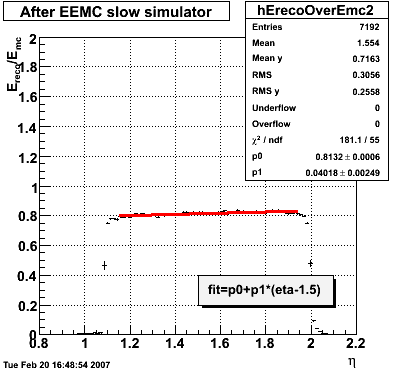
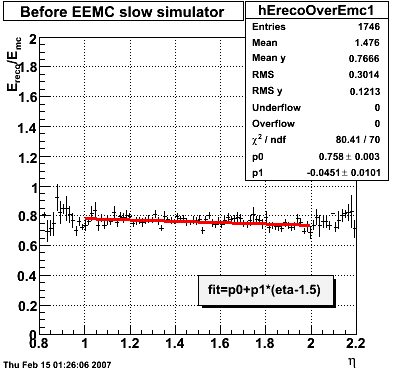
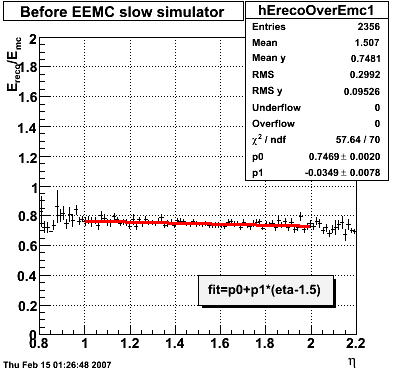
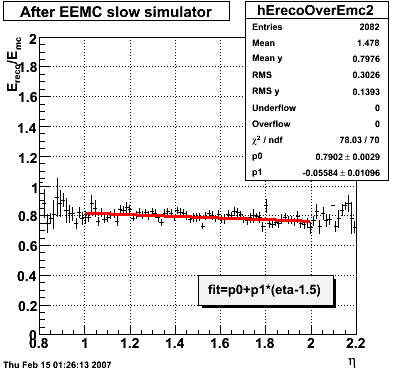
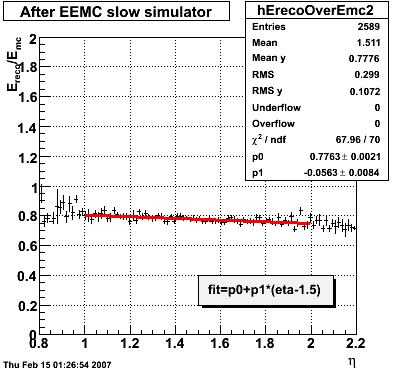
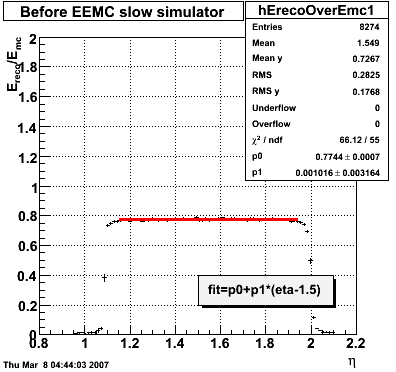
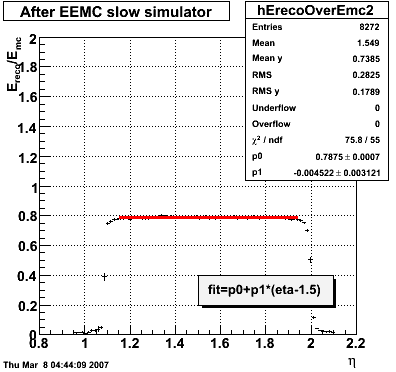
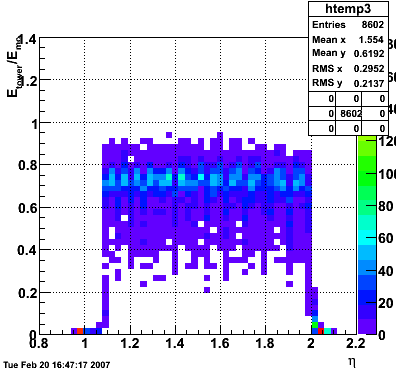
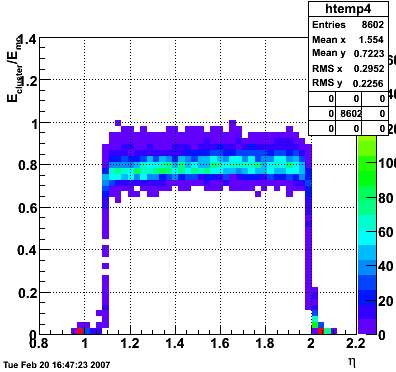
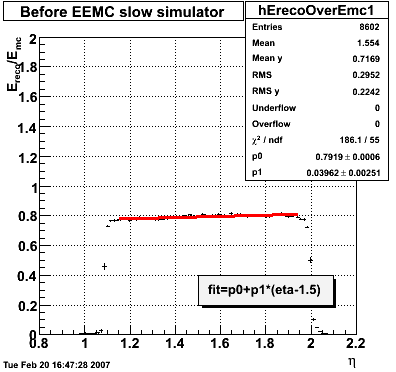
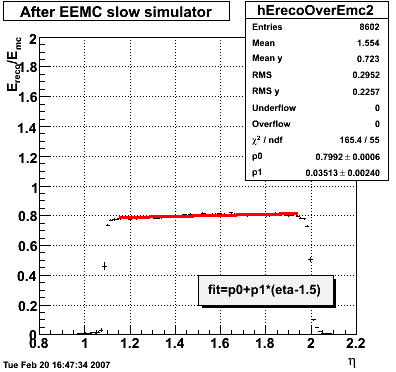
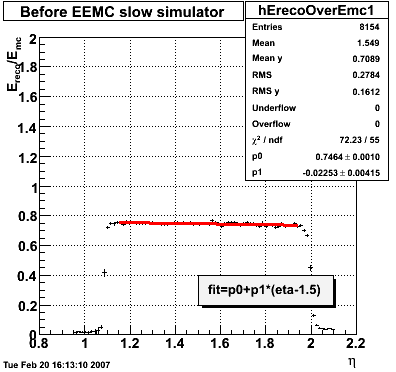
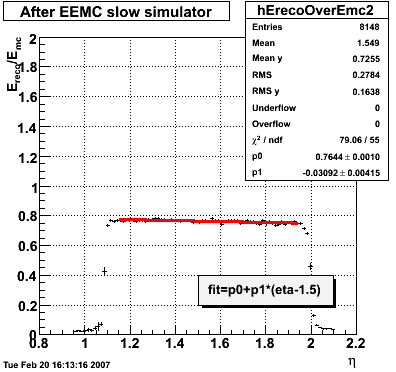
2007.02.08 E_reco / E_mc vs. eta
E_reco / E_mc vs. eta
Legend
- black curve: before EEMC slow simulator
- red curve: after EEMC slow simulator
Jason's Monte Carlo
- 4.4k single gamma's
- No SVT
- Nominal vertex
- Flat in pt 4-12 GeV
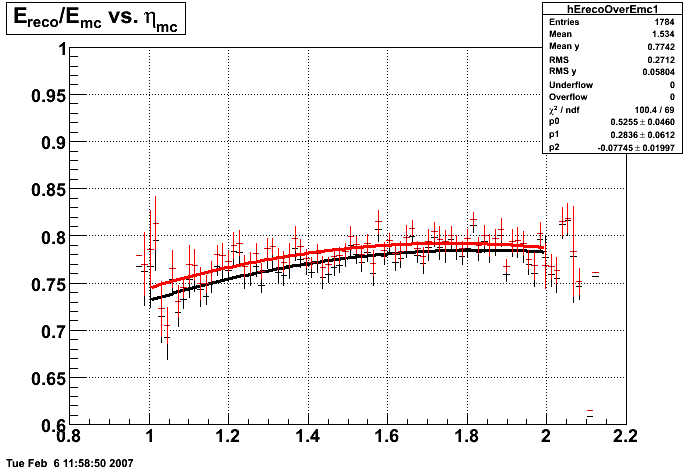
Will's Monte Carlo
- 10k single gamma's
- SVT/SSD out
- Vertex at 0
- Flat in pt 5-60 GeV
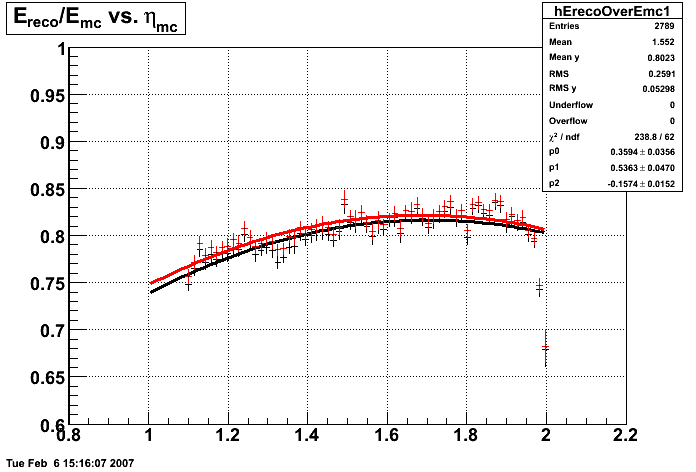
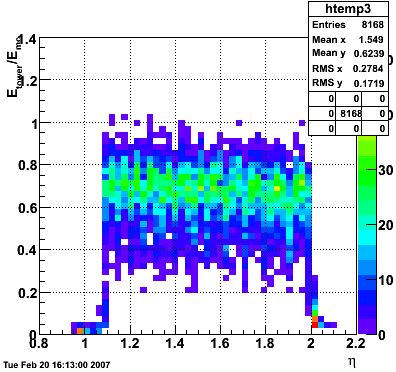
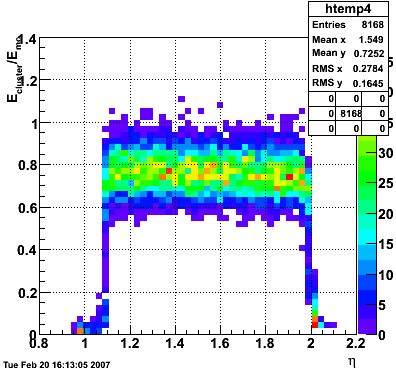
In the plot below, I use the energy of the single tower (tower with max energy) presumably the tower the photon hit. The nonlinearity seems to disappear.
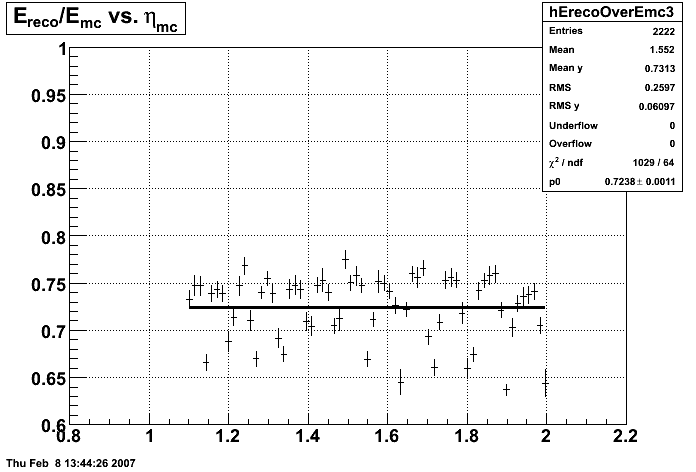
In the plot below, I use the energy of the 3x3 cluster of tower centered around the tower with the max energy. The nonlinearity is restored.
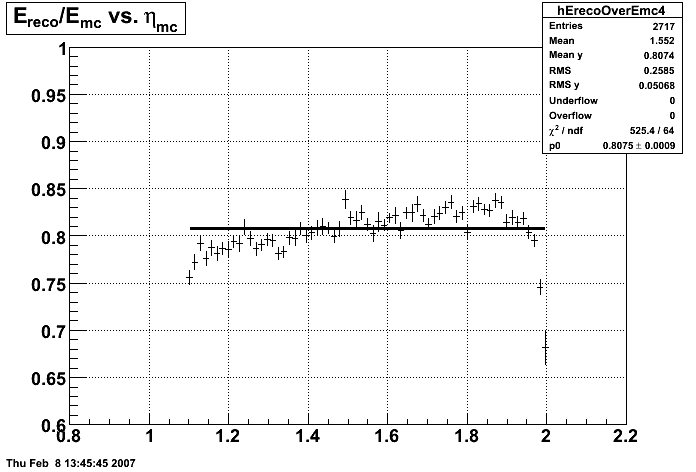
The plot below shows Etower/Ecluster vs. eta where the cluster consists of 3x3 towers centered around the max energy tower.
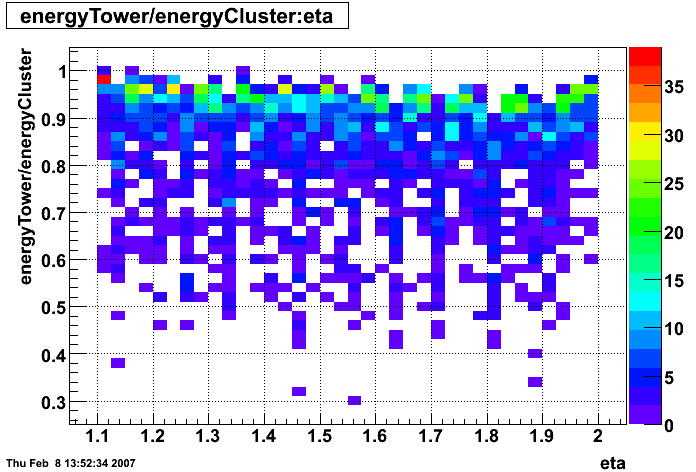
Below is the profile of E_tower/E_cluster vs. eta.
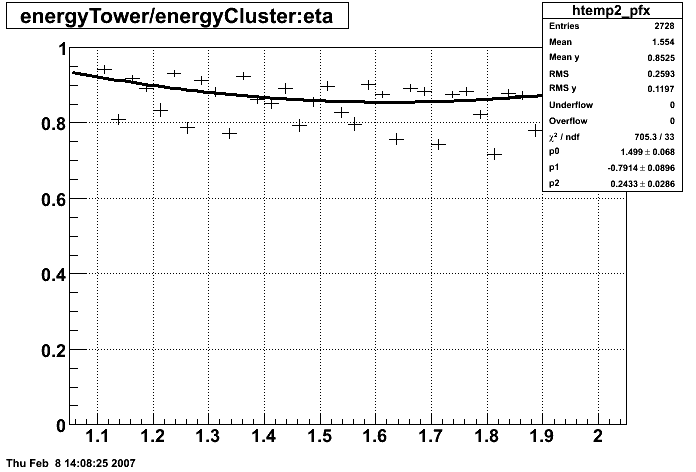
The plot below shows the energy sampled by the entire calorimeter as a function of eta, i.e. sampling fraction as a function of eta.
Sampling fraction integrated over all eta's.
Pibero Djawotho Last updated Thu Feb 8 13:59:29 EST 2007
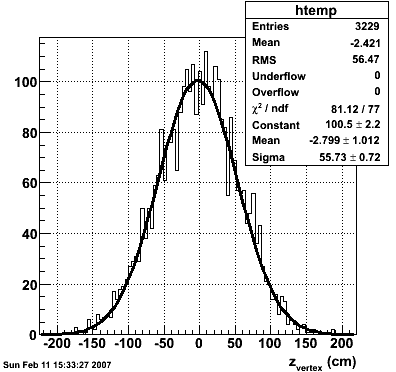
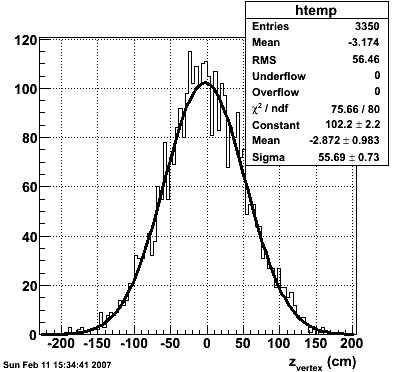
2007.02.11 Reconstructed/Monte Carlo Muon Energy
Reconstructed/Monte Carlo Muon Energy
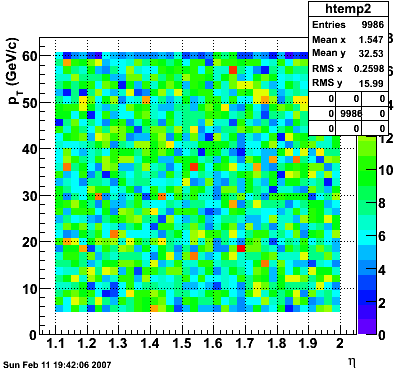
10k muons thrown by Will with:
- zvertex=0
- Flat in pT 5-60 GeV/c
- Flat in η 1.1-2
zvertex
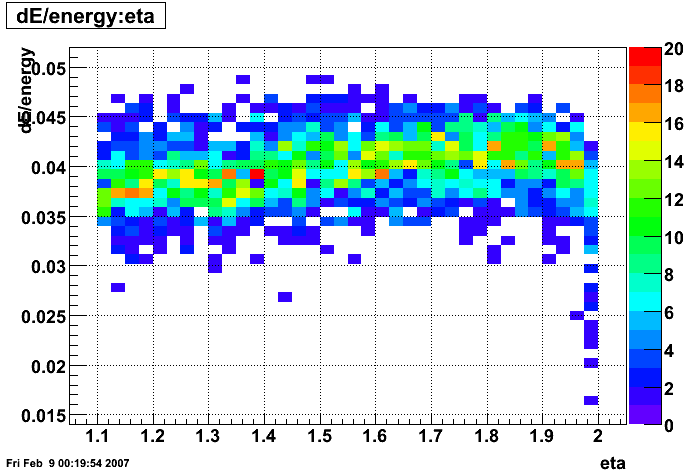
pT vs. η
EMC
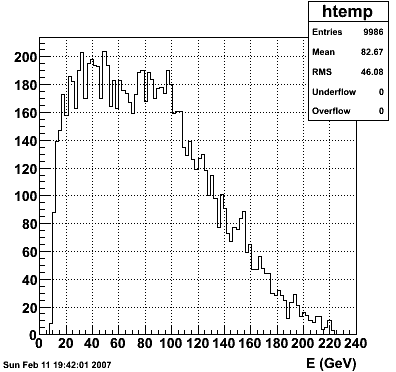
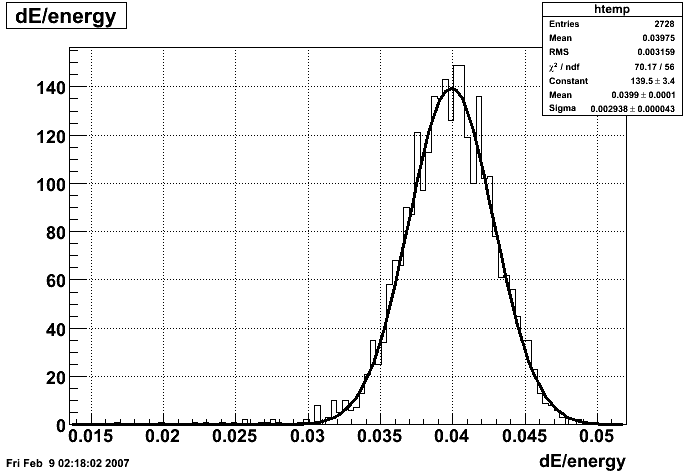
Etower/EMC vs. η
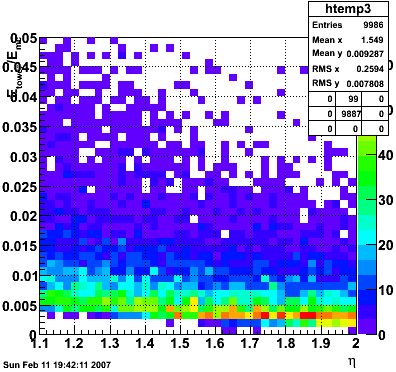
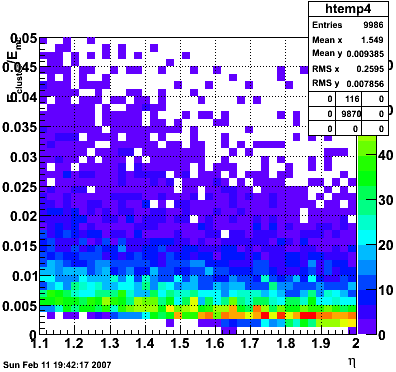
Ecluster/EMC vs. η
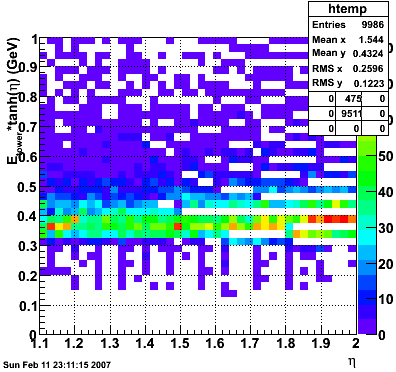
Etowertanh(eta) vs. eta
Pibero Djawotho Last modified Sun Feb 11 19:51:55 EST 2007
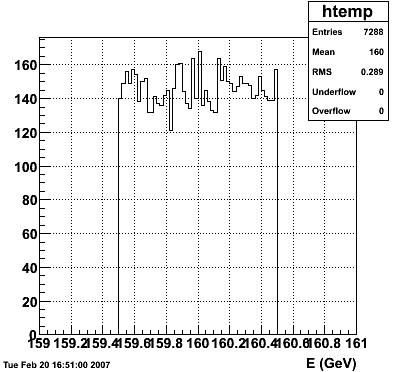
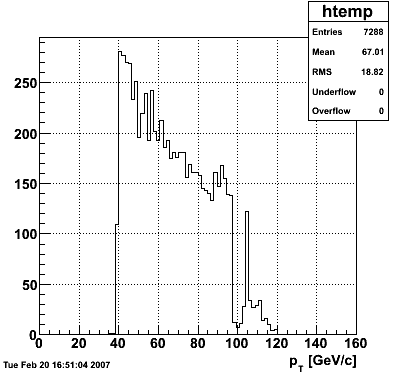
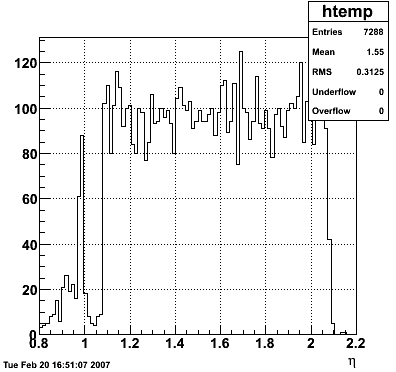
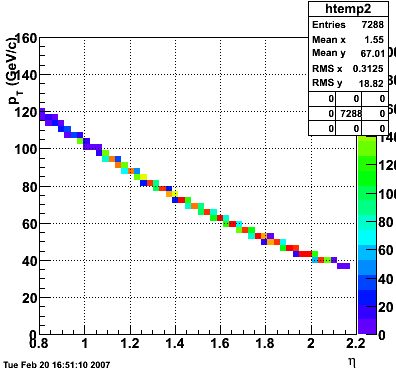
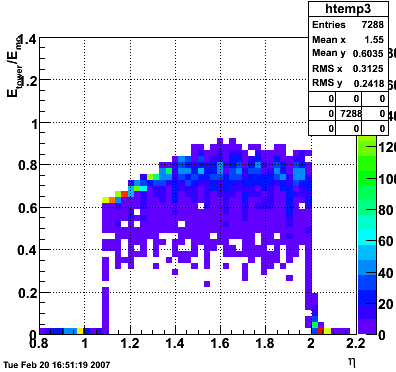
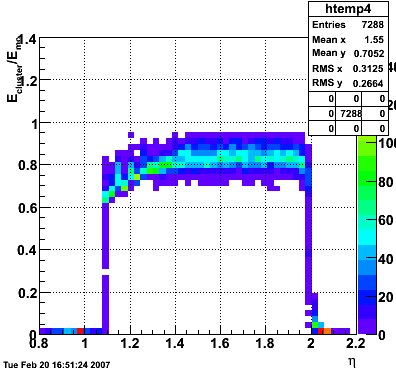
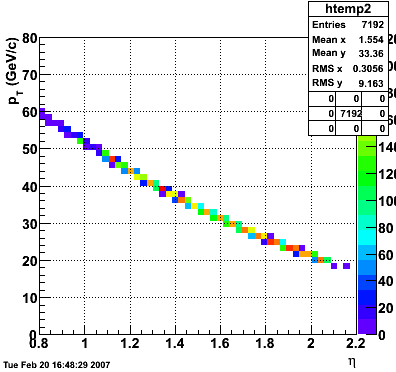
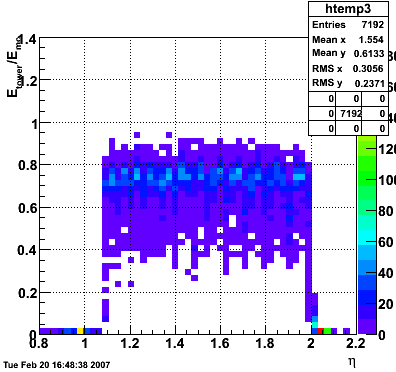
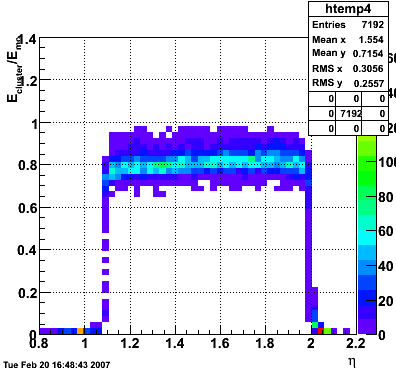
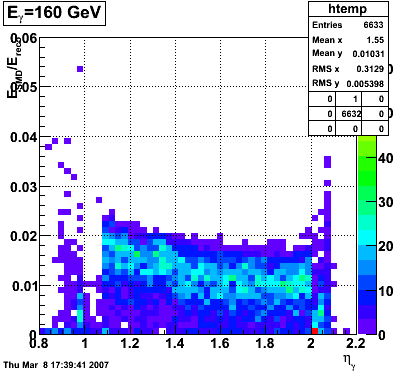
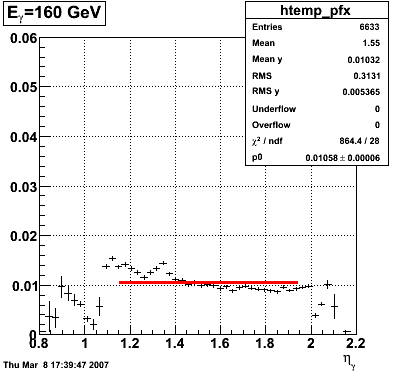
2007.02.15 160 GeV photons
160 GeV photons
- 10k 160 GeV photons
- zvertex=0
- η range 0.8-2.2
- SVT/SSD out
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Pibero Djawotho Last updated Thu Feb 15 04:33:09 EST 2007
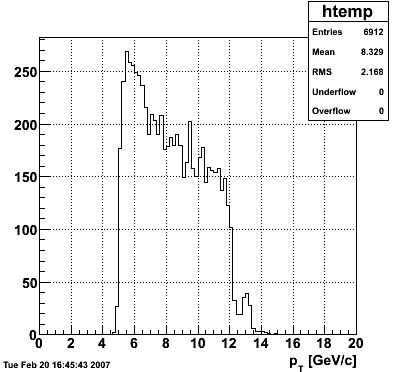
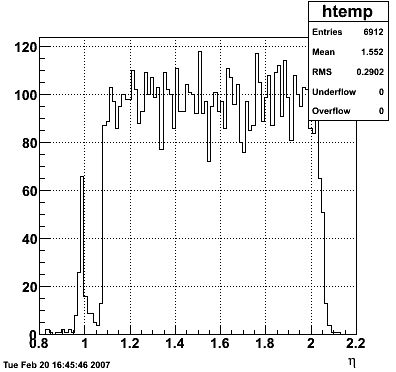
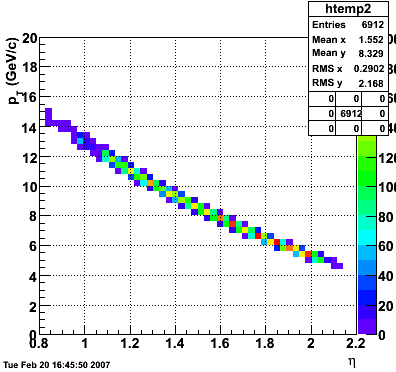
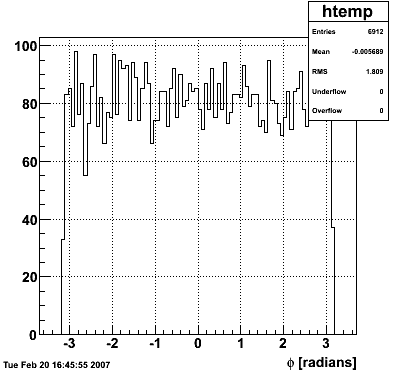
2007.02.15 20 GeV photons
20 GeV photons
- 10k 20 GeV photons
- zvertex=0
- η range 0.8-2.2
- SVT/SSD out
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Pibero Djawotho Last updated Thu Feb 15 04:32:25 EST 2007
2007.02.15 80 GeV photons
80 GeV photons
- 10k 80 GeV photons
- zvertex=0
- η range 0.8-2.2
- SVT/SSD out
 |
 |
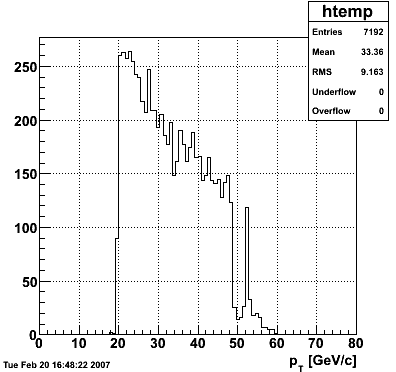 |
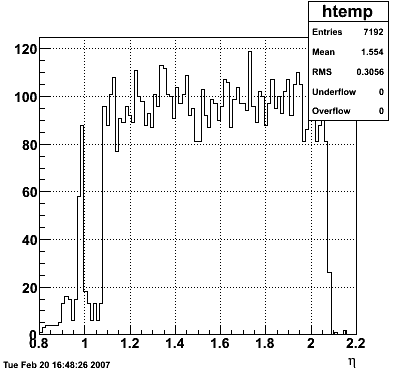 |
 |
 |
 |
 |
 |
 |
Pibero Djawotho Last updated Thu Feb 15 03:16:54 EST 2007
2007.02.15 Reconstructed/Monte Carlo Electron Energy
Reconstructed/Monte Carlo Electron Energy
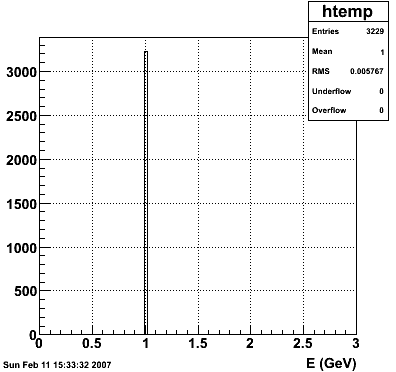
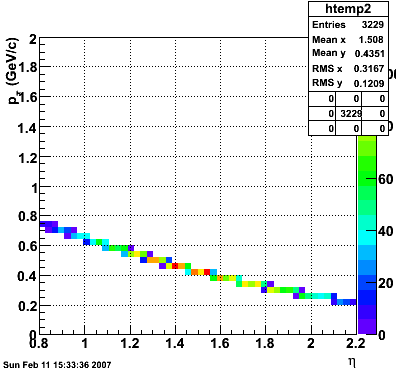
E=1 GeV |
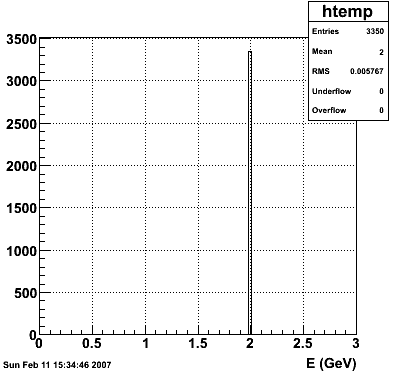
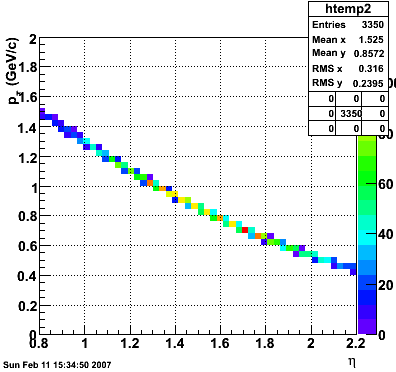
E=2 GeV |
 |
 |
 |
 |
 |
 |
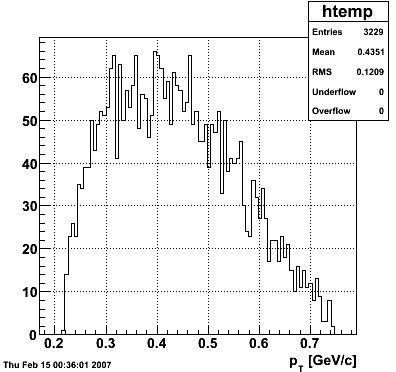 |
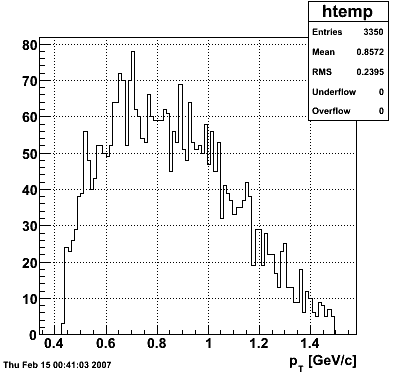 |
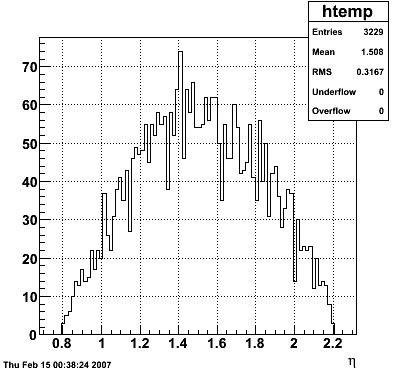 |
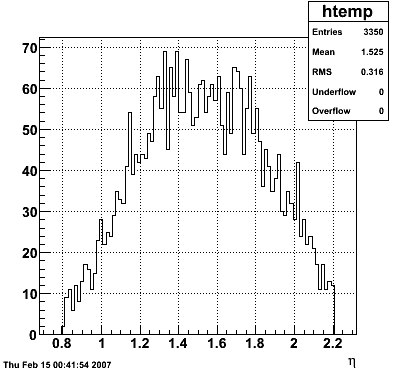 |
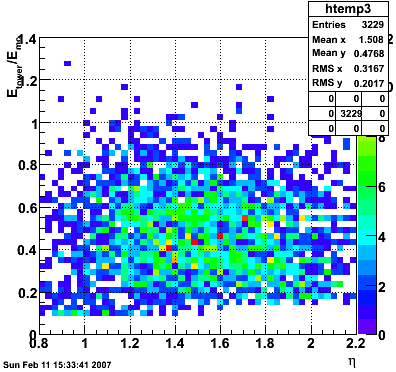 |
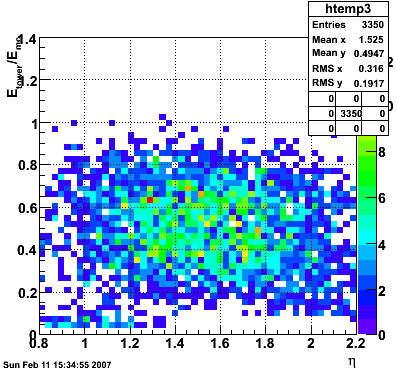 |
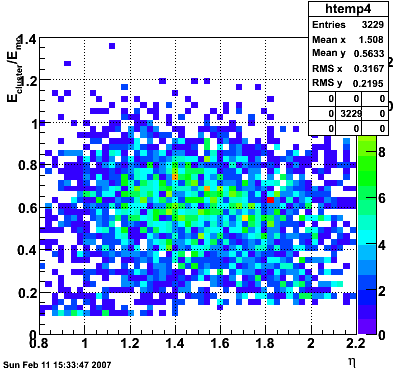 |
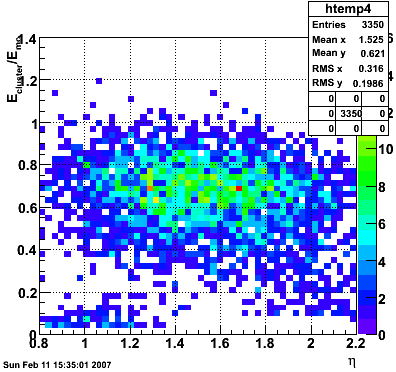 |
 |
 |
 |
 |
Pibero Djawotho Last modified Thu Feb 15 00:42:30 EST 2007
2007.02.19 10 GeV photons
10 GeV photons
- 10k 10 GeV photons
- zvertex=0
- η range 0.8-2.2
- SVT/SSD out
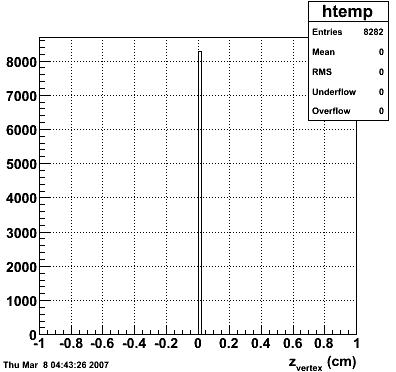 |
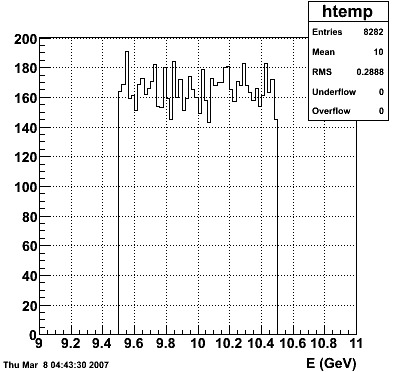 |
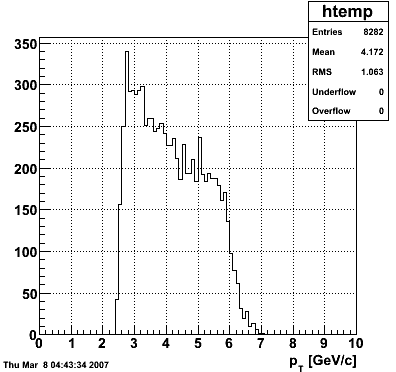 |
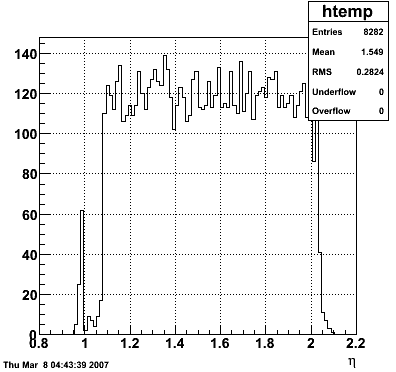 |
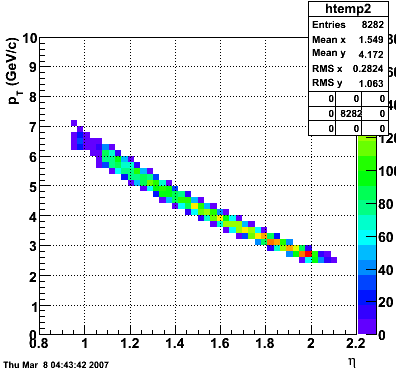 |
 |
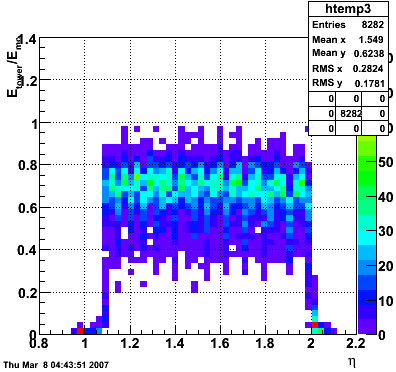 |
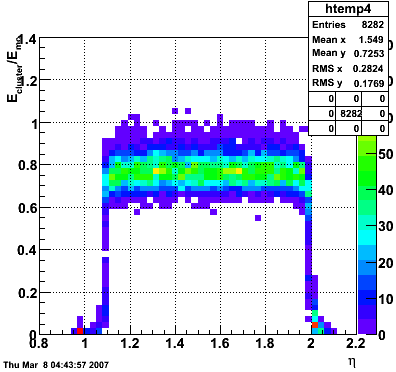 |
 |
 |
Pibero Djawotho Last updated Mon Feb 19 20:35:13 EST 2007
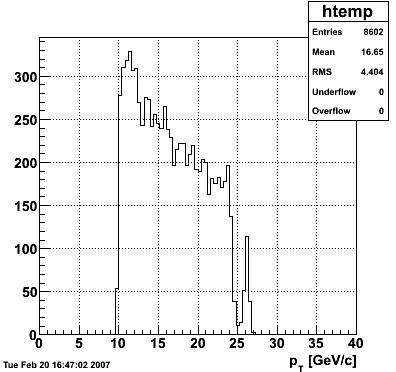
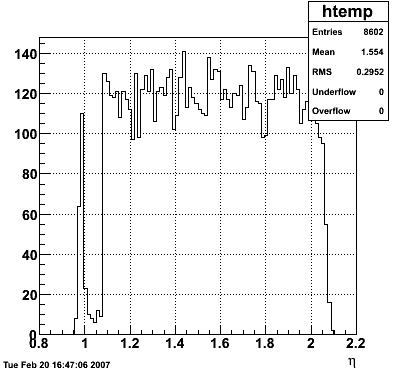
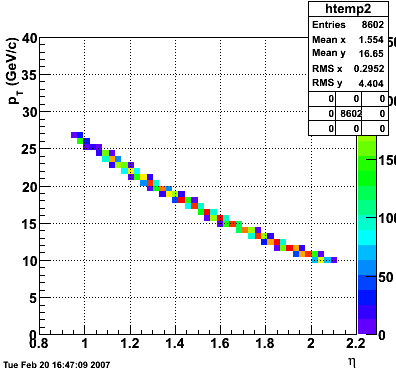
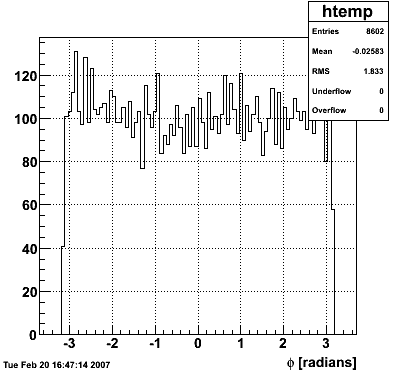
2007.02.19 40 GeV photons
40 GeV photons
- 10k 40 GeV photons
- zvertex=0
- η range 0.8-2.2
- SVT/SSD out
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Pibero Djawotho Last updated Mon Feb 19 20:37:37 EST 2007
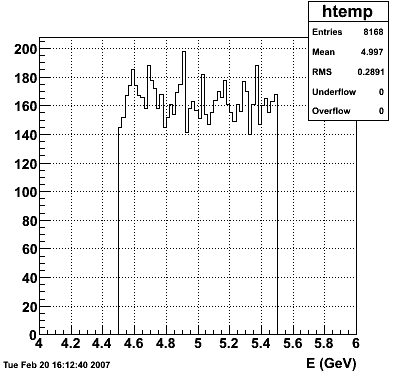
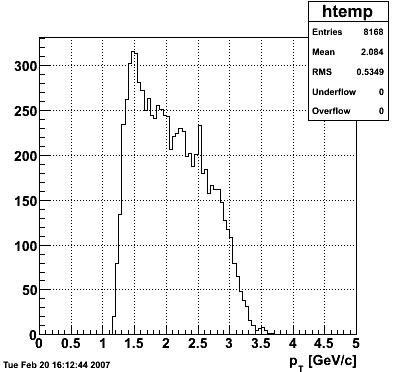
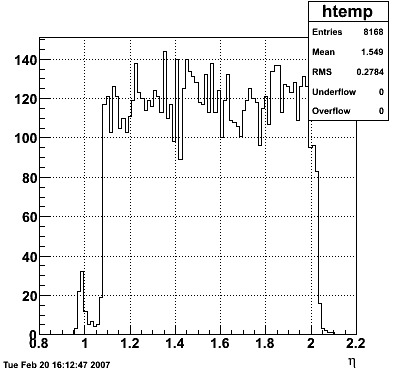
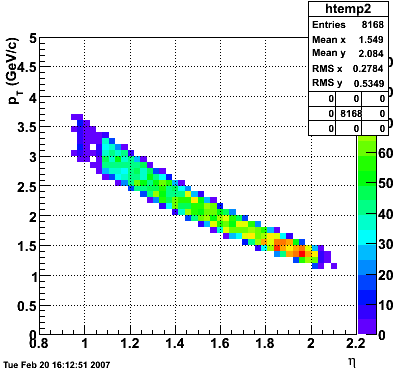
2007.02.19 5 GeV photons
5 GeV photons
- 10k 5 GeV photons
- zvertex=0
- η range 0.8-2.2
- SVT/SSD out
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Pibero Djawotho Last updated Mon Feb 19 20:13:39 EST 2007
2007.02.19 Summary of Reconstructed/Monte Carlo Photon Energy
Summary of Reconstructed/Monte Carlo Photon Energy |
Description |
The study presented here uses Monte Carlo data sets generated by Will Jacobs at different photon energies (5, 10, 20, 40, 80, 160 GeV):
- 10k photons
- vertex at 0
- eta 0.8-2.2
- SVT/SSD out
For each photon energy, the ratio E_reco/E_MC vs. eta was plotted and fitted to the function p0+p1*(1-eta), where E_reco is the reconstructed photon energy integrated over the
entire
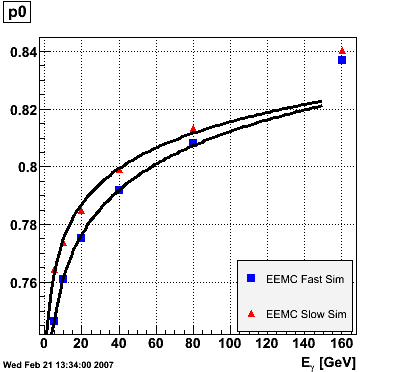
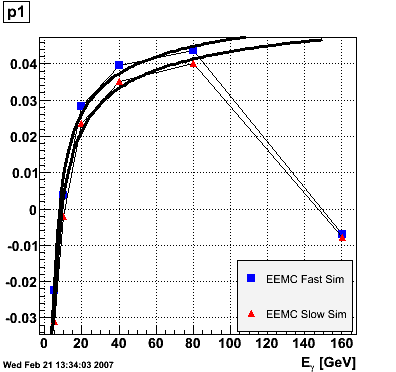
EEMC. The range of the fit was fixed from 1.15 to 1.95 to avoid EEMC edge effects. The advantage of parametrizing the eta-dependence of the ratio in this way is that p0 is immediately interpretable as the ratio in the middle of the EEMC. The parameters p0 and p1 vs. photon energy were subsequently plotted for the EEMC fast and slow simulator.
EEMC Fast/Slow Simulator Results |
 |
 |
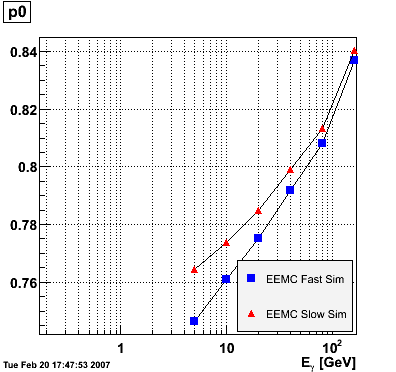 |
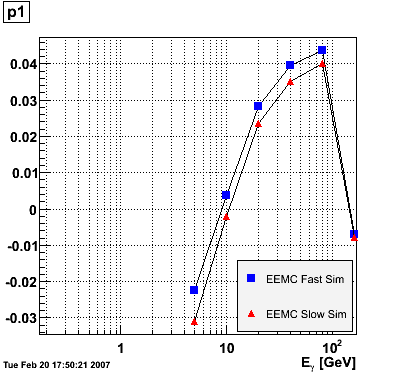 |
Conclusions |
The parameter p0, i.e. the ratio E_reco/E_MC in the mid-region of the EEMC, increases monotonically from 0.74 at 5 GeV to 0.82 at 160 GeV, and the parameter p1, i.e. the slope of the eta-dependence, also increases monotonically from -0.035 at 5 GeV to 0.038 at 160 GeV. There appears to be a magic energy around 10 GeV where the response of the EEMC is nearly flat across its entire pseudorapidity range. The anomalous slope p1 at 160 GeV for the EEMC slow simulator is an EEMC hardware saturation effect. The EEMC uses 12-bit ADC's for reading out tower transverse energies and is set for a 60 GeV range. Any particle which deposits more than 60 GeV in E_T will be registered as depositing only 60 GeV as the ADC will return the maximum value of 4095. This translates into a limit on the eta range of the EEMC for a particular energy. Let's say that energy is 160 GeV and the EEMC tops at 60 GeV in E_T, then the minimum eta is acosh(160/60)=1.6. This limitation is noticeable in a plot of E_reco/E_MC vs. eta. This anomaly is not observed in the result of the EEMC fast simulator because the saturation behavior was not implemented at the time of the simulation (it has since been corrected). The energy-dependence of the parameter p0 is fitted to p0(E)=a+b*log(E) and the parameter p1 to p1(E)=a+b/log(E). The results are summarized below:
EEMC fast simulator fit p0(E)=a+b*log(E) a = 0.709946 +/- 0.00157992 b = 0.022222 +/- 0.000501239 EEMC slow simulator fit p0(E)=a+b*log(E) a = 0.733895 +/- 0.00359237 b = 0.0177537 +/- 0.0011397 EEMC fast simulator fit p1(E)=a+b/log(E) a = 0.0849103 +/- 0.00556979 b = -0.175776 +/- 0.0138241 EEMC slow simulator fit p1(E)=a+b/log(E) a = 0.0841488 +/- 0.0052557 b = -0.187769 +/- 0.0130445
Pibero Djawotho Last updated Mon Feb 19 23:18:44 EST 2007
2007.05.24 gamma/pi0 separation in EEMC using linear cut
gamma/pi0 separation in EEMC using linear cut
 |
 |
 |
 |
 |
 |
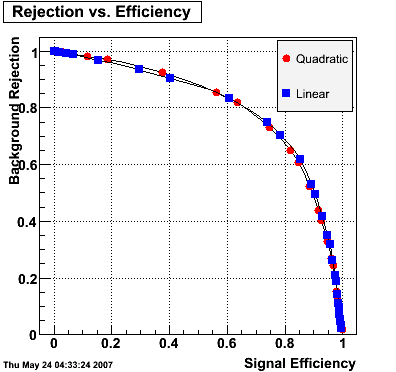 |
Pibero Djawotho Last updated Thu May 24 04:41:13 EDT 2007
2007.05.24 gamma/pi0 separation in EEMC using quadratic cut
gamma/pi0 separation in EEMC using quadratic cut
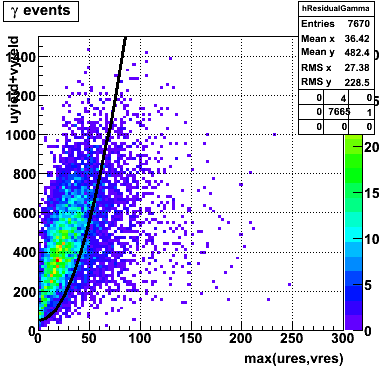 |
 |
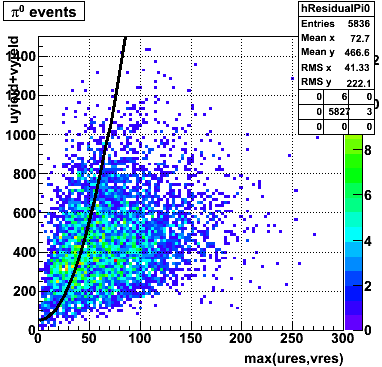 |
 |
 |
 |
 |
Pibero Djawotho Last updated Thu May 24 04:41:13 EDT 2007
2007.05.24 gamma/pi0 separation in EEMC using quadratic cut
gamma/pi0 separation in EEMC using quadratic cut
 |
 |
 |
 |
 |
 |
 |
Pibero Djawotho Last updated Thu May 24 04:41:13 EDT 2007
2007.05.30 Efficiency of reconstructing photons in EEMC
Efficiency of reconstructing photons in EEMC
Monte Carlo sample
- 10k photons
- STAR y2006 geometry
- z-vertex=0
- Flat in pt 10-30 GeV
- Flat in eta 1.0-2.1
SMD gamma/pi0 discrimination algorithm
The following
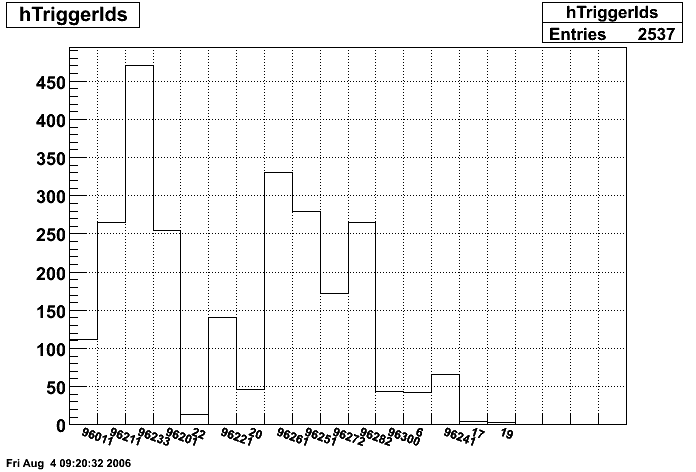
from the IUCF STAR Web site gives a brief overview of the SMD gamma/pi0 discrimination algorithm using the method of maximal sided fit residual (data - fit). This technique comes to STAR EEMC from the Tevatron via Les Bland via Jason Webb. The specific fit function used in this analysis is:
f(x)=[0]*(0.69*exp(-0.5*((x-[1])/0.87)**2)/(sqrt(2*pi)*0.87)+0.31*exp(-0.5*((x-[1])/3.3)**2)/(sqrt(2*pi)*3.3))
x is the strip id in the SMD-u or SMD-v plane. The widths of the narrow and wide Gaussians are determined from empirical fits of shower shape response in the EEMC from simulation.
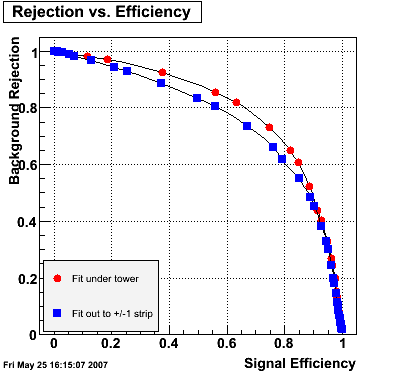
Optimizing cuts for gamma/pi0 separation
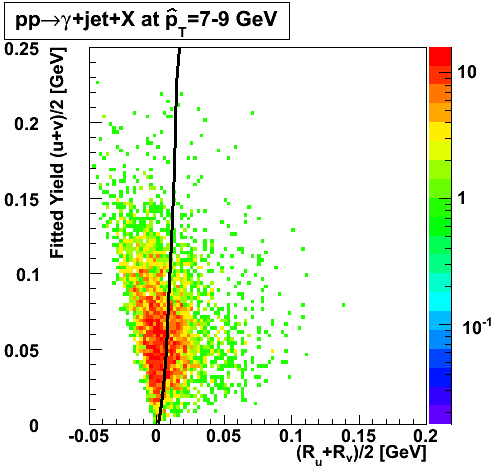
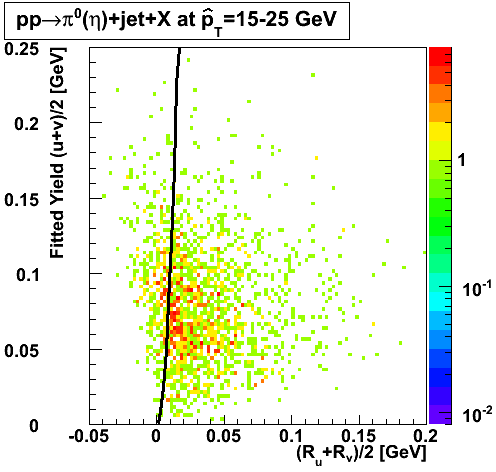
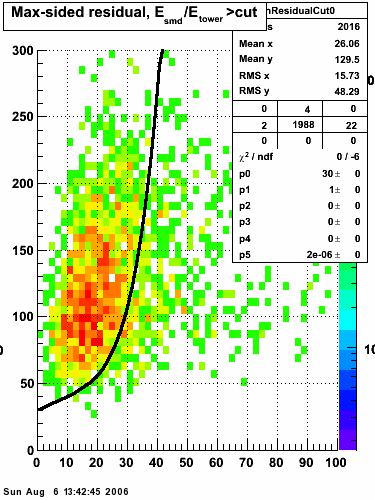
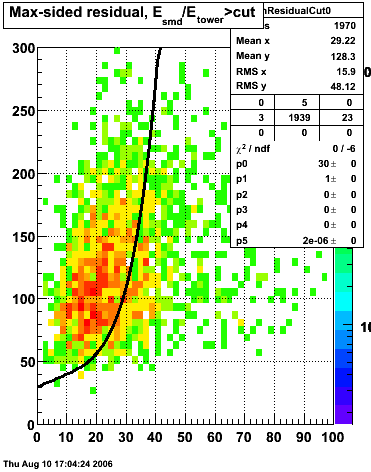
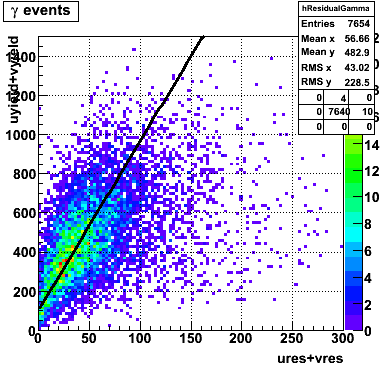
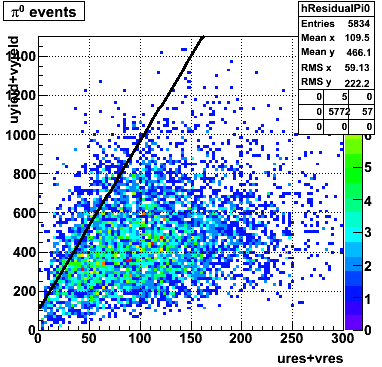
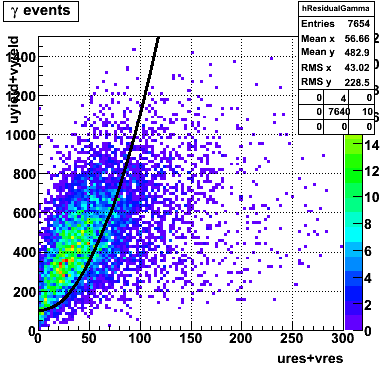
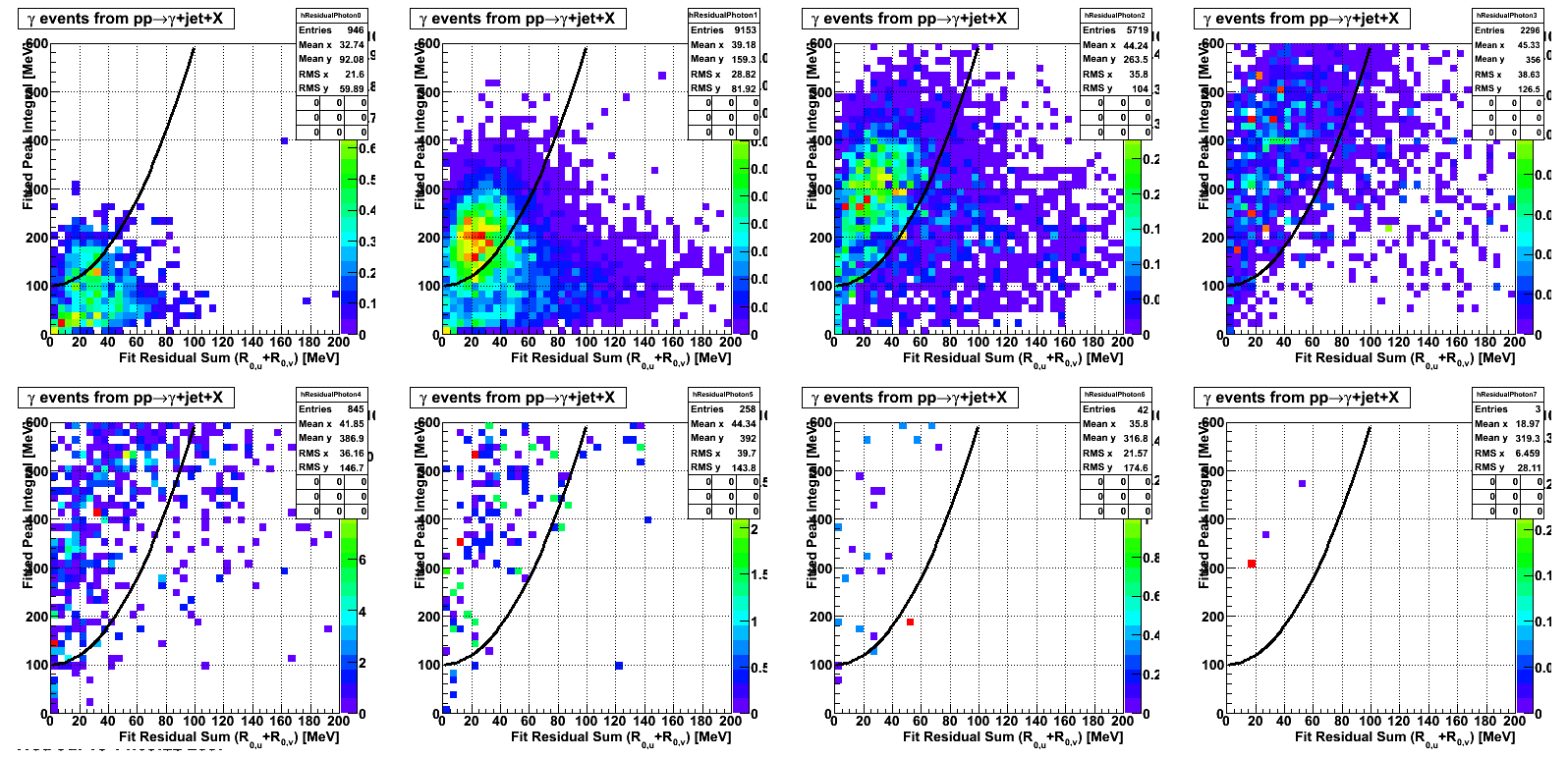
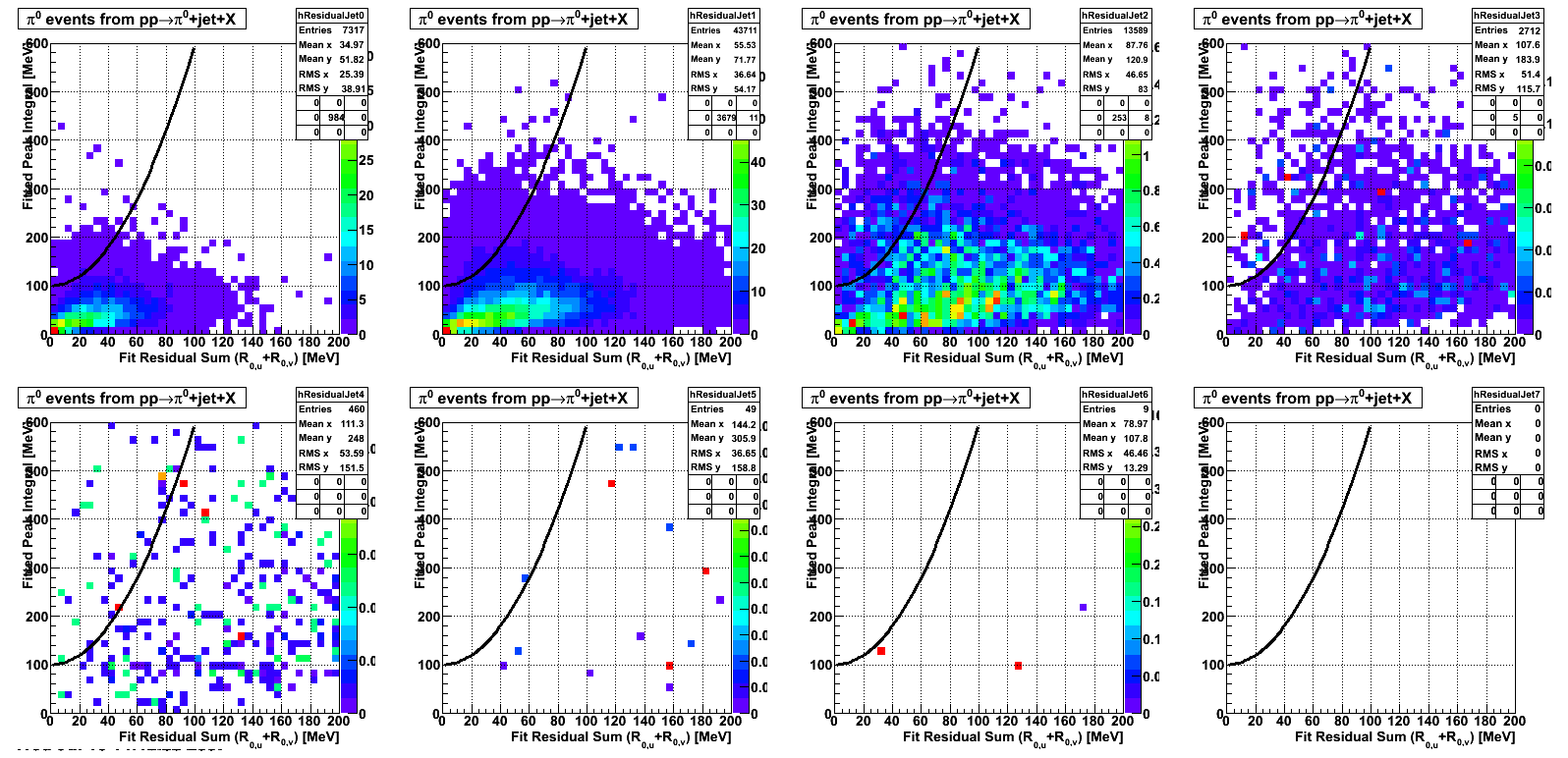
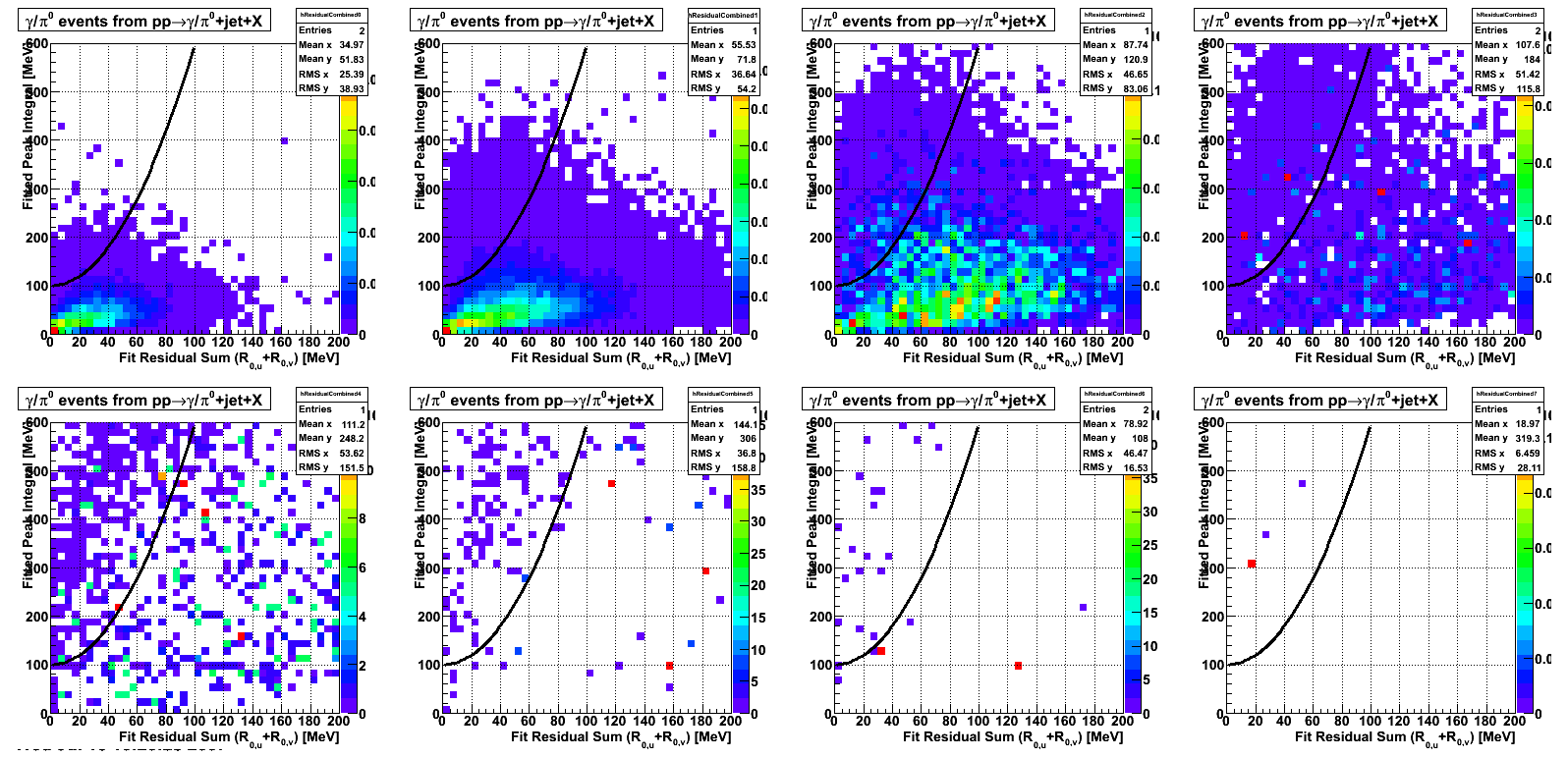
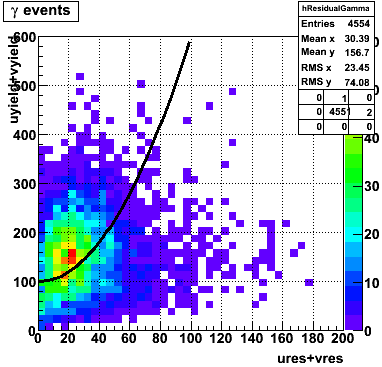
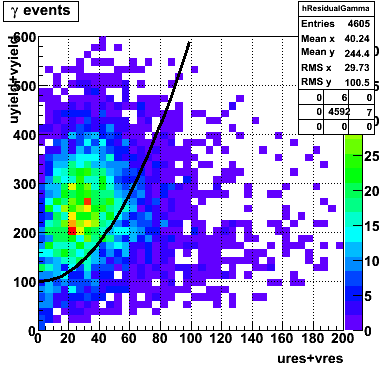
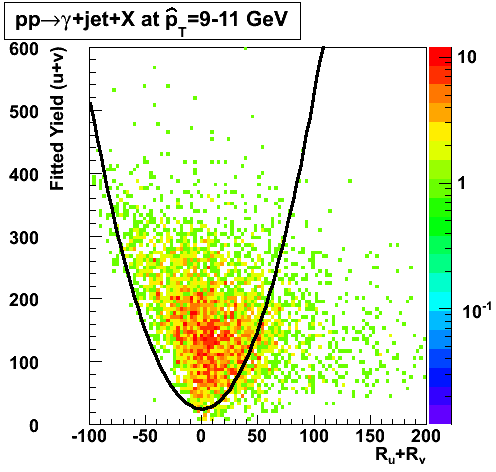
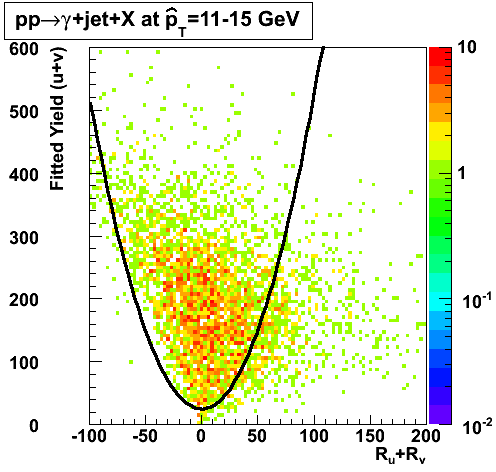
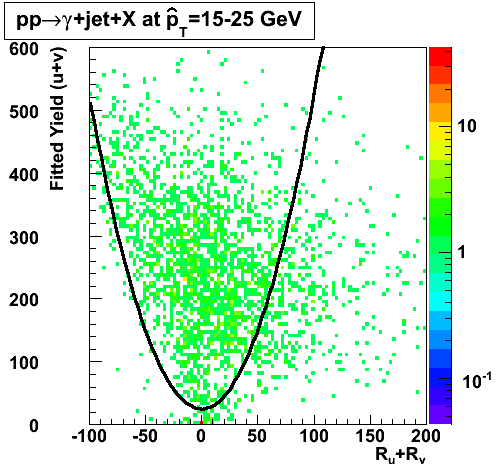
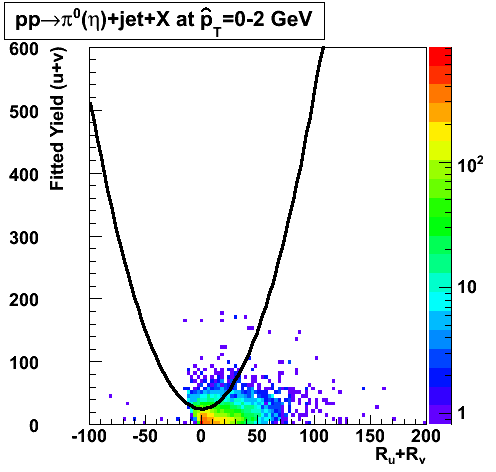
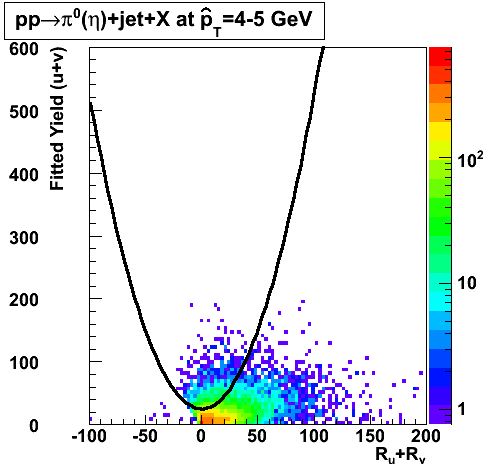
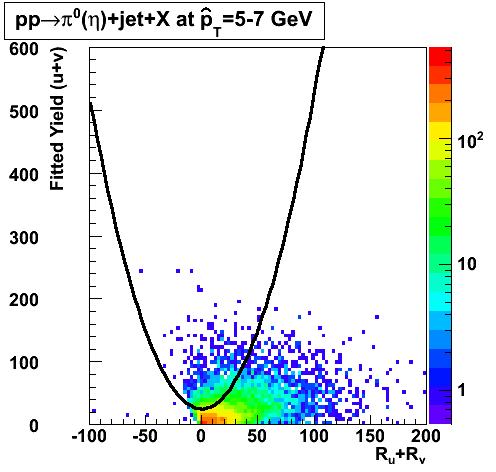
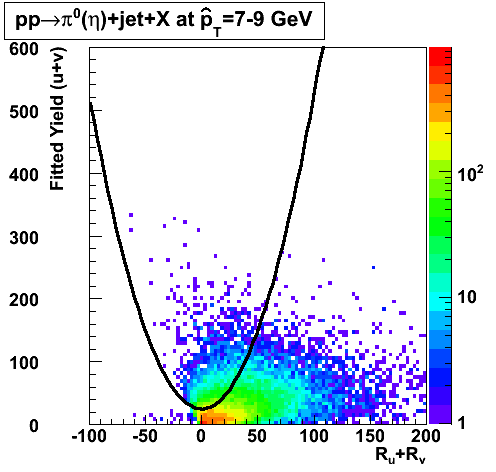
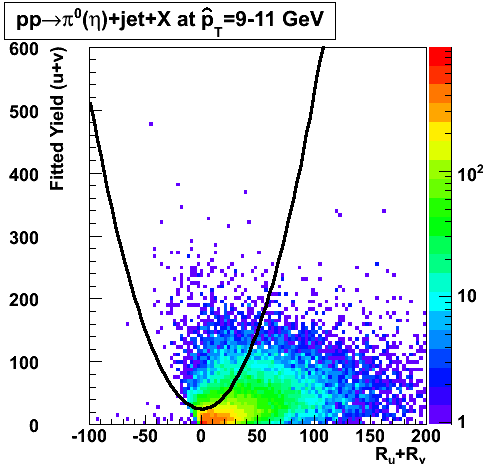
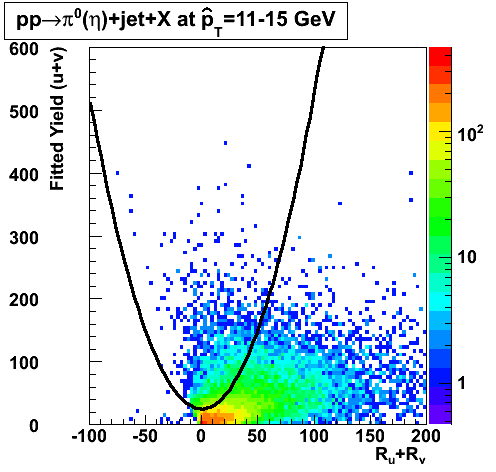
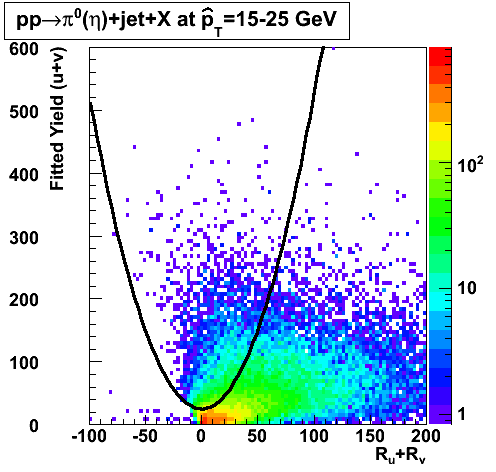
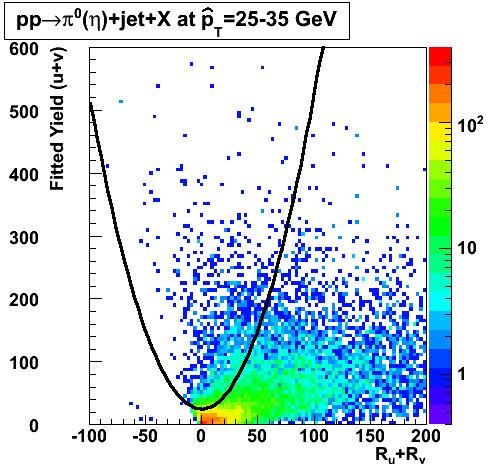
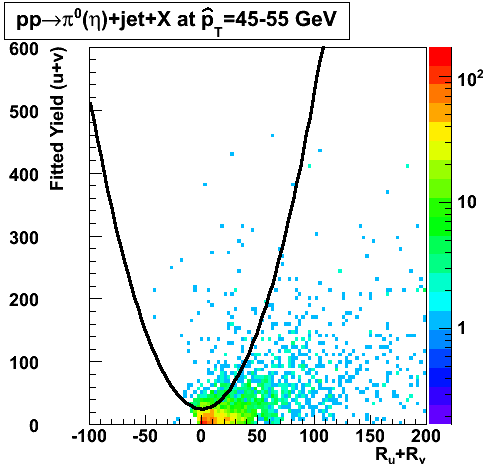
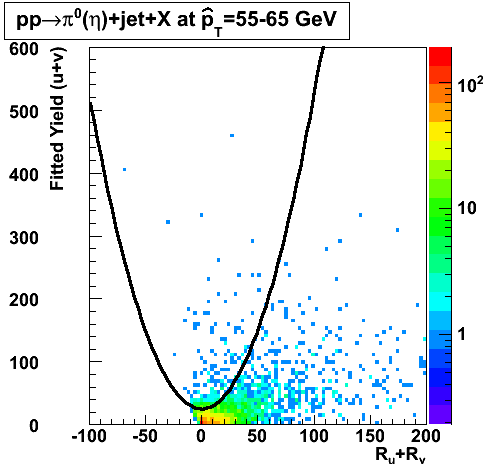
In the rest of this analysis, only those photons which have reconstructed pt > 5 GeV are kept. There is no requirement that the photon doesn't convert. The dividing curve between photons and pions is:
f(x)=4*x+1e-7*x**5
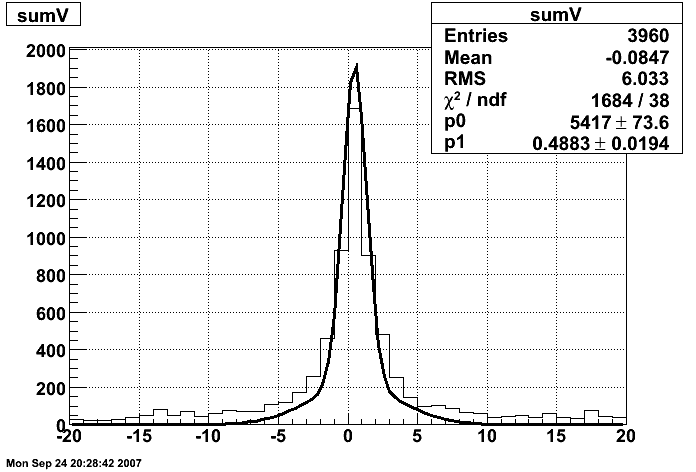
The y-axis is integrated yield over the SMD-u and SMD-v plane, and the x-axis is the sum of the maximal sided residual of the SMD-u and SMD-v plane.
 |
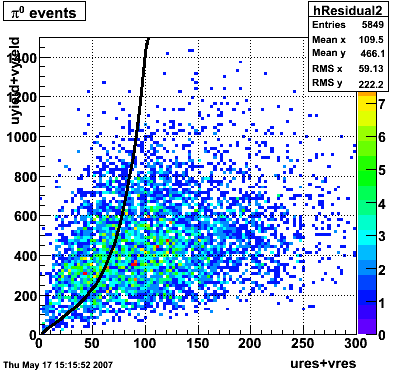 |
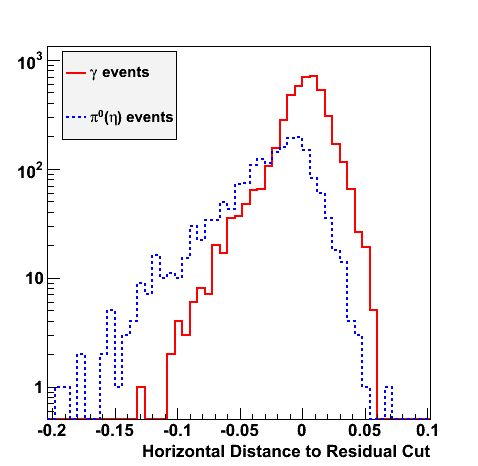
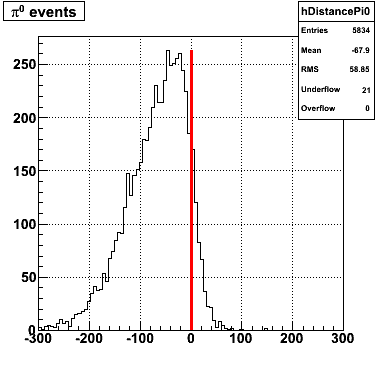
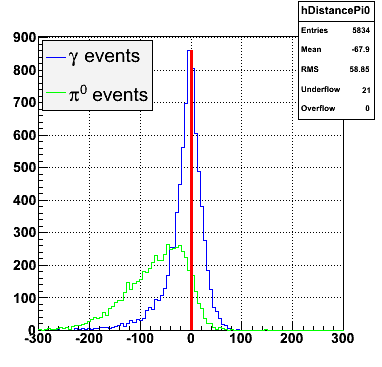
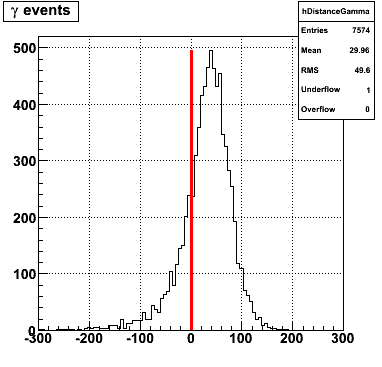
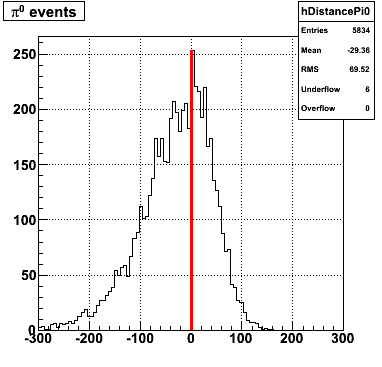
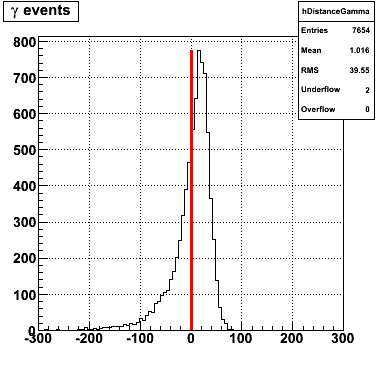
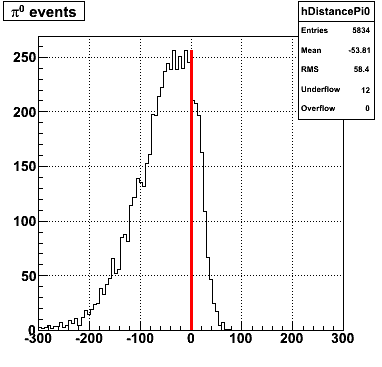
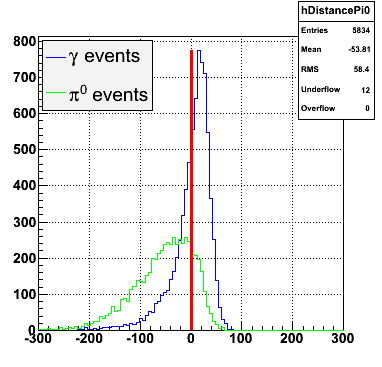
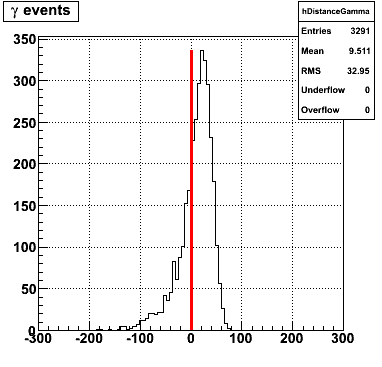
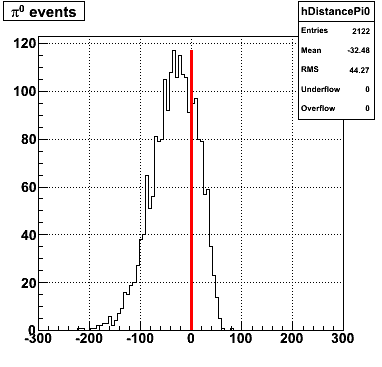
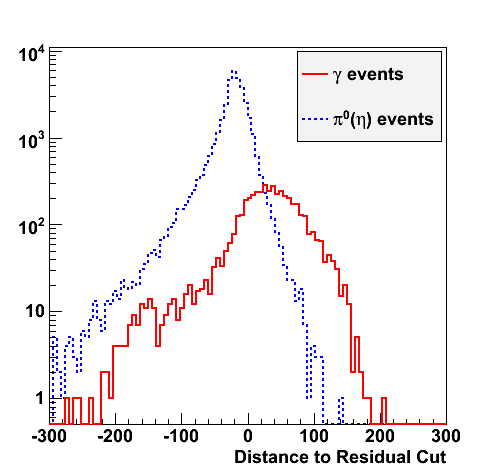
Following exchanges with Scott Wissink, the idea is to move from a quintic to a quadratic to reduce the number of parameters. In addition, the perpendicular distance between the curve and a point in the plane is used to estimate the likelihood of a particle being a photon or pion. Distances above the curve are positive and those below are negative. The more positive the distance, the more likely the particle is a photon. The more negative the distance, the more likely the particle is a pion.
Hi Pibero, With your new "linear plus quintic" curve (!) ... how did you choose the coefficients for each term? Or even the form of the curve? I'm not being picky, but how to optimize such curves will be an important issue as we (hopefully soon) move on to quantitative comparisons of efficiency vs purity. As a teaser, please see attached - small loss of efficiency, larger gain in purity. Scott
Hi Pibero,
I just worked out the distance of closest approach to a curve of the form
y(x) = a + bx^2
and it involves solving a cubic equation - so maybe not so trivial after
all. But if you want to pursue this (not sure it is your highest
priority right now!), the cubic could be solved numerically and "alpha"
could be easily calculated.
More fun and games.
Scott
 |
 |
 |
 |
 |
 |
Hi Pibero,
I played around with the equations a bit more, and I worked out an
analytic solution. But a numerical solution may still be better, since
it allows more flexibility in the algebraic form of the 'boundary' line
between photons and pions.
Here's the basic idea: suppose the curved line that cuts between
photons and pions can be expressed as y = f(x). If we are now given a
point (x0,y0) in the plane, our goal is to find the shortest distance to
this line. We can call this distance d (I think on your blackboard we
called it alpha).
To find the shortest distance, we need a straight line that passes
through (x0,y0) and is also perpendicular to the curve f(x). Let's
define the point where this straight line intersects the curve as
(x1,y1). This means (comparing slopes)
(y1 - y0) / (x1 - x0) = -1 / f'(x1)
where f'(x1) is the derivative of f(x) evaluated at the point (x1,y1).
Rearranging this, and using y1 = f(x1), yields the general result
f(x1) f'(x1) - y0 f'(x1) + x1 - x0 = 0
So, given f(x) and the point (x0,y0), the above is an equation in only
x1. Solve for x1, use y1 = f(x1), and then the distance d of interest
is given by
d = sqrt[ (x1 - x0)^2 + (y1 - y0)^2 ]
Example: suppose we got a reasonable separation of photons and pions
using a curve of the form
y = f(x) = a + bx^2
Using this in the above general equation yields the cubic equation
(2b^2) x1^3 + (2ab + 1 - 2by0) x1 - x0 = 0
Dividing through by 2b^2, we have an equation of the form
x^3 + px + q = 0
This can actually be solved analytically - but as I mentioned, a
numerical approach gives us more flexibility to try other forms for the
curve, so this may be the way to go. I think (haven't proved
rigorously) that for positive values of the constants a, b, x0, and y0,
the cubic will yield three real solutions for x1, but only one will have
x1 > 0, which is the solution of interest.
Anyway, it has been an interesting intellectual exercise!
Scott
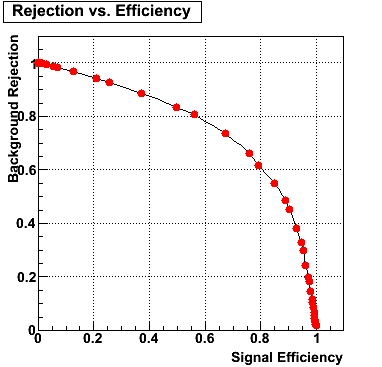
I made use of the ROOT function TMath::RootsCubic to solve the cubic equation numerically for computing distances of each point to the curve. With the new quadratic curve f(x)=100+0.1*x^2 the efficiency is 63% and the rejection is 82%.
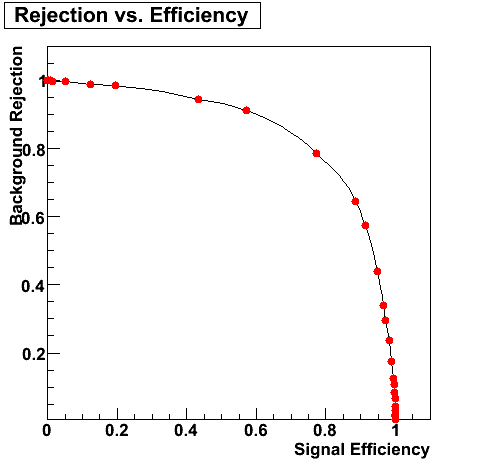
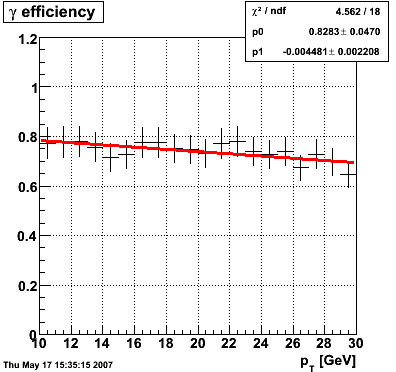
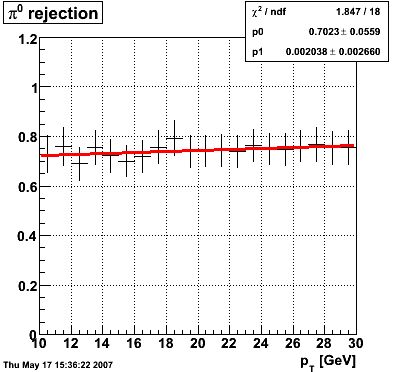
Efficiency and Rejection
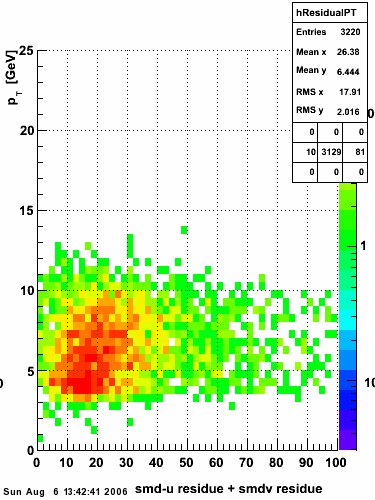
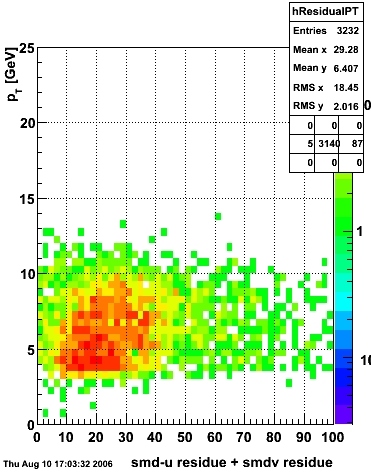
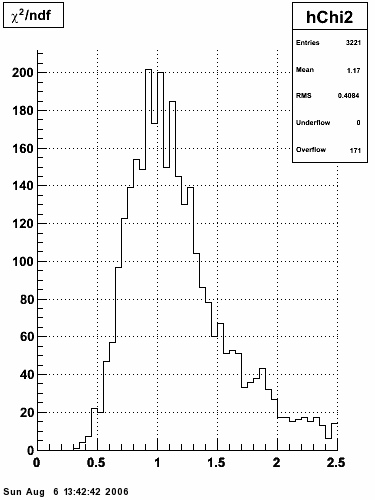
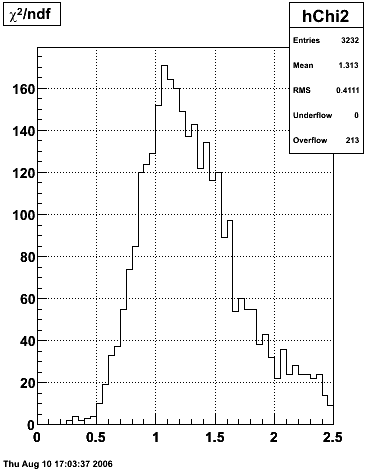
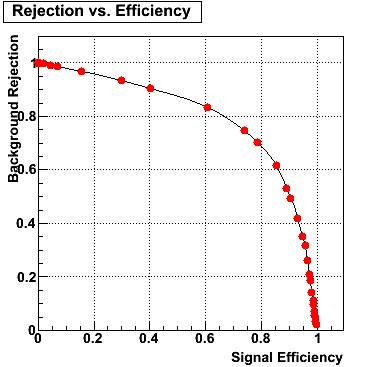
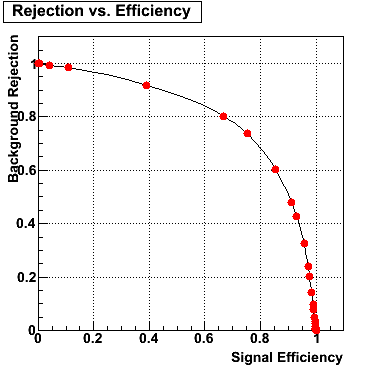
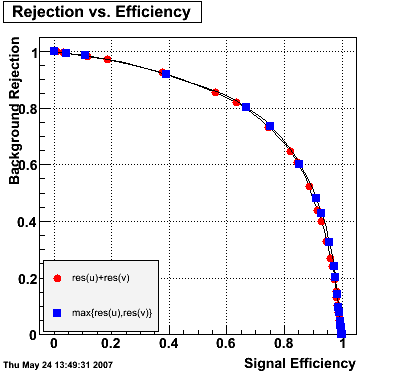
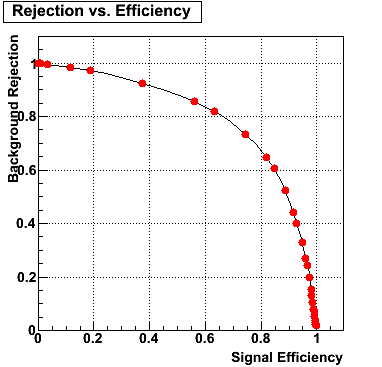
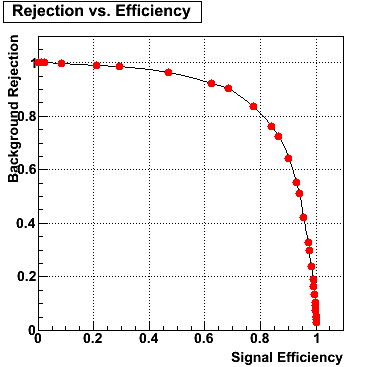
The plot on the left below shows the efficiency of identifying photons over the pt range of 10-30 GeV and the one on the right shows the rejection rate of single neutral pions. Both average about 75% over the pt range of interest.
 |
 |
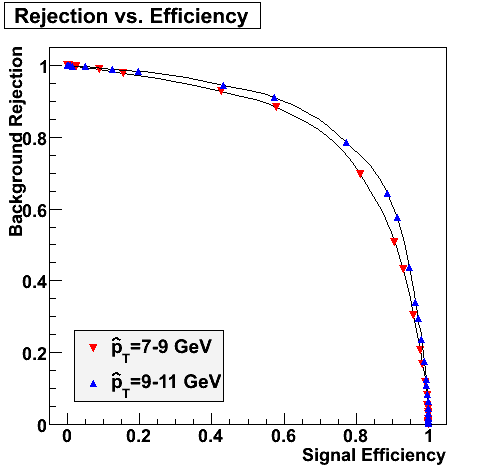
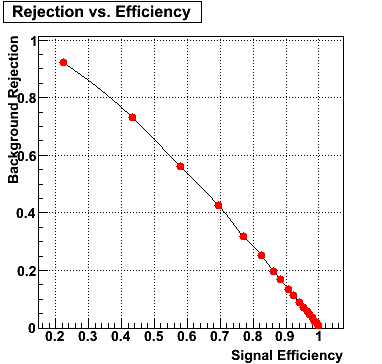
Rejection vs. efficiency at different energies
The plot below shows background rejection vs. signal efficiency for different energy ranges of the thrown gamma/pi0.

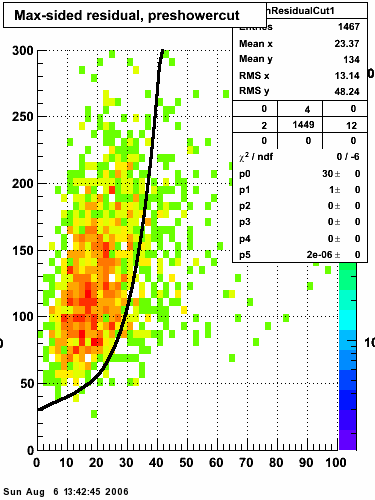
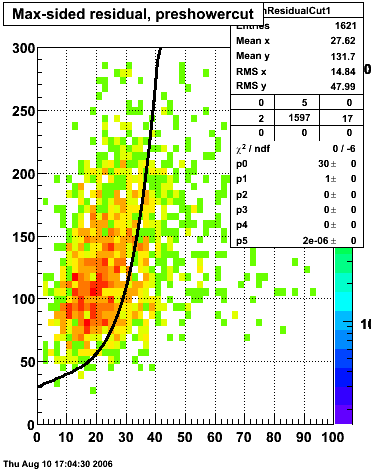
Rejection vs. efficiency with preshower cut
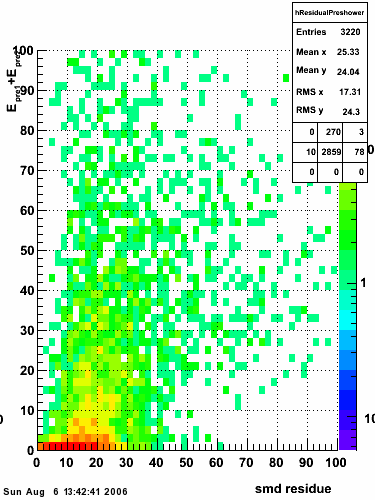
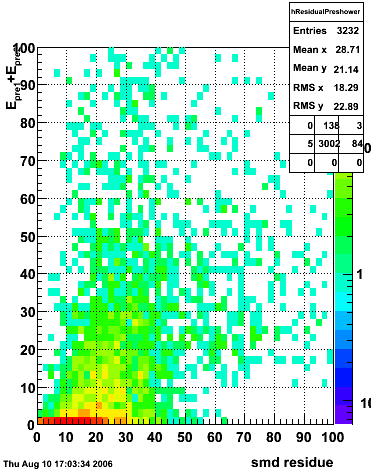
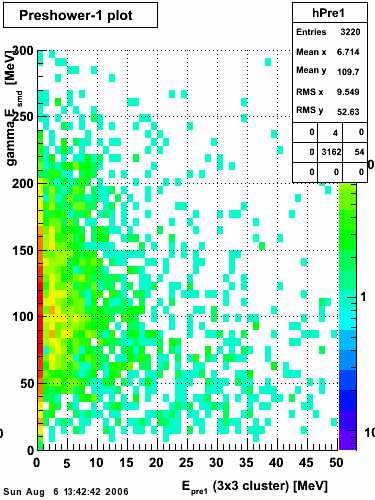
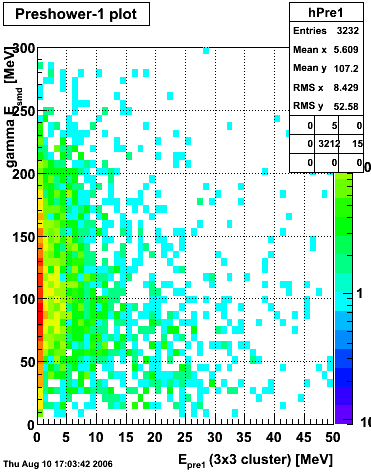
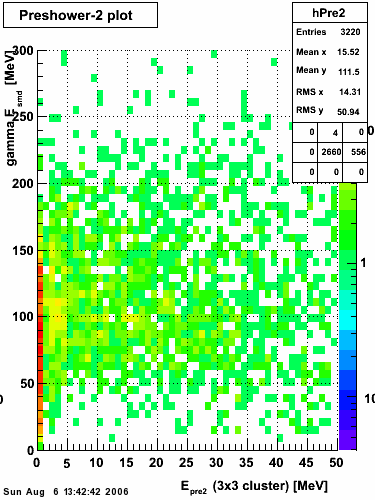
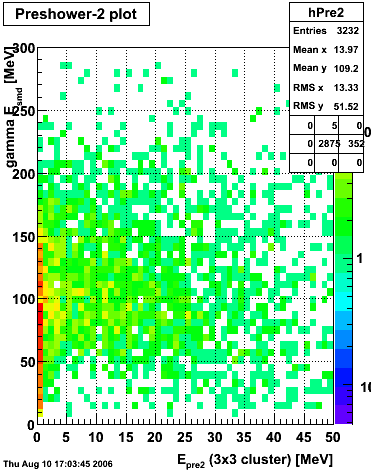
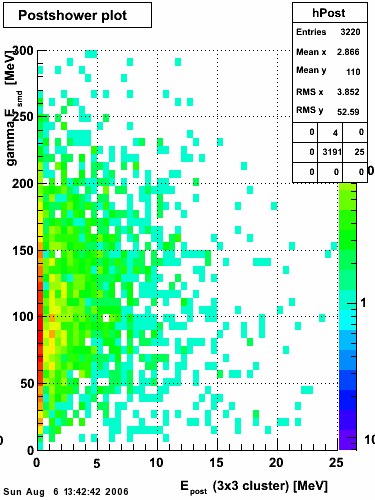
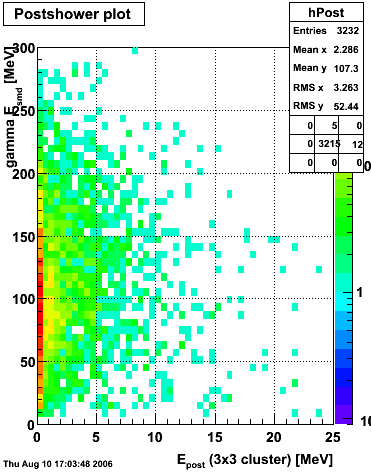
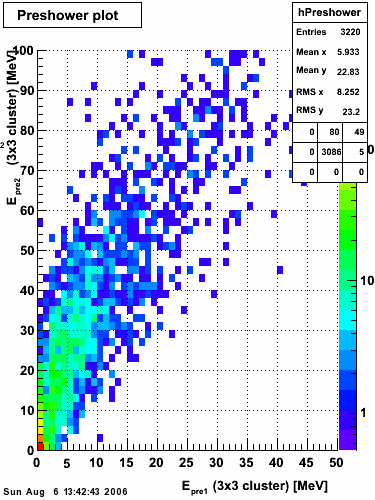
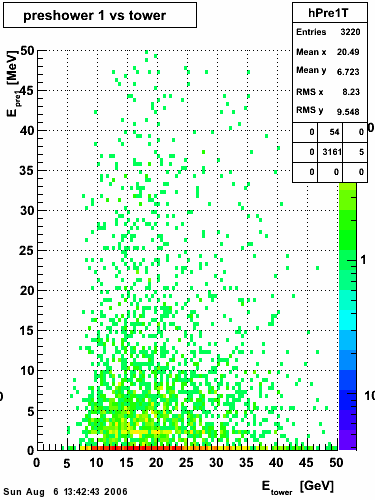
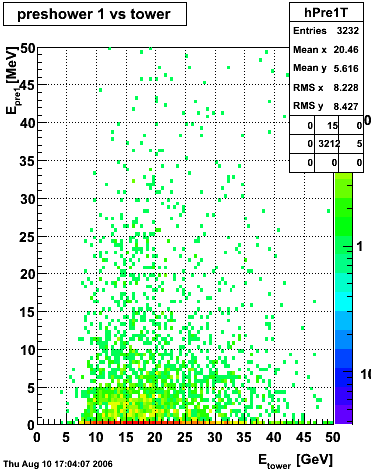
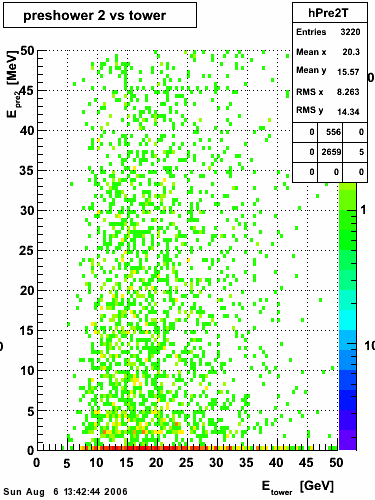
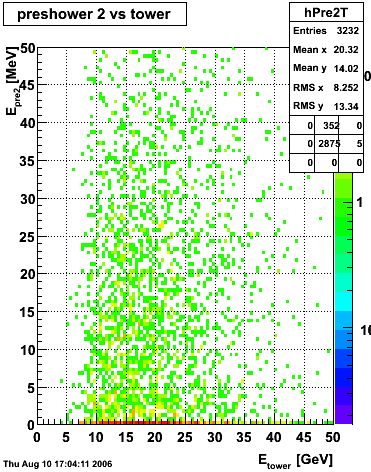
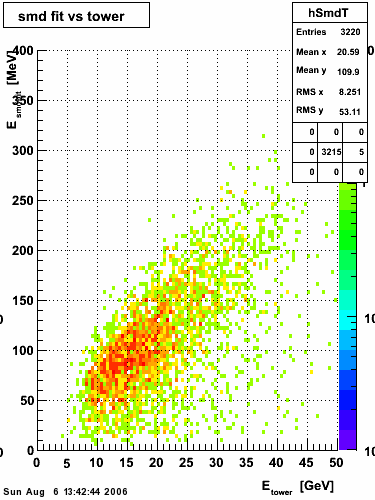
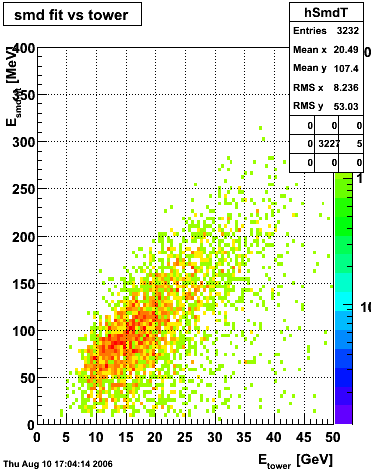
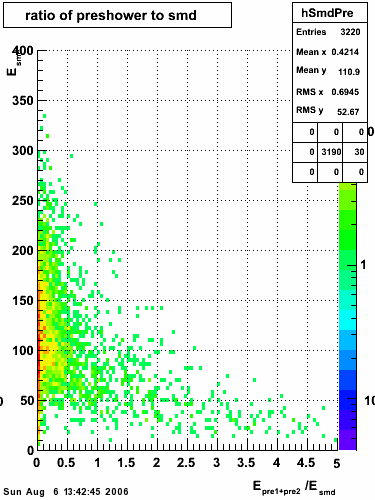
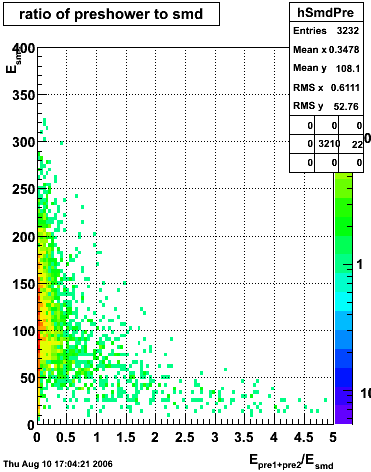
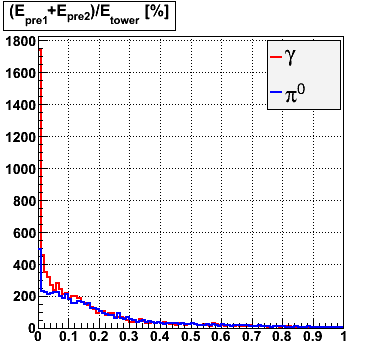
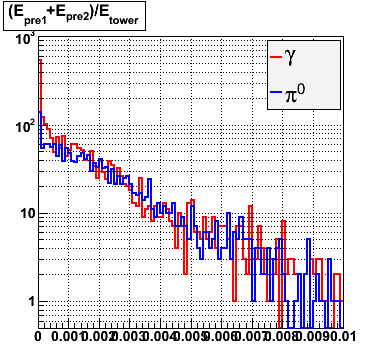
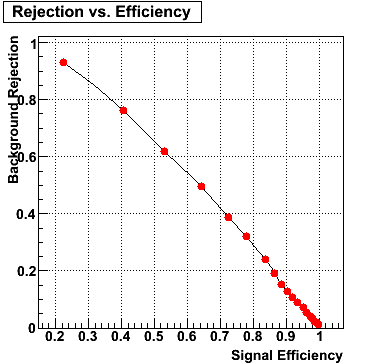
Below on the left is a plot of the ratio of the sum of preshower 1 and 2 to tower energy for both photons (red) and pions (blue). On the right is the rejection of pions vs. efficiency of photons as I cut on the ratio of preshower to tower. It is clear from these plots that the preshower layer is not a good gamma/pi0 discriminator, although can be used to add marginal improvement to the separation preovided by the shower max.
ALL ENERGIES |
|
 |
 |
E=20-40 GeV |
|
 |
 |
E=40-60 GeV |
|
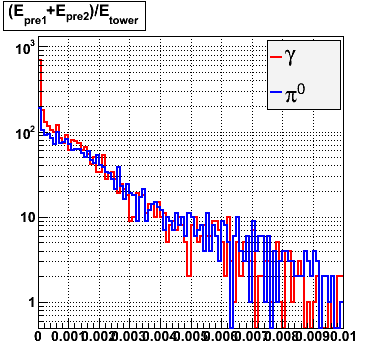 |
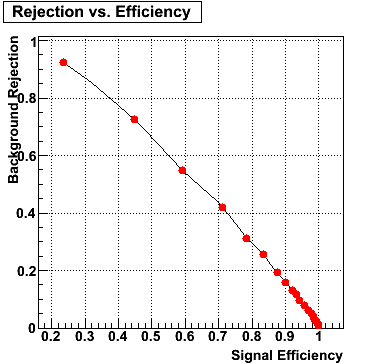 |
E=60-80 GeV |
|
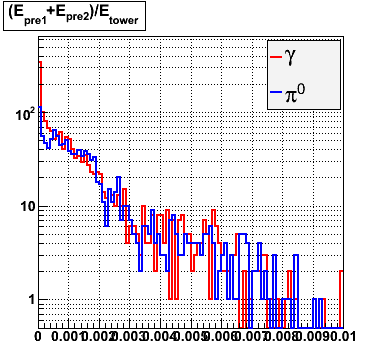 |
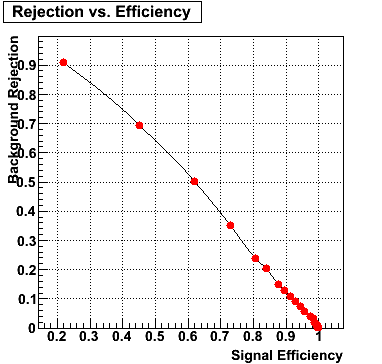 |
E=80-90 GeV |
|
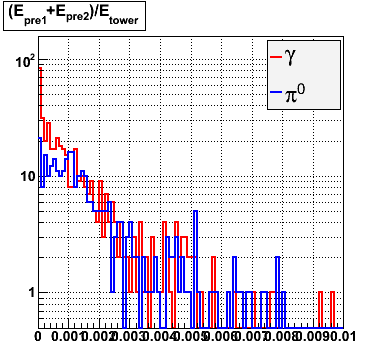 |
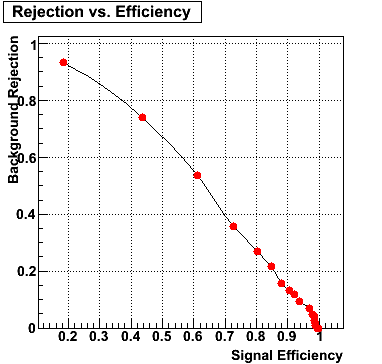 |
Pibero Djawotho Last updated Wed May 30 00:32:16 EDT 2007
2007.06.12 gamma/pi0 separation in EEMC at pT 5-10 GeV
gamma/pi0 separation in EEMC at pT 5-10 GeV
 |
 |
 |
 |
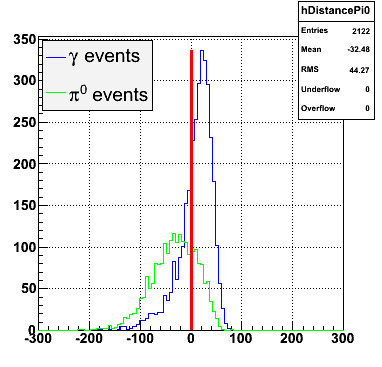 |
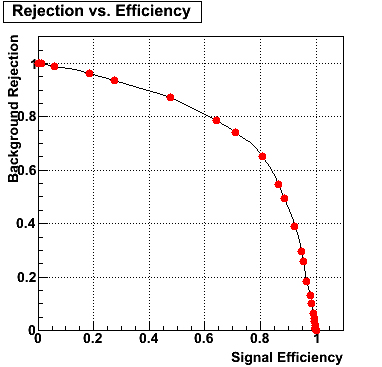 |
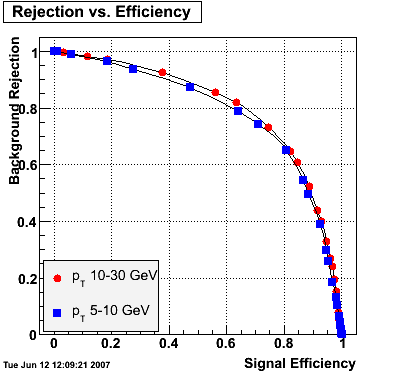 |
Pibero Djawotho Last updated Tue Jun 12 11:59:42 EDT 2007
2007.06.28 Photons in Pythia
Pythia Simulations
Pythia Simulations
All partonic pT
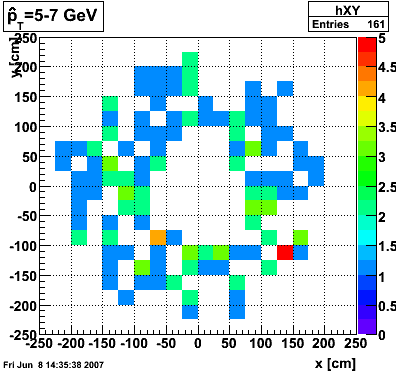
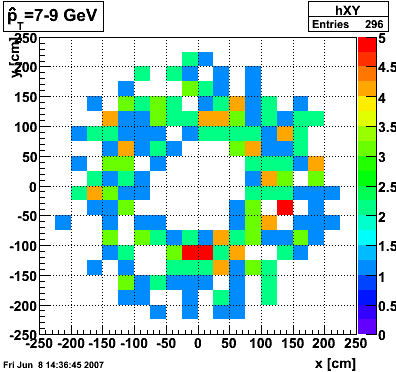
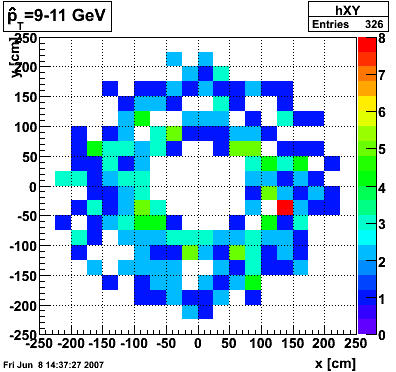
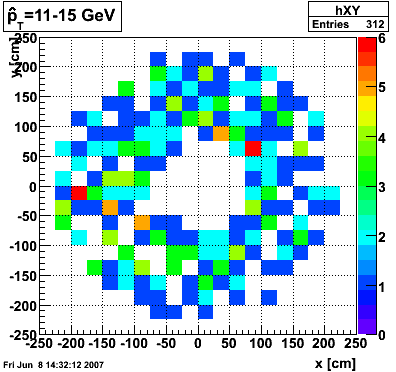
The plots below show the distribution of clusters in the endcap calorimeter for different partonic pT ranges. 2000 events were generated for each pT range. A cluster is made up of a central high tower above 3 GeV in pT and its surounding 8 neighbors. The total cluster pT must exceed 4.5 GeV.
 |
 |
 |
 |
 |
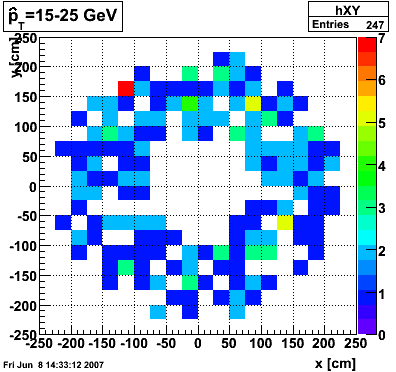 |
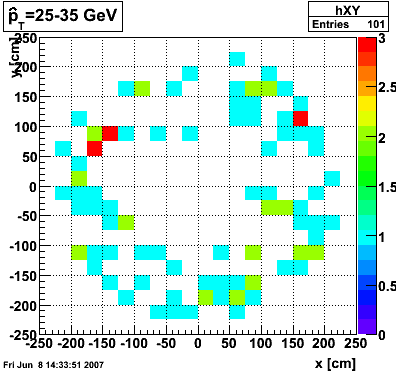 |
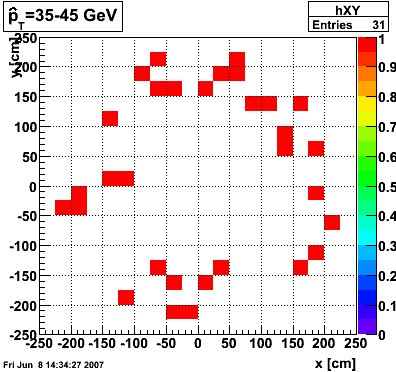 |
pT=9-11 GeV
Below is the pT of direct and decay photons from the Pythia record. Note how the two subsets are well separated at a given partonic pT. Any contamination to the direct photon signal would have to come from higher partonic pT.
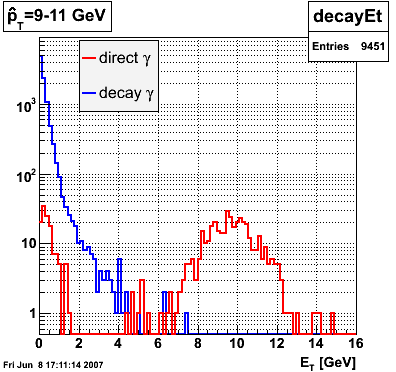 |
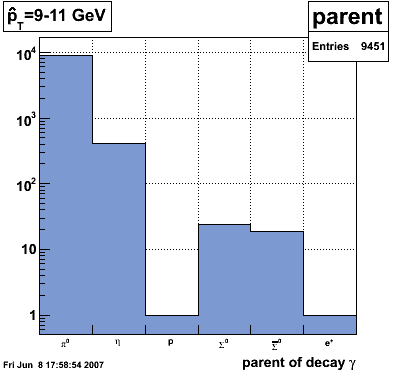 |
Differences between Renee's and Manuel's Pythia records?
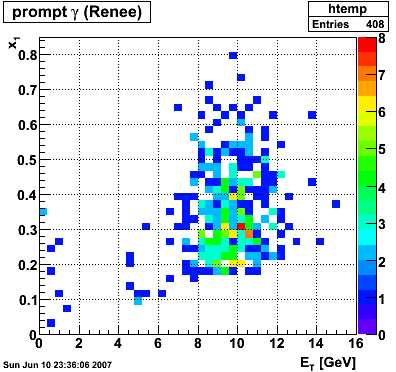 |
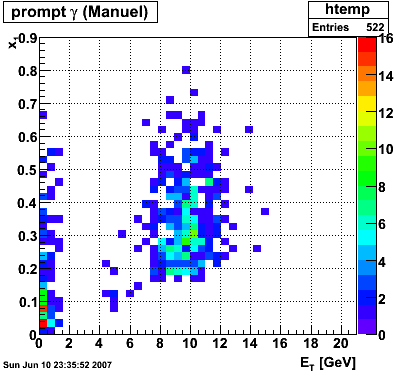 |
Number of prompt photons per event from GEANT record
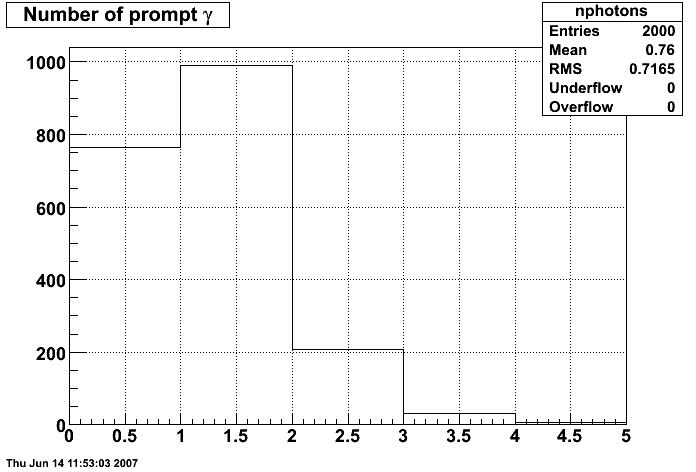
Pibero Djawotho Last updated Fri Jun 8 16:08:27 EDT 2007
a_LL
Partonic aLL
Jet |
Gamma |
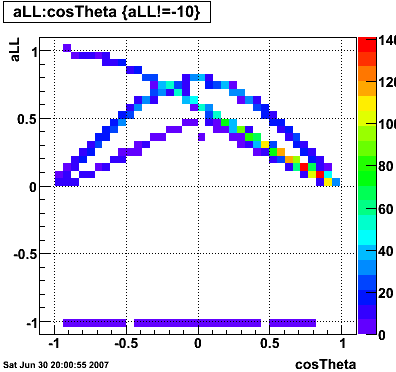 |
 |
Pibero Djawotho Last updated Sat Jun 30 20:14:21 EDT 2007
gamma-jet kinematics
gamma-jet kinematics
Clusters without parent track
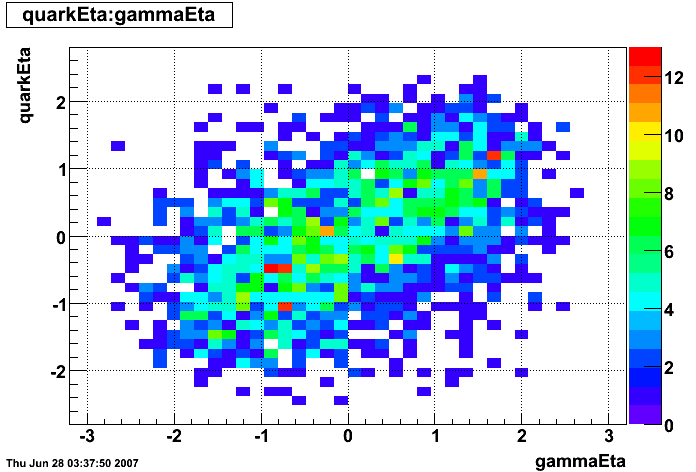 |
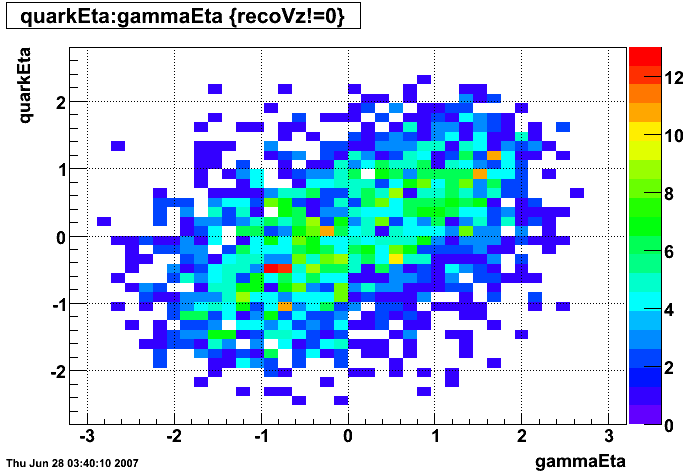 |
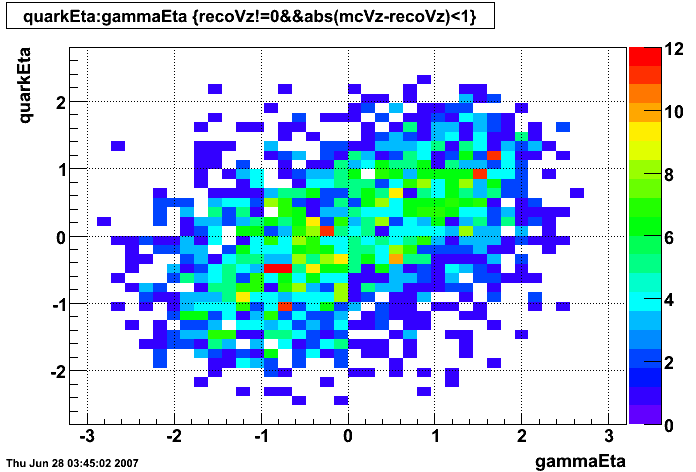 |
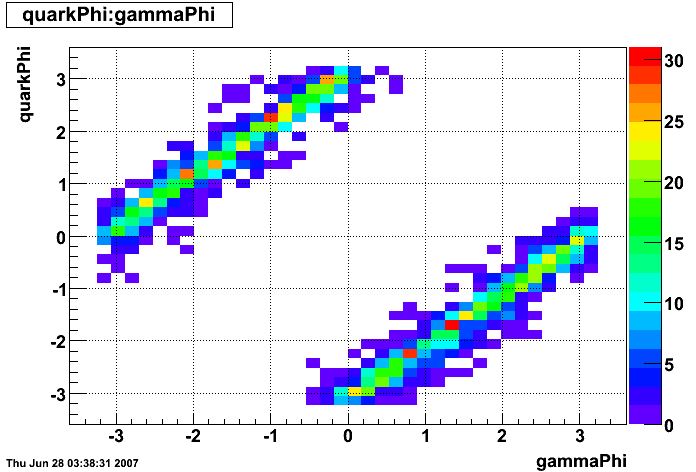 |
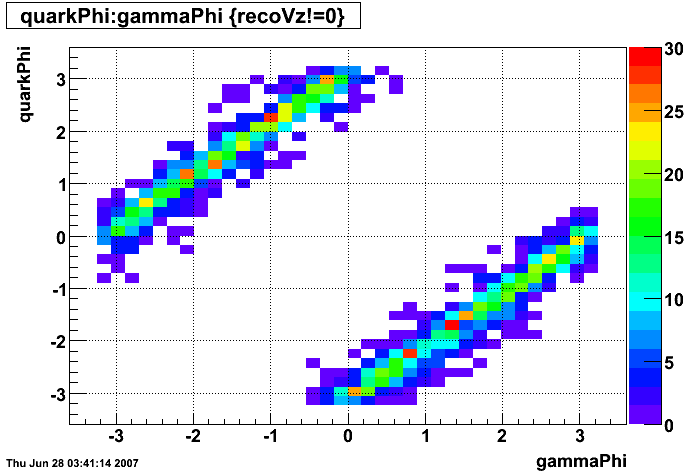 |
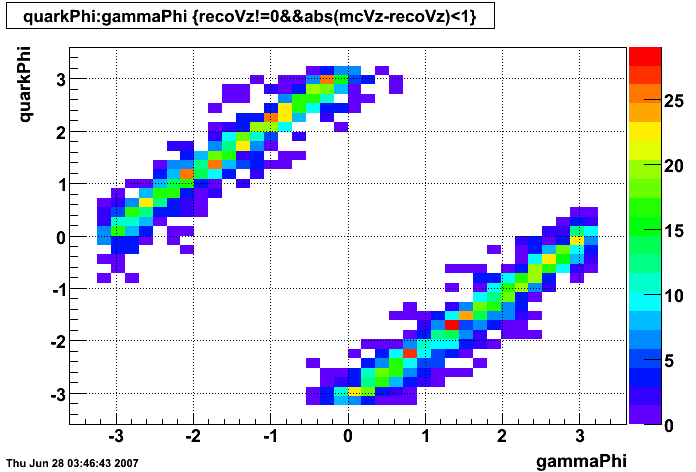 |
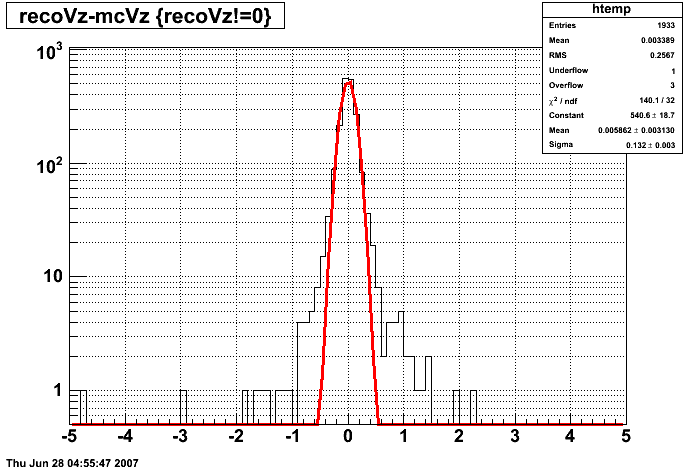 |
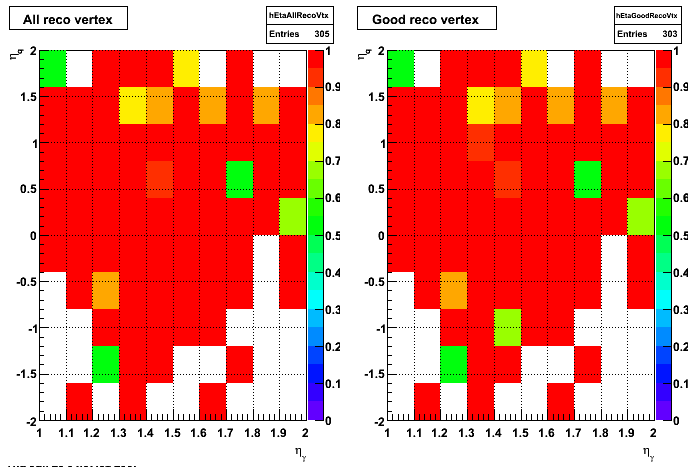 |
Pibero Djawotho Last updated Thu Jun 28 04:43:57 EDT 2007
gamma/X separation by energy
gamma/X separation by energy
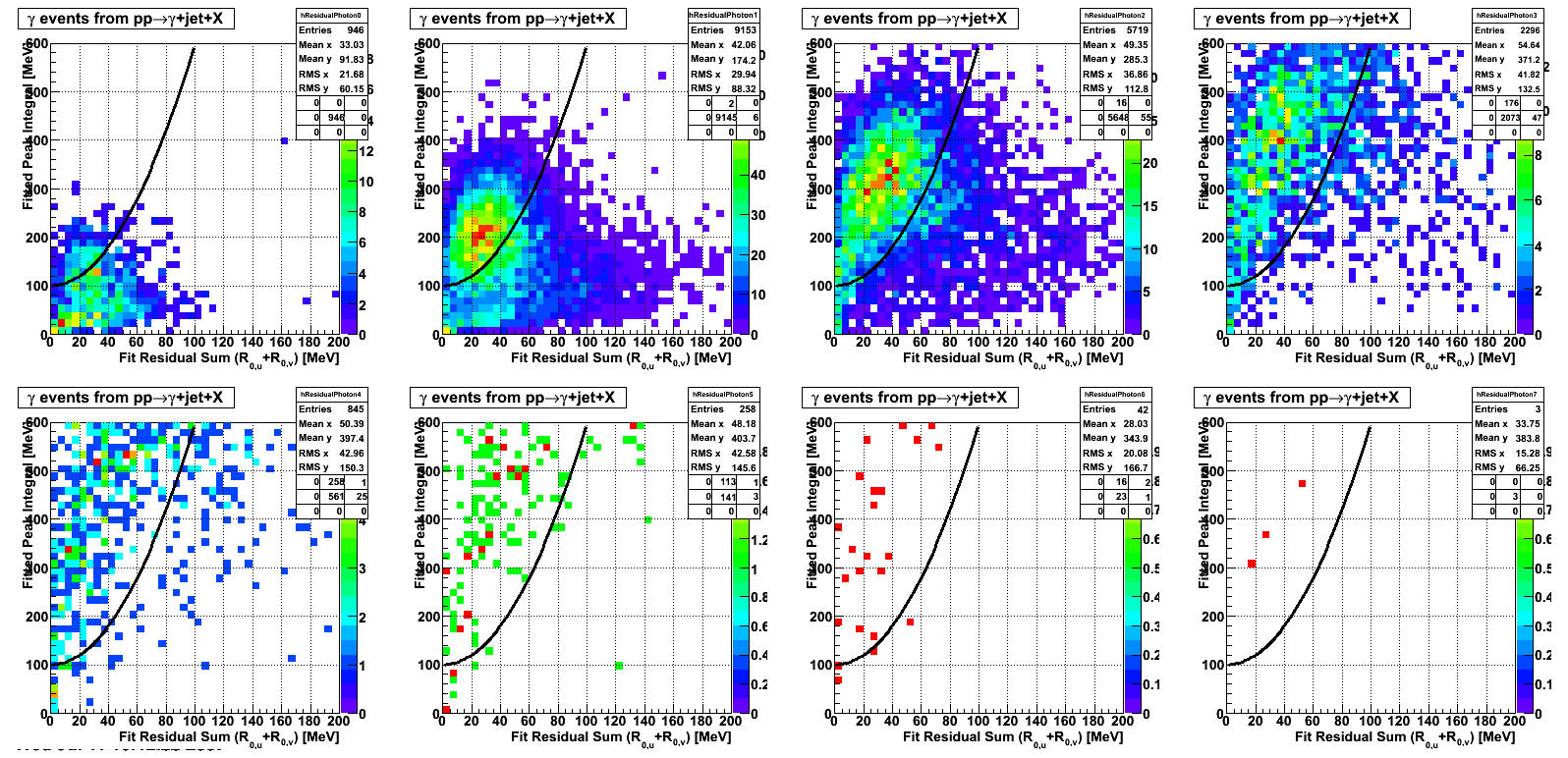 |
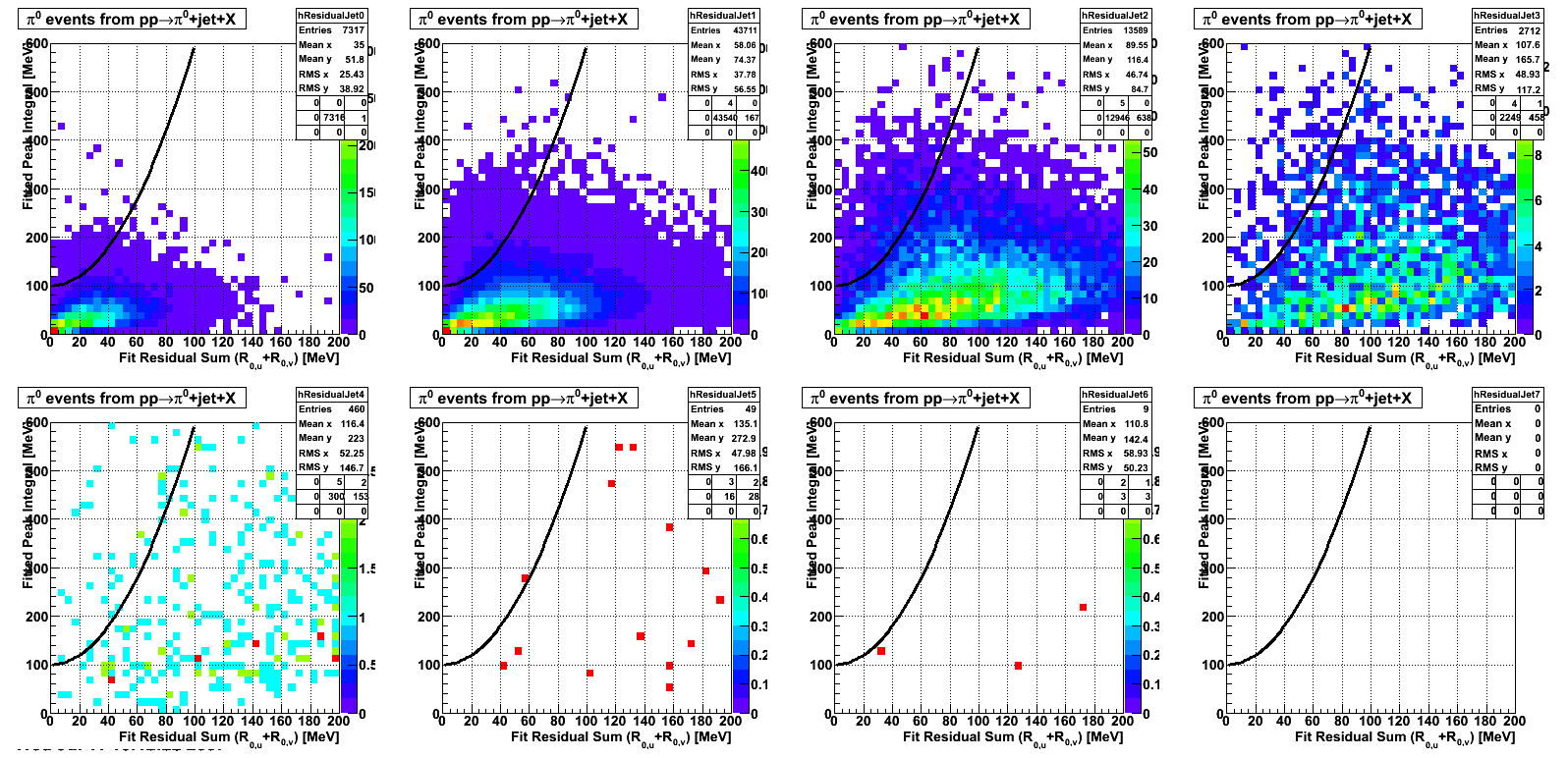 |
Pibero Djawotho Last updated Wed Jul 11 11:10:26 EDT 2007
gamma/X separation by energy with pT weights
gamma/X separation by energy with pT weights
 |
 |
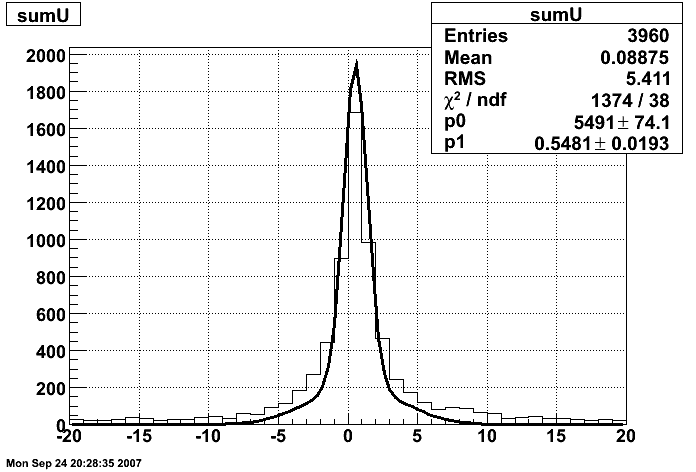
Pibero Djawotho Last updated Thu Jul 12 00:28:35 EDT 2007
gamma/X separation by energy with pT weights and normalized by number of events
gamma/X separation by energy with pT weights and normalized by number of events
 |
Pibero Djawotho Last updated Wed Jul 18 14:55:08 EDT 2007
gamma/pi0 separation efficiency and rejection at pT=5-7 GeV
gamma/pi0 separation efficiency and rejection at pT=5-7 GeV
 |
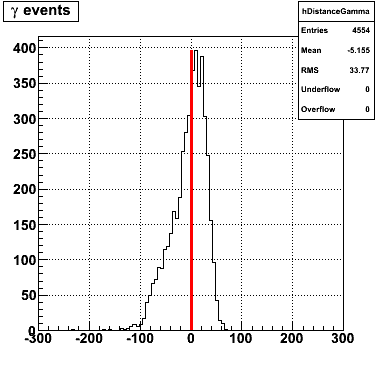 |
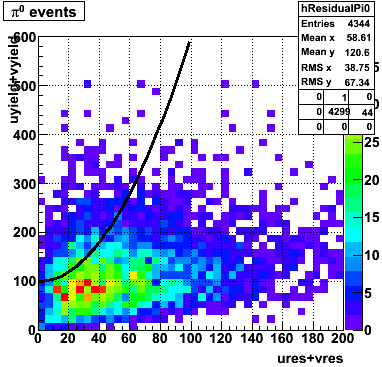 |
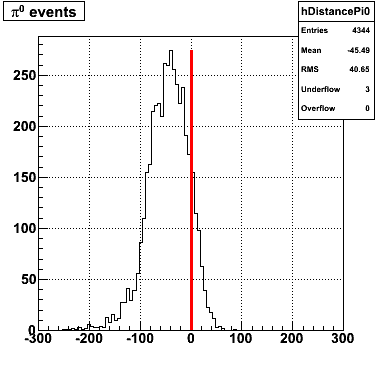 |
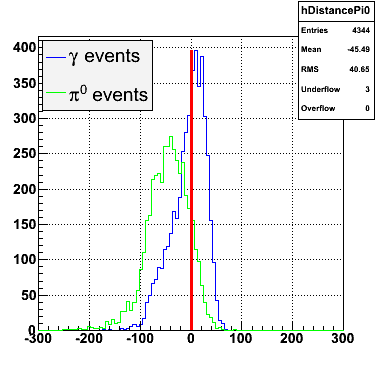 |
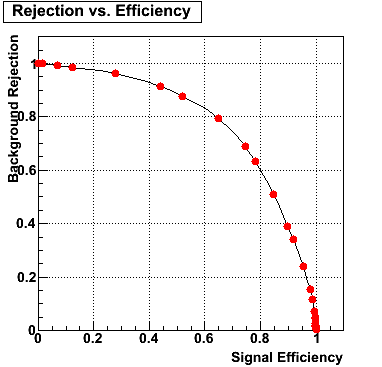 |
Pibero Djawotho Last updated Wed Jul 4 17:45:26 EDT 2007
gamma/pi0 separation efficiency and rejection at pT=9-11 GeV
gamma/pi0 separation efficiency and rejection at pT=9-11 GeV
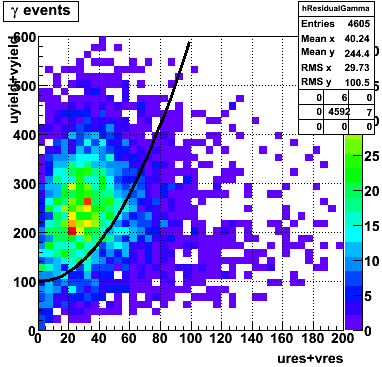 |
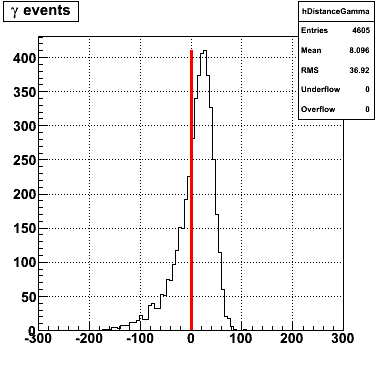 |
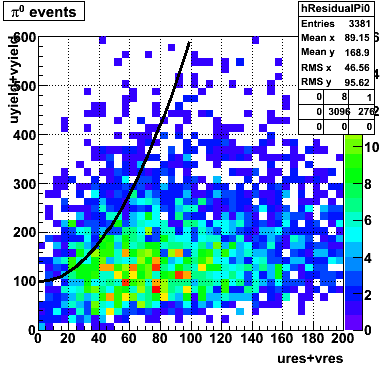 |
 |
 |
 |
Pibero Djawotho Last updated Wed Jul 4 13:23:41 EDT 2007
gamma/pi0 separation efficiency and rejection at pT=9-11 GeV
gamma/pi0 separation efficiency and rejection at pT=9-11 GeV
 |
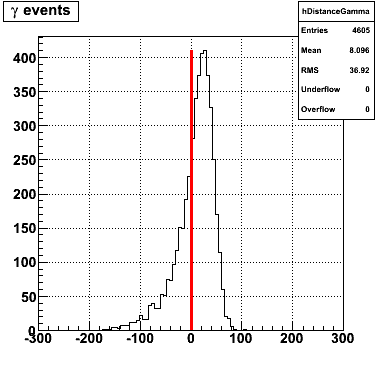 |
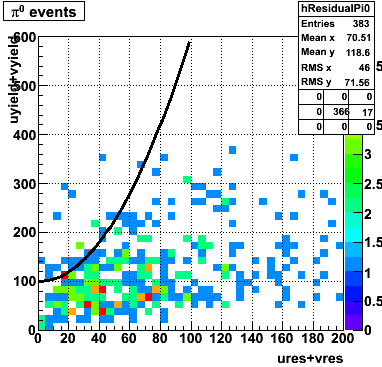 |
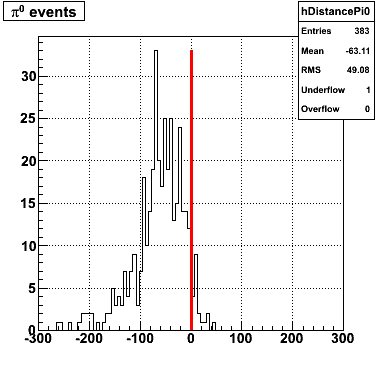 |
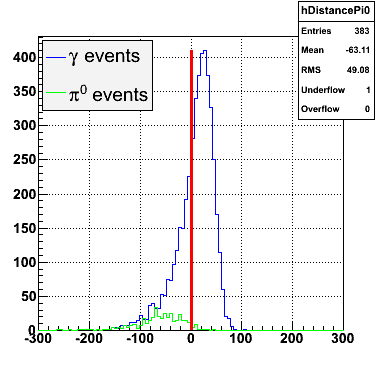 |
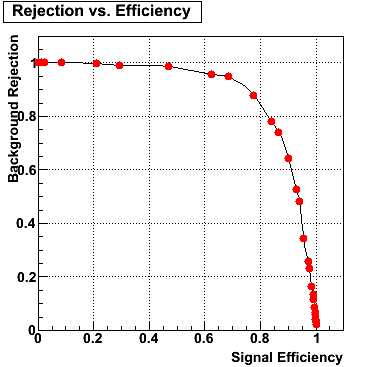 |
Pibero Djawotho Last updated Wed Jul 4 13:23:41 EDT 2007
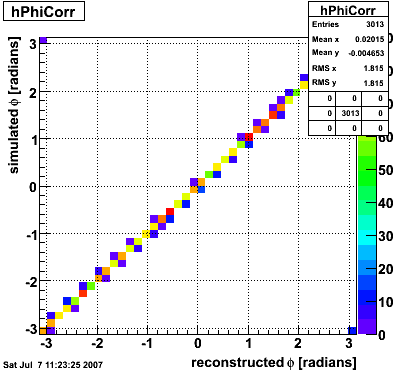
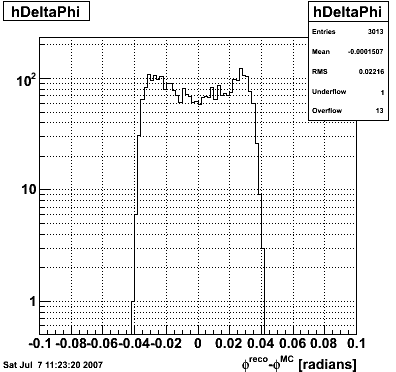
2007.07.09 How to run the gamma fitter
How to run the gamma fitter
The gamma fitter runs out of the box. The code consists of the classes StGammaFitter and StGammaFitterResult in CVS. After checking out a copy of offline/StGammaMaker, cd into the offline directory and run:
root4star StRoot/StGammaMaker/macros/RunGammaFitterDemo.C
The following plots will be generated on the ROOT canvas and dumped into PNG files.
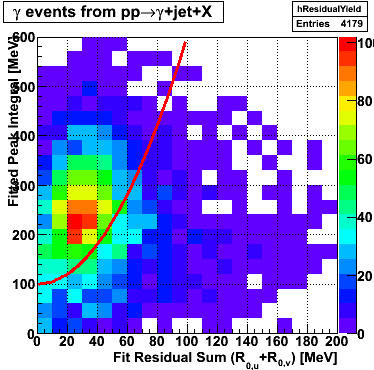 |
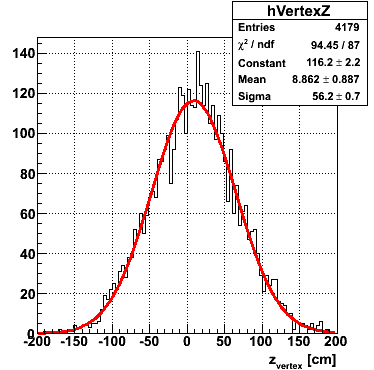 |
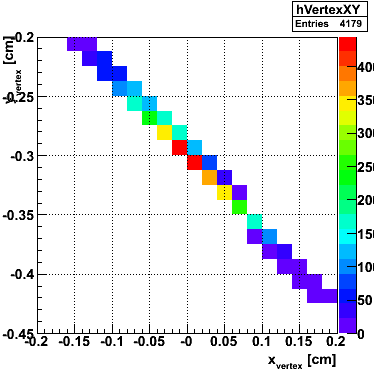 |
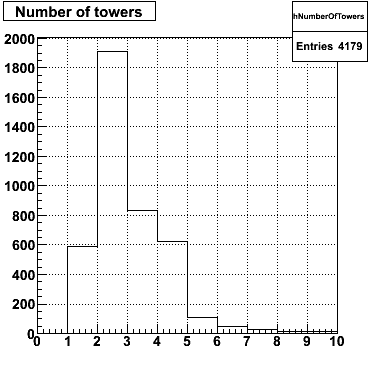 |
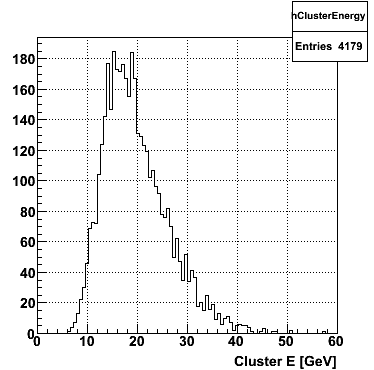 |
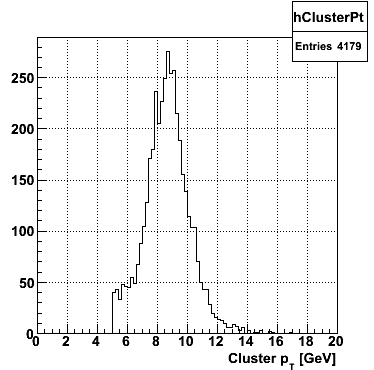 |
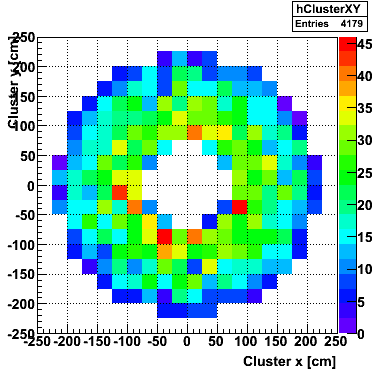 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Pibero Djawotho Last modified Mon Jul 9 18:40:07 EDT 2007
2007.07.25 Revised gamma/pi0 algorithm in 2006 p+p collisions at sqrt(s)=200 GeV
Revised gamma/pi0 algorithm in 2006 p+p collisions at sqrt(s)=200 GeV
Description
The class
computes the maximal sided residual of the SMD response in the u- and v-plane for gamma candidates. It is based on C++ code developed by Jason Webb from the original code by Les Bland who got the idea from CDF (?) The algorithm follows the steps below:
- The SMD response, which is SMD strips with hits in MeV, in each plane (U and V) is stored in histogram hU and hV.
- Fit functions fU and fV are created. The functional form of the SMD peak is a double-Gaussian with common mean and fixed widths. The widths were obtained by the SMD response of single photons from the EEMC slow simulator. As such, the only free parameters are the common mean and the total yield. The actual formula used is:
[0]*(0.69*exp(-0.5*((x-[1])/0.87)**2)/(sqrt(2*pi)*0.87)+0.31*exp(-0.5*((x-[1])/3.3)**2)/(sqrt(2*pi)*3.3))- [0] = yield
- [1] = mean
- The mean is fixed to the strip with maximum energy and the yield is adjusted so the height of the fit matches that of the mean.
- The residual for each side of the peak is calculated by subtracting the fit from the data (residual = data - fit) from 2 strips beyond the mean out to 40 strips.
- The maximal sided residual is the greater residual of each side.
Code
Candidates selection
- 2006 p+p at 200 GeV dataset from Sivers analysis (from Jan Balewski)
/star/institutions/iucf/balewski/prodOfficial06_muDst/ - Gamma candidate from gamma maker: 3x3 clusters with pt > 5 GeV
- No track pointing to cluster
- Minimum of 3 SMD hits in each plane
- Cuts from Jan & Naresh electron analysis:
- Preshower 1 energy > 0.5 MeV
- Preshower 2 energy > 2.0 MeV
- Postshower energy < 0.5 MeV
- The triggers caption in the PDF files shows the trigger id's satisfied by the event. A red trigger id is a L2-gamma trigger. I observe that generally the L2-gamma triggered event are a bit cleaner. Also shown is the pt and energy of the cluster.
Raw SMD response
- No additional cuts
- Pick only L2-gamma triggers
- Pick only L2-gamma triggers but no jet patch trigger
- Make isolation cut (see below)
The parameters of the isolation cut were suggested by Steve Vigor:
Hi Pibero,
In general, I believe people have used smaller cone radii for isolation
cuts than for jet reconstruction (where the emphasis is on trying to
recover full jet energy). So you might try something like requiring
that no more than 10 or 20% of the candidate cluster E_T appears
in scalar sum p_T for tracks and towers within a cone radius of
0.3 surrounding the gamma candidate centroid, excluding the
considered cluster energy. The cluster may already contain energy
from other jet fragments, but that should be within the purview of
the gamma/pi0 discrimination algo to sort out. For comparison, Les
used a cone radius of 0.26 for isolation cuts in his original simulations
of gamma/pi0 discrimination with the endcap. Using much larger
cone radii may lead to accidental removal of too many valid gammas.
Steve
Pibero Djawotho Last updated Wed Jul 25 10:07:07 EDT 2007
2007.09.12 Endcap Electrons
Endcap Electrons
This analysis is based on the work of Jan and Justin on SMD Profile Analysis for different TPC momenta. See here for a list of cuts. The original code used by Jan and Justin is here.
- Transverse running
- Analysis uses 64 out of 300 runs from 2006 pp transverse run
- MuDst are located at:
/star/institutions/iucf/balewski/prodOfficial06_muDst/
- No trigger selection
- Click here for SMD profiles of transverse electron candidates.
- Click here for ROOT file with transverse electrons ntuple.
- Longitudinal running
- MuDst are located at:
/star/institutions/iucf/hew/2006ppLongRuns/
- Click here for SMD profiles of longitudinal electron candidates.
- Click here for ROOT file with longitudinal electrons ntuple.
- Code
-
f(x)=p0*(0.69*exp(-0.5*((x-p1)/0.87)**2)/(sqrt(2*pi)*0.87)+0.31*exp(-0.5*((x-p1)/3.3)**2)/(sqrt(2*pi)*3.3))
-
p0 = yield
-
p1 = centroid

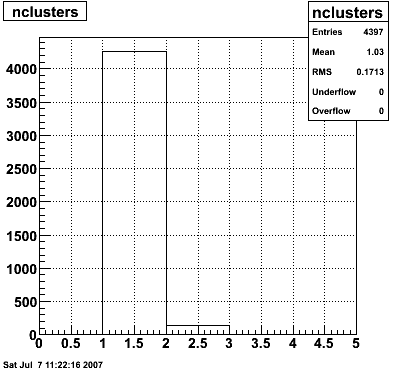
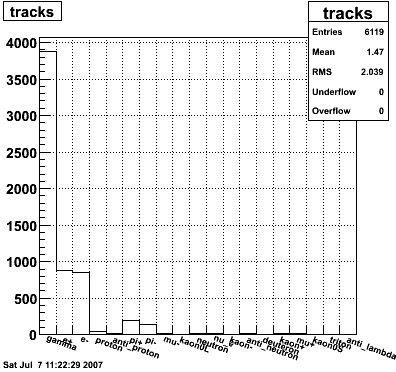
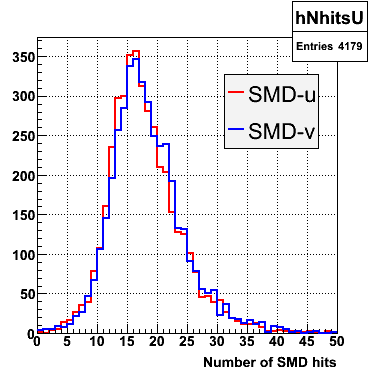
Figure 1: Number of tracks surviving each successive cut
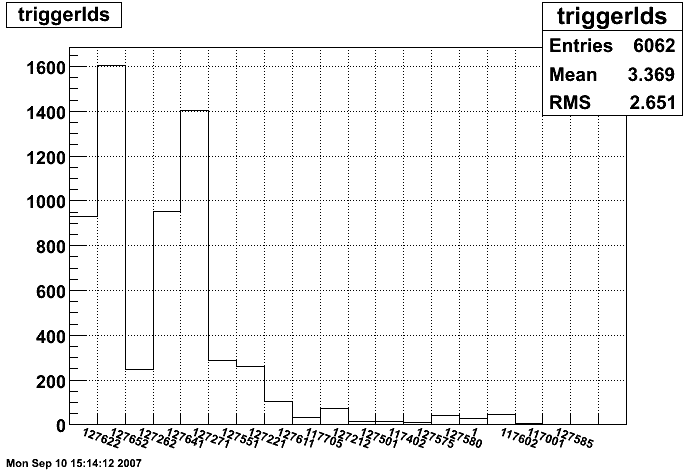
Figure 2a: Number of tracks per trigger id for all electron candidates. Most common trigger ids are:
127652
eemc-jp0-etot-mb-L2jet
EEMC JP > th0 (32, 4 GeV) and ETOT > TH (109, 14 GeV), minbias condition, L2 Jet algorithm, reading out slow detectors, transverse running
127271
eemc-jp1-mb
EEMC JP > th1 (49, 8 GeV) && mb, reading out slow detectors, transverse running
127641
eemc-http-mb-l2gamma
EEMC HT > th1 (12, 2.6 GeV, run < 7100052;13, 2.8 GeV, run >=7100052) and TP > TH1 (17, 3.8 GeV, run < 710052; 21, 4.7 GeV, run>=7100052 ), minbias condition, L2 Gamma algorithm, reading out slow detectors, L2 thresholds at 3.4, 5.4, transverse running
127622
bemc-jp0-etot-mb-L2jet
BEMC JP > th0 (42, 4 GeV) and ETOT > TH (109, 14 GeV), minbias condition, L2 Jet algorithm, reading out slow detectors, transverse running; L2jet thresholds at 8.0,3.6,3.3
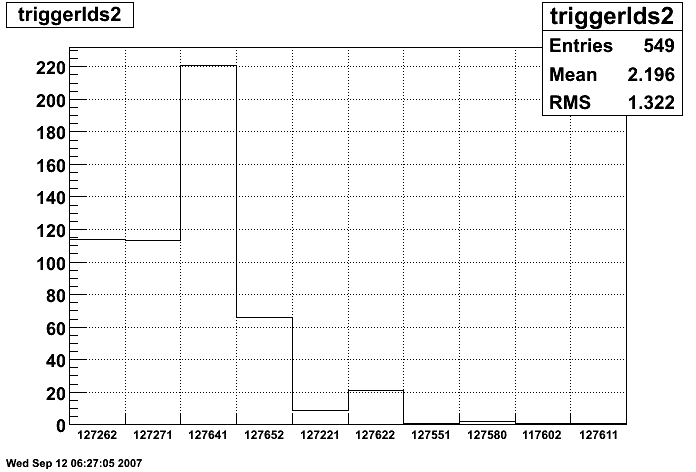
Figure 2b: Number of tracks per trigger id for all electron candidates for pT > 4 GeV. The dominant trigger ids become:
| 127641 | eemc-http-mb-l2gamma | EEMC HT > th1 (12, 2.6 GeV, run < 7100052;13, 2.8 GeV, run >=7100052) and TP > TH1 (17, 3.8 GeV, run < 710052; 21, 4.7 GeV, run>=7100052 ), minbias condition, L2 Gamma algorithm, reading out slow detectors, L2 thresholds at 3.4, 5.4, transverse running |
| 127262 | eemc-ht2-mb-emul | EEMC HT > th2 (22, 5.0 GeV) && mb, reading out slow detectors, emulated in L2, transverse running, different threshold from 117262 |
| 127271 | eemc-jp1-mb | EEMC JP > th1 (49, 8 GeV) && mb, reading out slow detectors, transverse running |
| 127652 | eemc-jp0-etot-mb-L2jet | EEMC JP > th0 (32, 4 GeV) and ETOT > TH (109, 14 GeV), minbias condition, L2 Jet algorithm, reading out slow detectors, transverse running |
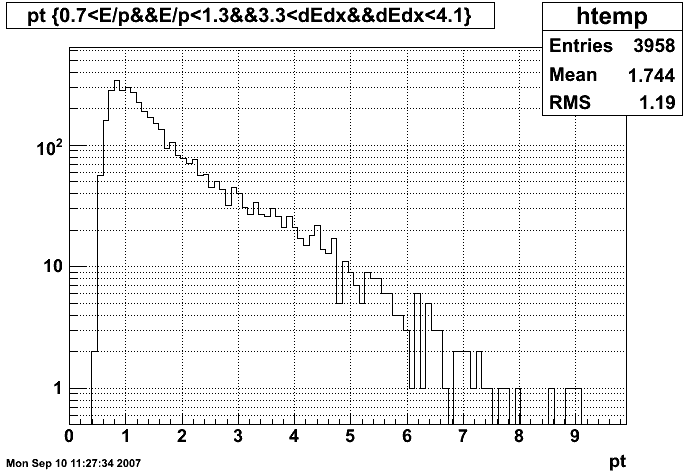
Figure 3: pT distribution of tracks before E/p, dE/dx and pT cut
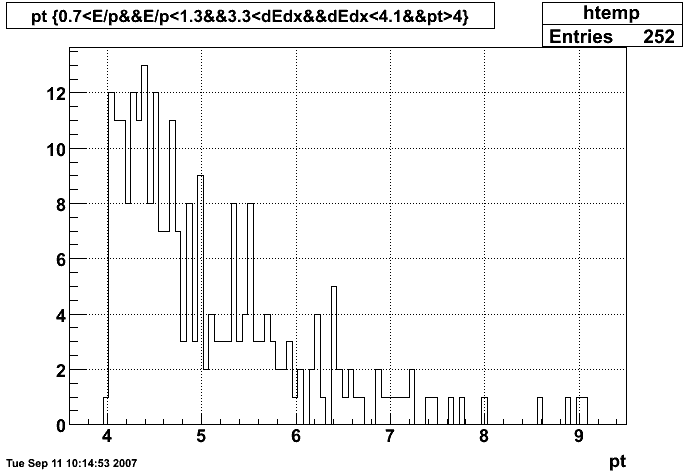
Figure 4: pT distribution of electron candidates with pT > 4 GeV
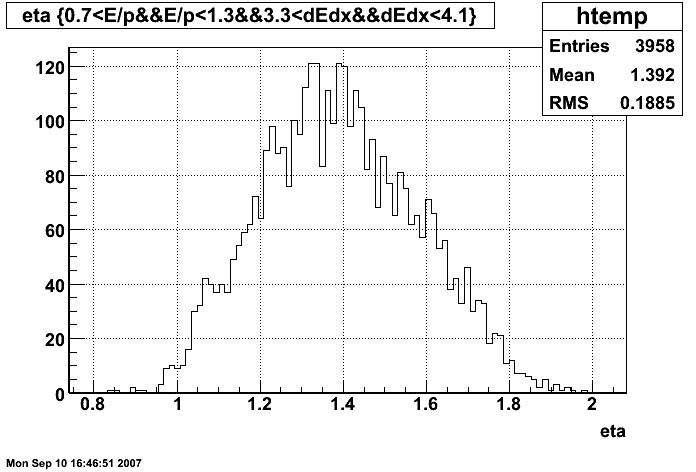
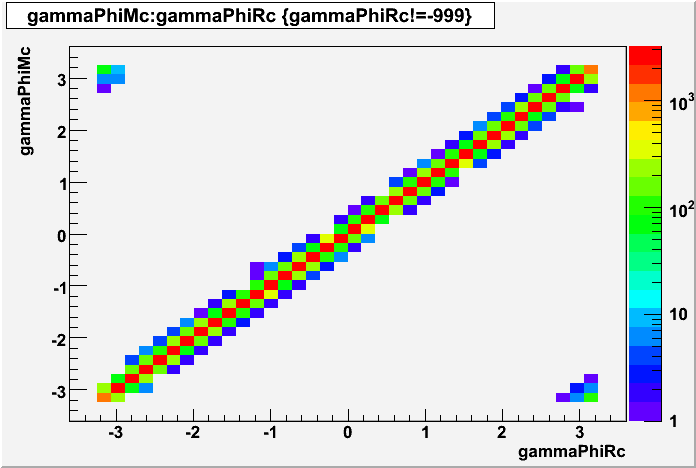
Figure 5: η distribution of electron candidates (all pT)
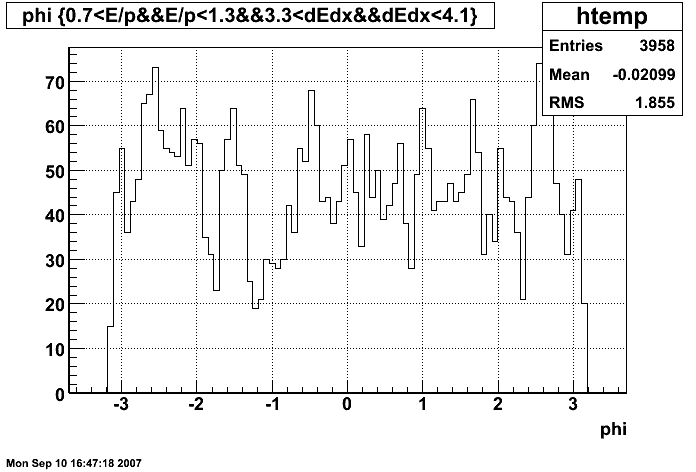
Figure 6: φ distribution of electron candidates (all pT)
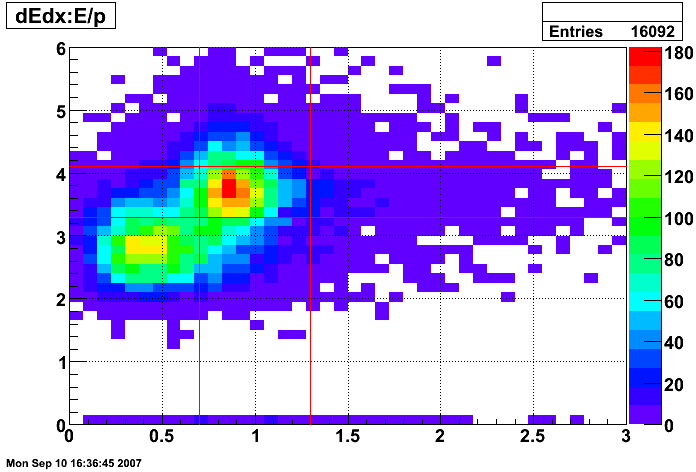
Figure 7: dE/dx of tracks before E/p and dE/dx cuts (all pT)
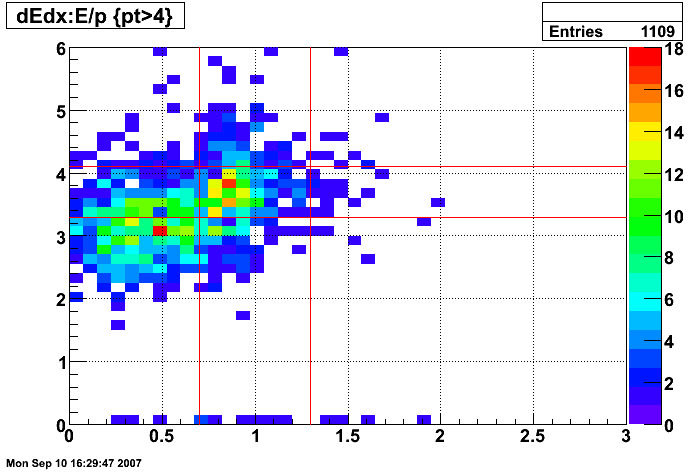
Figure 8: dE/dx of tracks before E/p and dE/dx cuts (pT > 4 GeV)
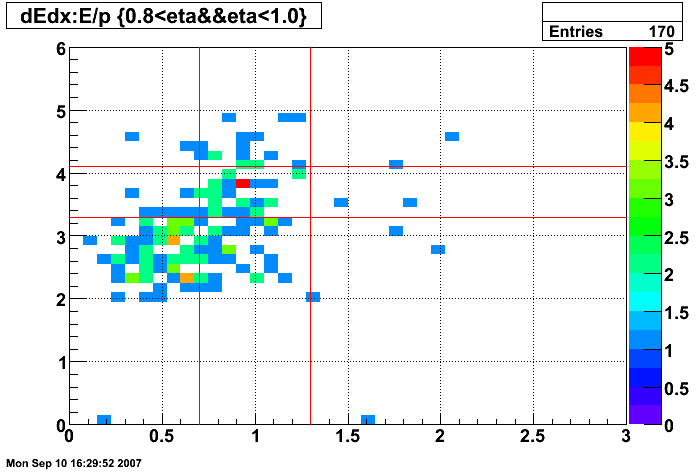
Figure 9: dE/dx of tracks before E/p and dE/dx cuts (all pT and 0.8 < η < 1.0)
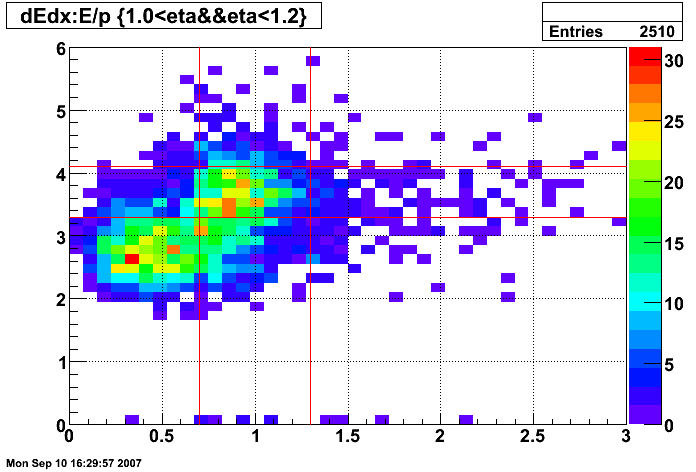
Figure 10: dE/dx of tracks before E/p and dE/dx cuts (all pT and 1.0 < η < 1.2)
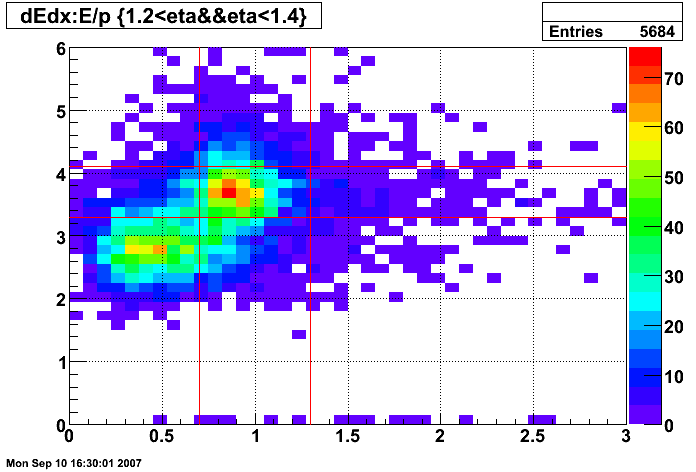
Figure 11: dE/dx of tracks before E/p and dE/dx cuts (all pT and 1.2 < η < 1.4)
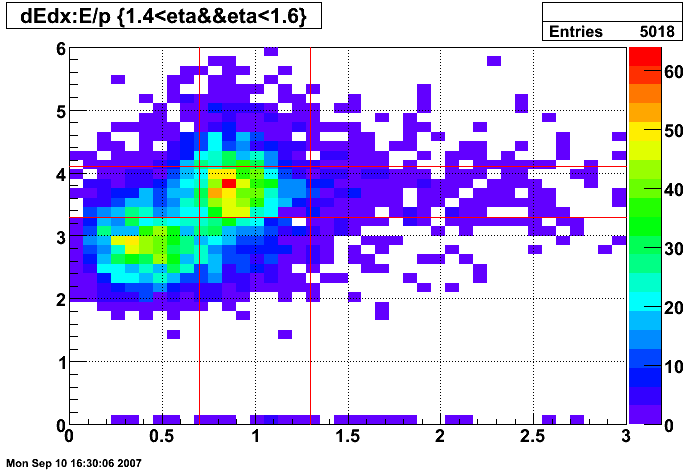
Figure 12: dE/dx of tracks before E/p and dE/dx cuts (all pT and 1.4 < η < 1.6)
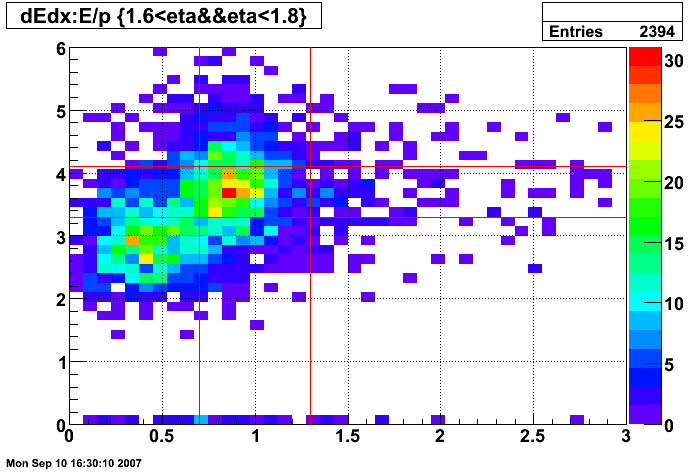
Figure 13: dE/dx of tracks before E/p and dE/dx cuts (all pT and 1.6 < η < 1.8)
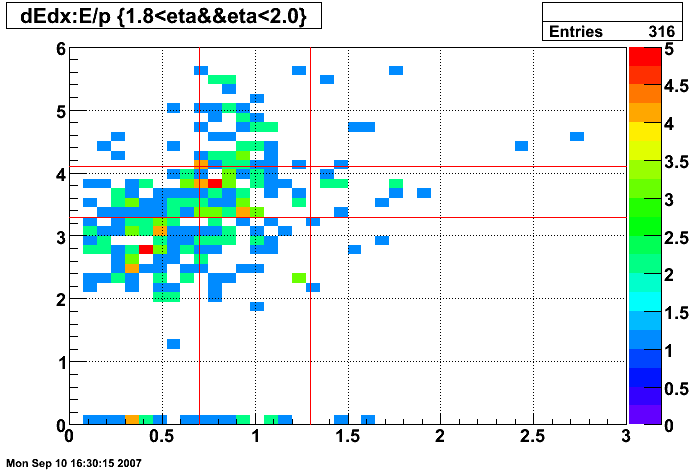
Figure 14: dE/dx of tracks before E/p and dE/dx cuts (all pT and 1.8 < η < 2.0)
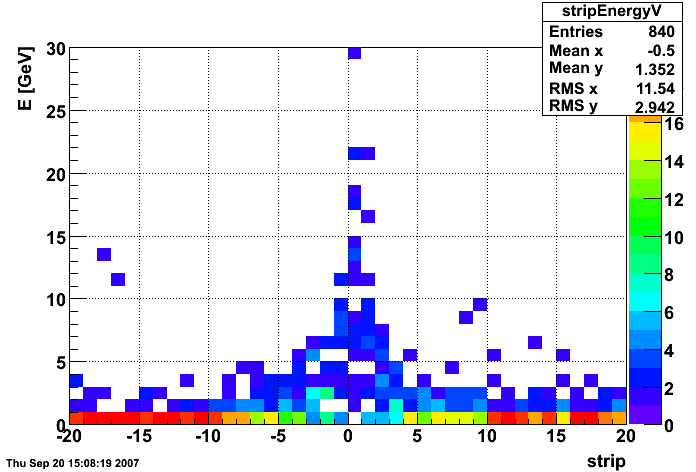
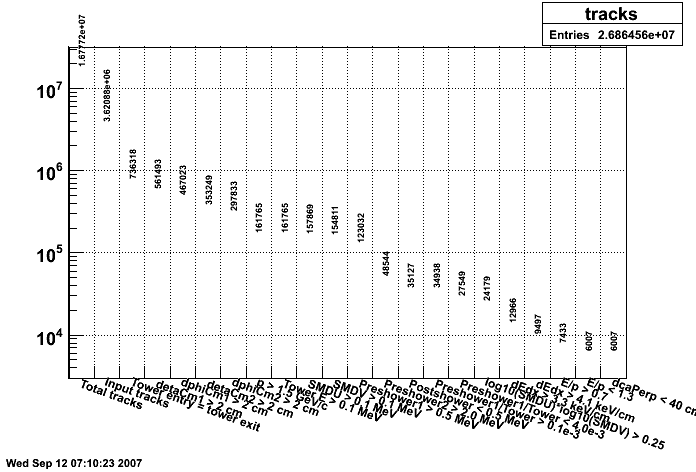
Figure 2.1
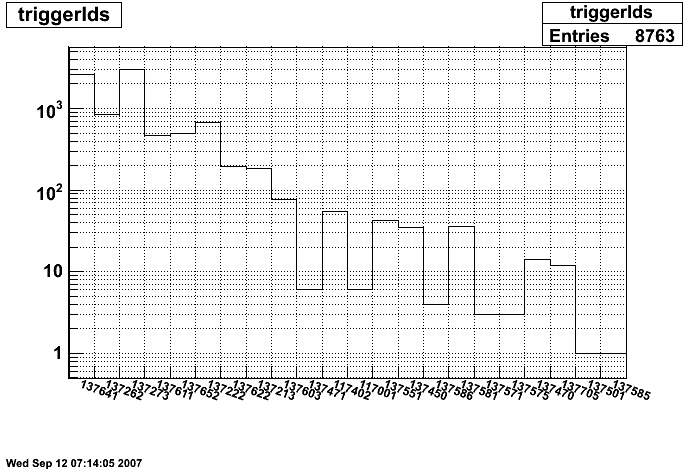
Figure 2.2: The dominant trigger ids are:
| 137273 | eemc-jp1-mb | EEMC JP > th1 (52, 8.7 GeV) && mb, reading out slow detectors, longitudinal running 2 |
| 137641 | eemc-http-mb-l2gamma | EEMC HT > th1 (16, 3.5 GeV) and TP > th1 (20, 4.5 GeV), minbias condition, L2 Gamma algorithm, reading out slow detectors, L2 thresholds at 3.7, 5.2, longitudinal running 2 |
| 137262 | eemc-ht2-mb-emul | EEMC HT > th2 (22, 5.0 GeV) && mb, reading out slow detectors, emulated in L2, longitudinal running 2 |
| 137222 | bemc-jp1-mb | BEMC JP > th1 (60, 8.3 GeV) && mb, reading out slow detectors, longitudinal running 2 |
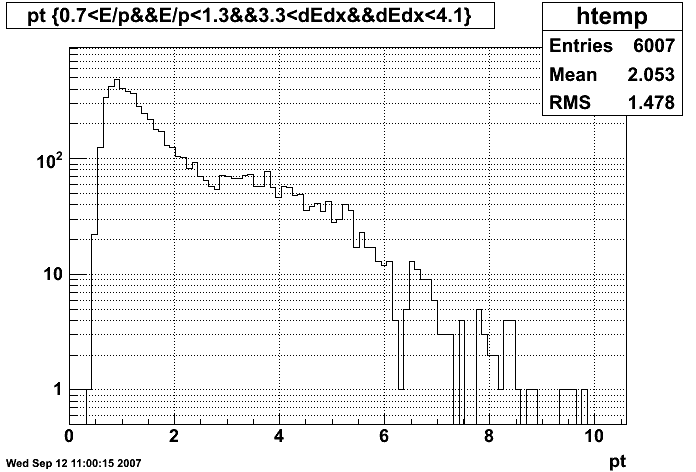
Figure 2.3a
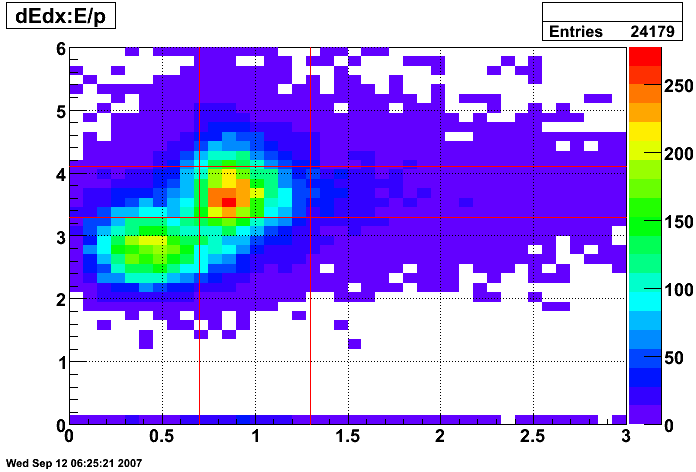
Figure 2.3
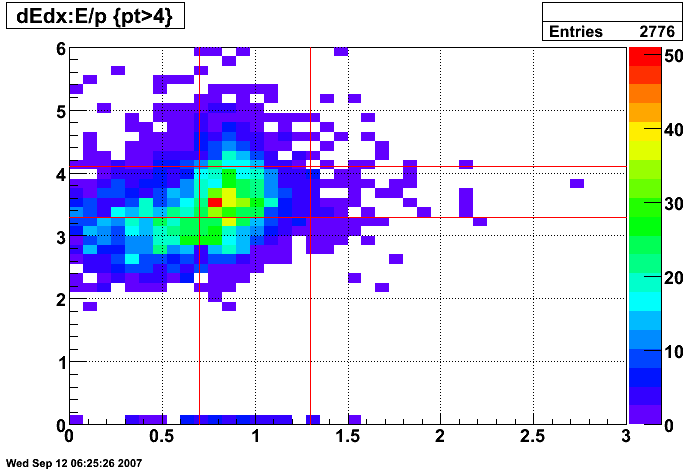
Figure 2.4
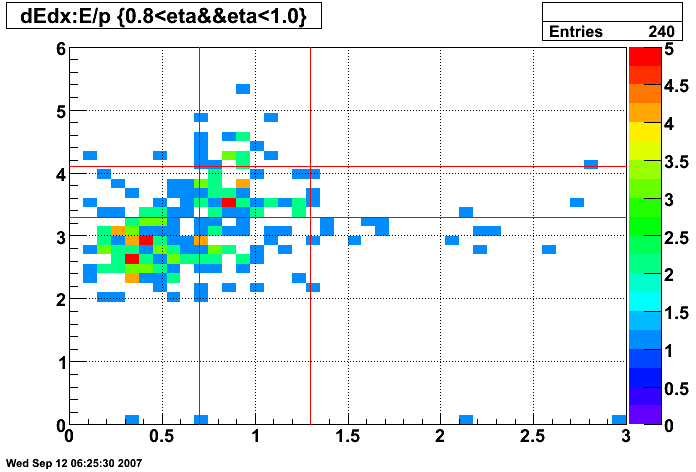
Figure 2.5
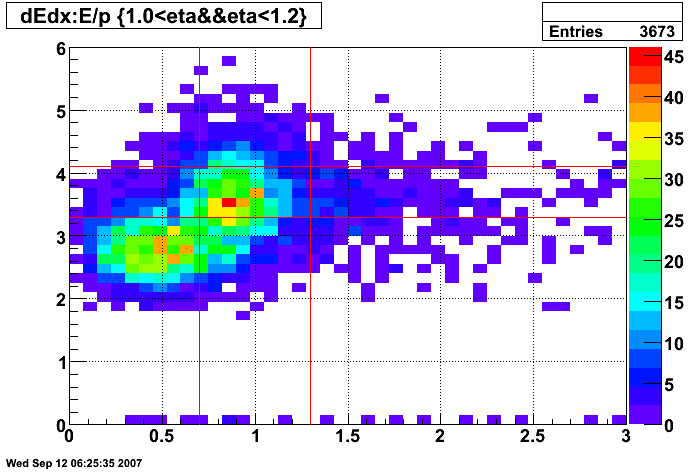
Figure 2.6
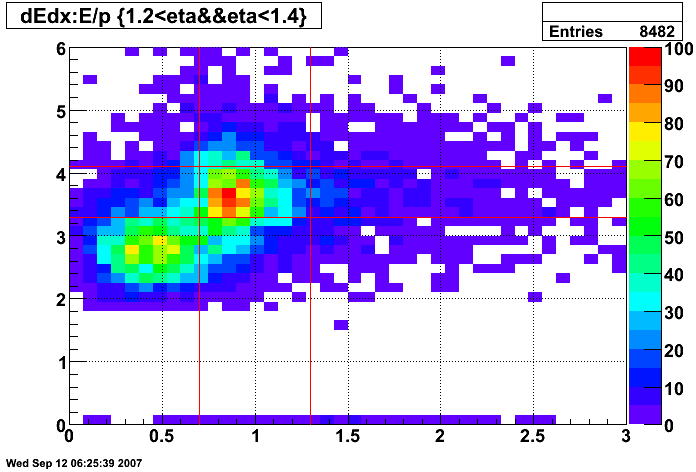
Figure 2.7
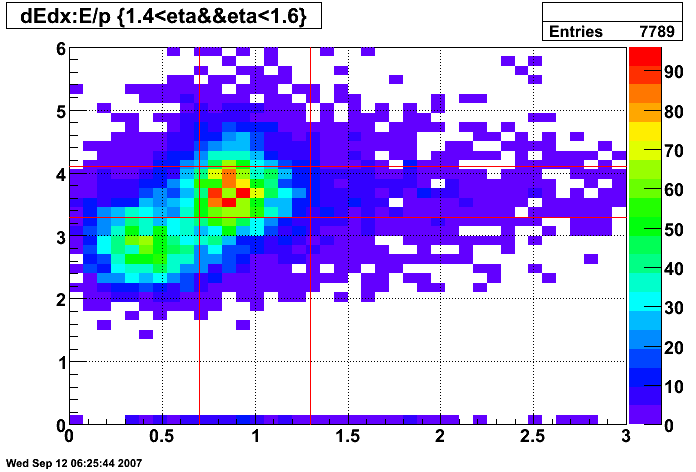
Figure 2.8
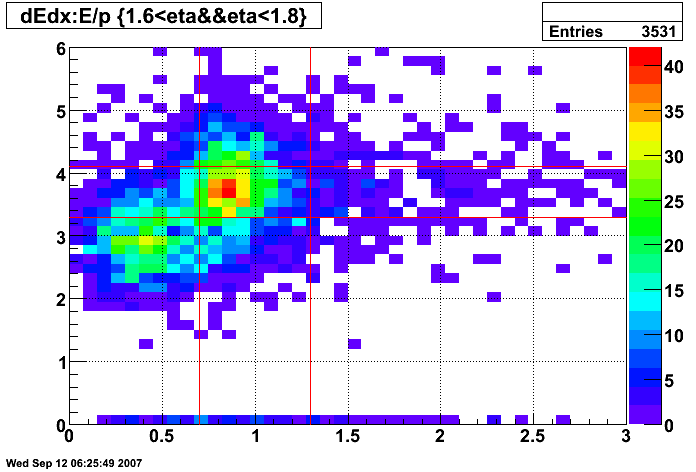
Figure 2.9
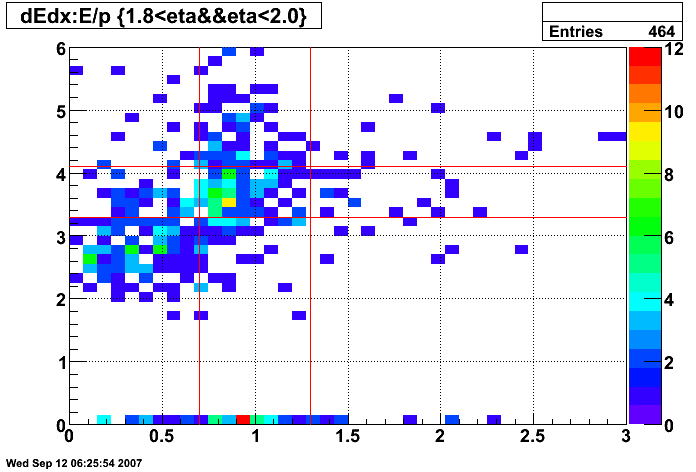
Figure 2.10
Click here for a tarball of the code used in this analysis.
SMD response function
Transverse
21 electrons
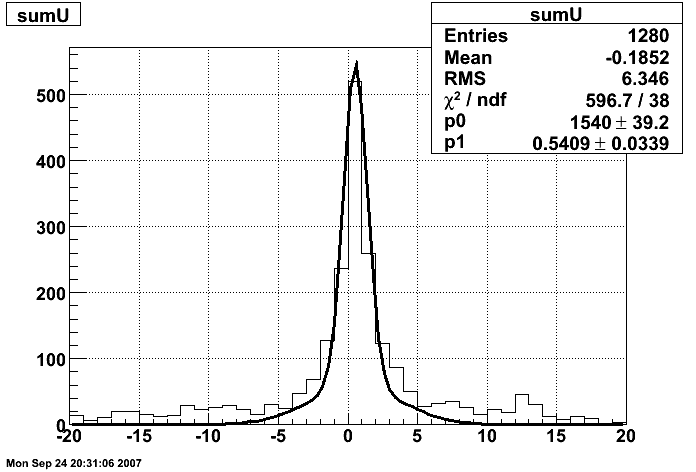
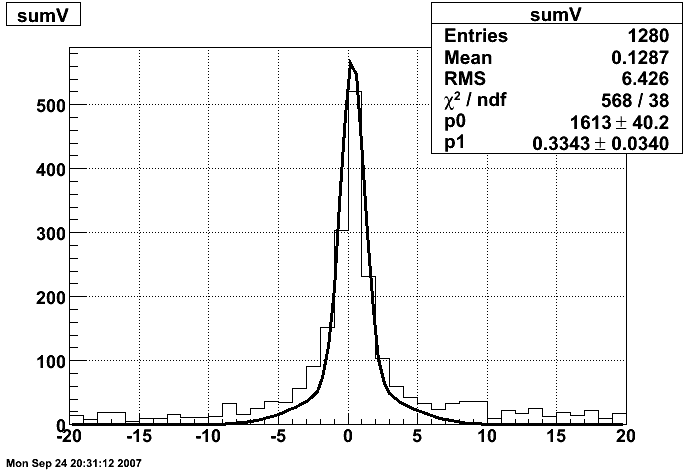
Longitudinal
99 electrons
Pibero Djawotho Last updated Wed Sep 12 08:29:53 EDT 2007
2008.01.23 Endcap etas
Endcap etas
Endcap etas
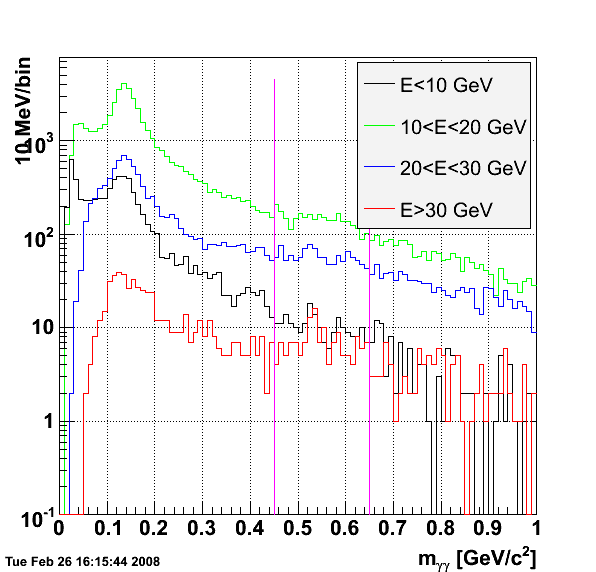
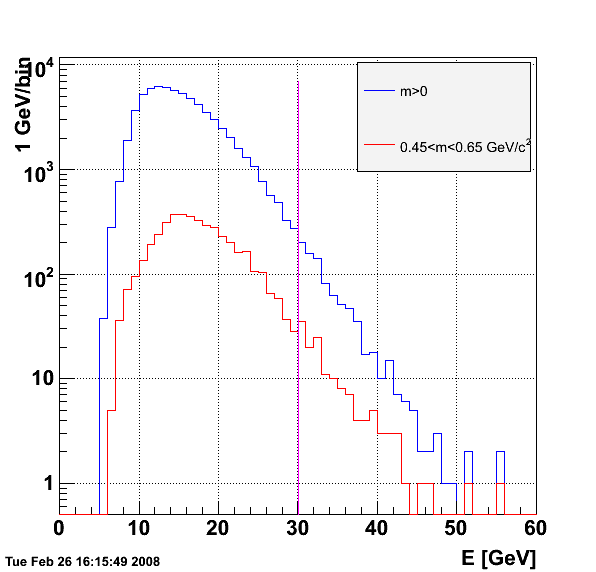
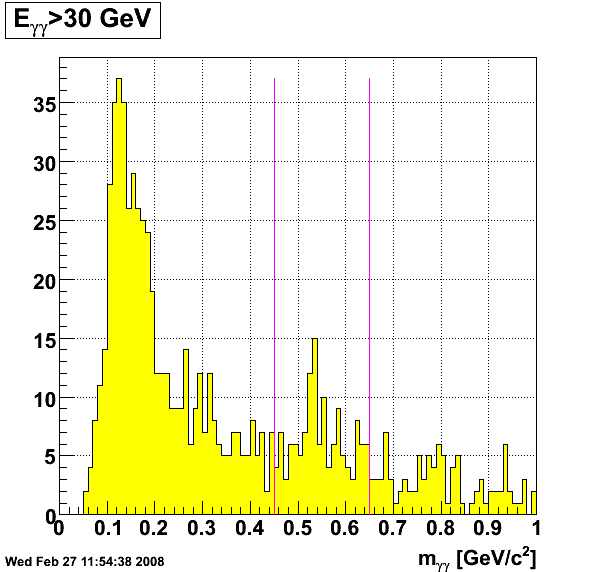
This analysis to look for etas at higher energy is in part motivated by this study. The interest in etas, of course, is that their decay photons are well separated at moderate energies (certainly more separated than the photons from pi0 decay). I ran Weihong's pi0 finder with tower seed threshold of 0.8 GeV and SMD seed threshold of 5 MeV (I believe his default SMD seed setting is 2 MeV). I then look in the 2-photon invariant mass region between 0.45 and 0.65 GeV (the PDG nominal mass for the eta is 0.54745 +/- 0.00019 GeV). I observe what looks like a faint eta peak. The dataset processed is the longitudinal 2 run of 2006 from the 20 runs sitting on the IUCF disk in Weihong's directory (/star/institutions/iucf/hew/2006ppLongRuns/).
Within the reconstructed mass window 0.45 to 0.65 GeV, I take a look at the decay photon shower profiles in the SMD. The samples are saved in the file etas.pdf. For the most part, these shower shapes are cleaner than the original sample. Although the statistics are not great.
Additional Material
- List of etas from Weihong (text file)
- List of etas from Weihong (pdf file)
- List of etas from Weihong using gammma maker
- List of etas from Weihong (all 12 sectors)
- Hal's eta spreadsheet
- Hal's revised eta spreadsheet
Documents
- Direct photon center-of-mass angular distributions in proton-antiproton collisions at sqrt(s)=1.8 TeV (Leslie Nakae Thesis)
- Measurement of the cross section for production of two isolated prompt photons in 1.8-TeV proton-antiproton collisions (Mikio Takano Thesis)
- Measurement of sqrt(s) dependence of isolated direct photon production in proton-antiproton collisions (Dana Partos)
- Prompt photon cross section measurement in pbar-p collisions at sqrt(s)=1.8 TeV (PRD 48 2998, 1993)
- A prompt photon cross section measurement in pbar-p collisions at sqrt(s)=1.8 TeV (FERMILAB-Pub-92/001-E)
Pibero Djawotho Last updated Wed Jan 23 12:35:43 EST 2008
2008.02.27 ESMD shape library
ESMD shape library
Shower Widths for Monte Carlo and Data
Description
Hal did a comparison of the widths of the shower shapes between Monte Carlo and data. Below is a description of what was done.
I took the nominal central value, either from the maxHit or the
nominal central value, and added the energy in the +/- 12 strips. Then I
computed the mean strip (which may have been different from the nominal
central value!!). I normalized the shape to give unit area for each smd
cluster, and added to the histograms separately for U and V and for MC and
data (= Will's events). I did NOT handle Will's events correctly, just
using whatever event was chosen randomly, rather than going through his
list sequentially. Note I ran 1000 events, and got 94 events in my shower
shape histos.
So, there are several minor problems. 1) I didn't go through Will's
events sequentially. 2) I normalized, but perhaps not to the correct 25
strips, because the mean strip and the nominal strip may have differed.
3) there may have been a cutoff on some events due to being close to one
end of the smd plane (near strip 0 or 287). My sense from looking at the
plots is that these don't matter much.
The conclusion is that the MC shape is significantly narrower than
the shape from Will's events, which is obviously narrower than the random
clusters we were using at first with no selection for the etas. Hence, we
are not wasting our time with this project.
- Monte Carlo U shower shape
- Monte Carlo V shower shape
- SMDU shower shape (Will's selection)
- SMDV shower shape (Will's selection)
- Energy Asymmetry
- Index of Library Entry
Decsription of Pythia Sample
A few histograms were added to the code:
- MC is Pythia gamma-jet at partonic pT 9-11 GeV with gamma in the Endcap
- Data is from Will Jacobs golden events from Weihong sample
- Require no conversion
- Require all hits from direct photon in same sector
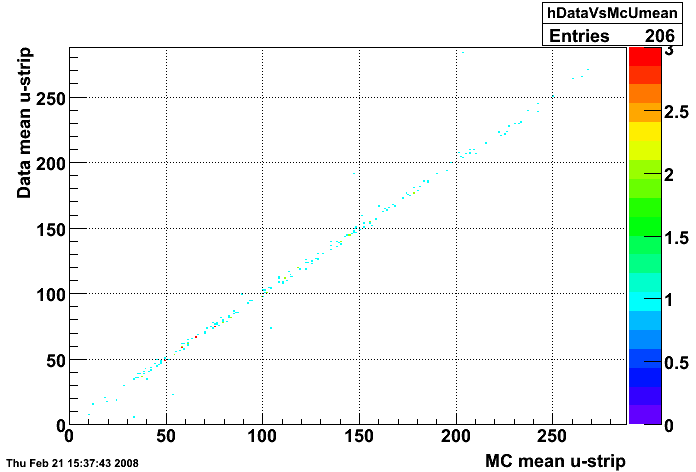
Figure 1:
Data vs. MC mean u-strip
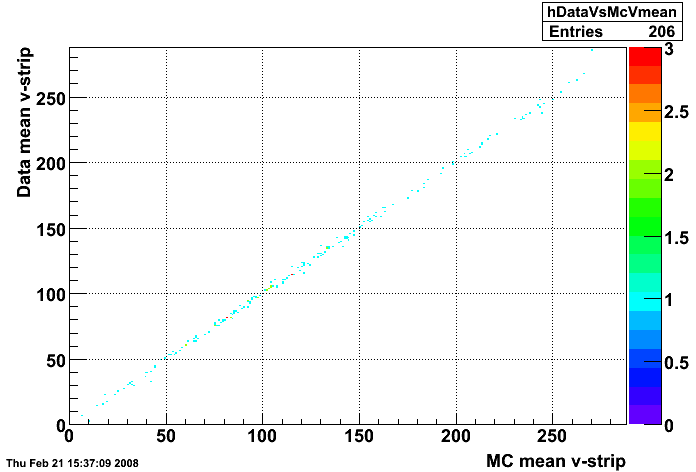
Figure 2:
Data vs. MC mean v-strip
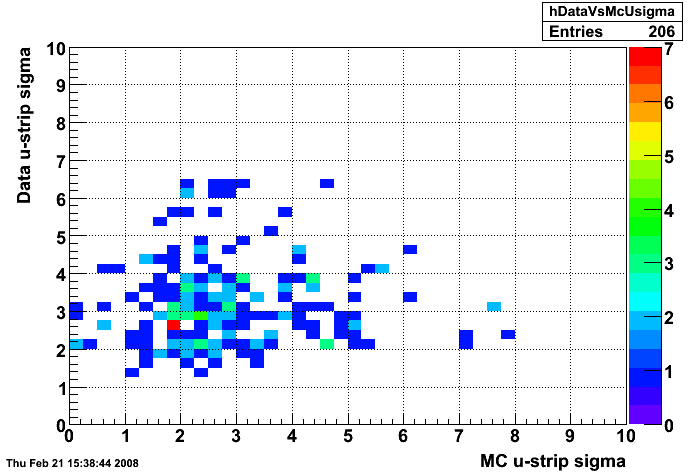
Figure 3:
Data vs. MC u-strip sigma
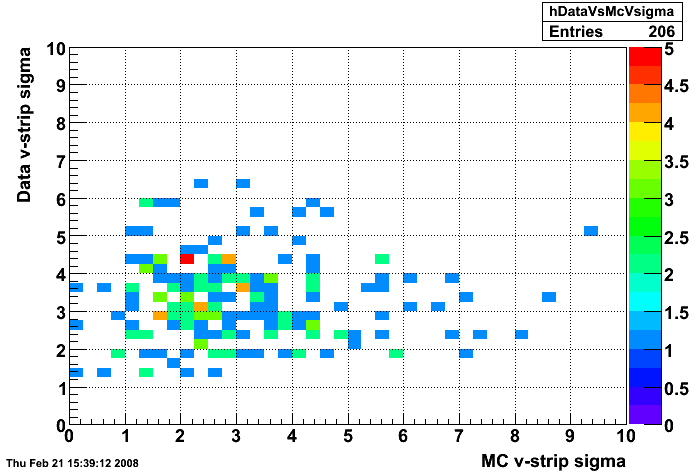
Figure 4:
Data vs. MC v-strip sigma
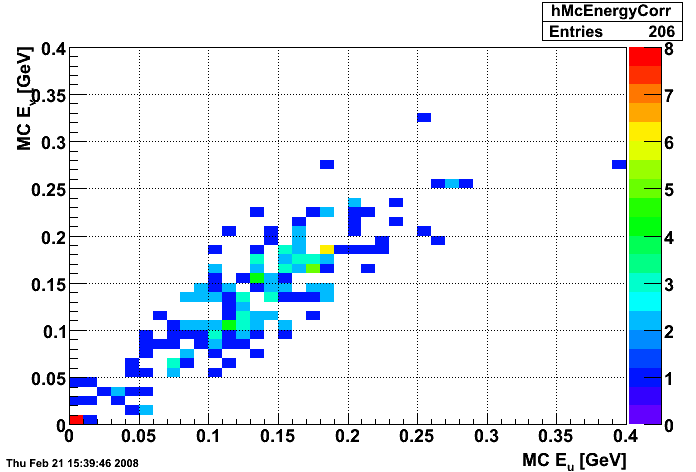
Figure 5:
MC E
v
vs. E
u
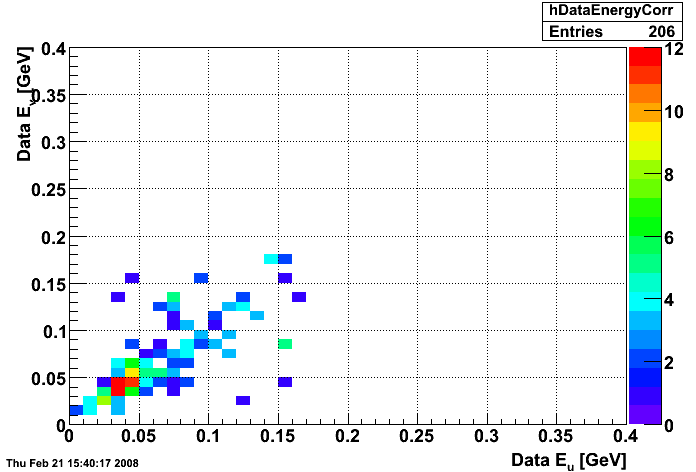
Figure 6:
Data E
v
vs. E
u
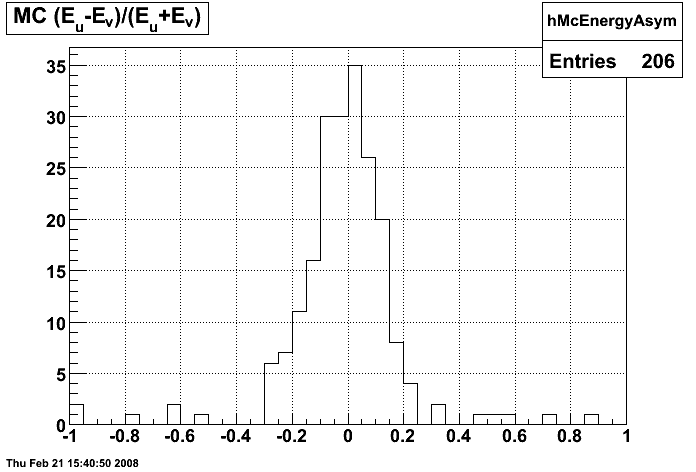
Figure 7:
MC energy asymmetry in SMD planes
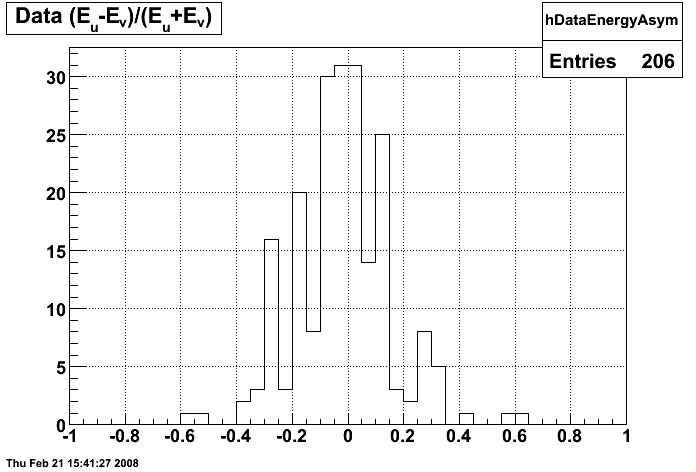
Figure 8:
Data energy asymmetry in SMD planes
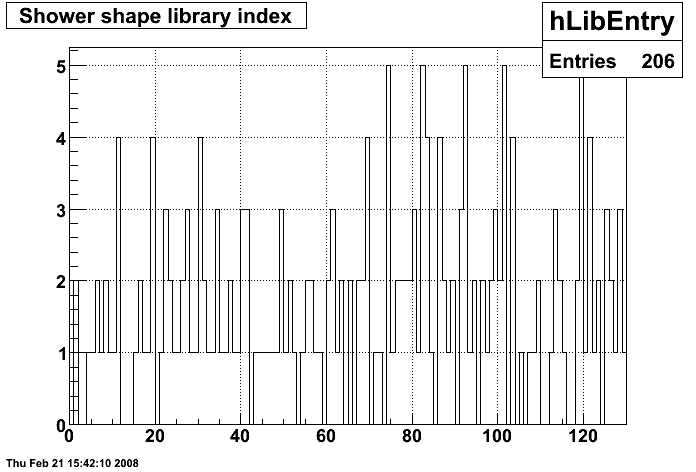
Figure 9:
Shower shape library index used (picked at random)
Single events shower shapes are displayed in
or
.
- green = projected position of direct photon in the Endcap
- blue = Monte Carlo SMD response
- red = Data SMD response
Hal Spinka Pibero Djawotho Last modified Wed Feb 27 09:51:27 EST 2008
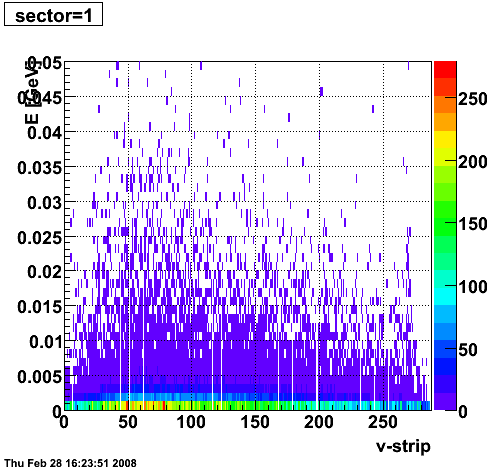
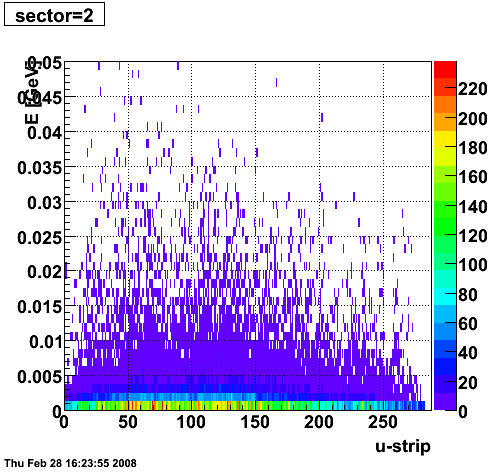
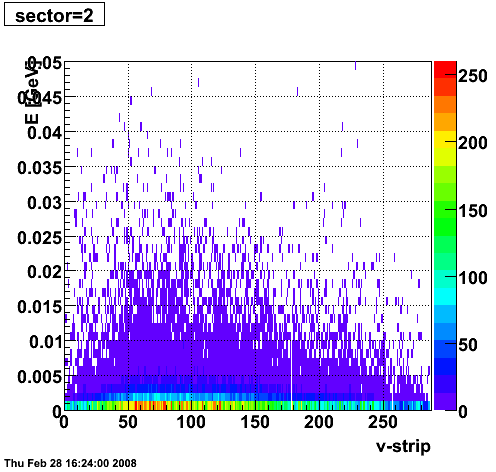
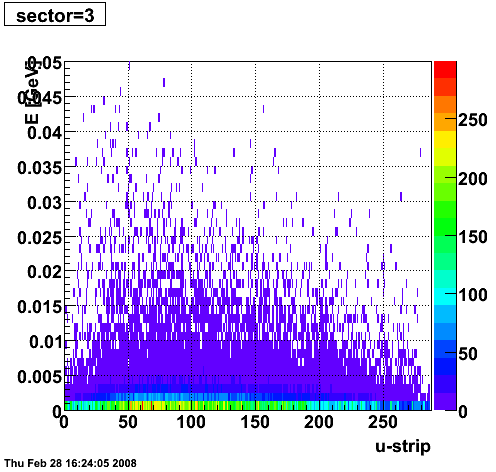
2008.02.28 ESMD QA for run 7136033
ESMD QA for run 7136033
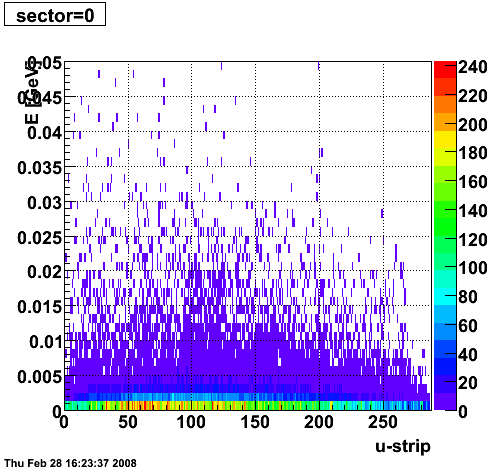 |
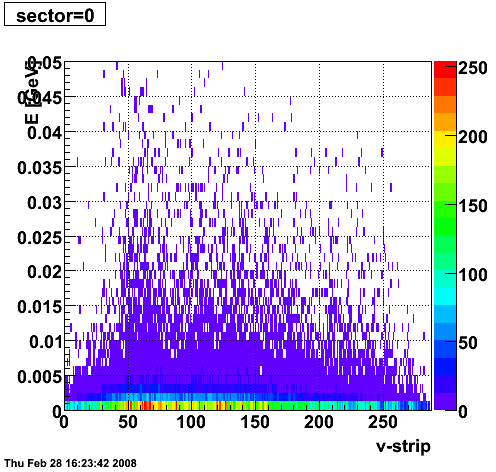 |
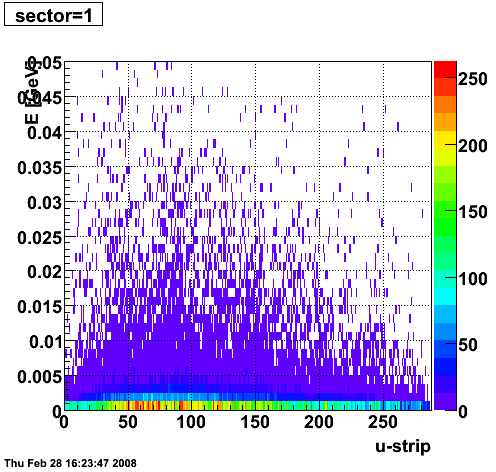 |
 |
 |
 |
 |
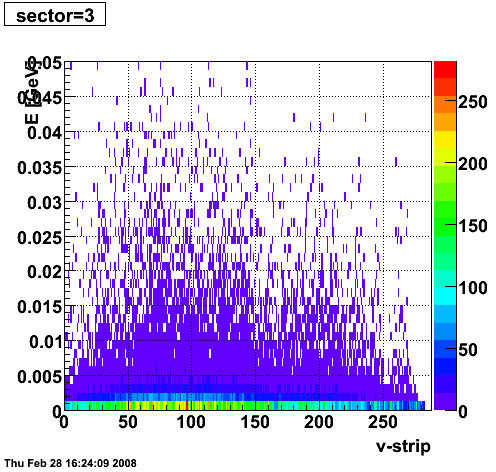 |
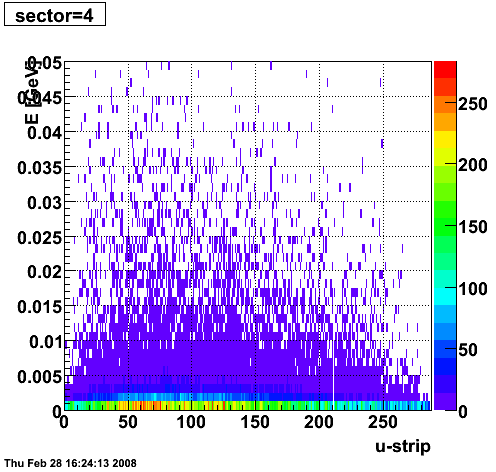 |
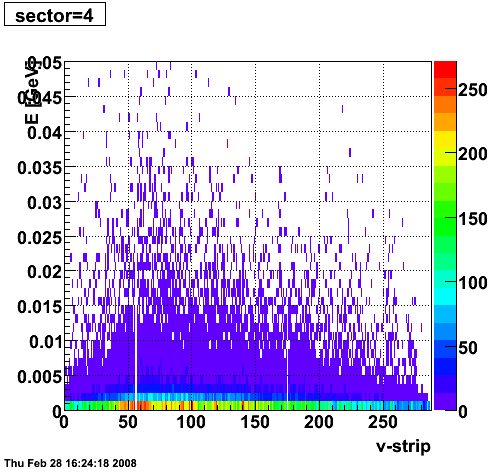 |
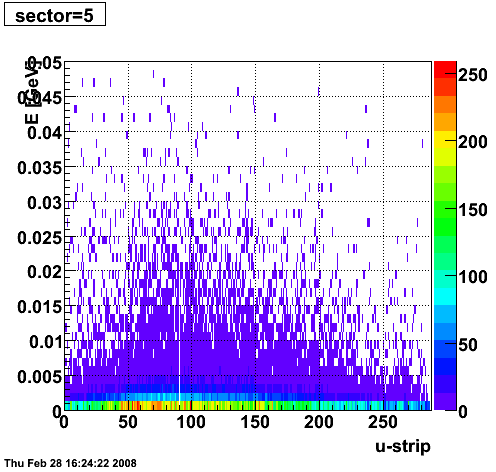 |
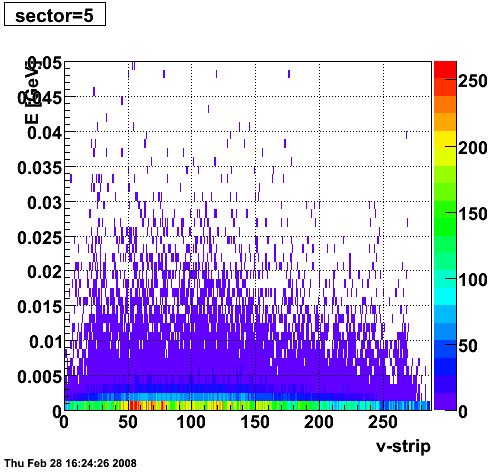 |
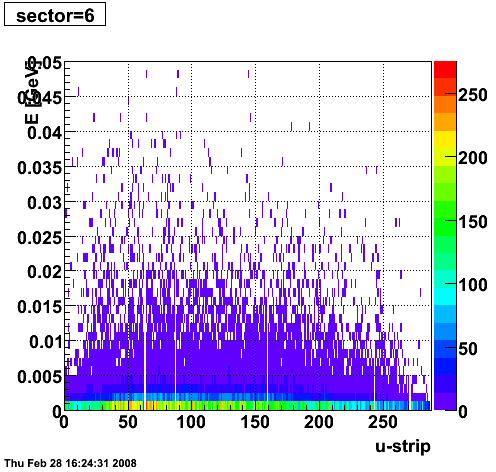 |
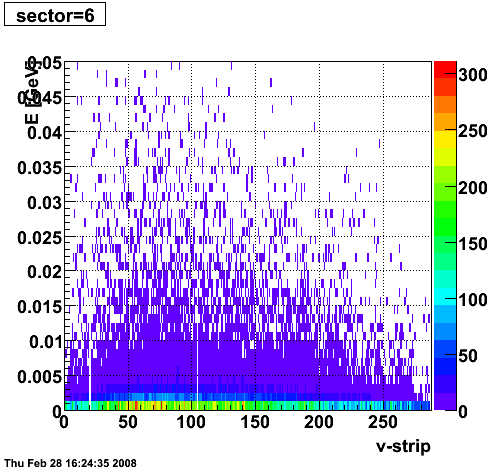 |
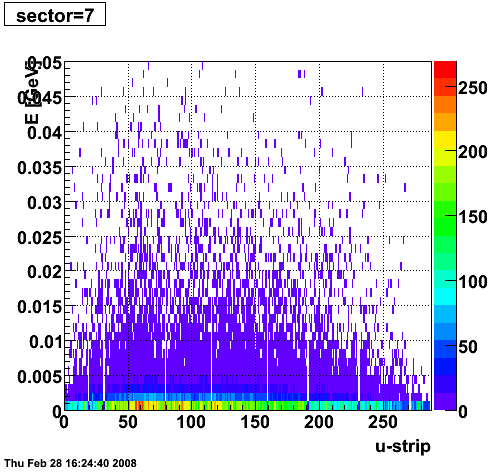 |
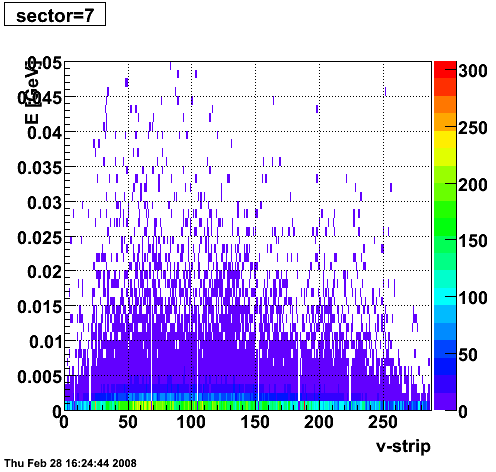 |
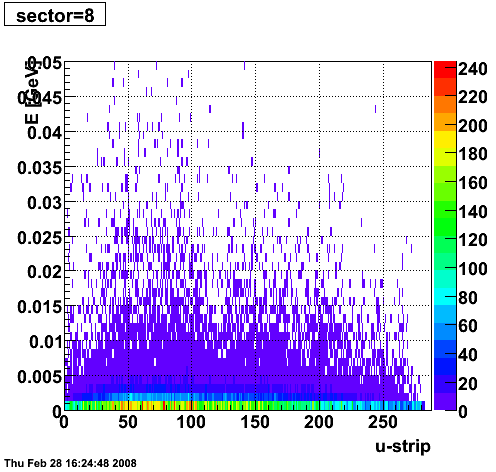 |
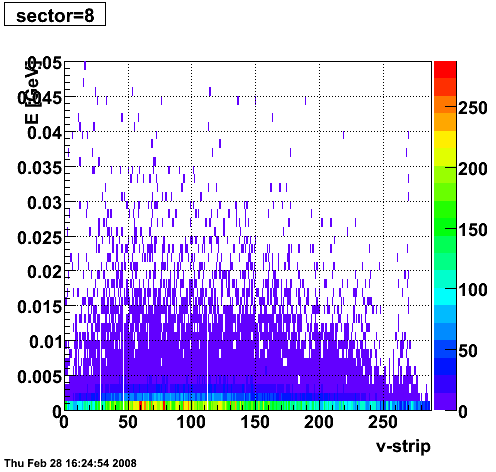 |
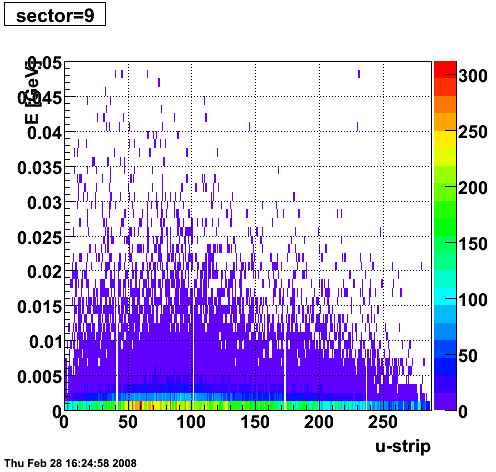 |
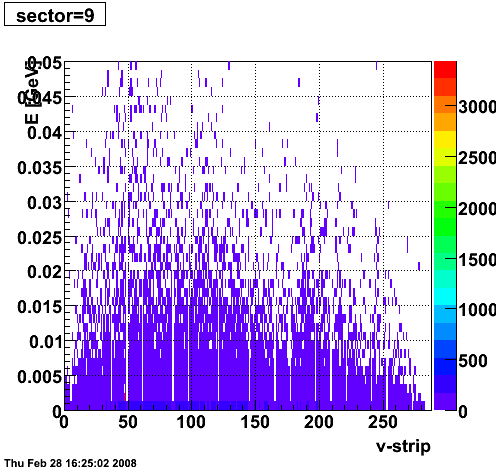 |
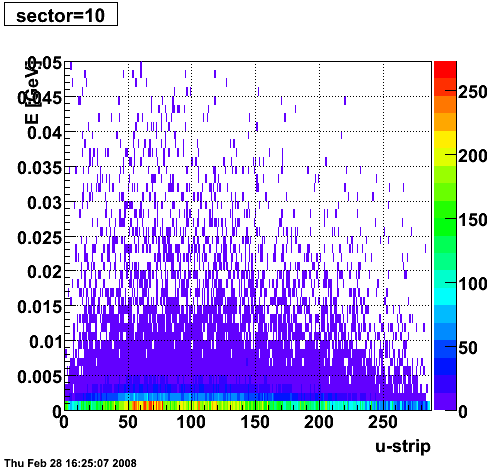 |
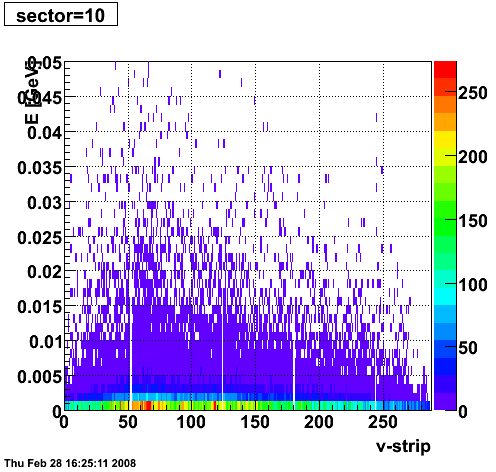 |
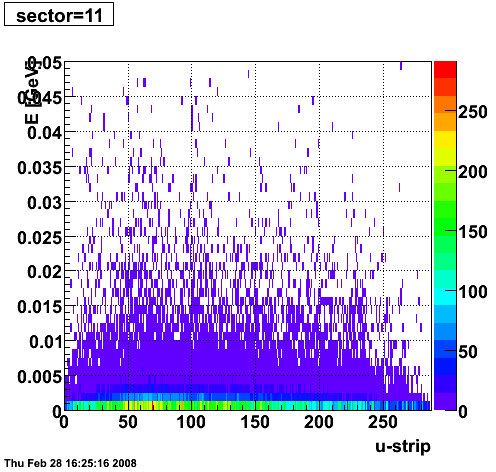 |
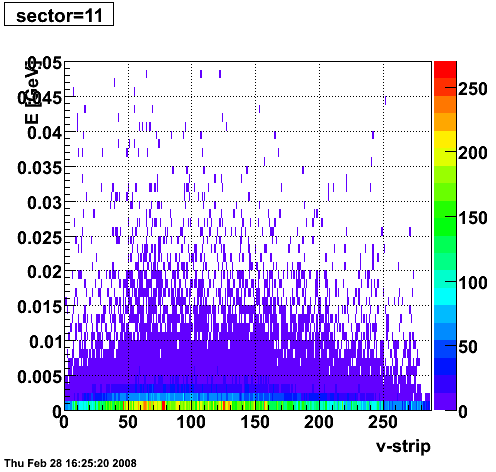 |
Pibero Djawotho Last updated Thu Feb 28 16:17:55 EST 2008
2008.03.04 A second look at eta mesons in the STAR Endcap Calorimeter
A second look at eta mesons in the STAR Endcap Calorimeter
Introduction
In case you missed it, the first look is
. I processed
from the 2006 pp longitudinal 2 runs and picked events tagged with the L2gamma trigger id (137641). I ran the StGammaMaker on the MuDst files from these runs and produced gamma trees. These gamma trees are available at
/star/institutions/iucf/pibero/2007/etaLong/
. Within the StGammaMaker framework, I developed code to seek candidate etas with emphasis on high purity. The macros and source files are:
Note, the workhorse function is
StEtaFinder::findTowerPoints()
.
Algorithm
- Find seed tower with pT > 0.8 GeV
- Require no TPC track into the seed tower
- Get the ranges of SMD U & V strips that span the volume of the seed tower
- Find the strips with maximum energy within these ranges
- Require that the maximum strips have more than 2 MeV in each SMD plane
- Get the intersection of the maximum strips and ensures that it lies within 70% of the fiducial volume of the seed tower
- Make sure the photon candidate responsible for the SMD clusters above enters and exits the same seed tower
- Form a 11-strip cluster in each plane with +/-5 strips around the max strip and require that it contains 70% of the energy in a range +/-20 strips around the max strip
- Require that the energy asymmetry between the 11-strip clusters in the U and V planes be less than 20%
- Create a point using the energy of the seed tower and the position of the intersection of the max strips in the SMD U and V planes
- Repeat until seed towers in the event are exhausted
- Combine different points in the event to calculate the invariant mass
- Diphoton pairs with invariant mass between 0.4 and 0.6 GeV are saved to a PDF file
Invariant mass
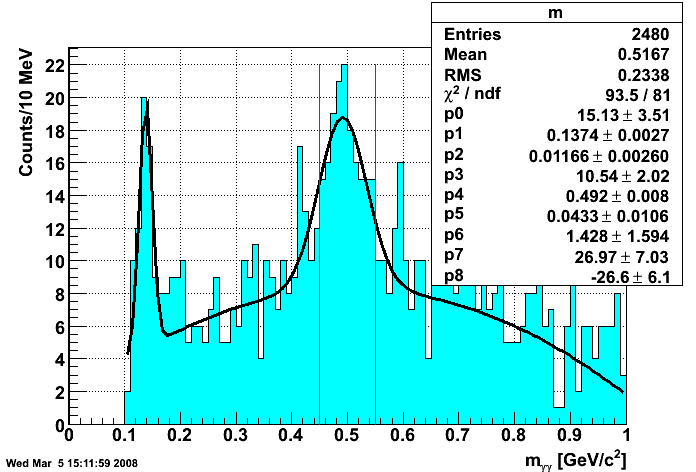
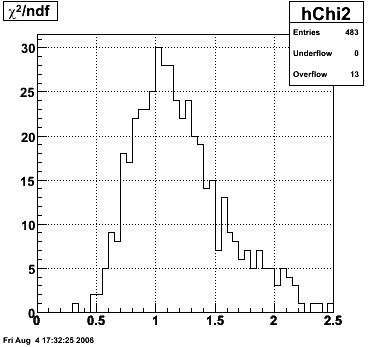
I fit the diphoton invariant mass with two Gaussians, one for the pi0 peak (p0-p2) and another one for the eta peak (p3-p5) plus a quadratic for the background (p6-p8). The Gaussian is of the form p0*exp(0.5*((x-p1)/p2)**2) and the quadratic is of the form p6*+p7*x+p8*x**2. A slightly better chi2/ndf in the fit is achieved by using Breit-Wigner functions instead of Gaussians for the signal here. I calculate the raw yield of etas from the fit as p3*sqrt(2*pi)*p5/bin_width = 85 where each bin is 0.010 GeV wide. I select candidate etas in the mass range 0.45 to 0.55 GeV and plot their photon response in the shower maximum detector here. Since we are interested in collecting photons of pT > 7 GeV, only those candidate photons with pT > 5 GeV will be used in the shower shape library. I also calculate the background under the signal region by integrating the background fit from 0.45 to 0.55 GeV and get 82 counts.
- S = 85
- B = 82
- S:B = 1.03:1
- S/√S+B = 6.6
Additional plots
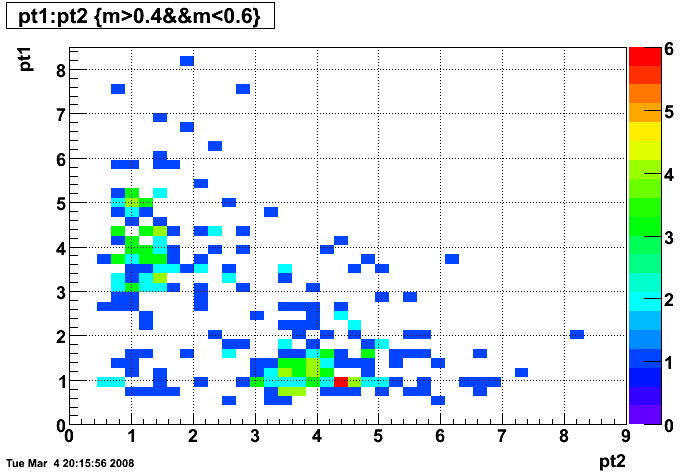
Pibero Djawotho Last updated at Tue Mar 4 16:21:13 EST 2008
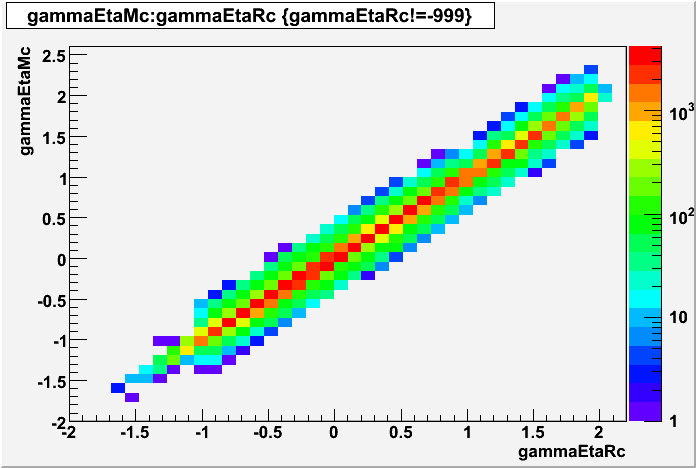
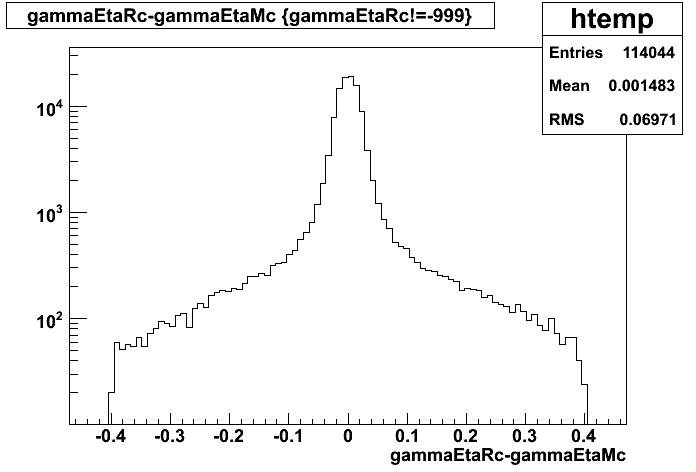
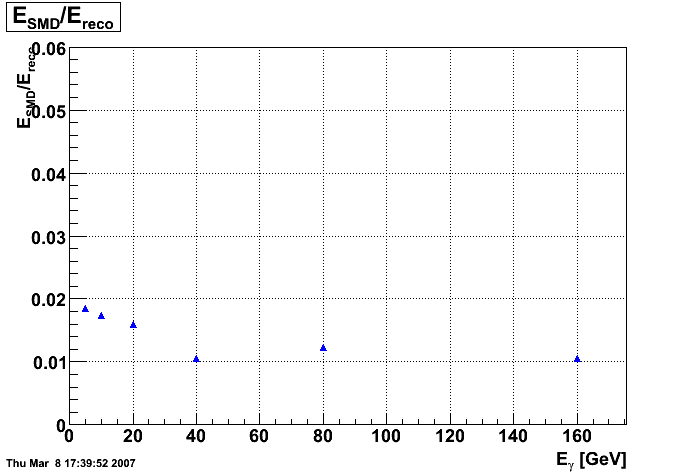
2008.03.08 Adding the SMD energy to E_reco/E_MC for Photons
Adding the SMD energy to E_reco/E_MC for Photons
The following is a revisited study of E_reco/E_MC for photons with the addition of the SMD energy to E_reco.
QA plots for each energy
E_SMD/E_reco vs. eta
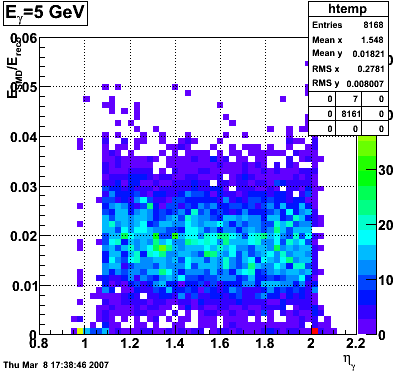 |
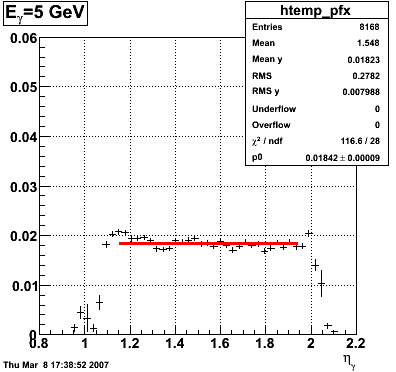 |
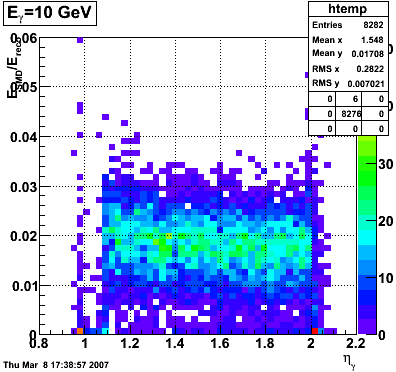 |
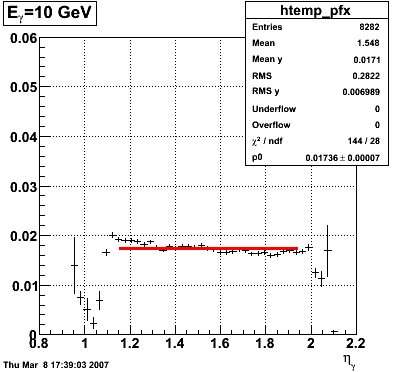 |
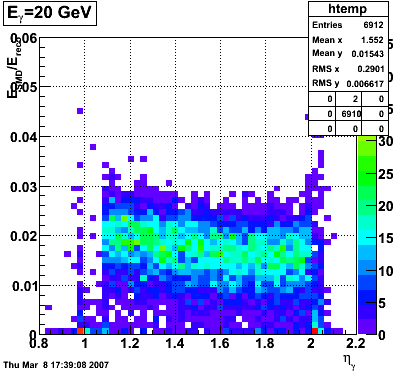 |
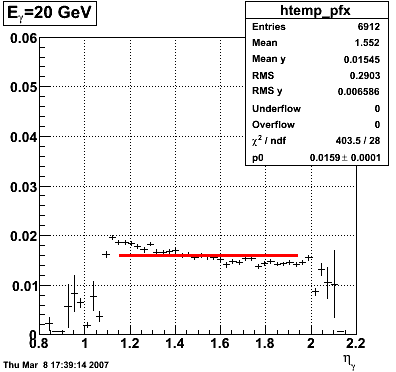 |
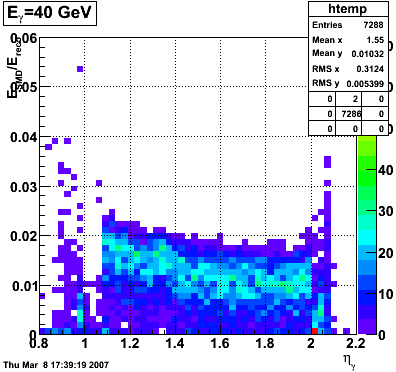 |
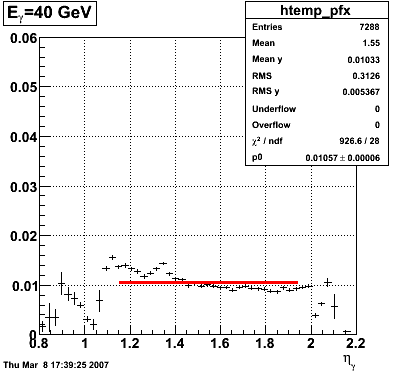 |
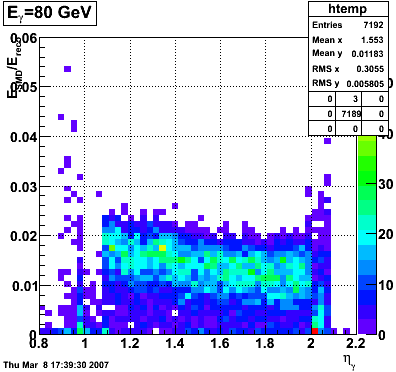 |
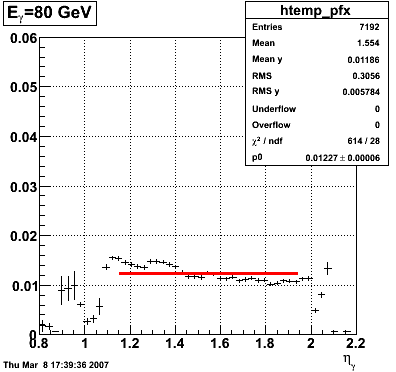 |
 |
 |
Pibero Djawotho Last updated Thu Mar 8 04:27:28 EST 2007
2008.03.21 Chi square method
SectorVsRunNumber.png 10-Feb-2010 12:22 14K
ShowerShapes.png 10-Feb-2010 12:22 17K
chiSquareMC.png 10-Feb-2010 12:22 13K
chiSquarePibero.png 10-Feb-2010 12:22 16K
chiSquareWill.png 10-Feb-2010 12:22 16K
chiSquareWillAndMC.png 10-Feb-2010 12:22 17K
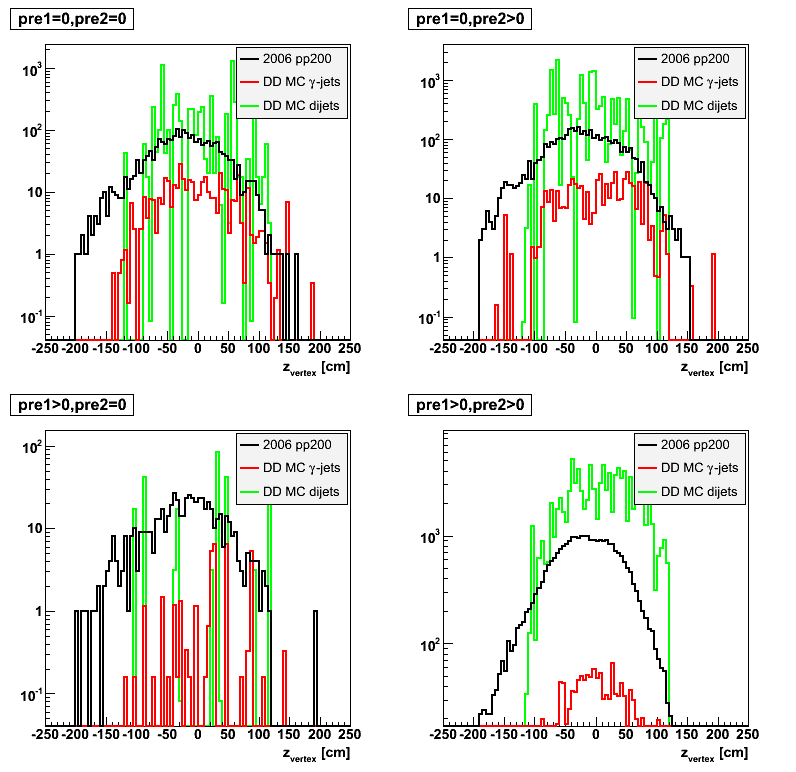
2008.04.08 Data-Driven Shower Shapes
Data-Driven Shower Shapes
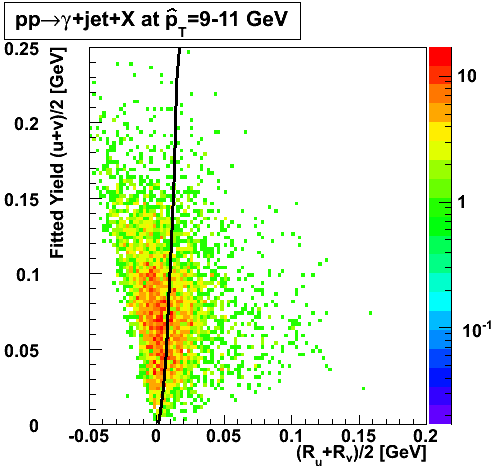
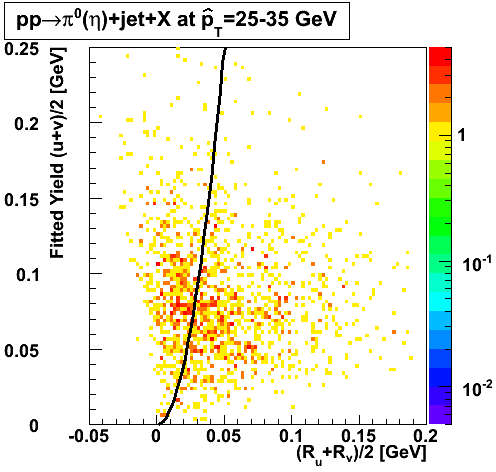
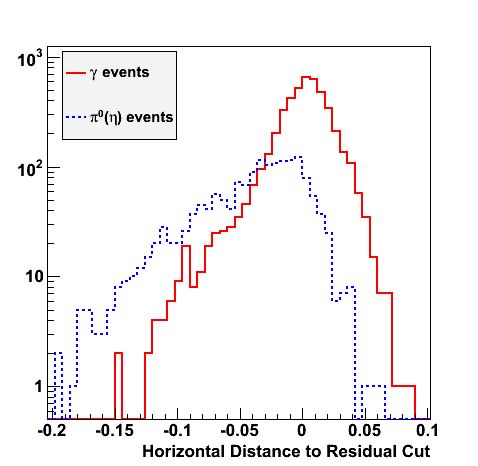
Gamma Conversion before the Endcap
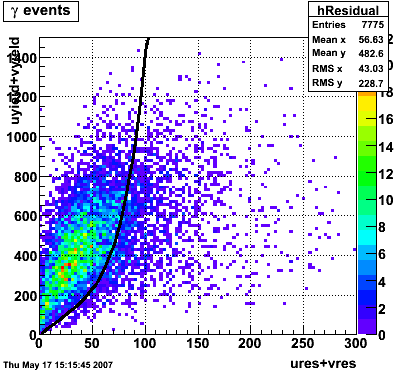
The plots below show the conversion process before the Endcap. I look at prompt photons heading towards the Endcap from a MC gamma-jet sample with a partonic pT of 9-11 GeV. I identify those photons that convert using the GEANT record. The top left plot shows the total number of direct photons and those that convert. I register a 16% conversion rate. This is consistent with Jason's 2006 SVT review. The top right plot shows the source of conversion, where most of the conversions emanate from the SVT support cone, also consistent with Jason's study. The bottom left plot shows the separation in the SMD between the projected location of the photon and the location of the electron/positron from conversion.
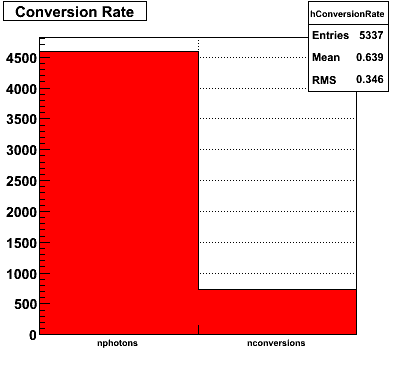 |
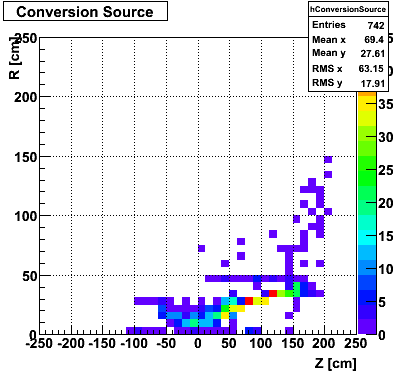 |
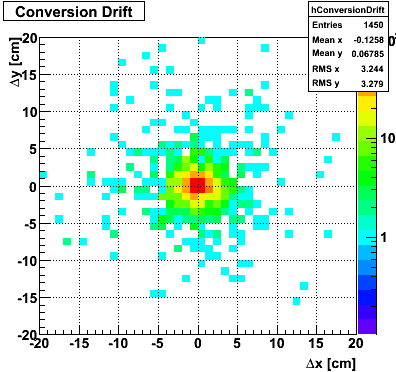 |
Shower shapes comparison
This
file shows several shower shapes in a single plot for comparison:
- MC - Monte Carlo shower shape from the 9-11 GeV pT gamma-jet Pythia sample
- DD - Data-driven Monte Carlo shower shape (Each final state photon shower shape is replaced with a corresponding shower shape from data in the same sector configuration, energy, preshower, and U/V-plane bin).
- Standard MC - Monte Carlo shower shape parametrized by Hal (also from the 9-11 GeV pT gamma-jet Pythia sample)
- Will - Data shower shape derived from photons from eta decays by Will using a modified version of Weihong/Jason meson pi0 finder
- Pibero - Data shower shape derived from photons from eta decays by Pibero using a crude eta finder
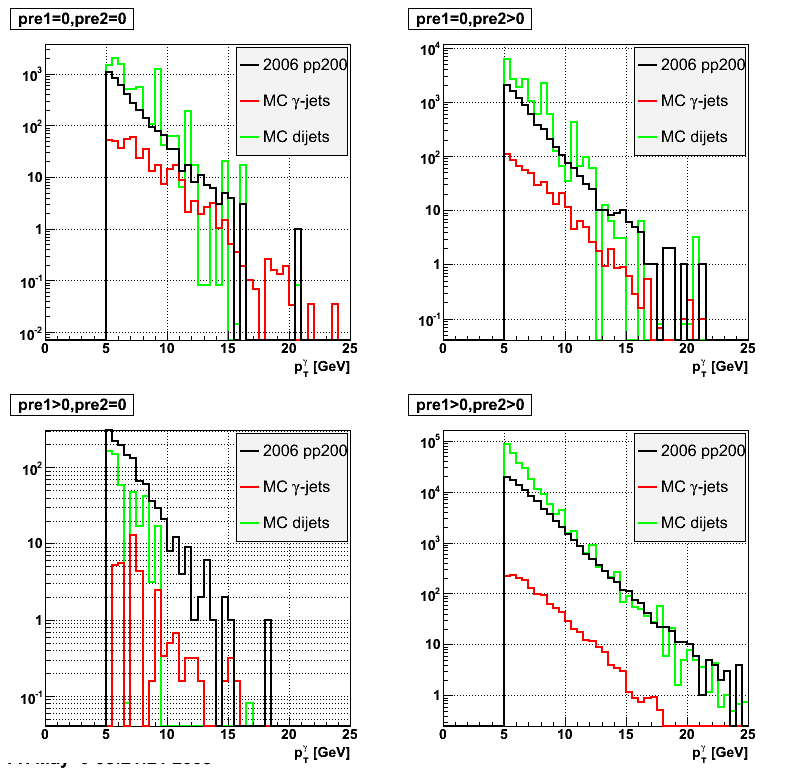
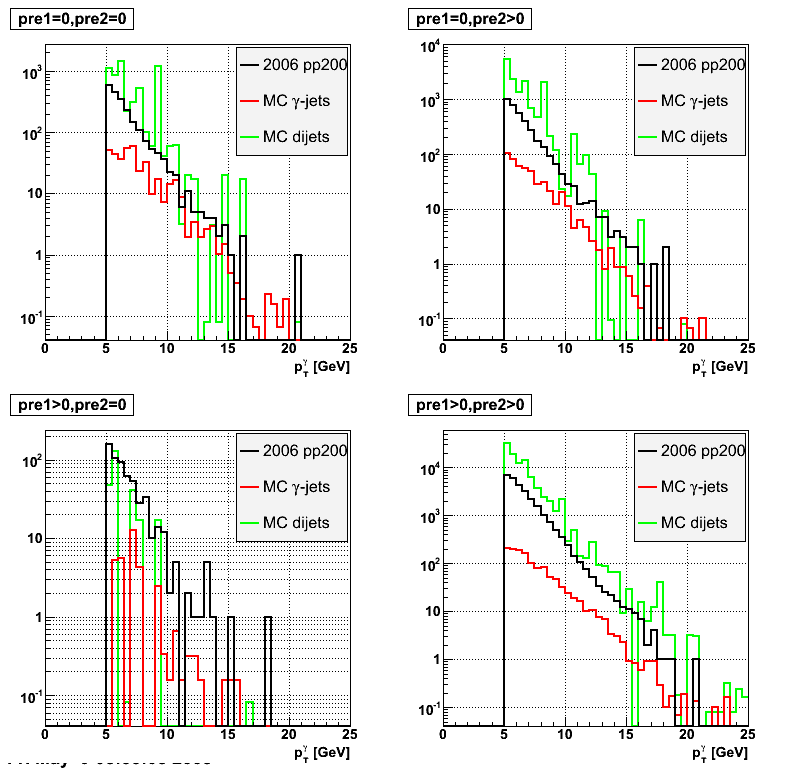
Shower Shapes Sorted by SMD Plane, Sector Configuration, Energy and Preshower
These Shower Shapes are binned by:
- SMD plane (U and V)
- Sector configuration with the formula sector%3 where sector=1..12, so 3 different bins. More details can be found at the EEMC Web site under the Geometry link.
- Energy of the photon (E < 8 GeV and E > 8 GeV)
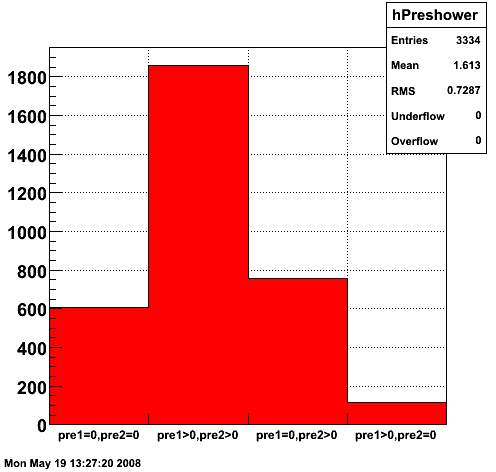
- Preshower energy
(pre1==0&&pre2==0)and(pre1>0||pre2>0)
They are then fitted with a triple-Gaussian of the form:
[0]*([2]*exp(-0.5*((x-[1])/[3])**2)/(sqrt(2*pi)*[3])+[4]*exp(-0.5*((x-[1])/[5])**2)/(sqrt(2*pi)*[5])+(1-[2]-[4])*exp(-0.5*((x-[1])/[6])**2)/(sqrt(2*pi)*[6]))
Comparison of Sided Residuals for Monte Carlo (MC) and Data-Driven (DD) Shower Shapes
All fits to MC are with reference to the old Monte carlo fit function:
[0]*(0.69*exp(-0.5*((x-[1])/0.87)**2)/(sqrt(2*pi)*0.87)+0.31*exp(-0.5*((x-[1])/3.3)**2)/(sqrt(2*pi)*3.3))
All fits to the data are with reference to a single
. The fit function is:
[0]*([2]*exp(-0.5*((x-[1])/[3])**2)/(sqrt(2*pi)*[3])+[4]*exp(-0.5*((x-[1])/[5])**2)/(sqrt(2*pi)*[5])+(1-[2]-[4])*exp(-0.5*((x-[1])/[6])**2)/(sqrt(2*pi)*[6]))
- All Shower Shapes
- No Conversion
- Conversion
- No Preshower
- Preshower
- No Conversion and Preshower
- Sector Configuration 0
- Sector Configuration 1
- Sector Configuration 2
Comparison of Sided Raw Tails for Monte Carlo (MC) and Data-Driven (DD) Shower Shapes
- All Shower Shapes
- No Conversion
- Conversion
- No Preshower
- Preshower
- No Conversion and Preshower
- Sector Configuration 0
- Sector Configuration 1
- Sector Configuration 2
Pibero Djawotho Last updated Tue Apr 8 17:29:40 EDT 2008
2008.04.12 Data-Driven Residuals
Data-Driven Residuals
Gammas
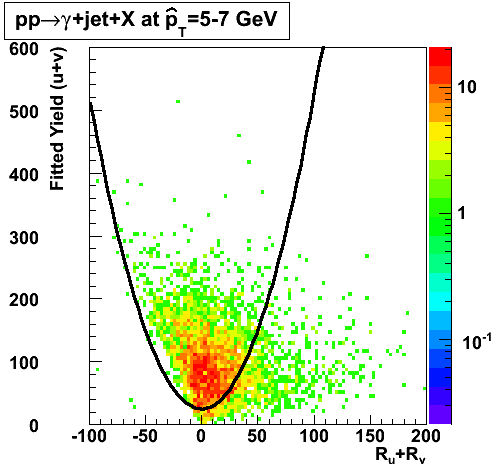 |
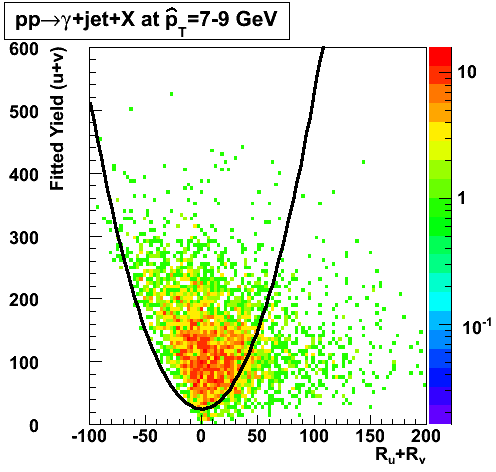 |
 |
 |
 |
 |
Jets
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
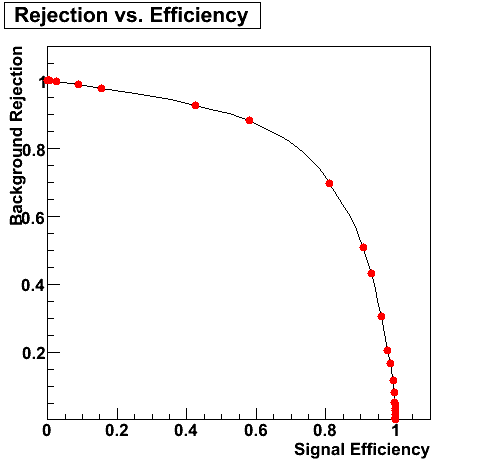
Background Rejection vs. Signal Efficiency
| Partonic pT=9-11 GeV | Partonic pT=9-11 GeV |
 |
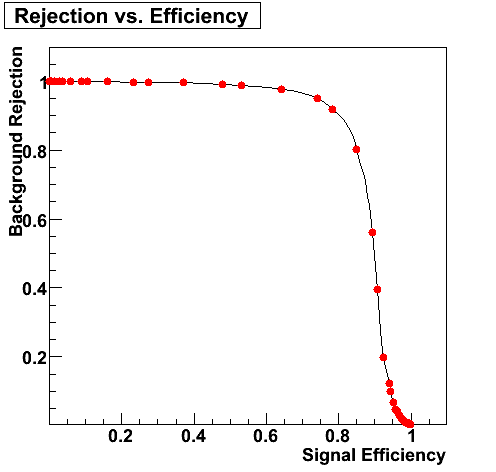 |
Background Rejection vs. Signal Efficiency (Neutral Meson pT > 8 GeV)
 |
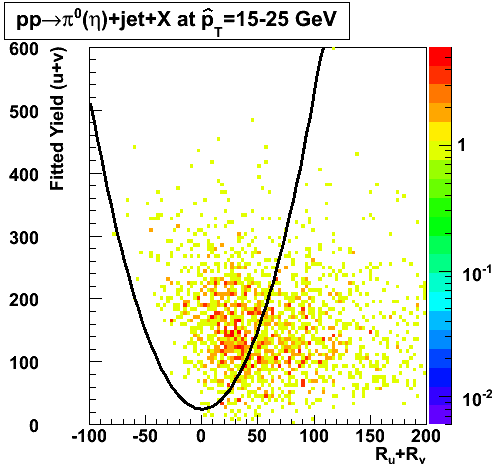 |
 |
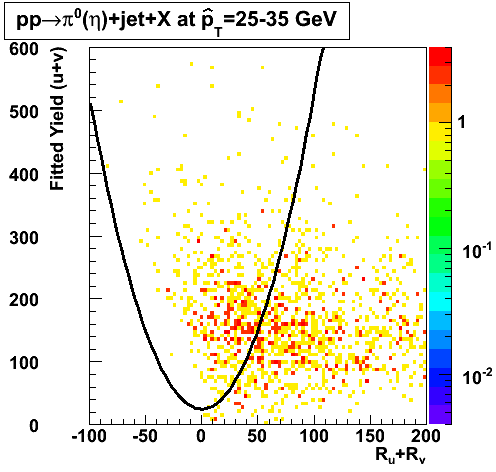 |
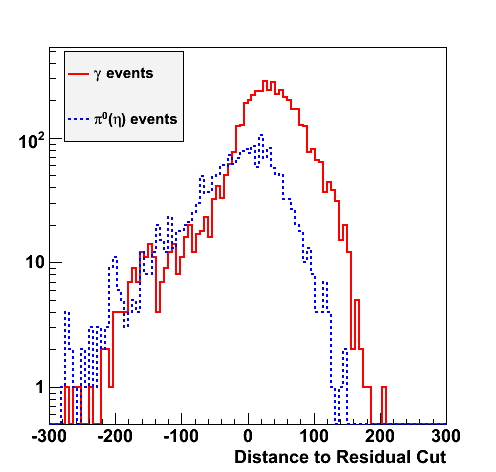 |
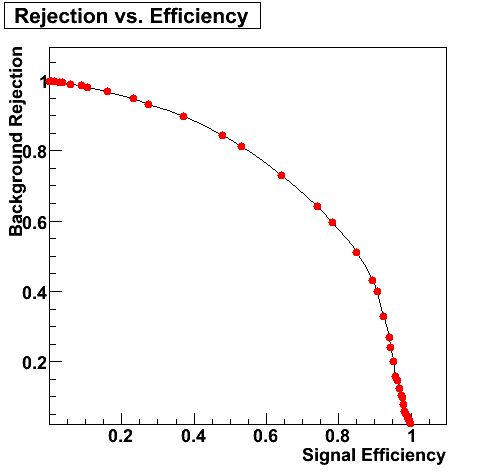 |
Pibero Djawotho Last updated Sat Apr 12 13:27:50 EDT 2008
2008.04.12 Pythia Gamma-Jets
Pythia Gamma-Jets
Gamma-Jet Yields
During Run 6, the L2-gamma trigger (trigger id 137641) sampled 4717.10 nb-1 of integrated luminosity. By restricting the jet to the Barrel, |ηjet|<1, and the gamma to the Endcap, 1<ηgamma<2, the yield of gamma-jets is estimated as the product of the luminosity, the cross section, and the fraction of events in the phasespace above. The total cross section reported by Pythia for gamma-jet processes at different partonic pT thresholds is listed in the table below. No efficiencies are included.
| pT threshold [GeV] | Total cross section [mb] | Fraction | Ngamma-jets |
| 5 | 6.551E-05 | 0.0992 | 30654 |
| 6 | 3.075E-05 | 0.1161 | 16840 |
| 7 | 1.567E-05 | 0.1150 | 8500 |
| 8 | 8.654E-06 | 0.1131 | 4617 |
| 9 | 4.971E-06 | 0.1223 | 2868 |
| 10 | 2.953E-06 | 0.1151 | 1603 |
Gamma-Jets pT slope
The pT slope is exp(-0.69*pT)=2^(-pT), so the statistics are halved with each 1 GeV increase in pT.
References
- Yield estimates based on single-particle MC sample, and comparison w/ pythia (Jason Webb)
- Pythia estimates of gamma-jet yields (Jim Sowinski)
Pibero Djawotho Last updated Sat Apr 12 15:15:56 EDT 2008
2008.04.22 Run 6 Photon Yield Per Trigger
Run 6 Photon Yield Per Trigger
Introduction
The purpose of this study is to estimate the photon yield per trigger in the Endcap Electromagnetic Calorimeter during Run 6. The trigger of interest is the L2-gamma trigger. Details of the STAR triggers during Run 6 were compiled in the 2006 p+p run (run 6) Trigger FAQ by Jamie Dunlop. The triggers relevant to this study are reproduced in the table below for convenience.
| Trigger id | Trigger name | Description |
| 117641 | eemc-http-mb-l2gamma | EEMC HT > th1 (12, 2.6 GeV) and TP > TH1 (17, 3.8 GeV), minbias condition, L2 Gamma algorithm, reading out slow detectors, L2 thresholds at 2.9, 4.5 |
| 127641 | eemc-http-mb-l2gamma | EEMC HT > th1 (12, 2.6 GeV, run < 7100052;13, 2.8 GeV, run >=7100052) and TP > TH1 (17, 3.8 GeV, run < 710052; 21, 4.7 GeV, run>=7100052 ), minbias condition, L2 Gamma algorithm, reading out slow detectors, L2 thresholds at 3.4, 5.4, transverse running |
| 137641 | eemc-http-mb-l2gamma | EEMC HT > th1 (16, 3.5 GeV) and TP > th1 (20, 4.5 GeV), minbias condition, L2 Gamma algorithm, reading out slow detectors, L2 thresholds at 3.7, 5.2, longitudinal running 2 |
The luminosity sampled by each trigger was also caclulated here by Jamie Dunlop. The luminosity for the relevant triggers is reproduced in the table below for convenience. The figure-of-merit (FOM) is calculated as FOM=Luminosity*PB*PY for transverse runs and FOM=Luminosity*PB2*PY2 for longitudinal runs where PB is the polarization of the blue beam and PY is the polarization of the yellow beam. Naturally, in spin physics, the FOM is the better indicator of statistical precisison.
| Trigger | First run | Last run | Luminosity [nb-1] | Figure-of-merit [nb-1] |
| 117641 | 7093102 | 7096017 | 118.88 | 11.89 |
| 127641 | 7097009 | 7129065 | 3219.04 | 1099.43 |
| 137641 | 7135050 | 7156028 | 4717.10 | 687.65 |
Event selection
Trigger selection
For this study, only the trigger of longitudinal running 2 (137641) is used. As mentioned above, at level-0, an EEMC high tower above 3.5 GeV and its associated trigger patch above 4.5 GeV in transverse energy coupled with a minimum bias condition, which is simply a BBC coincidence to ensure a valid collision, is required for the trigger to fire. The EEMC has trigger patches of variable sizes depending on their location in pseudorapidity. (The BEMC has trigger patches of fixed sizes, 4x4 towers.) At level-2, a high tower above 3.7 GeV and a 3x3 patch above 5.2 GeV in transverse energy is required to accept the event.
Gamma candidates
In addition to selecting events that were tagged online by the L2-gamma trigger, the offline
looks for tower clusters with minimum transverse energy of 5 GeV. These clusters along with their associated TPC tracks, preshower and postshower tiles, and SMD strips form gamma candidates. Gamma trees for the 2006 trigger ID 137641 with primary vertex are located at
/star/institutions/iucf/pibero/2006/gammaTrees/
.
Track isolation
The gamma candidate is required to have no track pointing to any of its towers.
EMC isolation
The gamma candidate is required to have 85% of the total transverse energy in a cone of radius 0.3 in eta-phi space around the position of the gamma candidate. That is E
Tgamma
/E
Tcone
> 0.85 and R=√Δη
2
+Δφ
2
=0.3 is the cone radius.
Jet Reconstruction
The gamma candidate is matched to the best away-side jet with neutral fraction < 0.9 and cos(φ
gamma
-φ
jet
) < -0.8. The 2006 jet trees are produced by Murad Sarsour at PDSF in
/eliza13/starprod/jetTrees/2006/trees/
. A local mirror exists at RCF under the directory
/star/institutions/iucf/pibero/2006/jetTrees/
.
Spin Information
Jan Balewski has an excellent write-up, Offline spin DB at STAR, on how to get spin states. I obtain the spin states from the skim trees in the jet trees directory. In brief, the useful spin states are:
| Blue Beam Polarization | Yellow Beam Polarization | Spin4 |
| P | P | 5 |
| P | N | 6 |
| N | P | 9 |
| N | N | 10 |
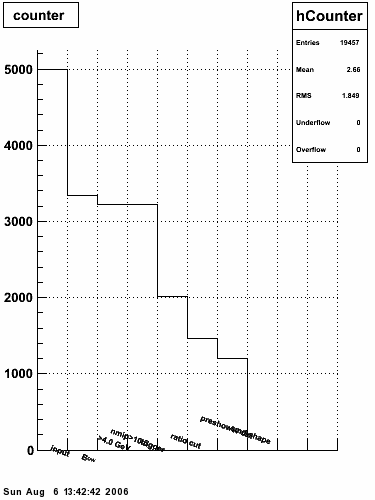
Event Summary
| L2-gamma triggers | 730128 |
| Endcap gamma candidates | 723848 |
| Track isolation | 246670 |
| EMC isolation | 225400 |
| Away-side jet | 99652 |
| SMD max sided residual | 19281 |
| Barrel-only jet | 15638 |
Note the number of L2-gamma triggers include only those events with a primary vertex and at least one gamma candidate (BEMC or EEMC).
Gamma-Jet Plots
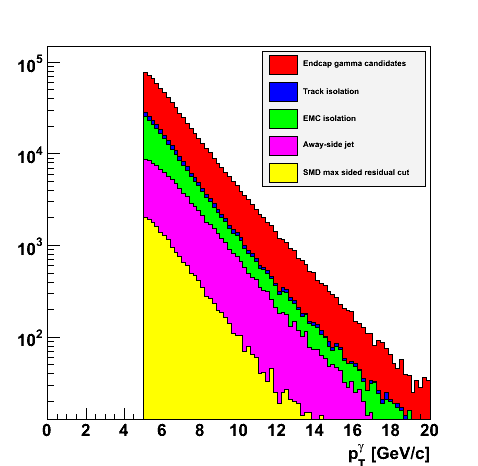 |
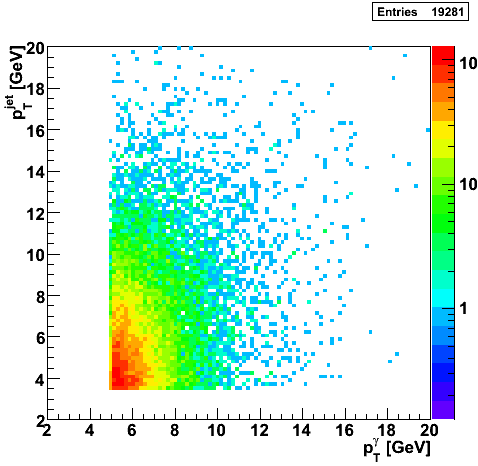 |
|
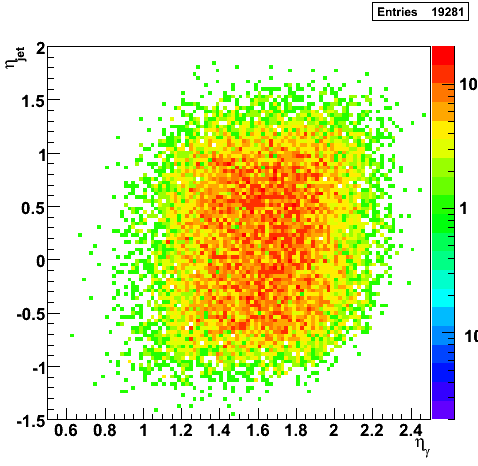 |
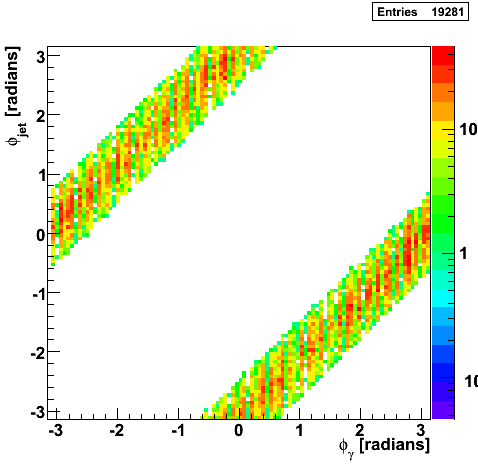 |
Comparison of pT Slope with Pythia
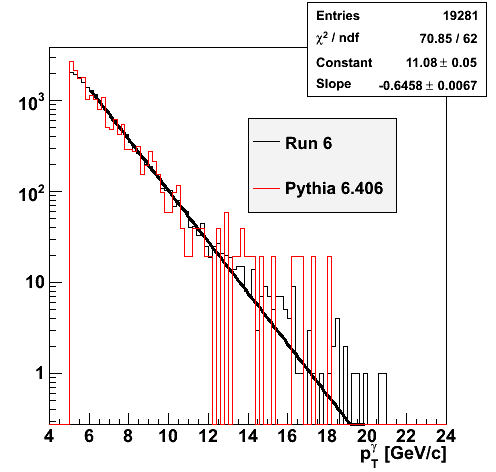 |
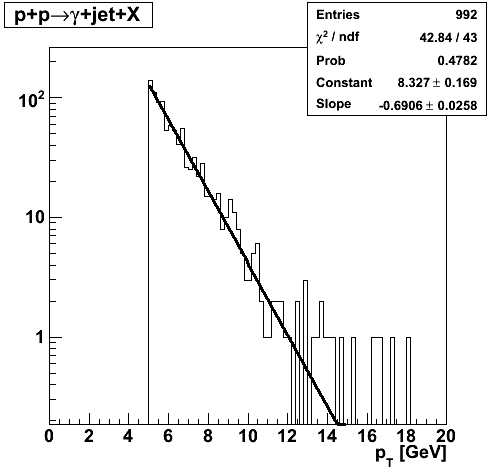 |
Partonic Kinematics Reconstruction

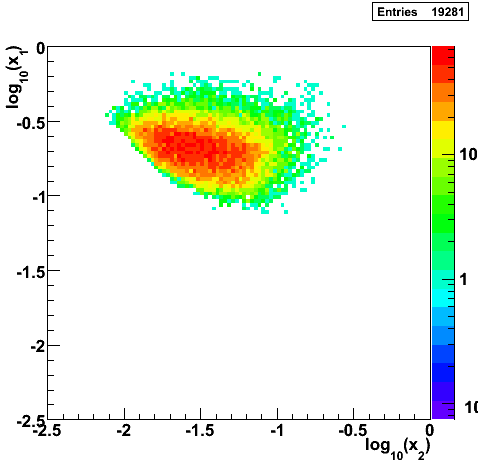 |
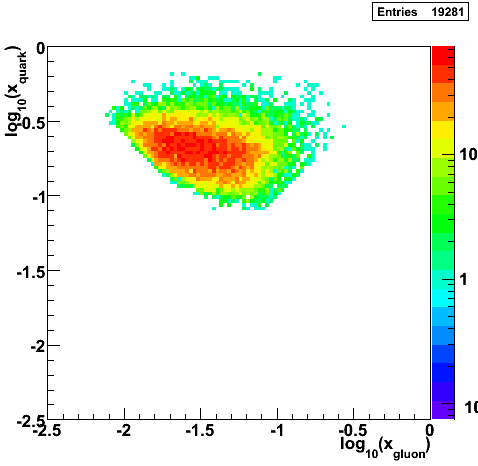 |
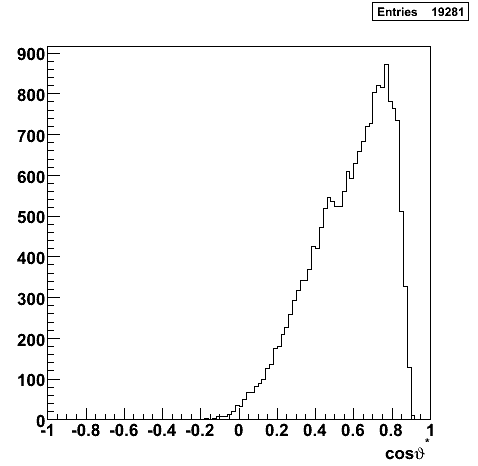 |
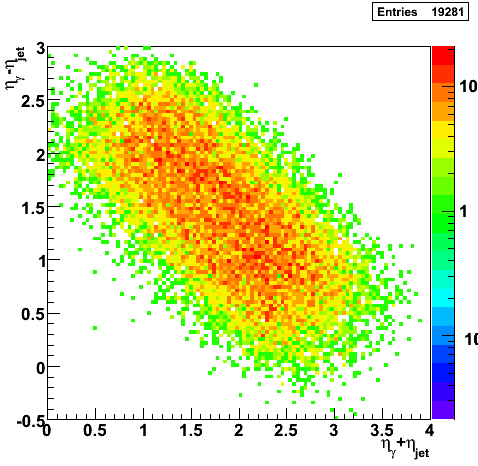 |
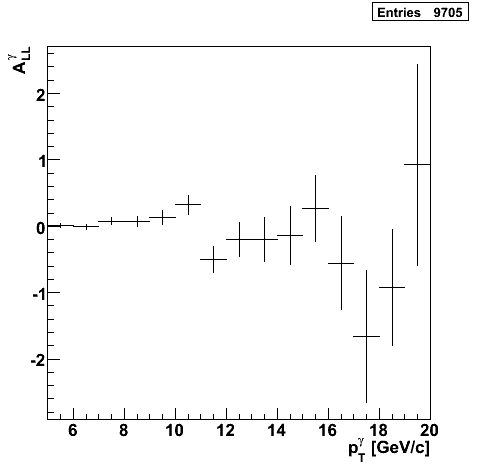 |
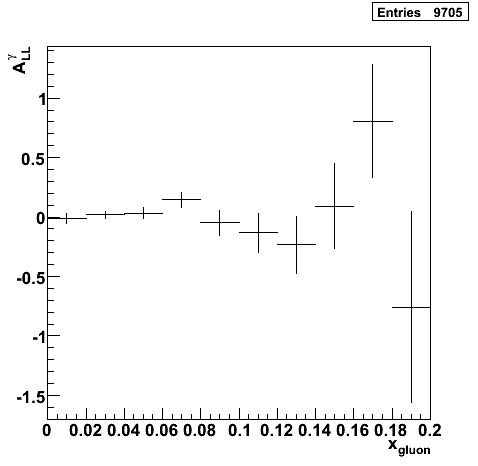 |
Open Questions
- I count ~2.4M events with trigger id 137641 using the Run 6 Browser, however my analysis only registers about ~0.78M.
Pibero Djawotho Last updated Tue Apr 22 11:40:18 EDT 2008
2008.05.07 Number of Jets
Number of Jets
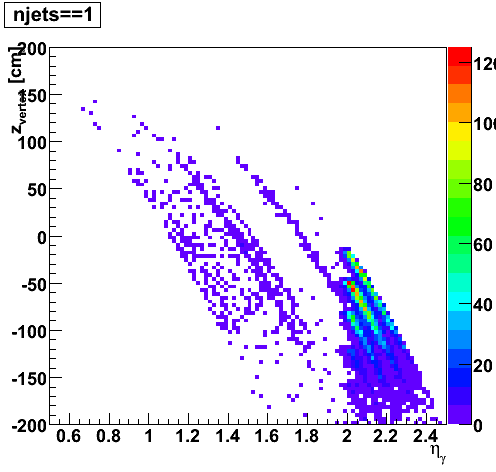
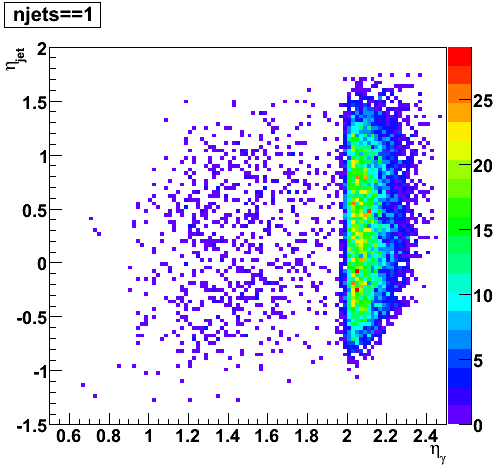
After selecting Endcap gamma candidates out of L2-gamma triggers, applying track and EMC isolation cuts, and matching the Endcap gamma candidate to an away-side jet, I record the number of jets below per event. Surprisingly, 8% of the events only have 1 jet. Those are events where the Endcap gamma candidate was not reconstructed as a neutral jet by the jet finder. The question is why.
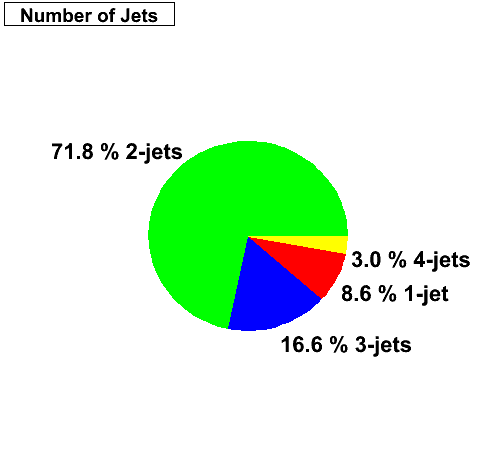 |
 |
 |
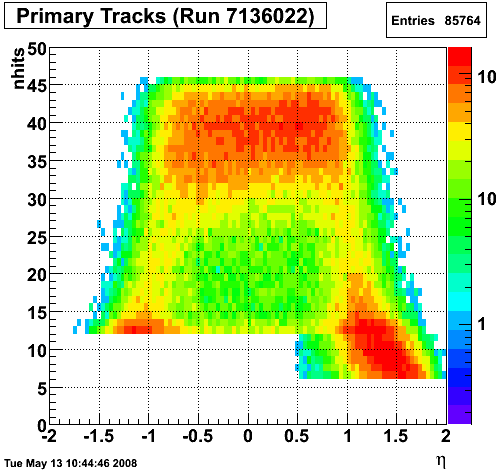 |
I display both Barrel and Endcap calorimeter towers (the z-axis represents tower energy) and draw a circle of radius 0.3 around the gamma candidate and a circle of radius 0.7 around the away-side jet for 2006 pp200 run 7136022. Even though many of the gamma candidates not reconstructed by the jet finder are at the forward edge of the Endcap, it is not at all clear why those that are well within the detector are not being reconstructed.
Pibero Djawotho Last updated Wed May 7 09:54:32 EDT 2008
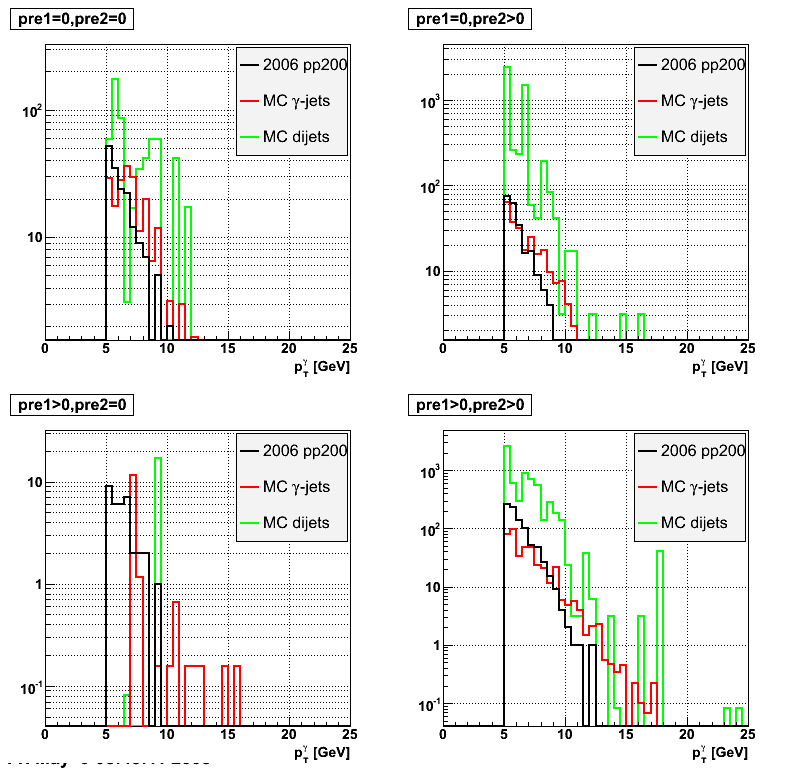
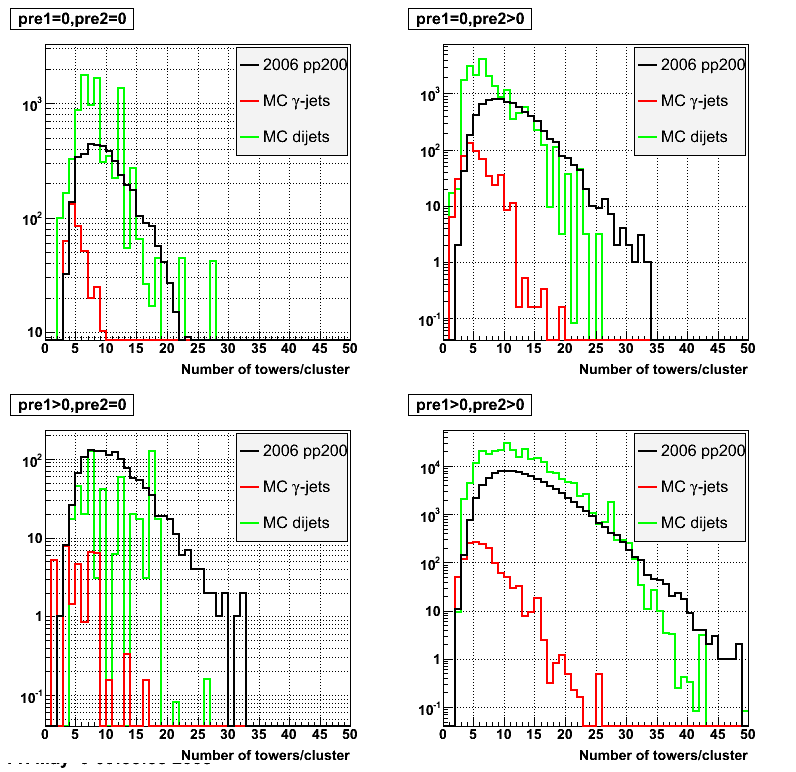
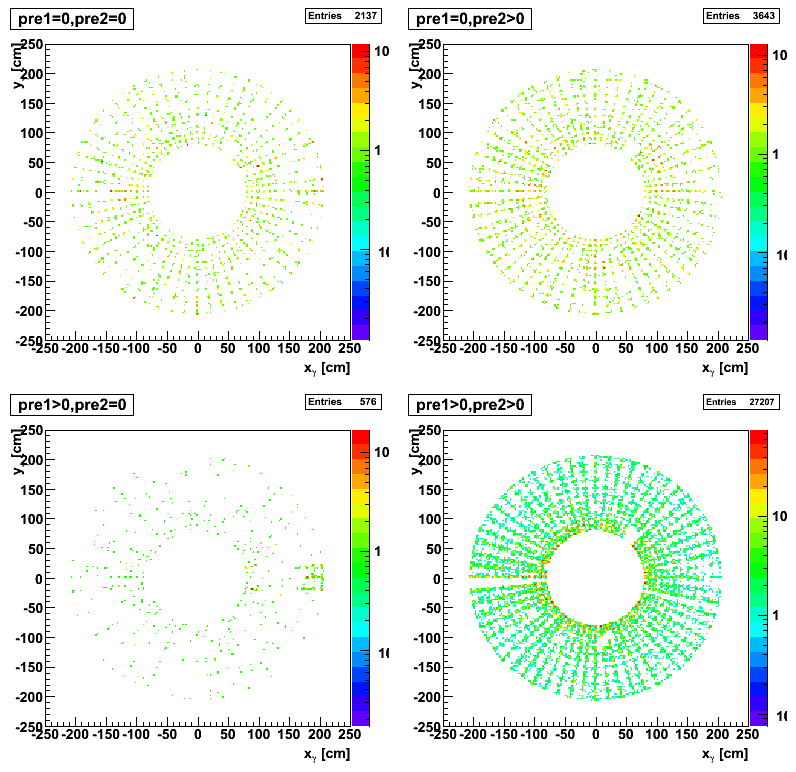
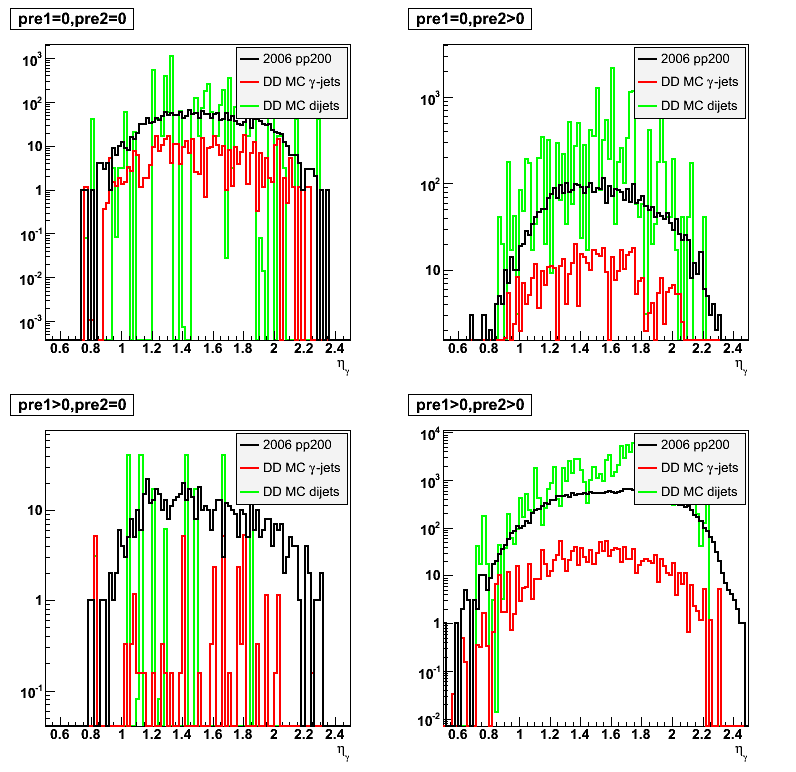
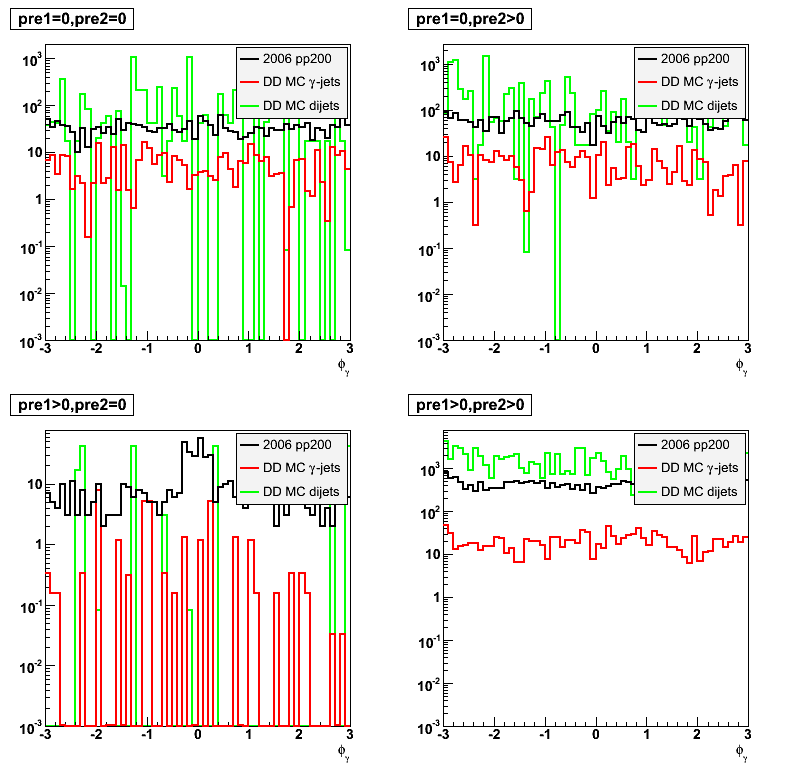
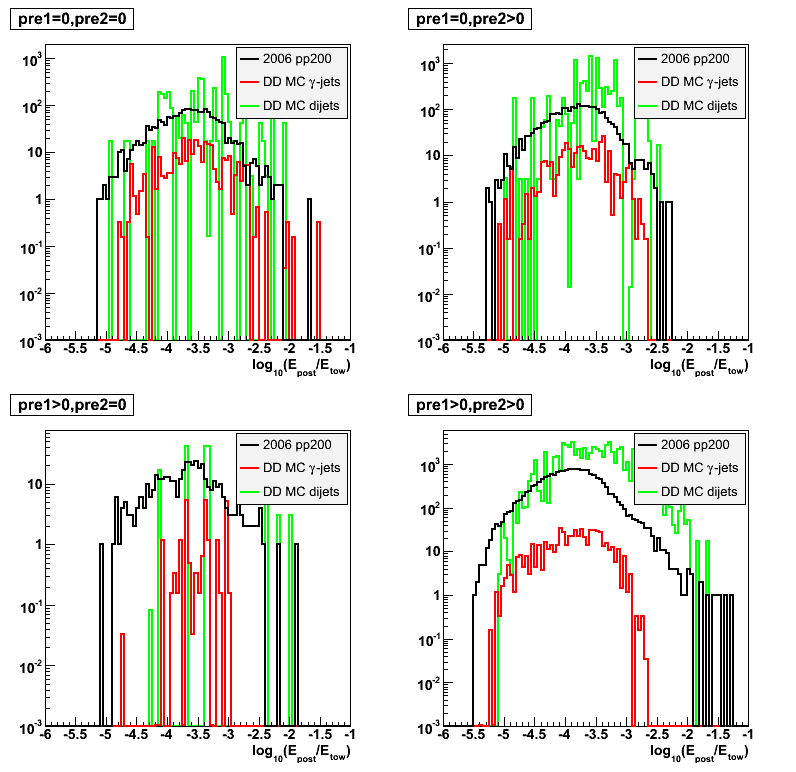
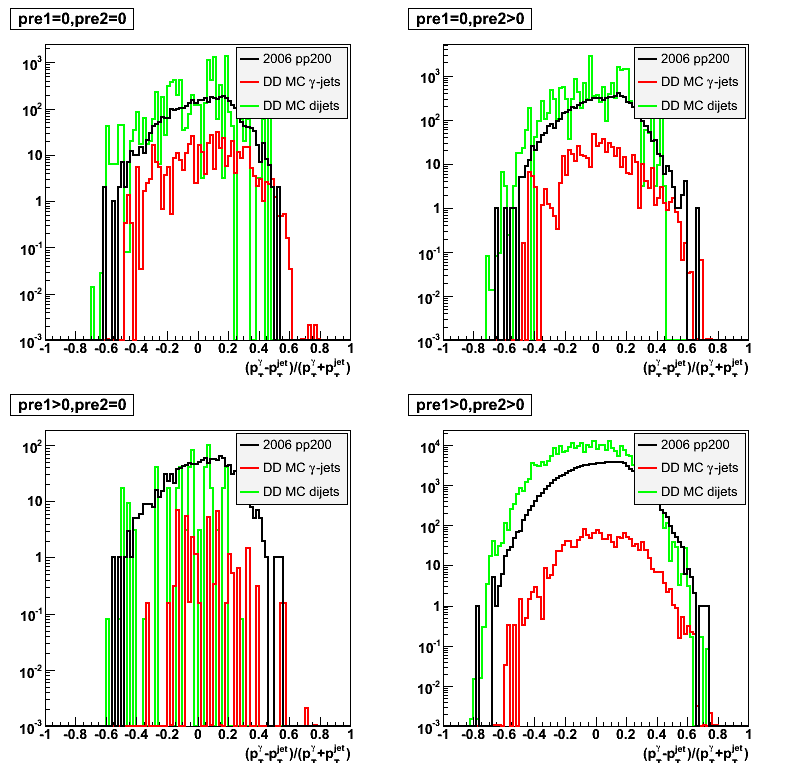
2008.05.09 Gamma-jets pT distributions
Gamma-jets pT distributions
Note:
No cuts on residuals applied.
Not cut on number of towers in gamma cluster
Number of towers in gamma cluster <= 9
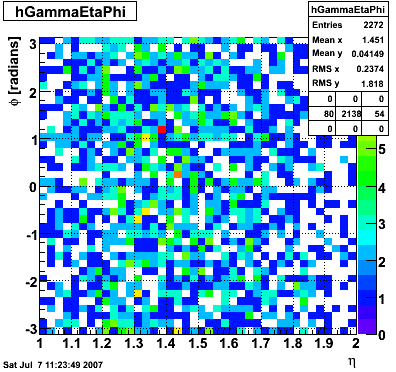
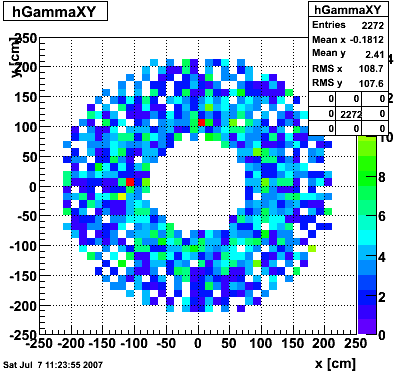
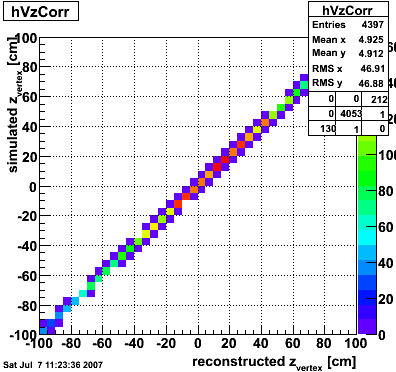
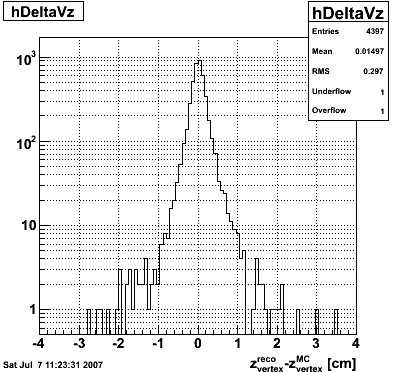
Number of towers in gamma cluster <= 4
Number of towers per cluster distributions
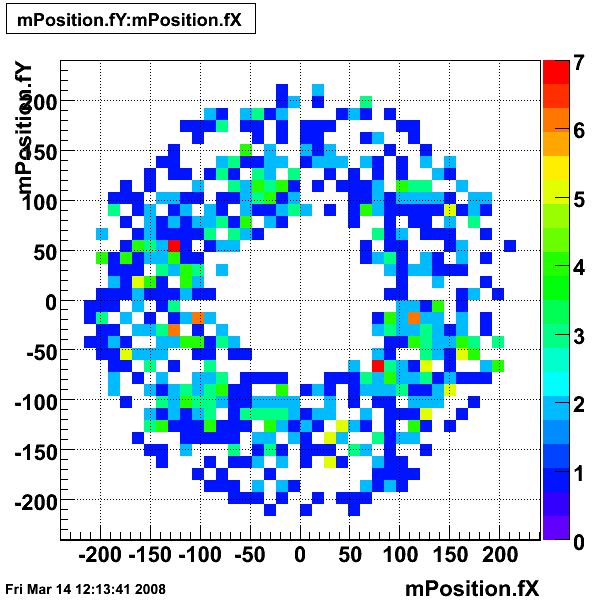
Gamma candidates xy-distribution
z-vertex distribution
Eta distribution
Phi distribution
log10(E_post/E_tow) distribution
pT asymmetry
References
Pibero Djawotho Last updated Fri May 9 08:19:00 EDT 2008
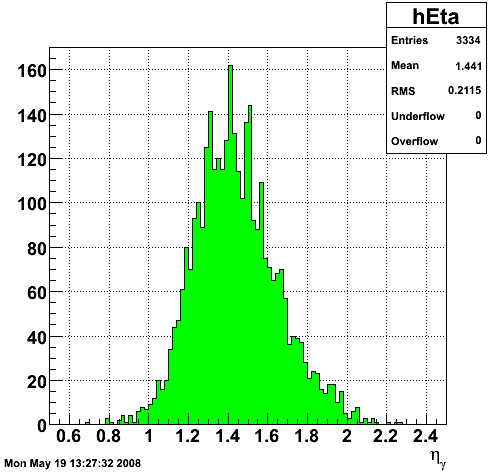
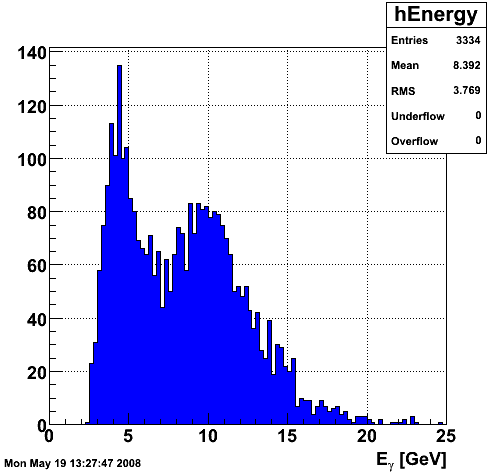
2008.05.19 Binning the shower shape library
Binning the shower shape library
Distributions
 |
 |
 |
Shower Shapes
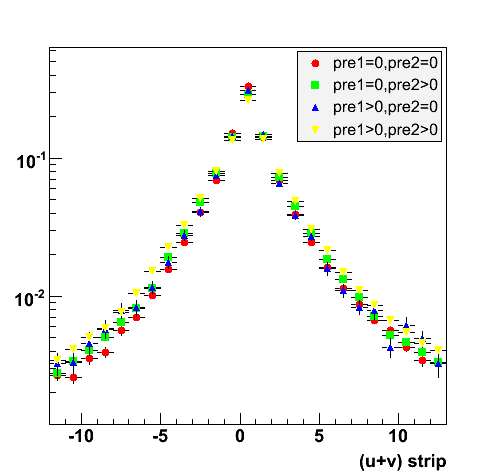 |
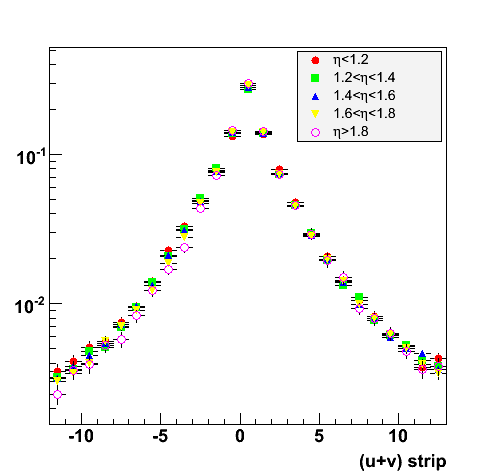 |
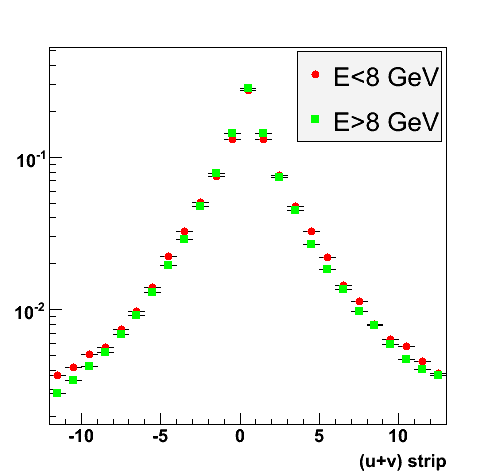 |
Pibero Djawotho Last updated Mon May 19 12:09:48 EDT 2008
2008.06.03 Jet A_LL Systematics
Jet A_LL Systematics
Hypernews discussion
jet A_LL systematic possibility
References
Pibero Djawotho Last updated Tue Jun 3 15:35:24 EDT 2008
2008.06.18 Photon-jet reconstruction with the EEMC - Part 2 (STAR Collaboration Meeting - UC Davis)
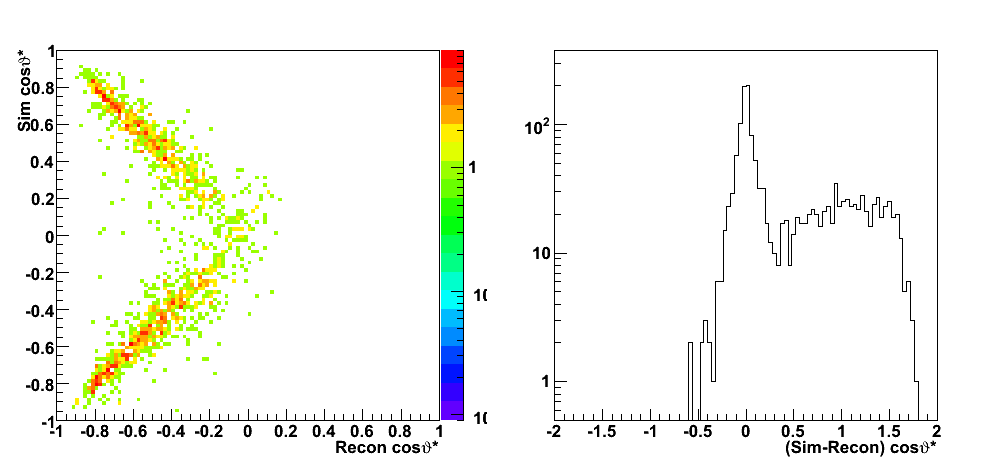
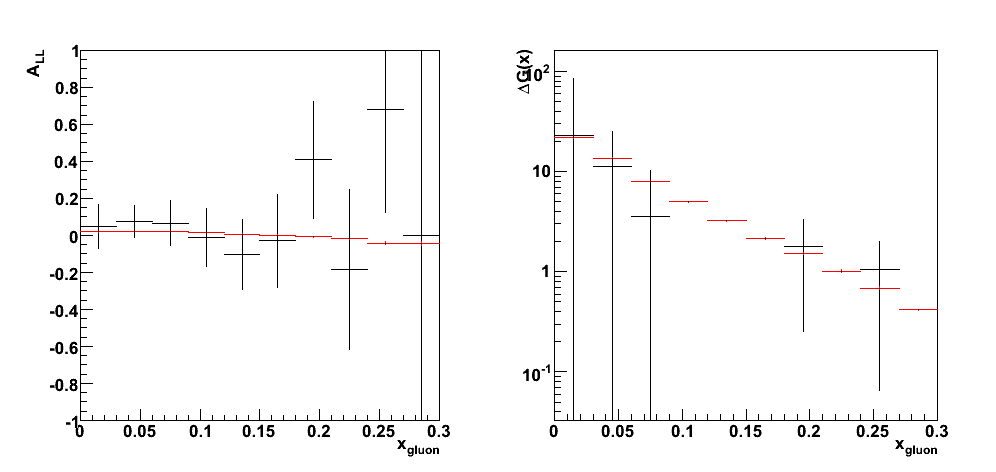
2008.07.16 Extracting A_LL and DeltaG
Extracting A_LL and DeltaG
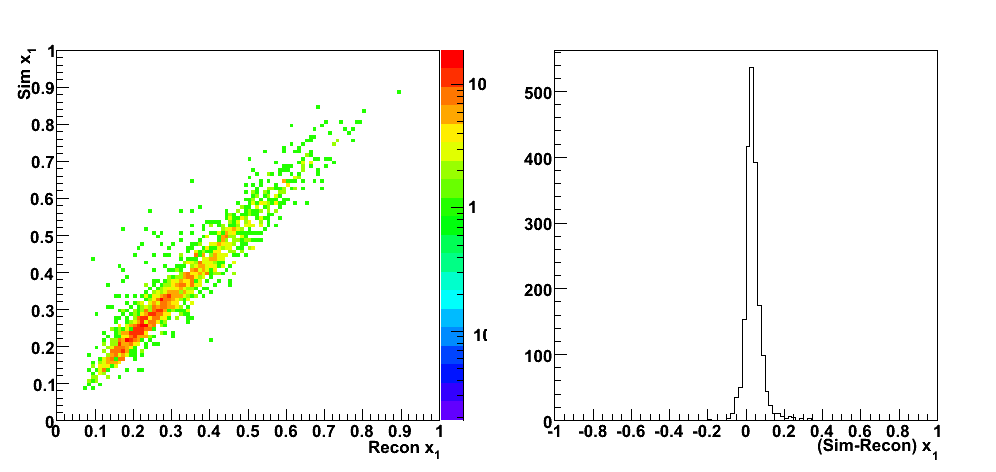
Determining state of beam polarization for Monte Carlo events
While Pythia does a pretty good job of simulating prompt photon production in p+p collisions, it does not include polarization for the colliding protons nor partons. A statistical method for assigning polarization states for each event based on ALL [1] is demonstrated in this section. For an average number of interactions for each unpolarized bunch crossing, Neff, the occurence of an event with a particular polarization state obeys a Poisson distribution with average yield of events per bunch crossing:
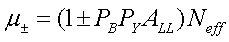
For simplicity, the polarizations of the blue and yellow beams are assumed to be P
B
=P
Y
=0.7 and N
eff
=0.01. The "+" spin state defines the case where both beams have the same helicities and the "-" spin state for the case of opposite helicities. The asymmetry A
LL
is calculated from the initial states polarized and unpolarized parton distribution functions and parton-level asymmetry:
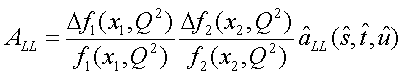
The algorithm then consists in alternatively drawing a random value N
int
from the Poisson distributions with mean μ
+
and μ
-
until N
int
>0 at which point an interaction has occured and the event is assigned the current spin state. The functioning of the algorithm is illustrated in Figure 1a where an input A
LL
=0.2 was fixed and N
trials
=500 different asymmetries were calculated. Each trial integrated N
total
=300 events. It is then expected that the mean A
LL
~0.2 and the statistical precision~0.1:
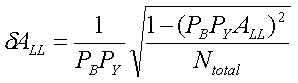
Indeed, both the A
LL
and its error are reproduced. In addition, variations on the number of events per trial were investigated (N
total
) in Figure 1b. The extracted width of the Gaussian distribution for A
LL
is consistent with the prediction for the error (red curve).
| Figure 1a | Figure 1b |
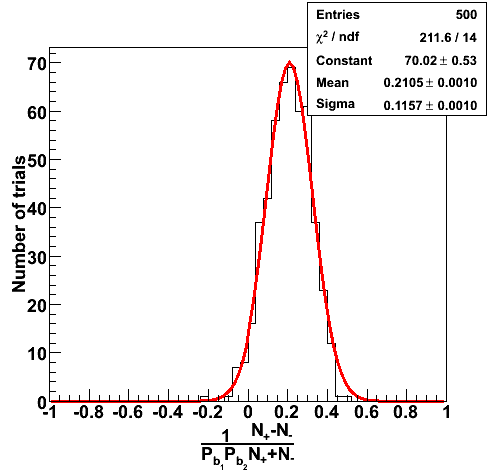 |
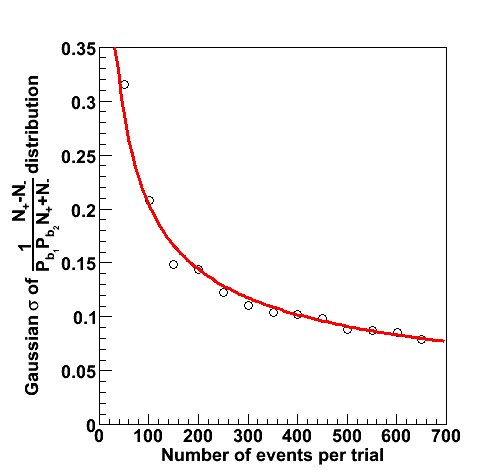 |
Event reconstruction
For this study, the gamma-jets Monte Carlo sample for all partonic pT were used. As an example, the prompt photon processes for the partonic pT bin 9-11 GeV and their total cross sections are listed in the table below. Each partonic pT bin was divided into 15 files each of 2000 events.
============================================================================== I I I I I Subprocess I Number of points I Sigma I I I I I I----------------------------------I----------------------------I (mb) I I I I I I N:o Type I Generated Tried I I I I I I ============================================================================== I I I I I 0 All included subprocesses I 2000 9365 I 3.074E-06 I I 14 f + fbar -> g + gamma I 331 1337 I 4.930E-07 I I 18 f + fbar -> gamma + gamma I 2 8 I 1.941E-09 I I 29 f + g -> f + gamma I 1667 8019 I 2.579E-06 I I 114 g + g -> gamma + gamma I 0 1 I 1.191E-10 I I 115 g + g -> g + gamma I 0 0 I 0.000E+00 I I I I I ==============================================================================
The cross sections for the different partonic pT bins has been tabulated by Michael Betancourt and is reproduced here for convenience.
| Partonic pT [GeV] | Cross Section [mb] |
| 3-4 | 0.0002962 |
| 4-5 | 0.0000891 |
| 5-7 | 0.0000494 |
| 7-9 | 0.0000110 |
| 9-11 | 0.00000314 |
| 11-15 | 0.00000149 |
| 15-25 | 0.000000317 |
| 25-35 | 0.00000000990 |
| 35-45 | 0.000000000449 |
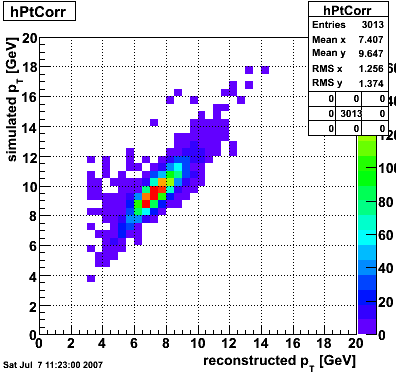
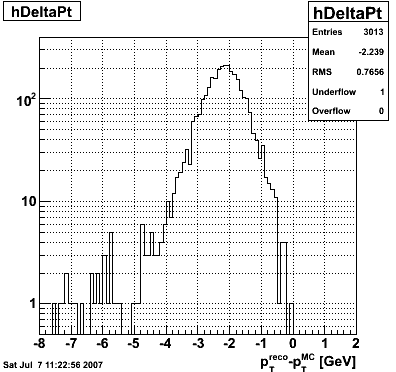
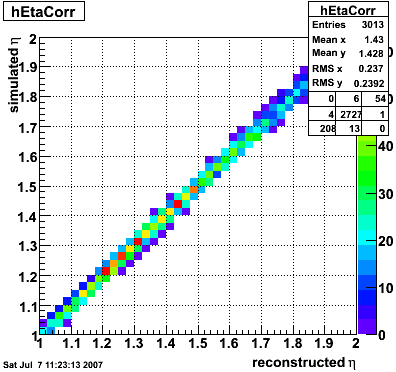
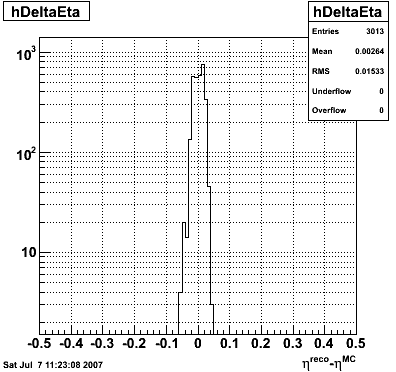
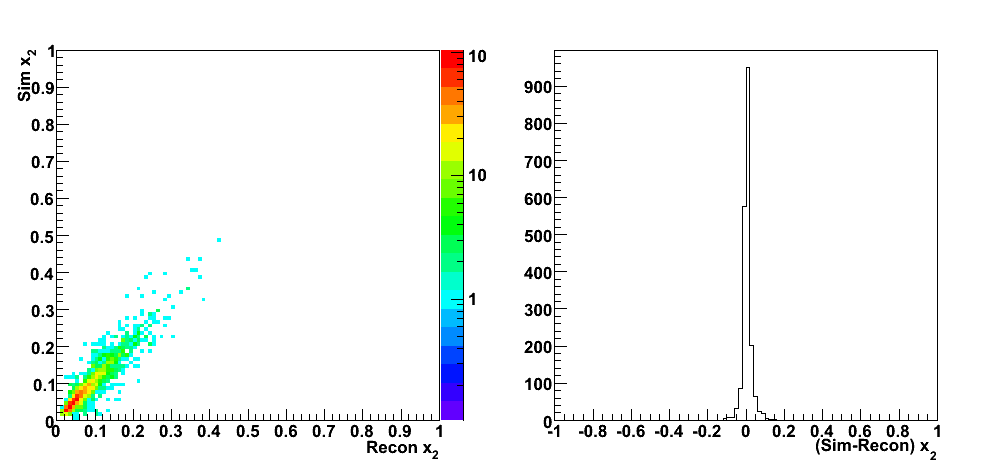
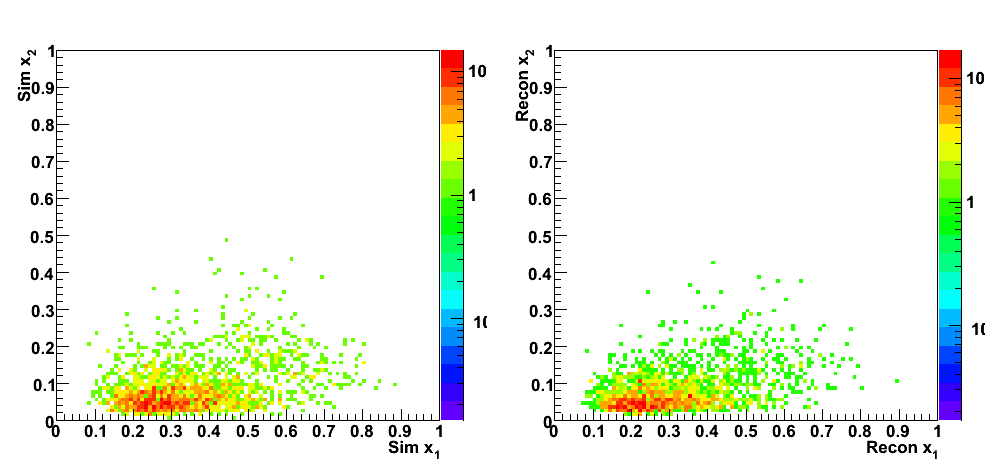
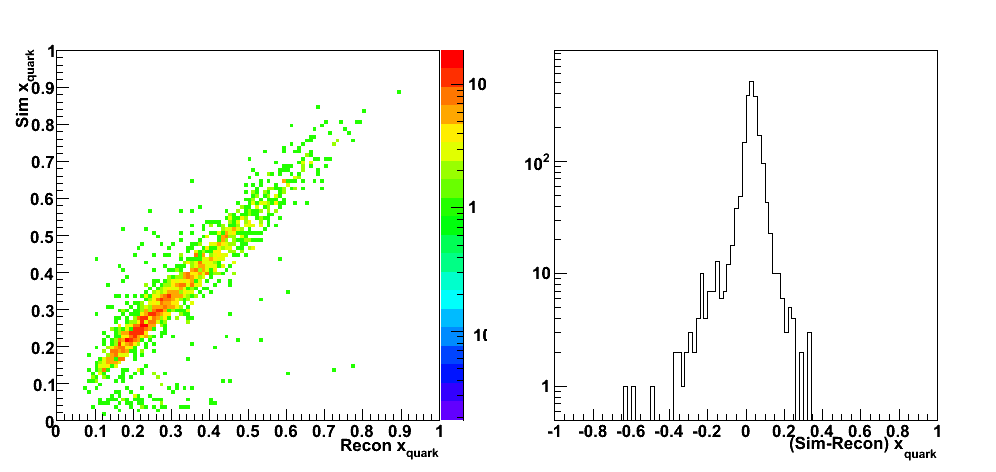
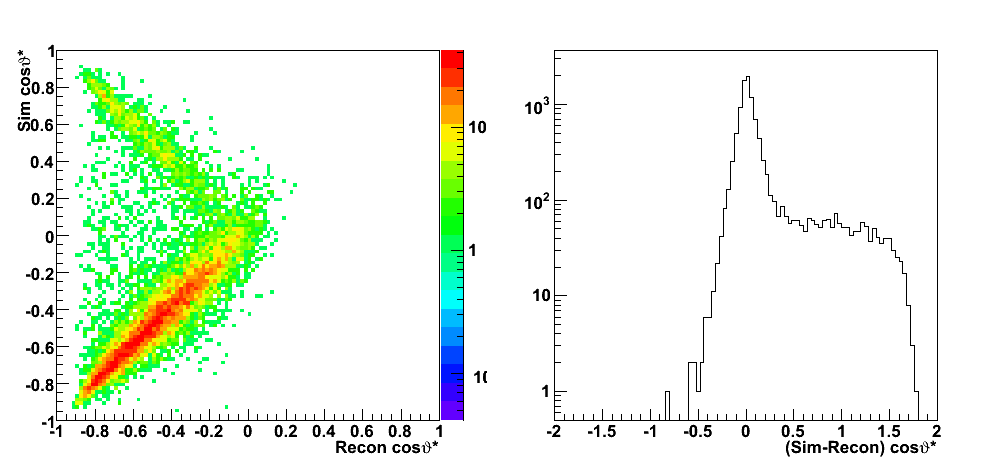
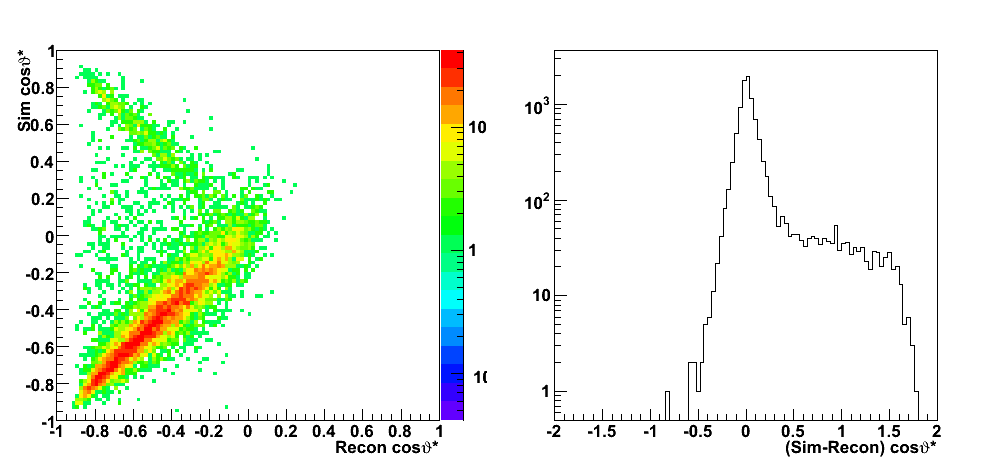
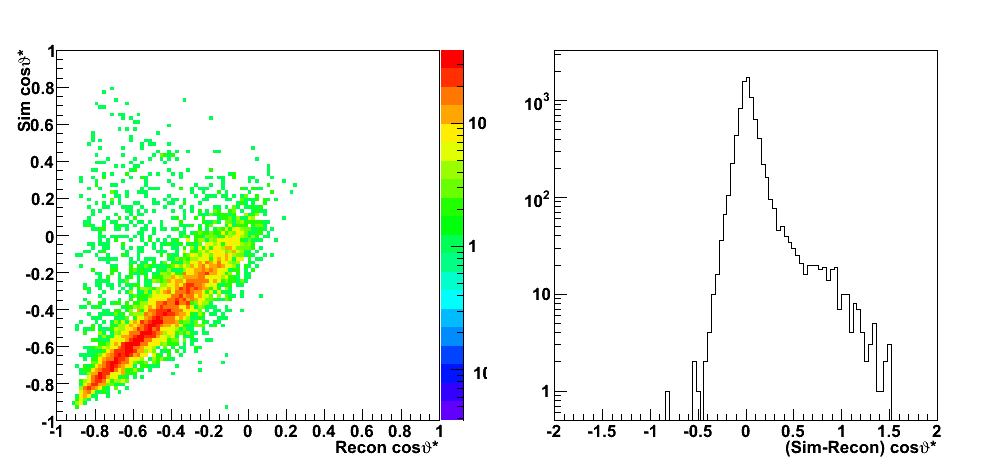
These events were processed through the 2006 pp200 analysis chain, albeit without any cuts on the SMD. The simulated quantities were taken from the Pythia record and the reconstructed ones from the analysis.
| Figure 2 |
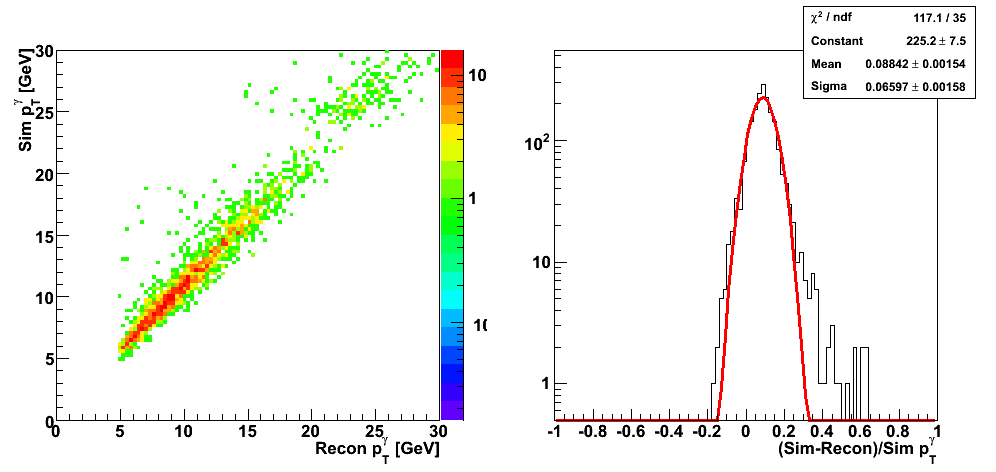 |
| Figure 3 |
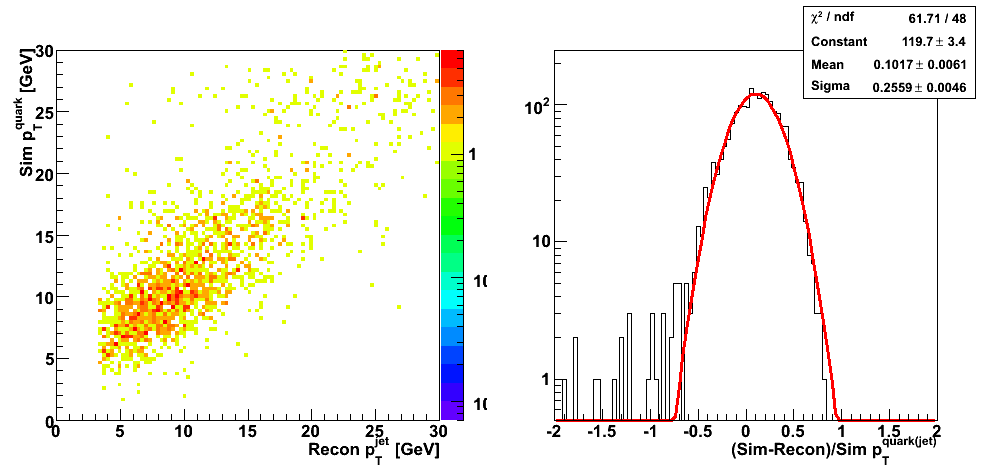 |
| Figure 4 |
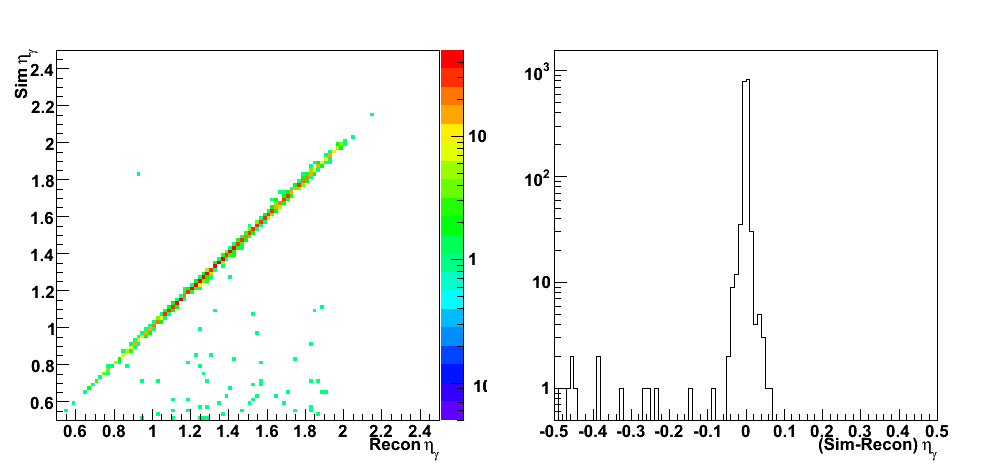 |
| Figure 5 |
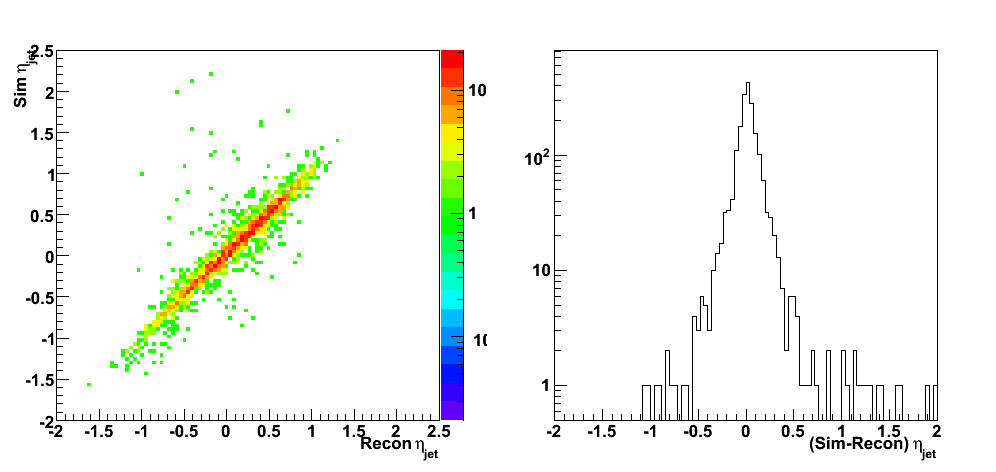 |
| Figure 6 |
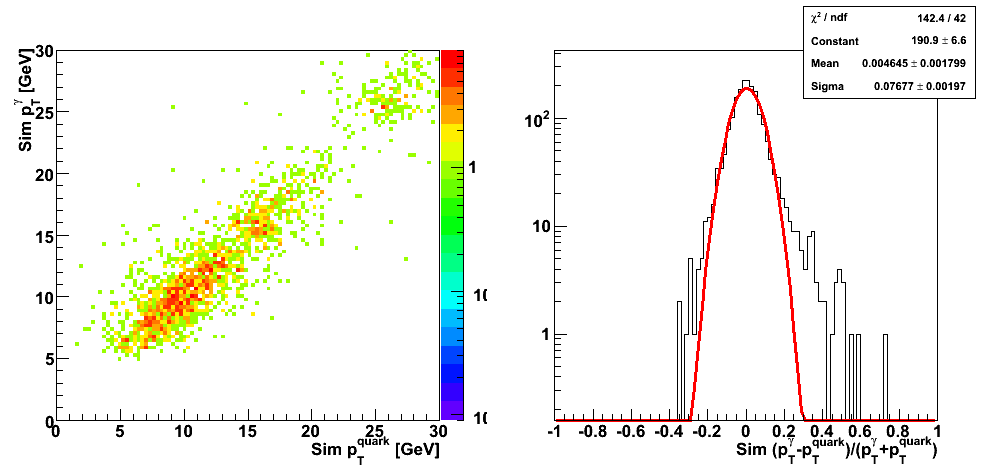 |
| Figure 7 |
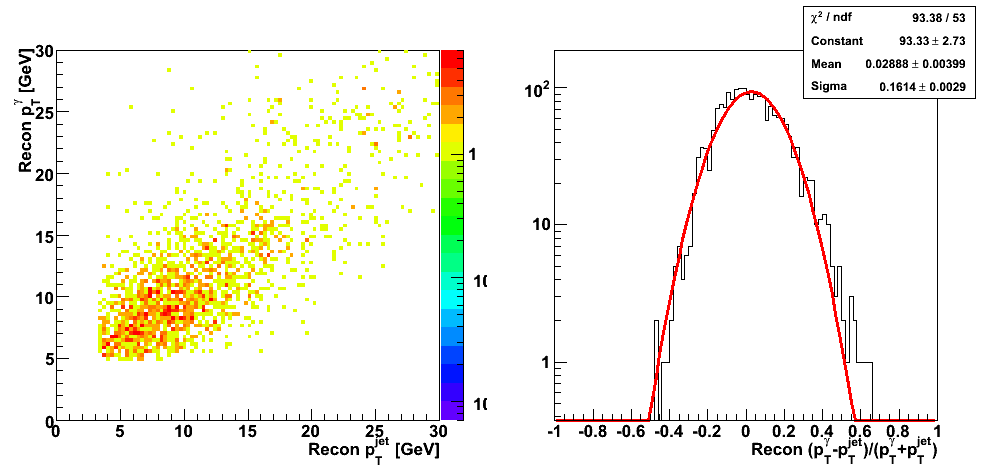 |
| Figure 8 |
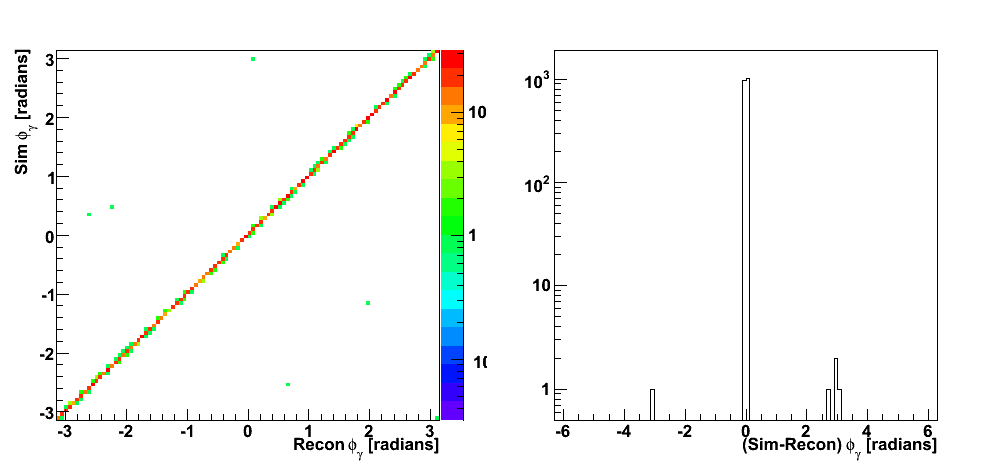 |
| Figure 9 |
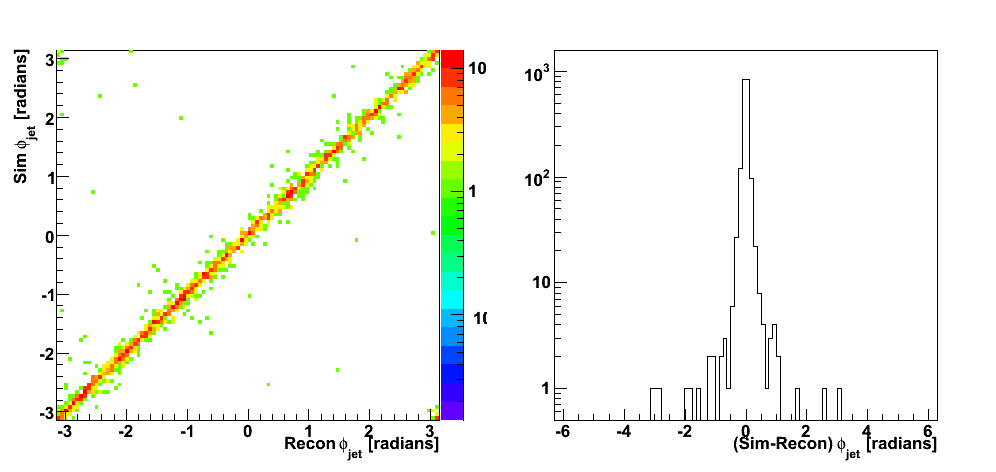 |
Partonic kinematics reconstruction
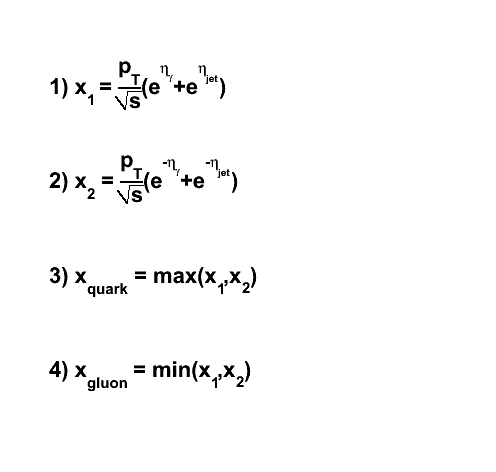 |
| PartonicKinematics.C |
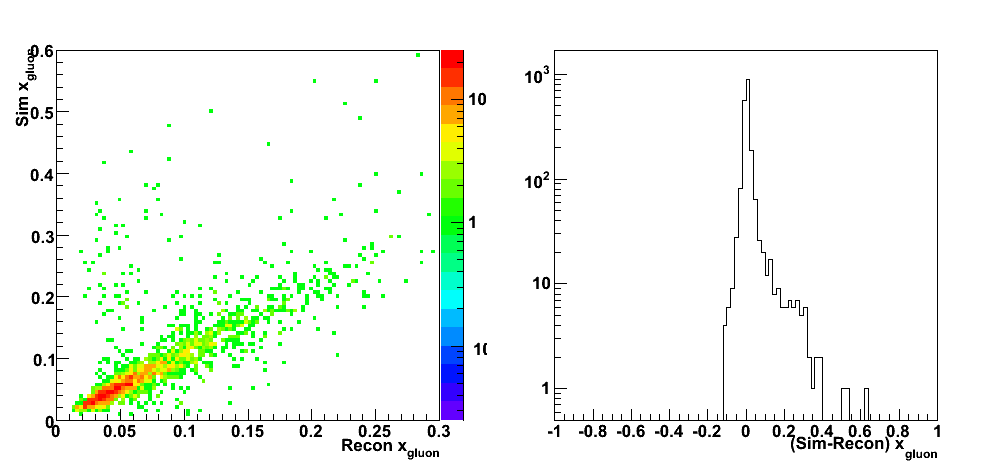
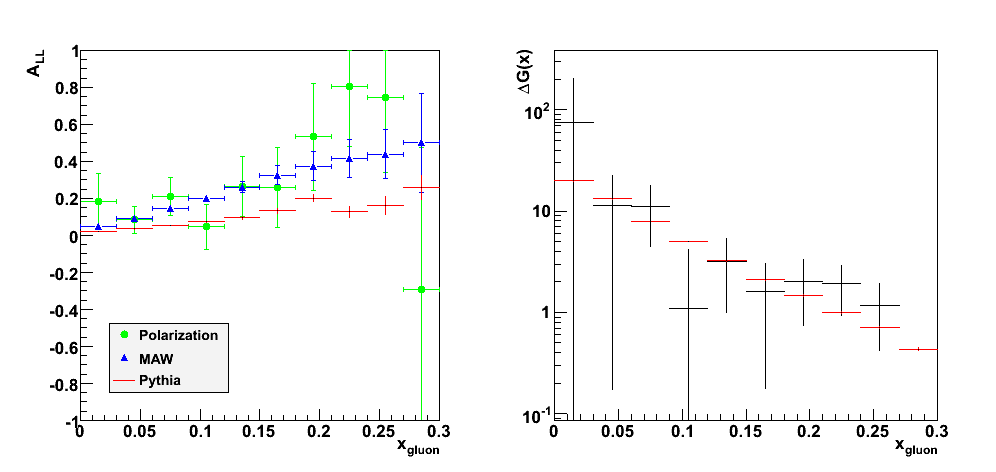
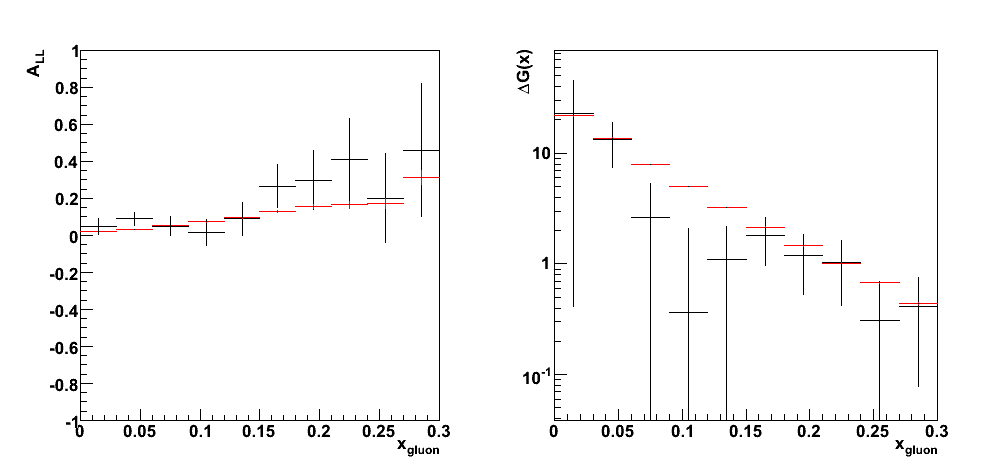
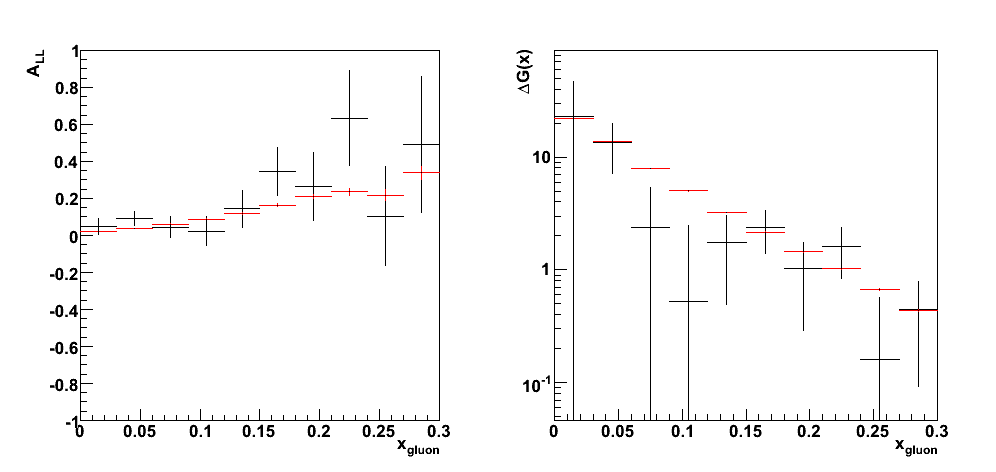
Predictions for A_LL and direct determination of DeltaG(x)
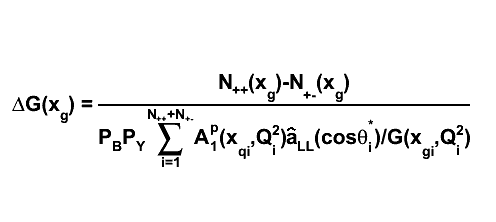 |
| DeltaG.C |
References
- Appendix Simulation Studies of Direct Photon Production at STAR
- DeltaG(x,mu^2) from jet and prompt photon production at RHIC arXiv:hep-ph/0005320
Pibero Djawotho Last updated Wed Jul 16 10:29:22 EDT 2008
2008.07.20 How to install Pythia 6 and 8 on your laptop?
How to install Pythia 6 and 8 on your laptop?
- Install Pythia 6 and build the interface to ROOT
- Install Pythia 8
- Install ROOT from source
Download the file pythia6.tar.gz from the ROOT site ftp://root.cern.ch/root/pythia6.tar.gz and unpack.
tar zxvf pythia6.tar.gzA directory
pythia6/ will be created and some files unpacked into it. Cd into it and compile the Pythia 6 interface to ROOT.
cd pythia6/ ./makePythia6.linuxFor more information, consult Installing ROOT from Source and skip to the section Pythia Event Generators.
Download the latest version of Pythia from http://home.thep.lu.se/~torbjorn/Pythia.html and unpack.
tar zxvf pythia8108.tgzA directory
pythia8108/ will be created. Cd into it and follow the instructions in the README file to build Pythia 8. Set the environment variables PYTHIA8 and PYTHIA8DATA (preferably in /etc/profile.d/pythia8.sh):
export PYTHIA8=$HOME/pythia8108 export PYTHIA8DATA=$PYTHIA8/xmldocRun configure with the option for shared-library creation turned on.
./configure --enable-shared make
Download the source code for ROOT from http://root.cern.ch/ and compile.
tar zxvf root_v5.20.00.source.tar.gz cd root/ ./configure linux --with-pythia6-libdir=$HOME/pythia6 \ --enable-pythia8 \ --with-pythia8-incdir=$PYTHIA8/include \ --with-pythia8-libdir=$PYTHIA8/lib make make installSet the following environment variables (preferably in
/etc/profile.d/root.sh):
export ROOTSYS=/usr/local/root export PATH=$PATH:$ROOTSYS/bin export LD_LIBRARY_PATH=$LD_LIBRARY_PATH:$ROOTSYS/lib:/usr/local/pythia6 export MANPATH=$MANPATH:$ROOTSYS/manYou should be good to go. Try running the following Pythia 6 and 8 sample macros:
root $ROOTSYS/tutorial/pythia/pythiaExample.C root $ROOTSYS/tutorial/pythia/pythia8.C
Pibero Djawotho Last updated on Sun Jul 20 23:35:39 EDT 2008
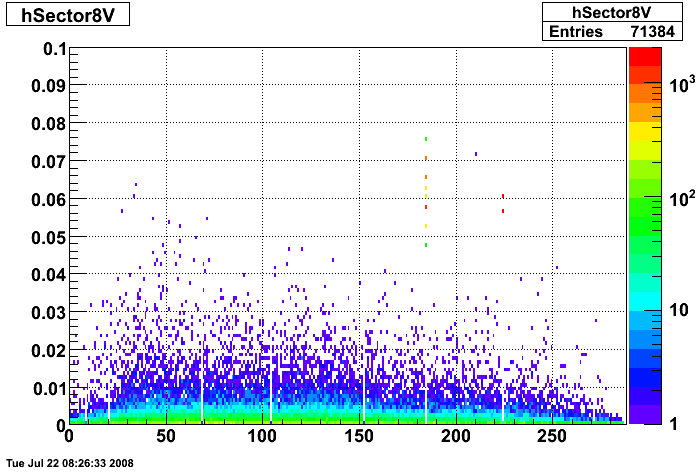
2008.07.23 Hot Strips Identified by Hal Spinka
Hot Strips Identified by Hal Spinka
- Run 7136034 Sector 8
- Run 7137036 Sector 9
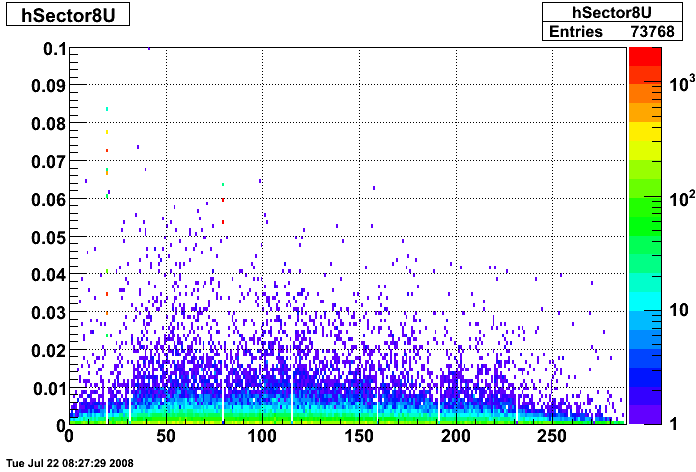
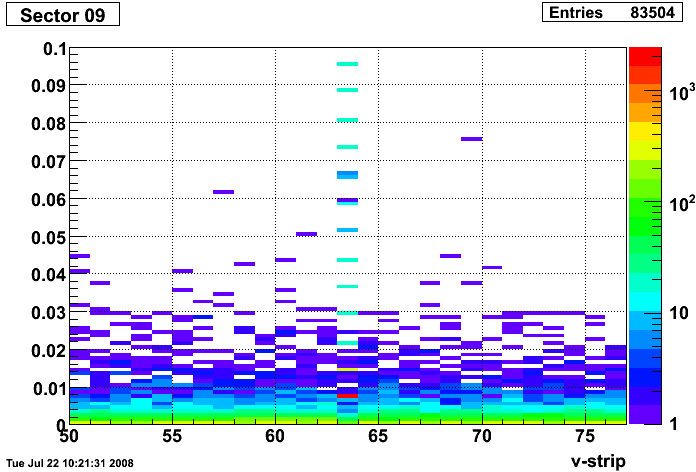
Strips 08U020, 08U080, 08V185 and 08V225
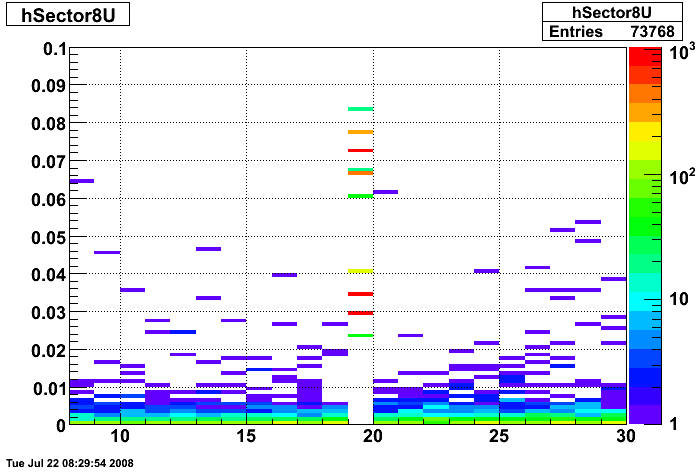
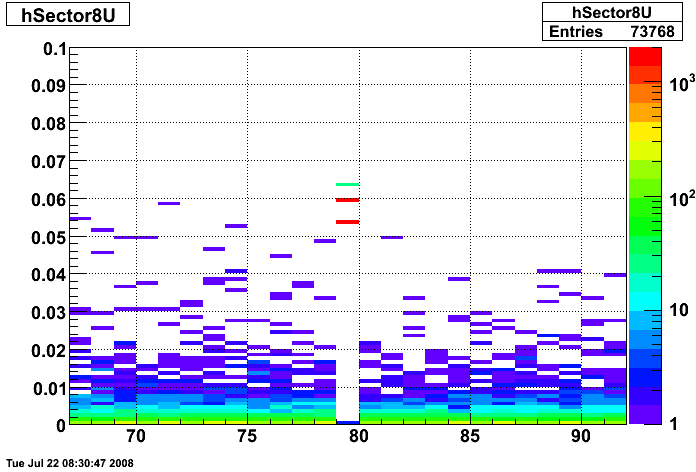
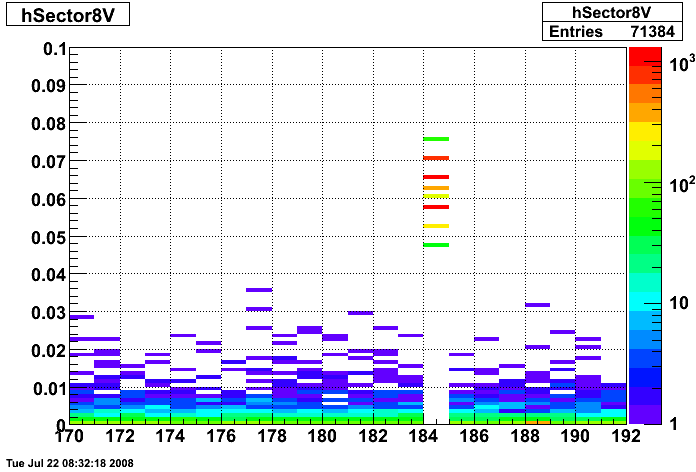
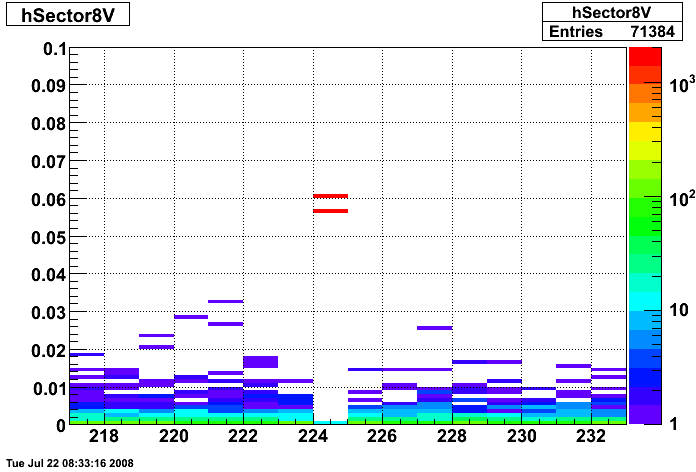
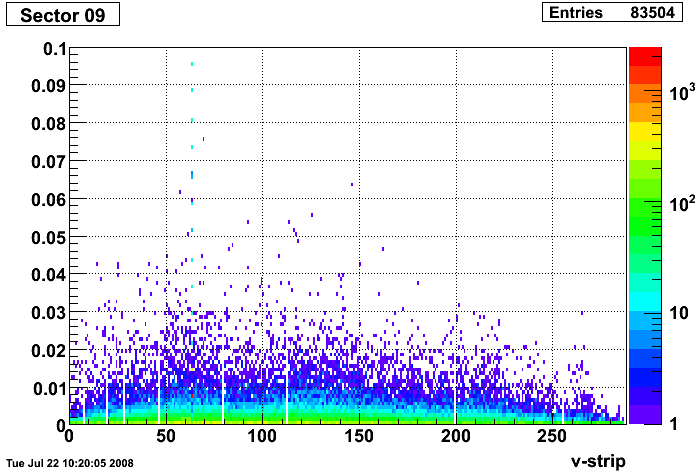
Strips 09V064
Pibero Djawotho Last updated Wed Jul 23 03:40:54 EDT 2008
2008.07.24 Strips from Weihong's 2006 ppLong 20 runs
Strips from Weihong's 2006 ppLong 20 runs
Energy [GeV] vs. strip id
Raw ADC vs. strip id
7136022.pdf 7136033.pdf 7136034.pdf 7137036.pdf 7138001.pdf 7138010.pdf 7138032.pdf 7140046.pdf 7143012.pdf 7144014.pdf 7145018.pdf 7145024.pdf 7146020.pdf 7146077.pdf 7147052.pdf 7148027.pdf 7149005.pdf 7152062.pdf 7153008.pdf 7155052.pdf
Pibero Djawotho Last updated Thu Jul 24 10:35:50 EDT 2008