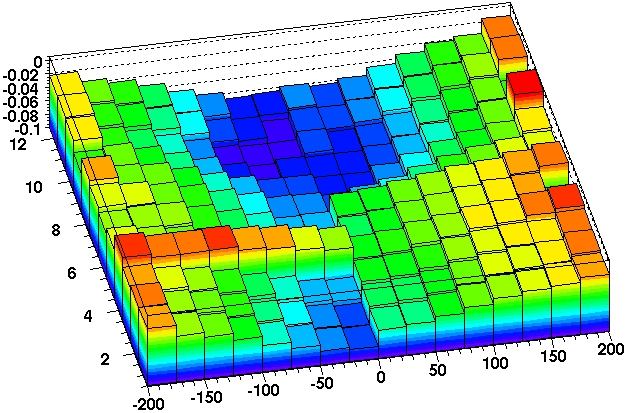
GridLeak: Gain Study
In February 2005, Blair took some special runs with altered TPC gains so we could study the effect on the GridLeak distortion. What is shown in the following plots is the distortion (represented by the profile of residuals at padrows 12 and 14, which amounts to 0.5 * [residual at padrow 12 + residual at padrow 14]) as a function of Z in the TPC. Black points are the distortions from sectors 7-24, and red are 1-6, which are the sectors where the TPC gain was reduced. I have chosen as labels "Norm", "Half", and "Low" for these three conditions of no gain change, half gain change on the inner pads only, and half gain change on both inner and outer.
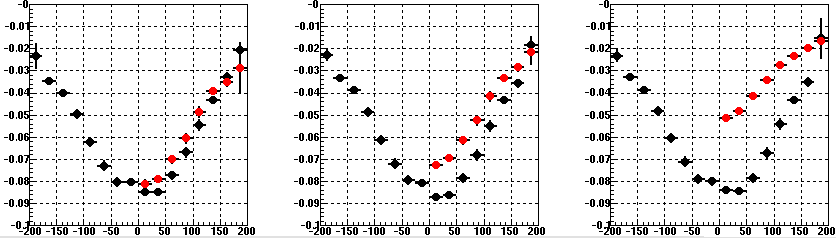
First note: the ever-present problem that our model goes to zero distortion at the endcaps, while the measured distortions do not appear to do so (though the distortion curves should flatten out [as seen in the above plots] as a function of Z near the endcap and central membrane due to boundary conditions on the fields in the TPC).
Second note: I have not excluded sector 20 from these plots, which is partly to explain why the east half (z<0) has slightly less distortions than the west in these profile plots. In reality, east and west were about even for a normal run (distortions excluding sector 20).
Here is the z-phi plot for Low (it's almost difficult to see the distortion reduction in the z-phi (in "o'clock") plot for Half):
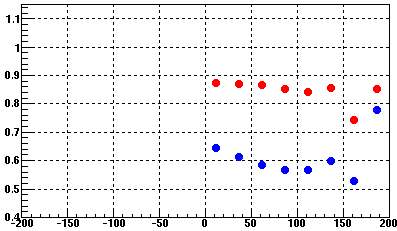
Third note: (though not too important for this study because we generally ignore east/west comparisons) the sectors between 1-6 o'clock already tend to show somewhat less distortion than the sectors at 7-12 o'clock, and because it is true on both halves of the TPC, it is more likely to be due SpaceCharge azimuthal anisotropy than asymmetries in the endplanes. Here are the distortions at |z|<50 for east (red) and west (blue) as a function of phi in "o'clock" where one can see the already present asymmetry, explaining why sectors 1-6 are already less distorted in the Norm run than sectors 7-12:
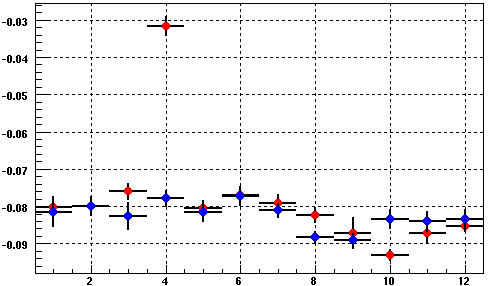
We have to normalize to sectors 7-12 to see the drop in distortions as it the runs are taken at different times when the luminosity of the machine, and therefore the distortion normalizations, are different. Here are the ratios from sectors 1-6 / sectors 7-12:
And the double ratios to see the drop in the Half and Low runs w.r.t. the Norm run:
These plots show ratios in the Z = 25-150cm range of about 0.86 and 0.59 respectively, or reductions of about 14% and 41% give or take a few percentage points. Data beyond 150cm tends to be poor and there's little reason to believe that the ratio really changes by much there. However, there does appear to be some shape to the data, which is not understood at this time.
Another way to calculate the difference in distortions is to take a linear fit to the slope of the distortions between z = 25-150cm. Those fit slopes are:
Low: 1-6: 0.000250 +/- 0.000019 7-12: 0.000420 +/- 0.000024 Half: 1-6: 0.000365 +/- 0.000023 7-12: 0.000433 +/- 0.000025 Norm: 1-6: 0.000401 +/- 0.000024 7-12: 0.000422 +/- 0.000023Again, we need the ratio of ratios:
[Half(1-6)/Half(7-12)] / [(Norm(1-6)/Norm(7-12)] = 0.89+/-0.11 (12%) [Low(1-6)/Low(7-12)] / [(Norm(1-6)/Norm(7-12)] = 0.63+/-0.08 (12%) Inner reduction = (11 +/- 11)% Outer reduction = (26 +/- 11)% Total reduction = (37 +/- 8)%These numbers are smaller than the reductions indicate by the above plot of double ratios of the distortions themselves. This likely reflects the errors in fitting the slopes. In that sense, the plot values may be more accurate. We need not worry in this study about getting the reduction numbers exact, but it is perhaps accurate enough to say that the inner sector gain drop reduces the distortion by about 13%, and the outer sector gain drop reduces it further by about 27% (about twice as much as the inner) from the original distortion. It is clear that both inner and outer TPC sectors contribute to the distortion, and that the outer TPC contributes significantly more to the distortion. If hardware improvements can only be implemented for either the inner or outer, then the outer is the optimal choice in this respect. It is not obvious offhand whether this is consistent with the GridLeak Simulations which we have done so far for these ion leaks.