Heavy Flavor
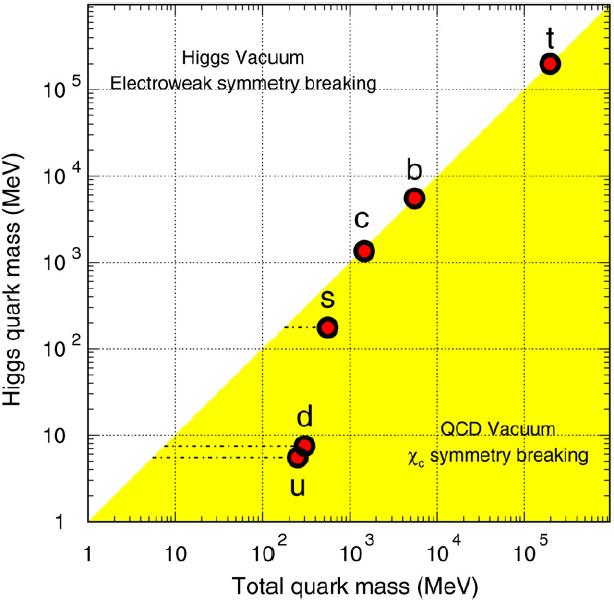Depending on the energy scale, there are two mechanisms that generate quark masses with different degrees of importance: current quark masses are generated by the electroweak symmetry breaking mechanism (Higgs mass) and spontaneous chiral symmetry breaking leads to the constituent quark masses in QCD (QCD mass). The QCD interaction strongly affects the light quarks (u, d, s) while the heavy quark masses (c, b, t) are mainly determined by the Higgs mechanism. In high-energy nuclear collisions at RHIC, heavy quarks are produced through gluon fusion and qq¯ annihilation. Heavy quark production is also sensitive to the parton distribution function. Unlike the light quarks, heavy quark masses are not modified by the surrounding QCD medium (or the excitations of the QCD medium) and the value of their masses is much higher than the initial excitation of the system. It is these differences between light and heavy quarks in a medium that make heavy quarks an ideal probe to study the properties of the hot and dense medium created in high-energy nuclear collisions.
Heavy flavor analyses at STAR can be separated into quarkonia, open heavy flavor and heavy flavor leptons.
Abstracts, Presentations and Proceedings
Abstracts
This page is maintained by Gang Wang.
#9995# DNP (fall meeting) 2010
Abstracts for DNP (fall meeting) 2010 (Nov. 2-6, 2010, Santa Fe, NM)
- Wenqin Xu
Title: Extracting bottom quark production cross section from p+p collisions at RHIC
The STAR collaboration has measured the non-photonic electron (NPE) production at high transverse momentum (pT ) at middle rapidity in p + p collisions at sqrt(s) = 200 GeV at the Relativistic Heavy Ion Collider (RHIC). The relative contributions of bottom and charm hadrons to NPE have also been obtained through electron hadron azimuthal
correlation studies. Combining these two, we are able to determine the high pT mid-rapidity electron spectra
from bottom and charm decays, separately.
PYTHIA with different tunes and FONLL calculations have been compared with this measured electron spectrum
from bottom decays to extract the bb-bar differential cross section after normalization to the measured spectrum.
The extrapolation of the total bb-bar production cross section in the whole kinematic range and its dependence
on spectrum shapes from model calculations will also be discussed.
- Yifei Zhang
Title: Open charm hadron reconstruction via hadronic decays in p+p collisions at $sqrt{s}$ = 200 GeV
Heavy quarks are believed to be an ideal probe to study the properties of the QCD medium produced in the relativistic heavy ion collisions. Heavy quark production in elementary particle collisions is expected to be better calculated in the perturbative QCD. Precision understanding on both the charm production total cross section and the fragmentation in p+p collisions is a baseline to further explore the QCD medium via open charm and charmonium in heavy ion collisions.
Early RHIC measurements in p+p collisions which were carried out via semi-leptonic decay electrons provides limited knowledge on the heavy quark production due to the incomplete kinematics, the limited momentum coverage and the mixed contribution from various charm and bottom hadrons in the electron approach. In this talk, we will present
the reconstruction of open charm hadrons (D0 and D*) via the hadronic decays in p+p collisions at $sqrt{s}$ = 200 GeV in the STAR experiment. The analysis is based on the large p+p minimum bias sample collected in RHIC Run9. The Time-Of-Flight detector, which covered 72% of the whole barrel in Run9, was used to improve the decay daughter
identification. Physics implications from this analysis will be presented.
- Xin Li
Title: Non-photonic Electron Measurements in 200 GeV p+p collisions at RHIC-STAR
Compared to the light quarks, heavy quarks are produced early in the collisions and interact very differently with the strongly couple QGP(sQGP) created at RHIC. In addition, their large masses are created mostly from the spontaneous symmetry breaking. All these features make heavy quark an ideal probe to study the sQGP. One of the critical references in these studies is the heavy quark production in p+p collisions, which also provides a crucial test to the pQCD. Measuring electrons from heavy quark semi-leptonic decay (non-photonic electron) is one of the major approaches to study heavy quark production at RHIC.
We will present STAR measurements on the mid-rapidity non-photonic electron production at pT>2 GeV/c in 200 GeV p+p collisions using the datasets from the 2008 and 2005 runs, which have dramatically different photonic backgrounds. We will compare our measurements with the published results at RHIC and also report the status of the analysis at pT<2 GeV/c using the dataset from the 2009 run.
- Jonathan Bouchet
Title: Reconstruction of charmed decays using microvertexing techniques with the STAR Silicon Detectors
Due to their production at the early stages, heavy flavor particles are of interest to study the properties of the matter created in heavy ion collisions. Direct topological reconstruction of $D$ and $B$ mesons, as opposed to indirect methods using semi-leptonic decay channels [1], provides a precise measurement and thus disentangles the $b$ and $c$ quarks contributions [2].
In this talk we present a microvertexing technique used in the reconstruction of $D^{0}$ decay vertex ($D^{0} \rightarrow K^{-}\pi^{+}$) and its charge conjugate. The significant combinatorial background can be reduced by means of
secondary vertex reconstruction and other track cut variables. Results of this method using the silicon detector information of the STAR experiment at RHIC will be presented for the Au+Au system at $\sqrt{s_{NN}}$ = 200 GeV.
[1]A. Abelev et al., Phys. Rev. Lett. {\bf 98} (2007) 192301
[2]N. Armesto et al., Phys. Lett. B{\bf 637} (2006) 362-366.
#9996# Hard Probe 2010
Abstracts for 2010 Hard Probe Meeting (Oct. 10-15, 2010, Eilat, Israel)
- Wei Xie
Heavy quarks are unique probes to study the strongly coupled Quark-Gluon Plasma created at RHIC. Unlike light quarks, heavy quark masses come mostly from spontaneous symmetry breaking, which makes them ideal for studying the medium's QCD properties. Due to their large masses, they are produced early in the collisions and are expected to interact with the medium quite differently from that of light quarks. Detailed studies on the production of open heavy flavor mesons and heavy quarkonium in heavy-ion collisions and the baseline $p+p$ and $d+A$ collisions provide crucial information in understanding the medium's properties. With the large acceptance TPC, Time of Flight, EM Calorimeter and future Heavy-Flavor Tracker, STAR has the capabilities to study heavy quark production in the dense medium in all different directions. In this talk, we will review the current status as well as the future perspectives of heavy quark studies in STAR experiment.
- Zebo Tang
Title: $J/\psi$ production at high pT at STAR
The $c\bar{c}$ bound state $J/\psi$ provides a unique tool to probe the hot dense medium produced in heavy-ion collisions, but to date its production mechanism is not understood clearly neither in heavy-ion collisions nor in hadron hadron collisions. Measurement of $J/\psi$ production at high $p_T$ is particularly interesting since at high $p_T$
the various models give different predictions. More over some model calculations on $J/\psi$ production are only applicable at intermediate/high $p_T$. Besides, high $p_T$ particles are widely used to study the parton-medium interactions in heavy-ion collisions. In this talk, we will present the measurement of mid-rapidity (|y|<1) $J/\psi \rightarrow
e^+e^-$ production at high $p_T$ in p+p and Cu+Cu collisions at 200 GeV, that used a trigger on electron energy deposited in Electromagnetic Calorimeter. The $J/\psi$ $p_T$ spectra and nuclear modification factors will be compared to model calculations to understand its production mechanism and medium modifications. The $J/\psi$-hadron azimuthal angle correlation will be presented to disentangle $B$-mesons contributions to inclusive $J/\psi$. Progresses
from on-going analyses in p+p collisions at 200GeV taken in year 2009 high luminosity run will be also reported.
-
Rosi Reed
Title: $\Upsilon$ production in p+p, d+Au, Au+Au collisions at $\sqrt{{S}_{NN }} = $ 200 GeV in STAR
Quarkonia is a good probe of the dense matter produced in heavy-ion collisions at RHIC because it is produced early in the collision and the production is theorized to be suppressed due to the Debye color screening of the potential between the heavy quarks. A model dependent measurement of the temperature of the Quark Gluon Plasma (QGP) can be determined by examining the ratio of the production of various quarkonia states in heavy ion collisions versus p+p collisions because lattice calculations indicate that the quarkonia states will be sequentially suppressed. Suppression is quantified by calculating ${R}_{AA}$, which is the ratio of the production in p+p scaled by the number of binary collisions to the production in Au+Au. The $\Upsilon$ states are of particular interest because at 200 GeV the effects of feed down and co-movers are smaller than for J/$\psi$, which decreases the systematic uncertainty of the ${R}_{AA} calculation. In addition to hadronic absorption, additional cold nuclear matter effects, such as shadowing of the PDFs, can be determined from d+Au collisions. We will present our results for mid-rapidity $\Upsilon$ production in p+p, as well as our preliminary results in d+Au and Au+Au at $\sqrt{{S}_{NN }}$ = 200 GeV. These results will then be compared with theoretical QCD calculations.
-
Wei Li
Title: Non$-$Photonic Electron and Charged Hadron Azimuthal Correlation in 500 GeV p+p Collisionsions at RHIC
Due to the dead cone effect, heavy quarks were expected to lose less energy than light quarks since the current theory predicted that the dominant energy loss mechanism is gluon radiation for heavy quarks. Whereas non-photonic electron from heavy quark decays show similar suppression as light hadrons at high $p_{T}$ in central Au+Au collisions. It is important to separate the bottom contribution to non-photonic electron for the better understanding of heavy flavor
production and energy loss mechanism in ultra high energy heavy ion collisions. B decay contribution is approximately 50$\%$ at a transverse momentum of $p_{T}$$\geq$5 GeV/c in 200 GeV p+p collisions from STAR results. In this talk, we will present the azimuthal correlation analysis of non-photonic electrons with charged hadrons at $p_{T}$$\geq$6.5 GeV/c in p+p collisions at $\sqrt{s}$ = 500 GeV at RHIC. The results are compared to PYTHIA simulations to disentangle
charm and bottom contribution of semi-leptonic decays to non-photonic electrons.
-
Gang Wang
Title: B/D Contribution to Non-Photonic Electrons and Status of Non-Photonic Electron $v_2$ at RHIC
In contrast to the expectations due to the dead cone effect, non-photonic electrons from decays of heavy quark carrying hadrons show a similar suppression as light hadrons at high $p_{T}$ in central 200 GeV Au+Au collisions at RHIC. It is important to separate the charm and bottom contributions to non-photonic electrons to better understand the heavy flavor production and energy loss mechanism in high energy heavy ion collisions. Heavy quark energy loss and heavy quark evolution in the QCD medium can also lead to an elliptic flow $v_2$ of heavy quarks which can be studied through $v_2$ of non-photonic electrons.
In this talk, we present the azimuthal correlation analysis of non-photonic electrons with charged hadrons at 1.5 GeV/c < $p_{T}$ < 9.5 GeV/c in p+p collisions at $\sqrt{s}$ = 200 GeV at RHIC, with the removal of J/$\Psi$ contribution to non-photonic electrons. The results are compared with PYTHIA simulations to disentangle charm and bottom contributions of semi-leptonic decays to non-photonic electrons. B decay contribution is approximately 50$\%$ at the electron transverse momentum of $p_{T}$ > 5 GeV/c in 200 GeV p+p collisions from STAR results. Incorporating the spectra and energy loss information of non-photonic electrons, we further estimate the spectra and energy loss of the electrons from B/D decays. Status of $v_2$ measurements for non-photonic electrons will also be discussed for 200 GeV Au+Au collisions with RHIC run2007 data.
#9997# APS 2010 April Meeting
Abstracts for 2010 APS April Meeting (Feb. 13-17, 2010, Washington DC)
- Jonathan Bouchet
Title: Performance studies of the Silicon Detectors in STAR towards microvertexing of rare decays
Abstract: Heavy quarks production ($b$ and $c$) as well as their elliptic flow can be used as a probe of the thermalization of the medium created in heavy ions collisions. Direct topological reconstruction of charmed and bottom decays is then needed to obtain this precise measurement. To achieve this goal the silicon detectors of the STAR experiment are explored. These detectors, a Silicon Drift (SVT) 3-layer detector[1] and a Silicon Strip one-layer detector[2] provide tracking very near to the beam axis and allow us to search for heavy flavour with microvertexing methods. $D^{0}$ meson reconstruction including the silicon detectors in the tracking algorithm will be presented for the Au+Au collisions at $\sqrt{s_{NN}}$ = 200 GeV, and physics opportunities will be discussed.
[1]R. Bellwied et al., Nucl. Inst. Methods A499 (2003) 640.
[2]L. Arnold et al., Nucl. Inst. and Methods A499 (2003) 652.
- Matt Cervantes
Title: Upsilon + Hadron correlations at the Relativistic Heavy-Ion Collider (RHIC)
Abstract: STAR has the capability to reconstruct the heavy quarkonium states of both the J/Psi and Upsilon particles produced by the collisions at the Relativistic Heavy Ion Collider (RHIC). The systematics of prompt production of heavy quarkonium is not fully described by current models, e.g. the Color Singlet Model (CSM) and the Color Octect Model. Hadronic activity directly around the heavy quarkonium has been proposed [1] as an experimental observable to measure the radiation emitted off the coloured heavy quark pair during production. Possible insight into the prompt production mechanism of heavy quarkonium can be obtained from this measured activity. Using STAR data from dAu collisions at sqrt(s_NN)= 200 GeV, the high S/B ratio found in Upsilon reconstruction [2] can enable us to perform an analysis of Upsilon + Hadron correlations. We will present our initial investigation of such an analysis.
[1] Kraan, A. C., arXiv:0807.3123.
[2] Liu, H., STAR Collaboration, arXiv:0907.4538.
PWG convener to press the approval button
On this page, we collect the information about which PWG convener to press the final approval button for which conference.
| Conference | Convener |
| 2018 Hot Quarks | Rongrong Ma |
| 2018 Hard Probes | Petr Chaloupka |
| 2018 EJC | Petr Chaloupka |
| 2018 ATHIC | Zebo Tang |
| 2018 Zimanyi School | Petr Chaloupka |
| 2019 Bormio | Rongrong Ma |
| 2019 IIT Indore | Zebo Tang |
| 2019 QCD Moriond | Petr Chaloupka |
| 2019 APS April Meeting | Sooraj Radhakrishnan |
| 2019 QWG | Zebo Tang |
| 2019 FAIRness | Zebo Tang |
| 2019 SQM | Petr Chaloupka |
| 2019 AUM | Sooraj Radhakrishnan |
Presentations
#9997# WWND2010
Jan 2-9, 2010 Winter Workshop on Nuclear Dynamics (Ocho Rios, Jamaica)
- Manuel Calderon: Quarkonia in STAR: Results and Future Plans
- Sarah LaPointe: Heavy Flavor Measurements in STAR and Future Measurements Using the HFT
#9998# DNP/JPS 2009 meeting
Oct. 13-17, 2009 DNP/JPS 2009 meeting (Big Island, Hawaii)
- Daniel Kikola: J/psi production in Au+Au and Cu+Cu collisions at sqrt(sNN) = 200 GeV at STAR
- Chris Powell: Low pT J/psi production in d+Au collisions at sqrt(sNN) = 200 GeV in STAR
- Rosi Reed: Upsilon production in p+p, d+Au, Au+Au collisions at 200 GeV in STAR
- Barbara Trzeciak (poster): Production of high pT J/psi in p+p collisions at sqrt(s) = 200 GeV in STAR
#9999# SQM 2009 meeting
Sept. 27-Oct. 2, 2009 SQM 2009 meeting (Buzios, Brazil)
Proceedings
Comparisons between STAR and PHENIX
This is a page that Thomas will edit to work on comparisons between STAR and PHENIX Non-Photonic electrons
HF PWG QM2011 analysis topics
Random list of collected topics for HF PWG QM2011 (as 10.8.2010)
Gang Wang: NPE v2 and possible NPE-h correlation
based on 200 GeV data
Wenqin Xu: Non-photonic electron spectrum in available Run10 AuAu data, and calculate the R_AA
Rosi Reed: Upsilon RAA in the 200 GeV
Yifei,David,Xin: Charm hadron measurement via the hadronic decays in both Run9 p+p and
Run10 AuAu 200 GeV collisions
Zebo Tang: High-pT J/psi spectra and correlations in run9 p+p and its R_AA in run10 200GeV Au+Au
Xin Li/ Mustafa Mustafa: Run09 p+p and Run10 Au+Au NPE cross section.
Matt Cervantes: Upsilon+hadron correlations
Chris Powell: low pT J/Psi in run 10 200GeV Au+Au to obtain R_AA and polarization measurement
Barbara Trzeciak: J/psi polarization with large
statistic p+p sample (run 9).
HF PWG Embedding page
This page is maintained by Jaroslav Bielcik
10: 2010/JUL/20 Updated HF embedding list
20.7.2010
HF embedding priority list
J/psi in pp2008 (done 10.2.2010)
D0/D0bar in CuCu 2005 (done 4.3.2010)
pi0 (newDalitz) in pp 2008 (QA of completed sample) (19.4.2010 closed)
Gamma in pp2008 re-production (20.7.2010 closed)
1) D0 in AuAu2007 (standby, expert look)
2) D0bar in AuAu2007 (standby, expert look)
8) pi0 (newDalitz) in CuCu 2005
9) Ds in AuAu 2007
10-13) electrons/pi0/gamma/eta in dAu 2008
14) J/psi in dAu 2008
q
11:2010/AUG/11 HF embedding
11.8.2010
HF embedding priority
J/psi in pp2008 (done 10.2.2010)
D0/D0bar in CuCu 2005 (done 4.3.2010)
pi0 (newDalitz) in pp 2008 (QA of completed sample) (19.4.2010 closed)
Gamma in pp2008 re-production (20.7.2010 closed)
1) D0 in AuAu2007 (standby, expert look)
2) D0bar in AuAu2007 (standby, expert look)
8) pi0 (newDalitz) in CuCu 2005
9) Ds in AuAu 2007
10-13) electrons/pi0/gamma/eta in dAu 2008
14) J/psi in dAu 2008
+
+
12:2010/AUG/17 QM&Paper proposal HF priority reevaluation
17.8.2010
HF embedding priority (31.8.2010 update)
J/psi in pp2008 (done 10.2.2010)
D0/D0bar in CuCu 2005 (done 4.3.2010)
pi0 (newDalitz) in pp 2008 (QA of completed sample) (19.4.2010 closed)
Gamma in pp2008 re-production (20.7.2010 closed)
J/psi in pp2006 (18.8.2010 closed)
1) D0 in AuAu2007 (standby, expert look)
2) D0bar in AuAu2007 (standby, expert look)
3) Upsilon in AuAu2007 ()
---------------------------------------------------------------------------------
D0 in AuAu 200 Run10
D* in AuAu 200 Run10
J/psi in AuAu200 Run10 (low pT and high pT)
Upsilon in AuAu 200 Run10
25) Ds in AuAu 2007
26-29) electrons/pi0/gamma/eta in dAu 2008
30) J/psi in AuAu2007
13: 2010/NOV/15 Updated HF embedding list STAR coll
15.11.2010
D* in AuAu 200 Run10
J/psi in AuAu200 Run10 (low pT and high pT)
Upsilon in AuAu 200 Run10
24) Ds in AuAu 2007
25-28) electrons/pi0/gamma/eta in dAu 2008
29) J/psi in AuAu2007
J/psi in dAu 2008 (paperdraft in PWG) (26.10.2010 closed)
14: 2010/NOV/16 Update of Run9
16.11.2010
Update 14.12.2010
D* in AuAu 200 Run10
J/psi in AuAu200 Run10 (low pT and high pT)
Upsilon in AuAu 200 Run10
22) Ds in AuAu 2007
23-26) electrons/pi0/gamma/eta in dAu 2008
27) J/psi in AuAu2007
15:2011/JAN/18 Update
18.1.2011
D* in AuAu 200 Run10
J/psi in AuAu200 Run10 (low pT and high pT)
Upsilon in AuAu 200 Run10
-) J/psi in AuAu2007
16:2011/JAN/24 QM2011 reordering
24.1.2011
D* in AuAu 200 Run10
J/psi in AuAu200 Run10 (low pT and high pT)
Upsilon in AuAu 200 Run10
-) J/psi in AuAu2007
17:2011/FEB/1 QM2011 reordering
1.2.2011
D* in AuAu 200 Run10
J/psi in AuAu200 Run10 (low pT and high pT)
Upsilon in AuAu 200 Run10
-) J/psi in AuAu2007
18:2011/MARCH/18 After Analysis Meeting
18.3.2011
D* in AuAu 200 Run10
J/psi in AuAu200 Run10 (low pT and high pT)
Upsilon in AuAu 200 Run10
-) J/psi in AuAu2007
19:2011/MAY/7 QM2011 done
7.5.2011
D* in AuAu 200 Run10
J/psi in AuAu200 Run10 (low pT and high pT)
Upsilon in AuAu 200 Run10
-) J/psi in AuAu2007
D0bar in AuAu2007 (14.2. 2011) high pT gamma in p+p 200 Run9 QM (low pT closed 1.3.;23.4. closed)
1: 2009/26/OCT HF Embeding List
Draft of current 26.10.2009 HF open issues based on collab. meeting LBNL
Electron/Pi0/Gamma/Eta in dAu2008 open
Pi0 (new Dalitz) in pp2005 open(simu)
Pi0 (new Dalitz) in pp2008 QA produced
Pi0 (new Dalitz) in CuCu2005 open
D0 in CuCu2005 work on new prod
D0 in AuAu2007 (P08ic finished, need re-production in P08ie)
Ds in AuAu2007 open
Low pT J/psi in AuAu2007 (sample produced)
High pT J/psi in dAu2008 (P08ic finished, need re-production in P08ie)
Low pT J/psi in dAu2008 (P08ic finished, need re-production in P08ie)
Low pT J/psi in pp 2008 open
Upsilon in AuAu2007 Issues with test sample (under investigation)
20:2011/JUN/21
D* in AuAu 200 Run10
J/psi in AuAu200 Run10 (low pT and high pT)
Upsilon in AuAu 200 Run10
-) J/psi in AuAu2007
D0bar in AuAu2007(14.2.2011)
high pT gamma in p+p 200 Run9 QM (low pT closed 1.3.;23.4. closed)
21:2011/AUG/06 Actual priority list
6.AUG.2011
13) electrons in dAu 2008 (20a9d52e9df73a2ebd9da10496e7b8e6)
-----------------------------------------------
D* in AuAu 200 Run10
J/psi in AuAu200 Run10 (low pT and high pT)
Upsilon in AuAu 200 Run10
D0bar in AuAu2007(14.2.2011)
high pT gamma in p+p 200 Run9 QM (low pT closed 1.3.;23.4. closed)
electrons in Au+Au 200GeV Run10 QM (23.4. done)
22:2011/NOV/16
16.NOV.2011
13) electrons in dAu 2008 (20a9d52e9df73a2ebd9da10496e7b8e6)
16) gamma in d+Au 2008 (36c1b4631b12157601a3c9684e57ae68)
electrons in AuAu 39 GeV
gamma in AuAu 39 GeV
pi0 in AuAu39 GeV
electrons in AuAu 62 GeV
gamma in AuAu 62 GeV
pi0 in AuAu 62 GeV
-----------------------------------------------
D* in AuAu 200 Run10
J/psi in AuAu200 Run10 (low pT and high pT)
Upsilon in AuAu 200 Run10
D0bar in AuAu2007(14.2.2011)
high pT gamma in p+p 200 Run9 QM (low pT closed 1.3.;23.4. closed)
electrons in Au+Au 200GeV Run10 QM (23.4. done)
23:2011/DEC/20
20.12.2011
16) gamma in d+Au 2008 (36c1b4631b12157601a3c9684e57ae68)
electrons in AuAu 39 GeV
gamma in AuAu 39 GeV
pi0 in AuAu39 GeV
electrons in AuAu 62 GeV
gamma in AuAu 62 GeV
pi0 in AuAu 62 GeV
-----------------------------------------------
D* in AuAu 200 Run10
J/psi in AuAu200 Run10 (low pT and high pT)
Upsilon in AuAu 200 Run10
D0bar in AuAu2007(14.2.2011)
high pT gamma in p+p 200 Run9 QM (low pT closed 1.3.;23.4. closed)
electrons in Au+Au 200GeV Run10 QM (23.4. done)
23:2011/DEC/20/OLD
20.11.2011
16) gamma in d+Au 2008 (36c1b4631b12157601a3c9684e57ae68)
electrons in AuAu 39 GeV
gamma in AuAu 39 GeV
pi0 in AuAu39 GeV
electrons in AuAu 62 GeV
gamma in AuAu 62 GeV
pi0 in AuAu 62 GeV
-----------------------------------------------
D* in AuAu 200 Run10
J/psi in AuAu200 Run10 (low pT and high pT)
Upsilon in AuAu 200 Run10
D0bar in AuAu2007(14.2.2011)
high pT gamma in p+p 200 Run9 QM (low pT closed 1.3.;23.4. closed)
electrons in Au+Au 200GeV Run10 QM (23.4. done)
24:2012/JAN/24 QM12 preparation
20.12.2011
13) gamma in d+Au 2008 (36c1b4631b12157601a3c9684e57ae68)
QM12
electrons in AuAu 39 GeV Run10 (20114301 and 20114302) SL10k
gamma in AuAu 39 GeV Run10 (20114308) SL10k
pi0 in AuAu39 GeV Run10 (20114307) SL10k
electrons in AuAu 62 GeV Run10 (20114305) SL10k
gamma in AuAu 62 GeV Run10 (20114303) SL10k
pi0 in AuAu 62 GeV Run10 (20114304) SL10k
pp500 Run11 ? NPE ele (2012801) ,gamma (2012801) ,pi0 (2012801), eta (2012801) SL11d
K,pi,D0,D* Run 11
J/Psi Run 11?
Upsilon Run 11?
-----------------------------------------------
D* in AuAu 200 Run10
J/psi in AuAu200 Run10 (low pT and high pT)
Upsilon in AuAu 200 Run10
D0bar in AuAu2007(14.2.2011)
high pT gamma in p+p 200 Run9 QM (low pT closed 1.3.;23.4. closed)
electrons in Au+Au 200GeV Run10 QM (23.4. done)
25:2012/FEB/21 QM 2012 list
21.2.2012
===================
pi0 in AuAu39 GeV Run10 (20114307) SL10k
pi0 in AuAu 62 GeV Run10 (20114304) SL10k
pp500 Run11 pi0 (2012801), eta (2012801) SL11d
Upsilon Run 11?
-----------------------------------------------
D* in AuAu 200 Run10
J/psi in AuAu200 Run10 (low pT and high pT)
Upsilon in AuAu 200 Run10
D0bar in AuAu2007(14.2.2011)
high pT gamma in p+p 200 Run9 QM (low pT closed 1.3.;23.4. closed)
electrons in Au+Au 200GeV Run10 QM (23.4. done)
26:2012/APR/24 QM update
29.5.2012 status
pi0 in AuAu39 GeV Run10 (20114307) SL10k
pi0 in AuAu 62 GeV Run10 (20114304) SL10k
pp500 Run11 pi0 (2012801), eta (2012801) SL11d
Upsilon Run 11?
-----------------------------------------------
D* in AuAu 200 Run10
J/psi in AuAu200 Run10 (low pT and high pT)
Upsilon in AuAu 200 Run10
D0bar in AuAu2007(14.2.2011)
high pT gamma in p+p 200 Run9 QM (low pT closed 1.3.;23.4. closed)
electrons in Au+Au 200GeV Run10 QM (23.4. done)
27:2012/02/OCT
Status (2016/04/05):
HF embedding helpers:
David Tlusty
STAR requests page:
New HF embedding requests
- pi/K/p in pp 200 GeV Run12: pi+/-, K+/-, proton/anti-proton
- charged hadron in pp 500 GeV Run9 (BBCMB)
- pi/K in AuAu 200 GeV Run14 (P16id, HFT)
- Quarkonia in pp 200 GeV Run15 (MTD)
- NPE in pp 200 GeV Run15 (BHT)
- Jpsi, Upsilon in pp 200 GeV Run15 (BHT)
- Charmonia in pAu 200 GeV Run15 (MTD)
- NPE in pAu 200 GeV Run15 (BHT)
- Jpsi, Upsilon in pAu 200 GeV Run15 (BHT)
- Upsilon in AuAu 200 GeV Run16 (MTD, HLT)
- pi/K/p in pp 200 GeV Run15 (BHT1)
- Jpsi, Upsilon in AuAu 200 GeV Run11 (BHT2)
- pi/K/p in AuAu 200 GeV Run16 (MB)
Closed samples:
Run14
- Upsilon->ee in AuAu 200 GeV Run14 (BHT2)
- e+/- in AuAu 200 GeV Run14 (BHT)
- gamma->ee in AuAu 200 GeV Run14 (BHT)
- pi0 Dalitz in AuAu 200 GeV Run14 (BHT)
- eta Dalitz in AuAu 200 GeV Run14 (BHT)
- Jpsi->mumu in AuAu 200 GeV Run14 (MTD)
- K+/- in AuAu 200 GeV Run14 VpdMB5
- pi+/- in AuAu 200 GeV Run14 VpdMB5
- Jpsi->ee in AuAu 200 GeV Run14 (HT1 & 2)
- Upsilon->mumu in AuAu 200 GeV Run14 (MTD)
Run13
- J/psi->mumu in pp 500 GeV Run13 (MTD)
- pi/K/p in pp 500 GeV Run13 (MTD): pi+/-, K+/-, proton/anti-proton
Run12
- pi in U+U 193 GeV (20124801, 20124802)
- K in U+U 193 GeV (20124804,20124803)
- e+/e- in U+U 193 Gev run 12 (central0-5%)
- gamma in U+U 193 GeV run 12 (central0-5%)
- J/psi in U+U 193 GeV run 12
- Upsilon in U+U 193 GeV run 12
- D0/D0bar in p+p 200 GeV run12 (VPDMB)
- D*+/D*- in p+p 200 GeV run12 (VPDMB)
- D*+/D*- p+p 200 GeV run 12 (HT)
- e+/e- in p+p 200 GeV run 12 (HT)
- gamma in p+p 200 GeV run 12 (HT)
- pi0 dalitz in p+p 200 GeV run 12 (HT)
- eta dalitz in p+p 200 GeV run 12 (HT)
- Ke3 in p+p 200 GeV run 12 (HT)
- e+/e- in p+p 200 GeV run 12 (VPDMB)
- gamma in p+p 200 GeV run 12 (VPDMB)
- pi0 dalitz in p+p 200 GeV run 12 (VPDMB)
- eta dalitz in p+p 200 GeV run 12 (VPDMB)
- Ke3 in p+p 200 GeV run 12 (VPDMB)
- J/psi->ee in p+p 200 GeV run 12 (MB)
- J/psi->ee in p+p 200 GeV run 12 (BHT0)
- J/psi->ee in p+p 200 GeV run 12 (BHT1)
- J/psi->ee in p+p 200 GeV run 12 (BHT2)
Run11
- pi/K in Run 11 p+p 500 (MB): pi+ , pi-, K+, K-
- pi/K/p in Run11 pp 500 (BHT1): pi+/-, K+/-, proton/anti-proton
- J/Psi in Run11 pp500 GeV
- pi0 pp500 Run11
- gamma pp500 Run 11
- electron in pp500 Run11
- eta pp 500 Run11
- Upsilon(1S+2S+3S) p+p 500 GeV run 11
- Psi(2s) in p+p 500 GeV run 11
- gamma in p+p 500 GeV run 11
- gamma in Au+Au 200 GeV run 11
- pi0 dalitz in Au+Au 200 GeV run 11
- eta dalitz in Au+Au 200 GeV run 11
- K,pi Run 11 Au+Au: pi+, pi-, K+, K-
- J/Psi in Au+Au Run 11
Run10
- pi in AuAu Run 10 pi+,pi-
- K in AuAu Run 10 K+, K-
- eta in Au+Au 200GeV Run10
- pi0 in Au+Au 200GeV Run10
- J/psi in AuAu200 Run10
- electrons in Au+Au 200GeV Run10
- gamma in Au+Au 200GeV Run10
- Ke3 in Au+Au 200GeV Run10
- K^{0}_{e3} in Au+Au 200 GeV run 10
- electrons in AuAu 62 GeV Run10
- gamma in AuAu 62 GeV Run10
- pi0 in AuAu 62 GeV Run10
- Ke3 in Au+Au 62 GeV run 10
- Eta in Au+Au 62 GeV run 10
- pi0 in AuAu39 GeV Run10
- Ke3 in Au+Au 39 GeV run 10
- gamma in AuAu 39 GeV Run10
- electrons in AuAu 39 GeV Run10
- pi in AuAu Run 10 pi+,pi-
- K in AuAu Run 10 K+, K-
- eta in Au+Au 200GeV Run10
- pi0 in Au+Au 200GeV Run10
- J/psi in AuAu200 Run10
- electrons in Au+Au 200GeV Run10
- gamma in Au+Au 200GeV Run10
- Ke3 in Au+Au 200GeV Run10
- K^{0}_{e3} in Au+Au 200 GeV run 10
- electrons in AuAu 62 GeV Run10
- gamma in AuAu 62 GeV Run10
- pi0 in AuAu 62 GeV Run10
- Ke3 in Au+Au 62 GeV run 10
- Eta in Au+Au 62 GeV run 10
- pi0 in AuAu39 GeV Run10
- Ke3 in Au+Au 39 GeV run 10
- gamma in AuAu 39 GeV Run10
- electrons in AuAu 39 GeV Run10
Run9
- pi0 in p+p 200 Run9
- High-pT J/Psi in p+p 200GeV Run9
- Upsilon in p+p 2009
- Upsilons in pp200 Run9
- Ke3 in p+p 200 Run9
- electron/positron in p+p 200 Run9
- D*+/D*- in p+p 200 GeV Run9
- D0/D0bar in p+p 200 GeV Run9
- electrons in p+p 500GeV
- gamma in p+p 500GeV
- pi0 in p+p 500GeV
- eta in p+p 500GeV
Run8
- J/psi in pp2008
- pi0 (newDalitz) in pp 2008
- Gamma in pp2008 re-production (20.7.2010 closed)
- electrons in pp2008 re-production
- eta in pp2008 re-production
- J/psi in dAu 2008
- electrons in dAu 2008
- gamma in d+Au 2008
- pi0 in d+Au 2008
- eta in d+Au 2008
Run7
Run6
Run5
- eta in p+p 200 Run9 (20104804) canceled
- Upsilons in d+Au Run 8 (6e3fc974bf5cc484daa76bd45969eb5b)
2: 2009/9/NOV Suggested HF Embedding Priority list
7.NOV.2009
HF embedding priority list for PWGC discussion
1) Upsilon in pp 2006 (done)
2) D0/D0bar in CuCu 2005
3) pi0 (new Dalitz) in pp 2008
4) Upsilon and Ds in AuAu2007
5) Upsilon in dAu2008
6) low pT J/psi in AuAu2007
7) electrons/gamma/eta in pp2008 re-production
8) pi0 (new Dalitz) in CuCu 2005
9) D0/D0bar in AuAu 2007
10) electrons/pi0/gamma/eta in dAu 2008
11) high and low pT J/psi in dAu 2008
12) high pT J/psi in pp2008
3:2009/9/NOV Upsilon in dAu 200 request
Primary contact: Haidong Liu
-----------------------------------------
d+Au 200 GeV (year 2008)
fast stream data st_upsilon
20K events for each states (1s, 2s, 3s)
flat in pT and y:
pT= 0 - 8 GeV/c
y= -1.5 - 1.5
1 Upsilon per event
let the Upsilon decay only into e+e-
production version: P08ie
starver: SL08e
geant geometry option: y2008(low material)
------------------------------------------
4: 2009/24/NOV: Gamma in AuAu200 (2007) request
Primary contact: Bertrand Biritz
----------------------------------------
AuAu 200 GeV (year 2007)
fast stream data st_btag
1M events for gamma conversions and then 1M for pi0 dalitz decay
flat in pT and y:
pT= 0 - 6 GeV/c
y= -1.5 - 1.5
production version: P08ie
starver: SL08e
geant geometry option: y2007
5:2009/2/DEC: Updated HF priority list
2.DEC. 2009
HF embedding priority list for PWGC discussion
1) Upsilon in pp 2006 (done)
2) D0/D0bar in CuCu 2005 (QA done, processing)
3) pi0 (new Dalitz) in pp 2008 (QA done, processing)
4) Upsilon and Ds in AuAu2007
5) Upsilon in dAu2008
6) low pT J/psi in AuAu2007
7) electrons/gamma/eta in pp2008 re-production
8) pi0 (new Dalitz) in CuCu 2005
9) D0/D0bar in AuAu 2007
10) electrons/pi0/gamma/eta in dAu 2008
11) high and low pT J/psi in dAu 2008
12) high pT J/psi in pp2008
13) pi0 and gamma in AuAu 2007
...
6: 2009/15/DEC Update of heavy flavor embedding priority list
15.DEC. 2009
exchange of Ds and D0 in AuAu2007 priority was done
HF embedding priority list
1) Upsilon in pp 2006 (done)
2) D0/D0bar in CuCu 2005 (QA done, processing)
3) pi0 (new Dalitz) in pp 2008 (QA done, processing)
4) Upsilon and D0 in AuAu2007
5) Upsilon in dAu2008
6) low pT J/psi in AuAu2007
7) electrons/gamma/eta in pp2008 re-production
8) pi0 (new Dalitz) in CuCu 2005
9) Ds in AuAu 2007
10) electrons/pi0/gamma/eta in dAu 2008
11) high and low pT J/psi in dAu 2008
12) high pT J/psi in pp2008
13) pi0 and gamma in AuAu 2007
7: 2010/JAN/12 J/Psi dAu2010 embedding on disk
The old J/Psi embedding files are on disk for period january 2010:
/eliza14/star/starprod/embedding/production_dAu/Jpsi_10{3-7}_1229459741
It is about 150 GB of files
Requested by Chris Powell and Olga Hajkova
8:2010/3/MARCH Updated HF priority list
9.MARCH. 2010
J/Psi pp2006 request switched with J/Psi AuAu2007 and moved to highest priority.
This is done because existing paper proposal and short time before Daniel leaves STAR
HF embedding priority list
J/psi in pp2008 (done 10.2.2010)
D0/D0bar in CuCu 2005 (done 4.3.2010)
1) pi0 (newDalitz) in pp 2008 (processing)
2) D0 in AuAu2007 (processing)
3) D0bar in AuAu2007
7) electrons/gamma/eta in pp2008 re-production
8) pi0 (newDalitz) in CuCu 2005
9) Ds in AuAu 2007
10) electrons/pi0/gamma/eta in dAu 2008
11) J/psi in dAu 2008
9:2010/APR/8 Updated HF priority list
8.APRIL. 2010
NPE p+p requests moved to higher priority.
This is done because existing paper proposal and urgency to resolve the issue
HF embedding priority list
J/psi in pp2008 (done 10.2.2010)
D0/D0bar in CuCu 2005 (done 4.3.2010)
1) pi0 (newDalitz) in pp 2008 (QA of completed sample) (19.4.2010 closed)
2) D0 in AuAu2007 (processing)
3) D0bar in AuAu2007 (processing)
10) pi0 (newDalitz) in CuCu 2005
11) Ds in AuAu 2007
12-15) electrons/pi0/gamma/eta in dAu 2008
16) J/psi in dAu 2008
HF PWG Preliminary plots
This page collects the preliminary plots approved by the HF PWG.
1) All the preliminary plots MUST contain a "STAR Preliminary" label.
2) Please include at least pdf and png versions for the figures
3) Where to put the data points: it is recommended to put the data point at the x position whose yield is equal to the averge yield of the bin.
-
Rongrong presented a couple of slides at the PWGC meeting: http://www.star.bnl.gov/protected/lfspectra/marr/Analysis/PlaceDataPoints.pdf.
- See also the classic paper by Lafferty and Wyatt, NIM A355 (1995) 541-547 or see http://inspirehep.net/record/374024.
Open Heavy Flavor
| Year | System | Physics figures | First shown | Link to figures |
| 2014+2016 | Au+Au @ 200 GeV | HFT: D+/- RAA | 2020 HP | plots |
| 2014+2016 | Au+Au @ 200 GeV | HFT: Ds+/- spectra, ratio | 2019 QM |
plots |
| 2016 | Au+Au @ 200 GeV | HFT: D+/- RAA | 2018 QM | plots |
| 2016 | d+Au @ 200 GeV | HFT: D0 | 2018 QM | plots |
| 2014 | Au+Au @ 200 GeV | HFT: D*/D0 ratio | 2018 QM | plots |
| 2014+2016 | Au+Au @ 200 GeV | HFT: D0 v1 | 2018 QM | plots |
| 2014+2016 | Au+Au @ 200 GeV | HFT: non-prompt Jpsi | 2017 QM | plots |
| 2014 | Au+Au @ 200 GeV | HFT: non-prompt D0 | 2017 QM | plots |
| 2014 | Au+Au @ 200 GeV | HFT: B/D->e | 2017 QM | plots |
| 2014 2014+2016 |
Au+Au @ 200 GeV | HFT: Lc/D0 Ds/D0 ratio HFT: Lc/D0ratio HFT: Lc/D0 Ds/D0 vs ALICE |
2017 QM 2018 QM 2019 Moriond |
plots plots plots |
| 2014 | Au+Au @ 200 GeV | HFT: Ds RAA and v2 | 2017 CPOD | plots |
| 2014 | Au+Au @ 200 GeV | HFT: D+/- | 2017 QM | plots |
| 2014 | Au+Au @ 200 GeV | HFT: D0 v3 | 2017 QM | plots |
| 2014 | Au+Au @ 200 GeV | D0-hadron correlation | 2017 QM | plots |
| 2014 | Au+Au @ 200 GeV | HFT: D0 RAA HFT: D0 RAA HFT: D0 RAA and v2 |
2019 SQM 2018 QM |
|
Quarkonium
| Year | System | Physics figures | First shown | Link to figures |
| 2018 | isobar @ 200 GeV | Minimum Bias: Jpsi RAA | 2022 QM | plots slides (USTC) slides (UIC) sildes (combined) |
| 2015 | p+p @ 200 GeV | Dimuon: Jpsi with jet activity | 2022 QM | plots slides |
| 2014 | Au+Au @ 200 GeV | Dimuon: Jpsi RAA, low pT | 2022 QM | plots slides |
| 2017 | Au+Au @ 54.4 GeV | Minimum Bias: Jpsi RAA | 2021 SQM | plots slides |
| 2011 | p+p @ 500 GeV | BEMC: Jpsi in jet | 2020 HP | plots |
| 2015 | p+Au @ 200 GeV | BEMC: Jpsi RpA | 2020 HP | plots |
| 2016 2014 2011 |
Au+Au @ 200 GeV | MTD/HT: Upsilon RAA | 2018 QM |
plots |
| 2015 | p+p, p+Au @ 200 GeV | MTD: Jpsi cross-section, RpA | 2017 QM | plots |
| 2015 | p+p @ 200 GeV | MTD: Jpsi polarization | 2017 PANIC | plots |
| 2015 | p+p, p+Au @ 200 GeV | BEMC: Upsilon RpAu | 2017 QM | plots |
| 2014 | Au+Au @ 200 GeV | MTD: Jpsi RAA, v2, Upsilon ratio | 2015 QM 2016 sQM |
plots |
| 2013 | p+p @ 500 GeV | MTD: Jpsi yield vs. event activity |
2015 HP |
plots |
| 2013 | p+p @ 500 GeV | MTD: Jpsi cross-section | 2016 sQM | plots |
| 2012 | U+U @ 193 GeV | MB: low-pT Jpsi excess | 2016 sQM | plots |
| 2012 | U+U @ 193 GeV | MB/BEMC: Jpsi v2 | 2017 QM | plots |
| 2012 | p+p @ 200 GeV | MB/BEMC: Jpsi cross-section, event activity BEMC: Jpsi polarization |
2016 QWG | plots plots |
| 2011 | Au+Au @ 200 GeV | MB/BEMC: Jpsi v2 | 2015 QM | plots |
| 2011 | Au+Au @ 200 GeV | MB: low-pT Jpsi excess | 2016 sQM | plots |
| 2011 | p+p @ 500 GeV | BEMC: Jpsi cross-section | WWND | plots |
| 2011 | p+p @ 500 GeV | HT: Upsilon cross-section HT: Upsilon event activity |
2017 QM 2018 PWRHIC |
plots |
Electrons from Heavy Flavor Decay
| Year | System | Physics figures | First shown | Link to figures |
| 2017 | Au+Au @ 27 & 54.4 GeV | NPE v2 | 2020 HP | plots |
| 2014+2016 | Au+Au @ 200 GeV | HF electron: fraction, RAA, double ratio | 2019 QM | plots |
| 2014 | Au+Au @ 200 GeV | NPE cross-section; RAA (without HFT) | 2017 QM | plots |
| 2012 | p+p @ 200 GeV | NPE-hadron correlation, b fraction | 2016 Santa Fe | plots |
| 2012 | p+p @ 200 GeV | NPE cross-section; udpated RAA | 2015 QM | plots |
HF PWG Weekly Meeting
Zoom info (from Oct 1st, 2020):
Bluejeans meeting info:
To join the Meeting: https://bluejeans.com/816517744
To join via Browser: https://bluejeans.com/816517744/browser
To join with Lync: https://bluejeans.com/816517744/lync
To join via Cisco Jabber Video: https://bluejeans.com/816517744/jabber
To join via Room System: Video Conferencing System: bjn.vc -or- 199.48.152.152 Meeting ID: 816517744
To join via Phone: 1) Dial: +1 888 240 2560(US Toll Free) 2) Enter Conference ID: 816517744
2022/05/26
1) D0 RAA in Isobar - Yuan Su
2) J/psi v2 in isobar (high-pT) - Yu-Ming Liu
3) J/psi v2 in isobar (low-pT) - Qian Yang
2022/05/19
1) Update on D+/- in Au+Au at 200 GeV- Jan Vanek
2) J/psi v2 in isobar - Qian Yang
2022/05/12
1) J/psi v2 in isobar (HF stream, high-pT) - Yu-Ming Liu
2022/05/5
1) Search for alpha + D in forward STAR - Cheng Wei Lin
2) Update on Au+Au 27 and 54 GeV NPE v2 paper - Yuanjing Ji
2022/04/21
1) Update on D+/- in Au+Au 200 GeV - Jan Vanek
2) Update on femtoscopic correlation function for D0-hadron in Au-Au @200 GeV - Roy Chowdhury Priyank
2022/03/17
1) Update on D+/- in Au+Au 200 GeV - Jan Vanek
2) J/psi RAA in Run18 isobar collisions - Ziyue Zhang
3) J/psi with jet activity - Hao Huang
4) J/psi production in isobar collisions - Yan Wang
- Video: https://bnl.zoomgov.com/rec/share/vBhs4DLV4LAYm3swh3GANtgUg52GYvtrsa4YHjqX5K6i15Uu6_iKmc5v0jAxbn8.spAeHTF1m6CwZ1vkPasscode: 7?%Gb+Vr
2022/03/10
1) Update on D+/- in Au+Au 200 GeV - Jan Vanek
2) Quarkonia R+AA in isobar Run18 - Ziyue Zhang
3) J/psi production in isobar collisions - Yan Wang
- Video: https://bnl.zoomgov.com/rec/share/akU6EY6j33iU2hc2G1smpjhfIxh2DiAO4A442ihrRNclk3ditiIq4F6B33o_Md2W.qjCt9P8WPrb3Ul5F(Passcode: *%1gp%4^)
2022/03/03
1) Items from PAC to discuss - Yi Yang
2) J/psi production in isobar - Yan Wang
3) J/psi v2 in isobar - Yu-Ming Liu
4) J/psi RAA in isobar - Ziyue Zhang
5) Update of D+/- in Au+Au 200 GeV - Jan Vanek
6) Update on femtoscopic correlation function for D0-hadron in Au-Au @200 GeV - Roy Chowdhury Priyank
- Video: https://bnl.zoomgov.com/rec/share/3Y4hKco3zXwSieTqDdSoysDpmeqhiphOIeopHnzbbUu-_YMbSAg7ZTjOKEiA6Lwy.KrvEfK-1-NWI0M0k
2022/01/27
1) Update of D+/- in Au+Au 200 GeV - Jan Vanek
2022/01/20
1) Embedding issue - Jian Zhou
2) J/psi v2 in isobar - Yu-Ming Liu
2022/01/13
1) J/psi elliptic flow measurement in isobar collision - Qian Yang
2) Improvement on J/psi reconstruction in isobar collisions - Jieke Wang
2021/12/30
1) D0 spectra and v2 in isobar - Yuan Su
2021/12/16
1) Isobar Run18 for J/psi and Upsilon - Ziyue Zhang
2) Isobar for Upsilon - Shuai Yang
3) B to D0 analysis - Xiaolong Chen
2021/12/02
1) D+/- in AuAu with HFT - Jan Vanek
2) Psi(2S) in isobar - Yan Wang
3) J/psi in AuAu at 54.4 GeV- Kaifeng Shen
2021/11/18
1) D0 meson and hadrons at Au-Au 200GeV - Priyanka Roy Chowdhury
2) B to D0 analysis - Xiaolong Chen
3) J/psi raw yield in Ru+Ru/Zr+Zr collisions - Yan Wang
2021/11/11
1) QM22 abstract discussion
Proposed abstracts:
* J/psi production with jet activity at p+p 200 GeV
(2) D+/- in AuAu with HFT - Jan Vanek
(3) J/psi RpAu in dielectron in Run15 - Ziyue Zhang
- minutes - Yi
2021/11/04
1) D+/- in AuAu with HFT - Jan Vanek
2) Run22 Trigger - All
3) QM22 abstract
- minutes - Yi
2021/10/21
1) D+/- in Au+Au with HFT - Jan Vanek
2) QA variables for BES-II - All
- minutes - Sooraj
2021/10/07
1) D+- in Au+Au with the HFT - Jan Vanek
2021/08/05
1) D+- in Au+Au@200Gev with the HFT - Jan Vanek
2) Trigger conditions for HF transverse spin asymmetry - Daniel Kikoła
- minutes - Yi
2021/07/29
1) Update on J/Psi with jet activity - Hao Huang
2) MTD Trigger for Run 22 - Rongrong Ma
3) BEMC and EEMC triggers for transverse spin asymmetry studies with HF in Run 22 - Daniel Kikola
4) Measurement of Forward D* and Implications for Intrinsic Charm - Matthew Kelsey
slides; minutes - Sooraj
2021/06/24
1) Update on electron hadron correlations in pp at 200 GeV - Yingjie Zhou
minutes - Barbara
2021/05/06
1) Upsilon spectra at pp500 GeV - Leszek Kosarzewski
2) Inclusive J/psi production at 54.4 GeV - Kaifeng Shen
minutes - Yi
2021/04/29
1) Update on the signal extraction for Run15 Jpsi RpA analysis - Rongrong Ma
2021/04/22
1) Upsilon production vs. multiplicity in pp collisions - Leszek Kosarzewski
2) Inclusive J/psi production at 54.4 GeV - Kaifeng Shen
minutes - Barbara
2021/03/25
1) Total charm cross-section in Au+Au 200 GeV from STAR - Xinyue Ju
2021/03/18
1) Run21 QA report - Kaifeng Shen
2) Update on Upsilon production vs. multiplicity - Leszek Kosarzewski
2021/3/1-12 STAR Collaboration Meeting (agenda)
HF Parallel 1
HF Parallel 2
HF Parallel 3
2021/02/25
1) D+/- in Au+Au collisions at 200 GeV with the HFT - Jan Vanek
minutes - Barbara
2021/02/18
1) J/psi v2 - Yu-Ming Liu
2021/01/21
1) Update on the Upsilon analysis with Run15pp/pAu 200 GeV data - Zaochen Ye
2020/12/17
1) Update on HFE analysis in AuAu collisions - Shenghui Zhang
minutes - Barbara
2020/12/3
1) Paper proposal for J/psi in jet - Qian Yang
2020/11/5
1) Update on trigger bias studies in 2015 p+p and p+Au data - Rongrong Ma
2) Feasibility study of reconstructing chi_c in Run-15 p+p data set - Aarif Chaudhary
minutes - Sooraj
2020/10/22
1) Update on HFE analysis in p+p collisions - replies to PWGC preview - Shenghui Zhang
2) Update on D+/- reconstruction with the HFT - Jan Vanek
minutes - Barbara
2020/10/15
1) Update on the trigger bias study for Run15 Jpsi RpA analysis - Rongrong Ma
2) Update on the study of J/psi production with jet activity - Hao Huang
minutes - Yi
2020/10/08
J/Psi production with jet activity - Hao Huang
minutes - Sooraj
2020/10/01
Running a collider mode during CeC for 2021, with 26.5 GeV/u beam - All
minutes - Barbara
2020/09/03
1) D0 in d+Au collisions - Lukas Kramarik
minutes - Sooraj
2020/08/20
1) Update on Heavy Flavor Decay Electron at high pT in p+p 200 GeV - Shenghui Zhang
2020/08/06
BUR - J/psi v1 and v2, Psi(2S) R_AA projection
minutes -Yi
2020/7/30
BUR - All
minutes -Yi
2020/7/23
1) Update on J/psi in pAu - Rongrong Ma
2) BUR 2023-2025 - All
Xin Dong's Snowmass presentation: link
2020/7/9
1) Update on D+- in Run16
- - Jan Vanek
2020/7/2
1) Update on inclusive J/Psi with dielectron channel at 200 GeV (run15) - Ziyue Zhang
2) Update on the study of trigger bias factor in pAu collisions - Rongrong Ma
minutes - Sooraj
2020/6/25
1) Update on D+- in Run16 Au+Au@200GeV - Jan Vanek
minutes - Zebo
2020/6/18
1) Brief update on run15 BEMC J/psi analysis - Ziyue Zhang (cancelled)
2020/6/11
1) Update on hot tower selection with Run15 pp and pAu BHT2 data - Zaochen Ye
2) Setup for full-event dAu - Lukas Kramarik
minutes - Yi
2020/5/28
1) Update on inclusive J/psi analysis in pp and pAu @200 GeV (2015) - Ziyue Zhang
2) Run14+16 D+/- and preliminary plots - Jan Vanek
3) Analysis of sample of embedding to zerobias d+Au - Lukas Kramarik
4) NPE v2 non-flow estimation in Au+Au 54 GeV- Yuanjing Ji
minutes - Sooraj
2020/5/21
1) Run14+16 D+/- - Jan Vanek
2) Update on Run15 J/psi->ee R_pAu - Ziyue Zhang
3) Run15 J/psi->ee R_pAu preliminary results - Ziyue Zhang
4) Update on trigger bias study for Run15 Jpsi->mu mu R_pAu - Rongrong Ma
minutes - Zebo
2020/5/14
1) D+- in Run16 Au+Au@200GeV - Jan Vanek
2) Inclusive Jpsi analysis Run15 (ee) - Ziyue Zhang
3) Run15 Jpsi and Upsilon RpA - Zhenyu Ye
4) Hpt_HPE_Run12_pp_Shenghui_05142020.pdf - Shenghui Zhang
minutes - Yi
2020/5/07
1) Systematic uncertainty for the trigger bias factor in pp collisions - Rongrong Ma
2) Study of J/psi production with jet activity - Hao Huang
3) Update on Au+Au 54GeV NPE reconstruction efficiency study - Yuanjing Ji
4) Update on inclusive Jpsi RpAu using Run15 data - Ziyue Zhang
2020/4/30
1) Trigger bias factor for J/psi R_pAu with MTD 2015 - Rongrong Ma
2) Update on D+/- in Run16 Au+Au - Jan Vanek
3) Update on J/psi in a jet - Qian Yang
4) Update on multiplicity distribution in pp for Upsilon analysis - Leszek Kosarzewski
5) QA of J/psi in run15 pp HT1 and HT2 - Ziyue Zhang
minutes - Zebo
2020/4/23
1) J/psi in 54 GeV AuAu collisions - Kaifeng Shen
2) J/psi in Jet production - Qian Yang
3) The projection of Upsilon measurement during 2023-2025 - Rongrong Ma
minutes - Yi
2020/4/16
1) Update on the D+- analysis in Run16 Au+Au 200GeV - Jan Vanek
2) Paper proposal on low energy NPE v2 analysis - Yuanjing Ji
minutes - Sooraj
2020/4/9
1) HFT NPE RAA/RCP paper proposal - Matthew Kelsey
minutes - Zebo
2020/4/2
1) Update on D+/- in Au+Au - Jan Vanek
2) Optimization of primary vertex selection J/psi and psi(2S) in 500 GeV p+p - Chan-Jui Feng
2020/3/11-15 STAR Collaboration Meeting (agenda)
HF Parallel 1
HF Parallel 2
HF Summary report
2020/2/20
1) Update on D+/- in Au+Au - Jan Vanek
2020/2/13
1) Efficiency calculation for D+/- in Au+Au - Jan Vanek
2020/1/16
1) First look at J/psi and dielectron from Run18 Isobar runs - Kaifeng Shen
2011
2011/12/20 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
o Barbara: E/p study from embedding and data in run09
o Leszek: update in J/psi in p+p
o Mustafa: embedding status report.
2011/12/13 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
o Daniel Kikola: NPE v2 projection from run12 U+U.
o Chris: low pt paper proposal
o Anthony: discussion on 2008 d+Au reproduction
o Mustafa: embedding status
2011/12/06 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
o Leszek: The effect of radiation tails on J/psi cross section in p+p
o Daniel Kikola: NPE v2 projection from run12 U+U.
o run12 trigger request: Wei and all
o Mustafa: embedding status
2011/11/08 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
-
Leszek: Low pt J/psi.
2011/11/01 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
-
Gang Wang: update on Collaboration meeting agenda.
-
Andrew Petersion: update on 2009 p+p Upsilon analysis
-
Greg Wimsatt: Update on the eID for Upsilon analysis
-
Daniel Kikola: NPE flow analysis
-
Mustafa: Embedding
2011/10/25 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
-
Chris: low pt J/Psi Au+Au
-
Mustafa: NPE in 39 GeV
-
Embedding
2011/10/18 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
-
Chris: low pt J/Psi Au+Au
-
Embedding
2011/10/4 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
-
Chris: low pt J/Psi Au+Au
-
Yasser:J/Psi and B simulations
-
Embedding
2011/09/13 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
-
Leszek: J/Psi update
-
Hao:J/Psi flow
-
Andrew: Upsilon in p+p
-
Greg: Upsilon in p+p
2011/08/30 Meeting Minutes
Time: 13:00 (EST), 10:00margin-top: 0.5em; margin-bottom: 0.9emo Barbara: (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
-
Leszek: J/Psi update
-
Barbara: J/Psi lineshapes
-
Mustafa: embedding news
2011/08/02 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
-
Xiangli: Update on J/psi v2
-
Mustafa: embedding news
2011/07/26 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
2011/07/19 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 101116. Password: 7999
-
Embedding update
2011/07/12 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 101116. Password: 7999
-
Wenqin: Update on Run10 NPE
-
Chris: EPS HEP presentation and study on lineshape
-
Embedding update
- All: New embedding priority list
- Zebo: QA on high pT J/psi
- Mustafa: Other updates
2011/06/21 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 101116. Password: 7999
-
Leszek Kosarzewski: update on J/Psi
-
Mustafa: embedding update
2011/06/14 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 93871. Password: 7999
-
Leszek Kosarzewski: update on J/Psi
-
Mustafa: embedding update
2011/05/10 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 93871. Password: 7999
-
Wei Xie: Update on NPE Run10 AuAu
-
Hao: Update J/psi v2
-
Barbara: Update on J/psi polarization
-
QM presentations:
2011/05/03 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 93871. Password: 7999
-
Wei Xie: Update of NPE Au+Au Run10
-
Wenqin: Update on NPE
-
Zebo: High-pT J/Psi
-
Barbara: J/Psi polarization
-
Mustafa:Embedding update
2011/04/26 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 93871. Password: 7999
-
Chris: Update on J/Psi
-
Wenqin: Update on NPE
-
Wei Xie: Update of NPE Au+Au Run10
-
Zebo: High-pT J/Psi
-
Mustafa: Embedding update
2012
2012/12/20
Time: 11:00 (EST), 8:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 1616
J/psi polarization paper proposal Barbara
NPE in d+Au Olga
2012/12/13
Time: 11:00 (EST), 8:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 1616
NPE v2 update - Daniel
2012/12/06
Time: 11:00 (EST), 8:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 1616
1. Upsilon trigger discussion for Run13 500 GeV Manuel
2. Upsilon analysis update Anthony
3. J/psi polarization update Barbara
4. NPE v2 update Daniel
5. Upsilon-h correlation Matt
2012/11/06
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 14 0849
1. D0 in 200 GeV U+U Zhenyu Ye
2. e-D0 analysis Witek Borowski
3. Upsilon-h analysis Matt Cervantes
3. embedding status update David and Mustafa
2012/10/31
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 14 0849
1. Upsilon update Anthony
2. Upsilon update Kurt
2. Embedding update David, Mustafa
2012/10/09
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 14 0849
1. NPE v2 Daniel Kikola
2. Embedding update David, Mustafa
2012/10/02
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 14 0849
1. NPE v2 Daniel Kikola
2. HF embedding priority list Jaro
2012/09/25
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 14 0849
1. NPE v2 Daniel Kikola
2012/09/18
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 14 0849
1. J/ps analysis in 500 GeV Qian Yang
2. run09 NPE analysis update Xin L, Yifei
3. update on NPE v2 Daniel Kikola
4. embedding priority list discussion Jaro
5. Hot datasets revisit all
2012/09/04
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 14 0849
1. update on D->e and B-> e Yifei Zhang
2012/09/04
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 14 0849
1. update on NPE v2 study. Dainel Kikola
2. update on J/psi in low energy Wangmeri Zha
3. embedding status David Tlusty and Mustafa.
2012/08/28
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 14 0849
1. HF PWG paper status and plan Wei Xie
2. NPE v2 jet correlation background Daniel Kikola
3. NPE v2 paper proposal. Daniel Kikola
4. run09 NPE update Xin Li
4. Who will be the next embedding helper?
2012/07/31
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 14 0849
. Password: 7999
http://evo.caltech.edu/evoNext/koala.jnlp?meeting=292I2iMeMt9M92Dv9aD9
1. NPE AuAu200 Wei/Wenquin
2.e-D0 in pp500 Witek
3.J/psi 62 Wangmei
4. NPE 62 Mustafa
5. NPE v2 Daniel
2012/07/24 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
1. e-D0 analysis in 500 GeV Witold Borowski (conitue from last week)
2. Update on Upsilon analysis Anthony
3. NPE spectra 200 GeV Update Wenqin, Wei
4. NPE high pT v2 update Wenqin
5. NPE v2 update Daniel
6 NPE low energy spectra update Mustafa.
7. D0 analysis update David
2012/07/17 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
1. D0 analysis using run10 and run11 data Yifei Zhang
2. D0 analysis in p+p 500 GeV David Tlusty
3. NPE flow analysis in Au+Au collisions Daniel Kikola
4. NPE analysis in 62 GeV Au+Au M. Mustafa
5. J/psi paper in p+p and d+Au Chris Powell
6. e-D0 analysis in 500 GeV Witold Borowski
5. Embedding status M. Mustafa
2012/07/10 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
1. Deadlines
2. Run 12 production priorities (need inputs)
3. Collaboration Meeting Agenda (update)
5. NPE v2 in 200 and 62 GeV Au+Au (Daniel)
6. NPE in 62 and 39 GeV Au+Au (Mustafa)
2012/07/03 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
1. Lezsek: Low-pT J/psi
2. Collaboration Meeting Agenda (Preliminary)
2012/06/26 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
1. Jonathan: update on TMVA analysis.
2. Daniel: update on NPE v2 analysis
3. Lezsek: J-psi
4. Anthony: Upsilon
2012/06/19 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
1. Leszek: nsigma_e cut effcieincy in p+p 200 GeV
2. Anothey: Upsilon update
3. Wei: run10 200 GeV NPE update.
4. Mustafa: Embedding update.
2012/06/12 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
1. Anthony: effect of h+/h- issue on Upsilon.
2. Wei: run10 200 GeV NPE update.
3. Chris: d+Au and p+p J/psi paper proposal.
4. Leszek: nsigma_e cut effcieincy in p+p 200 GeV
5. Mustafa: Embedding update.
2012/06/01 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
1. Anthony: Upsilon update
2. Mustafa, Jaro: Embedding update.
2012/05/22 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
1. Anthony Upsilon Update
2. Leszek Kosarzevski J/Psi
3. Mustafa Mustafa embeding update
2012/05/07 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
1. Olga Hajkova dAu Update
2. Mustafa Mustafa ele 62GeV QA
2012/05/01 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
1) Andrew Peterson: Upsilon pT Spectrum and fit
http://drupal.star.bnl.gov/STAR/system/files/DrewPeterson_PWGHF_PhoneMeeting_May_1_2012_0.pdf
2). Chris Powell: Low pT J/psi paper proposal update
http://drupal.star.bnl.gov/STAR/system/files/proposal_3.pdf
3). Greg Wimsatt:
http://drupal.star.bnl.gov/STAR/system/files/Wimsatt2012-04-28L0PotentialTriggerProblem_0.pdf
4). Pibero Djawotho
http://cyclotron.tamu.edu/pibero/jets/2011.10.18/JetMeeting-2011.10.18.pdf
2012/04/02 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
Agenda:
1) Matt: Upsilon correlation and spin update.
2) Hao: J/psi v2 update.
3) Wei: NPE purity.
4) Yifei: D0 signal in Run11 Au+Au.
2012/04/02 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
1. Spiros: HFT plan for run13.
2. Wei: NPE spectra requests in Cu+Au.
3. Daniel: NPE v2 request in Cu+Au.
4. all: HOT datasets request (last call).
5. Matt: Upsilon-h correlation update.
6. Wangmei: J/psi in 39 and 62 GeV Au+Au
7. Wenqin: J/psi->e contribution to NPE in 200 GeV Au+Au
2012/03/20 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
1) Lijuan: MTD Run13
http://www.star.bnl.gov/protected/lfspectra/ruanlj/BUR13/BUR13_MTD.pdf .
2) Wei: NPE Run10
www.star.bnl.gov/protected/heavy/weixie/PWG_presentation/NPE_run10_AuAu_03_27_2012.pptx
3) David: D0,D* in pp500
http://www.star.bnl.gov/protected/heavy/tlusty/pp500.pdf
4) Anthony: Upsilon in CuAu
http://nuclear.ucdavis.edu/~kesich/protected/CuAuFeasibilty_HFWeekly_27Mar12.pdf
5) Mustafa: NPE 62
http://www.star.bnl.gov/protected/heavy/mstftsm/NPE/AuAu62GeV/NPE_AuAu62GeV_March_27th_2012.pdf
6) Matt Upsilon-h
7)
QM2012 abstracts:
1) Mustafa NPE
http://www.star.bnl.gov/HyperNews-star/protected/get/heavy/3495.html
2) Yifei D in pp,AuAu 200 GeV
http://www.star.bnl.gov/HyperNews-star/protected/get/heavy/3500/1.html
3) Anthony Upsilon
http://www.star.bnl.gov/HyperNews-star/protected/get/heavy/3503.html
4) Wanqmei
http://www.star.bnl.gov/HyperNews-star/protected/get/heavy/3504.html
5) David D,D* in pp200, pp500 (AuAu200?)
http://www.star.bnl.gov/HyperNews-star/protected/get/heavy/3502/1.html
poster:
Daniel:
http://www.star.bnl.gov/HyperNews-star/protected/get/heavy/3500.html
2012/03/20 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
1) Discussion on the QM abstract.
2) J/psi v2 paper?
3) Other topics?
4) Embedding status
2012/03/13 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
2012/03/06 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
-
Daniel: K3e
-
Barbara:J/psi pol
-
Kurt: Upsilon eff
-
Mustafa: embedding update
2012/02/28 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
-
input for Cu+Au run
-
Mustafa: embedding update
2012/02/21 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
-
HP2010 abstract, e.g. J/psi
-
embedding request for Run11 data analyses.
-
Mustafa: embedding update
2012/02/14 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
-
Barbara: J/psi polarization systematic errors
-
Olga: NPE in dAu update
-
HP2012 abstacts discussion
-
Mustafa: embedding update
2012/02/07 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
-
Zebo: high pT J/psi
-
Chris: low pT J/psi
-
Mustafa: embedding update
2012/01/24 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
-
Paper discussion: J/Psi v2 and High pT J/Psi
-
Jaro: Embedding priority list
-
Reproduction of previous data
-
Wenqin: NPE v2
-
Daniel: NPE v2
-
Leszek: Low pT J/Psi
-
Embedding news:
2012/01/24 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
2012/01/17 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
-
Yifei: D in p+p 500GeV
-
Barbara: p+p 200GeV run9 E/p data x embedding
-
Reproduction list
-
Embedding update
2012/01/10 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
-
Mustafa: NPE in Au+Au 62GeV
-
QM12 plan
-
run11 data analysis plan
-
Embedding update
2012/01/03 Meeting Minutes
Time: 13:00 (EST), 10:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 104850. Password: 7999
o Xin Li: Run11 200 GeV Au+Au QA.
2013
2013/12/19
Time: 11:30 (EST), 8:30 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 2099
1) D* in pp 500 GeV David
2013/12/12
Time: 11:30 (EST), 8:30 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 2099
1) 2S+3S Upper Limit in AuAu 2010 - Anthony
2013/12/5
Time: 11:30 (EST), 8:30 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 2099
1) Upsilon in U+U - Robert
2) NPE in p+p (run 9) and d+Au (run 8) - Olga
3) NPE-h correlations in AuAu 200 GeV - Jay
2013/11/14
Time: 11:30 (EST), 8:30 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 2099
1). PID with TOF and dE/dx Lanny Ray
2). NPE spectra in run12 p+p Xiaozhi Bai
2013/10/31
Time: 11:30 (EST), 8:30 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 2099
1) NPE in p+p and d+Au 200 GeV - Olga
2)Purity for NPE in Au+Au 200 - 39 GeV - Daniel
2013/10/10
Time: 11:00 (EST), 8:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 2099
1) Upsilon spin alignment Matt
2) Upsilon embedding and E/p issue in U+U Robert
2013/10/03
Time: 11:00 (EST), 8:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 2099
1) NPE in d+Au (run 8) and p+p (run 9) Olga
2013/08/08
Time: 11:00 (EST), 8:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 2099
1). Update on Upsilon Anthony
2). J/psi in U+U Ota
3). J/psi in U+U Guannan
4). Update on J/psi in d+Au Leszek
2013/08/01
Time: 11:00 (EST), 8:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 2099
1) hadron nSigmaElectron calibration using ToF Daniel
2013/07/25
Time: 11:00 (EST), 8:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 2099
1) Update on upsilon 1S Anthony
2013/06/27
Time: 11:00 (EST), 8:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 2099
1) NPE in d+Au update Olga
2) Upsilon update Matt
2013/06/20
Time: 11:00 (EST), 8:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 2099
1) D* in p+p 500 GeV with BHT1 trigger Witak and David
2) update on J/psi in d+Au Leszek
3) Isolation of Upsilon 1S from the excited states Anthony
4) Upsilon in U+U 193 GeV Todd Kinghorn
2013/06/13
Time: 11:00 (EST), 8:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 2099
1) update on J/psi in d+Au Leszek
2013/06/06
Time: 11:00 (EST), 8:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 2099
1) update on J/psi in d+Au Leszek
2013/05/30
Time: 11:00 (EST), 8:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 2099
1). update on J/psi in d+Au Leszek
2013/05/16
Time: 11:00 (EST), 8:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 2099
1). Upsilin in U+U Collisions Robert Vertesi
2). Update on 62 GeV J/psi sys. errors. Wangmei
2013/05/16
Time: 11:00 (EST), 8:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 2099
1) D0 in U+U 193 GeV Zhenyu
2013/05/02
Time: 11:00 (EST), 8:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 2099
1) Upsilon updates Anthony
2013/04/25
Time: 11:00 (EST), 8:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 2099
1) Upsilon spin-aligment update Matt
2013/04/18
Time: 11:00 (EST), 8:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 2099
1). update on run11 J/psi analysis wangmei
2). Update on NPE analysis at 62.4 GeV Mustafa
3). J/psi v2 update Hao
4). discussion on systematic error Yifei
5). discussion on systematic error Daniel
6). Update on 500 GeV D meson analysis David
2013/04/11
Time: 11:00 (EST), 8:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 2099
1) MTD BUR request - Lijuan
2) J/psi in Au+Au 62 and 39 GeV: systematic errors - Wangmei
3) Efficiency uncertainties in D0 analysis - Yifei
2013/03/28
Time: 11:00 (EST), 8:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 2099
1) BUR 14/15 discussion with HFT Xin Dong
2) Run14 projection of J/psi Daniel
3) D0 Update Yifei
4) J/psi in U+U Ota
2013/03/21
Time: 11:00 (EST), 8:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 2099
update on Upsilon-h and Upsilon spin alignment Matt
2013/03/07
Time: 11:00 (EST), 8:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 2099
Upsilon: extending the AuAu measurement to |y| < 1.0 from |y| < 0.5 - Anthony
Upsilon: RdAu and its implications for theory and other experiments - Manuel Calderón de la Barca Sánchez
Low-pT J/psi in p+p run 9: Leszek
2013/02/07
Time: 11:00 (EST), 8:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 2099
NPE purity and photonic electron v2 Daniel (fit plot for NPE purity)
2013/01/31
Time: 11:00 (EST), 8:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 2099
Upsilon paper: Update on the status Anthony
J/psi polarization: Systematic error estimation of HT trigger efficiency Barbara
NPE in d+Au: Update Olga
J/psi in p+p 500 GeV: Embedding QA Qian
2013/01/24
Time: 11:00 (EST), 8:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 2099
Upsilon trigger request for p+p 500 GeV run 13 (Wei, Anthony ?)
J/psi WWND talk and request for preliminary status of J/psi results (pT spectra, RAA, RCP) for Au+Au 39 and 62 GeV Wangmei
Low-pT J/psi in p+p 200 GeV Leszek
2013/01/17
Time: 11:00 (EST), 8:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 2099
NPE in d+Au Olga
NPE talk at Bormio 51st International Winter Meeting Olga
Upsilon in d+Au: preliminary vs requested-to-be-preliminary Anthony
Low-pT J/psi in p+p 200 GeV Leszek
2013/01/10
Time: 11:00 (EST), 8:00 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 2099
NPE v2 update Daniel
D0 update Yifei
2014
2014/12/11
1) D* in pp 500 GeV Run11 HT - David
2) J/psi-h correlation in pp 500 GeV Run11 HT - Hui
Minutes - Zhenyu
2014/12/3
1) ccbar → e+μ simulation and projection for Au+Au 200 GeV with HFT - Bingchu
Minutes
2014/11/20
1) NPE in most central Central U+U Collisions - Katarina
2) B->J/psi with HFT and MTD in MC Simulation - Bingchu
Minutes - Zhenyu
2014/10/30
1) Upsilon spin alignment paper proposal - Matthew
Minutes
2014/10/21
1) MTD data production strategy for Run 14 - Group discussion
2) Run14 PicoDst Structure Update - Rongrong
3) J/psi in Au+Au 200 GeV Run10 vs Run11 - Wangmei
4) Upslion in p+p 500 GeV - Leszek
5) NPE in p+p 200 GeV Run12 - Xiaozhi
Minutes - Zhenyu
2014/10/16
1) MTD data production strategy for Run 14 - Rongrong
2) NPE in p+p 200 GeV - Xiaozhi
Minutes
2014/10/11
1) PicoDst for 2014 data - Rongrong
Meeting minutes - Zhenyu
2014/9/28
1) HQ2014 talk: Upsilon in p+p 500 GeV -Leszek
2014/9/4
1) Disk space -Xin et al.
2) Upsilon Spin Alignment -Matt
Meeting minutes - Zhenyu
2014/8/28
1) Upsilon in p+p 500 GeV -Leszek
Meeting minutes
2014/8/21
1) Upsilon Spin-Alignment - Matt
Meeting minutes
2014/8/14
1) Upsilon in pp 500 GeV - Leszek
Meeting Minutes - Zhenyu
2014/7/24
1) Upsilon in pp 500 GeV - Leszek
2014/7/17
1) Discussion on data production priorities
2) Upsilon spin alignment - Matt
Meeting minutes
2014/7/10
1) discussion on data production priorities
Meeting minutes
2014/7/3
1) discussion on data production priorities for QM15
Meeting minutes
2014/6/26
1) discussion on data production and physics priorities for QM15
2) pp200 baseline study - Long
Meeting minutes - Zhenyu
2014/6/12
1) NPE pp run12 - Shenghui
Meeting minutes
2014/6/5
Meeting minutes
2014/5/29
Meeting minutes - Zhenyu
2014/5/08
Time: 11:00 (EST), 8:00 (PST). EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 100 4409 Password: 7999
1) psi(2s) update run11 pp500 - Qian
2) D-meson update run12 pp200 - Mustafa
3) trigger efficiency run12 pp200 - Hao
4) J/psi update AuAu 200 GeV - Wangmei
2014/5/01
Time: 11:00 (EST), 8:00 (PST). EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 100 4409 Password: 7999
1) Upsilon updates in U+U - Robert
Meeting minutes
2014/4/24
Time: 11:00 (EST), 8:00 (PST). EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 100 4409 Password: 7999
1) J/psi in AuAu 200 - Wangmei
2) D* in p+p 500 Run11 - David
3) D0/D* in p+p 200 Run12 - Hao
4) J/psi polarization in p+p 500 GeV Run11 - Barbara
5) Upsilon in U+U Run12 - Robert
Meeting minutes - Zhenyu
2014/4/17
Time: 11:00 (EST), 8:00 (PST). EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 100 4409 Password: 7999
1) Upsilon in U+U - Robert
2) NPE in p+p 200 Run9 - Olga
3) Low pT J/psi in d+Au - Leszek
4) NPE in p+p 200 Run12 - Xiaozhi
5) J/psi in AuAu 200 - Wangmei
6) D0/D* in p+p 200 Run12 - Mustafa
7) D0/D* in p+p 200 Run12 - Hao
8) BUR15&16 - Daniel and all
BUR15&16 with HFT - Xin
2014/4/10
Time: 11:00 (EST), 8:00 (PST). EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 100 4409 Password: 7999
Meeting minutes
2014/4/3
Time: 11:00 (EST), 8:00 (PST). EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 100 4409 Password: 7999
1) low pT NPE in pp 2009 - Olga
2) high pT NPE in pp 2012 - Xiaozhi
Meeting minutes - Zhenyu
2014/3/27
Time: 11:00 (EST), 8:00 (PST). EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 686 8556
1) Upsilon in Au+Au - Anthony
2) Jpsi Polarization in pp500 - Barbara
3) D* in pp500 - David
2014/3/20
Time: 11:00 (EST), 8:00 (PST). EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 686 8556
1) Upsilon in Au+Au - Anthony
2014/3/13
Time: 11:00 (EST), 8:30 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 100 1507
1) Upsilon in Au+Au - Anthony
2) Heavy Flavor triggers for Au+Au run 14
3) Embedding QA for J/psi in U+U - Ota
2014/2/27
Time: 11:30 (EST), 8:30 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 100 1507
1) NPE in p+p 200 GeV run 12 - Xiaozhi Bai
2) Upsilon in U+U Robert
2014/1/16
Time: 11:30 (EST), 8:30 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 100 1507
1) Nonflow in NPE v2 in Au+Au 200 GeV - Daniel
2) Low-pT NPE in Au+Au 200 GeV run 10 - Kunsu
3) NPE in p+p 200 GeV run 12 - Xiaozhi Bai
4) J/psi to NPE contribution at 62.4GeV - Mustafa
2014/01/09
Time: 11:30 (EST), 8:30 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 100 1507
1) NPE in p+p 200 GeV run 12 - Xiaozhi Bai
2) J/psi in U+U 200 GeV - Ota
2014/01/02
Time: 11:30 (EST), 8:30 (PST). EVO password: heavy. EVO phone bridge #: +1 631 344 6100, +1 626 395 2112. Phone bridge Id: 15 2099
1) NPE in p+p run9 update Olga
2) D* in pp 500 GeV David
2015
2015/12/17
1) update of J/psi analysis in central UU collisions - signal corrections from data - Jana
2) Run16 triggers
3) projection for B->Jpsi in run16 - Bingchu
minutes
2015/12/3
1) D0 v2{event plane} in Au+Au 200 GeV run 14 - Hao
2) D0 v2{2 part. corr.} in Au+Au 200 GeV run 14 - Liang
minutes
2015/11/19
1) Jpsi-h correlation in Run11 p+p 500 GeV - Qian
2) D-h correlation in Run11 p+p 500 GeV systematic uncertainties - Long
3) NPE-h correlation in Run12 p+p 200 GeV - Zach
minutes - Zhenyu
2015/11/05
1) D0 analysis in Run 12 Cu+Au collisions - Pavol
minutes
2015/10/22
1) BEMC performance in 2014 HF PicoDsts - Rosi
2) Issues with in Au+Au 200 GeV run 14 data with HT trigger - Bingchu
Minutes
2015/10/15
1) Data production priority
2) Paper plans
3) Paper Proposal D0 v2 - Hao
3) D-h correlation systematic uncertainties in Run11 p+p 500 GeV - Long Ma
minutes - Zhenyu
2015/09/17
1) K0s spectra with the HTF and D0 double counting correction in Au+Au 200 GeV run 14 - Xin
2) Ds v2 and spectrum in Au+Au 200 GeV run 14 - Md. Nasim
3) Syst. uncertainties on J/psi->mu+mu- in Au+Au 200 GeV run 14 - Rongrong
4) J/psi->mu+mu- v2 and trigger efficiency in Au+Au 200 GeV run 14 - Takahito
5) J/psi v2 in Au+Au 200 GeV run 11 - Chensheng
Minutes
2015/09/11 - Low pT NPE in p+p Run12
Minutes - Zhenyu
2015/09/11
1) Data Driven Fast Simulator - Mustafa.
2) Corrected K_s - Xin.
3) D^0 spectra - Guannan.
4) Ds analysis - Nasim
5) Upsilon in p+p 500 GeV - Leszek
2015/09/10
1) J/psi-h correlation in run12 pp 200 GeV - Bingchu
2) Run 12 p+p 200 GeV, NPE-h deltaPhi Correlations - Zach
3) J/psi and Upsilon analysis using MTD data - Rongrong
4) J/psi->mumu v2 - Takahito
Minutes
2015/09/04
1) Systematic uncertainties for NPE from Run12 p+p 200 GeV MB - Shenghui
2) NPE from Run12 p+p 200 GeV - Xiaozhi
3) D0 Fast Simulation QA - Mustafa
4) Upsilon in p+p 500 GeV - Leszek
Minutes - Zhenyu
2015/09/03
1) pre-QM meeting agenda
2) D0 v2 from event plane - Hao
3) D0 v2 from 2-particle correlation - Liang
4) PID efficiency and Double-Counting for D0 Reconstruction - Xin
Minutes - Zhenyu
2015/08/27
J/psi in Au+Au 200 GeV run 14 with MTD -Rongrong
J/psi v2 in Au+Au 200 GeV Run 11 - Chensheng
MTD trigger efficiency study and J/psi->mumu v2 - Takahito
D0 v2{2} in Au+Au 200 GeV run 14 - Liang
Upsilon in p+p 500 run 11 - Leszek
minutes
2015/08/20-22
HFT Analysis and HFT+ Proposal Workshop
2015/08/13
1) NPE analysis in central UU collisions - Katarina
2) D0 v2 - Liang
minutes
2015/08/06
1) Ds efficiency and Rcp calculation- Nasim
2) Non-flow in Run14 D0 v2 - Malong
3) NPE analysis in central UU collisions - Katarina
4) D meson v2 - Michael
Minutes - Zhenyu
2015/07/30
1) background sources from angular correlations in the D0 invariant mass spectrum - Alexander
2) NPE in central UU collisions - Katarina
3) reconstruction efficiency of dimoun events - Rongrong
4) MTD partial tracking and trigger efficiency - Takahito
minutes
2015/07/23
1) Non-flow effect on D0 v2 - Hao
2) Vertex resolution studies with KFVertex and Minuit Vertex - Guannan
3) D0 Tree with KFVertex - Guannan
Minutes - Zhenyu
2015/07/16
1) D0 production in Au+Au 200 GeV run 14 - Guannan
2) Mixed event maker in RNC HF library - Micheal
3) K0S Efficiency calculation using toy MC model - Nasim
4) Purit estimation for NPE v2 in Au+Au 200, 62.4 and 39 GeV - Daniel
5) D0 foreground in Au+Au 200 GeV - Mustafa
minutes
2015/07/09
1) NPE in central UU - Katarina
2) trigger efficiency correction in D-hadron correlation study - Long Ma
3) update on Ds meson analysis - Long Zhou
minutes
2015/07/02
1) Run14 MTD results projection and data production strategy - Lijuan
2) Muon identification using J/psi signal in p+p 500 GeV - Te-Chuan/Yi Yang
3) Efficiency calculation for Ds in Au+Au 200 GeV run 14 using Toy Monte-Carlo simulation - Md. Nasim
4) J/psi in Run12 central U+U collisions - Jana
5) KFVertex and Hijing Simulation - Liang He
6) Upsilon in Run11 p+p 500 GeV - Leszek
Minutes - Zhenyu
2015/06/26
Hard Probes 2015 talk - Li Yi
J/psi vs event activity in p+p 500 GeV: analysis update, Hard Probes 2015 talk - Rongrong
D0 v2{2} in Au+Au 200 GeV - Liang He
J/psi polarization in p+p 500 GeV - Barbara
Minutes
2015/06/18
J/psi in BES paper status - Wangmei
NPE in Run10 Au+Au 62.4 GeV paper status - Mustafa
Event Plane Calibration status for Run14 MTD J/psi v2 - Takahito
D0 NMFs from Run14 - Mustafa
Mixed Event package for the RNC-HF analysis library as well as a quick case study using Mixed Event with D0 - Michael
KFVertex resolution and D0 correlation v2 - Liang
tracking/matching efficiency study in D triggered correlation in p+p collisions at 500GeV - Long Ma
D0 reconstruction with KFParticle - Amilkar
minutes
2015/06/11
1) Low pT NPE in Run12 p+p 200 GeV - Shenghui
2) NPE-h in Run11 p+p 500 GeV - Wei Li
3) Upsilon in Run12 U+U 193 GeV - Robert
4) J/psi from MTD in Run13 pp 500 GeV - Rongrong
5) e-mu correlation from HT and emu triggers in Run14 Au+Au 200 GeV - Bingchu
6) Run14 MTD data production strategy - Lijuan
7) KFVertex refitting I - Liang
8) KFVertex refitting II - Guannan
9) D0 Rcp Extraction - Mustafa
Minutes - Zhenyu
2015/05/21
1) Upsilon polarization paper proposal - Saskia
2) dsaAdc in the trigger simulator - Barbara
Minutes
2015/05/14
1) Introduction of D0 correlated v2 study - Leon
2) vertex refitting - Liang
3) Update centrality definition for Run14 AuAu200GeV - Guanna
4) Update on Charm correlation in pp 500 GeV - Long Ma
5) update on D+ and D- as well as some studies using a toy mc - Michael, Mustafa
6) the dsmAdc issue - Barbara
7) D0 reconstruction raw signals - Guannan
minutes
2015/05/07
1) MTD Data production - Lijuan
2) PicoDST production - Xin
3) J/psi polarization analysis in pp 500 GeV - Barbara
4) D0 reconstruction using KFParticle - Amilkar
Minutes - Zhenyu
2015/4/30
1) picoDst production for MTD data - Rongrong
2) J/psi v2 analysis for Run11 - Zhao
3) J/psi analysis in central U+U collisions - Jana
4) KF vertex refitting - Liang
Minutes
2015/04/23
1) Ds in Au+Au 200 GeV run 14 - Nasim
2) picoDST QA and Centrality Definition in Au+Au 200 GeV run 14 - Guannan
3) KF vertex refitting - Liang
4) Prospects of B-jet measurements with HFT - Yaping
Minutes - Zhenyu
2015/04/16
1) Gamma Conversion in Au+Au 14.5 GeV Run 14 - Mengzhen
2) E/p corrections of the Upsilons in U+U 193 GeV - Robert
3) D0 identification using TMVA - Jonathan
4) Charm correlation study with Pythia simulation -Long
5) D+/D- analsis in AU+Au 200 GeV with HFT - Michael
6) KF vertex re-fittiong - Liang
Minutes
2015/04/09
1) NPE v2 in Au+Au run 10 - purity vs momentum (postponed) - Daniel
2) NPE low-pT in p+p 200 GeV run 12 - Shenghui
3) Update on J/psi in BES paper status - Wangmei
4) B->J/psi projection for BUR16/17 - Bingchu
5) D analysis with HFT in Au+Au 200 GeV run 14 - Long
6) How to run simulations with HF particles embedded in a hijing background - Michael
Minutes - Zhenyu
2015/04/02
1) Beam User Request 2016-2017
- Unofficial information: Option 1: 22-week RHIC run in 2016, and no run in 2017, Option 2: 22-week runs in both 2016 and 2017
2) D0 v2 in Au+Au 200 GeV run 14 - Hao
3) Update on the picoD0Production and analysis code - Mustafa
4) Software package for general HF analysis with picoDsts - Jochen
5) Update on Upsilon Polarization paper proposal - Saskia and Yanfang
6) Update on Upsilon in U+U paper proposal - Robert
7) NPE pT spectrum in Au+Au 200 GeV run 10 - Kunsu
Minutes
2015/03/26
1) Run14 Au+Au picoDst production - Round table discussion
2) J/psi polarizaition in pp 500 GeV Run 11 - Barbara
3) NPE in pp 200 GeV Run12 - Xiaozhi
Minutes - Zhenyu
2015/03/19
1) Upsilon 2S/3S in U+U Run 12 - Robert
2) Upslion Npart weighting - Robert
3) Exercise with Kpis mass - Leon
4) D0 in Au+Au run 14 - Mustafa
5) PicoDst production for the Run14 AuAu200 GeV - Xin
6) J/psi production and J/psi-h correlation in p+p at 200 GeV - Bingchu
7) J/psi analysis using Run13 pp 500 GeV - Rongrong
Minutes
2015/03/12 (postponed to next week)
1) D0/D* in pp 500 GeV Run11 Paper Proposal - David
2) Upsilon 2S/3S in U+U Run 12 - Robert
2015/03/05
1) Upsilon in U+U - Robert
paper proposal
analysis update
2) J/psi pp reference at 39 and 62.4 GeV - Wangmei
3) Au+Au 200 GeV run 14 QA - Kpi pairs - Liang
2015/02/26
1) Event-Plane Dependent NPE-h correlations in AuAu 200 GeV - Jay
2) NPE in most central Central U+U Collisions - Katarina
Minutes - Zhenyu
2015/02/12
1) Primary Vertex Refitting for D Meson Simulation Studies - Mikhail
2) D0 Reconstruction Efficiency in Simulations with HFT in 200GeV p+p Collisions - Liang
3) Upsilon in U+U 193 GeV Run12 - Robert
4) D* in pp 500 GeV Run11 - David
Minutes - Zhenyu
2015/1/15
1) J/psi in pp 500 GeV Run13 MTD - Rongrong
2) J/psi and psi(2s) in pp 500 GeV Run11 - Qian
Minutes - Zhenyu
2016
2016/12/22
1) Consistency check between D0 and NPE v2 - Long Zhou
2) Run11 Au+Au Upsilon->ee - Zaochen ye
minutes - Zhenyu
2016/12/15
One-slide status for QM2017
Alena Harlenderova Guannan Xie Takahito Todoroki Jakub Kvapil Zac Miller
Bingchu Huang Pavol Federic Miroslav Saur Liang He Alex Jentsch
Xiaolong Chen Long Zhou Zaochen Ye Kunsu OH Xinjie Huang
minutes - Rongrong
2016/11/30
1) Upsilon in p+p 500 GeV - Leszek Kosarzeski
minutes - Zhenyu
2016/10/20
1) Upsilon in p+p 500 GeV - Leszek Kosarzeski2016/10/27
1) QA of Run16 st_hlt - Sooraj Radhakrishnan
minutes - Rongrong
2016/10/20
1) Upsilon in p+p 500 GeV - Leszek Kosarzeski
minutes - Rongrong
2016/10/06
1) Combined Upsilon analysis - Shuai Yang
2) Jpsi and Upsilon embedding in Run11 AuAu 200 GeV - Zaochen Ye
minutes - Rongrong
2016/09/29
1) Run15 p+Au st_physics data QA for NPE/Jpsi/Upsilon measurements - Zach
2) Run15 p+p 200 Jpsi polarization in dimuon channel - Zhen
minutes - Zhenyu
2016/09/22
1) Run15 centrality study using MB data - Yanfang Liu
minutes - Rongrong
2016/09/08
1) QA for Run15 pAu (MTD) - Takahito
2) J/psi v2 in Run12 U+U - Alena
3) Upslion in Run11 and Run14 Au+Au (BHT) - Zaochen
minutes - Zhenyu
2016/09/01
1) QA for Run15 st_physics pp/pA - Zachariah Miller
2) Non-prompt Jpsi using Run14 AuAu - Bingchu Huang
3) Quarkonium in Run15 pAu (BHT) - Zaochen Ye
minutes - Rongrong
2016/08/25
1) Vertex distribution in Run15 pp/pA - Yanfang
2) Upsilon in Run14 AuAu dielectron - Zaochen
minutes - Zhenyu
2016/08/11
1) Run-dependent QA of MTD events in Run15 pp 200 GeV - Takahito Todoroki
minutes - Rongrong
2016/08/04
1) EvtGen Implementation in STAR - Zhenyu
minutes - Zhenyu
2016/7/28
1) Centrality definition for Run14 AuAu 200 GeV, P16id - Xiaolong Chen
2) Jpsi in Run15 pp: how to determine the PID cuts range - Yanfang Liu
minutes - Rongrong
2016/7/21
1) Ds in Run14 Au+Au - Nasim
minutes - Zhenyu
2016/7/14
1) OSU collaboration meeting
2) J/psi efficiency from PID cuts - Yanfang
minutes - Rongrong
2016/07/07
1) data production priority and QM17 topics
2) Run14 Jpsi->dielectron embedding - Zaochen
3) PWG_TASK disk space request - Bingchu
4) Jpsi in Run15 p+p - Takahito
2016/6/23
1) NPE-h in Run11 pp 500 GeV - Wei Li
2) Jpsi x-sec from Run13 pp 500 GeV MTD data - Te-Chuan Huang
3) Jpsi in Run12 Cu+Au - Pavla Federicova
4) D+/- in Run14 Au+Au (P16id) - Jakub Kvapil
5) Jpsi in Run15 pp 200 GeV MTD - Yanfang Liu
6) Upsilon in pp 500 GeV - Leszek Kosarzewski
2016/6/16
1) Jpsi v2 from Run14 MTD data - Takahito Todoroki
2) Jpsi RAA from Run14 MTD data - Rongrong Ma
3) D0 v3 from Run14 AuAu HFT data - Michael Lominitz
4) Jpsi and Upsilon from Run14 AuAu BHT data - Zaochen Ye
5) NPE-h in Run11 p+p 500 GeV - Wei Li
6) Low-pT Jpsi enhancement - Wangmei
2016/6/9
1) D0 v2 with 2PC (P16id) - Liang He
2) Low-pT Jpsi enhancement in AuAu and UU - Wangmei
3) Jpsi v2 using Run14 MTD data - Takahito Todoroki
4) Jpsi cross section using Run14 MTD data - Rongrong Ma
minutes - Rongrong
2016/6/2
1) Jpsi-h correlation in Run12 pp200 - Bingchu Huang
2) Jpsi yield vs event activity in Run12 pp200 - Bingchu Huang
3) Jpsi cross section in Run13 pp500 using MTD - Te-Chuan Huang
minutes - Rongrong
2016/5/26
1) Jpsi polarization in Run12 pp200 - Siwei Luo
2) Jpsi-h correlation in Run11 pp500 - Qian Yang
3) Jpsi yield vs event activiity in Run12 pp200 - Bingchu Huang
4) MTD J/psi analysis in Run14 AuAu200 - Rongrong Ma
5) MTD Upsilon analysis in Run14 AuAu200 - Xinjie Huang
6) D0 v3 in Run14 AuAu200 - Michael Lomintz
2016/5/19
1) MTD J/psi analysis in Run14 AuAu200 - Rongrong Ma
2) D0 v2 in Run14 AuAu 200 (P16id) - Michael Lomnitz
3) J/psi polarization in pp 200 - Siwei Luo
4) Ds reconstrcution in Run14 AuAu 200 (P16id) - Long Zhou
5) Ds reconstruction in Run14 AuAu 200 (P16id) - Nasim
minutes - Rongrong
2016/05/12
1) J/psi polarization in Run12 pp200 - Siwei
2016/5/5
1) NPE in Run14 AuAu 200 - Shenghui
2) J/psi polarization in pp 200 - Siwei
3) D0 reconstruction in Run14 AuAu 200 (P16id) - Mustafa
minutes - Rongrong
2016/4/28
1) NPE v2 in 200, 62, 39 GeV - Daniel
2) Combinatorial Background Method study - Wangmei
minutes - Zhenyu
2016/4/21
1) Jpsi event activities in Run12 pp 200 - Bingchu
2) QA of Run15 pp200 for D0 analysis - Pavol
minutes - Rongrong
2016/4/14
1) sQM plan - Wangmei
2) Jpsi polarization in Run12 pp200 - Siwei
minutes - Zhenyu
2016/3/31
1) New production priorities
2) Run14 D0 production status - Guannan
3) J/psi-hadron correlation in Run13 - Te-Chuan
minutes - Rongrong
2016/3/24
1) Plan for MTD talk at sQM - Takahito
minutes - Rongrong
2016/3/10
1) Updates of Upsilon in UU 193 GeV (already in GPC) - Robert
minutes - Zhenyu
2016/3/3
1) D0 v3 in Run14 Au+Au 200 GeV - Michael
2) bug found in StPxlRawHitMaker - Hao
minutes - Rongrong
2016/2/11
1) D0 v2 in Au+Au 200 GeV run 14 - Hao
2) High tower trigger rates in run 16 - Zhenyu
3) D0 v3 in Au+Au 200 GeV run 14 -Michael
minutes
2016/2/4
1) NPE Raa in Run12 central U+U 193 GeV - Katarina
minutes - Zhenyu
2016/1/7
1) To run or not to run with the pileup protection on the MB trigger in Au+Au collisions in 2016 - Xin
2) B->e study in p+p 200 GeV run 12 - Zach
minutes
2017
2017/12/21
1) Update on Upsilon production in p+p 500 GeV - Leszek Kosarzewski
2) D+/- in d+Au collisions - Georgy Ponimatkin
minutes - Petr
2017/12/14
1) J/psi polarization using Run15 MTD data - Zhen Liu
minutes - Rongrong
2017/11/30
1) Latest results with KF Particle Finder - Maksym Zyzak
2) KF-Particle test results from run14 - Guannan Xie
3) Paper proposal: J/psi polarization in 200 GeV p+p with MTD - Zhen Liu
4) Update on Paper proposal: J/psi polarization in 200 GeV p+p with run12 data (ee) - Siwei Luo
5) Upsilon vs. event activity - Leszek Kosarzewski
minutes - Zebo
2017/11/16
1) Systematic uncertainties study for D0 paper - Guannan Xie
2) Upsilon event activity studies - Leszek Kosarzewski
minutes- Petr
2017/11/09
1) Upsilon in Run14 200 GeV AuAu via di-electron channel - Oliver Matonoha
2) MB events estimation for BBCMB trigger in Run15 200 GeV pp - Zaochen Ye
minutes - Rongrong
2017/11/02-04
Analysis Meeting
2017/10/26
1) Systematic uncertainties study for Run 12 J/psi polarization - Siwei Luo
2) Systematic uncertainties study for Run 14 MTD J/psi - Rongrong Ma
minutes - Zebo
2017/10/12
1) Upsilon production in p+p 500 GeV - trigger efficiency studies - Leszek Kosarzewski
2) Jpsi via the dimuon channel in Run14 200 GeV (slides 33+) - Rongrong Ma
minutes - Petr
2017/10/12
1) Jpsi via the dimuon channel in Run14 200 GeV (slides 1-33) - Rongrong Ma
minutes - Rongrong
2017/10/5
1) Update on D0 v1 for Run14+16 AuAu 200 GeV - Subash Singha
2) Trigger bias study for J/psi and Y in Run15 pp 200 GeV - Zaochen Ye
2017/9/28
1) Systematic uncertainty study for J/psi polarization in run15 p+p - Zhen Liu
2) Multiplicity dependence of J/psi and D0 trigger bias - Takahito Todoroki
3) Simulation of VPD efficiency in run15 p+p - Takahito Todoroki
minutes - Zebo
2017/9/14
1) Run14 D0 topological cuts re-tuning - Xiaolong Chen
2) Upsilon vs. event activity from Run11 pp500 - Leszek Kosarzewski
minutes - Rongrong
2017/9/7
1) J/psi v2 in Run12 UU 193 GeV - Alena Harlenderova
2) Embedding with HFT and open charm in y2016 data sample - Maksym Zyzak
3) Upsilon vs event activity from Run11 pp500 - Leszek Kosarzewski
minutes - Zhenyu
minutes - Rongrong
2017/8/31
1) J/psi v2 in Run12 UU 193 GeV - Alena Harlenderova
minutes - Zhenyu
2017/8/24
1) Tuning Lc cuts with Run14 AuAu 200 GeV - Sooraj Radhakrishnan
2) Ds with Run14 AuAu 200 GeV - Md. Nasim
minutes - Rongrong
2017/8/17
1) Trigger bias study for jpsi events for Run15 pAu200 - Takahito Todoroki
2) Toy MC study for J/psi polarization - Rongrong Ma
3) J/psi polarization in Run15 pp 200 GeV - Zhen Liu
minutes - Zhenyu
2017/8/10
1) D* from Run14 AuAu 200 GeV - Yuanjiang Ji
2) Lc from Run14 AuAu 200 GeV - Miroslav Simko
3) J/psi v2 in Run12 UU 193 GeV - Alena Harlenderova
4) Toy MC study for J/psi polarization - Rongrong Ma
5) J/psi polarization in Run15 pp 200 GeV - Zhen Liu
minutes - Rongrong
2017/8/3
1) Total charm cross section in AuAu200 - Xiaolong Chen
2) Upsilon vs event activity from Run11 pp500 - Leszek Kosarzewski
3) Centrality for Run15 pAu 200 GeV - Yanfang Liu
minutes - Zhenyu
2017/7/20
1) Trigger bias study for jpsi events for Run15 pp200 - Takahito Todoroki
2) Ds v2 for Run14 AuAu 200 GeV - Md Nasim
3) D0 v1 for Run14+16 AuAu 200 GeV - Subash Singha
minutes - Rongrong
2017/7/7
1) Trigger bias study for Run15 pp200 - Takahito Todoroki
2) Ds v2 from Run14 AuAu200 - Md. Nasim
3) D0 v1 from Run14+16 AuAu200 - Sooraj Radhakrishnan
minutes - Zhenyu
2017/6/29
1) Paper proposal: low pT j/psi production in AuAu 200 GeV - Wangmei Zha
2) Centrality study in Run15 pAu - Yanfang Liu
3) Run14 AuAu D0 v1 - Subhash Singha
minutes - Rongrong
2017/6/22
1) D0 v1 analysis with Run14+16 AuAu - Sooraj Radhakrishnan
minutes - Zhenyu
2017/6/15
1) D0 v1 analysis in Run14 AuAu - Subhash & Nasim
2) D0 v1 analysis in Run14+16 AuAu - Sooraj Radhakrishnan
3) Vertex resolution correction for Ds in Run14 AuAu - Md. Nasim
minutes - Rongrong
2017/6/8
1) MTD trigger efficiency - Rongrong
minutes - Zhenyu
2017/6/1
1) Systematic uncertainty for Run12 pp Jpsi polarization - Siwei Luo
minutes - Rongrong
2017/5/11
1) Centrality for 2015 p+Au 200 GeV - Yangfang Liu
minutes - Zhenyu
2017/5/4
1) Vertex reconstruction for 2016 d+Au200 GeV- Sooraj Radhakrishnan
minutes - Zhenyu
2017/4/27
1) Upsilon event activity study - Leszek Kosarzewski
minutes - Rongrong
2017/4/20
1) Centrality for 2015 p+Au 200 GeV - Yanfang Liu
minutes - Zhenyu
2017/4/13
1) Ds efficiency using FastSim package - Md. Nasim
minutes - Rongrong
2017/3/23
1) Request for storing Run16 KPiX tree on RCF - Shusu Shi
2) Jpsi RpA using Run15 MTD data - Takahito Todoroki
3) Upsilon di-electron analysis in Run14 AuAu - Oliver Matonoha
minutes - Rongrong
2017/3/16
1) J/psi polarization in Run12 pp - Siwei Luo
minutes - Zhenyu
2017/3/9
1) J/psi polarization in Run15 pp/A (MTD) - Zhen Liu
minutes - Rongrong
2017/3/2
1) D0 v1 from Run14 Au+Au - Subhash/Nasim
minutes - Zhenyu
2017/2/23
1) pA centrality
2017/2/16
1) D*-h in Run11 pp500 - Long Ma
2) Lc in Run16 AuAu200 - Sooraj
minutes - Zhenyu
2017/1/26
session 1-2 (Thursday)
1) Charmonium in Run15 pp/pAu - Takahito Todoroki
2) Upsilon in Run14 AuAu dimuon - Xinjie Huang
3) Upsilon in Run11 AuAu and Run15 pp/pAu - Zaochen Ye
4) B->D in Run14 AuAu - Xiaolong Chen
5) B->Jpsi in Run14+16 AuAu - Bingchu Huang
minutes - Zhenyu
6) Ds in Run14 AuAu - Long Zhou
7) NPE in Run14 AuAu - Shenghui Zhang
8) B/D->e in Run14 AuAu - Xiaozhi Bai
9) B/D->e in Run14 AuAu - Kunsu Oh
minutes - Rongrong
session 3-4 (Friday)
10) D and Lc in Run14 AuAu - Guannan Xie
11) Ds in Run14 AuAu - Md Nasim
12) D+/- in Run14 AuAu - Jakub Kvapil
13) D0-h in Run14 AuAu - Alex Jentsch
minutes - Zhenyu
14) D0 in Run12 Cu+Au - Miro Saur
15) Jpsi v2 in Run12 U+U - Alena Harlenderova
16) Upsilon in Run11 p+p 500 - Leszek Kosarzewski
17) Charmonion in Run15 p+p/Au - Takahito Todoroki
minutes - Rongrong
2017/1/19
1) Jpsi event activity in Run12 pp 200 GeV - Bingchu Huang
2) NPE in Run15 pp/pAu 200 GeV - Zach Miller
3) NPE without using HFT in Run15 AuAu 200 GeV - Shenghui Zhang
4) D0 v3 with HFT in Run14 AuAu 200 GeV - Michael Lomnitz
5) Jpsi polarization in Run 12 pp 200 GeV - Siwei Luo
6) Centrality study for Run15 pAu 200 GeV - Yanfang Liu
minutes - Rongrong
2017/1/12
1) J/psi and Psi(2s) from Run15 p+p and p+Au dimuon - Takahito
2) Upsilon from Run15 p+p and p+Au and Run11 Au+Au dielectron - Zaochen
3) D0 and Lc from Run14 Au+Au - Guannan
4) D0-h correlation from Run14 Au+Au - Alex
5) B->e from Run14 Au+Au - Xiaozhi
6) Upsilon from Run14+16 Au+Au dimuon - Xinjie
7) Upsilon from Run11 p+p 500 - Leszek
8) Upsilon from Run11 Au+Au - Zaochen
minutes - Zhenyu
2017/1/5
1) J/psi v2 in U+U collisions - Alena Harlenderova
2) Non-prompt J/psi in Au+Au collisions - Bingchu Huang
3) J/psi event activity in Run12 pp 200 GeV - Bingchu Huang
4) Upsilon in Run15 pp and pA collisions - Zaochen Ye
minutes - Rongrong
2018
2018/12/20
1) Update on Upsilon in p+p - Leszek Kosarzewski
minutes - Zebo
STAR 2018 Winter Analysis meeting (12/11-12/14)
https://drupal.star.bnl.gov/STAR/meetings/star-winter-analysis-meeting/
HF Parallel 1: https://drupal.star.bnl.gov/STAR/meetings/star-winter-analysis-meeting/heavy-flavor
HF Parallel 2: https://drupal.star.bnl.gov/STAR/meetings/star-winter-analysis-meeting/heavy-flavor-0
2018/11/29
1) MTD response efficiency in 2016 cosmics - Rongrong Ma
2) Update on J/psi polarization - Zhen Liu
3) Update on the single electron analysis - Matthew Kelsey
4) D+- analysis in Au+Au 200 GeV - Robert Licenik
minutes - Petr
2018/11/01
1) Update on Lc analysis - Sooraj Radhakrishan
2) Run14 J/psi Raa analysis - Rongrong Ma
minutes - Rongrong
2018/10/25
1) Update on D0 spectra paper - Guannan Xie
minutes - Zebo
2018/10/18
1) Upsilon->mumu l in Run14 Au+Au @ 200 GeV - Zhe-Jia Zhang
2) Update on the D0 v1 analysis - Subhash Singha
3) Update on D0 v3 analysis in 2016 + 2014 Au+Au@200GeV -Yue Liang
minutes - Petr
2018/10/11
1) Ds production in Run16 - Chuan Fu
2) Update on D* analysis - Yuanjing Ji
3) picoDst production of Run15 pAu st_mtd data - Yanfang Liu
minutes - Rongrong
2018/10/4
1) psi(2S)->J/psi+pipi in 500 GeV p+p - Chan-Jui Feng
2) Run13 J/psi->mumu update - Te-Chuan Huang
minutes - Zebo
2018/09/27
1) Update on the MB embedding for J/psi -> mumu analysis - Rongrong Ma
minutes - Petr
2018/09/20
1) Electron PID using a likelihood classifier - Matthew Kelsey
minutes - Rongrong
2018/13/9
1) Update on run14 MTD J/psi Raa Rongrong Ma
minutes - Petr
2018/9/6
1) Update on Run14+16 Upsilon->mumu - Pengfei Wang
minutes - Zebo
2018/8/9
1) Run15 Upsilon RpA - Zaochen Ye
minutes - Rongrong
2018/8/2
1) Update on D+- in Run16 Au+Au@200 GeV - Jan Vanel
2) Status report of D* in Run16 Au+Au@200 GeV - Yuanjing Ji
minutes - Zebo
2018/7/5
1) Update on run13 MTD J/psi cross-section - Te-Chuan Huang
minutes - Zebo
2018/6/14
1) Run15 pAu Embedding Comparison - Yanfang Liu
2) Update on J/psi->mu+mu in Run13 pp510 - Te-Chuan Huang
minutes - Petr
2018/6/7
1) Update on run14 MTD J/psi Raa - Rongrong Ma
minutes - Zebo
2018/5/31
1) Update on KFParticleFinder - Maksym Zyzak
2018/05/24
1) Update on pp reference for Run14 Jpsi Raa - Rongrong Ma
minutes - Rongrong
2018/05/03
1) RUN15 pp/pAu NPE -Kunsu
2)Update on Open HF semileptonic decays - Yifei
3)HFT effects on Upsilon reconstruction - Oliver
4)Update on D+ in AuAu run16 - Jan
5)MTD matching study - Rongrong
minutes-Petr
2018/05/01
1) D0 in dAu - Lukas
2) Lc analysis - Sooraj
3) D0 v2 in Run16 - Liang
4) D+/- in Run16 - Jan
5) Upsilon in Run14 BEMC - Oliver
6) D0 v1 - Subhash
7) D* in Run14 - Yuanjing
8) Upsilon from MTD - Pengfei
9) Lc+/Lc- - Miro
10) Update for D0 paper - Guannan
minutes - Petr
2018/04/26
1) Run16 D0 measurements - Xiaolong Chen
minutes - Rongrong
2018/04/19
1) D0 v2, v3 in Run16 Au+Au - Yue Liang
2) Run11 HT18 run-by-run QA - Shuai Yang
3) Upsilon from MTD in Run 16 Au+Au - Pengfei Wang, Shuai Yang
minutes - Zebo
2018/04/12
1) D+/- production in run16 AuAu - Jan Vanek
2) D* production in run14 AuAu - Yuanjing Ji
3) Update - bottom analysis - Yifei Zhang
minutes - Rongrong
4) Signal extraction of Upsilon in run14 AuAu BHT2 - Oliver Matonoha
5) Update on the D0 v1 analysis - Subhash Singha
6) Status of my D0 in dAu - Lukas Kramarik
minutes - Petr
2018/04/05
1) Systematics for J/psi in Run11 pp 500 GeV - Qian Yang
2) NPE in Run15 pp/pAu - Kunsu OH
3) Upsilon in Run16 AuAu 200 GeV (MTD) - Pengfei Wang
minutes - Rongrong
2018/03/29
1) Summary of HFT embedding tuning and validation - Sooraj Radhakrishnan
2) Run16 Upsilon reconstruction efficiency - Pengfei Wang
minutes - Zebo
2018/03/22
1)Upsilon->ee reconstruction efficiency and systematics in BHT2 AuAu14 - Oliver Matonoha
minutes -Petr
2018/03/15
1) Run16 fastsim and D0 - Xiaolong Chen
2) J/psi polarization measurement in Run12 - Siwei Luo
minutes -Petr
2018/03/01
1) MTD muon PID efficiency for Run15 pp & pAu - Rongrong Ma
2) Trigger bias factor for Run13 MTD Jpsi analysis - Te-Chuan Huang
minutes - Rongrong
2018/02/22
1) D0 v1 in 200 GeV Au+Au - Liang He
minutes - Zebo
2018/02/15
1) Upsilon->ee reconstruction efficiency study in AuAu14 BHT2 - Oliver Matonoha
2) QA of dAu data - Lukas Kramarik
minutes - Petr
2018/02/08
1) Paper proposal: Jpsi cross section in p+p 500 GeV - Te-Chuan
minutes - Rongrong
2018/02/01
1) Trigger bias of J/psi in Run15 p+p and p+Au - Takahito Todoroki
2) Update on Run14 MTD J/psi study - Rongrong Ma
minutes - Zebo
2018/01/24 - 28
STAR Collaboration Meeting
2018/01/18
1) Vz diff cut study in dAu 200 GeV for picoDst production - Liang He
2018/01/11
1) Centrality determination for Run14 prod_high - Xiaolong Chen
minutes - Rongrong
2018/1/4
1) Bad run determination for Run14 AuAu 200 GeV MTD data - Rongrong Ma
2) D0 v1 with Au+Au Run14 and Run16 data - Liang He
minutes - Zebo
2019
2019/12/19
1）D+/- in Run16 Au+Au - Jan Vanek
2) J/psi in Jet with Run11 pp 500 - Qian Yang
3) Glauber MC for dAu centrality - Lukas
2019/12/12
1) uncertainty estimation of p+p reference for Upsilon measurements -Pengfei
2019/10/23
1) Update on the analysis on single electrons with HFT - Matthew Kelsey
2) Update on J/Psi and Psi(2S) via the dimuon channel - Feng Chan-Jui
3) Update on D0 v2 event shape analysis- Yue Liang
4) Update on J/Psi RpA analysis in centrality bins- Yanfang Liu
minutes - Sooraj
2019/10/17
1) Systematic uncertainty of J/psi in pAu - Yanfang Liu
2) Systematic uncertainty of single electron in Au+Au with HFT - Matthew Kelsey
3) Update on D0 in d+Au - Lukas Kramarik
minutes - Zebo
2019/10/10
1) D0 v2 with event-shape-engineering - Yue Liang
2) Update on c/b NPE anlaysis - Matthew Kelsey
3) Bottom in Run14 Central-5 Au-Au - Yingjie Zhou
4) Improvement on J/psi signal extraction - Rongrong Ma
5) Update on D0 in d+Au - Lukas Kramarik
minutes -Petr
2019/10/03
1) Run 16 D+/- update - Jan Vanek
2) Update on NPE v2 in 54 GeV Au+Au - Yuanjing Ji
3) HF electron analysis with Run 16 Au+Au - Matthew Kelsey
4) D0 production in d+Au - Lukas Kramarik
5) Paper proposal for Run15 Jpsi RpA analysis - Rongrong Ma
minutes - Sooraj
2019/9/26
1) NPE in Run16 with HFT - Matthew Kelsey
2) Jpsi->mumu in Run15 p+p - Rongrong Ma
2019/9/19
1) Bad run determination for Run15 pp 200 GeV MTD data - RongRong Ma
2019/8/29
1) Bug fix in Upsilon efficiency in dielectron channel - Shuai Yang
2) Update on Ds analysis- Chuan Fu
minutes - Sooraj
2019/8/8
1) Study of non-flow effect in NPE v2 in 200 GeV Au+Au - Yingjie Zhou
2) Study with FMS in Run 16 - Matthew Kelsey
3) D+- reconstruction efficiency in Run16 Au+Au@200GeV sst+nosst streams - Jan Vanek
2019/8/1
1) Update on the D+- in Au+Au@200GeV - Jan Vanek
2) MTD matching efficiency study in Run15 - RongRong Ma
3) NPE v2 in 54 GeV Au+Au - Yuanjing Ji
4) Update on Upsilon ->nu+nu in Au+Au - Pengfei Wang
minutes -Petr
2019/7/25
1) Update on Upsilon studies in p+p 500 GeV - Leszek Kosarzewski
2) MTD trigger efficiency studies in Run17 p+p 500GeV - Feng Chan-Jui
3) Estimate of equivalent MB events for dimuon triggers in 2015 p+Au data - Rongrong Ma
minutes - Sooraj
2019/7/18
1) TPC tracking efficiency for the Jpsi analysis using Run15 p+Au data - Rongrong Ma
minutes - Zebo
2019/6/20
1) D0 v2 + event-shape-engineering - Yue Liang
2) Bottom electron RAA and v2 systematic uncertainties - Matthew Kelsey
minutes - Petr
2019/6/13
1) NPE v2 at 54 and 27 GeV - Yuanjing Ji
minutes - Zebo
2019/5/30
1) HF electron v1 in Au+Au 2014 - Matthew Kelsey
2) Update on Upsilon signal fitting - Leszek Kosarzewski
3) Update on J/Psi analysis in Run 15 p+Au- Yanfang Liu
4) Efficiency studies on J/Psi analysis in Run 15 p+Au - Rongrong Ma
2019/5/16
1) Upsilon ->e+e in Au+Au date - Shuai Yang
2) Charm v2 in Au+Au run16 with KFP - Pavol Federic
3) Upsilon ->nu+nu in Au+Au- Pengfei Wang
4) Bad run determination for Run15 pAu - Rongrong Ma
minutes-Petr
2019/5/9
1) Report on the Lambda_c paper - Sooraj Radhakrishnan
2) Update on single electron analysis with HFT - Matthew Kelsey
minutes - Zebo
2019/4/25
1) HFT Embedding pT Resolution Studies - Jan Vanek
minutes - Sooraj
2019/4/18
1) Update on La_c analysis - Sooraj Radhakrishnan
2) Upsilon paper proposal - Pengfei Wang
minutes-Petr
2019/4/11
1) updates for the Uplsion->ee (run11 AuAu@200 GeV) analysis - Shuai Yang
2) update on the Run16 embedding QA - Jan Vanek
3) update on Upsilon analysis via di-muon channel in run14+run16 Au+Au@200GeV - Pengfei Wang
4) the effects of MC-RC embedding issue on the Upsilon analysis - Zaochen Ye
minutes - Zebo
2019/3/30
STAR Collaboration meeting
2019/3/21
1) PID efficiency for D+- in Run16 Au+Au@200GeV - Jan Vanek
2) Effect of RC-MC issue for very low pT Jpsi analysis - Wangmei Zha
3) Number of equivalent MB events estimation for run11 HT2 triggered data - Shuai Yang
4) Update on PID efficiencies studies for D0 in d+Au - Lucas Kramarik
minutes - Zebo
2019/3/14
1) Run11 Upsilon update - Shuai Yang
2) Update on HF electron analysis Mathew Kelsey
2019/2/28
1) Ds analysis update - Chuan Fu
2) Upsilon signal fitting in p+p 500 - Leszek Kosarzewski
minutes -Petr
2019/2/21
1) QA of Run16 200GeV Au+Au pi+ embedding - Jan Vanek
2) Update on psi(2S) in run17 p+p@500GeV - Chan-Jui Feng
minutes - Zebo
2019/2/14
1) Upsilon analysis using Run11 HT2 data: Shuai Yang
minutes - Sooraj
2019/1/31
1) QA of run16 Au+Au@200GeV SL18f- Jan Vanek
2) K and pi PID efficiency for D0 in d+Au - Lukas Kramarik
3) Update on electron purity for Run14 single e analysis - Matthew Kelsey
minutes -Petr
2020
2020/04/02
1) D+/- in Run14 and Run16 : Jan Vanek
2) Vertex using MTD hits in Run17: Chan-Jui Feng
Minute
Minutes HF meeting 2010/08/10
2010/10/03 Meeting Minutes
- Chris: Low pT J/psi update
E/p show difference in width and shift MC/data. Should be investigated in different p bins to see p dependence
- All: HF QM2011 Topics
List will be ranked with priority based on possible impact/feasibility.
List will be revisited to push new paper low pt J/Psi further and also make sure that HF topics are covered.
New EH needed to make HF QM2011 embedding done
Minutes for HF PWG meeting on 04/03/2014
0) General
* Zhenyu has replaced Wei as a HF PWGC.
* Reminder of QM2014 deadlines
1) low pT NPE in pp 2009 - Olga
Olga updated the analysis to try to understand the enhancement at low pT w.r.t. Phenix and FONLL calculations.
She had previouly used a |eta|<1 cut and used a TOF matching efficiency as a function of pT integrated over
eta and phi from Babara. This time she derives the TOF matching eff by herself for different pT bins and phi
regions as a function of eta. She is using a |eta|<0.7 cut. Another change was to extract and use Gamma 2009
and Dalitz 2008 embedding samples to extract the photonic electron efficiencies. The third update was a
recaculation of the purity. With all these changes, the enhancement at low pT is now gone. A comment was made
on slide 4 where the eta-dependent tof matching efficiency shows rapid falling offs for -123<phi<-63. Suggested
to cut away these fall-off eta regions for -123<phi<-63
Action items:
1. Dalitz embedding 2009 samples for publication. Requests were in place but were not approved. The convenors
will follow this up. For conferences, using Dalitz 2008 samples are fine, as the photonic electron efficiencies
for gamma samples are similar between 2008 and 2009. For publication, Dalitz embedding 2009 samples are needed.
2. Olga will send around the purity extraction QA plots
3. Olga will put a cut to remove eta<0.3 and -123<phi<-63
2) high pT NPE in pp 2012 - Xiaozhi
Xiaozhi presented electron/gamma embedding QA plots. For data, he used photonic electrons with a requirement on
pair DCA and inv mass to select pure electrons, while for embedding he used the MC particle info to select pure
electrons. He found that nhitfit and global DCA distributions are different between data and embedding. Such a
difference should not have a large influence on the results, as the cuts he applied are far away from the majority
of the electron candidate distributions.
Action items:
1. Xiaozhi updates the study with the same selection cuts applied to both data and embedding to ensure there is
no bias introduced.
Heavy Quark Physics in Nucleus-Nucleus Collisions Workshop at UCLA
We will organize a workshop on heavy quark physics in nucleus-nucleus collisions from January 22-24, 2009. The workshop will be hosted by the Department of Physics and Astronomy, University of California at Los Angeles.
NPE Analyses
NPE Weekly Meeting
*******************************************************************************************************************
Meeting URL
https://bluejeans.com/500155369?src=join_info
Meeting ID
500 155 369
Want to dial in from a phone?
Dial one of the following numbers:
+1.408.740.7256 (US (San Jose))
+1.408.317.9253 (US (Primary, San Jose))
(see all numbers - https://www.bluejeans.com/premium-numbers)
Enter the meeting ID and passcode followed by #
Connecting from a room system?
Dial: bjn.vc or 199.48.152.152 and enter your meeting ID & passcode
*******************************************************************************************************************
2020/11/04
pp eh correlation updates summary since 0917 STAR Collaboration Meeting by Yingjie
2020/10/14
pp eh correlation_hadron track efficiency correction by Yingjie
2020/09/09
pp run12 eh correlation_systematic uncertainty continue by Yingjie
2020/07/22
pp run12 eh correlation_systematic uncertainty continue by Yingjie
2020/07/08
pp run12 eh correlation_systematic uncertainty by Yingjie
2020/6/30
Hpt_HPE_ppAuAu_Shenghui_06302020 by Shenghui
pp run12 eh correlation_systematic uncertainty by Yingjie
2020/06/23
Hpt_HPE_ppAuAu_Shenghui_06232020 by Shenghui
2020/06/16
Hpt_HPE_ppAuAu_Shenghui_06162020 by Shenghui
2020/03/12
pp run12 eh correlation collaboration meeting by Yingjie
2019/09/18
NPE_analysis_status_for_NPE_meeting_09182019 by Shenghui
2018/09/19
Electron PID with Likelihood method by Matthew
2018/09/13
Run14 HFT NPE by kunsu
2018/09/12
Electron PID with MVA by Matthew
2018/08/30
Run15 NPE by Peipei
2018/08/23
Run14 HFT NPE by kunsu
2018/08/16
Run14 PicoDst BEMC Check by Matthew
2018/07/26
Run14 HFT NPE by Kunsu
2018/07/05
Run14 HFT NPE by Kunsu
2018/06/21
Run14 HFT NPE by Kunsu
minutes
2018/06/07
Run14 HFT NPE by Kunsu
2018/04/19
Run15 pp/pA 200 NPE analysis by Kunsu
minutes by Kunsu
2018/03/22
Run15 pp 200 NPE analysis by Kunsu
2018/03/08
NPE updates by Kunsu
minutes by Kunsu
2018/01/23
NPE updates (DCAz in Run14 AuAu200, purity in Run15 pp200) and some updates about DCAz by Kunsu
minutes by Kunsu
2018/01/09
NPE updates (2nd peak on DCAz distribution) and plan by Kunsu
minutes by Kunsu
2018/01/02
NPE production in Run15 pp and pA by Peipei
2017/11/28
NPE production in Run15 pp and pA by Peipei
2017/11/14
work status summary by xiaozhi
Status Report: NPE Run14 AuAu@200GeV by Jongsik
2017/11/07
c+b->e with subtraction method by Yifei
2017/10/24
1)
NPE analysis update by xiaozhi
Update the slides by xiaozhi
minutes - Yaping
2017/10/19
1) NPE analysis update by xiaozhi
2) Status of NPE in Au+Au 200 GeV without HFT by Jongsik
2017/10/10
1) NPE analysis update by xiaozhi
2017/9/28
1) NPE analysis update by xiaozhi
2) Current status by Jongsik
2017/9/12
1) NPE analysis update by Xiaozhi
2) NPE analysis update by Shenghui
minutes - Yaping
2017/9/5
1) NPE analysis proposal by Kunsu, Jongsik and In-Kwon
2017/8/29
1) NPE updates by Shenghui
2) NPE updates by Xiaozhi
3) NPE updates by Kunsu
minutes - Yaping
2017/1/24
1) NPE updates by Kunsu
2017/01/20
minutes - Zhenyu
2017/01/17
1) NPE updates by Kunsu
minutes - Zhenyu
2017/01/13
1) NPE updates by kunsu
2017/01/10
1) NPE updates by Kunsu
2) Npe undate By xiaozhi
minutes - Zhenyu
2016/12/13
1) NPE update by Xiaozhi
2016/12/13
1) NPE updates by Kunsu
minutes - Zach
2016/12/06
1) NPE updates by Kunsu
2) DCAXY Updates by Xiaozhi
minutes - Zach
2016/11/22
1) PhE and inclusive e DCAxy in HIJING by Kunsu
2) PHE and inclusive DcaXy in Hijing by xiaozhi
minutes - Zhenyu
2016/11/01
1) HIJING QA by Kunsu
minutes - Zhenyu
2016/10/25
1) NPE updates by Kunsu
minutes - Zhenyu
2016/10/04
1) NPE w/o HFT by Shenghui
2016/09/20
1) NPE updates by Kunsu
2) update by Xiazohi
minutes - Zhenyu
2016/09/13
1) NPE updates by Kunsu
2016/08/30
1) QM2017 NPE Abstract Topics by Zach
2) NPE updates and QM2017 abstract by Kunsu
3) QM2017 abstract draft by Shenghui
minutes -Zhenyu
2016/03/18
1) single muon simulation by Jie
2) SL15c vs SL15k comparison by Xiaozhi
3) PXL simulator update by Kunsu
minutes - Zhenyu
2016/03/11
1) new simulator update (clustering and PXLBug) by Kunsu
2016/03/04
1) new simulator update (clustering) by Kunsu
2016/02/26
1) new simulator (clustering) by kunsu
2016/02/19
1) updates by Xiaozhi
2016/02/12
1) update by Kunsu
2) single muon by Jie
minutes - Zhenyu
2016/02/05
1) update by Kunsu
minutes - Zhenyu
2016/1/15
1) Data and simulation update - Kunsu
2) Data and simulation update -Xiaozhi
Minutes - Zhenyu
2015/12/18
1) search for Beam Pipe - Kunsu
2) photonic electrons in data and simulation - Xiaozhi
2015/12/11
1) Photonic electrons in Run14 data - Shenghui
2) Photonic electrons in Run14 data - Xiaozhi
Minutes - Zhenyu
2015/12/4
1) eK pair - Jie
Minutes - Zhenyu
2015/11/20
1) Phtonic Electrons Run14 data - Shenghui
2) Simulation -Xiaozhi
3) eK pair - Jie
Minutes - Zhenyu
2015/11/13
1) eK pair - Jie
2) First look into Run14 Data - Shenghui
3) Simulation -Xiaozhi
Minutes - Zhenyu
2015/11/06
1) Data - Kunsu
2) Simulation - Xiaozhi
3) eK pair - Jie
Minutes - Zhenyu
2015/10/23
1) Data and Simulation DCA comparison - Kunsu
2) Simulation updates - Xiaozhi
3) Updates - Jie
Minutes - Zhenyu
2015/10/16
1) Status - Zhenyu
2) Plan - Jie
2015/09/04
1) Data - Kunsu
2) Simulation - Zhenyu
Minutes - Zhenyu
2015/08/28
1) Data - Kunsu
Minutes - Xin
2015/08/14
1) Data - Kunsu
Minutes - Zhenyu
2015/08/07
1) Simulation - Xiaozhi
2) Data - Kunsu
Minutes - Zhenyu
2015/07/31
1) Simulation - Xiaozhi
2) Data - Kunsu
Minutes - Zhenyu
2015/07/24
1) Simulation - Xiaozhi
Minutes - Zhenyu
2015/07/17
1) Data - Kunsu
2) Simulation - Xiaozhi
Minutes - Xin
2015/07/10
1) Simulation - Xiaozhi
Minutes - Zhenyu
2015/06/26
1) Data - Kunsu
2015/05/29
0) QM Abstract
1) Simulation - Xiaozhi
Minutes - Zhenyu
2015/05/22
0 Code Review - Mustafa
1) Run14 Data - Kunsu
2) Simulation - Xiaozhi
Minutes - Zhenyu
2015/06/26
1) Data - Kunsu
2015/05/15
1) Simulation - Xiaozhi
Minutes - Zhenyu
2015/05/08
1) Run14 Data - Kunsu
2) Simulation - Xiaozhi
Minutes - Zhenyu
2015/05/01
1) Run14 Data - Kunsu
2) Presenation at LBNL RNC Group on April 27 - Kunsu
Minutes - Zhenyu
2015/04/17
1) Run14 Data - Kunsu
2) Simulation - Xiaozhi
Minutes - Zhenyu
2015/04/10
1) Run14 Data - Kunsu
Minutes - Zhenyu
PWG members and analysis
Current active PWG members
| Institute | Name | Position | Analysis Topics | Comment |
| BNL | Thomas Ullrich | Staff | Non-photonic electrons, quarkonia production | |
| Zhangbu Xu | Staff | Non-photonic electrons, J/psi production | ||
| Lijuan Ruan | Postdoc | High pT J/psi | ||
| UCLA | Huan Z. Huang | Staff | Non-photonic electrons, open charm hadron via hadronic decays | |
| Gang Wang | Postdoc | Non-photonic electron spectrum and v2, NPE-hadron correlations | ||
| Wenqin Xu | Student | Non-photonic electrons in d+Au, open charm hadron recon., HF PWG embedding helper | ||
| SINAP | Wei Li | Student | Non-photonic electrons in p+p 500 GeV | |
| Purdue Univ. | Wei Xie | Staff | Non-photonic electrons | |
| Xin Li | Student | Non-photonic electrons in d+Au / p+p Run 8, and p+p Run9 | ||
| Mustafa Mustafa | Student | D0 in p+p Run9 | ||
| UC Davis | Manuel Calderon | Staff | Upsilon production | |
| Haidong Liu | Postdoc | Upsilon in d+Au Run 8 | Left STAR in 2010 | |
| Debasish Dash | Postdoc | Upsilon in Au+Au Run 7 | Left STAR in 2010 | |
| Rosi Reed | Student | Upsilon in p+p Run 6, Au+Au Run 7 | ||
| LBNL | Grazyna Odyniec | Staff | J/psi production | |
| Xin Dong | Postdoc | Non-photonic electrons, open charm hadron recon. | ||
| Yifei Zhang | Postdoc | Non-photonic electrons, open charm hadron recon. | ||
| Daniel Kikola | Student | Low pT J/psi in Cu+Cu and Au+Au collisions | ||
| Chris Powell | Student | Low pT J/psi in d+Au collisions | ||
| Warsaw Tech. Univ. | Barbara Trzeciak | Student | J/psi polarization in p+p collisions | |
| Univ. of Sao Paulo | Alex Suaide | Staff | Non-photonic electrons, J/psi production | |
| Mauro Cosentino | Student | Low pT J/psi in p+p Run 6 | Graduated in 2008 (Theses) | |
| Lucas Lima | Student | Low pT J/psi L2 trigger | ||
| Texas A&M Univ. | Saskia Mioduszewski | Staff | Quarkonia production | |
| Rory Clarke | Postdoc | Upsilon production, BPRS calibration | Left in 2009 | |
| Pibero Djawotho | Postdoc | Upsilon in p+p Run 6 | In Spin PWG since 2009 | |
| Matt Cervantes | Student | Upsilon - h correlation, BPRS calibration | ||
| CTU, Prague | Jaro Bielcik | Staff | Non-photonic electrons, open charm hadron recon. | |
| Mira Krus | Student | Non-photonic electron - hadron correlation in A + A collisions | left STAR in 2010 | |
| Olga Hajkova | Student | Low pT J/psi in d+Au Run 8 | ||
| NPI, Prague | David Tlusty | Student | Non-photonic electrons in d+Au, open charm hadron recon. | |
| Yale | Stephen Baumgart | Student | D0 in Cu+Cu, open charm hadron recon. | Graduated in 2009 (Theses) |
| Anders Knospe | Student | Non-photonic electrons in Cu+Cu collisions | ||
| Wayne State Univ. | Sarah LaPointe | Student | D0 in Au+Au Run 7 with SVT/SSD | |
| Kent State Univ. | Spiros Margetis | Staff | Open charm hadron recon. | |
| Jonathan Bouchet | Postdoc | Open charm hadron recon. with SVT/SSD, microVertexing | ||
| Jaiby Joseph | Postdoc | Open charm hadron recon. with SVT/SSD, microVertexing | ||
| Naresh Subba | Student | Non-photonic electrons at forward region | ||
| SUBATECH | Sonia Kabana | Staff | Open charm hadron recon. in A+A with SVT/SSD | |
| Raghunath Sahoo | Postdoc | Non-photonic electron tagged D0 in Cu+Cu with SVT/SSD | ||
| Artemios Geromitsos | Student | Non-photonic electron tagged D0 and open charm hadron recon. with SVT/SSD | ||
| Witold Borowski | Student | Non-photonic electron tagged D0 and open charm hadron recon. with SVT/SSD | ||
| UC Berkeley | Chris Perkins | Student | J/psi in the forward region from FMS | |
| USTC, China | Zebo Tang | Student | High pT J/psi production | Graduated in 2009 (Theses) |
| SINAP, China | Fu Jin | Student | Non-photonic electrons in p+p 2008 | Graduated in 2010 |
Grouped by Analysis Topics
| Analysis Topics | PAs | Status | Comment |
| D0 reconstruction in dAu Run 3 | Haibin Zhang | Published | |
| D*, D+ reconstruction in dAu Run 3 | An Tai | Paper proposal to PWG (on hold as PA left) | PA left STAR |
| D0 reconstruction in AuAu 200 GeV Run 4 | Haibin Zhang | Paper hold from re-submission | |
| D0 reconstruction in CuCu 200 GeV Run 5 |
Stephen Baumgart Alexandre Shabetai |
Paper proposal to PWG (with NPE) | |
| D0 reconstruction in AuAu 200 GeV w/ SVT/SSD Run 7 | Sarah LaPointe | Preliminary result presented at QM09 | |
| D-meson reconstruction with micro-Vertexing |
Jonathan Bouchet Jaiby Joseph |
Preliminary | |
| Ds reconstruction in dAu (Run3), CuCu (Run5), AuAu (Run7) | Stephen Baumgart | Preliminary result presented at WWND2010 | |
| D0 reconstruction in dAu Run8 |
Wenqin Xu David Tlusty |
Preliminary (no strong signal) | Not consistent with Run3 |
| D*-jet correlation in pp Run 5 | Xin Dong | Published | |
| D0 reconstruction in p+p 200 GeV Run 9 |
David Tlusty Yifei Zhang Mustafa Mustafa |
Preliminary | |
| D* reconstruction in p+p 200 GeV Run 9 | Xin Dong | Preliminary | |
| NPE in dAu and pp Run 3 with TOF | Xin Dong | Published | |
| NPE in pp, dAu (Run 3) and AuAu (Run 4) with EMC |
Alexandre Suaide Weijiang Dong Jaro Bielcik |
Published | |
| NPE in AuAu Run 4 with TOF | Yifei Zhang | Paper hold from re-submission | |
| Low pT muon in AuAu Run 4 with TOF | Chen Zhong | Paper hold from re-submission | |
| NPE in pp Run 5/6 with EMC |
Shingo Sakai Gang Wang Wei Xie |
Paper in GPC | |
| NPE in CuCu Run 5 | Anders Knospe | Preliminary result presented at SQM09 | |
| NPE with Endcap EMC | Naresh Subba | Preliminary | |
| NPE in pp Run 8 with EMC | Wei Xie | Paper in GPC | |
| NPE in dAu Run 8 with EMC |
Xin Li Wenqin Xu David Tlusty |
Preliminary | |
| NPE in pp Run 8 with TOF | Fu Jin | Preliminary result presented at SQM08 | |
| NPE ALL in p+p | Priscilla Kurnadi | Preliminary | Joint with Spin PWG |
| NPE in pp Run9 (TOF+EMC) |
Yifei Zhang Xin Li |
Preliminary | |
| NPE-h in p+p 500 GeV | Wei Li | Preliminary | |
| NPE-h correlation in pp Run5/6 |
Xiaoyan Lin Shingo Sakai |
Published | |
| NPE-D0 correlation in pp Run5/6 | Andre Mischke | Published | |
| NPE-h correlation in CuCu and AuAu |
Gang Wang Bertrand Biritz Mira Krus |
Preliminary result presented at QM09 | |
| NPE-D0 correlation in CuCu and AuAu |
Artemios Geromitsos Witold Borowski Raghunath Sahoo |
Preliminary | |
| NPE v2 in AuAu Run 4 | Frank Laue | Preliminary result presented at QM05 (proceeding withdrawed) | |
| NPE v2 in AuAu Run 7 | Gang Wang | Preliminary result presented in HP2010 | |
| NPE in p+p Run9 with TOF+BEMC |
Xin Li Yifei Zhang |
Preliminary | |
| J/psi in AuAu Run 4 | Johan Gonzalez | Preliminary result presented at QM05 | |
| J/psi in pp with toplogical trigger | Mauro Cosentino | PWGC review | |
| High pT J/psi in pp Run 5/6 and CuCu Run 5, J/psi-h correlation | Zebo Tang | Published | |
| J/psi in CuCu Run 5 and AuAu Run 7 | Daniel Kikola | PWGC review | |
| High pT J/psi in AuAu Run 7 | Zebo Tang | Preliminary | |
| J/psi in dAu Run 8 |
Chris Powell Olga Hajkova |
PWGC review | |
| High pT J/psi in dAu Run 8 | Zebo Tang | Preliminary | |
| J/psi in dAu from FMS Run 8 | Chris Perkins | Preliminary | |
| High pT J/psi in pp Run 8/9 and polarization | Barbara Trzeciak | Preliminary | |
| High pT J/psi in pp Run9 | Zebo Tang | Preliminary | |
| Low pT J/psi in pp Run9 | Leszek Kosarzewski | Preliminary | |
| J/psi in AuAu Run10 with HLT | Hao Qiu | Preliminary | |
| Upsilon in pp Run 6 |
Pibero Djawotho Rosi Reed |
Published | |
| Upsilon in AuAu Run 7 |
Debasish Das Rosi Reed |
Preliminary result presented at QM08 New preliminary result presented at HP2010 |
|
| Upsilon in dAu Run 8 | Haidong Liu | Preliminary result presented at QM09 | |
| Upsilon-h correlation | Matt Cervantes | Preliminary | |
| Upsilon, correlation/polarization in Run9 | Matt Cervantes | Preliminary |
PicoDst production requests
This page collects the picoDst (re)production requested made by the HF PWG| Priority | Dataset | Data stream | Special needs | Chain option | Production status | Comments |
| 0 | production_pAu200_2015 | st_physics st_ssdmb |
BEMC | PicoVtxMode:PicoVtxVpdOrDefault, TpcVpdVzDiffCut:6 | Done with SL18b | Needed for QM2018 |
| 2 | dAu200_production_2016 | st_physics | BEMC, FMS | PicoVtxMode:PicoVtxVpdOrDefault, TpcVpdVzDiffCut:6 | Benefit QM2018 analysis | |
| 3 | production_pAu200_2015 | st_mtd | BEMC | PicoVtxMode:PicoVtxVpdOrDefault, TpcVpdVzDiffCut:6 | ||
| 4 | AuAu200_production_2016 AuAu200_production2_2016 |
st_physics | BEMC, FMS | PicoVtxMode:PicoVtxVpdOrDefault, TpcVpdVzDiffCut:3 | ||
| 5 | AuAu_200_production_2014 AuAu_200_production_low_2014 AuAu_200_production_mid_2014 AuAu_200_production_high_2014 |
st_mtd |
BEMC | mtdMatch, y2014a, PicoVtxMode:PicoVtxVpdOrDefault, TpcVpdVzDiffCut:3 | ||
| 1 | AuAu_200_production_low_2014 AuAu_200_production_mid_2014 |
st_physics | BEMC | mtdMatch, y2014a, PicoVtxMode:PicoVtxVpdOrDefault, TpcVpdVzDiffCut:3 | ||
| 6 | production_pp200long_2015 production_pp200long2_2015 production_pp200long3_2015 production_pp200trans_2015 |
st_physics st_ssdmb |
BEMC | mtdMatch, y2015c,PicoVtxMode:PicoVtxVpdOrDefault, TpcVpdVzDiffCut:6 | ||
| production_pp200_2015 | st_mtd | mtdMatch, y2015c, PicoVtxMode:PicoVtxVpdOrDefault, TpcVpdVzDiffCut:6, PicoCovMtxMode:PicoCovMtxSkip |
Upsilon Analysis
Links related to Upsilon Analysis.
- Upsilon paper page from Pibero.
- Technical Note is located in Attachments to this page.
- TeX source (saved as .txt so drupal doesn't complain) for Technical Note is also in Attachments.
- Upsilon paper drafts are found below.
Combinatorial background subtraction for e+e- signals
It is common to use the formula 2*sqrt(N++ N--) to model the combinatorial background when studying e+e- signals, e.g. for J/psi and Upsilon analyses. We can obtain this formula in the following way.
Assume we have an event in which there are Nsig particles that decay into e+e- pairs. Since each decay generates one + and one - particle, the total number of unlike sign combinations we can make is N+- = Nsig2. To obtain the total number of pairs that are just random combinations, we subtract the number of pairs that came from a real decay. So we have
N+-comb=Nsig2-Nsig=Nsig(Nsig-1)
For the number of like-sign combinations, for example for the ++ combinations, there will be a total of (Nsig-1) pairs that can be made by the first positron, then (Nsig-2) that can be made by the second positron, and so on. So the total number of ++ combinations will be
N++ = (Nsig-1) + (Nsig - 2) + ... + (Nsig - (Nsig-1)) + (Nsig-Nsig)
Where there are Nsig terms. Factoring, we get:
N++ = Nsig2 - (1+2+...+Nsig) = Nsig2 - (Nsig(Nsig+1))/2 = (Nsig2 - Nsig)/2=Nsig(Nsig-1)/2
Similarly,
N-- = Nsig(Nsig-1)/2
If there are no acceptance effects, either the N++ or the N-- combinations can be used to model the combinatorial background by simply multiplying them by 2. The geometric average also works:
2*sqrt(N++ N--) = 2*Nsig(Nsig-1)/sqrt(4) = Nsig(Nsig-1) = N+-comb.
The geometric average can also work for cases where there are acceptance differences, with the addition of a multiplicative correction factor R to take the relative acceptance of ++ and -- pairs into account. So the geometric average is for the case R=1 (similar acceptance for ++ and --).
Estimating Acceptance Uncertainty due to unknown Upsilon Polarization
The acceptance of Upsilon decays depends on the polarization of the Upsilon. We do not have enough statistics to measure the polarization. It is also not clear even at higher energies if there is a definite pattern: there are discrepancies between CDF and D0 about the polarization of the 1S. The 2S and 3S show different polarizations trends than the 1S. So for the purposes of the paper, we will estimate the uncertainty due to the unknown Upsilon polarization using two extremes: fully transverse and fully longitudinal polarization. This is likely an overestimate, but the effect is not the dominant source of uncertainty, so for the paper it is good enough.
There are simulations of the expected acceptance for the unpolarized, longitudinal and transverse cases done by Thomas:
http://www.star.bnl.gov/protected/heavy/ullrich/ups-pol.pdf
Using the pT dependence of the acceptance for the three cases (see page 9 of the PDF) we must then apply it to our measured upsilons. We do this by obtaining the pT distribution of the unlike sign pairs (after subtracting the like-sign combinatorial background) in the Upsilon mass region and with |y|<0.5. This is shown below as the black data points.
.gif)
The data points are fit with a function of the form A pT2 exp(-pT/T), shown as the solid black line (fit result: A=18.0 +/- 8.3, T = 1.36 +/- 0.16 GeV/c). We then apply the correction for the three cases, shown in the histograms (with narrow line width). The black is the correction for the unpolarized case (default), the red is for the longitudinal and the blue is for the transverse case. The raw yield can be obtained by integrating the histogram or the function. These give 89.7 (histo) and 89.9 (fit), which given the size of the errors is a reasonable fit. We can obtain the acceptance corrected yield (we ignore all other corrections here) by integrating the histograms, which give:
- Unpol: 158.9 counts
- Trans: 156.4 counts
- Longi: 163.6 counts
We estimate from this that fully transverse Upsilons should have a yield lower by -1.6% and fully longitudinal Upsilons should have a higher yield by 2.9%. We use this as a systematic uncertainty in the acceptance correction.
In addition, the geometrical acceptance can vary in the real data due to masked towers which are not accounted for in the simulation. We estimate that this variation is of order 25 towers (which is used in the 2007 and 2008 runs as the number of towers allowed to be dynamically masked). This adds 25/4800 = 0.5% to the uncertainty in the geometrical acceptance.
Estimating Drell-Yan contribution from NLO calculation.
Ramona calculated the cross section for DY at NLO and sent the data points to us. These were first shown in the RHIC II Science Workshop, April 2005, in her Quarkonium talk and her Drell-Yan (and Open heavy flavor) talk.
The total cross section (integral of all mass points in the region |y|<5) is 19.6 nb (Need to check if there is an additional normalization with Ramona, but the cross section found by PHENIX using Pythia is 42 nb with 100% error bar, so a 19.6 nb cross section is certainly consistent with this). She also gave us the data in the region |y|<1, where the cross section is 5.24 nb. The cross section as a function of invariant mass in the region |y|<1 is shown below.
.gif)
The black curve includes a multiplication with an error function (as we did for the b-bbar case) and normalized such that the ratio between the blue and the black line is 8.5% at 10 GeV/c to account for the efficiency and acceptance found in embedding for the Upsilon 1s. The expected counts in the region 8-11 are 20 +/- 3, where the error is given by varying the parameters of the error function within its uncertainty. The actual uncertainty is likely bigger than this if we take into account the overall normalization uncertainty in the calculation.
I asked Ramona for the numbers in the region |y|<0.5, since that is what we use in STAR. The corresponding plot is below.
.gif)
The integral of the data points gives 2.5 nb. The integral of the data between 7.875 and 11.125 GeV/c2 is 42.30 pb. The data is parameterized by the function shown in blue. The integral of the function in the same region gives 42.25 pb, so it is quite close to the calculation. In the region 8<m<11 GeV/c2, the integral of the funciton is 38.6 pb. The expected counts with this calculation are 25 for both triggers.
Response to PRD referee comments on Upsilon Paper
First Round of Referee Responses
Click here for second round.
-------------------------------------------------------------------------
Report of Referee A:
-------------------------------------------------------------------------
This is really a well-written paper. It was a pleasure to read, and I
have only relatively minor comments.
We thank the reviewer for careful reading of our paper and for providing
useful feedback. We are pleased to know that the reviewer finds the
paper to be well written. We have incorporated all the comments into a
new version of the draft.
Page 3: Although there aren't published pp upsilon cross sections there
is a published R_AA and an ee mass spectrum shown in E. Atomssa's QM09
proceedings. This should be referenced.
We are aware of the PHENIX results from
E. Atomssa, Nucl.Phys.A830:331C-334C,2009
and three other relevant QM proceedings:
P. Djawotho, J.Phys.G34:S947-950,2007
D. Das, J.Phys.G35:104153,2008
H. Liu, Nucl.Phys.A830:235C-238C,2009
However, it is STAR's policy to not reference our own preliminary data on the manuscript we submit for publication on a given topic, and by extension not to reference other preliminary experimental data on the same topic either.
Page 4, end of section A: Quote trigger efficiency.
The end of Section A now reads:
"We find that 25% of the Upsilons produced at
midrapidity have both daughters in the BEMC acceptance and at least one
of them can fire the L0 trigger. The details of the HTTP
trigger efficiency and acceptance are discussed in Sec. IV"
Figure 1: You should either quote L0 threshold in terms of pt, or plot
vs. Et. Caption should say L0 HT Trigger II threshold.
We changed the figure to plot vs. E_T, which is the quantity that is
measured by the calorimeter. For the electrons in the analysis, the
difference between p_T and E_T is negligible, so the histograms in
Figure 1 are essentially unchanged. We changed the caption as suggested.
Figures 3-6 would benefit from inclusion of a scaled minimum bias spectrum
to demonstrate the rejection factor of the trigger.
We agree that it is useful to quote the rejection factor of the trigger.
We prefer to do so in the text. We added to the description of Figure
3 the following sentence: "The rejection factor achieved with Trigger
II, defined as the number of minimum bias events counted by the trigger scalers
divided by the number events where the upsilon trigger was issued, was
found to be 1.8 x 105."
Figure 9: There should be some explanation of the peak at E/p = 2.7
We investigated this peak, and we traced it to a double counting error.
The problem arose due to the fact that the figure was generated from
a pairwise Ntuple, i.e. one in which each row represented a pair of
electrons (both like-sign and unlike-sign pairs included), each with a
value of E and p, instead of a single electron Ntuple. We had plotted
the value of E/p for the electron candidate which matched all possible
high-towers in the event. The majority of events have only one candidate
pair, so there were relatively few cases where there was double
counting. We note that for pairwise quantities such as opening angle and
invariant mass, each entry in the Ntuple is still different. However,
the case that generated the peak at E/p = 2.7 in the figure was traced
to one event that had one candidate positron track, with its
corresponding high-tower, which was paired with several other electron
and positron candidates. Each of these entries has a different invariant
mass, but the same E/p for the first element of the pair. So its entry
in Figure 9, which happened to be at E/p=2.7, was repeated several times
in the histogram. The code to generate the data histogram in Figure 9
has now been corrected to guarantee that the E/p distribution is made
out of unique track-cluster positron candidates. The figure in the paper
has been updated. The new histogram shows about 5 counts in that
region. As a way to gauge the effect the double counting had on the
E/p=1 area of the figure, there were about 130 counts in the figure at
the E/p=1 peak position in the case with the double-counting error, and
there are about 120 counts in the peak after removing the
double-counting. The fix leads to an improved match between the data
histogram and the Monte Carlo simulations. We therefore leave the
efficiency calculation, which is based on the Monte Carlo Upsilon
events, unchanged. The pairwise invariant mass distribution from which
the main results of the paper are obtained is unaffected by this. We
thank the reviewer for calling our attention to this peak, which allowed
us to find and correct this error.
-------------------------------------------------------------------------
Report of Referee B:
-------------------------------------------------------------------------
The paper reports the first measurement of the upsilon (Y) cross-section
in pp collisions at 200 GeV. This is a key piece of information, both
in the context of the RHIC nucleus-nucleus research program and in its
own right. The paper is rather well organized, the figures are well
prepared and explained, and the introduction and conclusion are clearly
written. However, in my opinion the paper is not publishable in its
present form: some issues, which I enumerate below, should be addressed
by the authors before that.
The main problems I found with the paper have to do with the estimate
of the errors. There are two issues:
The first: the main result is obtained by integrating the counts above
the like-sign background between 8 and 11 GeV in figure 10, quoted to
give 75+-20 (bottom part of table III). This corresponds the sum Y +
continuum. Now to get the Y yield, one needs to subtract an estimated
contribution from the continuum. Independent of how this has been
estimated, the subtraction can only introduce an additional absolute
error. Starting from the systematic error on the counts above background,
the error on the estimated Y yield should therefore increase, whereas
in the table it goes down from 20 to 18.
Thanks for bringing this issue to our attention. It is true that when
subtracting two independently measured numbers, the statistical
uncertainty in the result of the subtraction can only be larger than the
absolute errors of the two numbers, i.e. if C = A - B, and error(A) and
error(B) are the corresponding errors, then the statistical error on C
would be sqrt(error(B)2+error(A)2) which would yield a larger absolute
error than either error(A) or error(B). However, the extraction of the
Upsilon yield in the analysis needs an estimate of the continuum
contribution, but the key difference is that it is not obtained by an
independent measurement. The two quantities, namely the Upsilon yield
and the continuum yield, are obtained ultimately from the same source:
the unlike sign dielectron distribution, after the subtraction of the
like-sign combinatorial background. This fact causes an
anti-correlation between the two yields, the larger the continuum yield,
the smaller the Upsilon yield. So one cannot treat the subtraction of
the continuum yield and the Upsilon yield as the case for independent
measurements. This is why in the paper we discuss that an advantage of
using the fit includes taking automatically into account the correlation
between the continuum and the Upsilon yield. So the error that is
quoted in Table III for all the "Upsilon counts", i.e. the Fitting
Results, the Bin-by-bin Counting, and the Single bin counting, is quoted
by applying the percent error on the Upsilon yield obtained from the
fitting method, which is the best way to take the anti-correlation
between the continuum yield and the Upsilon yield into account. We will
expand on this in section VI.C, to help clarify this point. We thank the referee for
alerting us.
The second issue is somewhat related: the error on the counts (18/54, or
33%) is propagated to the cross section (38/114) as statistical error,
and a systematic error obtained as quadratic sum of the systematic
uncertainties listed in Table IV is quoted separately. The uncertainty on
the subtraction of the continuum contribution (not present in Table IV),
has completely disappeared, in spite of being identified in the text as
"the major contribution to the systematic uncertainty" (page 14, 4 lines
from the bottom).
This is particularly puzzling, since the contribution of the continuum
is even evaluated in the paper itself (and with an error). This whole
part needs to be either fixed or, in case I have misunderstood what the
authors did, substantially clarified.
We agree that this can be clarified. The error on the counts (18/54, or
33%) includes two contributions:
1) The (purely statistical) error on the unlike-sign minus like sign
subtraction, which is 20/75 or 26%, as per Table III.
2) The additional error from the continuum contribution, which we
discuss in the previous comment, and is not just a statistical sum of
the 26% statistical error and the error on the continuum, rather it must
include the anti-correlation of the continuum yield and the Upsilon
yield. The fit procedure takes this into account, and we arrive at the
combined 33% error.
The question then arises how to quote the statistical and systematic
uncertainties. One difficulty we faced is that the subtraction of the
continuum contribution is not cleanly separated between statistical and
systematic uncertainties. On the one hand, the continuum yield of 22
counts can be varied within the 1-sigma contours to be as low as 14 and
as large as 60 counts (taking the range of the DY variation from Fig.
12). This uncertainty is dominated by the statistical errors of the
dielectron invariant mass distribution from Fig. 11. Therefore, the
dominant uncertainty in the continuum subtraction procedure is
statistical, not systematic. To put it another way, if we had much
larger statistics, the uncertainty in the fit would be much reduced
also. On the other hand, there is certainly a model-dependent component
in the subtraction of the continuum, which is traditionally a systematic
uncertainty. We chose to represent the combined 33% percent error as a
statistical uncertainty because a systematic variation in the results
would have if we were to choose, say, a different model for the continuum
contribution, is smaller compared to the variation allowed by the
statistical errors in the invariant mass distribution. In other words,
the reason we included the continuum subtraction uncertainty together in
the quote of the statistical error was that its size in the current
analysis ultimately comes from the statistical precision of our
invariant mass spectrum. We agree that this is not clear in the text,
given that we list this uncertainty among all the other systematic
uncertainties, and we have modified the text to clarify this. Perhaps a
more appropriate way to characterize the 33% error is that it includes
the "statistical and fitting error", to highlight the fact that in
addition to the purely statistical errors that can be calculated from
the N++, N-- and N+- counting statistics, this error includes the
continuum subtraction error, which is based on a fit that takes into
account the statistical error on the invariant mass spectrum, and the
important anti-correlation between the continuum yield and the Upsilon
yield. We have added an explanation of these items in the updated draft of
the paper, in Sec VI.C.
There are a few other issues which in my opinion should be dealt with
before the paper is fit for publication:
- in the abstract, it is stated that the Color Singlet Model (CSM)
calculations underestimate the Y cross-section. Given that the discrepancy
is only 2 sigma or so, such a statement is not warranted. "Seems to
disfavour", could perhaps be used, if the authors really insist in making
such a point (which, however, would be rather lame). The statement that
CSM calculations underestimate the cross-section is also made in the
conclusion. There, it is even commented, immediately after, that the
discrepancy is only a 2 sigma effect, resulting in two contradicting
statements back-to-back.
Our aim was mainly to be descriptive. To clarify our intent, the use of
"underestimate" is in the sense that if we move our datum point lower by the
1-sigma error of our measurement and this value is higher than the top
end of the CSM calculation. We quantify this by saying that the
size of the effect is about 2-sigma. We think that the concise statement
"understimate by 2sigma" objectively summarizes the observation, without
need to use more subjective statements, and we modified
the text in the abstract and conclusion accordingly.
- on page 6 it is stated that the Trigger II cuts were calculated offline
for Trigger I data. However, it is not clear if exactly the same trigger
condition was applied offline on the recorded values of the original
trigger input data or the selection was recalculated based on offline
information. This point should be clarified.
Agreed. We have added the sentence: "The exact same trigger condition was
applied offline on the recorded values of the original trigger input data."
- on page 7 it is said that PYTHIA + Y events were embedded in zero-bias
events with a realistic distribution of vertex position. Given that
zero-bias events are triggered on the bunch crossing, and do not
necessarily contain a collision (and even less a reconstructed vertex),
it is not clear what the authors mean.
We do not know if the statement that was unclear is how the realsitic
vertex distribution was obtained or if the issue pertained to where the analyzed collision comes from.
We will try to clarify both instances. The referee has correctly understood
that the zero-bias events do not necessarily contain a collision.
That is why the PYTHIA simulated event is needed. The zero-bias events
will contain additional effects such as out of time pile-up in the Time
Projection Chamber, etc. In other words, they will contain aspects of
the data-taking environment which are not captured by the PYTHIA events.
That is what is mentioned in the text:
"These zero-bias events do not always have a collision in the given
bunch crossing, but they include all the detec-
tor effects and pileup from out-of-time collisions. When
combined with simulated events, they provide the most
realistic environment to study the detector e±ciency and
acceptance."
The simulated events referred to in this text are the PYTHIA events, and
it is the simulated PYTHIA event, together with the Upsilon, that
provides the collision event to be studied for purposes of acceptance
and efficiency. In order to help clarify our meaning, we have also added
statements to point out that the dominant contribution to the TPC occupancy
is from out of time pileup.
Regarding the realistic distribution of vertices,
this is obtained from the upsilon triggered events (not from the zero-bias events, which
have no collision and typically do not have a found vertex, as the referee correctly
interpreted). We have added a statement to point this out and hopefully this will make
the meaning clear.
- on page 13 the authors state that they have parametrized the
contribution of the bbar contribution to the continuum based on a PYTHIA
simulation. PYTHIA performs a leading order + parton shower calculation,
while the di-electon invariant mass distribution, is sensitive to
next-to-leading order effects via the angular correlation of the the two
produced b quarks. Has the maginuted of this been evaluated by comparing
PYTHIA results with those of a NLO calculation?
We did not do so for this paper. This is one source of systematic
uncertainty in the continuum contribution, as discussed in the previous
remarks. For this paper, the statistics in the dielectron invariant
mass distribution are such that the variation in the shape of the b-bbar
continuum between LO and NLO would not contribute a significant
variation to the Upsilon yield. This can be seen in Fig. 12, where the
fit of the continuum allows for a removal of the b-bbar yield entirely,
as long as the Drell-Yan contribution is kept. We expect to make such
comparisons with the increased statistics available in the run 2009
data, and look forward to including NLO results in the next analysis.
- on page 13 the trigger response is emulated using a turn-on function
parametrised from the like-sign data. Has this been cross-checked with a
simulation? If yes, what was the result? If not, why?
We did not cross check the trigger response on the continuum with a
simulation, because a variation of the turn-on function parameters gave
a negligible variation on the extracted yields, so it was not deemed
necessary. We did use a simulation of the trigger response on simulated
Upsilons (see Fig. 6, dashed histogram).
Finally, I would like to draw the attention of the authors on a few less
important points:
- on page 6 the authors repeat twice, practically with the same words,
that the trigger rate is dominated by di-jet events with two back-to-back
pi0 (once at the top and once near the bottom of the right-side column).
We have changed the second occurrence to avoid repetitiveness.
- all the information of Table I is also contained in Table 4; why is
Table I needed?
We agree that all the information in Table I is contained in Table 4
(except for the last row, which shows the combined efficiency for the
1S+2S+3S), so it could be removed. We have included it for convenience
only: Table I helps in the discussion of the acceptance and
efficiencies, and gives the combined overall correction factors, whereas
the Table IV helps in the discussion of the systematic uncertainties of
each item.
- in table IV, the second column says "%", which is true for the
individual values of various contributions to the systematic uncertainty,
but not for the combined value at the bottom, which instead is given
in picobarn.
Agreed. We have added the pb units for the Combined error at the bottom of the
table.
- in the introduction (firts column, 6 lines from the bottom) the authors
write that the observation of suppression of Y would "strongly imply"
deconfinement. This is a funny expression: admitting that such an
observation would imply deconfinement (which some people may not be
prepared to do), what's the use of the adverb "strongly"? Something
either does or does not imply something else, without degrees.
We agree that the use of "imply" does not need degrees, and we also
agree that some people might not be prepared to admit that such an
observation would imply deconfinement. We do think that such an
observation would carry substantial weight, so we have rephrased that
part to "An observation of suppression of Upsilon
production in heavy-ions relative to p+p would be a strong argument
in support of Debye screening and therefore of
deconfinement"
We thank the referee for the care in reading the manuscript and for all
the suggestions.
Second Round of Referee Responses
> I think the paper is now much improved. However,
> there is still one point (# 2) on which I would like to hear an
> explanation from the authors before approving the paper, and a
> couple of points (# 6 and 7) that I suggest the authors should
> still address.
> Main issues:
> 1) (errors on subtraction of continuum contribution)
> I think the way this is now treated in the paper is adequate
> 2) (where did the subtraction error go?)
> I also agree that the best way to estimate the error is
> to perform the fit, as is now explicitly discussed in the paper.
> Still, I am surprised, that the additional error introduced by
> the subtraction of the continuum appears to be negligible
> (the error is still 20). In the first version of the paper there
> was a sentence – now removed – stating that the uncertainty
> on the subtraction of the continuum contribution was one
> of the main sources of systematic uncertainty!
> -> I would at least like to hear an explanation about
> what that sentence
> meant (four lines from the bottom of page 14)
Response:
Regarding the size of the error:
The referee is correct in observing that the error before
and after subtraction is 20, but it is important to note
that the percentage error is different. Using the numbers
from the single bin counting, we get
75.3 +/- 19.7 for the N+- - 2*sqrt(N++ * N--),
i.e. the like-sign subtracted unlike-sign signal. The purely
statistical uncertainty is 19.7/75.3 = 26%. When we perform
the fit, we obtain the component of this signal that is due
to Upsilons and the component that is due to the Drell-Yan and
b-bbar continuum, but as we discussed in our previous response,
the yields have an anti-correlation, and therefore there is no
reason why the error in the Upsilon yield should be larger in
magnitude than the error of the like-sign subtracted unlike-sign
signal. However, one must note that the _percent_ error does,
in fact, increase. The fit result for the upsilon yield alone
is 59.2 +\- 19.8, so the error is indeed the same as for the
like-sign subtracted unlike-sign signal, but the percent error
is now larger: 33%. In other words, the continuum subtraction
increases the percent error in the measurement, as it should.
Note that if we one had done the (incorrect) procedure of adding
errors in quadrature, using an error of 14.3 counts for the
continuum yield and an error of 19.7 counts for the
background-subtracted unlike-sign signal, the error on the
Upsilon yield would be 24 counts. This is a relative error of 40%, which
is larger than the 33% we quote. This illustrates the effect
of the anti-correlation.
Regarding the removal of the sentence about the continuum
subtraction contribution to the systematic uncertainty:
During this discussion of the continuum subtraction and
the estimation of the errors, we decided to remove the
sentence because, as we now state in the paper, the continuum
subtraction uncertainty done via the fit is currently
dominated by the statistical error bars of the data in Fig. 11,
and is therefore not a systematic uncertainty. A systematic
uncertainty in the continuum subtraction would be estimated,
for example, by studying the effect on the Upsilon yield that
a change from the Leading-Order PYTHIA b-bbar spectrum we use
to a NLO b-bbar spectrum, or to a different Drell-Yan parameterization.
As discussed in the response to point 6), a complete
removal of the b-bbar spectrum, a situation allowed by the fit provided
the Drell-Yan yield is increased, produces a negligible
change in the Upsilon yield. Hence, systematic variations
in the continuum do not currently produce observable changes
in the Upsilon yield. Varying the continuum yield
of a given model within the statistical error bars does, and
this uncertainty is therefore statisitcal. Therefore, we removed the
sentence stating that the continuum subtraction is one
of the dominant sources of systematic uncertainty because
in the reexamination of that uncertainty triggered by the
referee's comments, we concluded that it is more appropriate
to consider it as statistical, not systematic, in nature.
We have thus replaced that sentence, and in its stead
describe the uncertainty in the cross
section as "stat. + fit", to draw attention to the fact that
this uncertainty includes the continuum subtraction uncertainty
obtained from the fit to the data. The statements in the paper
in this respect read (page 14, left column):
It should be noted that
with the statistics of the present analysis, we find that the
allowed range of variation of the continuum yield in the fit is
still dominated by the statistical error bars of the invariant mass
distribution, and so the size of the 33% uncertainty is mainly
statistical in nature. However, we prefer to denote
the uncertainty as “stat. + fit” to clarify that it includes the estimate of the anticorrelation
between the Upsilon and continuum yields obtained
by the fitting method. A systematic uncertainty due to
the continuum subtraction can be estimated by varying
the model used to produce the continuum contribution
from b-¯b. These variations produce a negligible change in
the extracted yield with the current statistics.
We have added our response to point 6) (b-bbar correlation systematics)
to this part of the paper, as it pertains to this point.
> Other issues:
> 3) (two sigma effect)
> OK
> 4) (Trigger II cuts)
> OK
> 5) (embedding)
> OK
> 6) (b-bbar correlation)
> I suggest adding in the paper a comment along the lines of what
> you say in your reply
> 7) (trigger response simulation)
> I suggest saying so explicitly in the paper
Both responses have been added to the text of the paper.
See page 13, end of col. 1, (point 7) and page 14, second column (point 6).
> Less important points:
> 8) (repetition)
> OK
> 9) (Table I vs Table IV)
> OK…
> 10) (% in last line of Table IV)
> OK
> 11) (“strongly imply”)
> OK
We thank the referee for the care in reading the manuscript, and look forward to
converging on these last items.
Upsilon Analysis in Au+Au 2007
Paper Title: Observation of Upsilon mesons in Au+Au collisions at sqrt(sNN) = 200 GeV
Target Journal: PRC
PAs: Rosi Reed, Debasish Das, Haidong Liu, Pibero Djawotho, Thomas Ullrich and Manuel Calderón de la Barca Sánchez.
Links.
Rosi Reed's Upsilon-related presentations.
Abstract:
We report on a measurement of the dielectron mass spectrum from 7 to 15 GeV/c2 at midrapidity in Au+Au collisions at √sNN = 200 GeV. The main contributions to the spectrum in this range are the ϒ(1S+2S+3S) states as well as the Drell Yan and b-bbar continuum. We compare the ϒ yield to the measured cross-section measured in p+p, scaled by the number of binary collisions, to obtain a nuclear modification factor of RAA (1S+2S+3S) = 0.92 +/- 0.37 (stat.) +0 -0.14 (syst.). The measured yield, which is dominated by the ϒ(1S) state, is consistent with no suppression within the available statistics.
Conclusion:
We report on a measurement of the dielectron mass spectrum near the ϒ mass region with the STAR detector. Our result opens a new era of bottomonium studies in heavy-ion collisions. The yield of ϒ(1S+2S+3S) states in 0-60% central Au+Au collisions is found to be 83 +/- 17 (stat) +/- X (syst). Given a cross-section of ϒ in p+p of 114 pb, we find that the nuclear modification factor RAA for ϒ(1S+2S+3S) → e+e is 0.92 +/- 0.37 (stat.) +0 -0.14 (syst.). Our measured yield is dominated by the ϒ(1S), so our result indicates that this state shows little suppression in Au+Au collisions at RHIC energies. We see a slight indication of suppression in the 0-10% most central collisions, but more statistics are needed to make definite conclusions. Lattice QCD results on quarkonium suppression due to color screening indicate that the ϒ(1S) state survives to ~4Tc, so the observed yield places a model-dependent upper limit on the temperature reached in Au+Au collisions at RHIC.
Figures:
Figure 1a: The black histogram shows the η−φ radial distance R = √(Δη)2+(Δφ)2 where Δη and Δφ are the differences in η−φ between the candidate electron tracks in the TPC and the centroid of the triggered cluster in the BEMC.
Figure 1b: The E/p distribution for towers between 6.0 < E < 7.0 GeV, and tracks which have satisfied the conditions R < 0.04 and -2.0 < nσelectron < 3.0. An electron should leave all of its energy in the calorimeter, so we would expect this distribution to be a Gaussian centered about 1. The Energy measurment includes contributions from the underlying-event, which is high in Au+Au collisions, shifting the E/p peak to values greater than 1. The tail at high E/p results from pi0 events, as the Upsilon trigger also selects dijet events.
Figure 4: Invariant mass spectrum for unlike-sign (closed circles) and like-sign (line histogram) electron pairs. The like-sign spectra were combined as B = 2√N++N--.
Figure 5: The solid circles depict the invariant-mass spectrum after subtraction of the like-sign combinatorial background. The fit (solid line: functional form; dashed histogram: integral in each bin) includes contributions from the ϒ states, as well as Drell-Yan and b-bbar. The ϒs are represented in the fit by three Crystal-Ball functions. The dot-dashed curve illustrates the Drell-Yan and b-bbar continuum as extracted in the fit.
Invariant Mass
0-60% Centrality
From ntuple generated on 5/25/2010. Macro MacroUpsAAInvMassMakeHistosFromTree06012010.C is attached.
Figure 1: Invariant mass plots for 0-60% centrality. Generated with cuts -1.4<nSigmaElectron<3.0, 0.8<E/p<1.4, refMult>47. m_0 shfit was calculated to be 6.36+/-0.20 and wdith is 1.10+/-0.15. For 8<=m<=11 n+- = 258, n++ = 90, n-- = 74.
Figure 2: Invariant Mass versus rapdity for 0-60% centrality.
For refMult > 50 all values remained the same. For refMult>44, n+- =259 but everything else remained the same.
This indicates that the systematic uncertainty on dN/dy for the 0-60% centrality is extremely small.
0-10%
Figure 3: Invariant mass plots for 0-10% with the same cuts as Figure 1 except refMult>430. m_0shift = 6.39 +/- 0.25 and width 0.99 +/- 0.15. n+- = 112, n-- = 28, n++ = 37.
Figure 4: Invariant mass versus rapidty for 0-10% centrality.
For refMult>449 m_0 shift = 6.50 +/- 0.32 width = 1.05 +/- 0.18
n+- = 104, n-- = 28, n++ = 35
For refMult>411 m_0 shift 6.41 +/- 0.28 width = 1.10 +/- 0.17
n+- = 140, n-- = 35, n++ = 44
ref>449
N++ = 34
N-- = 28
N+- = 98
ref>411
N++ = 43
N-- = 35
N+- = 133
Figure 5: Invariant mass plots for 10-60% with the same cuts as Figure 1 except 47<refMult<430. m_0shift = 6.20 +/- 0.33 and width 1.16 +/- 0.29. n+- = 146, n-- = 46, n++ = 53.
The lower cut in refMult does not change the value much, see discussion for Figures 1 and 2. If we vary the higher refMult cut, the results are:
47<ref<449
N++ = 56
N-- = 46
N+- = 157
47<ref<411
N++ = 46
N-- = 39
N+- = 125
For the 3 cases, we can calculate the signal (upsilon+DY+b-bbar) as:
0-10% S = 48 +/- 13(stat) +7/-12 (sys)
10-60% S = 47 +/-16(stat) +8/-7 (sys)
0-60% S = 95 +/- 21(stat) +1/-0 (sys)
Where the systematic errors here are only related to the uncertainty in the centrality definition. The uncertainty in the efficiency due to the centrality selection will be calculated using embedding. I looked at the differences in the yield from data because the refMult distribution of upislon candidates is drastically different than the triggered or minbias distribution. It is heavily weighted towards the central end, which is why uncertainty on the cut for 60% central events doesn't make a large difference. We don't really have any upsilon candidate events with refMult < 47 (candidate defined as a trigger cluster with tracks extrapolated to the clusters with basis PID cuts).
In the 0-60% centrality case, we unfortunately have a downward fluctuation in the background curve right under the upsilon peak. Instead of using the background histogram, I populated a histogram using the fit to the background and filled it with the same number of counts as the original background. I then set the error bars in each bin of the new histogram to the same values as in the original background histogram.
Figure 5: Purple histogram on the left is the created histogram and the histogram on the right is the subtracted histogram using the purple histogram instead of the red background histogram. The resulting counts are 101 in the signal region. The number when using the background histogram is 103.
Invariant Mass fits
In order to calculate the yield of the Upsilon (1S+2S+3S) state, we need to be able to subtract out the contribution from Drell Yan (DY) and the b-bbar continuum. This is difficult because the yields are not known precisely for this mass range in p+p, and in Au+Au the b-bbar continuum is hypothesized to experience some supression.
0-60% Centrality
First, fit leaving the amplitude for the DY, b-bbar and total upsilon yield free. The ratio of the 1S, 2S and 3S states is kept the same as in p+p.
Figure 1: 0-60% centrality fit with 3 free parameter, the yield of DY, b-bbar and upislon. The chi^2/dof for this fit is 1.28. The number of b-bbar counts is 0, and the number of DY counts is 1.15 +/- 22.3. The upsilon yield in 5<m<16 from the fit is 88.2+/-17.7 and is 100.4+/-20.2 from a bin-by-bin counting.
Given our statistics and the very similar shape of the DY and b-bbar curve, the fit in Figure 1 convinced me that it is best to fit with only 1 parameter that is the sum of the DY and b-bbar background.
Next, the question must be asked, do we see any evidence for upsilons in this region? Or can we explain the entire unlike sign subtracted yield by the combination of Drell-Yan and b-bbar background?
Figure 2: 0-60% Centrality fit with only the DY and b-bbar background. It is obvious that this fit can not explain the peak, which indicates that we do observe Upsilons in Au+Au collisions. The chi^2/dof was 2.56. The yield of b-bbar was 12.7 +/- 25.3 and the DY yield was 11.2 +/- 24.4. The total counts in the region 8<m<11 is 94, which is much larger than the yield from the fit.
Figure 3: Fit to data assuming that there is no Drell-Yan or b-bbar background. This fit will give the largest yield of upsilons and will be used for the systematic uncertainty. The chi^2/dof is 1.14. The upsilon yield in 5<m<16 is 88.9+/- 16.3 by fit and 101.6 +/- 18.7 by a bin by bin counting method.
If we assume no suppression of a particular physics process, we are assuming RAA = 1. Rearranging this equation gives us:
In our p+p paper, we quote a combined yield of (sigma DY + sigma b-bbar )||y|<0.5, 8<m<11 GeV/c^2 = 38 ± 24 pb.
For 0-60% NmbAA = 1.14e9 and Nbin = 395. Sigma_pp is 42 mb at sqrt(s)=200 GeV. This means the number of expected DY and b-bbar counts in the 8<m<11 GeV mass range is (1.14e9)x395x38e-12/42e-3 = 407 +/- 257 if Nbin scaling were true.
If we assume the efficiency for the DY and b-bbar->e+e- is the same as the upsilon within this range, we can use the calculated upsilon efficiency of 4.4%. This means we'd expect to observe 18+/- 11 DY and b-bbar counts in 8<m<11.
The cross section for Upsilon(1S+2S+3S) was reported as 114 +/- 38(stat) pb, over all ranges. Doing the same calculation, we'd expect 1222 +/- 407 counts if Nbin scaling were true. With the calculated efficiency, this number becomes: 54 +/- 18 counts.
L2 Parameters
Figure 1: Red points are the bit-shifted adc-pedestal value of the tower with the highest adc value. The blue curve is from embedding series 120-123 upsilon 1S scaled by 5000.
NmbAA calculation
NmbAA = #upsilon minbias events in the given centrality bin
upsilon minbias trigger ID 200611
Total # of ups-mb events = sum #ups-mb(i)*prescale(i) where i is done on a run by run basis
To calculate this #, I used Jamie's bytrig.pl script, which returns a cross-section per run #
This cross-section was calculated assuming a "minbias" cross-section of 3.12 b. This number is comes from Jamies assumption that 10 b is the ZDC cross-section, but 3 b is from E&M processes that don't produce any particles and won't fire the vpd-mb trigger. 7 b is the hadronic cross-section as calculated by Glauber, but the vpd will miss about 1 b in the peripheral region. Then, the vpd vertex cut will remove ~1/2 of all triggers giving a cross-section ~3.12 b. This number is very ad hoc, but is necessary to use in order to get the # of events from the macro. To get from the integrated luminosity per run number to the # of minbias events, one calculates int L(i)/min-bias cross section = #minbias triggers(i) x prescale(i). I have confirmed that this works by checking some run numbers calculated by the script versus the runlog.
Summing over all "good" runs gives a total number of upsilon minbias triggers x prescale of 1.57 x 10^9. Attached is a spread sheet of each run number, the number of L2 upsilon triggers, the integrated luminosity per run # and the # of ups-mb triggers x prescale for that run #.
This information was presented to the HF list in presentation at:
http://drupal.star.bnl.gov/STAR/system/files/HF05112010.ppt
The error on this number is essentially zero because the statistical error of a number of order 10^9 is of order 1/10000, see: http://www.star.bnl.gov/HyperNews-star/protected/get/heavy/2753.html for discussion.
Next, we need the number of these events that are in the 0-60% or the 0-10% centrality bin. Since the vpd is inefficient for peripheral collisions, the total number of upsilon minbias events should be higher than what we see in the detector. First, we need to know the reference multiplicity cut for these centrality bins. See:
http://drupal.star.bnl.gov/STAR/system/files/HF06012010.ppt
Centrality
This trigger could not use the standard STAR centrality definitions because the base upsilon minbias trigger had a much wider vpd cut then the +/-30 cm that the more generic minbias trigger had. Beyond 30 cm the acceptance of the TPC changes, which means that the reference Multiplicity will not be constant. The centrality definitions are calculated by integrating a glauber model calculation of the reference Multiplicity.
First, I used Hiroshi Masui's code "run_glauber_mc.C" which runs the actual glauber simulation to generate Ncoll and Npart for 100k throws. The default values are for AuAu 200 GeV. The created root file along with the refMult from the upsilon minbias data set are then analyzed with NbdFitMaker. This code attempts to take Npart and Ncol and turn those into a reference multiplicity by using the two component model to describe the reference multiplicity. See Hiroshi's talk at:
dN/deta = npp[(1-x)Npart/2 + xNcoll] and is convoluted with a negative binomial distribution with 2 free parameters. The calculated RefMult is then matched to the data refMult at high refMults where the trigger efficiency should be 100%. Minuit is not used because it doeos not converge. I found that it was difficult to get these distributions to match exactly at the high end. Stepping through the allowed range of parameters, I found that mu = 2.2, x = 0.145 and k = 2.0 gave the closest result of chi^2/dof of 2.2 (for refMult>100). This resulted in a total efficiency of 84.6% and 100% for centrality 0-60%. Changing x and k by a reasonable amount did not significantly change the centrality defintion. Changing mu did change the centrality defintion slightly.
Figure 1: RefMult distributions versus changes in mu. The default mu was set to 2.4 which is ~npp the mean multipliclity of p+p collisions. This was changed to match the upsilon trigger minbias refmult distribution.
The calculated refMult cuts are > 47+/-3 for 0-60% centrality and >430+/-19 for 0-10% centrality.
Output and input files for this calculation can be found at:
/star/u/rjreed/UpsilonAA2007Paper/GlauberRefMult/
Hiroshi's code used for this exercise can be found at:
/star/u/rjreed/glauber/Try02/
Attached to this note is the "Centcut.C" macro used to generate Figure 1 and calculate the centrality versus refMult and the systematic uncertainty in that number.
Also of interest is the refMult distributions of the L2 upsilon triggered data set and the candidates. I normalized all these distributions to the glauber calculation at the high end. This is especially true of the candidate distribution as there can be more than one candidate per vertex. For these purposes, I limited the distributions to the index 0 vertices.
Figure 2: Normalized refMult distributions for the upsilon minbias trigger in black, the glauber calculation in red, the L2 upsilon triggered sample in pink and the upsilon candidates in blue. Candidates were chosen from index 0 vertices where the two daughter particles had an R<0.04, -2<nsigmaElectron<3 and E/p<3. Macro used to generate this graph, drawRef2.C is attached to this post.
Another number that is needed from this calculation is Nbin, the number of binary collsisions. I altered Hiroshi's code so that it created a text file with Ncoll, Nbin and refMult. This allowed me to calculate the average Nbin for a particular refMult. For 0-60% centrality, Nbin = 395 +/- 6.5(sys) and for 0-10% centrality Nbin = 964 +/- 27(sys). Additional systematic uncertainties due to the cross-section, Woods-Saxon distribution and exclusion region need to be checked. Attached is a spreadsheet I made from the output text file that allowed me to calculate these numbers. The values were generated with the mu=2.2 k=2.0 x=0.145 values, but the different centrality cuts were applied.
The corrected yield for upsilons is calculated as (1/NmbAA)*(dN/dy). We can cancel out the base minbias efficiency from this number by using the exact same cuts for NmbAA and dN/dy. This means that we merely need to calculate the number of minbias triggers that pass the reference multiplicity cut. For 0-60% centrality, NmbAA = 1.14e9 +0.2e9/-0.1e9 (sys due to centrailty determination) and for 0-10% centrality NmbAA = 1.78e8 +0.25e8/-0.24e8 (sys due to centrality determination)
Upsilon Analysis in d+Au 2008
Upsilon yield and nuclear modification factor in d+Au collisions at sqrt(s)=200 GeV.
PAs: Anthony Kesich, and Manuel Calderon de la Barca Sanchez.
- Dataset QA
- Trigger ID, runs
- Trigger ID = 210601
- ZDC East signal + BEMC HT at 18 (Et>4.3 GeV) + L2 Upsilon
- Total Sampled Luminosity: 32.66 nb^-1; 1.216 Mevents
- http://www.star.bnl.gov/protected/common/common2008/trigger2008/lum_pertriggerid_dau2008.txt
- Trigger ID = 210601
- Run by Run QA
- Integrated Luminosity estimate
- Systematic Uncertainty
- Trigger ID, runs
- Acceptance (Check with Kurt Hill)
- Raw pT, y distribution of Upsilon
- Accepted pT, y distribution of Upsilons
- Acceptance
- Raw pT, eta distribution of e+,e- daughters
- Accepted pT, eta distribution of e+,e- daughters
- Comparison plots between single-electron embedding, Upsilon embedding
- L0 Trigger
- DSM-ADC Distribution (data, i.e. mainly background)
- DSM-ADC Distribution (Embedding) For accepted Upsilons, before and after L0 trigger selection
- Systematic Uncertainty (Estimate of possible calibration and resolution systematic offsets).
- "highest electron/positron Et" distribution from embedding (Accepted Upsilons, before and after L0 trigger selection)
- L2 Trigger
- E1 Cluster Et distribution (data, i.e. mainly background)
- E1 Cluster Et distribution (embedding, L0 triggered, before and after all L2 trigger cuts)
- L2 pair opening angle (cos theta) data (i.e. mainly background)
- L2 pair opening angle (cos theta) embedding. Needs map of (phi,eta)_MC to (phi,eta)_L2 from single electron embedding. Then a map from r1=(phi,eta, R_emc) to r1=(x,y,z) so that one can do cos(theta^L2) = r1.dot(r2)/(r1.mag()*r2.mag()). Plot cos theta distribution for L0 triggered events, before and after all L2 trigger cuts. (Kurt)
- L2 pair invariant mass from data (i.e. mainly background)
- L2 pair invariant mass from embedding. Needs simulation as for cos(theta), so that one can do m^2 = 2 * E1 * E2 * (1 - cos(theta)) where E1 and E2 are the L2 cluster energies. Plot the invariant mass distribution fro L0 triggered events, before and after all L2 trigger cuts. (Check with Kurt)
- PID
- dE/dx
- dE/dx vs p for the Upsilon triggered data
- nsigma_dE/dx calibration of means and sigmas (done by C. Powell for his J/Psi work)
- Cut optimization (Maximization of electron effective signal)
- Final cuts for use in data analysis
- E/p
- E/p distributions for various p bins
- Study of E calibration and resolution between data and embedding (for L0 Trigger systematic uncertainty)
- Resolution and comparison with embedding (for cut efficiency estimation)
- dE/dx
- Yield extraction
- Invariant mass distributions
- Unlike-sign and Like-sign inv. mass
- Like-sign subtracted inv. mass
- Crystal-Ball shapes from embedding/simulation. Crystal-ball parameters to be used in fit
- Fit to Like-sign subtracted inv. mass, using CB, DY, b-bbar
- Contour plot (1sigma and 2sigma) of b-bbar cross section vs. DY cross section
- Upsilon yield estimation and stat. + fit error
- Invariant mass distributions
- Cross section calculation.
- Yield, dN/dy
- Integrated luminosity (for 1/N_events, where N_events were the total events sampled by the L0 trigger)
- Efficiency (Numbers for each state, and cross-section-branching-ratio-weighted average)
- Uncertainty
- pt Distribution (invariant, i.e. 1/N_event 1/2pi, 1/pt dN/dpt dy) in |y|<0.5 vs pt) This might need one to do the CB, DY, bbbar fit in pt bins.
- Nuclear Modification Factor
- Estimation of <Npart> for the dataset, and uncertainty.
- Putting it all together: dN/dy in dAu, Npart, Luminosity (N_events), divided by the pp numbers (dsigma/dy, sigma_pp)
- Plot of R_dAu vs y, comparison with theory
- Plot of R_dAu vs Npart, together with Au+Au
- Plot of R_dAu vs pt. Try to do together with Au+Au (minbias, maybe in centrality bins, but maybe not enough stats)
Upsilon Analysis in p+p 2009
Upsilon cross-section in p+p collisions at sqrt(sNN) = 200 GeV, 2009 data.
PAs: Kurt Hill, Andrew Peterson, Gregory Wimsatt, Anthony Kesich, Rosi Reed, Manuel Calderon de la Barca Sanchez.
- Dataset QA (Andrew Peterson)
- Trigger ID, runs
- Run by Run QA
- Integrated Luminosity estimate
- Systematic Uncertainty
- Acceptance (Kurt Hill)
- Raw pT, y distribution of Upsilon
- Accepted pT, y distribution of Upsilons
- Acceptance
- Raw pT, eta distribution of e+,e- daughters
- Accepted pT, eta distribution of e+,e- daughters
- Comparison plots between single-electron embedding, Upsilon embedding
- L0 Trigger
- DSM-ADC Distribution (data, i.e. mainly background) (Drew)
- DSM-ADC Distribution (Embedding) For accepted Upsilons, before and after L0 trigger selection
- Systematic Uncertainty (Estimate of possible calibration and resolution systematic offsets).
- "highest electron/positron Et" distribution from embedding (Accepted Upsilons, before and after L0 trigger selection)
- L2 Trigger
- E1 Cluster Et distribution (data, i.e. mainly background)
- E1 Cluster Et distribution (embedding, L0 triggered, before and after all L2 trigger cuts)
- L2 pair opening angle (cos theta) data (i.e. mainly background)
- L2 pair opening angle (cos theta) embedding. Needs map of (phi,eta)_MC to (phi,eta)_L2 from single electron embedding. Then a map from r1=(phi,eta, R_emc) to r1=(x,y,z) so that one can do cos(theta^L2) = r1.dot(r2)/(r1.mag()*r2.mag()). Plot cos theta distribution for L0 triggered events, before and after all L2 trigger cuts. (Kurt)
- L2 pair invariant mass from data (i.e. mainly background)
- L2 pair invariant mass from embedding. Needs simulation as for cos(theta), so that one can do m^2 = 2 * E1 * E2 * (1 - cos(theta)) where E1 and E2 are the L2 cluster energies. Plot the invariant mass distribution fro L0 triggered events, before and after all L2 trigger cuts. (Kurt)
- PID (Greg)
- dE/dx
- dE/dx vs p for the Upsilon triggered data
- nsigma_dE/dx calibration of means and sigmas
- Cut optimization (Maximization of electron effective signal)
- Final cuts for use in data analysis
- E/p
- E/p distributions for various p bins
- Study of E calibration and resolution between data and embedding (for L0 Trigger systematic uncertainty)
- Resolution and comparison with embedding (for cut efficiency estimation) (Kurt and Greg)
- dE/dx
- Yield extraction
- Invariant mass distributions
- Unlike-sign and Like-sign inv. mass (Drew)
- Like-sign subtracted inv. mass (Drew)
- Crystal-Ball shapes from embedding/simulation. (Kurt) Crystal-ball parameters to be used in fit (Drew)
- Fit to Like-sign subtracted inv. mass, using CB, DY, b-bbar.
- Contour plot (1sigma and 2sigma) of b-bbar cross section vs. DY cross section. (Drew)
- Upsilon yield estimation and stat. + fit error. (Drew)
- (2S+3S)/1S (Drew)
- Invariant mass distributions
- pT Spectra (Drew)
- Cross section calculation.
- Yield
- Integrated luminosity
- Efficiency (Numbers for each state, and cross-section-branching-ratio-weighted average)
- Uncertainty
- h+/h- Corrections
Upsilon Analysis in p+p 2009 - L0 Trigger
Upsilon Analysis in p+p 2009 - PID
- PID (Greg)
- dE/dx
- dE/dx vs p for the Upsilon triggered data
- nsigma_dE/dx calibration of means and sigmas
- Electron Mean: -0.263
- Electron Width: - 1.016
- Pion Width: 0.943
- Hadron Width: 1.071
- Cut optimization (Maximization of electron effective signal)
- Final cuts for use in data analysis
- E/p
- E/p distributions for various p bins
- Study of E calibration and resolution between data and embedding (for L0 Trigger systematic uncertainty)
- Resolution and comparison with embedding (for cut efficiency estimation) (Kurt and Greg)
- dE/dx
Upsilon Analysis in p+p 2009 - pT Spectra
Upsilon cross-section in p+p collisions at sqrt(sNN) = 200 GeV, 2009 data - pT Spectra
Note: All data plots are currently using -2 < nσe < 3 which is not optimized for this analysis!
Note: All data plots are using every run; run-by-run QA has not yet been completed!
- pT Spectra (Drew)
- First stab at pT spectrum of Upsilons from ee daughters. This does not have efficiency corrections yet.
- DY and bbbar are "subtracted" by multiplying the bin by the ratio of Yeild(Upsilon)/Yeild(Upsilon+DY+bbbar).
- The errors are added in quadrature, which is correct only to first order for this DY and bbbar "subtraction".
- <pT> is just the mean of the bin, not the mean of the hits in the bin
- Improvements on the way
- pQCD Upsilon pT Spectra
- p+p √S = 200 GeV
- Pythia 8.1.53 with the following cuts:
- Upsilon -> ee pair
- Can only detect this decay channel
- Ee1 > 4.0 GeV, Ee2 > 2.5 GeV
- L2 trigger
- need to verify the actual trigger.. changed from 2006 to 2008/9
- L2 trigger
- |ηe1| < 0.5, |ηe2| < 0.5
- mid-rapidity
- cos(θe1e2) < 0.5
- Ensure the electrons are roughly back-to-back
- pT e1 > 200 MeV, pT e2 > 200 MeV
- Upsilon -> ee pair
- 2.5 M p+p->bbbar events for each pTHatMin
- 1 GeV <= pTHatMin <= 10 GeV in steps of 0.10 GeV
- Boosts the statistics of less likely collisions
- Stacked histograms together
- normalization factor: (cross section at X GeV) / (cross section at 1.0 GeV)
- First bin is basically divided by 0 and is cutoff
Upsilon Analysis in p+p 2009 data - Acceptance
- Acceptance (Kurt Hill) - Upsilon acceptance aproximated using a simulation that constructs Upsilons (flat in pT and y), lets them decay to e+e- pairs in the Upsilon's rest frame, and uses detector response functions generated from a single electron embedding to model detector effects. An in depth study of this method will also be included.
- Raw pT, y distribution of Upsilon
- Accepted pT, y distribution of Upsilons
- Acceptance
- Raw pT, eta distribution of e+,e- daughters
- Accepted pT, eta distribution of e+,e- daughters
- Comparison plots between single-electron embedding, Upsilon embedding
Upsilon Analysis in p+p 2009 data - Acceptance
- Acceptance (Kurt Hill)
- Raw pT, y distribution of Upsilon
- Accepted pT, y distribution of Upsilons
- Acceptance
- Raw pT, eta distribution of e+,e- daughters
- Accepted pT, eta distribution of e+,e- daughters
- Comparison plots between single-electron embedding, Upsilon embedding
Upsilon Analysis in p+p 2009 data - Dataset QA
- Dataset QA (Andrew Peterson)
- Trigger ID, runs
-
Name
Trigger id
Lum [pb-1]
P4 L [pb-1]
Nevents [M]
First Run
Last Run
Description
Stream
-
Upsilon 22.855 1.978 1.381 10114071 10180030 Upsilon, reading ETOW BTOW TOF ESMD TPX BSMD upsilon Upsilon 240640 1.293 0.105 0.049 10114071 10117052 Broken, do not use upsilon Upsilon 240641 21.563 1.873 1.331 10117085 10180030 18 (4.3 GeV) < BHT && BBCMB && Upsilon at L2 upsilon
-
- Run by Run QA
-
- X-Axis is scaled because ROOT seemed to not want to fit anything that small
- Z-Axis on first 2 and Y-Axis on second 2 are weighted by 1/(error on trigger ratio)
- Once I have completed going through the run logs to throw out bad runs on that alone I will fit with Gaussians and keep up to 3 sigma
- Runs thrown out:
- 0 Magnetic Field (how did this even get flagged for Upsilon?)
- 10172027
- Δ Integrated Luminocity: 0.024188 pb-1
- Fewer than 10,000 events in run
- 10131011, 10137047, 10142045, 10143046, 10144033, 10144097, 10169015, 10172086 , 10173054
- Δ Integrated Luminocity: 0.000276 pb-1
- Marked as "bad" in the shift log
- 10127044, 10128037, 10128051, 10128064, 10155017
- Δ Integrated Luminocity: 4e-06 pb-1
- Note: only 10127044 was presnet in the Luminocity files from Jamie
- Note: only 10127044 was presnet in the Luminocity files from Jamie
- 0 Magnetic Field (how did this even get flagged for Upsilon?)
-
- Integrated Luminosity estimate: 21.539 pb-1
- Not final number, still needs more shift log reviews and Gaussian fit rejection
- Has trigger id 240640 thrown out, 0 magnetic field, fewer than 10k events in a run, and marked "bad" from shift logs (see above)
- Using http://www.star.bnl.gov/protected/common/common2009/trigger2009/lumi200GeV/lum_perrun_Upsilon.txt to determine integrated Luminocity
- Need to see if there is a better way, Jamie said he wouldn't trust these to within more than about 10-15%
- http://www.star.bnl.gov/protected/common/common2009/trigger2009/triggers2009.html
- Systematic Uncertainty
- Trigger ID, runs
Upsilon analysis in p+p 2009 - Yield Extraction
Upsilon cross-section in p+p collisions at sqrt(sNN) = 200 GeV, 2009 data - Yield Extraction
Note: All plots are currently using -1.8 < nσe < 3 which is not optimized for this analysis!
Note: All plots are using every run using Trigger ID 240641; run-by-run QA has not yet been completed or implemented!
- Invariant mass distributions
- Unlike-sign and Like-sign inv. mass (Drew)
- Like-sign subtracted inv. mass (Drew)
- Fit is from 5 GeV/c2 to 16 GeV/c2
- Crystal-Ball shapes from embedding/simulation. (Kurt)
- 0<pt<10 & 0<|y|<0.5
Param 1S 2S 3S alpha 1.18 1.16 1.21 n 1.83 2.06 2.04 mu 9.46 10.02 10.35 sigma 0.125 0.143 0.150 0<pt<10 & 0.5<|y|<1
-
Param 1S 2S 3S alpha 1.21 1.21 1.27 n 1.85 1.96 1.89 mu 9.46 10.02 10.35 sigma 0.124 0.145 0.154 - 0<pt<2 & 0<|y|<0.5
-
Param 1S 2S 3S alpha 1.30 1.43 1.12 n 1.81 1.65 2.78 mu 9.46 10.02 10.35 sigma 0.119 0.139 0.141 - 0<pt<2 & 0.5<|y|<1
-
Param 1S 2S 3S alpha 1.72 1.53 1.25 n 1.23 1.86 2.37 mu 9.46 10.02 10.35 sigma 0.141 0.151 0.163 - 2<pt<4 & 0<|y|<0.5
-
Param 1S 2S 3S alpha 1.30 1.14 1.31 n 1.72 2.12 1.85 mu 9.46 10.02 10.35 sigma 0.126 0.134 0.155 2<pt<4 & 0.5<|y|<1
-
Param 1S 2S 3S alpha 1.59 1.25 1.65 n 1.52 2.13 1.23 mu 9.46 10.02 10.35 sigma 0.135 0.139 0.159 - 4<pt<6 & 0<|y|<0.5
-
Param 1S 2S 3S alpha 1.11 1.22 1.30 n 1.97 2.17 2.07 mu 9.46 10.02 10.35 sigma 0.117 0.152 0.155 - 4<pt<6 & 0.5<|y|<1
-
Param 1S 2S 3S alpha 1.17 1.60 1.30 n 2.20 1.46 1.66 mu 9.46 10.02 10.35 sigma 0.136 0.179 0.162 - 6<pt<8 & 0<|y|<0.5
-
Param 1S 2S 3S alpha 1.08 1.11 .984 n 2.07 2.18 2.82 mu 9.46 10.02 10.35 sigma 0.138 0.154 0.154 - 6<pt<8 & 0.5<|y|<1
-
Param 1S 2S 3S alpha 1.06 1.22 1.03 n 2.16 2.16 2.75 mu 9.46 10.02 10.35 sigma 0.133 0.166 0.165 - 0<pt<2 & 0<|y|<1
-
Param 1S 2S 3S alpha 1.39 1.46 1.18 n 1.66 1.63 2.42 mu 9.46 10.02 10.35 sigma 0.124 0.142 0.146 - 2<pt<4 & 0<|y|<1
-
Param 1S 2S 3S alpha 1.33 1.16 1.35 n 1.72 2.10 1.78 mu 9.46 10.02 10.35 sigma 0.128 0.135 0.152 - 4<pt<6 & 0<|y|<1
-
Param 1S 2S 3S alpha 1.10 1.25 1.32 n 2.06 1.90 1.93 mu 9.46 10.02 10.35 sigma 0.121 0.157 0.157 - 6<pt<8 & 0<|y|<1
-
Param 1S 2S 3S alpha 1.08 1.25 1.00 n 2.06 2.18 2.71 mu 9.46 10.02 10.35 sigma 0.138 0.156 0.156 - Crystal-ball parameters to be used in fit (Drew)
0<pt<10 & 0<|y|<1
Param 1S 2S 3S alpha 1.21 1.21 1.27 n 1.85 1.96 1.89 mu 9.46 10.02 10.35 sigma 0.124 0.145 0.154 - Unlike-sign and Like-sign inv. mass (Drew)
- Fit to Like-sign subtracted inv. mass, using CB, DY, b-bbar.
- Contour plot (1sigma and 2sigma) of b-bbar cross section vs. DY cross section. (Drew)
- This plot is flawed -- using 2006 background fit and integrated luminocity
- Upsilon yield estimation and stat. + fit error. (Drew)
- Contour plot (1sigma and 2sigma) of b-bbar cross section vs. DY cross section. (Drew)
- (2S+3S)/1S
- Method 1
- Fix the 1S, 2S, and 3S to PDG ratios
- f = (CB1 + (CB2+CB3)*B ) / N
- B = (pp2009 2S+3S) / (PDG 2S+3S)
- Method 2
- Fix the 1S, 2S, and 3S to PDG ratios
- f = (CB1 + CB2*B2 + CB3*B3) / N
- Need to think more about what B2 and B3 are
- B2 = pp2009(2S / 1S)?
- B3 = pp2009(3S / 1S)?
- Method 1
Upsilon cross-section in p+p collisions at sqrt(sNN) = 200 GeV, 2009 data - h+/h-
h+/h-: Comparison Between the Reproduction vs the Original Production
~10% of the 2009 p+p 200 GeV was reproduced (http://www.star.bnl.gov/public/comp/prod/prodsum/production2009_200Gev_Single.P11id.html). We ran over the available Upsilon stream reproduction and compared with the results from the original production. The reproduction was generally found to have a different index for each set of electron pairs, so the following cuts were used to match Upsilon candidates:
Same Run ID and Event ID
|Delta Vz| < 1.0 cm
Same Charge (daughter 1 reproduction = daughter 1 original production, daughter 2 reproduction = daughter 2 original production)
-1.29 < nSigmaElectron 3.0 (used in the analysis for the original production)
We projected the m_{old} over the range of 8 to 11 GeV to see the effect on the Upsilon candidate:
There is a smearing of mass, ~1/3 GeV, with the reproduction compared to the original production. We specifically chose the 8 < m_{old} < 11 GeV/c^2 range to see how the Upsilons would be affected for a cross section measurement.
Upsilon Paper: pp, d+Au, Au+Au
Page to collect the information for the Upsilon paper based on the analysis of
Anthony (4/24):
in data, the electrons were selected via 0<nSigE<3, R<0.02. For pt<5, we fit to 0<adc<303. For pt>5, 303<adc<1000.
In embedding, the only selections are the p range, R<0.02, and eleAcceptTrack. The embedding pt distro was reweighted to match the data.
Anthony (4/5): Added new Raa plot with comparison to strickland's supression models
Anthony (4/4): I attached some dAu cross section plots on this page. The eps versions are on nuclear. The cross sections are as follows:
all: 25.9±4.0 nb
0-2: 1.8±1.7 nb
2-4: 10.9±2.9 nb
4-6. 5.2±5.3 nb
6-8: 0.57±0.59 nb
I expect the cross sections to change once I get new efficiences from embedding, but not by a whole lot.
Drew (4/6): Got Kurt's new lineshapes, efficiencies, and double-ERF parameters today. Uploading the fits to them. I'm not sure I believe the fits...
Bin-by-Bin Counting Cross Section by pT (GeV/c):
|y|<1.0 all: 134.6 ± 10.6 pb
0-2: 27.6 ± 6.3 pb
2-4: 39.1 ± 5.8 pb
4-6: 19.9 ± 3.8 pb
6-8: 13.6 ± 5.1 pb
|y|<0.5 all: 119.2 ± 12.4 pb
0-2: 23.8 ± 6.8 pb
2-4: 35.9 ± 7.4 pb
4-6: 19.0 ± 4.5 pb
6-8: 14.2 ± 4.6 pb
The double ERF is a turn-off from the L2 trigger's mass cut. Kurt used the form: ( {erf*[(m-p1)/p2]+1}*{erf*[(p3-m)/p4]+1} )/2, but I used /4 in the actual fit because each ERF can be at most 2. By fits are also half a bin shifted from Tony's, we'll need to agree on it at some point. The |y|<1 are divided by 2 units in rapidity, and the |y|<0.5 by 1 unit.
Upsilon 200 GeV AuAu 2010
E/p Cut Efficiencies
We cut on E/p for our candidate daughter electrons and positrons for
the AuAu analysis. To find the efficiencies of these cuts, we find
the efficiency of the cuts on embedded single electrons from the
file AuAu2010_singleE_emb_4May12.root, located in /home/khill/upsAuAu/ on
the nuclear server, appropriately modified to match the data, as described
below. We used data from the file AuAu10_ups_10Jun12.root, located in
/home/kesich/AuAu2010_Upsilons/ on the nuclear server.
For the first, L0, daughter from the data we select only positively charged
particles with nSigmaElectron > 1 and with cluster energies between 5 and
6. We compared these to embedded electrons with Adc > 303 and cluster
energy between 5 and 6. They also must have been reconstructed in the tpc
and have been from an event with at least one fired calorimeter tower. We
plotted both these real particles' and embedded electrons' Ecluster/p
spectrum. We fit the data around the peak (from 0.7 to 1.5) and the
embedding in the full range to gaussians.
However, the embedded particles were modified to match the data. Firstly,
since the embedding was thrown flat in momentum, we weighed the momentum
spectrum to the data. Secondly, we smeared the Ecluster values to better
simulate the resolution of the calorimeter. Thirdly, we still found the
mean of this modified electron embedding signal to not fall on top of the
peak in the data. Realizing that contamination from other particles in
the event can add to the measured energy from the calorimeter, we felt
justified in simply shifting the mean of the electron embedding to match
this peak. To instantiate these last two modifications, we convolved the
embedding E/p spectrum with another gaussian, iteratively tweaking the mean
and width of the convolving gaussian until the embedding's and data's
gaussian fits matched.
For the second daughter from the data, we again select only positively
charged particles with nSigmaElectron > 1. We found that the second
daughters' cluster energies were not well correlated to their momentum,
indicating contamination from particles unrelated to Upsilon production.
Note that the energy requirement of the L0 trigger on the first daughter
probably ensures the much cleaner correlation of momentum and cluster
energy for the first daughters. Tower energies did, however, show close
equality to momentum values in the second daughter. Cutting on tower
energy between 5 and 6 provided inadequate statistics so we cut instead on
tower energy from 3 to 4. The embedded electrons were cut with Adc > 303,
as for the comparison with the first daughters, but now necessarily with
tower energy between 3 and 4 for comparison to the second daughters. We
fit the data around the peak (now, from 0.7 to 1.4) and the embedding in
the full range to gaussians, like for the first daughters.
A similar process for analysis of the first daughters was done with the
second daughters to match embedding to the data; the embeddding momentum
spectrum was weighed to data and a gaussian was convolved over the
embedding, as described above.
For the first daughter, we cut on Ecluster/p between 0.7 and 1.4.
One can calculate the resultant efficiency by considering our matched
embedding distribution in two ways. Firstly, we can integrate the
gaussian fit to the embedding between the cuts and divide by its integral
over all E/p. Secondly, we can integrate the histrogram between the cuts
and divide by the histograms integral over all E/p. Using the fit, the
efficiency of the first daughter's cut is calculated to be ~90%.
Using the histogram, the efficiency is calculated to be ~88%.
For the second daughter, we cut on Etower/p between 0.7 and 1.4. We can
calculate the efficiency, again, in two ways. Using the fit, the efficiency
is calculated to be ~87%. Using the histogram, the efficiency is ~84%.
Upsilon pp, dAu, AuAu Paper Documents
This page is for collecting the following documents related to the Upsilon pp (2009), dAu (2008) and AuAu (2010) paper:
- Paper Proposal (Most Recent: Version 3)
- New in v3: Now says we're going for PLB and has the E772 and MC plots included. Also has |y|<1.0 results
- Technical Note (Most Recent: Version 6)
- New in v3: AuAu consistency analysis and expanded summary table
- New in v4: Added JPsi study of linewidth and 1S numbers
- New in v6 : Final version for paper as resubmitted to PLB
- Paper Draft (Latest: Version 25)
- New in v26: Updated with changes made in PLB proof
- v25-resub: Version as re-submitted to PLB (no line numbers).
- New in v25: Updated acknowledgements.
- New in v24: Minor changes to discussion or TPC misalignment
- New in v23.1: Added systematics to Fig. 3
- New in v23: Updated with comments from Lanny and Thomas. Changes are in red.
- New in v22: Made changed based on GPC responses to our responses to the referees. Also, all Tables are now correct. Changes are in blue.
- New in v21: Changed in response to PLB referee comments. Changed results to likelihood fits. Added binding energy plot. Tabs. II and III are NOT correct.
- New in v20: ???
- New in v19: Updated with minor comments from Thomas on Nov 25.
- New in v18: Incorporated lost changes from v16. Added 3 UC Davis undergrads to the author list.
- New in v17: A few more changes from GPC comments and addition of AuAu cross sections
- New in v16: Changes from GPC comments after collaboration review
- New in v15: Collaboration review changes
- New in v14: English QA changes
- New in v13: Mostly minor edits suggested by Lanny and Thomas
- New in v12: Updated the MC section to addredd |y|<0.5. Also did some other, minor graphwork on fig 3b
- New in v11: Updated with latest comments from the GPC. Official version before the first GPC meeting
- New in v10: Updated from PWG discussion. Cleaned and enchanced plots
- New in v9: Cleaned up v8
- New in v8: Added analysis of 1S state and discussion of E772
- New in v7: Made many changes based on first round of GPC e-mails. Summaries of changes and responses can be found on the responses sub-page.
- New in v6: Cleaned up most plots. Reworded end of intro. Cleaned up triggering threshold discussion. Added labels for subfigures.
- New in v5.1: Made stylistic clarifications and fixed a few typos. Updated dAu mass spectrum legend to explain grey curve.
- New in v5: PLB formatting and some plot clean-up
- New in v4: E772 results and |y|<1.0 and |y|<0.5 both included for AuAu
Responses to Collaboration comments
- Comments from JINR
- Comments from Tsinghua
- Comments from UCLA
- Comments from Creighton
- Comments from WUT
- Comments from BNL
Thanks to all the people who submitted comments. These have helped to improve the draft. Please find the responses to the comments below.
Comments from JINR (Stanislav Vokal)
1) Page 3, line 40, „The cross section for bottomonium production is smaller than that of charmonium [8-10]...“, check it, is there any cross section for bottomonium production in these papers?
Answer: Both papers report a quarkonium result. The PHENIX papers quote a J/psi cross section of ~178 nb. Our paper from the 2006 data quotes the Upsilon cross section at 114 pb.
2) Page 3, lines 51-52, „compared to s_ccbar approx 550 - 1400 mb [13, 14]). ...“. It should be checked, in [13] s is about 0.30 mb and in [14], Tab.VII, s is about 0.551 – 0.633 mb.“.
Answer: In Ref. 13, the 0.3 mb is for dsigma/dy, not for sigma_cc. To obtain sigma_cc, one has to use a multiplicative factor of 4.7 that was obtained from simulations (Pythia), as stated in that reference. This gives a cross section of ~ 1.4 mb, which is the upper value we quote (1400 \mu b). In reference 14, in Table VIII the low value of 550 \mu b is the lower value we use in the paper. So both numbers we quote are consistent with the numbers from those two references.
3) Page 3, line 78, „...2009 (p+p)...“ and line 80 „20.0 pb-1... “, In Ref. [10] the pp data taken during 2006 were used, 7.9 pb-1, it seems that this data sample was not included in the present analysis. Am I true? If yes – please explain, why? If the data from 2006 are included in the present draft, then add such information in the text, please.
Answer: That is correct: the data from 2006 was not included in the present analysis. There were two major differences. The first difference is the amount of inner material. In 2006 (and 2007), the SVT was still in STAR. In 2008, 2009, and 2010, which are the runs we are discussing in this paper, there was no SVT. This makes the inner material different in 2006 compared to 2009, but it is kept the same in the entire paper. This is the major difference. The inner material has a huge effect on electrons because of bremsstrahlung, and this distorts the line shape of the Upsilons. The second difference is that the trigger in 2006 was different than in 2009. This difference in triggers is not insurmountable, but given the difference in the amount of inner material, it was not worth to try to join the two datasets. We have added a comment to the text about this:
4) Page 4, Fig.1, numbers on the y-axe should be checked, because in [10], Fig.10, are practically the same acounts, but the statistic is 3 times smaller;
Answer: The number that matters is the counts in the Upsilon signal. In Fig. 10 of Ref. 10, there is a lot more combinatorial background (because of the aforementioned issue with the inner material), so when looking at the total counts one sees a similar number than in the present paper. However, in the case of the 2006 data, most of the counts are from background. The actual signal counts in the highest bin of the 2006 data are ~55-30 = 25, whereas the signal counts in the present paper are ~ 50 - 5 = 45 in the highest bin. When you also notice that the 2006 plot had bins that were 0.5 GeV/c^2 wide, compared to the narrower bins of 0.2 GeV/c^2 we are using in Figure 1 (a), it should now be clear that the 2009 data has indeed more statistics.
5) Page 5, line 31, „114 ± 38+23-14 pb [10]“, value 14 should 24;
Answer: Correct. We have fixed this typo. Thank you.
6) Page 5, Fig.2, yee and yY should be identical;
Answer: We will fix the figures to use one symbol for the rapidity of the upsilons throughout the paper.
7) Page 5, Fig.2 – description, „Results obtained by PHENIX are shown as filled tri-angles.“ à diamond;
Answer: Fixed.
8) Page 6, Fig.3a, here should be hollow star for STAR 1S (dAu) as it is in Fig.3b;
Answer: Fixed.
9) Page 8, line 7, „we find RAA(1S) = 0.44 ± ...“ à should be 0.54;
Answer: Fixed.
10) Page 8, lines 9-12, „The ratio of RAA(1S) to RAA(1S+2S+3S) is consistent with an RAA(2S+3S) approximately equal to zero, as can be seen by examining the mass range 10-11 GeV/c2 in Fig. 4.“, it is not clear, check this phrase, please;
Answer: We have modified this phrase to the following: "If 2S+3S states were completely dissociated in Au+Au collisions, then R_AA(1S+2S+3S) would be approximately equal to $R_AA(1S) \times 0.69$. This is consistent with our observed R_AA values, and can also be inferred
11) Page 8, line 26, „CNM“, it means Cold Nuclear Matter suppression? – should be explained in text;
Answer: The explanation of the CNM acronym is now done in the Introduction.
12) Page 9, line 30-31, „The cross section in d+Au collisions is found to be = 22 ± 3(stat. + fit)+4- 3(syst.) nb.“, but there is no such results in the draft before;
Answer: This result is now given in the same paragraph where the corresponding pp cross section is first
stated, right after the description of Figure 1.
13) Page 9, line 34, „0.08(p+p syst.).“ à „0.07(p+p syst.).“, see p.7;
Answer: Fixed. It was 0.08
14) Page 10, Ref [22], should be added: Eur. Phys. J C73, 2427 (2013);
Answer: We added the published bibliography information to Ref [22].
15) Page 10,, Ref [33] is missing in the draft.
Answer: We have now removed it. It was left over from a previous version of the draft which included text that has since been deleted.
Comments from Tsinghua
1) Replace 'Upsilon' in the title and text with the Greek symbol.
Answer: Done.
2) use the hyphen consistently across the whole paper, for example, sometimes you use 'cold-nulcear matter', and at another place 'cold-nuclear-matter'. Another example is 'mid-rapidity', 'mid rapidity', 'midrapidity'...
Answer: On the hyphenation, if the words are used as an adjectivial phrase, then those need to be hyphenated. In the phrase "the cold-nuclear-matter effects were observed", the words "cold-nuclear-matter" are modifying
the word "effects", so they are hyphenated. However, from a previous comment we decided to use the acronym "CNM" for "cold-nuclear matter", which avoids the hyphenation. We now use "mid-rapidity" throughout the paper.
3) For all references, remove the 'arxiv' information if the paper has been published.
Answer: We saw that published papers in PLB do include the arxiv information in their list of references. For the moment, we prefer to keep it there since not all papers are freely available online, but arxiv manuscripts are. We will leave the final word to the journal, if the editors ask us to remove it, then we will do so.
4) Ref. [33] is not cited in the text. For CMS, the latest paper could be added, PRL 109, 222301 (2012).
Answer: Ref [33] was removed. Added the Ref. to the latest CMS paper on Upsilon suppression.
5) For the model comparisons, you may also compare with another QGP suppression model, Y. Liu, et al., PLB 697, 32-36 (2011)
Answer: This model is now included in the draft too, and plotted for comparison to our data in Fig. 5c.
6) page 3, line 15, you may add a reference to lattice calculations for Tc ~ 175 MeV.
Answer: Added a reference to hep-lat/0305025.
7) Fig 1a, \sqrt{s_{NN}} -> \sqrt{s}. In the caption, |y| -> |y_{ee}|
Answer: Fixed.
8) For the dAu rapidity, the directions of Au-going and p-going should be explicitly defined.
Answer: We also realized that this was important to do. This is now done by adding the sentence: "Throughout this paper, the positive rapidity region is the deuteron-going direction, and the
negative rapidity region is the Au-going direction. "
9) Fig.2a, the label of x-axis, 'y_{ee}' -> 'y_{\Upsilon}'. In the caption for Fig. 2a, Ref. [21] should be cited after 'EPS09 nPDF'.
Answer: We moved the citation to the first part of the caption.
10) page 5, around line 28-29, please mention explicitly this result is for p+p 200 GeV.
Answer: Done. The text now reads "we calculate a production cross section in p+p collisions..."
11) page 7, line 33, add space after N_{part}
Answer: Fixed.
12) page 7, line 36, Fig. 5c -> Figure 5c
Answer: Done.
13) page 7, line 46, remove 'bin from'
Answer: Done.
14) page 7, line 55, 'the latter' -> 'the former' ?
Answer: Split the sentence into two, and explicitly stated "The level of suppression we observe for
|y|<0.5 stays approximately constant from dAu up to central AuAu collisions. " to make it clear.
15) Fig. 4 a, b, and c, '30%-60%' -> 30-60%, '10%-30%' -> '10-30%', '0%-10%' -> '0-10%' In the caption, |y| -> |y_{ee}|
Answer: Fixed.
16) Fig. 5, the label of the y axis better to be the same style as Fig. 2
Answer: Fixed.
17) Page 9, line 33, line 45, when quoting the RdAu and RAA, why omit the p+p stat. errors? Also the p+p syst. err. in line 34 is not the same as that in page 7, line 41, please check.
Answer: The p+p stat. errors are combined together with the Au+Au stat. errors because it is straightforward to combine stat. errors, and we just quote the combined stat. error. Syst errors are fixed.
Comments from UCLA
1. In the legends of Fig 1 and Fig 4, the line color for the like-sign and unlike-sign should be blue and red, instead of black.
Answer: Fixed.
2. On page 5, line 29, it is not specified whether this is for p+p or dAu.
Answer: Done. The text now reads "we calculate a production cross section in p+p collisions..."
3. The directions of the d and Au beams were not defined: which goes forward and which backward in y? It will be good to specifiy the direction, and briefly discuss the different physics we expect from the forward and backward regions.
Answer: We also realized that this was important to do. This is now done by adding the sentence: "Throughout this paper, the positive rapidity region is the deuteron-going direction, and the
negative rapidity region is the Au-going direction. "
4. Page 7, line 50, "Pb+Pb" should be upright.
Answer: Done.
5. Page 7, line 55-56, "the latter" should be the model, which doesn't look constant. It seems you are talking about the measurements. Then it should be "the former".
Answer: Split the sentence into two, and explicitly stated "The level of suppression we observe for
|y|<0.5 stays approximately constant from dAu up to central AuAu collisions. " to make it clear.
6. Page 8, line 13-14, "in d+Au to be $2\sigma$ from unity and consistent with unity in peripheral" -> "to be $2\sigma$ from unity in d+Au and consistent with unity in peripheral"
Answer: Done.
7. Page 8, line 22, "modeling"
Answer: There are two aims: to incorporate... and to model ... Since we use the infinitive form in the description of the first aim ("to incorporate") we also use the infinitive form ("to model") in the second aim.
8. Page 3, line 82, "pQCD" -> "perturbative QCD (pQCD)"
9. Page 5, line 6, "perturbative QCD" -> "pQCD"
Answer: Both are now fixed.
10. Page 5, Fig 2, the caption says "Results obtained by PHENIX are shown as filled triangles", but they are "diamonds", not triangles in figure.
Answer: Fixed.
11. Pg 4 Line 1 : Barrel Electro-Magnetic Calorimeter (EMC) - Barrel Electro-Magnetic Calorimeter (BEMC) and replace EMC with BEMC throughout.
Answer: Done.
12. Pg 4 Line 65 : |y_{\upsilon}| - |y|. In the following Figure 1, its |y_{ee}| < 0.5 in figure panels and |y| < 0.5 in caption. Inconsistency, if all of them are same.
Answer: Fixed.
13. Pg 5 Line 1 : The data are fit .. - The data are fitted ..
Answer: Both forms are grammatically correct. The past participle can be either "fit" or "fitted".
http://en.wiktionary.org/wiki/fit#Verb
We kept the text as is.
14. Pg 5 Line 6 : via a perturbative (pQCD) next to leading order (NLO) - via a next to leading order (NLO) pQCD
Answer: Done.
15. Pg 5 Line 41 : ... with respect to ... - ... with respect to the ...
Answer: It is correct as written, usage: with respect to (something). One could also use "with respect to the" but then we would need to add another noun, for example as in, "with respect to the binary-collision-scaling expectation". We felt the original form was ok.
16. Pg 5 Line 46 : ... yield ... - ... yields ...
Answer: Done.
17. Pg 6 Line 25 : The present data ... - The present data in which figure ?
Answer: It is now made clear in the text that this refers to Figure 2b.
18. Pg 6 Caption for Fig. 3 : Use a) and b) instead of top and bottom
Answer: Done.
19. Pg 6 Caption for Fig. 3 : x_{F} in caption and X_{F} in figure
Answer: Fixed.
20. Pg 8 Line 26 : when CNM first appears, it needs to be spelled out.
Answer: Done, it is now given in the Introduction.
21. Pg 9 Line 28 & 31 : The term B_{ee} \times is missing in front of d\sigma/dy
Answer: Done.
Comments from Creighton
Page 3, Line 71. Why only p+p and d+Au? Why is the Au+Au cross-section not extracted?
Answer: We typically extract the yield per event in AA. This can be transformed into a cross section if we use the integrated luminosity. To get from a total number of minimum-bias events to an integrated luminosity all that is needed is the hadronic cross section for AuAu collisions, which is typically obtained using a Glauber model. We typically don't quote it mainly because what the community wants to know is R_AA itself. That is the quantity that the theorists typically calculate, and so we had received guidance to not include a cross section. (It was actually included in earlier versions of the draft.) Given this call for including it, we have now brought it back to the draft.
Figure 2. It might be more appropriate to include the description of the symbols in the figure caption rather than in the text. The legend might be reformatted so the description of symbols has the same structure for STAR, PHENIX, and Ramona Vogt. Why not use a consistent label for what we understand to be the same quantity expressed on the horizontal axis? (Figure 2a uses the rapidity for e+e- while Figure 2b uses rapidity for the upsilon.)
Answer: The caption now describes the symbols too. We left the description in the text also, to help the reader.
Page 5, Line 4. The wording in the text makes it sound like the red line in Figure 2 could refer exclusively to the upsilon production.
Answer: We have reworded this part to:
"The data are fit with a parameterization consisting of the sum of various contributions to the
Page 6, Line 18. It might be more appropriate to discuss here why the mid-rapidity point is lower than the prediction (rather than later in the text).
Answer: In a sense, the next paragraphs and figures are meant to discuss this point being low. We use R_dAu to have more discussion of the model predictions (and show their uncertainties). We next compare our result to previous measurements, which show a similar suppression. We added the sentence "To study this observation for \dAu\ further, we make a closer comparison to models and to previous measurements of \upsi\ production in p+A collisions. " to highlight this.
Page 7, Line 11/Figure 3b. It is unclear how the plot in terms of Feynman-x improves the comparison of rapidity coverage.
Answer: We added the x_F plot because the E772 data were given in x_F. We can massage our data to get x_F from rapidity making some estimates about the pT, which we can do because we have all the information on the Upsilon 4-momenta for our data, but we do not have this information for E772. So in order to compare to their result, it was best to not touch their data and massage ours, with intimate knowledge of ours, than to keep everything in y_Upsilon but having to massage their data without knowledge of their pT distribution so that we would only be guessing as to the correct y_Upsilon that would correspond to a particular x_F range.
Page 9, Line 30. This result in the conclusions does not seem to have been presented in the body of the paper.
Answer: This result is now given in the same paragraph where the corresponding pp cross section is first
stated, right after the description of Figure 1.
Comments from WUT
Reader 1:
1. legend of Fig. 1b
--------------------
I would rather put R_{dA}=1 (not R_{AA}) to be consistent with the figure caption and the main text
Answer: Fixed.
2. Fig 2a and discussion in the text
of the results for pp at positive and negative rapidities.
----------------------------------------------------------
I found it a bit awkward that we are presenting results just after folding in data at positive and negative y.
Of course the physics for pp is symmetric wrt y=0,
but it would be better to present separately results
for -1 < y < -0.5 and 0.5 < y < 1.0 to show that indeed the results are consistent.
(Also as a cross check of correctness of including all experimental corrections, and nothing to hide)
Answer: We did check that the results were consistent for pp, but we wanted to maximize the statistical power of the data, given that we are still somewhat statistics limited. Note that the acceptance and efficiency is lower for the 0.5 < |y|< 1.0 region, so that is why we wanted to add the two in pp, thanks to the symmetry, to show our best results. For the d+Au case, as we say in the paper, we did leave the analysis in distinct rapidity regions because the system is not symmetric.
3. legend of Fig. 2a
--------------------
For STAR and PHENIX points it would be more transparent,
if the legend would have similar layout as for NLO pQCD CEM.
I.e. 'STAR' in a single line followed by two lines
'pp' and 'dAu/1000' and analogously for
PHENIX/
Answer: Fixed.
4. line 2 on page 7
------------------
"their deuterium result" => "their pd result"
would be more straightward statement
(I assume E772 had a liquid deuterium target to study pd collisions)
Answer: Done. And yes, we say in the text that they had a liquid deuterium target.
5. Fig. 4
---------
The curves for combinatorial background should be made smooth
like for all other curves, not going in steps.
Answer: Fixed.
Reader 2:
page 4, line 1 and in further occurences: shouldn't it be BEMC instead of EMC ?
--------------------
Answer: Done.
page 5, line 1: shouldn't it be "The data are fitted"
---------------------------------------
Answer: Both forms are grammatically correct. The past participle can be either "fit" or "fitted".
http://en.wiktionary.org/wiki/fit#Verb
We kept the text as is.
Reader 3:
Overall it is a very well written paper and important results.
1. Acronyms in the introduction should be defined there (RHIC, LHC, pQCD or even QCD)
--------------------
Answer: Done.
p. 3, l. 60: you use "cold-nuclear-matter effects" without defining what "cold" and "hot" nuclear matter is. It would be good to introduce these terms when you talk about QGP and then other possible sources of suppression (line 52-63)
--------------------
Answer: Added short phrases to better define these terms.
p.8 l.26 - CNM should be defined
--------------------
Answer: It is now defined in the Introduction.
p.8 l.44-48 - it is not clear from the text how exactly CNM and QGP effects were combined for the scenario 4.
--------------------
Answer: We now state "For scenario 4), the expected suppression is simply taken to be the product of the suppression from scenario 2) and scenario 3)."
p.9 l.29 "with NLO" -> with "pQCD NLO"
--------------------
Answer: In the rest of the paper, we have used NLO pQCD, so at this point, it should be clear that when we are talking about
a Next-to-Leading Order calculation, we are implicitly talking about a perturbative QCD calculation (the fact that we are talking
about "orders" in a calculation implies
that we are talking about perturbation theory,
and this entire paper deals with QCD), so it should be clear from the context.
Figures: Caption of Fig 2: " from EPS09 with shadowing" - "EPS09" is nPDF which includes shadowing already, maybe write "due to shadowing using EPS09"?
--------------------
Answer: Changed the caption so it reads: "The dAu
Fig 2 and Fig 6 - the contrast of the figures could be improved - for instance lines for models in Fig. 2 are barely visible when printed in black and white
Answer: Fixed.
Reader 4: Fig. 1 and Fig 4 - The information on pT range,
in which the signal is presented, can be added.
-------------------------------------
Answer: We added a sentence at the end of the "Experimental Methods" section to state: "For all results we quote, the Upsilon data are integrated over all transverse momenta."
Comments from BNL
The new p+p result is significant, why is it not in title?
Answer: We already have one paper that is all about the pp cross section. Our result in this paper is an improvement, but the new results on suppression are the highlight of the paper, and we felt they deserved to be emphasized in the title. If we change the title to something like "Upsilon production in pp, d+Au, and Au+Au collisions at sqrt(s_NN) = 200 GeV" would include the pp result in the title, but it will not mention suppression. We prefer to emphasize the suppression, as that is the new, important result. Since we are attempting to publish in Physics Letters B, we felt it was more appropriate.
The paper is not clear in many places, and would be helped from a re-write keeping the audience in mind, i.e. not nesc. an expert in HI. It was commented that in particular the introduction on page 2 line 56 to 66 has much expert knowledge assumed, but does cover the field. Some examples are given below in the individual comments.
Answer: We tried to make the introduction section a short review of the field so that a non-expert could follow. We don't understand which expert knowledge is assumed in the introduction in lines 56-66. We certainly have strived to make the paper clear, and we will look for the specific comments and suggestions below.
The different RAA values appears multiple places in text. We think it is important to present these in tabular form, particular since so many numbers are presented RAA |y| <0.5, 1 centrality and collision system. Noted by several readers. Page 7,30-‐50 Page 8, 4-‐20
Answer: A table with all the values has now been added to the paper.
The definition of RAA seems a bit colloquial, normally this is defined vs. e.g pt, but in the case of the Upsilon it is our understanding this is an integral of the cross section over all (or some) pt-‐range divided by the pp . The paper should define this clearly.
Answer: We specifically wrote in the paper the equation used for R_AA. This is as clear a definition as we can make. We also now specify that our measurements are integrated over all pt.
The abstract should reflect the conclusion of the paper, this does not at present.
Our results are consistent with complete suppression of excited-state Υ mesons in Au+Au collisions. The additional suppression in Au+Au is consistent with the level expected in model calculations that include the presence of a hot, deconfined Quark-Gluon Plasma. However, understanding the effects seen in d+Au is still needed before fully interpreting the Au+Au results.
The most important observation, which is the unexpected observation that R_dAu is the same as R_AA for central events in the |y|<0.5 region, is the reason why we wrote the last sentence in the abstract.
Answer: We have discussed the differences in the |y|<1 and |y|<0.5 in the PWG, precisely to try to make sure that the results we are observing in |y|<1 and in |y|<0.5 are statistically consistent. One of the results is a subset of the other, so one must be careful to take into account the correlations. This study is in the technical note, in section 6A (page 33). We concluded that the results are self consistent. As to whether the result is statistical fluctuation, this is a possibility, but that is the case for any result, and the only way to remedy that situation is to run more dAu. As to whether it could be a systematic effect, we have done the analysis in |y|<0.5, in |y|<1, and in 0.5<|y|<1 where for each we use the same methods for extracting the signal, for applying efficiency and acceptance corrections, for estimating the backgrounds, etc. So if there is a systematic effect, it would affect the |y|<0.5 and the 0.5<|y|<1 region in the same way, and therefore it would not lead to differences between these two regions. We do not think that this "takes away" from the final conclusions, because it is an observation that is not expected if there should be binary scaling in dAu, and it makes the result more interesting. The reason why we included the E772 data was precisely because we observed such a striking suppression in dAu. So indeed, the fact that the data in Fig. 5b do not show a significant centrality dependence vs. Npart is one of the most important observations of the paper. And with the E772 data, we can point to a previous result that shows a similar level of suppression in pA. Therefore, this paper will serve to exhort the community to take a closer look at Upsilon suppression in pA or dA. We do not understand the comment about conclusions being "iffy". If there is a specific conclusion that does not seem to be supported by the data, then we can address that.
The last sentence in conclusion seem exaggerated, and not documented from text just remove.
Answer: One of the main points of the paper is that in Fig. 5b, as we explain in the previous answer, there is no evidence for a significant centrality dependence of Upsilon suppression in dAu. The models predict the level of suppression we see in AuAu, but one of the key results of the paper is the suppression seen in dAu. The GPC strongly advocated to include a sentence in the conclusions of the paper that cautions readers that one must understand the dAu suppression before any strong claims can be made. The last sentence was rephrased slighly to better reflect this.
In abstract suggest the remove the sentence “Our measurements p+p…” and add to the text where relevant in the introduction. Not really relevant.
Answer: Done.
Individual comments:
Page 3 line 34: it is not at all obvious how the 2 statements (deconfinement and high temperature phase of lattice QCD where color is an active degree of freedom) in this sentence are scientifically connected.
Answer: The connection is that color Debye screening, which is the original effect proposed by Matsui and Satz,
requires a quark-gluon plasma where the color charges of the high-temperature plasma screen the heavy-quark potential that binds the bottomonium (or charmonium) states. This is one of the key ideas in QGP physics.
Page 3 line 59 for a non HI guru this argumentation is basically impossible to follow. Also ccbar and bbar pairs are produced the same way through gg fusion so why should there be a difference.
Answer: It seems that the question arises because the inquirer did not follow that the arguments presented are about final state effects, since the comment about ccbar and b-bbar pairs being produced through gluon fusion is about their production in the inital state, not about the possible ways that they can be broken up in the final state. The comment about
the interaction cross section of the Upsilon with hadrons applies to the final state, once the hadrons are produced. The size of the upsilon meson is much smaller than the J/psi meson, and the corresponding cross section of an Upsilon to interact with a final state pion (and then break up into a pair of B mesons) is much smaller than the cross section for a J/psi to be broken up by a pion into a pair of D mesons. We will add a comment that the effects discussed in this section are final state effects.
Page 3 line 46. There is no reference to statistical recombination.
Answer: Added a reference to Thews et al.
Page 3 line 78 there is no issues using the 2008 dAu data even so other analysis claim they cannot publish because of the non perfect tpc alignment?
Answer: We put a lot of work to take into account the effect of the TPC misalignment. This is discussed in the Technical Note in Section V.F, page 29. In particular, the 2009 pp data was originally processed with the same misalignment that the 2008 dAu data and the 2010 AuAu data both have. The 2009 pp data was subsequently reprocessed with fixed calibrations, and we studied the effect that the distortions had on our invariant mass reconstruction on an event-by-event basis, i.e. comparing the mass obtained in the production with the misalignment and then with the misalignment fixed on the exact same event. This allowed us to characterize the effect of the misalignment and to take it into account in embedding for the line-shapes and then in the extraction of the Upsilon yield via the fits using those line-shapes. This was studied extensively in the PWG in large part because we wanted to make sure that any issues regarding the misalignment would be dealt with appropriately. We cannot comment on other analyses, but if they can also study the differences in the two pp 2009 productions, that could help them to account for the TPC misalignment in their own analyses.
Fig 1 caption – comment to fit: the chi^2 of the pp fit must be horrible, any reason why the fit does not describe the data better.
Answer: The chi^2/NDF is 1.37 in the pp fit. This is not something we would characterize as "horrible". Given the statistics, there is not a strong reason to change the fit from using components we expect to have, namely the Upsilon states, the Drell-Yan and b-bbar continuum, and the combinatorial background.
2nd question: was the setup of STAR, especially the material budget, the same? If not, which I assume, how different are they?
Answer: The material budget was the same. The TPC misalignment in dAu, and AuAu increases the width compared to pp. The higher occupancy in AuAu also contributes to a broadening compared to pp. As noted above, we now explicitly state
in the paper that the material budget in all three datasets is the same.
page 5 line 6 (fig caption) ‘band’ -> box/square
Answer: The NLO calculations are shown as a band, and that is what is mentioned in the caption.
page 6 line 48: the effect at mid rapidity taking the systematic uncertainty into account is 2 sigma max. I think this is a number which needs to be stated.
Answer: We state the value of R_dAu with statistic and systematic uncertainties. We will also provide a table with all the R_AA and R_dAu values. The sentence we use in page 6 line 48 says that the suppresion is "indicative" of effects beyond shadowing, initial-state parton energy loss, or absorption by spectator nucleons.
Using "indicative" is usually warranted for effects that are of ~2 to 3 sigma significance, we certainly not claim a "discovery" (5sigma).
Itʼs a bit hard to follow the various R_AA and R_dAu quoted in the paper. A table listing the R_{AB} for the various combinations might be more useful than scattering the values through the text.
Answer: A table is now provided.
Abstract: I realize that in the abstract you donʼt want to get too technical, but omitting the rapidity range and whether it is 1S or 1S+2S+3S makes the numbers not useful.
Answer: We added a short clarification in the abstract as to the result quoted being 1S+2S+3S, and in the rapidity range |y|<1.
p. 4: Lines 55-57: the tracking and electron identification efficiencies would be the same across the three datasets, but in the previous paragraph there was discussion about differences in efficiency. Needs to be made clearer.
Answer: The text is now clear that the main thing that was chosen to be the same was the electron identification efficiency.
Fig1 The N_{--} is unclear the – runs together with the N
Answer: Fixed
Fig. 2: Vogt band does not print well.
Answer: Increased the line weights and changed the colors to darken them so that they print better.
fig 2a needs ""Phenix"" in dAu/1000 (open diamonds)
Answer: Fixed
Fig 2: “are shown as triangles There are no triangles,
Answer: Done. It should be diamonds.
c) Fig 3a The label A^0.96 is not the actual black curve which is (A/2)^{-0.04) according" "to the text in pg 7. Maybe writting the A^{alpha} scaling of cross section in the figure may help.
Answer: Fixed
in Fig 4 where the CB in all three panels is not a smooth curve nor a histogram; it has an unusual "mexican pyramid" shape
Answer: What's wrong with Mexican pyramids? :-) The plot will now be a smooth curve.
The A to the 0.96 does not match the text in line 5 page 7
Answer: As noted above, the Figure will now display A^0.96 scaling to make clear that the line shown is not A^0.9, but
rather derived from a cross section that scales as A^0.96.
Fig. 5: Are the shaded boxes systematics in the AB system? If so, needs to be in the caption.
Answer: Fixed
Fig. 6: "Our data is shown as a red vertical line with systematics shown by the pink box. There are two systematics (pp and AB). What was done with these? The pp is common to d+Au and Au+Au, so not clear, actually, what should be done.
Answer: The two systematics were added in quadrature for Fig. 6, we now state that in the paper. (Agree that it is debatable how to best combine them, but we should state what was done.)
.p. 6, lines 43-44: Do you mean y<~-1.2, rather than 1.2? Otherwise the argument doesnʼt make sense. And, where is the 1.2 from (citation)?
Answer: Correct, it should be -1.2. We do give the reference (23) for this statement in the previous sentence.
p. 8, line 11: consistent with an RAA(2S+3S) approximately equal to zero. Would be better to quantify this as an upper limit.
Answer: This section was reworded based on suggestions from another reader. The argument now starts with the hypothesis of an approximately zero yield of the 2S+3S, states what that would imply for the R_AA(1S) and R_AA(1S+2S+3S) values, and
then notes that this is consistent with our data.
p. 9, line 1: at how many sigma was the exclusion? At 4.2 sigma, as quoted later?
Answer: The exclusion the "no-suppression" scenario had a p-value of less than 1 in 10^7 (better than 5 sigma) for all R_AA cases in AuAu. The R_dAu had a different p-value of 1.8 * 10^-5 (~4.2 sigma).
Line 18: result rather than effect reads better.
Answer: Done.
How were systematics taken into account in the quoting of “sigma”?"
Answer: The only time we quote "sigma" are for the exclusion of the "no-suppression" scenarios. For R_AA, they would still
be excluded at better than ~5 sigma even including systematics. For the dAu case, if the p-value is calculated with the systematic uncertainty shift we get 1.5 x 10^-3, which is about 3sigma.
a) The style of the paper is too colloquial for my taste, but I'm told that journals have relaxed their style requirements.
Answer: This is a style issue, we are certainly willing to discuss this with the editors of the journal if need be.
d) Reference [10] explains that the Combinatorial background is obtained by fitting the same charge sign pair distribution and that appears to be the case in this paper except in Fig 4 where the CB in all three panels is not a smooth curve nor a histogram; it has an unusual ""mexican pyramid"" shape.
Answer: The plots will all have a smooth curve.
Page 7 top (line)9 From the figs its not obvious there is 4.2 deviation, more like 3, can you cross check.
Answer: See previous comments on the deviations and statistical significance.
Clearly the difference between y 0.5 and 1.0 make the conclusion a bit waffly.
Answer: For dAu, in both scenarios we are excluding the no-suppression scenario. Both datasets are supporting this conclusion. Furthermore, the comment we make in about a 4.2sigma exclusion of the no-suppression scenario comes
from the |y|<1 measurement, which is the weaker exclusion of the two. The |y|<0.5 only serves to make this conclusion stronger.
The notation and fonts for RAA and Upsilon(1S+2S+3s) not not consistent across paper.
Answer: plots are now consistent (For Anthony).
Page 8 line 48 “ assumed a flat prior..” This reference to statistics may or may not come across well to the general reader,
Possible expand on this.
Answer: We have followed other papers in the Physics Letters B which use these same statistical techniques, and this usage was accepted.
One minor comment:" "In Fig.6, “CMN effects” should be “CNM effects”
Answer: Fixed.
Page 4 line 28&57, the three datasets” clarify to indicate “between the datasets from the three collisions systems”"
Answer: Done.
"line 57" "‘be the same” Really, should it not be “approximately the same".
Answer: Done.
Responses to GPC, April 2014
Thomas:
1. General: with the new text (in red) there's no a wild mix
of Au in roman and italic in normal text and in super/sub-scripts. Since Au is a chemical symbol I would put it all in roman
consistently.
This sentence doesn't say a lot and as I already mentioned that
I do not think the feed-down pattern is any more complex
than that in the charmomium sector. I attached a schematic
diagram. Replace Y with Psi and chi_b with chi_c and h_b with h_c
and that's it.
Why not simply saying here that the amount of feed-down into
the Y(states) is not measured at RHIC energies and then give
numbers of the next closest energy (which is Tevatron I guess).
3. Fig 1,: I already mentioned that I suggest to turn this
into a table. The plot doesn't really provide any new insight.
4. Page 9, line 13.
"*" -> "\times" or just leave it out
5. Page 11, Line 18.
I wonder if one should add one sentence mentioning the Y suppression
in high multiplicity pp events seen by CMS. Fits in the context.
6. Page 11, line 50.
Delete "However".
7. Fig. 6. The font size of the legend is a bit on the small side.
There's enough room to make it a tic bigger.
8. Table II.
Can we really say that d-Au is 0-100%? That would be zero bias.
Wasn't there a min-bias mixed with the Y trigger. To my knowledge
we never quoted anything above 80/90%. What about simply saying
min. bias instead of 0-100%.
Lanny:
P3 L30 -- remove "complex" (it is an unnecessary adjective here)
P4 (new) Fig.1 and red text lines 50-51, 65-69: The efficiencies are
about the same for the 30-60, 10-30 and 0-60 at each rapidity bin.
This information probably should be in the text since HF reco. eff.
are useful to know by others in the business. I recommend putting
this information in the text in place of the above Figure 1 and lines, e.g.
"The $\Upsilon$ acceptance $\times$ efficiency for three centrality
bins (30-60%, 10-30%, 0-60%) are XX, XX and XX for respective
rapidity bins |y|<0.5, |y|<1.0 and 0.5<|y|<1.0. For the 0-10% centrality
the corresponding total efficiencies are reduced by approximately XX%."
Please check that the various uses of "total efficiency", "reconstruction
efficiency", "acceptance times efficiency" etc are used consistently and
avoid extra such terms if possible.
P5 Fig2b -- The legend "p+p x <Ncoll>" is misleading and may be what ref.2
is asking about. The grey band in 2b is not simply the red curve in 2a
multiplied by a constant (Ncoll). There are resolution effects as discussed
on P6. The caption should say, "The grey band shows the expected yield if
RDAu = 1 including resolution effects (see text)."
P5 L8 -- Are b-bbar pair backgrounds NPE from open HF meson
decays (B-mesons)? Just curious.
P5 Tabel I -- I assume momentum resolution effects are included in
the line shape entries. Ref.1 is concerned about p-resolution and in
addition to the response, this table caption should note that p-resol.
is included in the line shape errors if that is true.
P5 L17-28 -- I did not find any discussion in the paper about the
use of max likelihood fitting. This turned out to be a big deal and
will be discussed in the response. This parag. would be the place
to say, briefly how the fits were done.
P6 L6 -- "miscalibration" sounds scary. Can this issue be explained
in the text, and more so in the responses, so that neither referee nor
the readers are put-off by the statement and dismiss the paper's results?
P6 L26 -- I recommend against arguing with the referee over simple
wording changes that have equivalent meanings. Is there a subtlety
here that I don't recognize?
P6 Fig.3a -- The referee is asking that the legend "Upsilon -> e+e-"
say explicitly "Upsilon(1S+2S+3S) -> e+e-". But also change to l+l-.
She/he wants the states listed explicitly.
P8 Fig 5c caption - same issue as above with the grey band. The
last sentence in the caption should read: "The grey band ... number
of binary collisions including resolution effects (see text)."
P9 L8 -- Referring to Fig. 6c, the 10-30% RAA is consistent with unity
also. This sentence should say, "..consistent with unity in peripheral
to more-central Au+Au collisions..." BTW, "events" is jargon which we
all use, but I think it is better to say "collisions" here and throughout
the paper unless we are specifically discussing a triggered event in
DAQ.
Also, I changed event to collision where approriate in the text. Those changes are unhighlighted.
P10 L8 -- "With two possibilities.." implies that CNM and QGP are
the only possibilities for reducing yields. There is at least the
possibility of modified fragmentation of HF quarks in a
dense system. I recommend saying "Considering two possible
sources..." which more accurately reflects what was done; we
considered these two effects and not others.
P10 L37-39 -- Isn't the "QGP only" preferred in Fig. 8b? Why
mention the other as "consistent" and not also mention the
Thorsten: - p3, l31-l32: I don't like the formulation too much, maybe "...there exists a feed-down pattern in the bottomonium sector, and thus melting of the higher states affects also the measured yield of the lower states."
- fig 1 take a lot of space for basically not much information, maybe a table would be sufficient?
- p6, l6: TPC miscalibration sounds scary, maybe non-perfect TPC calibration?
- p11, l5: I'm not too happy with the A^alpha discussion: after all it is a just a fit to the data. Have you used for this statement the alpha value from our own measurement, e.g. fig 4 bottom or the integrated one from fig 4 top? The integrated one is significantly above the midrapidity one, also for E772
Responses to PLB Referees
Responses to Reviewers' comments:
We would like to thank the referees for the insightful and constructive comments. We discuss below our detailed replies to your questions and the corresponding explanation of changes to the manuscript. But before we go into the replies to the comments, we want to make the referees aware of changes to the results that were prompted via our studies of the systematic effects on the yield extraction. Since this paper deals with cross sections and with nuclear-modification factors, both of which involve obtaining the yields of the Upsilon states, this change affects all the results in the paper. We therefore wanted to discuss this change first. Please note that the magnitude of these effects do not change the overall message of the paper.
We wanted to alert the referees up-front about this important change before we proceeded into the detailed responses. This study was indirectly prompted by one of the questions from Referee 2 regarding systematic effects from yield extraction.
In the process of investigating the systematic difference between extracting the upsilon yield through simultaneous fitting compared to background subtraction as requested by the referee, we also studied the effects of chi^2 fits (specifically of Modified Least-Squares fits) compared to maximum-likelihood fits. We used chi^2 fits in our original submission. We were aware that extracting yields using a chi^2 fit introduces a bias (e.g see Glen Cowan's "Statistical Data Analysis", Sec. 7.4). The size of the bias is proportional to the value of the chi^2 of the fit. In the case of the Modified Least-squares fit, when fitting a histogram including the total yield as a fit parameter, the yield will on average be lower than the true yield by an amount equal to chi^2. The relative bias, i.e. the size of the bias divided by the extracted yield, goes to zero in the large yield limit, which is why for cases with large statistics this effect can be negligible. We had attempted to mitigate the effects of this bias by using the integral of the data, since this removes the bias completely in the signal-only case. But a bias remains in the case where there are both signal and background present. For our case, the yield extracted from the fit for the background is also biased toward lower values, and since we used this background estimate to subtract from the integral of the data in the extraction of the Upsilon yields, these biased the Upsilon yields towards higher values. Through simulation studies, where we include signal and 3 background components as in our analysis, we were able to quantify these effects. Given that in some cases the biases could be of order 10-20%, the fits needed to be redone in order to remove the bias. The solution is straightforward since the extraction of yields using a maximum-likelihood fit is unbiased. We have studied the difference of a modified-least squares fit and a maximum-likelihood fit and confirmed that the yield extraction in the latter method is essentially unbiased. We therefore have redone all the fits to extract the Upsilon yields via maximum-likelihood fits. The revised results are now quoted in the paper. The overall message of the paper is not affected by these changes.
We proceed next to answer the specific points raised by the reviewers.
Reviewer #1: This paper reports results on Y production in pp, dAu, and AuAu
collisions at top RHIC energy. It contains original and important
results and clearly qualifies for publication in PLB. However, there
are many aspects of the paper which need attention and/or improvement
prior to publication. They are detailed below:
1. the introduction is carelessly written. For example, the value
quoted for the pseudo-critical temperature near mu = 0 of 173 MeV is
taken from an old publication in 2003. Recent lattice results from the
Wuppertal-Budapest group (PoS LATTICE2013 (2013) 155) and the Hot QCD
Collaboration (Phys.Rev. D81 (2010) 054504) imply much lower T values
near 150 MeV and are far superior in terms of lattice sizes and spacing.
the results from the Hot QCD collaboration (Phys.Rev. D81 (2010) 054504) do not imply
much lower T values. In that paper, in section IV "Deconfinement and Chiral aspects of the QCD transition", when discussing the deconfinement transition temperature range the authors write:
"...we have seen that the energy density shows a rapid rise in the temperature interval T = 170–200. MeV. This is usually interpreted to be due to deconfinement, i.e., liberation of many new degrees of freedom".
Therefore, this does not indicate T values near 150 MeV. In addition, they also mention this range when discussing their results for the renormalized Polyakov loop, which
is the parameter most closely related to the deconfiment transition, being that it is the exact order parameter in the pure
gauge case:
"The renormalized Polyakov loop rises in the temperature interval T = 170–200 MeV where we also see the rapid increase of the energy density."
Therefore, the results from the Hot QCD collaboration do not imply T values near 150 MeV.
In addition, in reference 9 of the Wuppertal-Budapest group (JHEP 1009 (2010) 073 arXv:1005.3508), which is a paper comparing the various results for Tc between the Wuppertal-Budapest and HotQCD groups, again the results for the renormalized Polyakov loop (figure 7, right) indicate a broad transition region in the region T=160-200 MeV. They do have a table discussing values of Tc of about 147 MeV, but that is for the chiral transition, which is not the most relevant one for quarkonium suppression.
When they look at the trace anomaly (e-3p)/T^4, they see 154 MeV for the Tc value. They in addtion make the point that the transition is a broad crossover, which is something we also say in our paper. The fact that the transition is a broad crossover leads to differences in the estimates of the pseudo-critical temperatures depending on which observable is used. As an example, in the caption of Table 2, where they give the values of Tc for many observables, they mention that the Bielefeld-Brookhaven-Columbia-Riken Collaboration obtained Tc=192. They also note "It is more informative to look at the complete T dependence of observables, than
just at the definition-dependent characteristic poins of them." So given the above, we will modify the paper to give a range of temperatures, 150-190, and cite the papers from the
Wuppertal-Budapest and HotQCD collaborations.
probe..' does not get to any of the real issues, such as the complex
feeding pattern in the Y sector and the crucial question of whether Y
mesons reach equilibrium in the hot fireball as required to interpret
the apparent sequential melting pattern in terms of 'break-up'
temperatures.
The reviewer also mentions that there is a crucial question as to whether the Upsilon mesons reach equilibrium with the fireball as a requirement to interpret the sequential melting pattern. We respectfully disagree with the referee in this matter. The Upsilon is by definition not in equilibrium. The only requirement of course is that the medium is deconfined. In lattice QCD studies only the medium is thermalized; the potential between the heavy quarks is screened independent of whether the Upsilon is in equilibrium or not. We discussed this issue with lattice expert Peter Petreczky who confirmed our view.
furthermore, statistical recombination is not a 'complication' but a
direct measure of deconfinement. And the smallness of off-diagonal
terms in the recombination matrix does not imply absence of
recombination as the diagonal terms can be substantial.
Also the newest results on p-Pb collisions from the LHC are entirely
ignored, see, e.g., arXiv:1308.6726.
2. section on experimental methods
no detail is given concerning the crucial momentum resolution but it
is stated at the end of this section that cuts were adjusted for
different systems such that 'tracking and electron id would be the
same across the 3 data sets'. On the other hand, already in Fig. 1 we
see a strong dependence of the mass resolution on the system even for
low multiplicities as in pp and p-Pb. The effect must be much stronger
in Pb-Pb as is indeed visible in Fig. 4. Especially in view of the
importance of resolution for the separation of excited Y states this
referee has to be convinced that the systematic errors are under
control for momentum and pid measurements as a function of
multiplicity. Also how the systematic errors for the separation of Y'
and Y'' from Y are determined as a function of multiplicity needs to
be demonstrated explicitely.
3. Fig. 2b
even at y = 0 the difference between data and models is less than 2
sigma, taking uncertainties due to the pp reference into account and I
don't believe it makes sense to argue about effects beyond shadowing
and initial state parton energy loss in these data.
4. in Fig. 3 the size of the systematic errors should be indicated.
5. in Fig. 5 it is demonstrated that the observed suppression near
midrapidity is independent of system size (N_part). This could imply
that the higher Y states are already disappeared in dAu
collisions. This is mentioned briefly in the conclusion, but could be
stressed more.
6. At LHC energy, the anisotropic model of Strickland reproduces well
the centrality dependence of R_AA but not the rapidity dependence,
see, e.g. the final session of the recent hard probes meeting in South
Africa.
7. The presentation in Fig. 6 on the quantitative evaluation of
different model assumptions compared to data depends again strongly on
the size of the systematic errors, see the comment in section 2.
----------------------------------------------------------------------------------------------------------------------------------------------------------------------
Reviewer #2: I have read the manuscript PLB-D-13-01645 submitted to me for review.
The authors present a detail analysis on the suppression of Y production in d+Au and Au+Au collisions at sqrt(s_NN)=200 GeV using the STAR detector at RHIC. The article is very well written and deserves publication. However, I would like to suggest considering the following remarks to improve the understandability of the article:
1. Page 1, column 1, paragraph 1: The now accepted value for the critical temperature (chiral transition) is Tc = 150 - 160 MeV (depending on the exact definition of the observables). Reference 3 is outdated and should be replaced by more recent publications, i.e. arXiv:1005.3508 [hep-lat]
2. Page 2, column 2, paragraph 1: Please quantify the corrections due to the trigger bias w.r.t. the event centrality. Same for the tracking efficiency as a function of N_part. How does acceptance times efficiency for detecting Y as a function of rapidity and N_part looks like?
3. Page 3, column 1, paragraph 1: statement "some information will be lost" is too general! What are the systematic uncertainties arising from the different methods (same-event like-sign CB, fit to the CB) of the combinatorial background subtraction? What is the signal significance, in particular in the d+Au measurement? How does the signal looks like after CB and physical background subtraction? Systematic errors should be clearly mentioned.
We have studied these effects through various MC simulations in order to extract the biases. The likelihood fits have negligible biases. Furthermore, and to get back to the original question posed by the referee, in these simulations we obtained the variance of our results when doing simultaneous fits when compared to background-subtracted fits. We found a reduction in the variance when using simultaneous fits which was our original impetus. We also found no systematic effect in the expectation values of the yields obtained by the two different fitting methods. However, given the reduction in the variance of the extracted yield (i.e. in their error) in the simultaneous fit, we favor this method since it introduces a smaller uncertainty. We have redone all of our fits using the likelihood method and we corrected for any extraction biases seen through simulation.
Regarding signal significance, in all cases we see significant signals in d+Au. This can be infered by examining Fig. 3a and comparing the size of the statistical+fit error bars to the measured value of the cross section. This ratio is a good indicator of the statistical significance of our signal. For example, the dAu signal at |y|<0.5 has a significance of 11.7/3.2 = 3.7 sigma.
Since the referee also asked about systematic uncertainties, we have added a full table covering all measured sources of systematic uncertainty and added additional comments about the main sources in the text.
4. Fig 1: It would be easier for reader if the range of the y axis would be the same in Fig 1a and Fig 1b. Why is the explanation of the grey curves in the figure discussed in this complicated way, to my understanding the gray band simply shows the pp yield scaled by the number of binary collisions? If so, the label could read simply pp*<N_coll>.
5. Fig 1a: From where the line shape for pp comes from? It seems NOT to fit experimental data, i.e. all data points around 9 GeV/c^2 and below. Is it then evident to take as a cross section the integral of the data points?
6. Page 3, column 2, paragraph 1: How was the measured Y(1S+2S+3S) yield transformed to cross section?
7. Page 3, column 2, paragraph 3 (wording): "Hence, averaging between forward and reverse rapidities is not warranted as it is in
p+p." --> "Hence, averaging between forward and backward rapidities is not justified as it is in p+p." sounds more understandable.
8. Page 4: Try to arrange the placement of Figs such that there will not be a single line of the text within one column.
9. Fig 2: also here Fig a and Fig b could be presented with the same range on the Y axis, e.g. from -3 to 3.
10. Fig 2a : what is shown here is Y(1S+2S+3S), moreover PHENIX results on Y -> mu+mu- are shown in the same plot, that is why the figure label should be changed, i.e. Y->e+e- should be replaced by Y(1S+2S+3S)
11. Page 4, column 2, paragraph 2: <N_coll> (not <N_bin>) is commonly used as notation for the number of binary collisions. Sigma_AA is sigma^tot_AA (same for pp). It is important to indicate in the text the values for the total inelastic cross sections in pp, dA and AA and <N_coll> used to calculate R_AA.
12. Page 4, column 2, paragraph 3: In view of the discussion would it be helpful to also show R_AuAu vs. Rapidity?
13. Page 6, column 1, paragraph 1: Which function has been used to fit the CB - exponential? Again, what are the systematic uncertainty arising from the different methods (same-event like-sign CB, fit to the CB) of the combinatorial background subtraction. See also comment 4. concerning the label.
The function used to model the CB is now discussed in the text. Systematics from the fit methods are summarized in Tab. I.
14. Page 6, column 1, paragraph 2: The statement "Similar suppression is found by CMS in PbPb collisions (37)" should be moved to the paragraph 4 where the authors discuss Y(1S) suppression. Actually, for the same value of N_part=325 R_AuAu=0.54+-0.09 as for R_PbPb=0.45
Done.
15. Page 6, column 1, paragraph 4: How did the authors derived: R_AA(1S+2S+3S) = R_AA(1S)*0.69?
We had aimed to keep the text brief, since we were mindful of the space constraints, but given this question, we have added a few more sentences and references to clarify the R_AA(1S+2S+3S)=R_AA(1S)*0.7 statement, and also reduced our significant figures, quoting only a factor of 0.7.
16. Page 6, column 2, paragraph 2: What are the uncertainties on Drell-Yan and bbbar cross sections and how does it influence the significance of the signal.
Various normalizations are used in the fit. This is accounted for in the correllation
17. http://arxiv.org/pdf/1109.3891.pdf reports on the first measurement of the Y nuclear modification factor with STAR. It is probably worth to mention this work in the ms.
18. The R_AA of J/psi (p_T > 5 GeV), Y(1S) and an upper limit on the R_AA (2S+3S) was obtained in STAR. I would like to suggest to add a plot showing R_AA as a function of binding energy as a summary figure (also as a key figure to the long discussion on the extraction of the upper limit on R_AA(2S+3S)).
In summary, this ms. contains very interesting results and I propose publication in Phys. Letter B after the authors have taken care of the remarks above.
We thank the referee for her/his comments and remarks, which have helped improve the paper. We hope that we have addressed the issues raised, and adequately answered the questions posed, and look forward to the publication of the paper.
Upsilon pp, dAu, AuAu GPC E-mail Responses
This is a page to house long e-mail responses.
Using Pythia 8 to get b-bbar -> e+e-
We used Pythia 8 to produce b-bbar events. First we used the default Pythia 8. Macro for running with default parameters is here. We then used the STAR Heavy Flavor tune v1.1 for Pythia 8. The macro for running with the STAR HF tune is here.
The cross-sections reported by Pythia (numbers after 5M events) using the default parameters:
*------- PYTHIA Event and Cross Section Statistics -------------------------------------------------------------*
| |
| Subprocess Code | Number of events | sigma +- delta |
| | Tried Selected Accepted | (estimated) (mb) |
| | | |
|-----------------------------------------------------------------------------------------------------------------|
| | | |
| g g -> b bbar 123 | 19262606 4198826 4198275 | 6.971e-04 1.854e-07 |
| q qbar -> b bbar 124 | 3126270 801174 800981 | 1.331e-04 8.216e-08 |
| | | |
| sum | 22388876 5000000 4999256 | 8.303e-04 2.028e-07 |
| |
*------- End PYTHIA Event and Cross Section Statistics ----------------------------------------------------------*
So gg initiated subprocess has a 0.697 ub cross section and the q-qbar initiated subprocess has a 0.133 ub cross section. The sum for both subprocesses pp -> b bbar is 0.830 ub.
Using the STAR HF Tune, the cross section statistics reported by Pythia change to the following:
*------- PYTHIA Event and Cross Section Statistics -------------------------------------------------------------*
| |
| Subprocess Code | Number of events | sigma +- delta |
| | Tried Selected Accepted | (estimated) (mb) |
| | | |
|-----------------------------------------------------------------------------------------------------------------|
| | | |
| g g -> b bbar 123 | 31956918 4520459 4520459 | 9.247e-04 2.542e-07 |
| q qbar -> b bbar 124 | 2259563 479541 479541 | 9.817e-05 8.544e-08 |
| | | |
| sum | 34216481 5000000 5000000 | 1.023e-03 2.682e-07 |
| |
*------- End PYTHIA Event and Cross Section Statistics ----------------------------------------------------------*
The cross section increases to 1.023 ub with the STAR HF Tune v1.1. The main changes to the default parameters are the reduction of the bottom quark mass from 4.8 (default) to 4.3 GeV/c2, the change of PDF from CTEQ5L (default) to the LHAPDF set MRSTMCal.LHgrid, and the choice of renormalization and factorization scales.
The selection of e+e- in the final state is done by following the fragmentation of the b or bbar quark into a B meson or baryon, and then looking at its decay products to find an electron or positron. The pT distribution of the genrated b quarks is shown below.
Fig. 1: Generated b quarks.
.gif)
The <pT> of the b quarks is 3.3 GeV. These then fragment into B mesons and baryons. As an example, we plot here the B0 and B0-bar pT distribution, below.
Fig. 2:Pt distribution of B0 and B0-bar mesons.
.gif)
The <pT> of the B mesons is 3.055 GeV/c, one can estimate the peak of the Z distribution (most of the momentum of the b quark is carried by the meson, so it should be close to 1) as 3.055/3.331=0.92.
After the beauty hadrons are produced, they can decay producing electrons and positrons. We search for the e+e- daughters of the beauty hadrons, their pT distribution is shown below.
Fig. 3: pT distribution of the e+ e- daughters of the b quarks.
.gif)
When an event has both an electron and positron from the b-bbar pair this can generate a trigger. However, these are generated in all of phase space, and we mainly have acceptance at mid-rapidity. The full rapidity distribution of the e+e- pairs is shown below:
Fig. 4: Rapidity distribution of the e+e- pairs from b decay.
.gif)
The distribution is well approximated by a Gaussian with mean ~ 0 and width close to 1 (off by 4.3%).
We calculate the invariant mass. This is shown below:
Fig 6. Invariant mass spectrum of e-e+ pairs originating from b-bbar pairs.
.gif)
The red histogram is for all e+e- pairs generated by Pythia. The blue histogram is for pairs with |y_pair|<0.5, which is the region of interest. The distributions are fit to a function to parameterize the shape, shown in the black lines. This is inspired by using a QCD tree-level power-law distribution multiplied with a phase-space factor in the numerator. The fit parameters for the blue line are:
- b = 1.59 +/- 0.06
- c = 27.6 +/- 5.8
- m0 = 29.7 +/- 7.8
Using the STAR HF Tune, the parameters are:
- b = 1.45 +/- 0.05
- c = 64.2 +/- 26.1
- m0 = 49.7 +/- 18.0
With the default parameters, in mass region 8 < m < 11 GeV/c2 and for |y|<0.5 the Pythia prediction is for a cross section of 29.5 pb.
With the STAR HF Tune, in the same phase space region the Pythia prediciton is for a cross section of 46.9 pb.
One can calculate from the Pythia cross section, the STAR efficiency*acceptance and the integrated luminosity the expected yield in the region 8< m < 11 GeV/c2. This gives 12 expected counts for trigger 137603, assuming the trigger doesn't affect the invariant mass shape.
However, tince the trigger has a turn-on region, we need to take this into account. The turn on can be obtained by looking at the background counts in the real data. By modeling the background with an error function of the form (erf((m-m0)/sigma)+1)/2 and multiplying by an exponential, we obtain the parameters m0=8.07 +/- 0.74 GeV/c2 and sigma = 1.75 +/- 0.45 GeV/c2. The fit to obtain the error function is shown below (it is one of the figures in the paper):
Fig. 7 Unlike-sign and like-sign invariant mass distributions from data. The like-sign is fit with and exponential multiplied by an erf.
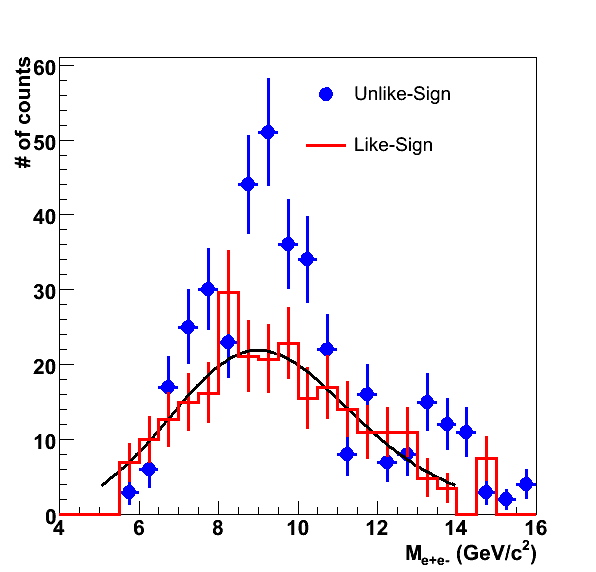
We then need to apply this function to parameterize the turn-on region of the trigger to the b-bbar e+e- invariant mass spectrum. We have one additional piece of information from the efficiency estimation: the overall acceptance * trigger efficiency * tracking efficiency and including additional PID cuts for the Upsilon(12) is 5.4%, we can use this to normalize the function after including the trigger turn-on so that at M=10 GeV/c2 it gives 5.4% of the yield before applying the trigger turn-on. This way we take care of the trigger turn-on shape and the overall normalization given by the acceptance, efficiency, etc. obtained from the upsilon embedding. This assumes that an e+e- pair with invariant mass identical to the upsilon will have identical efficiency and acceptance. Using this, we estimate the yield in the region 8<m<11 including the trigger turn-on and acceptance and efficiency to be 19 counts from b-bbar in the Upsilon mass region in the entire dataset.
For the STAR HF Tune, the cross section is larger and the expected counts are larger:
Code to run Pythia and produce b-bbar -> e+ e- events
// main00.cc
// Modified from the main01.cc
// which is a part of the PYTHIA event generator.
// Copyright (C) 2008 Torbjorn Sjostrand.
// PYTHIA is licenced under the GNU GPL version 2, see COPYING for details.
// Please respect the MCnet Guidelines, see GUIDELINES for details.
// This is a simple test program.
#include "Pythia.h"
#include "TROOT.h"
#include "TFile.h"
#include "TH1.h"
bool isBHadron(int id) {
// This snippet is meant to capture all B hadrons
// as given in the PDG.
if (id<0) id*=-1;
if (id<500) return false;
return (fmod(id/100,5.)==0.0 || id/1000==5);
}
using namespace Pythia8;
int main() {
// Initialize root
TROOT root("Manuel's ROOT Session","PYTHIA Histograms");
// Generator. Process selection. LHC initialization. Histogram.
Pythia pythia;
// Uncomment line below to turns on all HardQCD processses
// These are 111-116 and 121-124
//pythia.readString("HardQCD:all = on");
// Turn on only bbar production:
// g g -> b bbar (subprocess 123)
// q qbar -> b bbar (subprocess 124)
pythia.readString("HardQCD:gg2bbbar = on");
pythia.readString("HardQCD:qqbar2bbbar = on");
pythia.readString("PhaseSpace:pTHatMin = 20.");
// Random number Generator Should be Set Here if needed (before pythia.init())
// On seeds:
// seed = -1 : default (any number < 0 will revert to the default). seed = 19780503
// seed = 0 : calls Stdlib time(0) to provide a seed based on the unix time
// seed = 1 through 900 000 000: various numbers that can be used as seeds
//pythia.readString("Random.setSeed = on");// doesn't work needs fixing
//pythia.readString("Random.seed = 3000000");
pythia.init( 2212, 2212, 200.);
Hist mult("charged multiplicity", 100, -0.5, 799.5);
TH1D* multHist = new TH1D("multHist","Multiplicity",100,-0.5,99.5);
TH1D* bquarkPt = new TH1D("bquarkPt","bquarkPt",100,0,50);
TH1D* bbarquarkPt = new TH1D("bbarquarkPt","bbar quark Pt",100,0,50);
TH1D* B0mesonPt = new TH1D("BOmesonPt","B0mesonPt",100,0,50);
TH1D* B0barmesonPt = new TH1D("BObarmesonPt","B0bar meson Pt",100,0,50);
TH1D* electronFrombPt = new TH1D("electronFrombPt","electrons from b",100,0,30);
TH1D* positronFrombPt = new TH1D("positronFrombPt","positrons from b",100,0,30);
TH1D* epluseminusMinv = new TH1D("epluseminusMinv","e+ e- Inv. Mass",100,0,30);
// Begin event loop. Generate event. Skip if error. List first one.
for (int iEvent = 0; iEvent < 10000; ++iEvent) {
if (!pythia.next()) continue;
if (iEvent < 1) {pythia.info.list(); pythia.event.list();}
// Find number of all final charged particles and fill histogram.
// Find the b (id = 5) and bbar (id = -5), find their daughters,
// if daughters include electron (id = 11) and positron (id=-11), calculate their
// invariant mass
// Status flags:
// 21 incoming particles of hardest subprocess
// 23 outgoing particles of hardest subprocess
// 81-89 primary hadrons produced by hadronization process (B mesons, e.g.)
// 91-99 particles produced in decay process or by B-E effects (e.g. the electrons)
int nCharged = 0;
int indexBQuark(0), indexBbarQuark(0);
for (int i = 0; i < pythia.event.size(); ++i) {
if (pythia.event[i].isFinal() && pythia.event[i].isCharged()) {
++nCharged;
}
Particle& theParticle = pythia.event[i];
if (theParticle.id() == 5 ) {
indexBQuark = i;
//cout << "Mother 1, Mother 2 = " << theParticle.mother1() << ", " << theParticle.mother2() << endl;
}
if (theParticle.id() == -5) {
indexBbarQuark = i;
//cout << "Mother 1, Mother 2 = " << theParticle.mother1() << ", " << theParticle.mother2() << endl;
}
} // particle loop
cout << "Found b quark at index " << indexBQuark << endl;
cout << "Found bbar quark at index " << indexBbarQuark << endl;
bquarkPt->Fill(pythia.event[indexBQuark].pT());
bbarquarkPt->Fill(pythia.event[indexBbarQuark].pT());
mult.fill( nCharged );
multHist->Fill(nCharged);
//cout << "Event " << iEvent << ", Nch= " << nCharged << endl;
//Find hadronization products of b and bbar.
int bQuarkDaughter1 = pythia.event[indexBQuark].daughter1();
int bQuarkDaughter2 = pythia.event[indexBQuark].daughter2();
int bbarQuarkDaughter1 = pythia.event[indexBbarQuark].daughter1();
int bbarQuarkDaughter2 = pythia.event[indexBbarQuark].daughter2();
// Obtain the two hadrons from the fragmentation process
// Use the PDG id's for this. All B mesons id's are of the form xx5xx, and
// all B baryons are of the form 5xxx.
// So we obtain the id, (make it positive if needed) and then test
// to see if it is a meson with fmod(currId/100,5)==0.0
// to see if it is a baryon with currId/1000==5
int HadronFromBQuark(0), HadronFromBbarQuark(0);
if (bQuarkDaughter1<bQuarkDaughter2) {
cout << "Daughters of b Quark" << endl;
for (int j=bQuarkDaughter1; j<=bQuarkDaughter2; ++j) {
if (isBHadron(pythia.event[j].id())) {
cout << "Fragmentation: b -> " << pythia.event[j].name() << endl;
cout << " id " << pythia.event[j].id() << " at index " << j << endl;
HadronFromBQuark = j;
}
}
}
if (bbarQuarkDaughter1<bbarQuarkDaughter2) {
cout << "Daughters of bbar Quark" << endl;
for (int k=bbarQuarkDaughter1; k<=bbarQuarkDaughter2; ++k) {
if (isBHadron(pythia.event[k].id())) {
cout << "Fragmentation : bbar -> " << pythia.event[k].name() << endl;
cout << " id " << pythia.event[k].id() << " at index " << k << endl;
HadronFromBbarQuark = k;
}
}
}
// Search the daughters of the hadrons until electrons and positrons are found
// if there are any from a semileptonic decay of a beauty hadron
// Start with the b quark
int Daughter(HadronFromBQuark), electronIndex(0), positronIndex(0);
while (Daughter!=0) {
cout << "Checking " << pythia.event[Daughter].name() << " for e+/e- daughters" << endl;
if (pythia.event[Daughter].id()==-511) {
// This is a Bbar0, enter its pT
cout << "Filling Bbar0 pT" << endl;
B0barmesonPt->Fill(pythia.event[Daughter].pT());
}
if (pythia.event[Daughter].id()==511) {
// This is a B0, enter its pT
cout << "Filling Bbar0 pT" << endl;
B0mesonPt->Fill(pythia.event[Daughter].pT());
}
int nextDaughter1 = pythia.event[Daughter].daughter1();
int nextDaughter2 = pythia.event[Daughter].daughter2();
// search for electron or positron
for (int iDaughter = nextDaughter1; iDaughter<=nextDaughter2; ++iDaughter) {
if (pythia.event[iDaughter].id()==11) {
cout << "Found electron" << endl;
cout << pythia.event[iDaughter].name() << endl;
electronIndex=iDaughter;
electronFrombPt->Fill(pythia.event[electronIndex].pT());
break;
}
if (pythia.event[iDaughter].id()==-11) {
cout << "Found positron" << endl;
cout << pythia.event[iDaughter].name() << endl;
positronIndex=iDaughter;
positronFrombPt->Fill(pythia.event[positronIndex].pT());
break;
}
}// loop over daughters to check for e+e-
// If we get here, that means there were no electrons nor positrons.
// Set the Daughter index to zero now.
Daughter = 0;
// If any of the daughters is still a beauty-hadron, we can try again
// and reset the Daughter index, but only if one of the daughters contains a
// b quark.
for (int jDaughter = nextDaughter1; jDaughter<=nextDaughter2; ++jDaughter) {
if (isBHadron(pythia.event[jDaughter].id())) {
//One of the daughters is a beauty hadron.
Daughter = jDaughter;
}
}// loop over daughters to check for another b hadron
}// end of search for electrons in all the daughters of the b quark
// Now search among the daughters of the bbar quark
Daughter=HadronFromBbarQuark;
while (Daughter!=0) {
cout << "Checking " << pythia.event[Daughter].name() << " for e+/e- daughters" << endl;
if (pythia.event[Daughter].id()==-511) {
// This is a Bbar0, enter its pT
cout << "Filling Bbar0 pT" << endl;
B0barmesonPt->Fill(pythia.event[Daughter].pT());
}
if (pythia.event[Daughter].id()==511) {
// This is a B0, enter its pT
cout << "Filling B0 pT" << endl;
B0mesonPt->Fill(pythia.event[Daughter].pT());
}
int nextDaughter1 = pythia.event[Daughter].daughter1();
int nextDaughter2 = pythia.event[Daughter].daughter2();
// search for electron or positron
for (int iDaughter = nextDaughter1; iDaughter<=nextDaughter2; ++iDaughter) {
//cout << "daughter is a " << pythia.event[iDaughter].name() << endl;
if (pythia.event[iDaughter].id()==11) {
cout << "Found electron" << endl;
cout << pythia.event[iDaughter].name() << endl;
electronIndex=iDaughter;
electronFrombPt->Fill(pythia.event[electronIndex].pT());
break;
}
if (pythia.event[iDaughter].id()==-11) {
cout << "Found positron" << endl;
cout << pythia.event[iDaughter].name() << endl;
positronIndex=iDaughter;
positronFrombPt->Fill(pythia.event[positronIndex].pT());
break;
}
}// loop over daughters to check for e+e-
// If we get here, that means there were no electrons nor positrons.
// Set the Daughter index to zero now.
Daughter = 0;
// If any of the daughters is still a beauty-hadron, we can try again
// and reset the Daughter index, but only if one of the daughters contains a
// b quark.
for (int jDaughter = nextDaughter1; jDaughter<=nextDaughter2; ++jDaughter) {
if (isBHadron(pythia.event[jDaughter].id())) {
//One of the daughters is a beauty hadron.
Daughter = jDaughter;
}
}// loop over daughters to check for another b hadron
}//end of search for electron among daughters of bbar quark
if (electronIndex!=0 && positronIndex!=0) {
cout << "Found an e+e- pair from bbar" << endl;
cout << "Ele 4-mom = " << pythia.event[electronIndex].p() << endl;
cout << "Pos 4-mom = " << pythia.event[positronIndex].p() << endl;
Vec4 epluseminus(pythia.event[electronIndex].p()+pythia.event[positronIndex].p());
epluseminusMinv->Fill(epluseminus.mCalc());
}
else {
cout << "No e+e- pair in event" << endl;
}
// End of event loop. Statistics. Histogram. Done.
}// event loop
pythia.statistics();
//cout << mult << endl;
//Write Output ROOT hisotgram into ROOT file
TFile* outFile = new TFile("pythiaOutputHistos1M.root","RECREATE");
multHist->Write();
bquarkPt->Write();
bbarquarkPt->Write();
B0mesonPt->Write();
B0barmesonPt->Write();
electronFrombPt->Write();
positronFrombPt->Write();
epluseminusMinv->Write();
outFile->Close();
return 0;
}
Code to run with STAR HF Tune
// main00.cc
// Modified from the main01.cc
// which is a part of the PYTHIA event generator.
// Copyright (C) 2008 Torbjorn Sjostrand.
// PYTHIA is licenced under the GNU GPL version 2, see COPYING for details.
// Please respect the MCnet Guidelines, see GUIDELINES for details.
// This is a simple test program.
#include "Pythia.h"
#include "Basics.h"
#include "TROOT.h"
#include "TFile.h"
#include "TH1.h"
bool isBHadron(int id) {
// This snippet is meant to capture all B hadrons
// as given in the PDG.
if (id<0) id*=-1;
if (id<500) return false;
return (fmod(id/100,5.)==0.0 || id/1000==5);
}
using namespace Pythia8;
double myRapidity(Vec4& p) {
return 0.5*log(p.pPlus()/p.pMinus());
}
int main() {
// Initialize root
TROOT root("Manuel's ROOT Session","PYTHIA Histograms");
// Generator. Process selection. LHC initialization. Histogram.
Pythia pythia;
// Shorthand for some public members of pythia (also static ones).
//Event& event = pythia.event;
ParticleDataTable& pdt = pythia.particleData;
// The cmnd file below contains
// the Pythia Tune parameters
// the processes that are turned on
// and the PDFs used
// for the pythia run.
pythia.readFile("main00.cmnd");
UserHooks *oniumUserHook = new SuppressSmallPT();
pythia.setUserHooksPtr(oniumUserHook);
cout << "Mass of b quark " << ParticleDataTable::mass(5) << endl;
cout << "Mass of b bar " << ParticleDataTable::mass(-5) << endl;
// Extract settings to be used in the main program.
int nEvent = pythia.mode("Main:numberOfEvents");
int nList = pythia.mode("Main:numberToList");
int nShow = pythia.mode("Main:timesToShow");
int nAllowErr = pythia.mode("Main:timesAllowErrors");
bool showCS = pythia.flag("Main:showChangedSettings");
bool showSett = pythia.flag("Main:showAllSettings");
bool showStat = pythia.flag("Main:showAllStatistics");
bool showCPD = pythia.flag("Main:showChangedParticleData");
pythia.init();
if (showSett) pythia.settings.listAll();
if (showCS) pythia.settings.listChanged();
if (showCPD) pdt.listChanged();
Hist mult("charged multiplicity", 100, -0.5, 799.5);
TH1D* multHist = new TH1D("multHist","Multiplicity",100,-0.5,99.5);
TH1D* bquarkPt = new TH1D("bquarkPt","bquarkPt",100,0,50);
TH1D* bbarquarkPt = new TH1D("bbarquarkPt","bbar quark Pt",100,0,50);
TH1D* B0mesonPt = new TH1D("BOmesonPt","B0mesonPt",100,0,50);
TH1D* B0barmesonPt = new TH1D("BObarmesonPt","B0bar meson Pt",100,0,50);
TH1D* BplusmesonPt = new TH1D("BplusmesonPt","BplusmesonPt",100,0,50);
TH1D* BminusmesonPt = new TH1D("BminusmesonPt","Bminus meson Pt",100,0,50);
TH1D* BplusmesonPtCDFrap = new TH1D("BplusmesonPtCDFrap","BplusmesonPt |y|<1",100,0,50);
TH1D* BminusmesonPtCDFrap = new TH1D("BminusmesonPtCDFrap","Bminus meson Pt |y|<1",100,0,50);
TH1D* electronFrombPt = new TH1D("electronFrombPt","electrons from b",100,0,30);
TH1D* positronFrombPt = new TH1D("positronFrombPt","positrons from b",100,0,30);
TH1D* epluseminusMinv = new TH1D("epluseminusMinv","e+ e- Inv. Mass",300,0,30);
TH1D* epluseminusRapidity = new TH1D("epluseminusRapidity","e+ e- y",80,-4,4);
TH1D* epluseminusMinvMidRap = new TH1D("epluseminusMinvMidRap","e+ e- Inv. Mass |y|<0.5",300,0,30);
// Begin event loop. Generate event. Skip if error. List first one.
int nPace = max(1,nEvent/nShow);
int nErrors(0);
for (int iEvent = 0; iEvent < nEvent; ++iEvent) {
if (!pythia.next()) {
++nErrors;
if (nErrors>=nAllowErr) {
cout << "Reached error limit : " << nErrors << endl;
cout << "Bailing out! " << endl;
break;
}
continue;
}
if (iEvent%nPace == 0) cout << " Now begin event " << iEvent << endl;
if (iEvent < nList) {pythia.info.list(); pythia.event.list();}
// Find number of all final charged particles and fill histogram.
// Find the b (id = 5) and bbar (id = -5), find their daughters,
// if daughters include electron (id = 11) and positron (id=-11), calculate their
// invariant mass
// Status flags:
// 21 incoming particles of hardest subprocess
// 23 outgoing particles of hardest subprocess
// 81-89 primary hadrons produced by hadronization process (B mesons, e.g.)
// 91-99 particles produced in decay process or by B-E effects (e.g. the electrons)
int nCharged = 0;
int indexBQuark(0), indexBbarQuark(0);
for (int i = 0; i < pythia.event.size(); ++i) {
if (pythia.event[i].isFinal() && pythia.event[i].isCharged()) {
++nCharged;
}
Particle& theParticle = pythia.event[i];
if (theParticle.id() == 5 ) {
indexBQuark = i;
//cout << "Mother 1, Mother 2 = " << theParticle.mother1() << ", " << theParticle.mother2() << endl;
}
if (theParticle.id() == -5) {
indexBbarQuark = i;
//cout << "Mother 1, Mother 2 = " << theParticle.mother1() << ", " << theParticle.mother2() << endl;
}
} // particle loop
cout << "Found b quark at index " << indexBQuark << endl;
cout << "Found bbar quark at index " << indexBbarQuark << endl;
bquarkPt->Fill(pythia.event[indexBQuark].pT());
bbarquarkPt->Fill(pythia.event[indexBbarQuark].pT());
mult.fill( nCharged );
multHist->Fill(nCharged);
//cout << "Event " << iEvent << ", Nch= " << nCharged << endl;
//Find hadronization products of b and bbar.
int bQuarkDaughter1 = pythia.event[indexBQuark].daughter1();//first daughter index
int bQuarkDaughter2 = pythia.event[indexBQuark].daughter2();//last daughter index
int bbarQuarkDaughter1 = pythia.event[indexBbarQuark].daughter1();
int bbarQuarkDaughter2 = pythia.event[indexBbarQuark].daughter2();
// Obtain the two hadrons from the fragmentation process
// Use the PDG id's for this. All B mesons id's are of the form xx5xx, and
// all B baryons are of the form 5xxx.
// So we obtain the id, (make it positive if needed) and then test
// to see if it is a meson with fmod(currId/100,5)==0.0
// to see if it is a baryon with currId/1000==5
int HadronFromBQuark(0), HadronFromBbarQuark(0);
if (bQuarkDaughter1<bQuarkDaughter2) {
cout << "Daughters of b Quark" << endl;
for (int j=bQuarkDaughter1; j<=bQuarkDaughter2; ++j) {
if (isBHadron(pythia.event[j].id())) {
cout << "Fragmentation: b -> " << pythia.event[j].name() << endl;
cout << " id " << pythia.event[j].id() << " at index " << j << endl;
HadronFromBQuark = j;
}
}
}
if (bbarQuarkDaughter1<bbarQuarkDaughter2) {
cout << "Daughters of bbar Quark" << endl;
for (int k=bbarQuarkDaughter1; k<=bbarQuarkDaughter2; ++k) {
if (isBHadron(pythia.event[k].id())) {
cout << "Fragmentation : bbar -> " << pythia.event[k].name() << endl;
cout << " id " << pythia.event[k].id() << " at index " << k << endl;
HadronFromBbarQuark = k;
}
}
}
// Search the daughters of the hadrons until electrons and positrons are found
// if there are any from a semileptonic decay of a beauty hadron
// Start with the b quark, the b-bar quark loop comes after this
int Daughter(HadronFromBQuark), electronIndex(0), positronIndex(0);
while (Daughter!=0) {
cout << "Checking " << pythia.event[Daughter].name() << " for e+/e- daughters" << endl;
if (pythia.event[Daughter].id()==-511) {
// This is a Bbar0, enter its pT
cout << "Filling Bbar0 pT" << endl;
B0barmesonPt->Fill(pythia.event[Daughter].pT());
}
if (pythia.event[Daughter].id()==511) {
// This is a B0, enter its pT
cout << "Filling Bbar0 pT" << endl;
B0mesonPt->Fill(pythia.event[Daughter].pT());
}
Vec4 daughterVec4 = pythia.event[Daughter].p();
double daughterRap = myRapidity(daughterVec4);
if (pythia.event[Daughter].id()==-521) {
// This is a Bminus, enter its pT
cout << "Filling Bminus pT" << endl;
BminusmesonPt->Fill(pythia.event[Daughter].pT());
if (fabs(daughterRap)<1.0) {
BminusmesonPtCDFrap->Fill(pythia.event[Daughter].pT());
}
}
if (pythia.event[Daughter].id()==521) {
// This is a Bplus, enter its pT
cout << "Filling Bplus pT" << endl;
BplusmesonPt->Fill(pythia.event[Daughter].pT());
if (fabs(daughterRap)<1.0) {
BplusmesonPtCDFrap->Fill(pythia.event[Daughter].pT());
}
}
int nextDaughter1 = pythia.event[Daughter].daughter1();
int nextDaughter2 = pythia.event[Daughter].daughter2();
// search for electron or positron
for (int iDaughter = nextDaughter1; iDaughter<=nextDaughter2; ++iDaughter) {
if (pythia.event[iDaughter].id()==11) {
cout << "Found electron" << endl;
cout << pythia.event[iDaughter].name() << endl;
electronIndex=iDaughter;
electronFrombPt->Fill(pythia.event[electronIndex].pT());
break;
}
if (pythia.event[iDaughter].id()==-11) {
cout << "Found positron" << endl;
cout << pythia.event[iDaughter].name() << endl;
positronIndex=iDaughter;
positronFrombPt->Fill(pythia.event[positronIndex].pT());
break;
}
}// loop over daughters to check for e+e-
// If we get here, that means there were no electrons nor positrons.
// Set the Daughter index to zero now.
Daughter = 0;
// If any of the daughters is still a beauty-hadron, we can try again
// and reset the Daughter index, but only if one of the daughters contains a
// b quark.
for (int jDaughter = nextDaughter1; jDaughter<=nextDaughter2; ++jDaughter) {
if (isBHadron(pythia.event[jDaughter].id())) {
//One of the daughters is a beauty hadron.
Daughter = jDaughter;
}
}// loop over daughters to check for another b hadron
}// end of search for electrons in all the daughters of the b quark
// Now search among the daughters of the bbar quark
Daughter=HadronFromBbarQuark;
while (Daughter!=0) {
cout << "Checking " << pythia.event[Daughter].name() << " for e+/e- daughters" << endl;
if (pythia.event[Daughter].id()==-511) {
// This is a Bbar0, enter its pT
cout << "Filling Bbar0 pT" << endl;
B0barmesonPt->Fill(pythia.event[Daughter].pT());
}
if (pythia.event[Daughter].id()==511) {
// This is a B0, enter its pT
cout << "Filling B0 pT" << endl;
B0mesonPt->Fill(pythia.event[Daughter].pT());
}
Vec4 daughterVec4 = pythia.event[Daughter].p();
double daughterRap = myRapidity(daughterVec4);
if (pythia.event[Daughter].id()==-521) {
// This is a Bminus, enter its pT
cout << "Filling Bminus pT" << endl;
BminusmesonPt->Fill(pythia.event[Daughter].pT());
if (fabs(daughterRap)<1.0) {
BminusmesonPtCDFrap->Fill(pythia.event[Daughter].pT());
}
}
if (pythia.event[Daughter].id()==521) {
// This is a Bplus, enter its pT
cout << "Filling Bplus pT" << endl;
BplusmesonPt->Fill(pythia.event[Daughter].pT());
if (fabs(daughterRap)<1.0) {
BplusmesonPtCDFrap->Fill(pythia.event[Daughter].pT());
}
}
int nextDaughter1 = pythia.event[Daughter].daughter1();
int nextDaughter2 = pythia.event[Daughter].daughter2();
// search for electron or positron
for (int iDaughter = nextDaughter1; iDaughter<=nextDaughter2; ++iDaughter) {
//cout << "daughter is a " << pythia.event[iDaughter].name() << endl;
if (pythia.event[iDaughter].id()==11) {
cout << "Found electron" << endl;
cout << pythia.event[iDaughter].name() << endl;
electronIndex=iDaughter;
electronFrombPt->Fill(pythia.event[electronIndex].pT());
break;
}
if (pythia.event[iDaughter].id()==-11) {
cout << "Found positron" << endl;
cout << pythia.event[iDaughter].name() << endl;
positronIndex=iDaughter;
positronFrombPt->Fill(pythia.event[positronIndex].pT());
break;
}
}// loop over daughters to check for e+e-
// If we get here, that means there were no electrons nor positrons.
// Set the Daughter index to zero now.
Daughter = 0;
// If any of the daughters is still a beauty-hadron, we can try again
// and reset the Daughter index, but only if one of the daughters contains a
// b quark.
for (int jDaughter = nextDaughter1; jDaughter<=nextDaughter2; ++jDaughter) {
if (isBHadron(pythia.event[jDaughter].id())) {
//One of the daughters is a beauty hadron.
Daughter = jDaughter;
}
}// loop over daughters to check for another b hadron
}//end of search for electron among daughters of bbar quark
if (electronIndex!=0 && positronIndex!=0) {
cout << "Found an e+e- pair from bbar" << endl;
cout << "Ele 4-mom = " << pythia.event[electronIndex].p() << endl;
cout << "Pos 4-mom = " << pythia.event[positronIndex].p() << endl;
Vec4 epluseminus(pythia.event[electronIndex].p()+pythia.event[positronIndex].p());
epluseminusMinv->Fill(epluseminus.mCalc());
double epluseminusRap = 0.5*log((epluseminus.e()+epluseminus.pz())/(epluseminus.e()-epluseminus.pz()));
epluseminusRapidity->Fill(epluseminusRap);
if (fabs(epluseminusRap)<0.5) epluseminusMinvMidRap->Fill(epluseminus.mCalc());
}
else {
cout << "No e+e- pair in event" << endl;
}
// End of event loop. Statistics. Histogram. Done.
}// event loop
if (showStat) pythia.statistics();
//cout << mult << endl;
//Write Output ROOT hisotgram into ROOT file
TFile* outFile = new TFile("pythiaOutputHistosTest.root","RECREATE");
multHist->Write();
bquarkPt->Write();
bbarquarkPt->Write();
B0mesonPt->Write();
B0barmesonPt->Write();
BplusmesonPt->Write();
BminusmesonPt->Write();
BplusmesonPtCDFrap->Write();
BminusmesonPtCDFrap->Write();
electronFrombPt->Write();
positronFrombPt->Write();
epluseminusMinv->Write();
epluseminusRapidity->Write();
epluseminusMinvMidRap->Write();
outFile->Close();
return 0;
}
Varying the Continuum Contribution to the Dielectron Mass Spectrum
Initial Normalization
The normalization to the Drell-Yan and b-bbar cross sections are given by the calculation from Ramona in the Drell-Yan case and by Pythia in the b-bbar case. There is an uncertainty in the overall normalization of the contribution from these two sources to the dielectron continuum under the Upsilon peak. We can do a fit to obtain the Upsilon yield with the normalization fixed. This is shown below.
Fig. 1: Fit to the invariant mass spectrum. The data points are in blue. The Drell-Yan curve is the dot-dashed line and the b-bbar is the dashed line. The Red line is the sum of the Upsilon line shape (obtained from embedding for the 1S+2S+3S keeping their ratios according to the PDG values) plus the continuum contribution from DY+b-bbar. The red histogram is the integral of the red line, which is what is used to compare to the data in the fit (we fit using the "i" option to use the integral of the function in each bin).
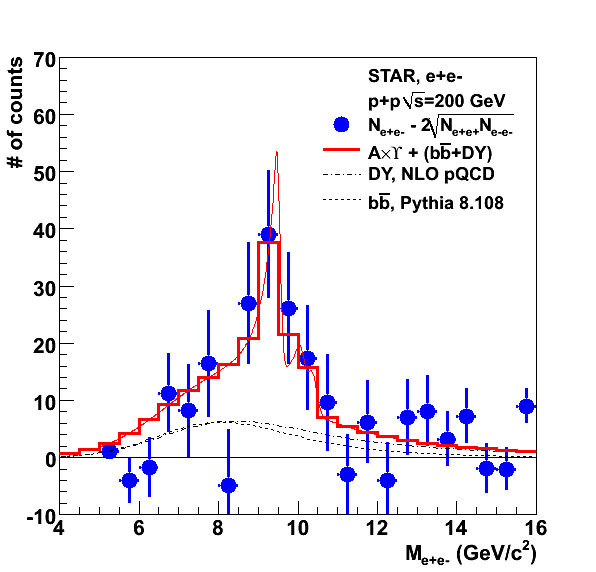
With the above fit, we obtain 64.3 counts after integrating the upsilon part (the yield of DY is 32.3 and the yield of b-bbar is 26.8, both are held fixed for the fit). This gives a cross section of 63.4/(1*0.054*9.6 pb-1) = 124 pb. The efficiency estimate of 5.4% for the overall efficiency is still being checked though, given the E/p shape not being gaussian due to the trigger bias near the L0 threshold, so this can still change.
It is also possible to let the yield of the continuum vary and study if the chisquare/dof of the fit improves. That way, we can not just assume a continuum yield, but actually measure it. Since the yields of the DY and the b-bbar are very similar and given our statistics we can't really discriminate one from the other, we are mainly sensitive to the sum. One way to study this is to keep their ratios fixed as in the plot above, but vary the overall yield of both of them This adds one extra parameter to the fit to account for the total sum of the continuum yield. We perform the fit in the region 5< m < 16 GeV/c2.
One issue is that the Crystal-Ball fit is a user defined function, and we use the integral of the function to fit, which seems to push ROOT to its limit in an interactive session with a macro interpreted on the fly. This is alleviated somewhat by cleaning up the code to do the one-parameter fit in a compiled macro. However, trying out the two-parameter fit directly seems to be too much for ROOT even in compiled mode and the code runs out of memory and seg-faults. A (rather inelegant) way around this is to scale the continuum yield by hand, compile the macro each time and do the one-parameter fit. For each of those fits, one can obtain the chisquare/deg. of freedom. This is shown in the plot below:
Fig. 2. Chisquare per degree of freedom as a function of the continuum yield (Drell-Yan + b-bbar).
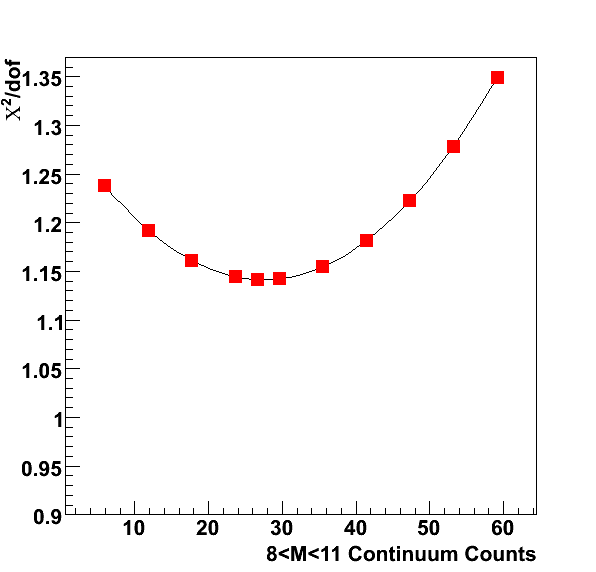
We find a clear minimum, indicating that our data do have some sensitivity to the continuum yield. The Rightmost point with 59.1 counts is the yield obtained directly from Pythia 8.108 and from Ramona's calculation. Our data indicate that the yield is likely smaller by about a factor of 2, we obtain at the minimum a yield of 26.6 counts. Since the yield of Upsilons is obtained from the same fit, our fitted Upsilon yield will increase with decreasing counts from the continuum. This is shown below.
Fig. 3: Fitted yield of Upsilons for a given continuum yield. The minimum found above is illustrated by the vertical line.
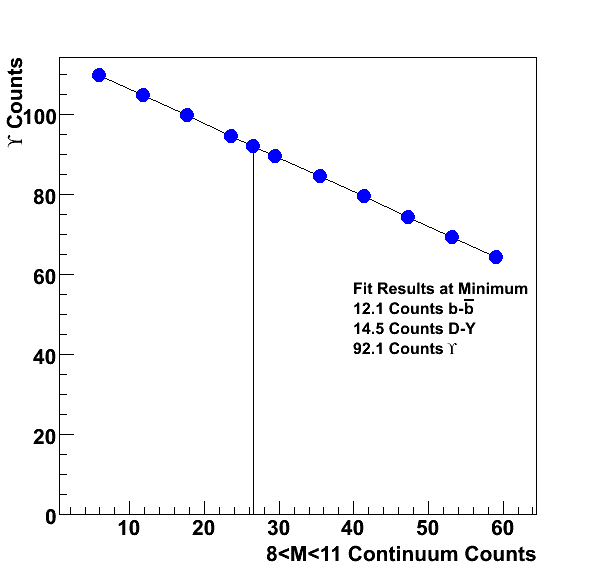
The corresponding plot with the fit at the minimum is shown below.
Fig. 4: Dielectron data with the curves for the DY and b-bbar at the yield which minimizes the chi-square. In other words, the result of a (poor man's) two-parameter fit to find both the Upsilon yield and the Continuum yield.
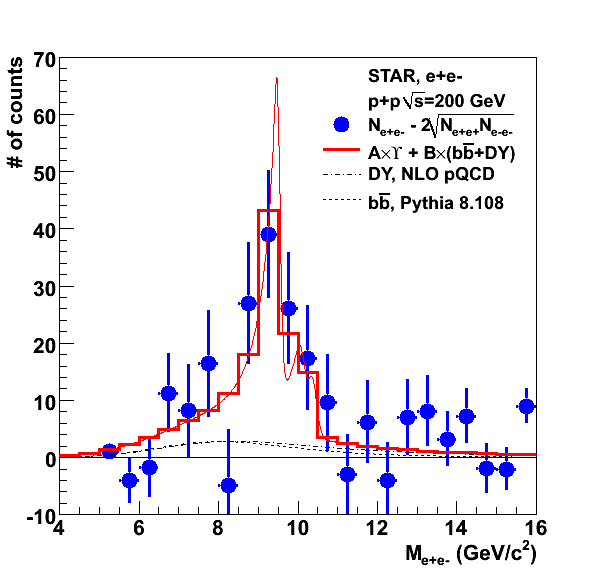
The results of this fit give 14.5 counts for DY and 12.1 counts for b-bbar, i.e a factor 0.45 lower than the 32.3 counts for DY and the 26.8 counts for b-bbar is 26.8 obtained before. Ramona's calculation for dsigma/dm |y|<1 gave 5.25 nb and the Pythia cross section b-bbar cross section times the BR into e+e- gives 6.5 nb, so our data indicate that we can decrease these by a factor 0.45 (or decrease one by essentially 100% and leave the other one unchanged). The Upsilon yield in this case increases to 92.1 counts, which gives a cross section of 92.1/(1*0.054*9.6) = 178 pb. So this has a large effect on the yield (92.1-64.338)/92.1 = 0.3, i.e. a 30% change in the yield (and hence in the cross section). Note also that 178 pb is quite larger than our first estimate for the cross section. This highlights the importance of getting the efficiency estimates right.
WWW
Heavy Flavor Lepton
Heavy flavor leptons provide an extra handle on the open heavy flavor mesons, since they come from semi-leptonic decays of D and B mesons with significant branching ratios. Once produced, leptons do not participate in the strong interaction in the later stages of the collision, and remain a clean probe into the whole evolution of the system. Apart from TPC and TOF, BEMC is used to improve electron identification, and MTD is used for muon detection.
Heavy flavor muons
Non-photonic electrons
Hidden Heavy Flavor
J/psi suppression was one of the proposed QGP signatures in the early days. Later, various cold nuclear matter effects were brought up to complicate the interpretation of J/psi measurements. Still, the study of J/psi collective motion deepens our understanding of the coalescence mechanism and the charm quark collectivity. We also reconstructed Upsilon and observed the suppression of Upsilon(1S+2S+3S).
J/psi
Upsilon
Open Heavy Flavor
More than 99% of charm quarks hadronize into open charm, D mesons. So the measurement of D mesons is a must for the determination of charm cross section. Due to the short life time, the low production rate and the high combinatorial background, the direct reconstruction of D mesons is difficult with the TPC pointing resolution. HFT will be employed to reconstruct the displaced vertex and greatly suppress the combinatorial background. This will also enable the D0 flow analysis, to ascertain the charm quark collectivity. Other open heavy flavor hadrons like Ds and Lambdac will also be studied with HFT.
D mesons
D0 v1 analysis documents
This page is designed to assemble the D0 v1 analysis details.
==> Section 1 <===
Dataset:
Event cuts:
4) ! ( PV_x < e-5 & PV_y < e-5 & PV_z < e-5)
Good run list:
https://drupal.star.bnl.gov/STAR/blog/rksooraj/good-run-lists-hft-embedding
RunQA:
==> Section 2 <===
D0 reconstruction
Single track cuts:
D0 topological cuts:
==> Section 3 <===
Efficiency calculation and spectra
https://drupal.star.bnl.gov/STAR/system/files/Status_D0v1_PreQM_23Mar.pdf
==> Section 4 <===
D0 v1 results
==> Section 5 <===
Systematics
Charged hadron v1 (Run14 vs. Run16)
v2 in different rapidity bins Run14 vs. Run16
Luminosity dependence
drupal.star.bnl.gov/STAR/system/files/Luminosity_effect_on_D0v1.pdf
Link to Overleaf page for analysis note preparation: