Introduction

The purpose here is somewhat two(three?)-fold.  I want to repeat some studies that Jason did with the isolation cut described here with the new Monte Carlo and with the trigger fully simulated.  I want to see not only what gives the best rejection vs. efficiency but what gives the best agreement with the conversion method.  Also I want to investigate the hadronic veto.  I found here that the conversion method gets the right answer in Monte Carlo only when I add hadronic veto by cutting on the energy in the postshower around the gamma candidate.  However, the hadronic veto really kills the statistics so I would like to see how I can lossen that and still maintain the agreement.  The thing I'm going to try is as follows: if there is no energy in a postshower cone of radius R=0.3 around the candidate then it passes.  If there is energy I look at the ratio of the energy in a cone of radius R=0.1 to R=0.3.  Real photons do deposit some energy in a very narrow cone so this will be like a "hadronic isolation."  The plan is to scan the hadronic isolation just like the energy isolation and see what gives the best rejection vs. efficiency and agreement with the Monte Carlo.

Method

1.  Fix the hadronic veto at nominal - energy in a postshower cone of radius R=0.3 is 0.

2.  Scan the energy isolation cut for agreement in data vs. Monte Carlo, rejection vs. efficiency and conversion method accuracy.

3.  Fix the energy isolation cut at the value found in (2) and then repeat while scanning the hadronic veto.

4.  Repeat steps 2 & 3 if necessary to find the optimal point for both cuts.

Results

First I look at the agreement between data and Monte Carlo of the isolation varaible = ET(1x1c)/ET(0.3) in different pT and eta bins.  The only cut applied here is that the candidate has transverse momentum > 5 GeV.

Left plot: Isolation ratio in signal vs. background, both normalized to 1.  Middle plot: isolation ratio compared to data (absolute norm from the data).  Right Plot: rejection & eff vs. isolation cut.

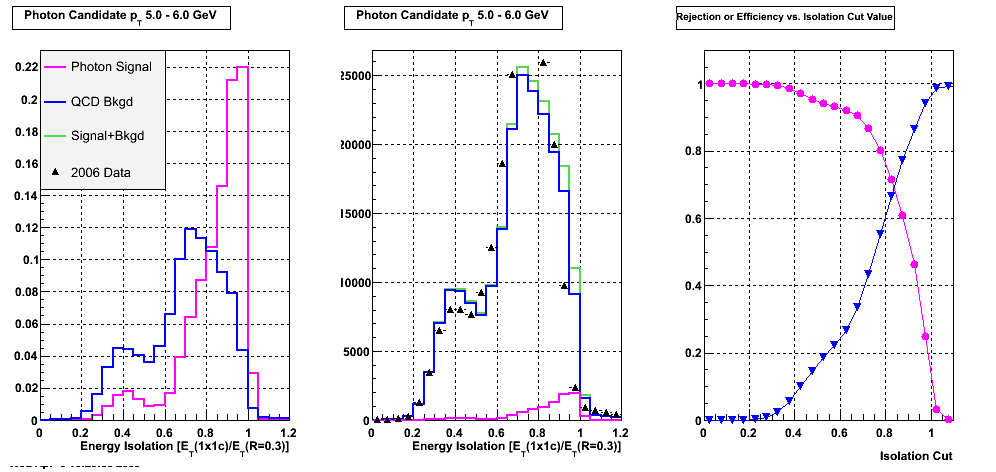
 Figure 1: Energy Isolation for photons with 5<pT<6

Figure 2:  Energy isolation for candidates with 6<pT<8.

 Figure 3: Energy isolation for candidates with 8< pT< 12.

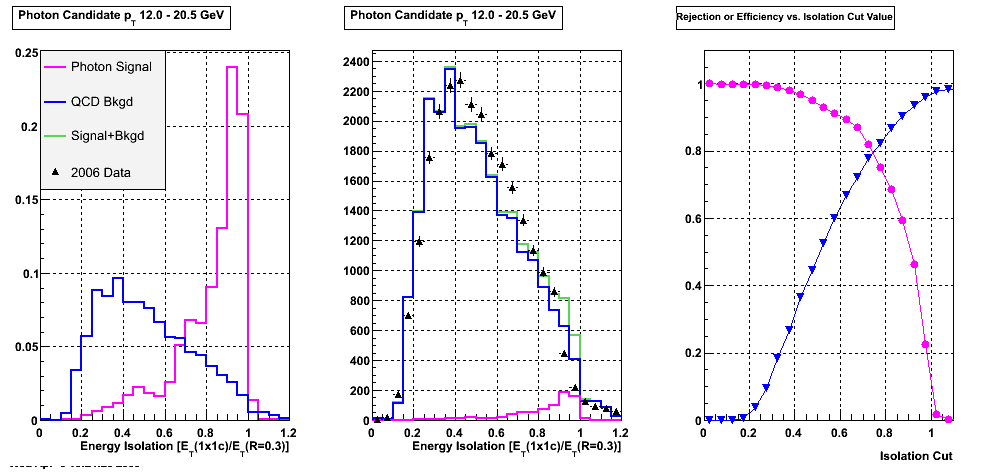
Figure 4: Energy isolation for candidates with pT> 12.  pT is not cut off at 20  - label is wrong.

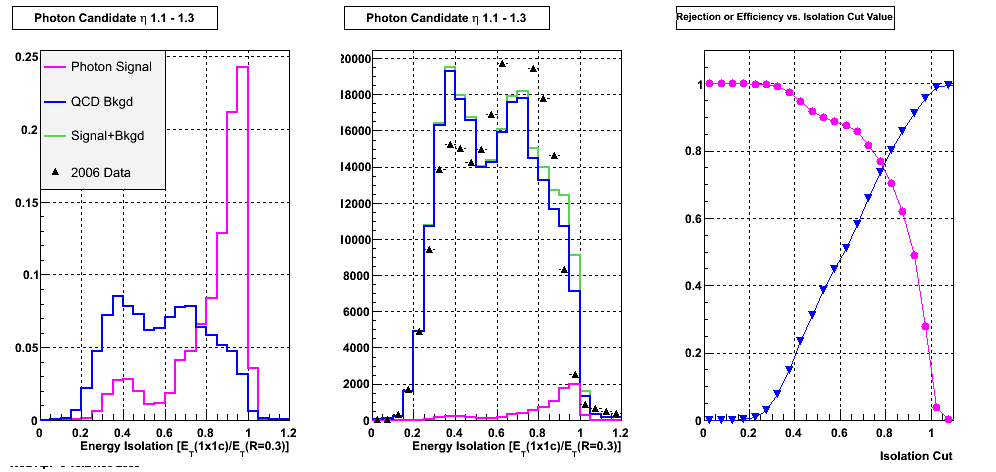
Figure 5: Energy isolation eta < 1.3.  Label is not quite right again.

Figure 6: Energy isolation for for candidates with 1.3< eta< 1.7.

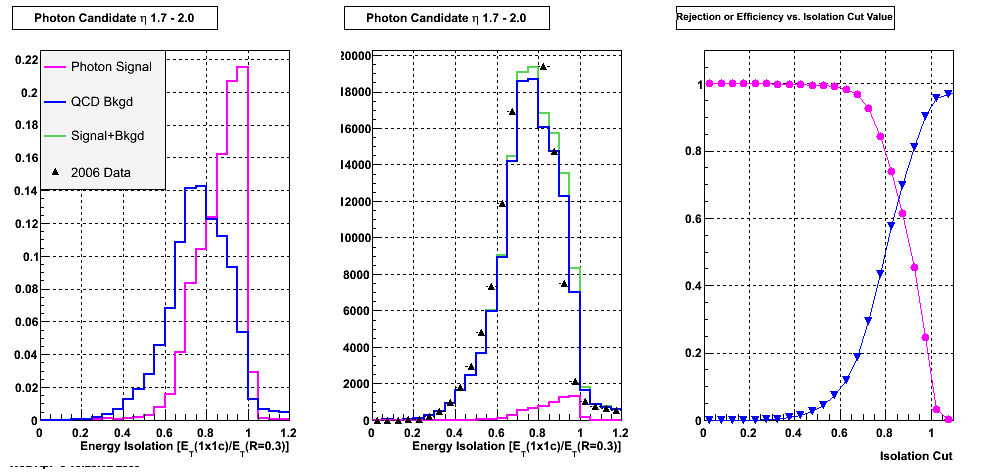
Figure 7: Energy isolation for candidates with 1.7 < eta< 2.0

Comments on Energy isolation agreement: I guess this isn't too bad, given the overall agreement between data and Monte Carlo in general.  Based on rejection vs. efficiency it seems that a cut anywhere between Iso > 0.8 and Iso> 0.9 would be OK. 

Now to get additional input on where to make the cut, I look at the number of photons the conversion method predicts (after all cuts) versus the number matched in a cone of R=0.3 in the QCD Monte Carlo.  I set the hadronic vet to nominal, requiring no energy in the postshower.  Results are in the plot below.

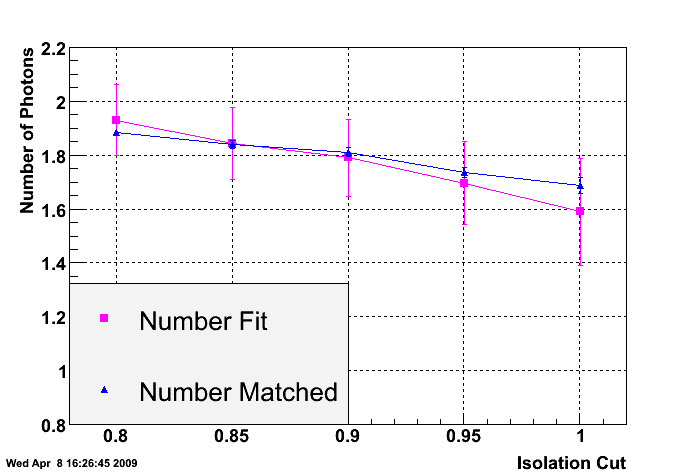
So the agreement between the Monte Carlo and the conversion method is relatively insensitive to the isolation cut value. 

For the next part I fix the minimum isolation to 0.8 and try to scan the hadronic veto.  First, let's look at the energy in the postshower cone of radius R=0.3 for the signal and background in the Monte Carlo.  Here I select gamma candidates with pT> 5 GeV and energy isolation ratio > 0.8. In this plot black is the photons and red is QCD background.

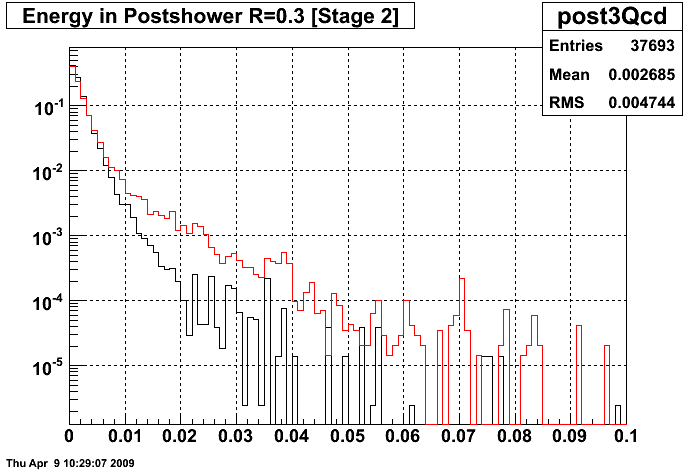
Now the above plot doesn't look very good for discriminating signal from background because there is too much background in the 0 bin.  So there is really no point to trying to do ratios, etc.

Another way to use the posthower is to use the "D variable" where D is a ratio between postshower energy and energy in the smd strips:

D = Ln(Epost/(Eu+Ev+delta).

I apply the same cuts as above and get the following plot.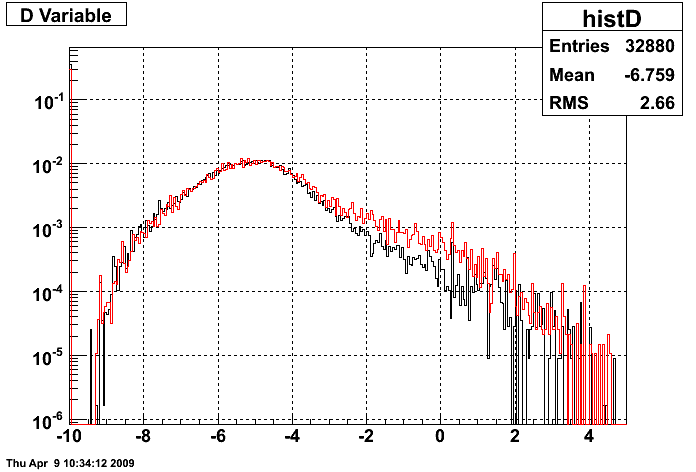

The discrimation here also looks lousy.

Comments

So I've seen, and I believe Jason has seen, that the conversion method doesn't work unless a hadronic veto is applied.  However, using the postshower does a really lousy job of distinguishing signal from background.  Can we justify a cut on the postshower energy based on the plots above?