Determining efficiencies, yields for signal and background, take 1
Updated on Fri, 2008-05-02 14:47. Originally created by jwebb on 2008-04-27 15:59.



Contents:
0.0 Data sample and cuts
Data:
Use the 178 run "electrum" runlist defined Gamma tree production.
Cuts:
1) Reconstruct 3x3 tower clusters w/in EEMC with pT>5 GeV
2) Isolation cut -- ET/ET(0.3) > 90%
3) CPV cut -- Epre1(0.3) == 0
We then examine various distributions for the events which satisfy the CPV cut. We may also apply the double CPV cut, requiring Epre2==0 in addition to the Epre1==0 condition, to further enhance the signal/background.
0.1 Section 0.1
1.0 Single photon efficiency
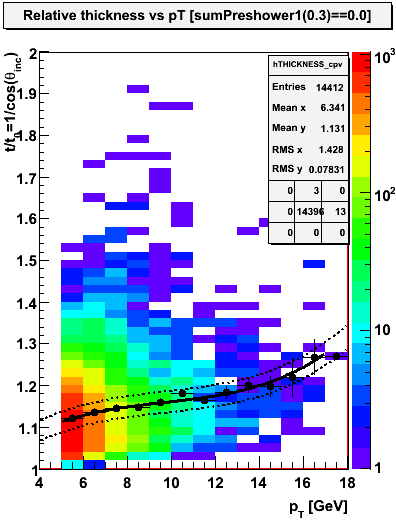
Below we show a plot of the mean thickness seen by photon candidates as a function of transverse momentum.
Figure 1.1 -- Plot of 1/cos(θ) = (thickness)/(thickness at normal incidence) versus pT. The fit is to a 3rd degree poly. The two dashed bands represent the upper and lower tolerance of 0.4mm noted in the master geometry file. Data points represent the mean w/in each pT bin. Error bars represent the uncertainty in the mean.
Observations:
1. This is the mean thickness of the first absorber vs. pT for all events which satisify the cuts above.
2. The detailed behavior is a convolution of several effects, including
a. The vertex vs trigger bias
b. The cross section (dN/deta)
c. The effectiveness of the cuts versus eta
2.0 Photonic background efficiency
3.0 Hadronic background yields
In this section we examine energy ratios between the SMD and towers in an attempt to quantify the contamination due to hadronic showers. We focus on events which satisfy
a charged-particle veto, but note that the method should be valid for events which have Epre1>0 as well.
Subsections:
3.1 Sampling fraction of the SMD versus number of hit strips
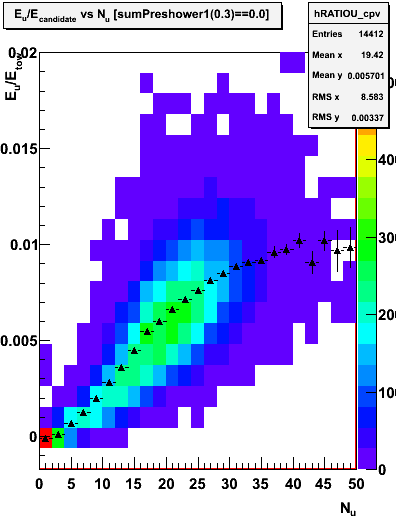
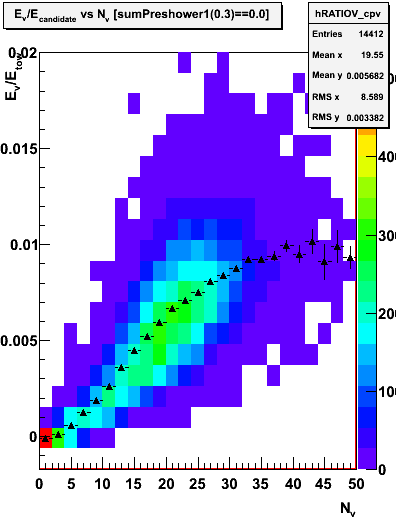
Figure 3.1 -- Measured SMD sampling fraction versus N smd strips with ADC > 3 sigma + ped. U left, V right. Events satisfy the CPV. Triangles (error bars) represent the mean (spread) of the distribution.


Observations:
1. As Nstrips --> 0, the yield should be dominated by hadronic showers. We see no energy deposited in the SMD (relative to the tower) for these events.
2. For large N strips, we expect the signal to be dominated by photonic backgrounds and single gammas. Here we approach a 1% sampling fraction per plane.
3. There is no reason to expect that the sampling fraction for single gammas and the photonic background events will be identical.
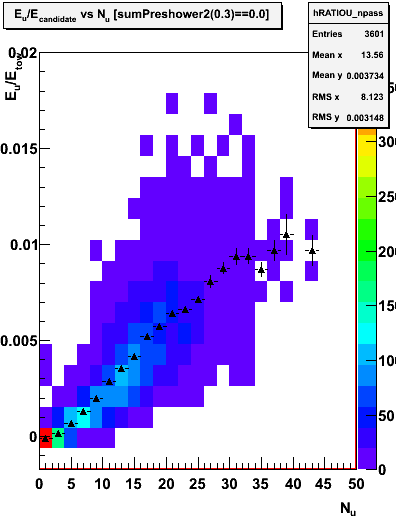
Figure 3.2 -- Measured SMD sampling fraction versus N smd strips with ADC > 3 sigma + ped. U left, V right. Events satisfy a double CPV (pre1 and pre2 == 0). Trangles (error bars) represent the mean (spread) of the distribution.


3.2 Sampling fraction of the SMD versus D
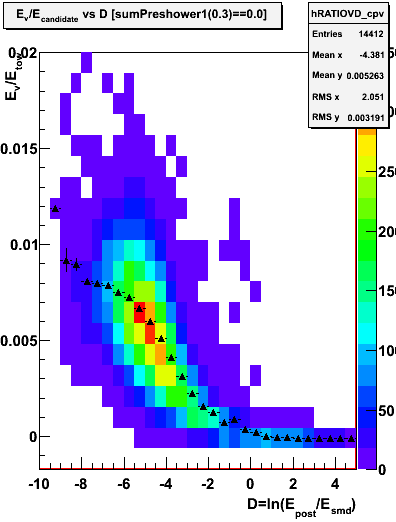
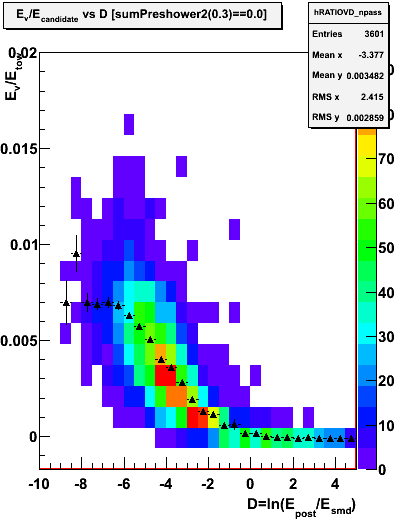
Figure 3.3 -- Eu/Etower vs D and Ev/Etower vs D right. Events satisfy the CPV cut. Triangles (error bars) represent the mean (spread) of the distribution.


Figure 3.4 -- Eu/Etower vs D and Ev/Etower vs D right. Events satisfy a double CPV cut (Epre1==0 and Epre2==0). Triangles (error bars) represent the mean (spread) of the distribution.


3.3 Attempt to extract hadronic background
Given figure 3.1-3.4, and some reasonable estimates for the SMD sampling fraction for single gammas and/or photonic background events, it should be possible to determine the fraction of photons (including photonic backgrounds) to hadronic events. Here are the estimates and assumptions which I am making:
1. Assume that the sampling fraction for an event type is independent of both Nstrips and D. (Note-- I will discuss this assumption below). Given this assumption,
2. Estimate a single-photon sampling fraction of 0.007 (per plane) from behavior as D-->0 in figure 3.4. These should be our least contaminated photons.
3. Estimate a multi-photon sampling fraction of 0.0095 (per plane) from behavior as D-->0 in figure 3.3. This number is somewhat soft, but we're only trying to get a rough idea of what's going on here.
4. From figures 3.3 and 3.4 it's pretty clear that the sampling fraction for an hadronic event is zero. (Again, for hadrons which convert well w/in the stack).
5. For events with Epre1==0, assume "photon" signal is a mix of 1/2 single photons and 1/2 pi0-like backgrounds.
6. For events with Epre1==0 and Epre2==0, assume "photon signal" is pure single photon.
Then for Epre1==0:
N(>=1gamma) = Ntotal * ( measured s.f. ) / ( 0.007/2 + 0.0095/2 )
For Epre1==0 and Epre2==0
N(>=1gamma) = Ntotal * ( measured s.f. ) / 0.007
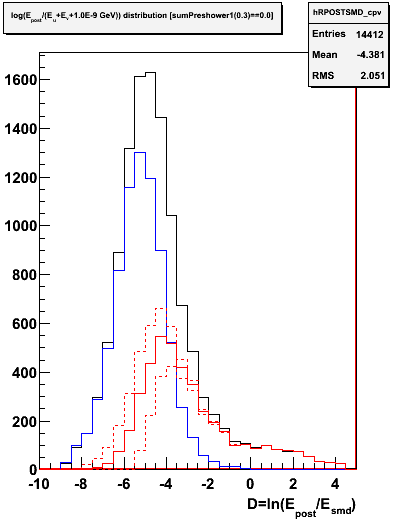
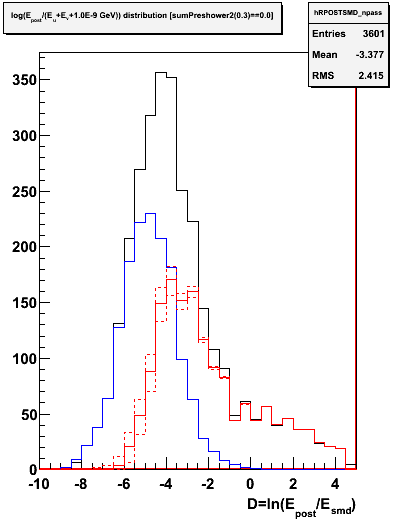
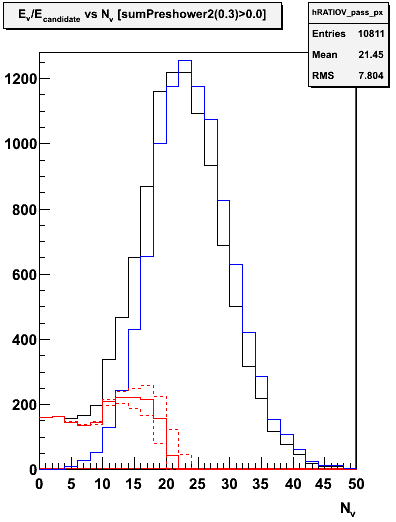
Figure 3.5 -- Left: events which pass the CPV cut (Epre1==0). Right: events which pass a double CPV cut (Epre1==0&&Epre2==0). Solid black histogram indicates the total number of events. Blue histogram the number of photons and photonic background events estimated using the above equations. Red histograms denote the hadronic background estimated from the above (Nhadron = Ntotal - Ngamma). The dashed red lines show a WAG at systematics.


Observations:
1) For Epre1==0 I estimate 28% of the events with -10<D<-1 are from hadronic showers, based on the above figure.
2) For Epre1==0&&Epre2==0, I estimate 42% of the events with -10<D<-1 are from hadronic showers, based on the above figure.
3) Compare with ~7% as estimated from a 2-gaussian fit to the Epre1==0 distribution.
4) The increased fraction of hadronic showers in the (Epre1==0&&Epre2==0) is expected since the Epre2==0 condition supresses electromagnetic showers much more heavily than hadronic showers.
Next I'll try to extract the Nstrip dependence for the hadronic background. I'll play a little loose here. The photonic-backgrounds tend towards higher numbers of SMD strips hit. So we'll estimate a 0.007 sampling fraction for single photons at low Nstrips. Also, as a hadronic shower deposits energy across more strips, it is almost certainly depositing a larger fraction of its energy. Thus it is unlikely that sf(hadron)=0 will hold. The point of this exercise is to get a qualitative feel for what's happening, not to pin it down to 3 significant figures.
Figure 3.6 -- Estimate hadron yields vs N strips with ADC > 3 sigma + ped for SMDU (left) and SMDV (right). Events satisfy the CPV (Epre1==0) condition. No cut on Epre2. We use sf(gamma) = 0.007, and do not attempt to average in the photonic background sampling fraction (this should be OK as these backgrounds tend to be higher strip numbers).


Observations:
1) Hadronic backgrounds are fairly significant, even near ~15 hit SMD strips.
2) The total integral appears smaller than indicated by the upper-left panel in figure 3.5. We have different assumptions about sampling fractions (figure 3.5 averages gamma and pi0, but the dashed lines in figure 3.5 indicate pure photon and pure pi0 assumptions). So these estimates are pretty soft right now.
3) I would guess that the peak in D around D=-4 for the neutral hadrons would be associated with the hadronic events showing up at larger numbers of SMD strips... i.e. they both indicate large hadronic energy deposited w/in the SMD.
3.4 Some Obsertvations and Conclusions and Random Thoughts
1) There is a potentially large contamination of hadronic showers in the event sample.
2) I expect figure 3.5 may be an underestimate of this contamination. Why?
The estimate of the hadronic contamination was based on several assumptions, one of which was that the SMD sampling fraction for such events was constant and zero. This assumption should fail for the ~25% of events which convert near the SMD. When a neutral (or charged) hadron first converts, it dumps ~1/3 of its energy as a prompt-electromagnetic signal. This will clearly be sampled by the SMD at some level. So the sampling fraction for this class of events will be higher, and it will take more of these events to "pull down the average".
3) This technique for estimating the hadronic background should be viable for events with Epre1>0, so useful for a purely shower-shape driven analysis.
4) We're clearly going to need to understand the calorimeter's response to neutral hadrons better. At some level we can probably use charged hadrons which we track into the calorimeter acceptance as a cross check of the Monte Carlo... and/or to develop cuts which we can use to reject this stuff.
5) We're going to need some additional handles to suppress hadronic backgrounds and/or estimate their yields.
»
- jwebb's blog
- Login or register to post comments
