- jwebb's home page
- Posts
- 2019
- 2018
- 2017
- 2016
- 2015
- 2014
- 2013
- November (1)
- October (1)
- September (1)
- July (1)
- June (1)
- April (1)
- March (3)
- February (1)
- January (1)
- 2012
- 2011
- December (2)
- September (3)
- August (5)
- July (6)
- June (6)
- May (1)
- April (5)
- March (5)
- February (2)
- January (2)
- 2010
- December (3)
- October (3)
- September (2)
- August (2)
- June (2)
- May (4)
- April (4)
- March (2)
- February (4)
- January (10)
- 2009
- 2008
- 2007
- 2006
- July (1)
- My blog
- Post new blog entry
- All blogs
Improving the Isolation Cut
Abstract: Our goal is to improve the isolation cut by
- Reducing the size of the tower cluster
- Correcting for energy leakage into neighboring towers
which will (1) decrease the likelyhood that the 2nd photon from a meson decay contributes energy to the gamma candidate, and (2) reduces the amount of energy which the gamma candidate contributes to the isolation energy sum.
1.0 Illustration of the Problem
To illustrate some of the tradeoffs associated with cluster size, figure 1 compares three different cluster sizes: a 2x2 cluster, a 2x1 or 1x2 cluster and Ahmed's prescription of only adding the neighboring tower if the leading photon candidate in the SMD is found near the edge of the tower. In this study, Monte Carlo events were generated w/ a
realistic pT and vertex distribution. Only single gammas and single pi0s were thrown for each event. Gamma candidates are found using the default conditions (5 GeV 3x3 clusters).
Slow simulator uses default configuration (i.e. no gain variations).
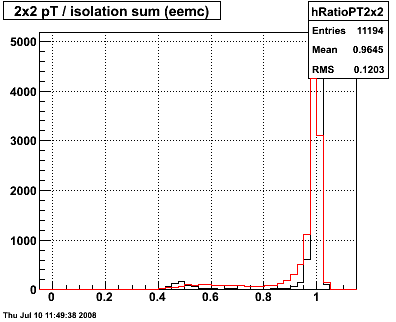
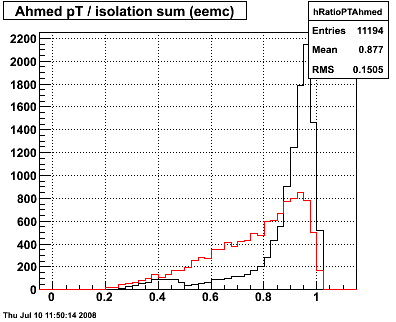
Figure 1.1 -- Isolation ratio: ET (gamma) / ET (w/in R<0.3). Black is single photons. Red is single pi0 decays.
The three figures correspond (in order) to 2x2, 2x1 or 1x2 and Ahmed's clustering.

Observations:
Two things become immediately obvious. As one decreases the cluster size, it is more likely that the 2nd photon is excluded from the tower cluster, thus making it more likely that
one can reject a pi0. It's a bit surprising, but a 2x2 cluster size has almost no rejection power against (single) pi0 decays. Secondly, as one decreases the size of the cluster, the energy resolution for the photon candidate is decreased. So in order to maintain high efficiency for photon reconstruction we have to establish a looser cut that we otherwise would like.
n.b. This also underscores the imporatance of good calibrations. At present, a 99% isolation cut doesn't make any sense, because the towers aren't calibrated to 1%.
I was a bit puzzled by the result that a 2x2 cluster doesn't work well... (my intuition skewed by too many years of trying to reconstruct pi0's...) To set the scale, figure 1.2 compares the size of towers at the inner and outer radius to a ET = 6 GeV pi0's minimum opening angle, and it's opening angle for decays with zgg <= 0.95. The tower boundaries are approximated by a trapezoid, and the (color) z-axis of the plot shows the fraction of energy which a photon at the given position will deposit w/in the tower.
Figure 1.2 -- Comparison of tower size to minimum opening angle between the photons for a ET = 6 GeV pi0 decay. The higher energy photon is assumed to be at the center of the tower, and the inner circle corresponds to the minimum radius where the second photon can be found. 95% of all pi0 decays will be contained between the inner and outer circles. The other features of the plot are described in the text.
.png)
.png)
Observations:
It is interesting to note that the size of the tower is comparable to the minimum separation of 6 GeV pi0's over the full acceptance of the detector. Towers at eta=1 are wider than this minimum separation, but not excessively wider. Therefore for lower pT gamma/pi0 separation, a single EEMC tower looks like an appropriate cluster size. To pull this off, we will need to understand and correct for energy sharing between the towers.
2.0 Next Steps
For my next round of studies, my plan is to
- Reduce the cluster size to a single tower for isolation cuts only,
- Correct the single-tower ET by a toy model for energy sharing
- Define the pT of the gamma candidate from either a 2x2 or (more likely) a 3x3 cluster for kinematic reconstruction
- Define a fiducial cut requiring that 80% of the energy of the photon (as assessed by the toy model) is w/in the single tower
The purpose of (1) is to maximize the discrimination power of the isolation cut against the 2nd photon from the pi0 decay. The purpose of (2) is to maximize the gamma reconstruction efficiency for fairly tight isolation cuts. The purpose of (3) is to ensure that we have the best pT resolution possible for the gamma candidates. The purpose of (4) is that I don't trust my toy model to reproduce energy sharing in detail at this point. So we restrict it in the initial studies so that it won't make a "large" correction to the pT.
The toy model:
We implement a purely geometric toy model to estimate energy sharing. The model described below can be easily changed to study systematics, or tuned to match Monte Carlo and/or data. It has the advantage of being fast. It works as follows:
- Throw a single "photon" w/in +/- 20cm of the center of a tower.
- For each photon, throw 1000 "mips" distributed according to a shower shape which mocks up an EM shower
- w/in R<2.5 cm throw a flat distribution for 90% of all mips
- w/in R<3.5*2.5 throw a flat distribution for 10% of all mips
- Count the total number of mips which hit the tower from a given (x,y) position for the photon, and divide by the total number thrown
As a side note, I've compared the above model to a model where we use a wide gaussian and a narrow gaussian (90% of energy w/in 1 RM, 10% w/ in 3.5 RM). Results qualitatively similar, and agree w/in the few % level (better agreement at eta=1 than eta=2).
Figure 2.1 -- Energy sharing according to toy model described above. The cross w/in the tower represents the approximate fiducial volume (delta x and delta y) where a photon can hit and 80% of its energy is depostied w/in that tower.

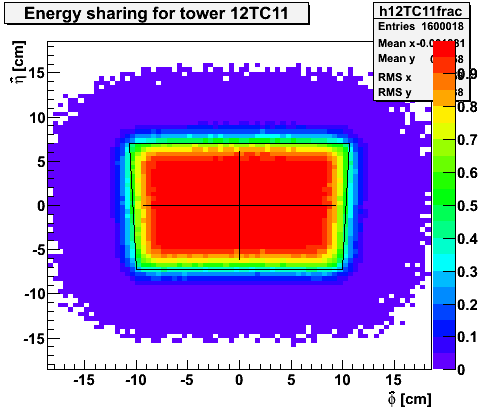
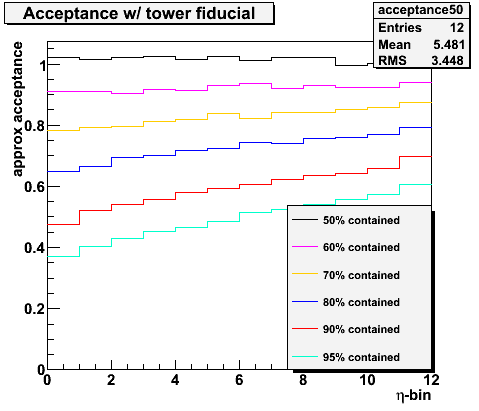
Figure 2.2 -- Estimated acceptance versus eta-bin for various percentages of photon energy contained w/in a single tower.
3.0 Isolation Cut with Fiducial Cut and Energy-Fraction Correction
We select gamma candidates which are 80% contained w/in the tower which they hit, and apply the energy correction discussed above.
Figure 3.1 -- Efficiency vs rejection for 1 tower clusters with energy sharing correction, fiducial cut applied.
.png)
.png)
Figure 3.2 -- Efficiency vs rejection for 1 tower clusters with energy sharing correction, NO fiducial cut applied.
.png)
.png)
Groups:
- jwebb's blog
- Login or register to post comments
