EEmc Gammas via conversion method, improving yield extraction using postshower information
Abstract: We have EEmc Gammas via conversion method, relaxing the hadronic veto cut identified a background contribution which appears consistent with neutral hadrons (or charged hadrons which slip through our cuts) initiating a hadronic shower w/in the calorimeter stack. Such a neutral background is not accounted for in our estimate of the background efficiency. Thus, the extraction method breaks down. For this study, we use the postshower response to estimate the fraction of hadron-like vs photon-like backgrounds, and extract a more reliable single photon yield.
1.0 Description of the Method
Begin by applying the following cuts to the event sample
Cuts:
1. Require candidate to be w/in the EEMC with pT > 5.0 GeV.
2. Isolation cut -- ET / ETR<0.3 > 0.9
3. Charged particle veto -- require sum of all preshower-1 tiles w/in R < 0.3 to be == 0
4. Analyzing cut -- sum preshower-2 tiles w/in R < 0.3 is greater than zero (i.e. at least one tile w/ ADC > 3 sigma + ped
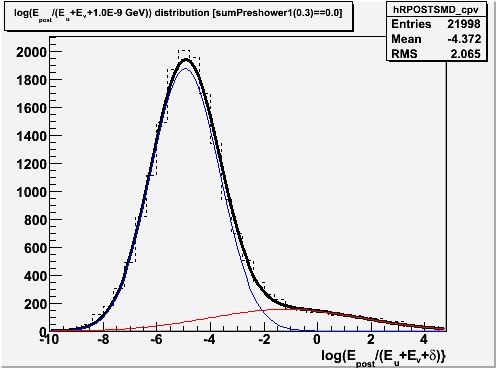
Plot the postshower-to-SMD energy ratio of these events. We see a broad gaussian on top of a much broader background. The gaussian "photonic" region occurs for relatively little energy in the postshower detector for relatively large SMD energy deposits. This is the type of signature we expect for electromagetic showers. It rides on top of a modest background of events, with a tail which extends to large energy deposits in the postshower with little energy showing up in the SMD. The events in this "hadronic" region are consistent with hadronic showers occuring w/in the endcap. We fit the distribution to the sum of two gaussians to estimate their relative contributions.
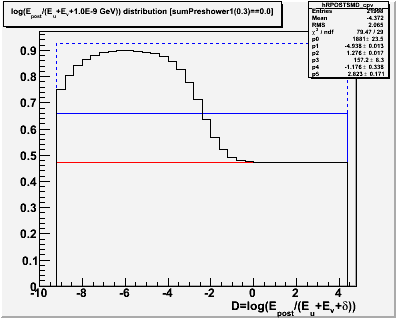
For the rest of this discussion, we define D = log(Epost/(Eu+Ev+delta)).
n.b. log is ln, i.e. natural logarithm. As in TMath::Log() ... which of course is undocumented in the root reference guide, and one has to look at the code to find out. Sheesh.
Figure 1 -- Fit to log(Epost/(Eu+Ev+delta)). The fit is to the sum of two gaussians. The fit chi2 (conviently left off of the plot) is somewhat poor... 79.47 per 29 dof. However, this gives us a starting point to estimate the relative fractions of (a) single photons, (b) photonic backgrounds, and (c) hadronic backgrounds.
To extract the number of gammas, we will try to use the formula
Ngamma = Ntotal × (ε - εbackground) / (εgamma - εbackground) (eqn 1)
from the conversion method. ε is the measured efficiency with which photon candidates leave a signal in the second preshower detector, εgamma and εbackground are the probabilities that a single gamma and "background" particle will leave a signal (determined through MC, pi0 reconstruction and/or other means). Since the composition of the background changes with D, we expect the background efficiency to also change. We first need to determine what the efficiency for "hadronic" events leaving a single in preshower-2.
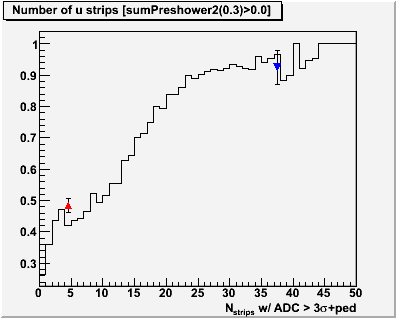
Figure 2 -- Extraction of the efficiency for "hadronic" candidates. At left the solid (dashed) histogram indicates the number of events which survived the CPV (analyzing) cut. At right, the ratio of the events which satisfy the analyzing cut to the events which satisfied the CPV. The fit is a p0 over the range [0.,2).
.png)
.png)
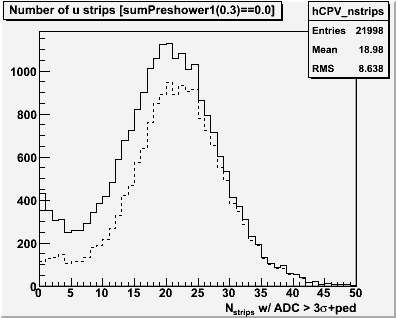
Approximately 46% of the "hadronic" events satifies the analyzing cut. Note that systematic errors on this estimate from fit ranges, possible dependence on D, should be investigated. And the error bars on the histogram are not properly calculated. Our purpose here is not to get to a final result, but rather to test the methodology. We can cross check this efficiency with another distribution. Specifically, the number of strips in the SMD (u) plane.
Figure 3 -- Number of candidates with a given number of SMD strips which fired. Events which satisfied the CPV cut (solid line) and analyzing cut (dashed) are shown at left. At right is the ratio of the number passing the analyzing cut to the number passing the CPV cut. The red data point shows the efficiency with which the hadronic background fires the analyzing cut. It is compared with the ratio for low number of strips firing (which we have taken to be one indication of a hadronic candidate). The blue data point shows the efficiency with which a pi0 satisfies the analyzing cut. It is compared with events which fired a large number of strips (very suggestive of a pi0 event).
Our next task is to determine the average background efficiency as a function of D. To do this, we need an answer we don't have at the moment -- the number of pi0's (or alternatively gammas) as a function of D. Once we have an estimated efficiency, we can iterate to improve it (and improve the estimated photon yield). So let's start with a reasonable estimate. Try splitting the events in the "photonic" region 60% photon and 40% pi0. This produces the following estimates for the composition of the D spectrum:
Figure 4 -- LEFT: Initial estimate for fractional number of events which are due to gammas (solid blue), photonic backgrouds (dashed blue) and hadronic backgrounds (red). RIGHT: Initial estimate of efficiency vs D for gammas (solid blue), photonic backgrouds (dashed blue) and hadronic backgrounds (red). The solid black line indicates the average background: eps_bg = f_pi0 * eps_pi0 + f_hadron * eps_hadron.
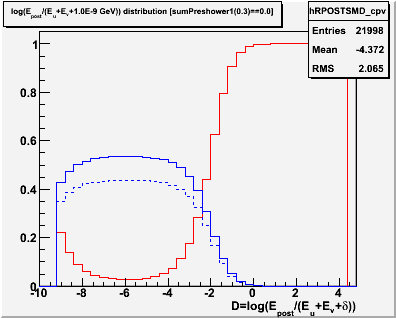
The above figure illustrates a serious problem. At D=-2, the average efficiency crosses the efficiency for detecting a single gamma. Equation 1 becomes singular at this point. Therefore, we can't utilize the conversion method to extract the single photon yield. But we don't need to. It is perfectly legal to extract the photonic background yield instead. Then we can solve for the single photon yield.
The procedure to extract the single gamma yield is as follows:1. Determine efficiencies for hadronic background
2. Generate initial estimate for composition and efficiency vs D.3. Bin-by-bin, extract the number of photonic background events using
Nphotonic-bg = Ncpv × (ε - εgamma+hadronic) / (εphotonic-bg- εgamma+hadronic)
where
εgamma+hadronic = fgamma * εgamma + fhadron * εhadron
4. Recalculate efficiencies and iterate. (But hold the number of hadronic candidates constant).
Figure 5 -- The result of the extraction. Total yield is 7176 +/- 206.5 events. Uncertainties have not been properly propagated.
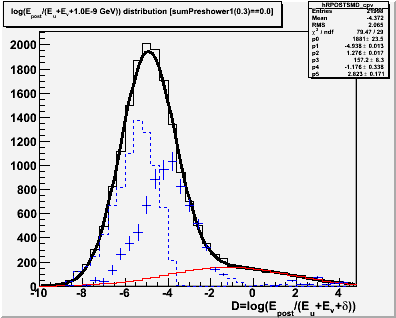
1. The extracted yield is in line with what we have found previously using cuts on the SMD energy ratio to reject hadronic background.
2. I am a little bit concerned that the extraction is "so pure" from -3 to -2 or so. I would really expect more pion like events there. But perhaps a more precisely measured pion efficicency will change things.
3. We should be able to independently measure the photonic background efficiency from (e.g.) figure 3.
Groups:
- jwebb's blog
- Login or register to post comments
