Due to the magnetic field in STAR, particles' helices will of course bend. In the TPC, a helix can be tracked to its origin, and the azimuthal angle of the particle's momentum can be taken at that point. In the EPD however, we can only measure the angle of a tile through which a particle traveled at the time it passed through that tile. It's important, then, to quantify the effect of track bending on the measurement of Psi_{1} from the EPD. This study focuses on the fixed-target running mode, where the target is at +201 cm and the magnetic field is at -0.5 T \hat{z}. For simplicity, we can just take a positively charged track with initial momentum in the +\hat{x} direction. The change in the track's azimuthal angle is then given by 
Equation 1: Track azimuthal angle
, where atan2(y,x) is the familiar C++ function (the derivation is attached). 

An interesting feature here is that there is no dependence on transverse momentum. This can also be simulated using StPhysicalHelix. Plotting this,
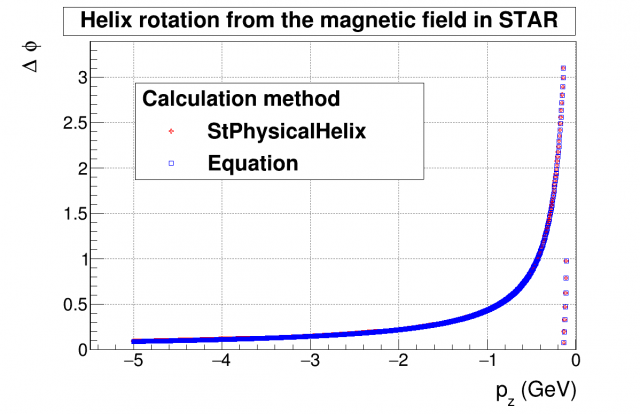Figure 1: Calculated rotation of positive tracks due to external magnetic field

we see the expected behavior of small rotation angle for large |p_{z}| tracks and a lot of rotation (to the point of looping) for low-|p_{z}| particles. The first loop happens at p_{z} ~ -0.13 GeV. Looking at the relevant p_{z} range at \sqrt{s_{NN}} = 3 GeV, 
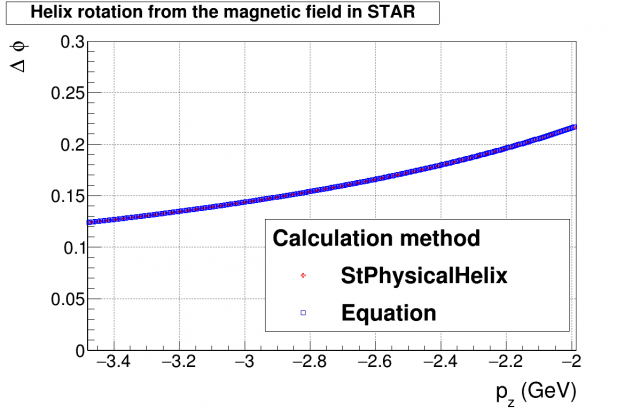Figure 2: Calculated rotation of positive tracks due to external magnetic field, for the relevant p_{z} for center-of-mass energy 3 GeV
we see rotations around 0.1 - 0.2 rad. We can compare this to data, where we correlate the#Psi_{1} from the TPC and rings of the EPD. Since the TPC's event plane is unaffected by this B-field rotation effect, this correlation gives us a measurement of the rotation effect in the EPD. We can fill a 1D histogram with a weighted nMip of each tile, rotated by Psi_{1} of the TPC, and fit it with a cosine functional form (or a Gaussian, which gives the same results). The parameters below are: f1 = [0]*cos(x+[1])+[2].
Figure 3: EPD hit phi rotated by #Psi_{1, TPC} and weighted by nMip
Note that the mean and the fit phase are different, which may (or may not) be surprising; however, the mean depends on the amplitude, frequency, and phase of the fit, so this is expected. For each ring, the shift is shown below:
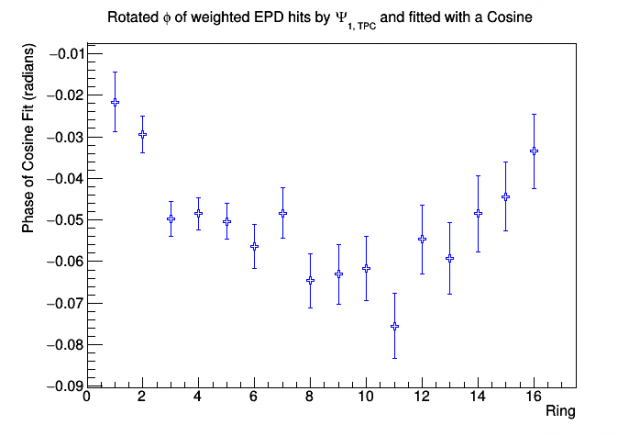Figure 4: Phases of cosine fits for each EPD ring
There is an observed rotation on the same order that we would expect. The effect of this rotation on the first-order event plane is much smaller:
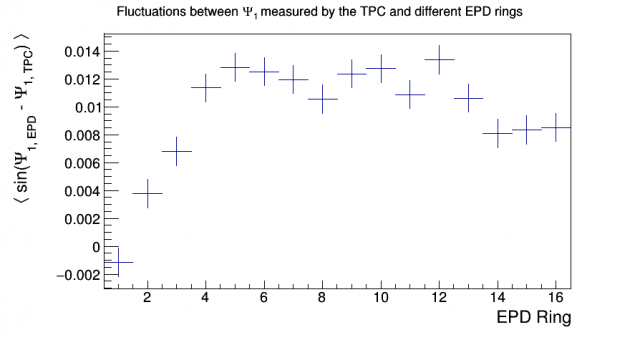Figure 5: Correlation between EPD and TPC first-order event planes

Initially, it seems that the above two measurements should be the same, only changed by a sign; however, this is incorrect thinking (the proof is attached). When EPD hits are rotated by the ring-dependent extracted values of the cosine-fit phases, we see the average sine go to zero, so this effect can be corrected for. 
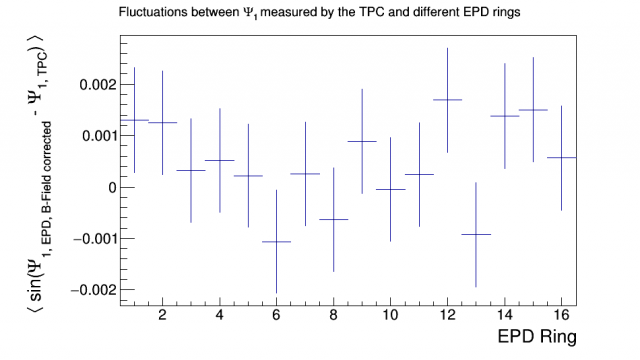Figure 6: Correlation between EPD and TPC first-order event planes, after EPD hits' azimuthal angles are corrected with the phases of the cosine fits

This can potentially be improved by using the cosine fits on a centrality-dependent basis, but in practice, the fit errors are too large and there is no improvement.
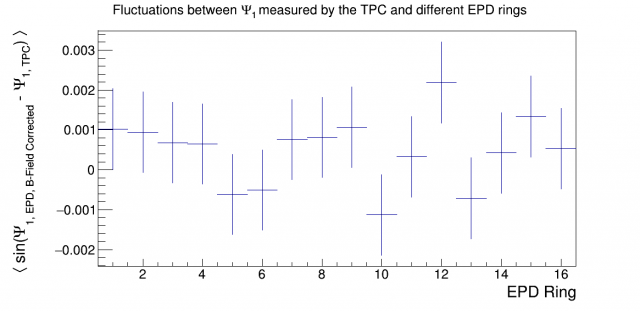Figure 7: Correlation between EPD and TPC first-order event planes, after EPD hits' azimuthal angles are corrected with the phases of the cosine fits on a centrality-dependent basis

In either case, one can notice a tendency towards positive values, and in fact, performing a Rebin(12) on this histogram gives an average sine of 4.68e-4 \pm 2.53e-4, making it about 2\sigma from 0. This should be consistent with zero, but it is at least greatly reduced. The weights in the nMip distribution are corrected for by using phi weighting, but the angles are not corrected for when using shifting; however, since we are looking at the angle of each hit relative to the event plane angle measured by the TPC, this lack in complete flatness cannot cause this problem of a non-zero average sign.