-angular resulution and momentum resolution is negligible compared to the binning.

The main systematic check is 'spin mixing', i.e. the random assignment of spin states. Doing this repeatedly checks if the error bars are correct and if there are false asymmetries induced in the extraction. Comparison between square root formula and relative luminosity  as well as the chi2 distribution of the fits adds extra confidence.

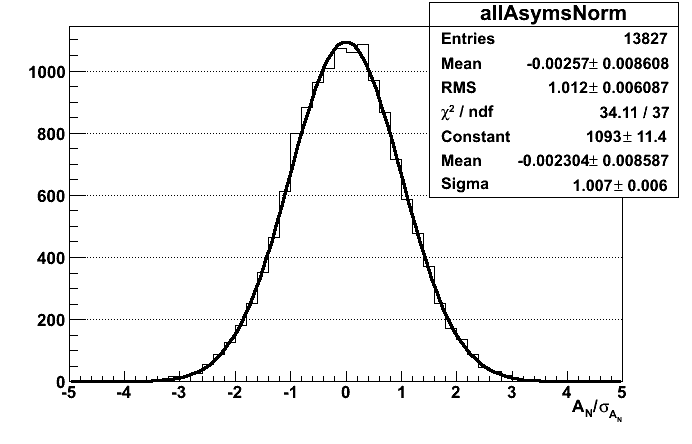
Spin Mixing: No false asymmetries and errors are correct, first rel lumi formula. Asymmetries are normalized by dividing by the fit error. There is one asymmetry per kinematic bin and fill. The process is repeated 10 times to collect enough statistics

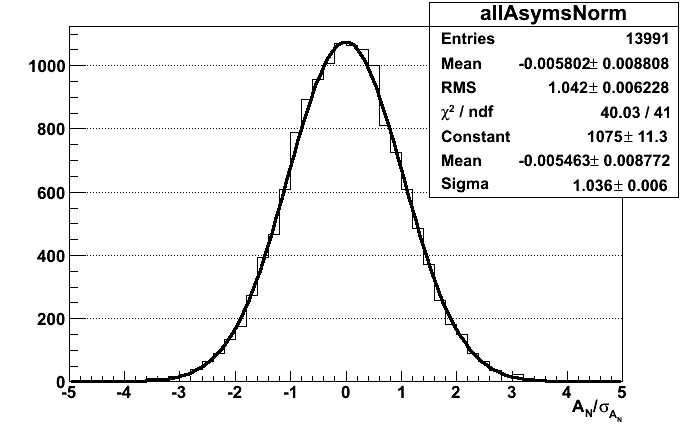
For square root formula:

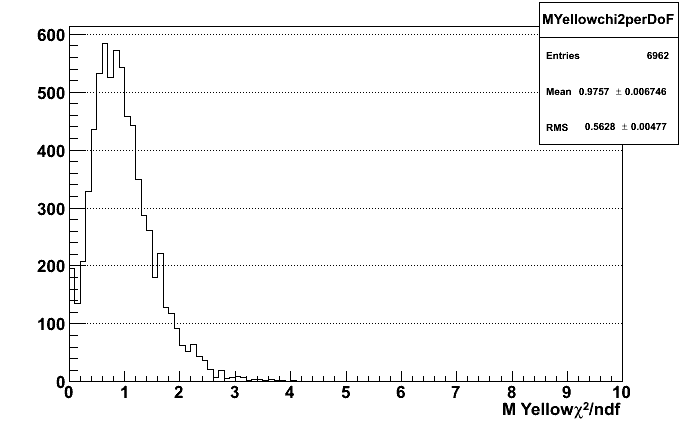
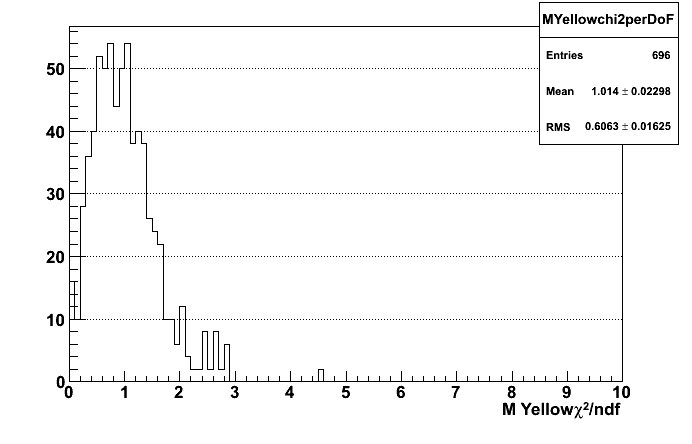
Chi2 of fits (here only for one beam an invariant mass binning, looks the same though...) In the analysis there is a cut chi2/NDF> 0.2 and <5

First for spin mixing, then for final analysis

Comparison of asymmetries for yellow and blue, shown are the asymmetries for p_t binning and eta <> 0:

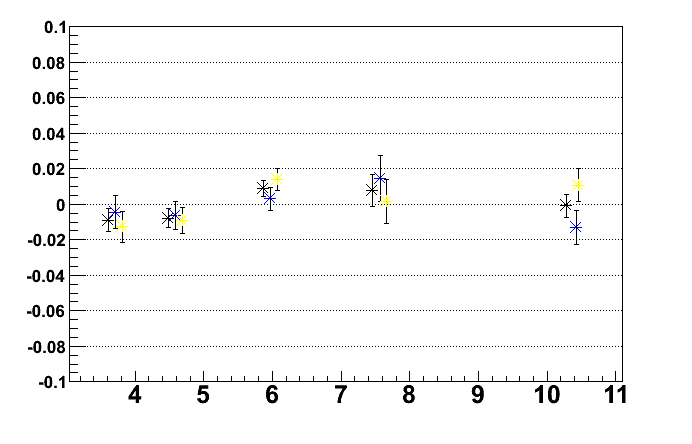
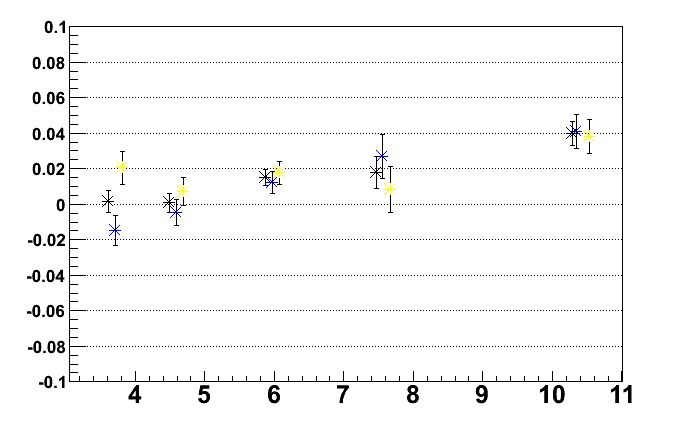
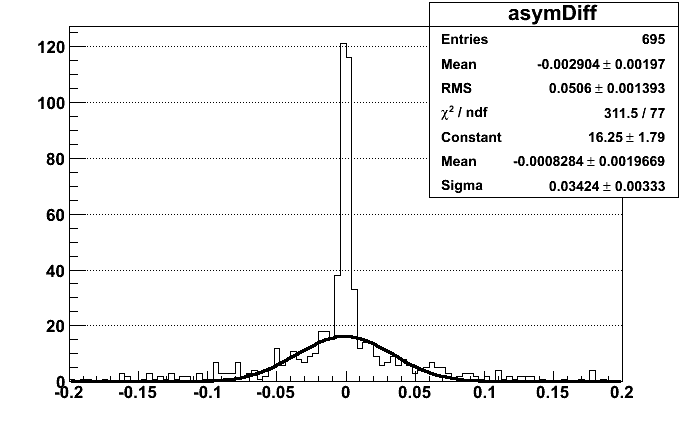
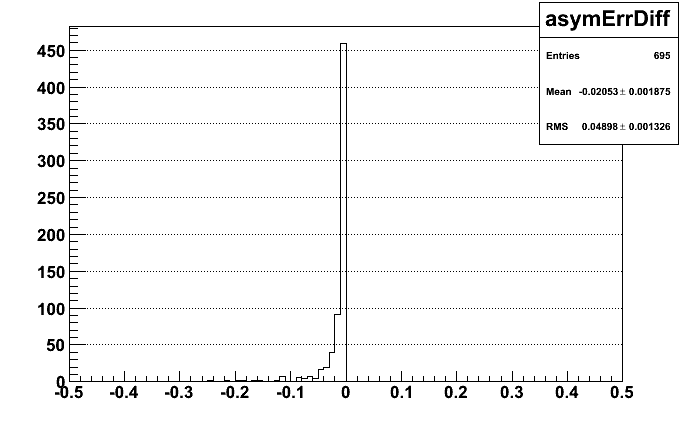
Difference between square root and rel lumi results:

For differences (As_relLumi-As_sqRoot)/Err_reLumi is plotted and (Error_relLumi-Err_sqRoot)/Err_sqRoot

using cosine instead of sine: ( for eta <> 0 )

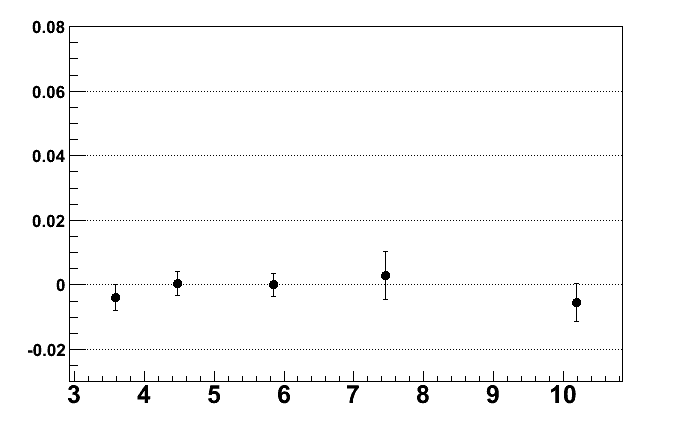
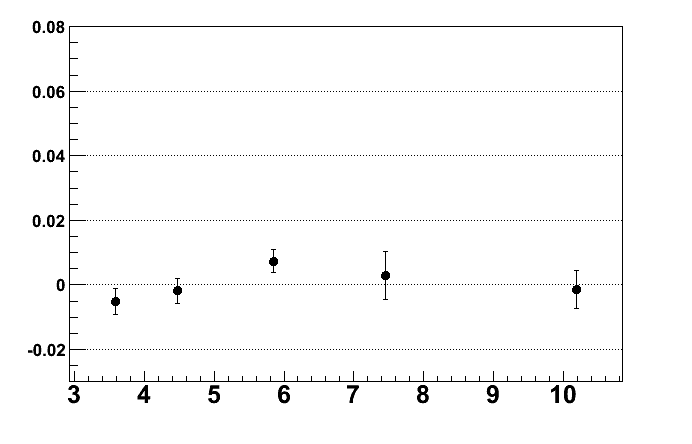
Zero test with randomized direction of \vec{R} (i.e. half the events R=h1-h2 and the other half R=h2-h1

First eta<0, m_inv binning

eta >0

and for p_t, eta<0

p_t binning, eta >0