I have begun considering the "rate-safe counting" method for computing the relative luminosities, using techniques from Andrew Manion's work on the PHENIX relative luminosity. His methods are documented in section 4.3 of his thesis (https://www.phenix.bnl.gov/phenix/WWW/publish/manion/Manion_Thesis.pdf). He also wrote a PHENIX analysis note, which has been attached to this blog entry (https://drupal.star.bnl.gov/STAR/system/files/manion_analysis_note.pdf)

Manion's Rate-Safe Counting Technique

Two Event Classes:

1. Double-sided events (DS) -- collisions which will trigger a coincidence
   • DS events occur an average of λ times per bXing
2. Single-sided events (SS) -- collisions which will trigger a single but not a coincidence
   • East SS events (ESS) occur an average of λ_E times per bXing
     
   • West SS events (WSS) occur an average of λ_W times ber bXing
     

Probability for detecting k_E hits in E-scaler from DS events, given that E-scaler has efficiency * acceptence = ε_E:

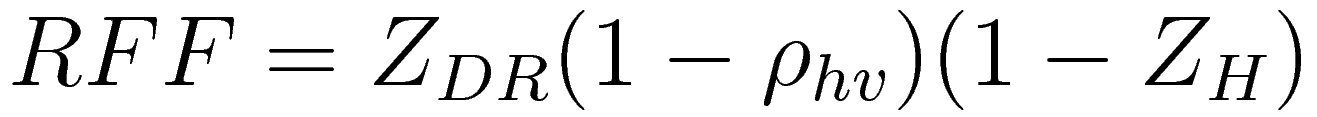
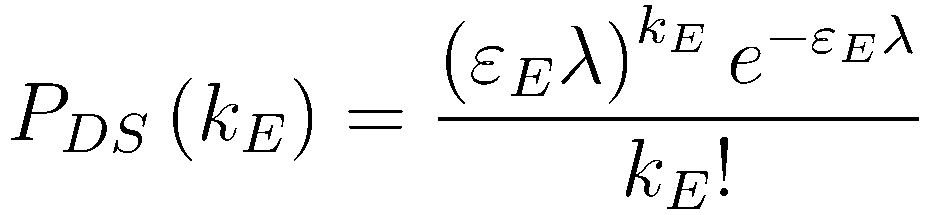
Probability for detecting k_W hits in W-scaler from DS events, given that W-scaler has efficiency * acceptence = ε_W:

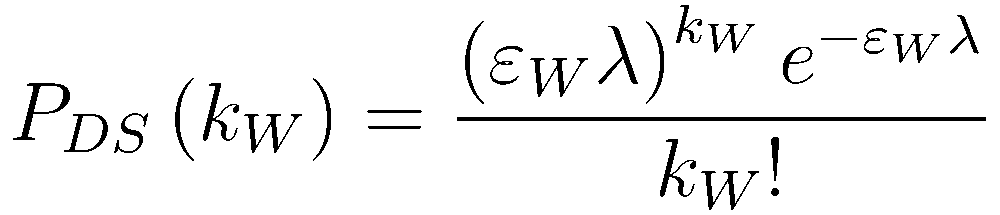
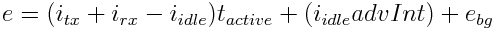
The joint probability that the E-scaler detects k_E hits AND the W-scaler detects k_W hits from DS events is

where P_DS(k_W|k_E) is the probability that the W-scaler detected k_W hits given that the E-scaler detected k_E hits.

Let i denote the number of collisions.

After a bit of effort (see references to Manion's papers above), one can show that this joint probability distribution may be written:

 

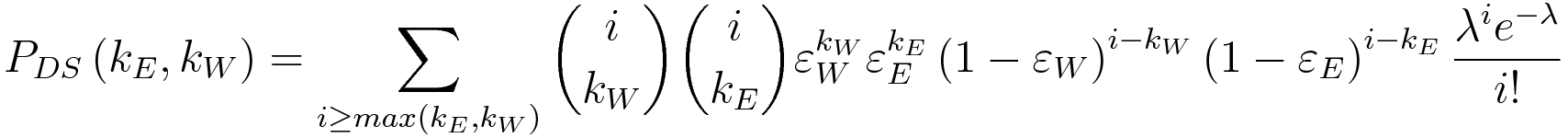
Now consider SS events.

Probability for detecting k_E hits in E-scaler from SS events:

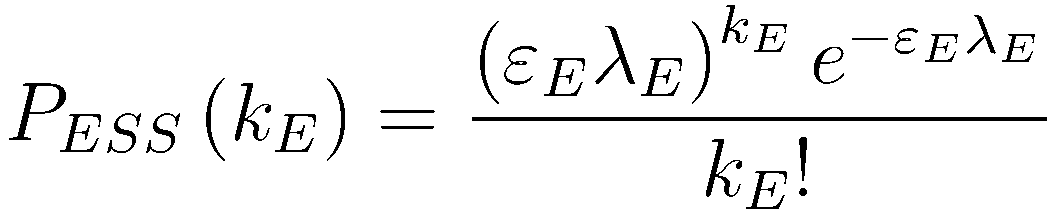
Probability for detecting k_W hits in W-scaler from SS events:

 

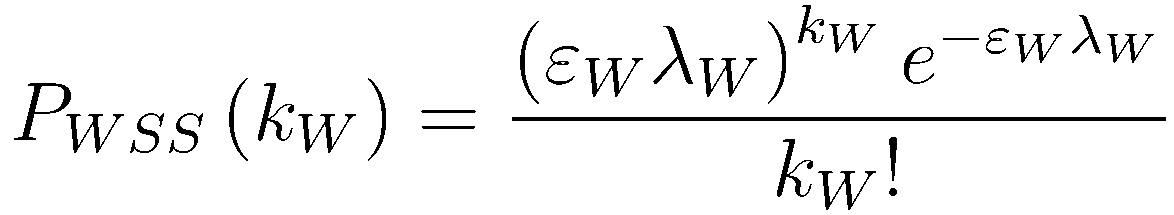
Consider the following three probability distributions:

1. zero hits in E-scaler:

2. zero hits in W-scaler:

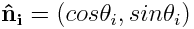
3. zero hits in 2-sided detector:

 

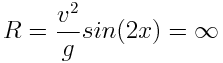
Let P* denote the probability that the 2-sided detecter detects zero hits in both E & W, given the condition that the single sided detectors each detected zero hits.

Using the Kolmogorov definition of conditional probability, P* is expressed as

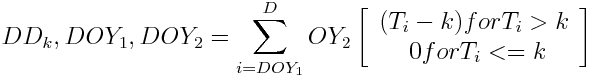
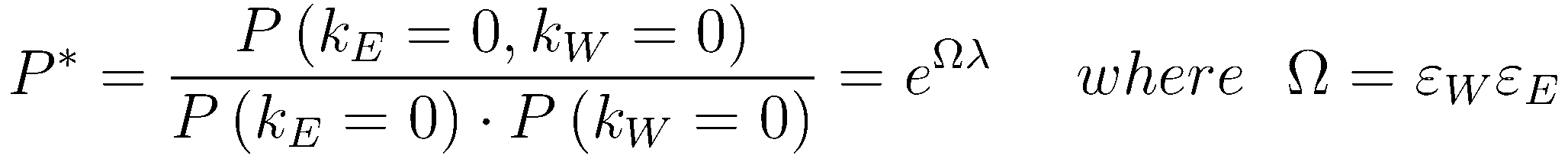
Let P_E(W) be the probability of detecting at least 1 E(W)-scaler singles, and P_EW the probability of detecting at least 1 coincidence. These probabilites are used

to rewrite the above three probability distributions for seeing zero hits in the form of "(probability of zero hits) = 1 - (probability of at least 1 hit)".

Take the logarithm of P* to obtain

 

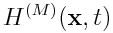
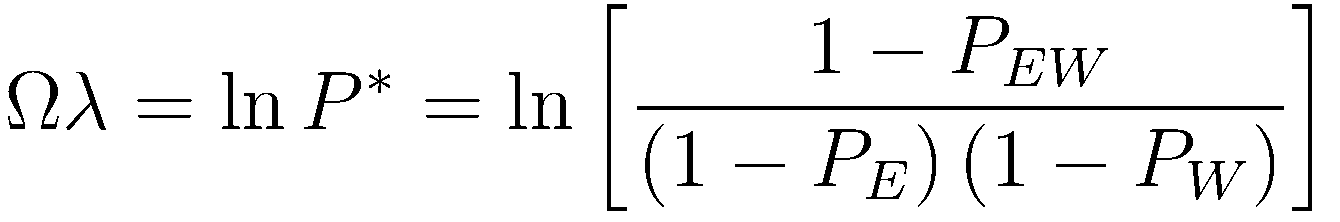
Assume the probability distributions of detecting N_E(W) hits in the E(W)-scaler and N_EW coincidences are all binomial, given N_bx bXings.

Manion argues this is needed since the probability of a trigger is significant for all filled bXings. Denoting the mean of these binomial distributions by <.>, we thus have

 

Finally, the product of E&W acceptances & efficincies times the rate-safe counts is written in terms of raw scaler counts {N_E,N_W,N_EW} as:

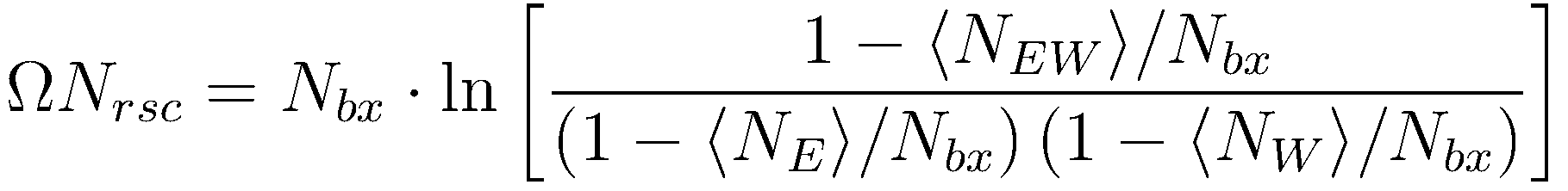        <===== rate-safe correction equation

where the subscript "rsc" stands for (rate-safe correction)

 

Note on Accidentals

1. For bXings with 1 collision, we either have a true coincidence from a DS-event or a single hit from a SS-event
   • No accidental coincidences occur in this case
     
2. For bXings with more than 1 collisions, we have the following possibilities
   • Detection of coincidence event: either one or both of the following cases must occur
     • At least 1 DS-collision -- occurs an average λ times per bXing
     • At least 1 ESS-collision and 1 WSS-collision -- occurs an average λ_E and λ_W times per bXing, respectively
       
   • Detection of single event
     • DS-event contribution
     • All SS events in the bXing are toward one detector -- occurs an average λ_E or λ_W times per bXing

Claim: P* only depends on λ, but not on λ_E or λ_W. Thus the above quantity N_rsc only counts "true coincidences"

 

Run 13 Relative Luminosity Impact

The rate-safe technique is implemented in the relative luminosity by using N_rsc, assuming the Ω factors are independent of initial spin

Important Note: the rate-safe error bars are currently not being propagated as done in Manion's papers. I am currently using the error bars which come from sqrt(counts), which is the
same uncertainty propagation used in the acc+mul corrections case.

The relative luminosity computed using the previous multiples+accidentals corrections differs at the 0.1% level from that using the rate-safe method;
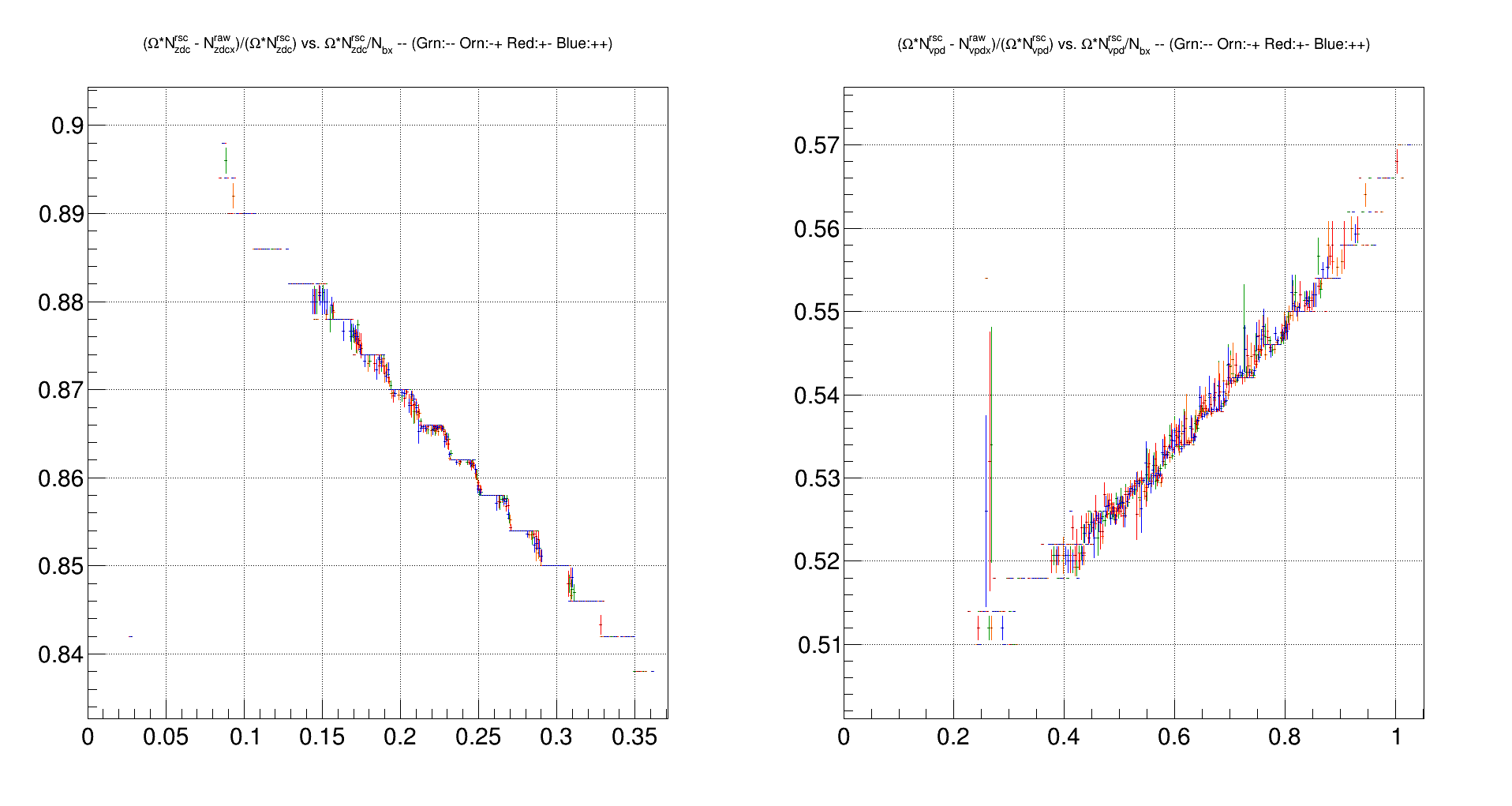
The plots below show the difference between rate-safe ZDC and mul+acc corrected ZDCX as well as that for the VPD:

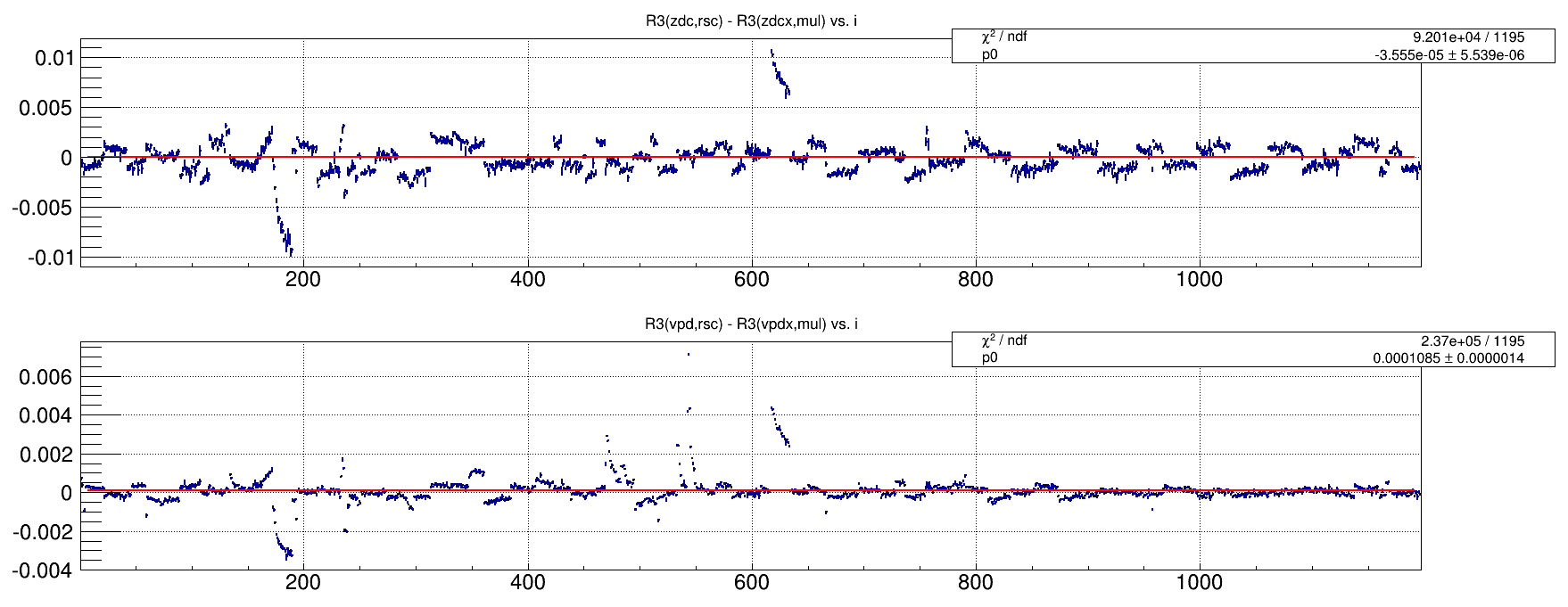
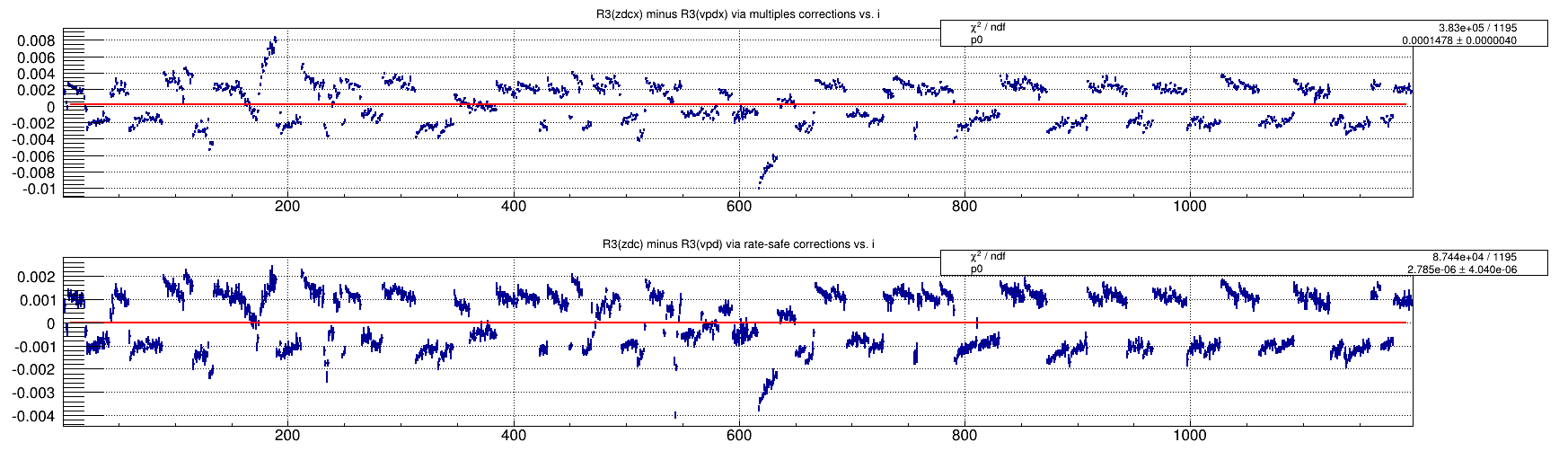
The rate safe technique improves the comparison between R3 computed using the ZDC vs. VPD by a factor of 2; this factor of 2 improvement is also seen
for other relative luminosities R1,R2,R4-9. The pair of plots below show the R3 value for ZDC minus VPD using old corrections method first and then rate-safe method second:

The following plots show the fraction of counts which undergo acc+mul corrections, plotted vs. acc+mul corrected count probability for the ZDC (left) and VPD (right)

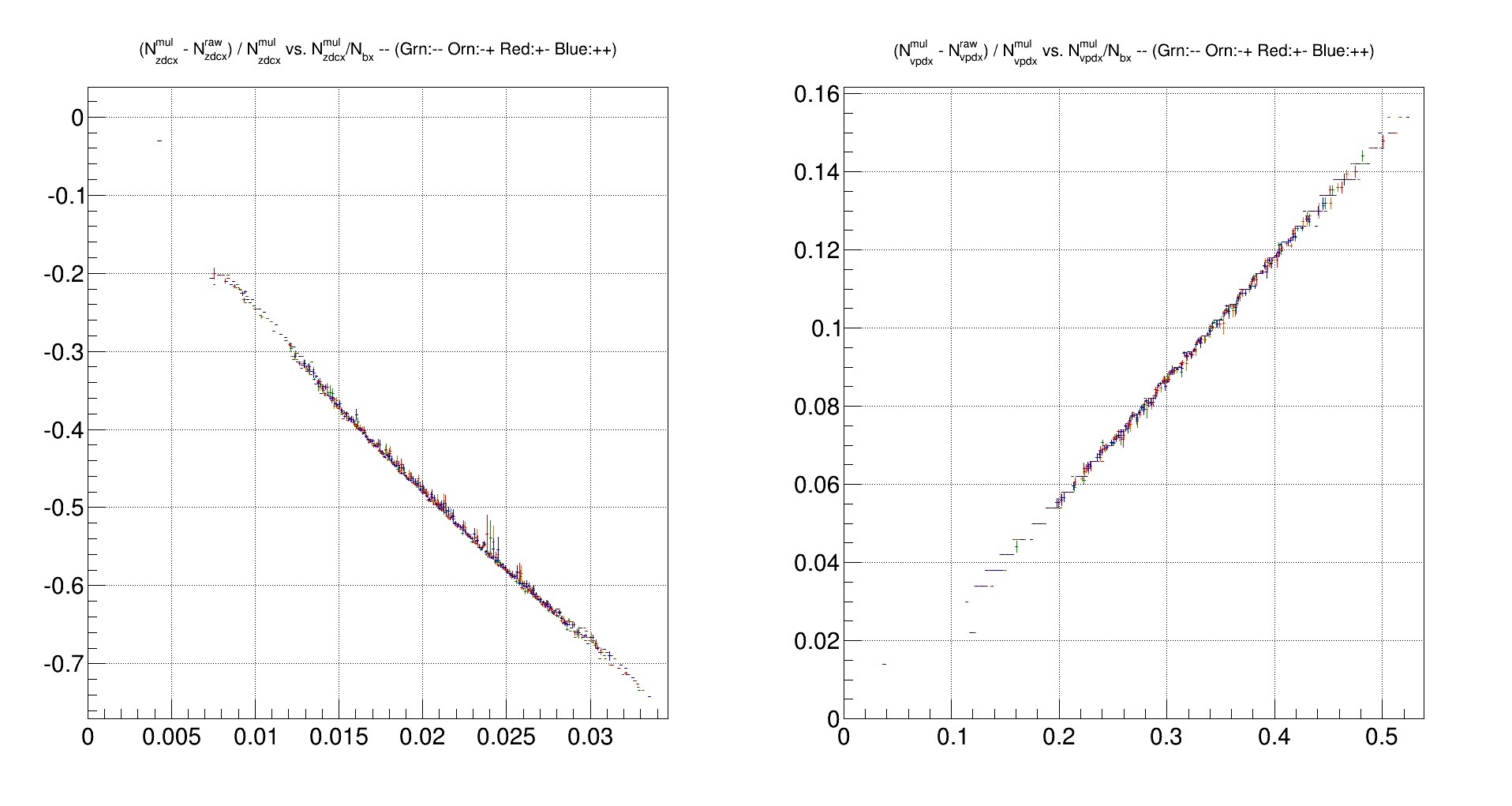
Then compare these plots to similar plots using the rate-safe counting method (note the Ω factors!)
Conclusion: the fraction of "undercounting" or "overcounting" is much less dependent on hit probability when using the rate-safe method
[n.b. the stepping structure in these plots is correctable by using finer binning; different colours are for different initial spin states]

The rate-safe method also impacts the scaler A_LL, determined using the bunch fitting technique
First, the distribution of scaler ZDCX A_LL w.r.t. VPDX using the acc+mul corrections is

The widths of the Gaussians are:

• left sigma = 0.001080
• right sigma = 0.000979

Comapare this to the same distribution, but using rate-safe corrections:

The widths of the Gaussians are:

• sigma left = 0.000418
• sigma right = 0.000457

The narrower distributions using the rate-safe method may cause a drop in the Run 13 A_LL systematic uncertainty by a factor of 2-3
The spin pattern correlation remains evident, however.