- dilks's home page
- Posts
- 2019
- 2018
- December (1)
- November (1)
- October (1)
- August (2)
- July (4)
- June (3)
- May (1)
- April (2)
- March (2)
- February (1)
- January (5)
- 2017
- December (3)
- November (1)
- October (2)
- September (3)
- August (2)
- July (2)
- June (1)
- May (2)
- March (3)
- February (3)
- January (3)
- 2016
- November (2)
- September (4)
- August (2)
- July (6)
- June (2)
- May (3)
- April (1)
- March (2)
- February (3)
- January (2)
- 2015
- December (3)
- October (3)
- September (2)
- August (6)
- June (3)
- May (3)
- April (4)
- March (3)
- February (5)
- January (3)
- 2014
- December (1)
- November (1)
- October (3)
- September (4)
- August (3)
- July (3)
- June (2)
- May (2)
- April (2)
- March (1)
- 2013
- 2012
- 2011
- My blog
- Post new blog entry
- All blogs
Review of Transversity and Rellum Systematics
This is a summary of methods used at estimating systematic uncertainties for previous A_LL measurements. The information was obtained from the following theses:
- Leight: STAR 2009 pi0 A_LL
- Betancourt: STAR 2009 direct photon A_LL
- Staszak: STAR 2006 jets A_LL
- Boyle: PHENIX 2005-06 pi0s A_LL
- Kocoloski: STAR pi+/- A_LL
- Fukao: PHENIX 2005 pi0 A_LL
| Transverse Polarization | Relative Luminosity | |
| Leight | A_sigma too small from pi0 analysis; used A_sigma from 2009 inclusive jets; ~2.5 e-4 (pT-independent) |
difference between pi0 A_LL computed using ZDC vs. BBC for rellum; ~1.7 e-4 (pT-dependent) |
| Betancourt | Approximated as 0.02 * A_LL ~10 e-4 (pT-dependent) |
difference between photon A_LL computed using ZDC vs. BBC for rellum; ~1.5 e-3 (pT-dependent) |
| Staszak | via A_sigma; used STAR scaler polarimetry to obtain polarization angles. A_TT was consistent with zero Ranges from ~0.09 e-3 to 1.28 e-3 (pT-dependent) |
Compare rellum using two different detectors; uncertainty contribution given by Equation 5 below deltaR ~ 9.4 e-4 |
| Boyle | A_TT measured in 2005 for 4 fills with spin rotators disabled; used local polarimetry to obtain polarization angles ~negligible contribution |
deltaR obtained from ZDC to BBC rellum comparison; deltaR propagates to deltaA_LL via equation 6 below (eq. 4.7-8 from thesis) ~5 e-4 Followed up with bXing-by-bXing analysis which is then width corrected and rate corrected Asymmetry of scalers ratio plus its uncertainty is the contribution to A_LL systematic |
| Kocoloski | Extracted A_sigma from 2005 data set | |
| Fukao | Size of A_TT term in "A_meas" equation below used as systematic ~5 e-3 from A_TT ~5 e-4 from A_L |
deltaR obtained from ZDC to BBC rellum comparison; followed up with bXing-by-bXing BBC/ZDC trigger ratio via MLM (see eq A.34-A.36) Contribution to A_LL systematic given by equation 6 below deltaR / R ~ 2 e-4 for longitudinal |
--------------------------------------------------------------------------------------------------------------------------------------------------------
Some relevant equations:
EQUATION 1: If the supposedly longitudinal proton beam polarization makes an angle Theta w.r.t. proton momentum, the yield is given in terms of asymmetries as:
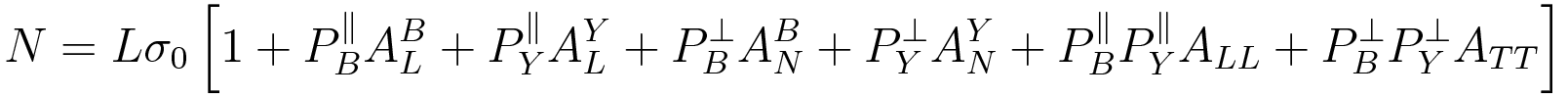
EQUATION 2: If the beams are transversely polarized, the yield is written i.t.o. azimuthal dependence as:
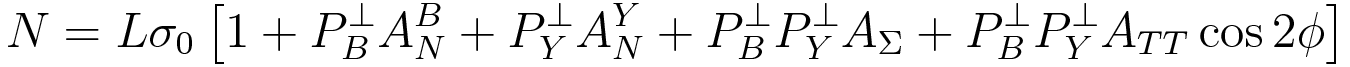
EQUATION 3: The systematic uncertainty of A_LL due to A_sigma is given by:
.png)
EQUATION 4: The systematic uncertainty of A_LL due to A_TT is given by:
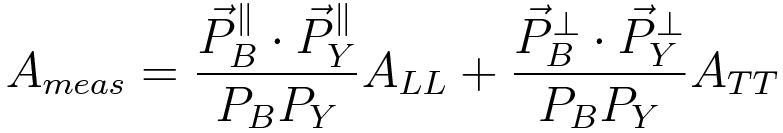
EQUATION 5: For relative luminosity, Staszak's thesis uses
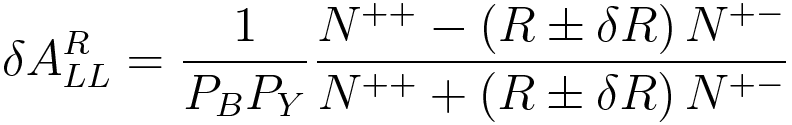
EQUATION 6: Boyle's thesis uses, where the approximation N^{++} \approx R N^{+-} is used:
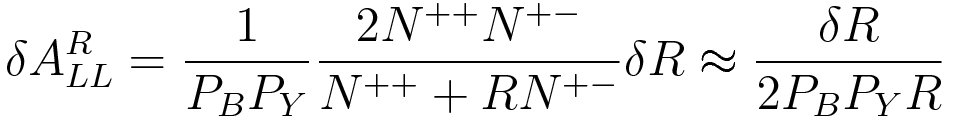
- dilks's blog
- Login or register to post comments
