Now that I figured out what was going on with the SVD algorithm (see link below), I went about estimating the systematic errors due to the choice of unfolding algorithm (Bayesian vs. SVD) and the choice of regularization parameter.

https://drupal.star.bnl.gov/STAR/blog/dmawxc/update-08022018-run-9-pp-follow-weird-svd-behavior

The errors presented below are calculated in the same way that I calculated the systematic errors due to the choice of unfolding prior:

https://drupal.star.bnl.gov/STAR/blog/dmawxc/update-07262018-run-9-pp-systematic-errors-prior-r-02
https://drupal.star.bnl.gov/STAR/blog/dmawxc/update-07312018-run-9-pp-systematic-errors-prior-r-05

The default distribution is chosen to be the Bayesian result with a regularization parameter of k = 3 (the same as the default for the two links above) for both R = 0.2 and 0.5.  The prior was, of course, the corresponding particle-level h+- triggered jet distribution from the Run9 dijet embedding sample that was used for generating the response matrix.

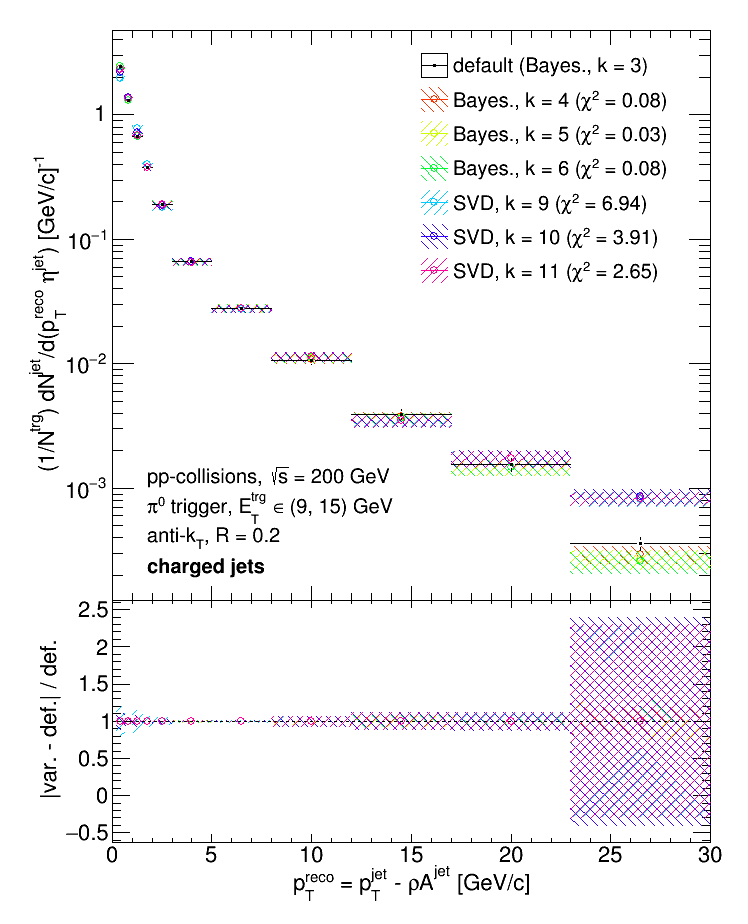
The regularization parameter for the default distribution was chosen st. the chi2 between the backfolded distribution and data was the closest to 1.  Then I used the next 3 iterations in the Bayesian algorithm to estimate the systematic error (since changes in the backfolded distribution are essentially negligible past the default regularization parameter).

For the SVD algorithm, I chose the regularization parameter that gave the best chi2 (i.e. closest to 1) between the backfolded distribution and data but still had reasonable error bars.  Past the highest value of k plotted above, the error bars on the unfolded SVD distribution explode.  Then I walked the regularization parameter back 2 steps to estimate the systematic error.  Below I show some examples of backfolded SVD distributions vs. data.

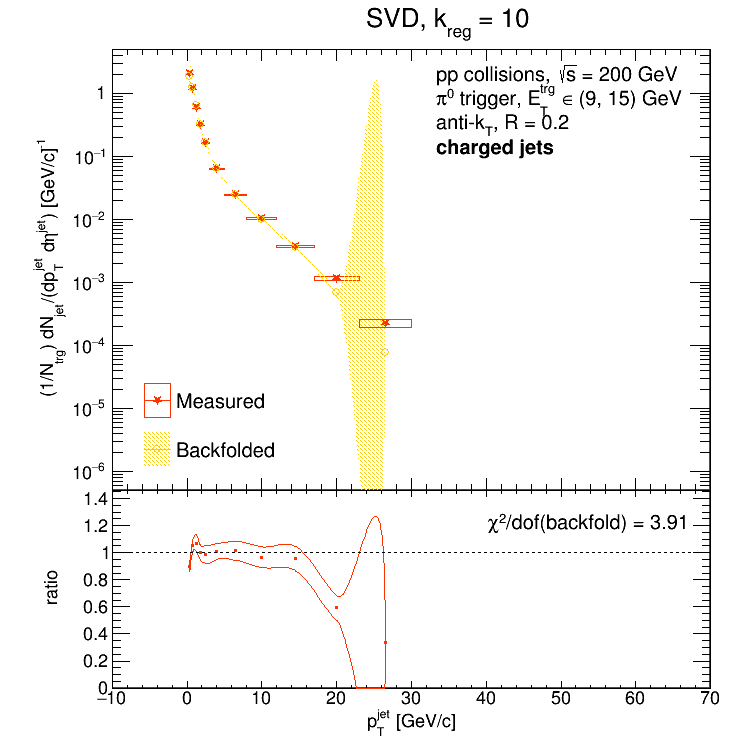
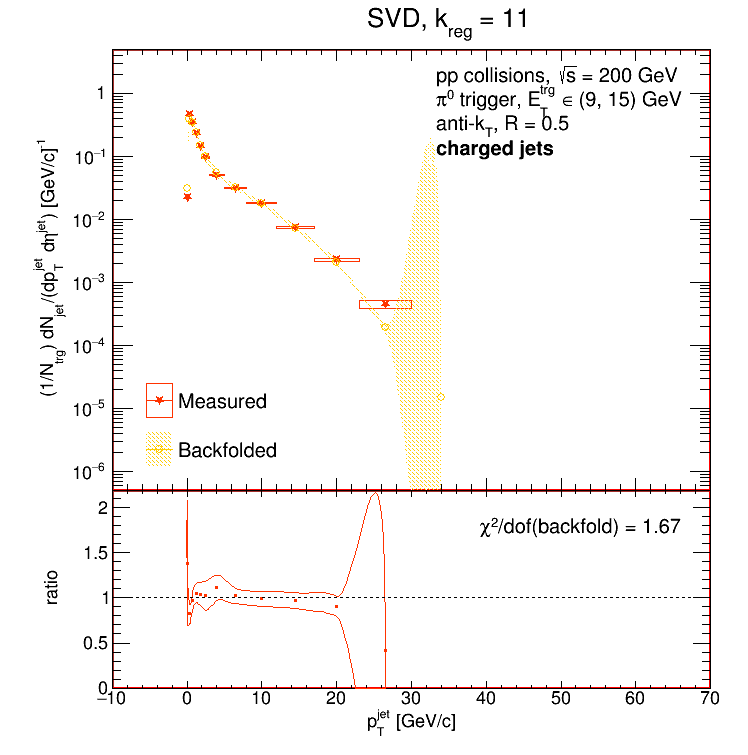
As always, the giant error bars on the last bin of the backfolded distribution are just ROOT misbehaving.