(January 18, 2012) NOTE: From this update until my December 31 update I incorrectly calculated the background-asymmetry systematic. I have subsequently changed my methodology. Instead of taking the largest asymmetry from among the bins, I take the largest average of the two bins surrounding the pion peak (turns out to be the yellow beam). This is ~2%. The sizes of the resulting systematics are quite comparable to what has been reported.

(December 6, 2012) NOTE: a typo resulted in a sizable increase in the systematic uncertainties for these calculations. The bug has been fixed and the systematics are greatly reduced. A newer calculation with the latest code implementations is forthcoming.

Here, I describe an alternative background-correction procedure. Hopefully, this will prove robust enough to move forward with a preliminary result for the neutral pion A_N. The basic idea is to utilize an "after-the-fact" correction, of the form

A_N = (A_{N, tot} - (1-f_sig)×A_{N, bg})/f_sig

instead of the direct calculation Steve developed. In time, we hope to revisit that method as it has several advantages. However, the hope is this procedure proves robust enough for the present.

Signal Fraction

First, we must determine the signal fraction. These we have from Steve's background template procedure. In Fig. 1 I show the signal fractions as a function of φ_S in each hemisphere and x_F bin. I have summed over all spin states and fit the data with the background templates.

Figure 1

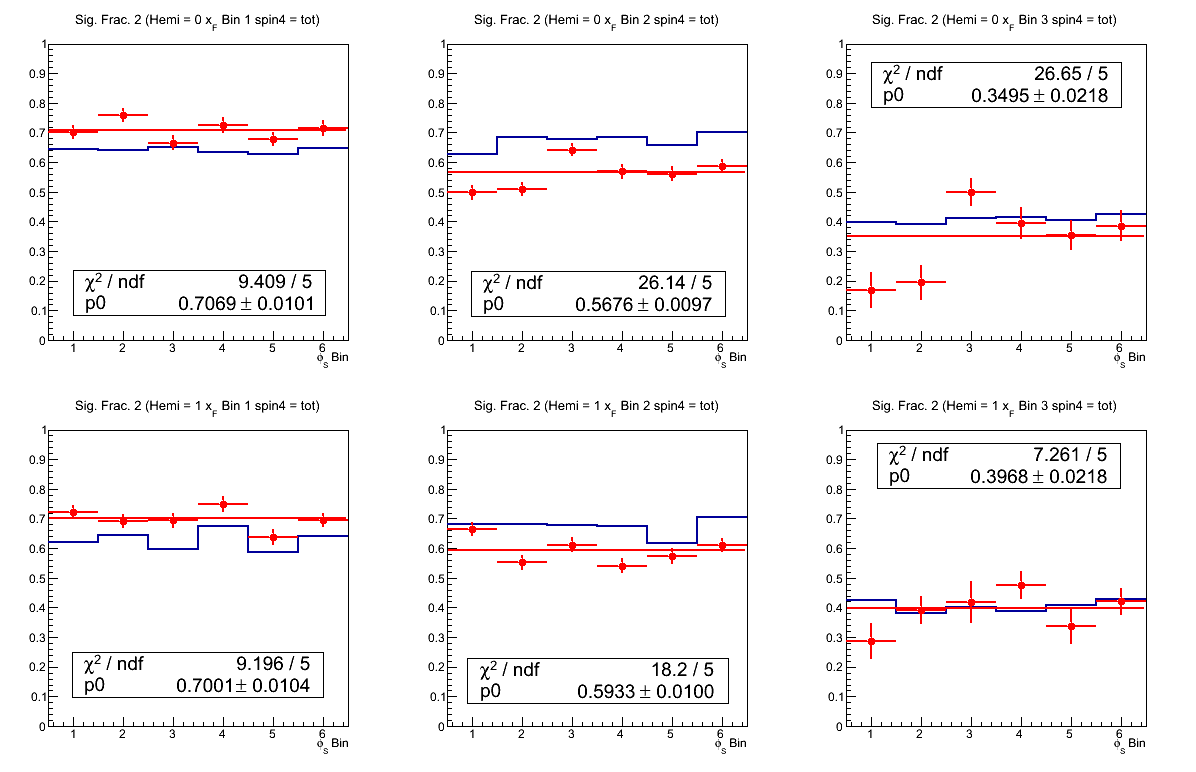
To extract the signal fractions I fit each distribution with a constant. The extracted values are fairly consistent across the hemispheres. I then average the fits for each hemisphere within an x_F bin for the final value.

The uncertainty on a quantity such as the signal fraction can be expressed

f_sig = N_sig/N_tot

(δf_sig)² = (f_sig×δN_sig/N_sig)²+(f_sig×δN_tot/N_tot)².

For Steve's method, there are two sources of systematic error concerning the signal fraction: the residual fit and the propagated systematic. To determine a conservative systematic estimate for Steve's fits, I calculate δN_sig/N_sig where in δN_sig I add the residual and propagated systematic in quadrature. Figure 2 shows the result of these calculations in hemispheres and x_F bins.

Figure 2

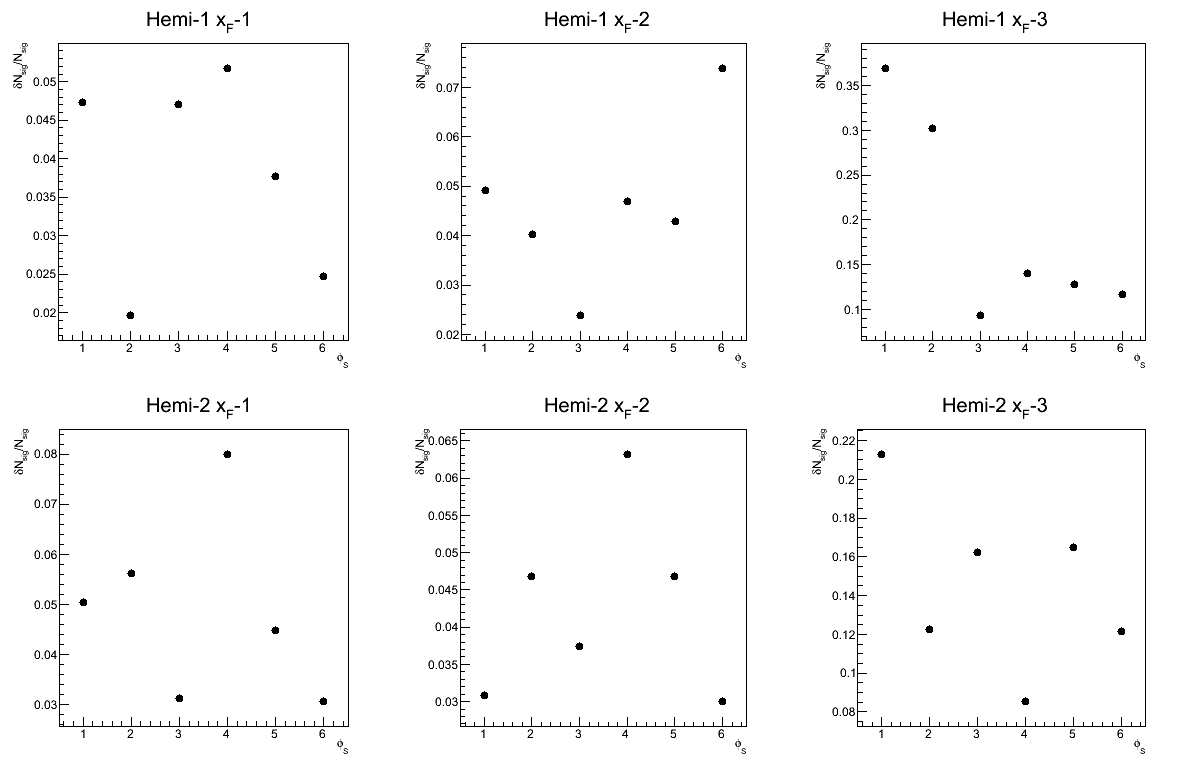
For each x_F bin I pick the highest value of the 12 φ bins to use in the systematic error calculation on A_N. For p_T there are a few complications. Namely, data-simulation agreement breaks down below 5 GeV/c. This gives one pause as to whether or not we can include these bins in the asymmetry calculation (including integrating over them for the x_F asymmetries). Furthermore, the mass fits for several phi bins did not converge. This yields hugh systematic uncertainties in the signal fractions. For the time being I have integrated over the suspect p_T bins for the x_F dependence but will not show them in the p_T dependence.

Background Asymmetry

To determine the background asymmetry I evaluate A_N as a function of invariant mass as seen in Fig. 3.

Figure 3

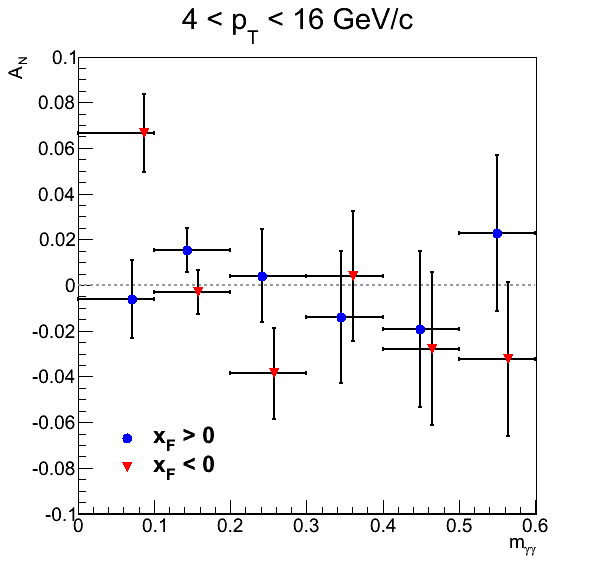
I take the average of the two bins surrounding the pion peak which turns out to be a rather small asymmetry. Because of the large asymmetry seen in the lowest bin of x_F < 0, I recalculate the pion asymmetry assuming a background asymmetry of 7%. The difference between the two calculations sets the background asymmetry systematic.

Asymmetries

There are a couple of items which remain. I would like to include for systematic considerations an alternative background estimation. Perhaps, something as simple as a polynomial fit would be enough. The PWG has expressed some nervousness about fits not including the low-mass background at lower kinematic ranges. Thus, it would be good to include these fits in estimating the systematic contribution from our signal-fraction fits. Also, it might also be useful to examine the asymmetries for a varied mass window. At present, we examine 0.1 < m_γγ < 0.2 GeV/c². It might be informative to recalculate the asymmetries with a range, e.g. 0.08 < mgg < 0.22 GeV/c².

Figure 4

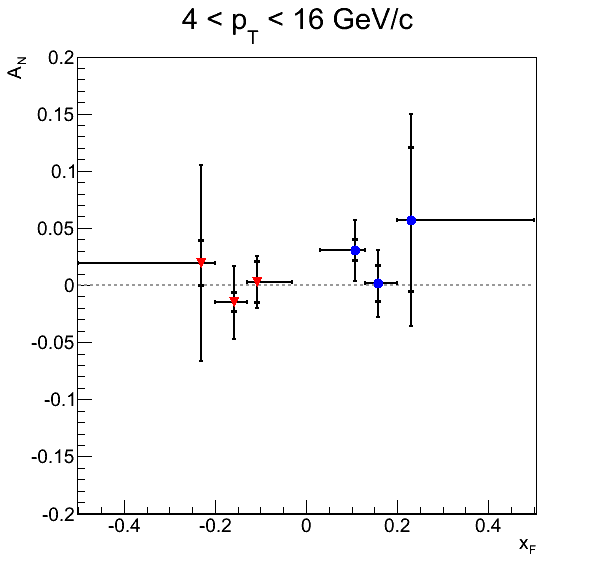
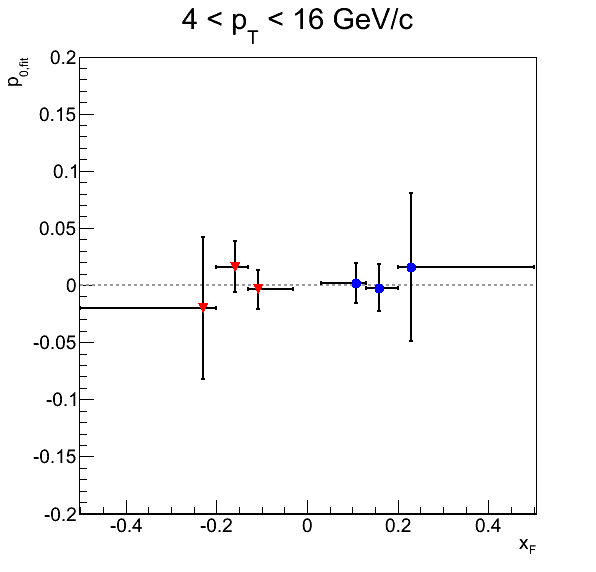
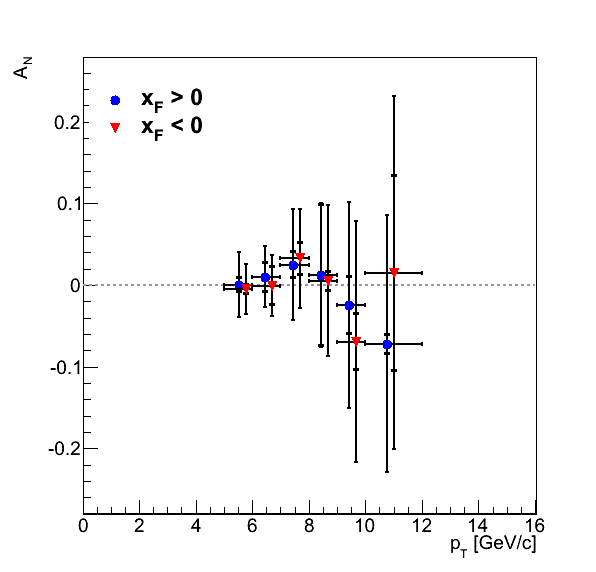
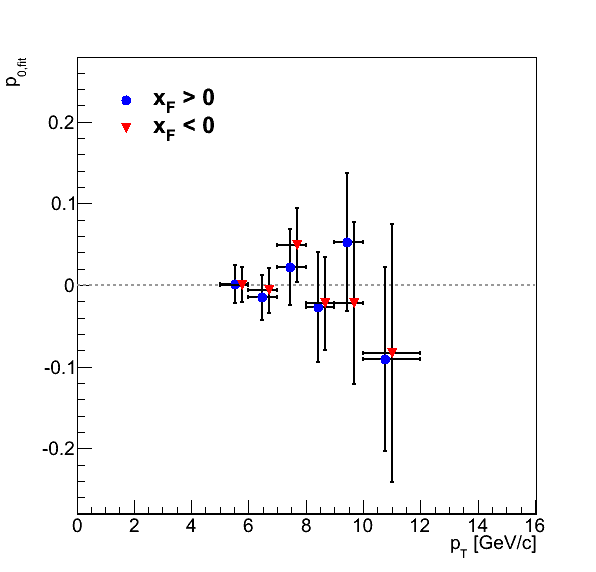
Figure 4 shows the current status of the background-corrected pion asymmetries as well as the p₀'s for the φ_S fits. Inner error bars are systematic errors, while outer error bars are statistical. The systematics included are background fractions and background asymmetries.