(January 18, 2012) NOTE: From this update until my December 31 update I incorrectly calculated the background-asymmetry systematic. I have subsequently changed my methodology. Instead of taking the largest asymmetry from among the bins, I take the largest average of the two bins surrounding the pion peak (turns out to be the yellow beam). This is ~2%. The sizes of the resulting systematics are quite comparable to what has been reported.

As I mentioned in my previous blog, I found a typo in my code which exacerbated the systematic uncertainty for the background asymmetry. In the meantime there has been quite a bit of code development. Here, I describe an update to my alternative background-correction procedure. With perhaps one additional systematic to include the next step is to revisit the direct calculation to see if that method will converge with the latest developments.

Signal Fraction

One update since last time is that I now calculate the signal fractions from fits to the mass distributions summed over the phi bins. This utilizes the statistics more efficiently and smooths over some of the divergent fits within the φ bins. The errors related to the signal fraction calculation are treated as systematic errors. There is, of course, embedded within these errors a statistical contribution. After all, the errors on the parameters are better determined with fits to more data. However, it is difficult in this procedure to separate the two contributions. To set a conservative limit, I include in the statistical uncertainties an error on the signal fraction equal to what we have deemed systematic uncertainties. The effect is negligible as we are dominated by statistical uncertainties from the yields.

Additionally, since last time, I have implemented an alternative signal fraction calculation for systematics purposes. I fit the φ-integrated invariant mass distribution with a Gaussian signal plus third-order polynomial background function. Again, to set a conservative limit, I recalculate the asymmetries utilizing the alternative signal fraction assuming the maximal background asymmetry of 7%. The difference between the calculation utilizing Steve's fits and this alternative fit determines the signal fraction systematic uncertainty.

Figure 1

xF Bins
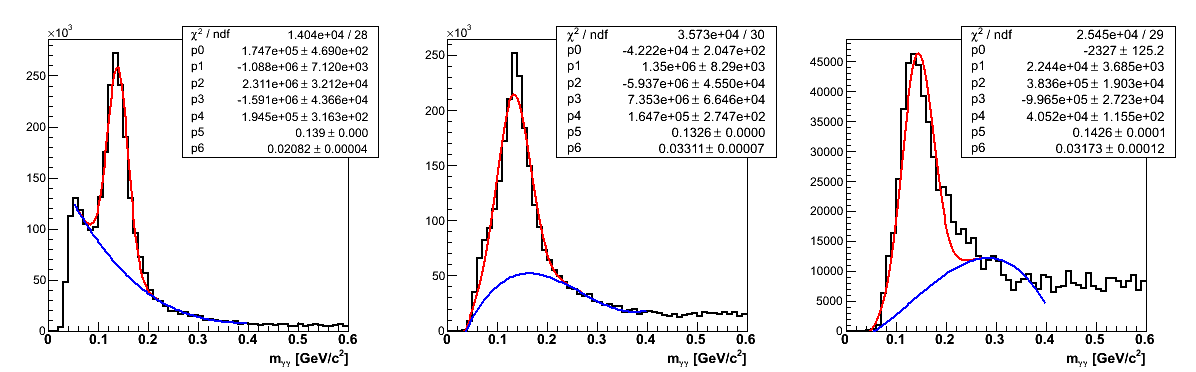pT Bins

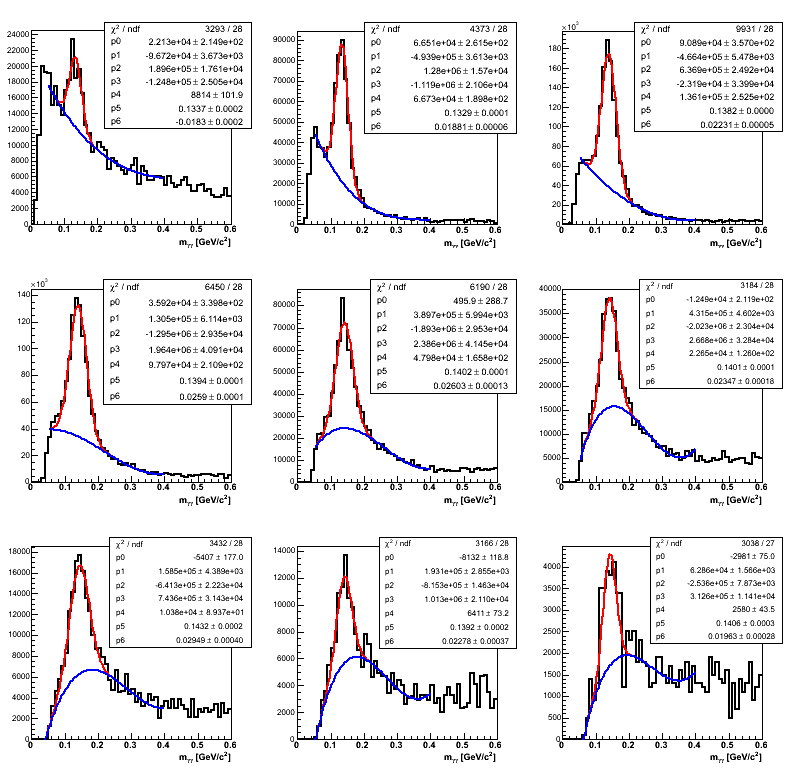Figure 1 shows the alternative mass fits. One can see they are not spectacular by any means. However, they are probably sufficient for the moment; and should provide an upper-limit to the systematic.

Mass Window

An additional systematic uncertainty I would like to check is to vary the mass window. At the moment all I do not have signal fraction calculations for the different mass window, so I will hold off on this for now.

Asymmetries

Here, I post the current status of the asymmetry calculations.

Figure 2

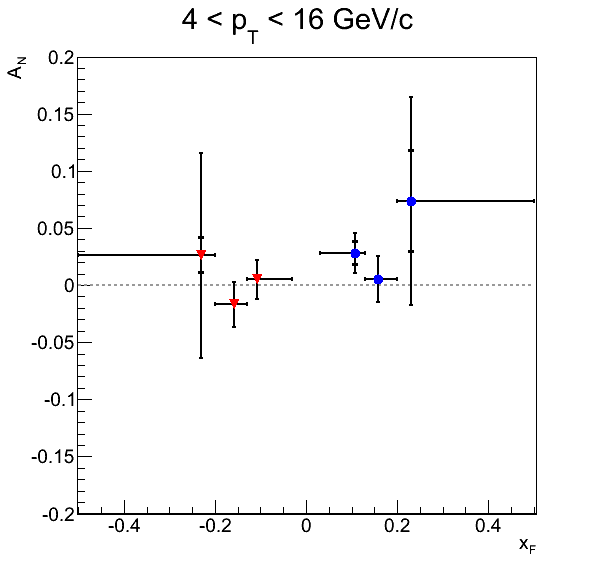
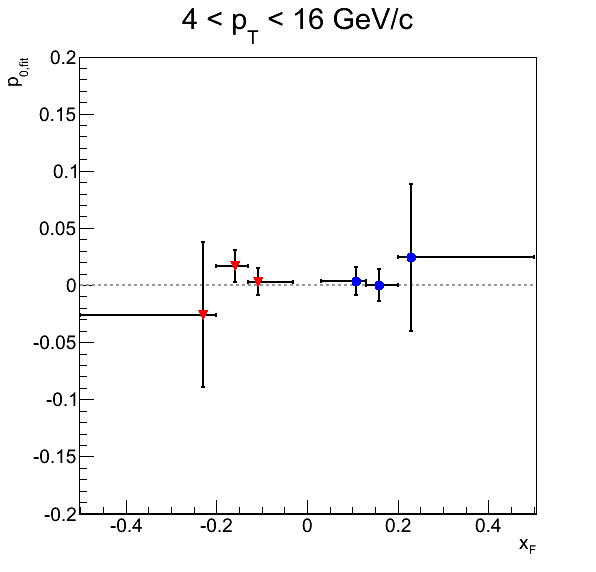
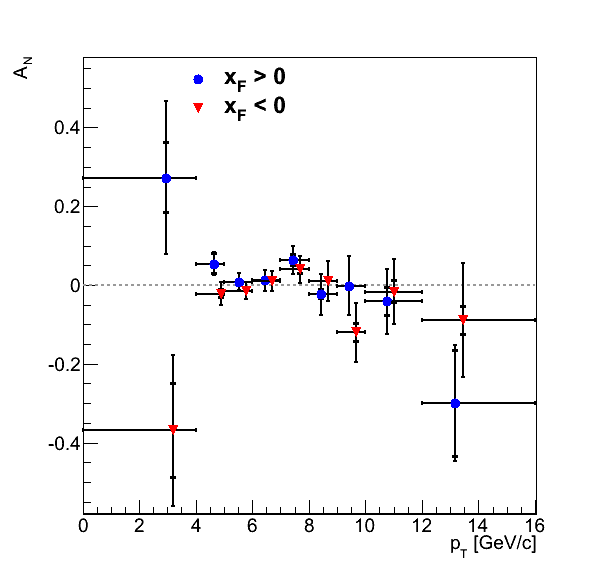
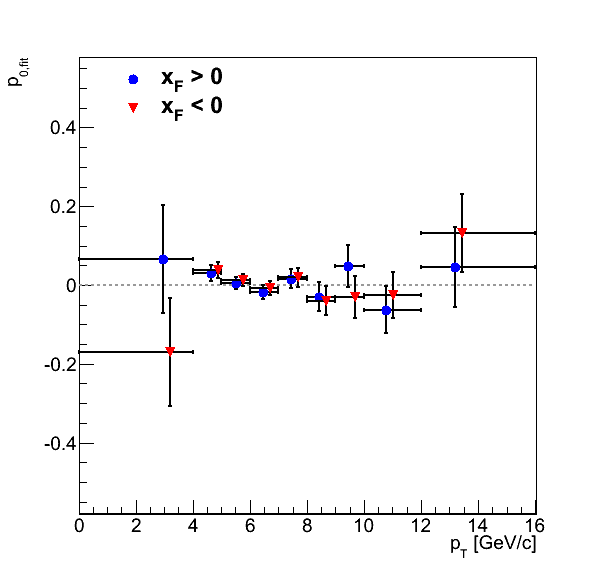
Figure 2 shows the background-corrected pion asymmetries as well as the p₀'s for the φ_S fits. Inner error bars are systematic errors, while outer error bars are statistical. The systematics included are signal fractions from propagated errors and an alternative calculation and background asymmetries.