drach09's blog

In my previous update I looked at Collins and Sivers asymmetries for the currently available jet trees. In this update I look at the Sivers asymmetry in bins of η_jet, rebinned Collins asymmetries in trying to even out much of the wild fluctuations due to a lack of statistics at high-z and high-j_T, and the Collins-like asymmetries for which we may have sensitivity. Finally, I also look at some statistical cross-checks of my analysis. The cuts are exactly as before and described in the previous update. Note that all asymmetries are shown prior to polarization correction.

Sivers Asymmetries

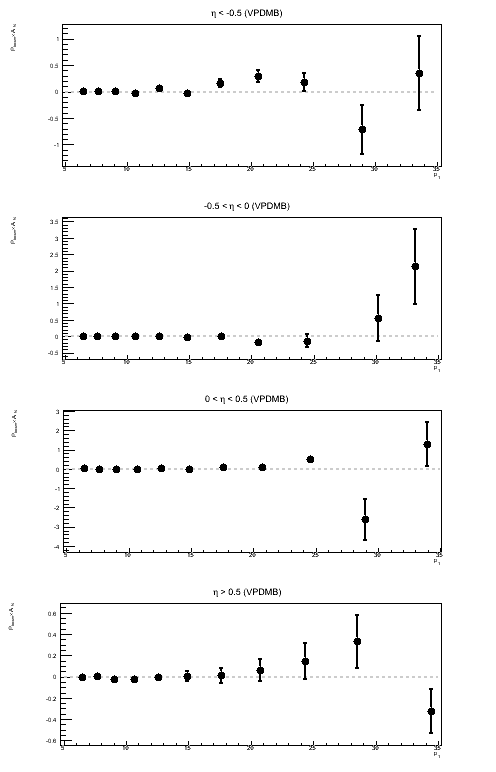
There is some hint of a nonzero Sivers effect in JP1 and VPDMB. I am cautious about drawing too many conclusions, given the lack of such evidence in the JP2 and AJP triggers. However, it is certainly worth investigation. One idea is to examine the η dependence, as was done in the recent jet PRD.

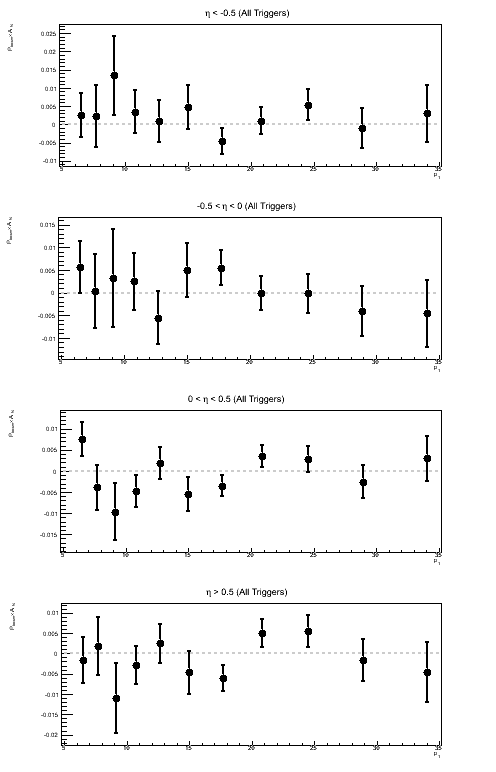
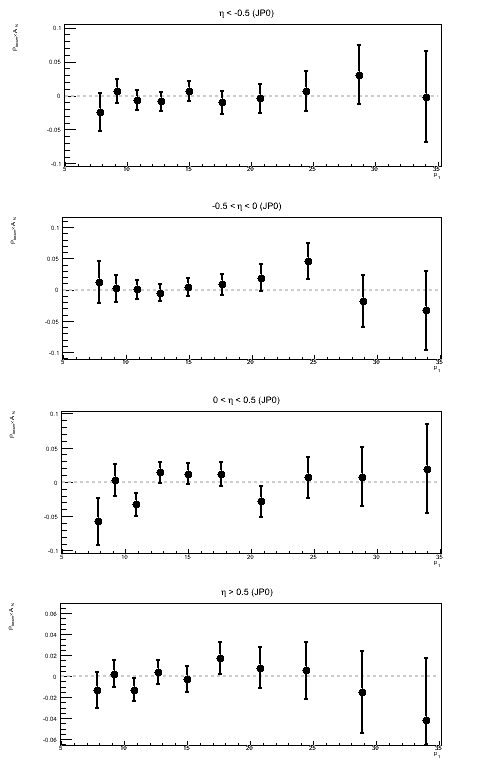
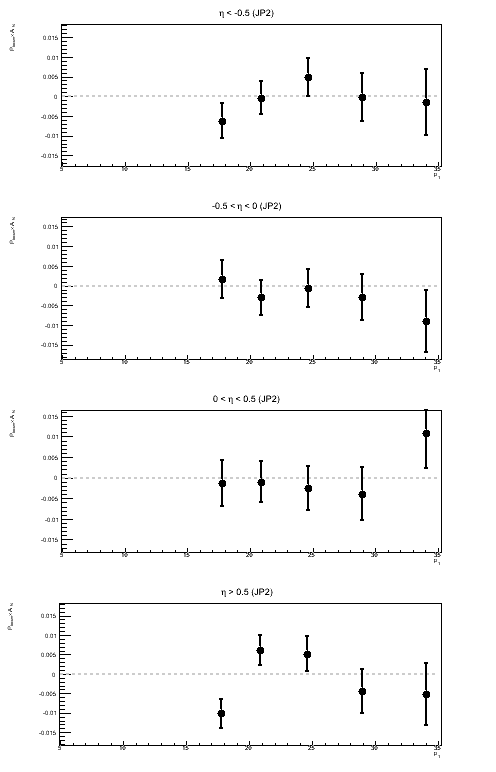
Figure 1: Sivers Asymmetry in Bins of η_jet

All Triggers	JP0	JP1

JP2	AJP	VPDMB

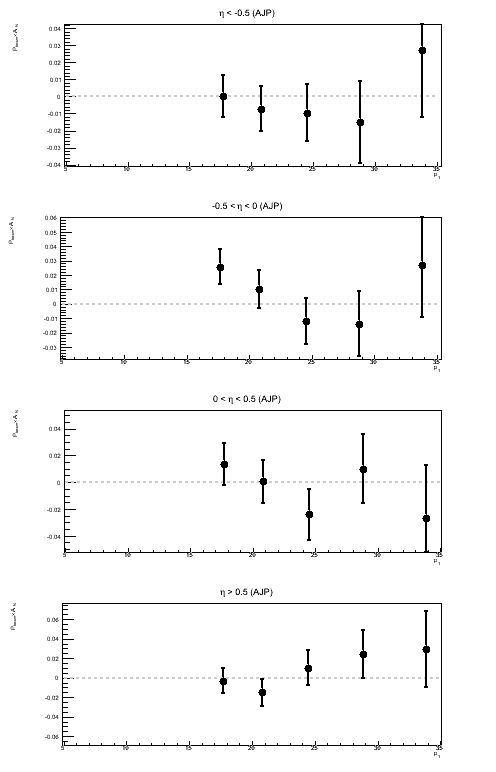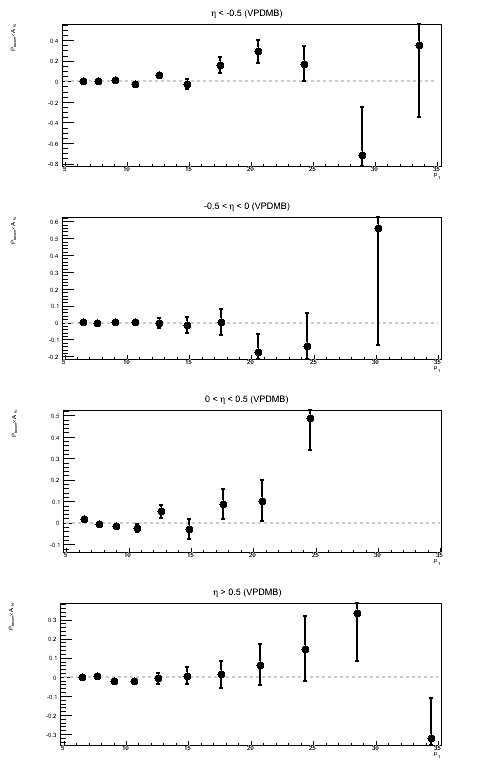Above, I show the Sivers asymmetry as a function of jet p_T for different bins of η_jet. Naïvely, I would assume a real Sivers effect would increase as one moves forward in η and exhibit something like a 1/p_T-dependence. I do not see anything resembling a 1/p_T-dependence. I am also wary of concluding anything from JP1 and VPDM at rather high p_T. As a follow-up to this, it is worth looking at the actual sin(φ_S) fits to see if the fit itself is believable.

Collins Asymmetries

The main change from before is a rebinning of the asymmetries. My code, now includes the following for z and j_T bins:

  const double zbins[nzbins+1] = { 0., 0.05, 0.1, 0.2, 0.3, 0.4, 0.5, 0.8, 1. };
  const double jtbins[njtbins+1] = { 0., 0.1, 0.2, 0.3, 0.5, 0.7, 1., 2., 10. };

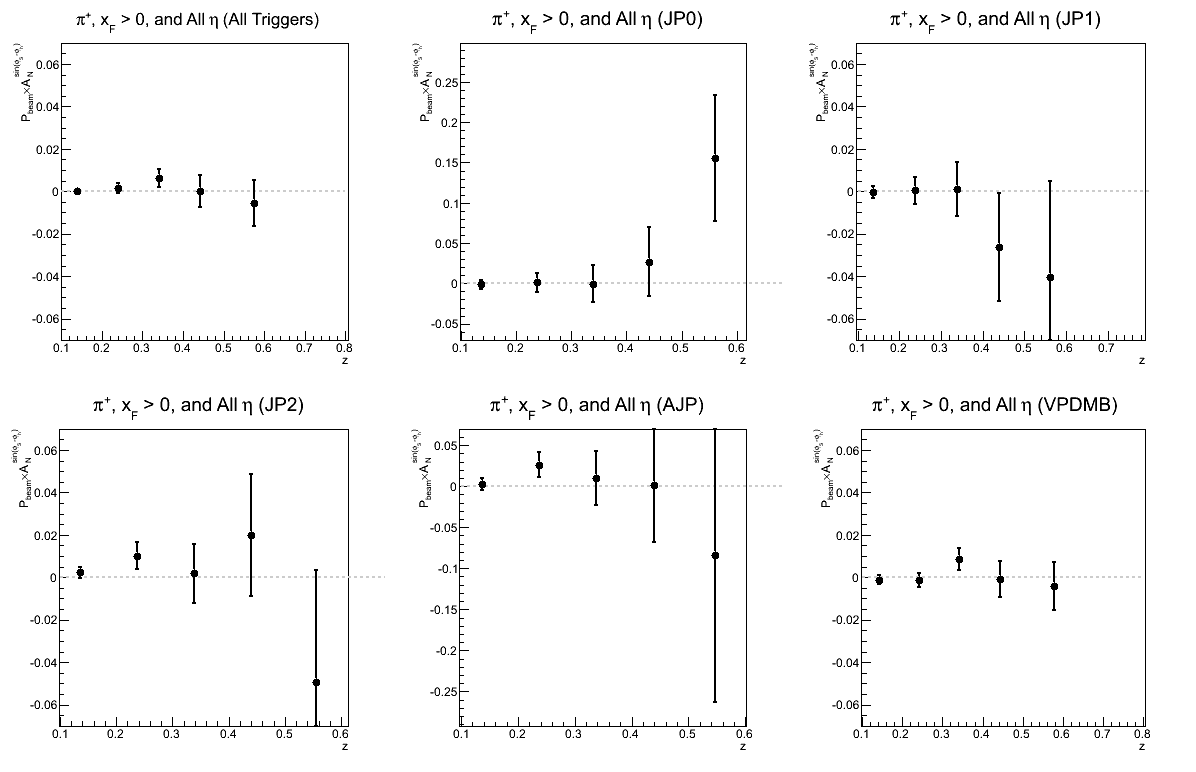
Figure 2: Collins Asymmetry as a Function of z

Triggers
charge > 0	charge < 0

Comparison of Hemispheres and x_F
charge > 0	charge < 0

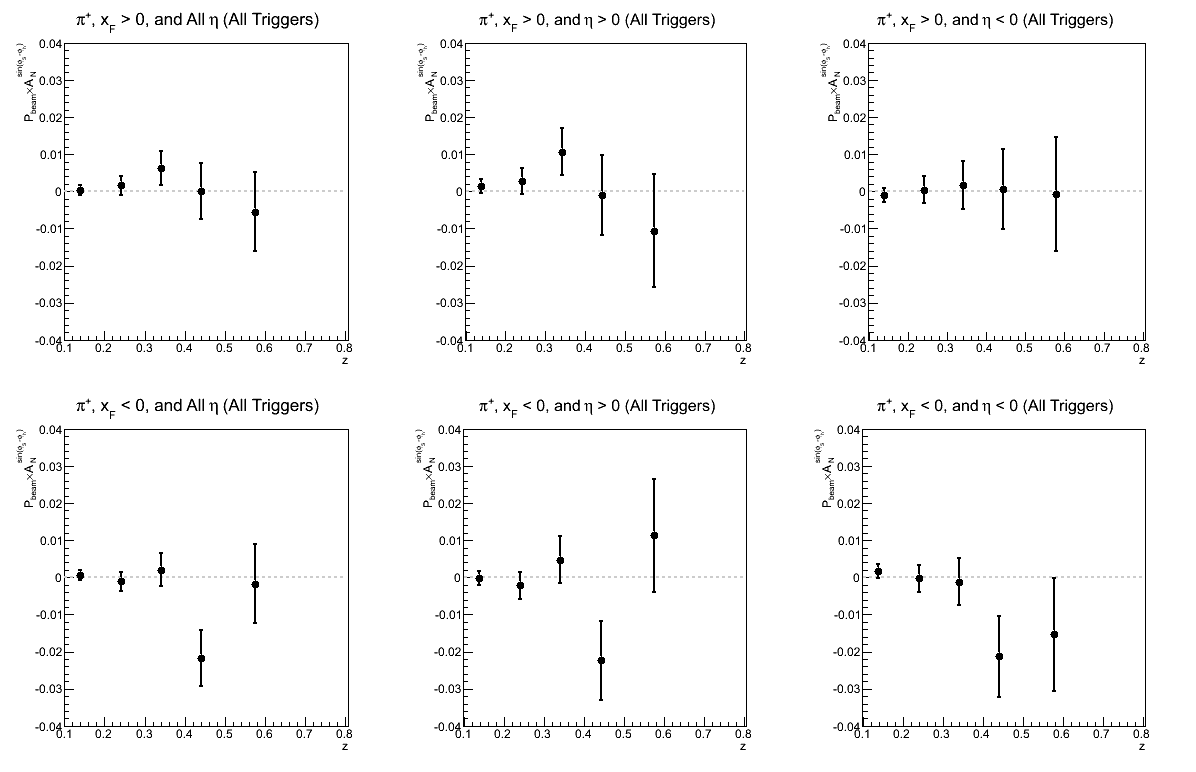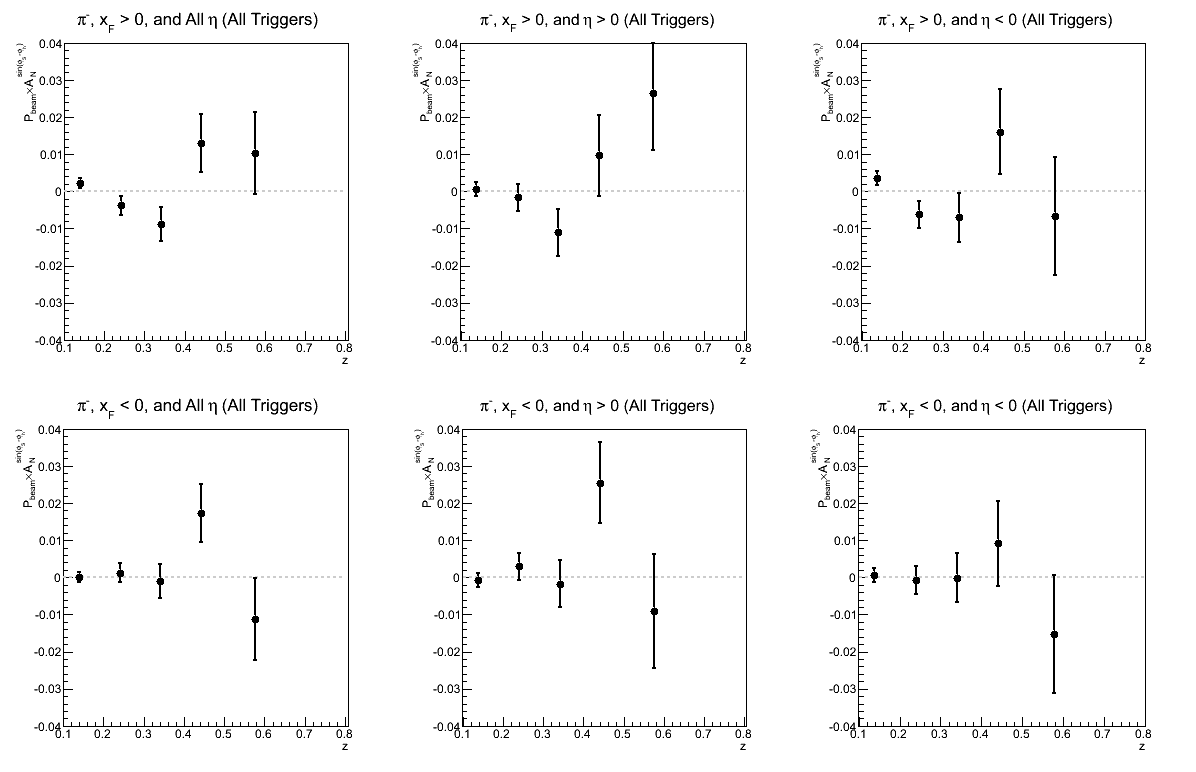While not necessarily optimal for one's eyes, I have kept the vertical scales the same to try to give a sense of which triggers are contributing and where. I have also dumped unzoomed histograms in the attic at the bottom of the blog. I'm still not ready to make any declarations. There does seem to be a hint of charge-sign dependence to the asymmetries in z, but I will definitely need more statistics before I can state so firmly.

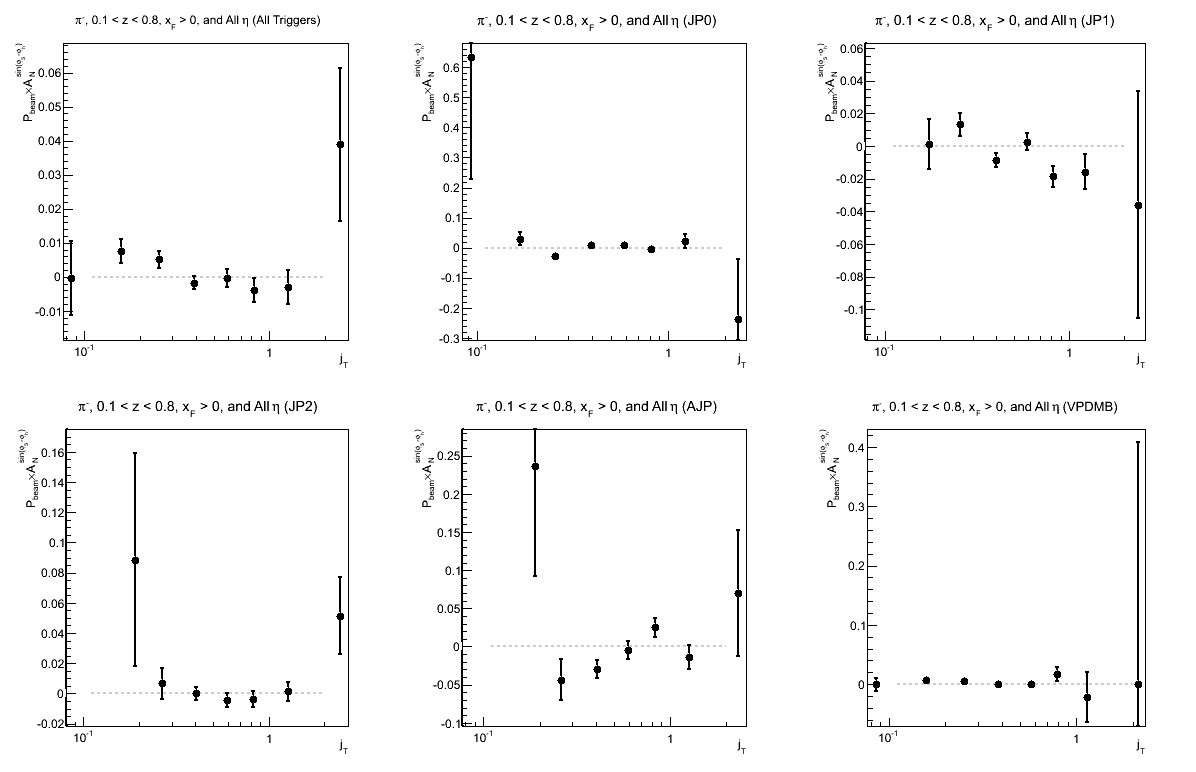
Figure 3: Collins Asymmetry as a Function of j_T (0.1 < z < 0.8)

Triggers
charge > 0	charge < 0

Comparison of Hemispheres and x_F
charge > 0	charge < 0

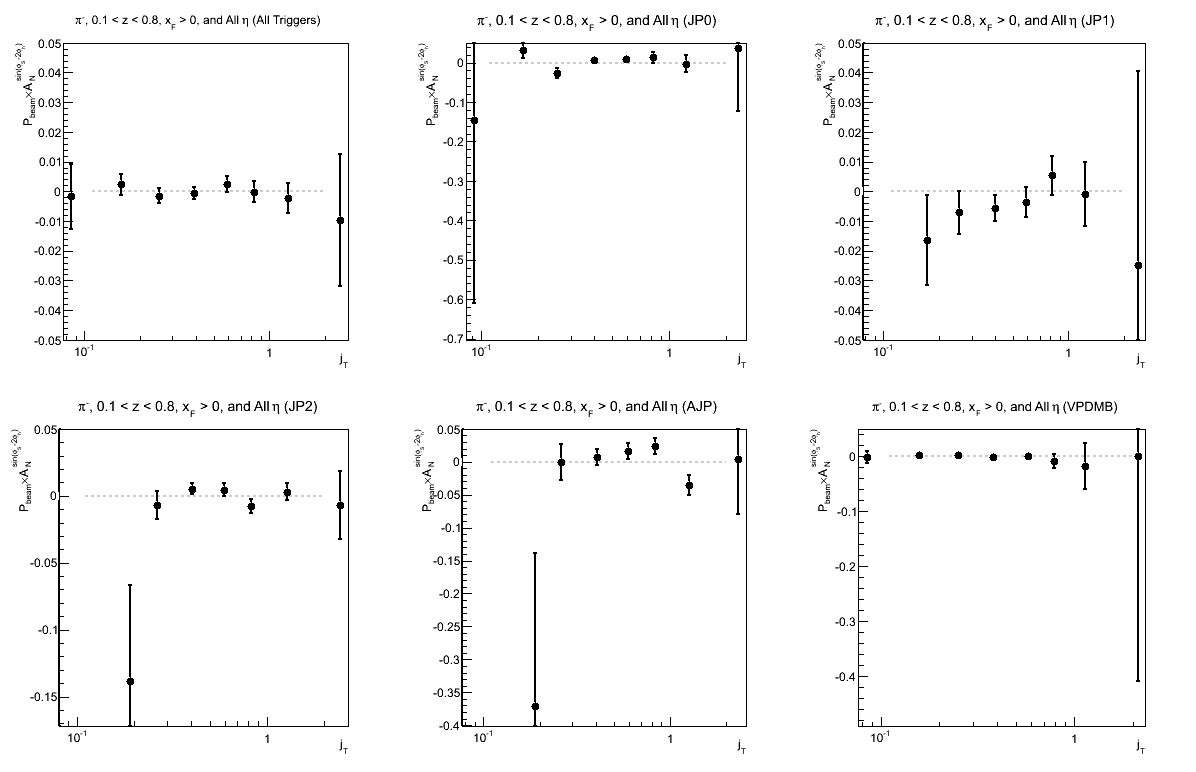
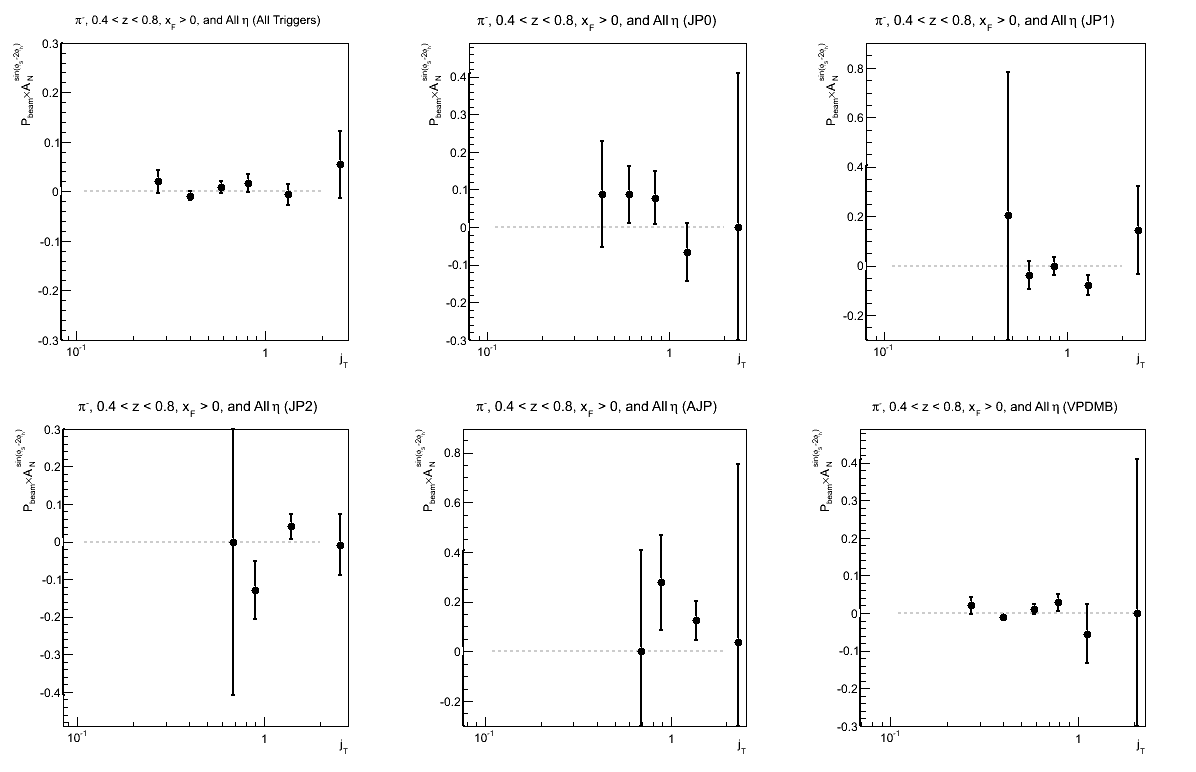
Again, we see hints of charge-sign dependence; but more statistics are needed for sensitivity to what appears to be a rather small effect, if any.

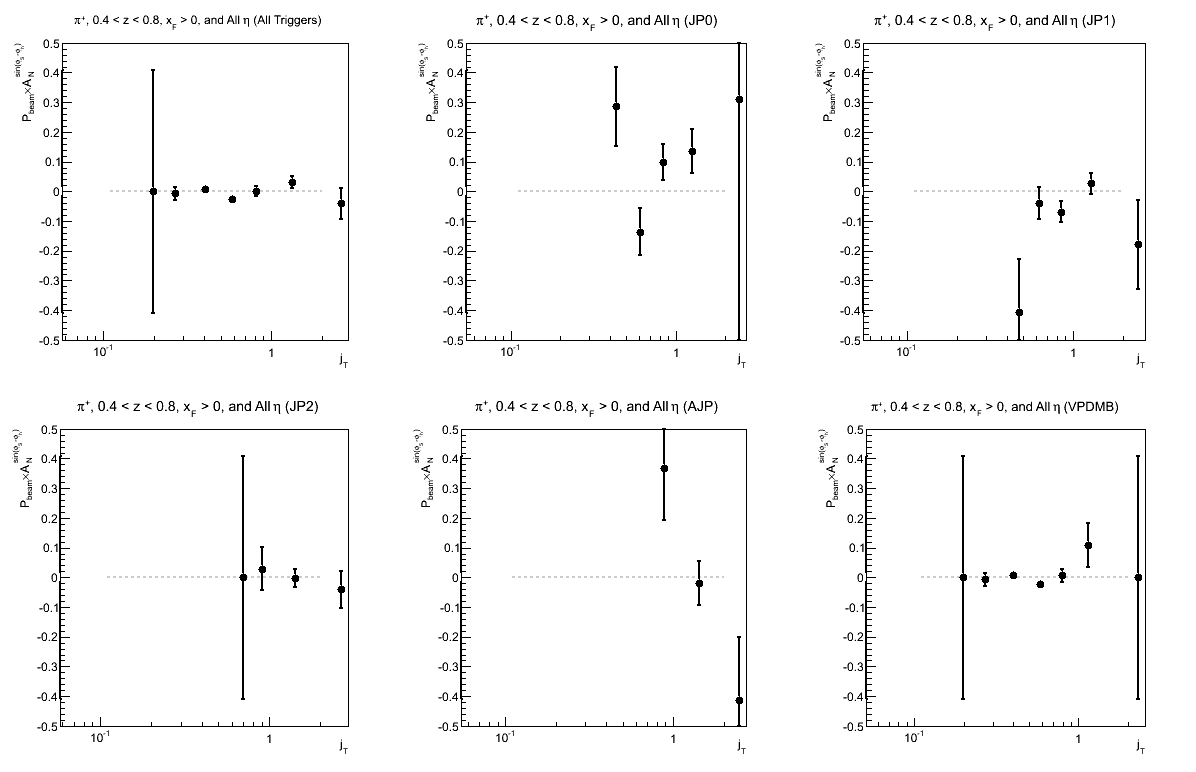
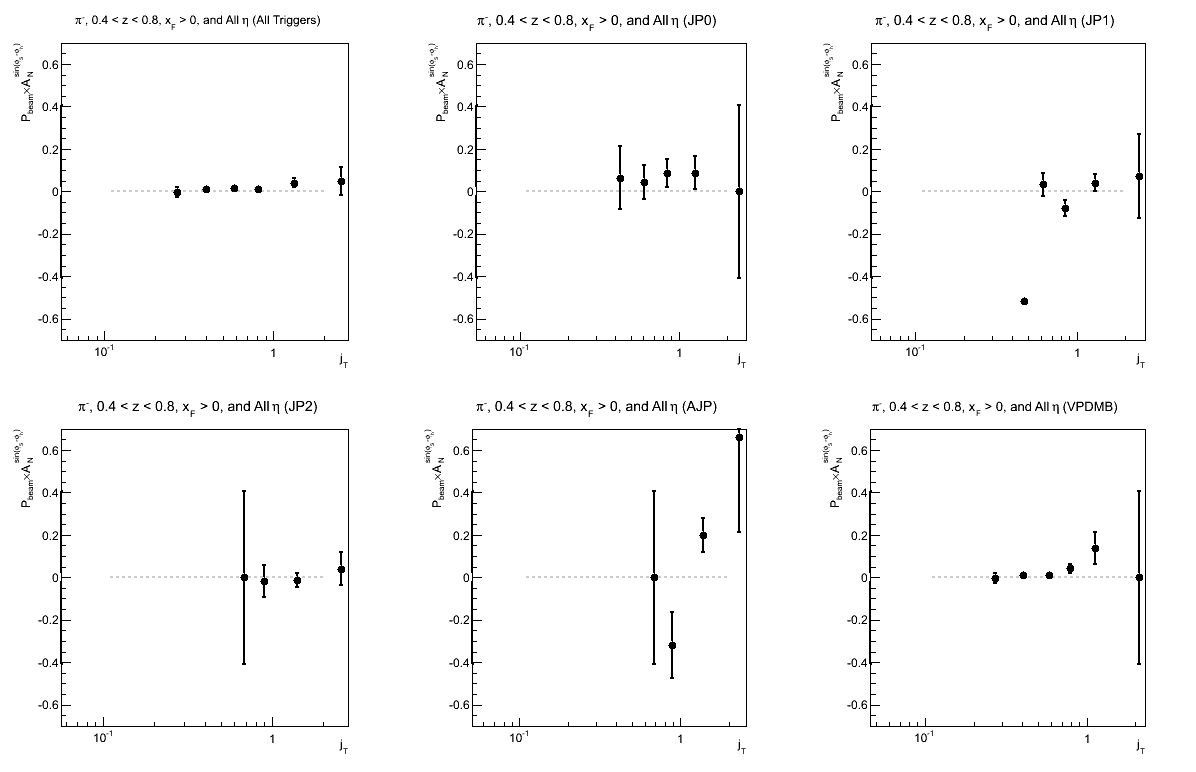
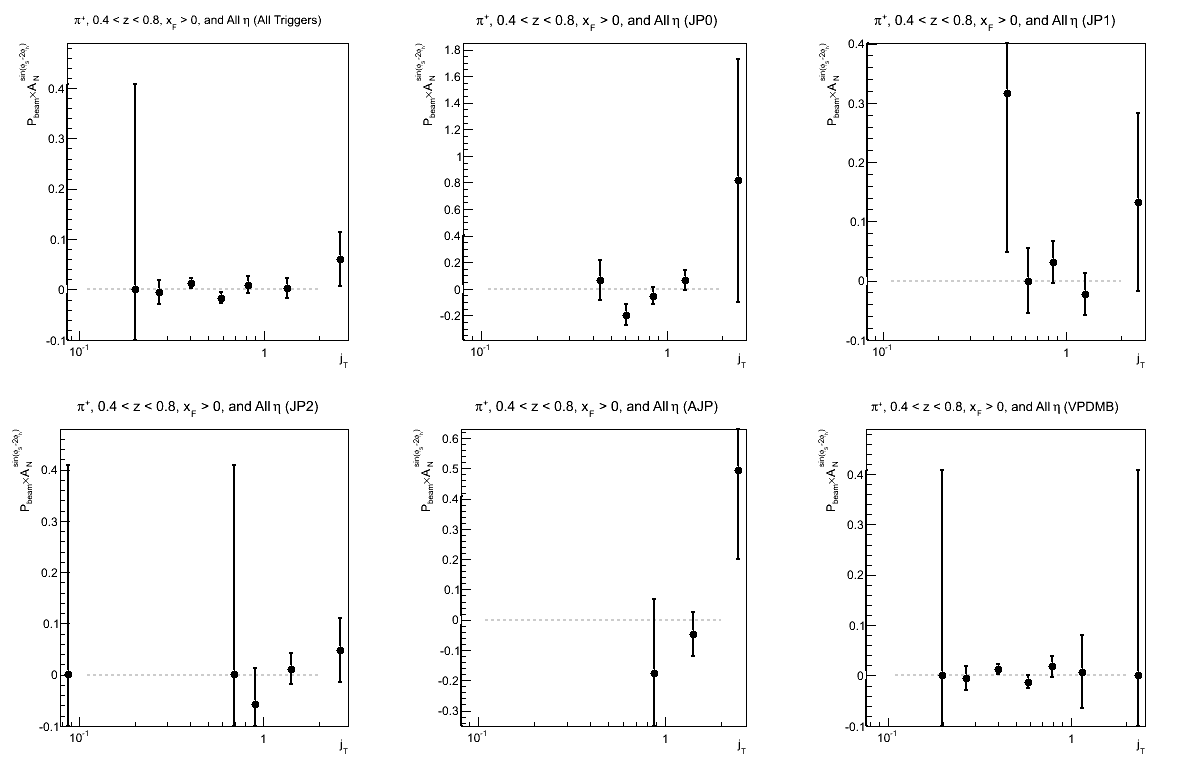
Figure 4: Collins Asymmetry as a Function of j_T (0.4 < z < 0.8)

Triggers
charge > 0	charge < 0

Comparison of Hemispheres and x_F
charge > 0	charge < 0

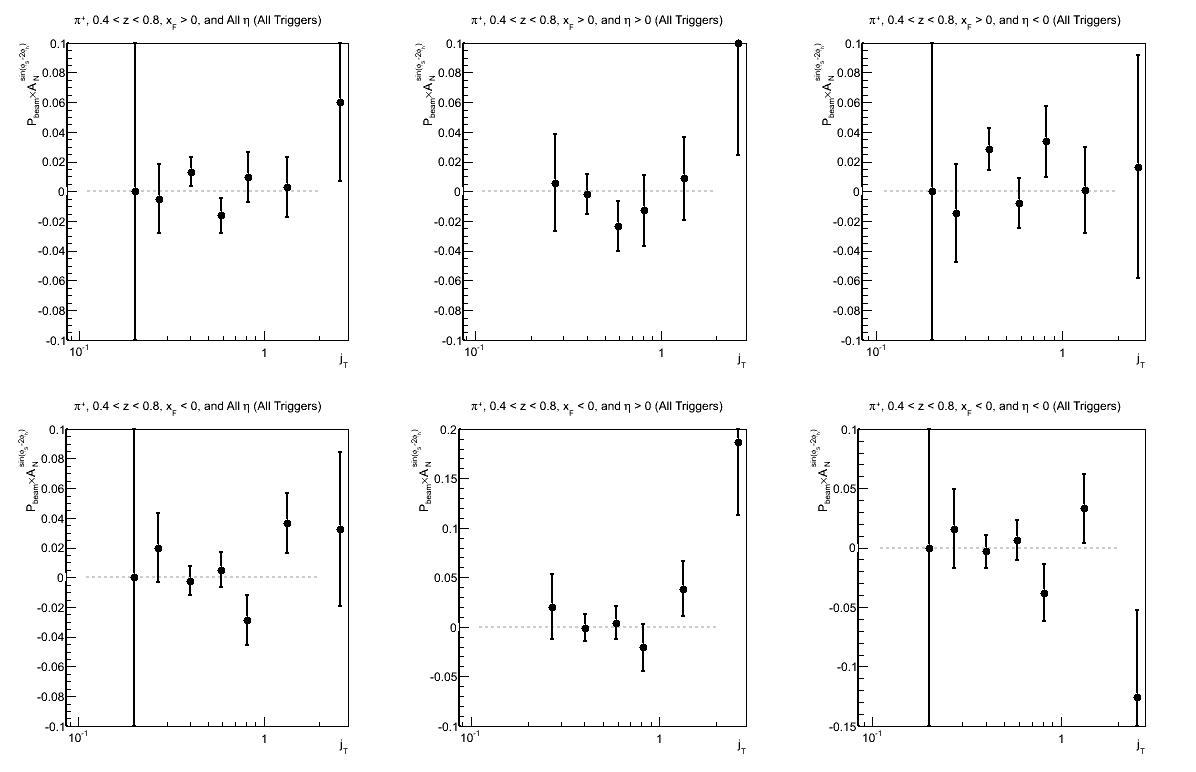
Again, I have so few statistics in the high-z region that it is difficult to draw conclusions.

Collins-like Asymmetries

This is the first time I have looked at the sin(φ_S-2φ_h) or "Collins-like" asymmetry. I have binned the same as the Collins asymmetry.

Figure 5: Collins-like Asymmetry as a Function of z

Triggers
charge > 0	charge < 0

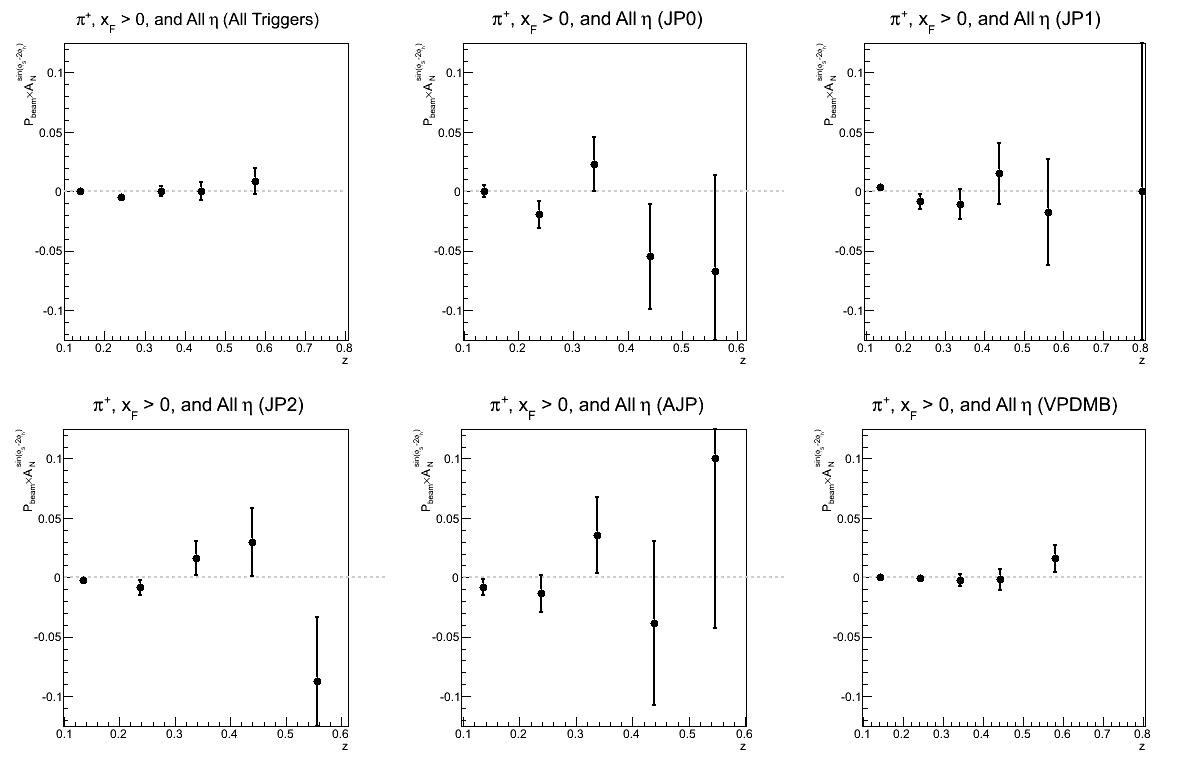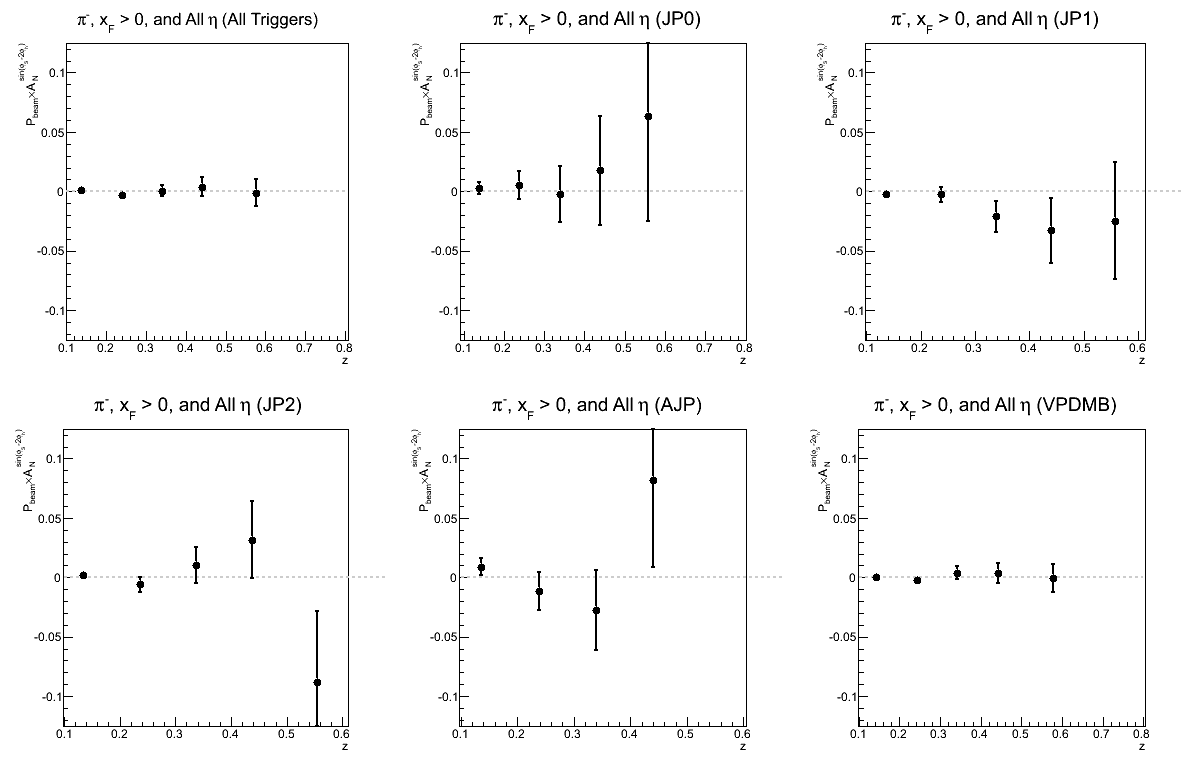Comparison of Hemispheres and x_F
charge > 0	charge < 0

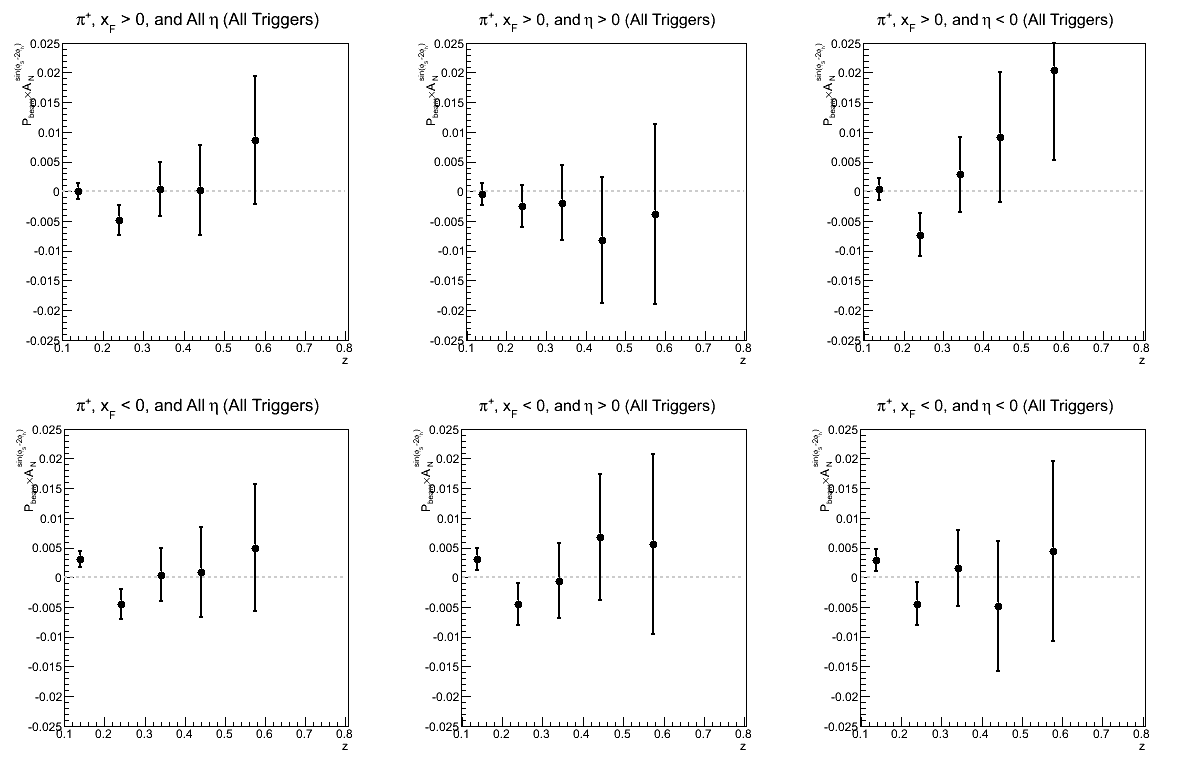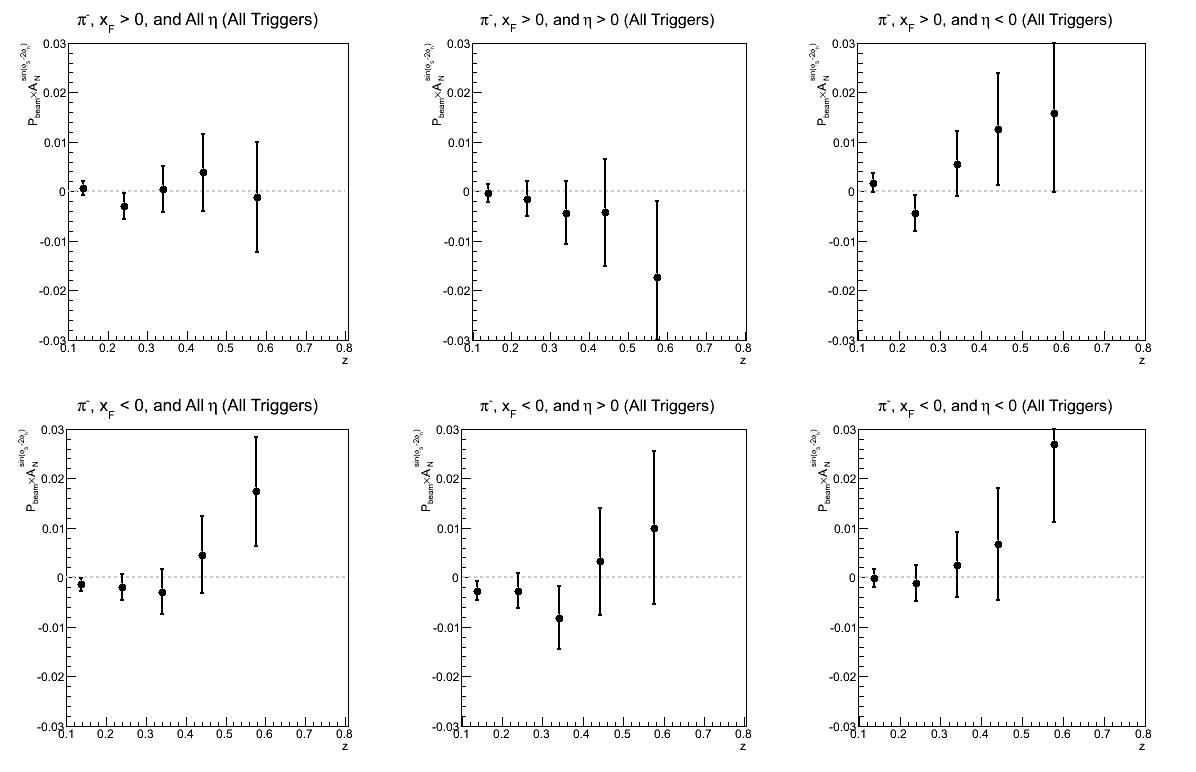Figure 6: Collins-like Asymmetry as a Function of j_T (0.1 < z < 0.8)

Triggers
charge > 0	charge < 0

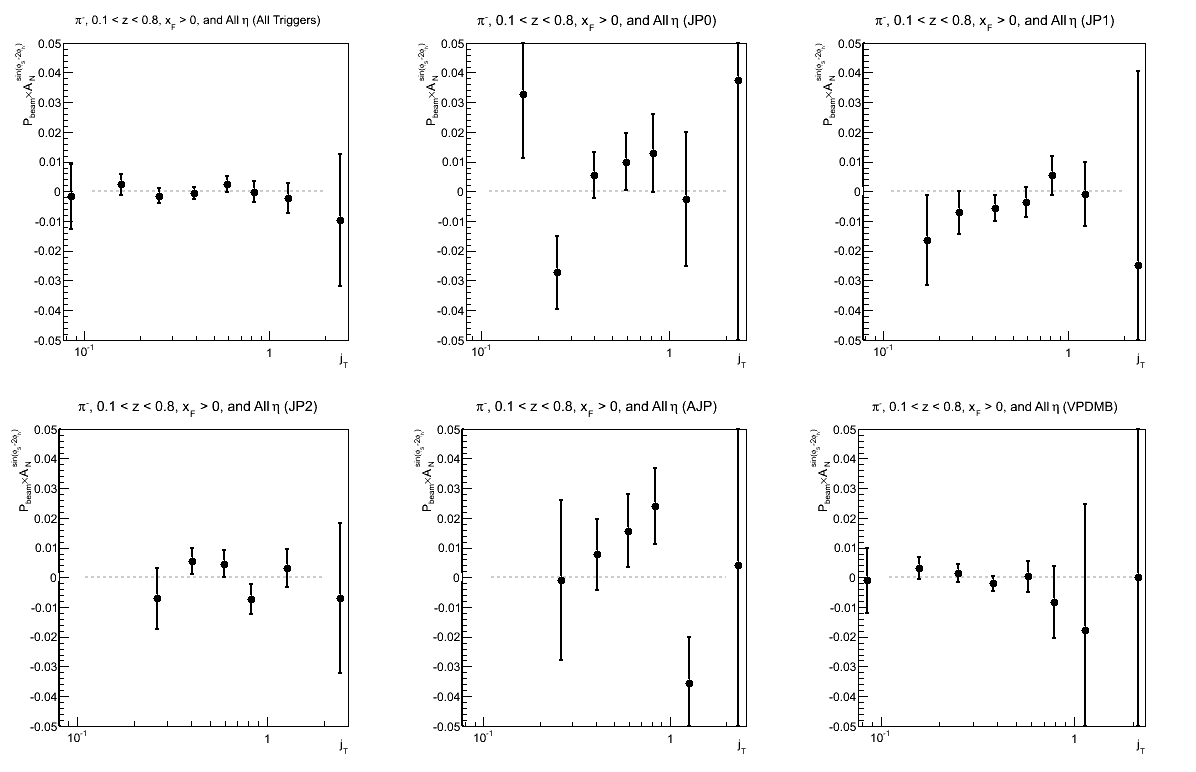Comparison of Hemispheres and x_F
charge > 0	charge < 0

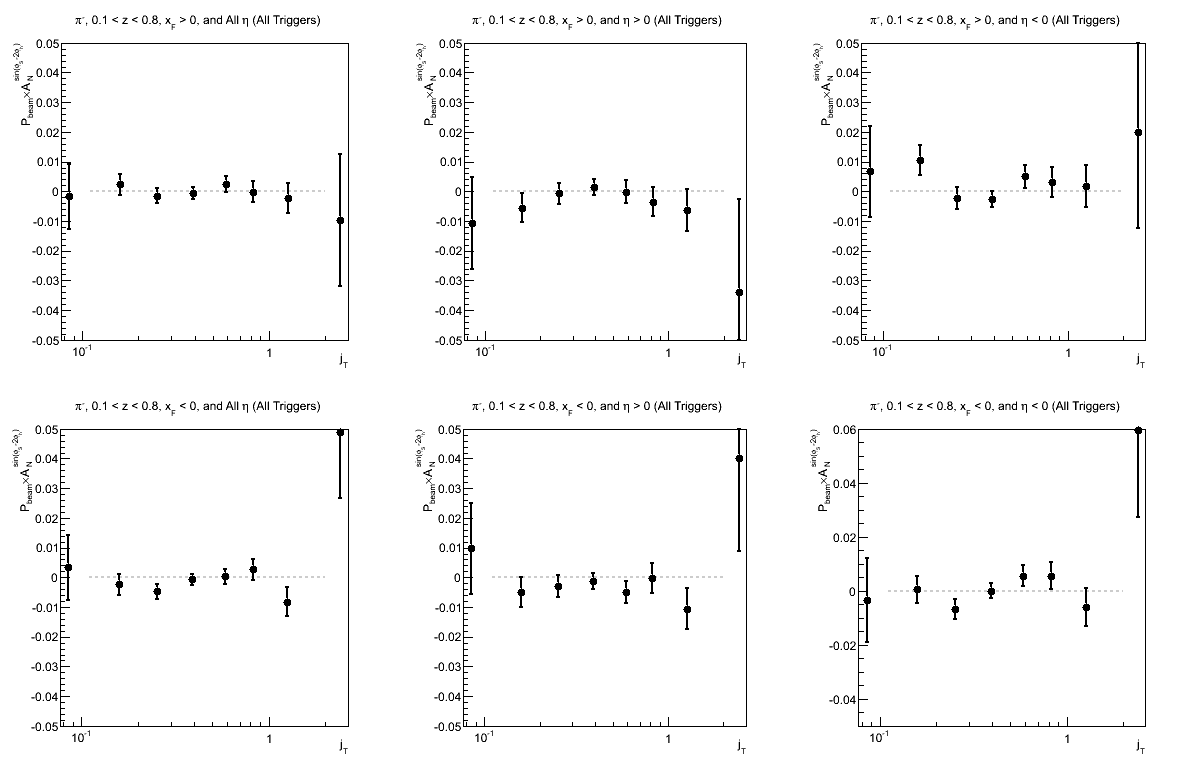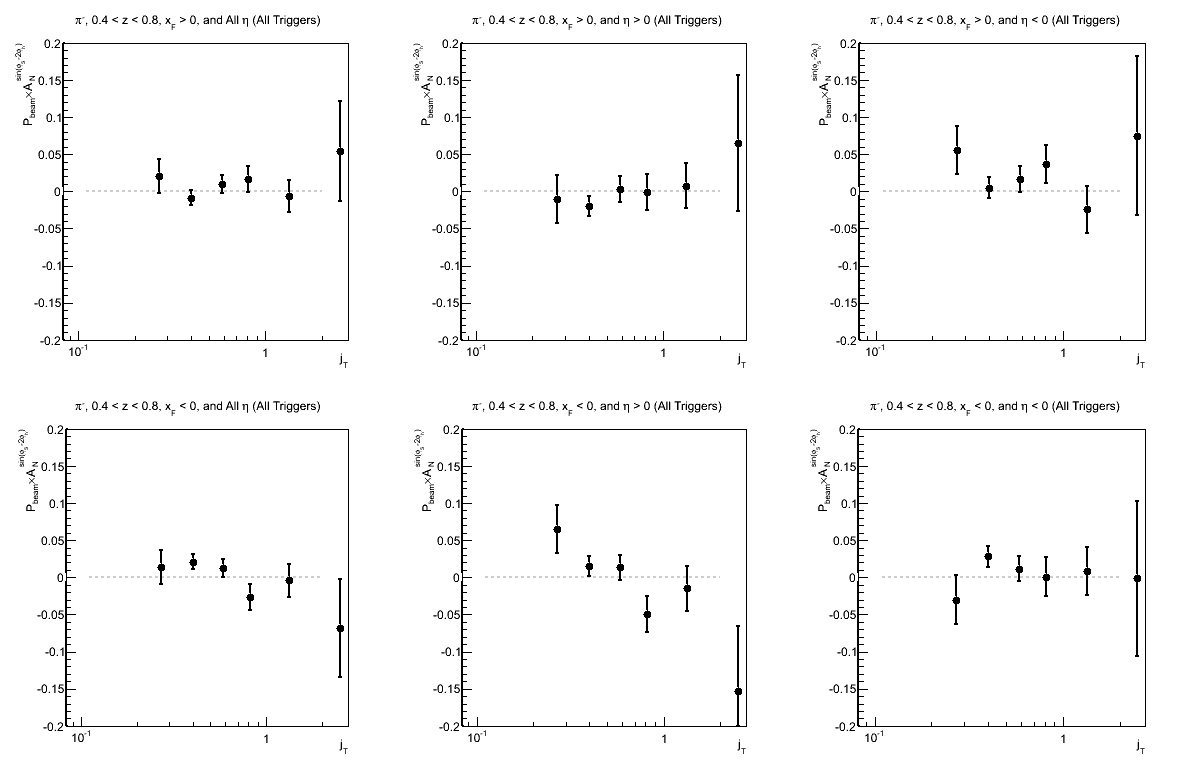
Figure 7: Collins-like Asymmetry as a Function of j_T (0.4 < z < 0.8)

Triggers
charge > 0	charge < 0

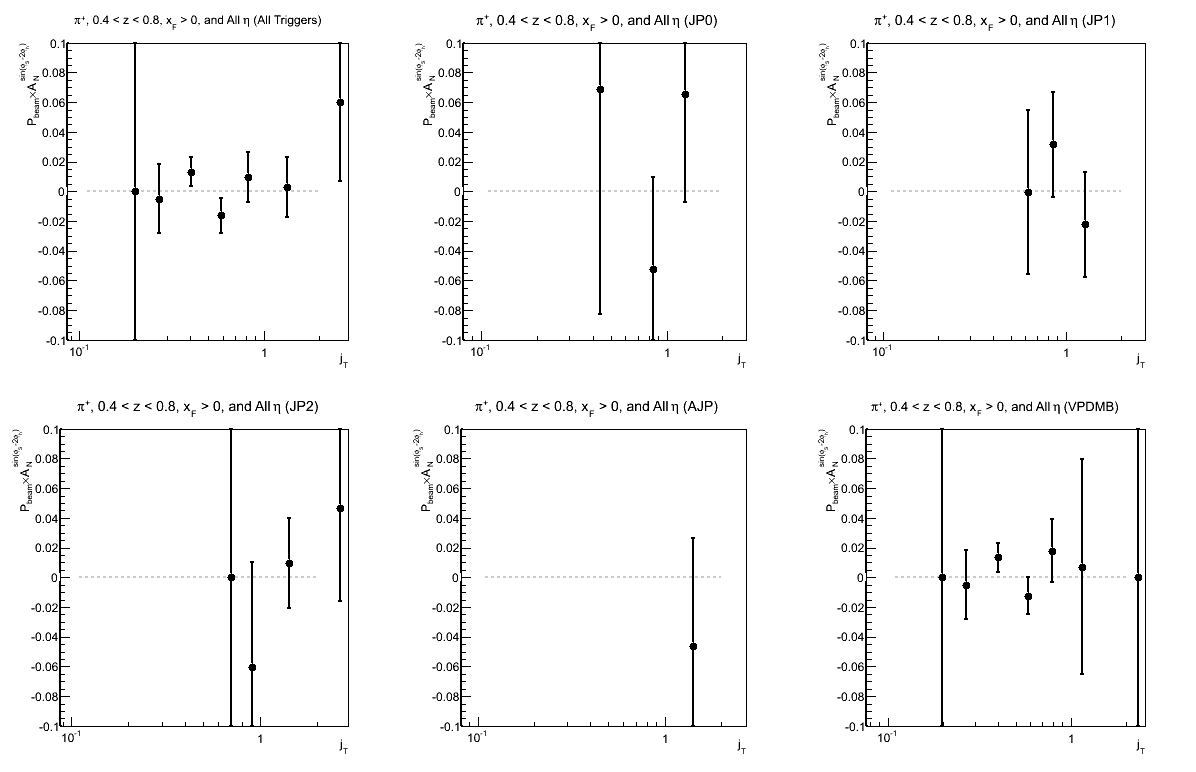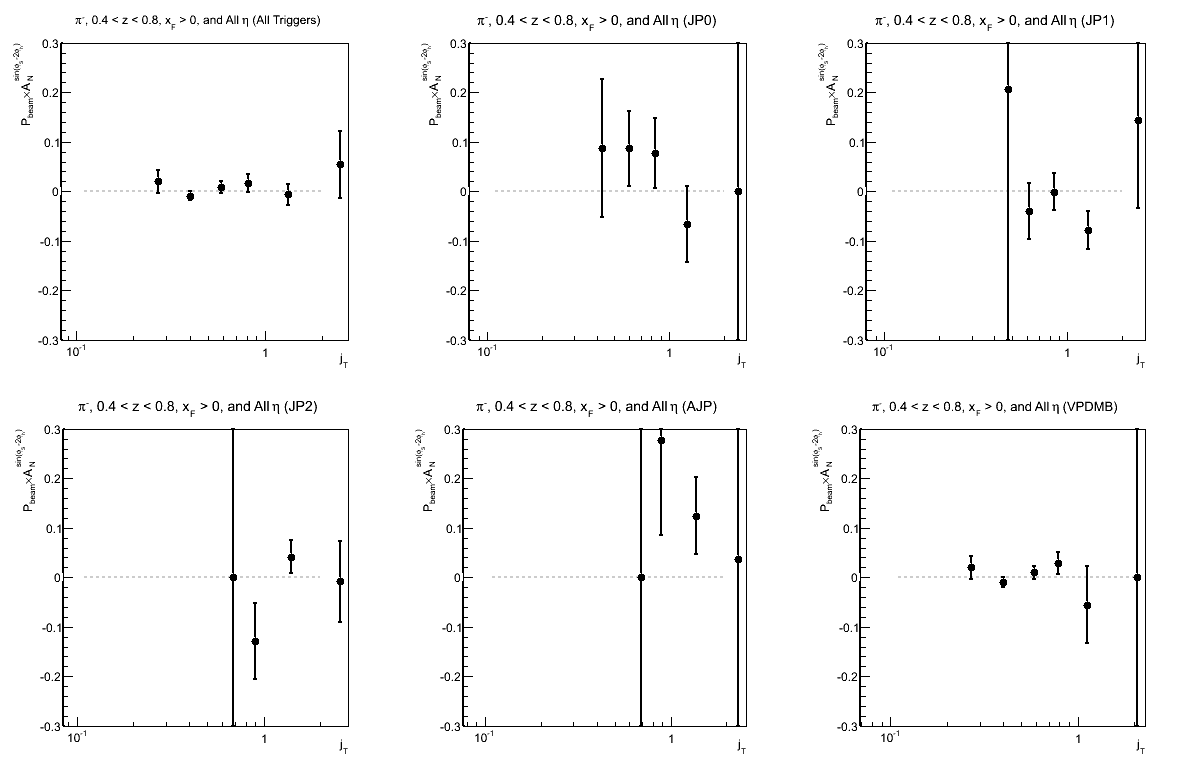Comparison of Hemispheres and x_F
charge > 0	charge < 0

Statistical Cross-checks

p₀ From Fits

In principle, the p₀'s from my fits should be the same. Thus, a good cross-check is to see if the p₀'s are consistent within statistical uncertainties.

Figure 8: p₀ for Sivers Asymmetry as a Function of p_T

Triggers

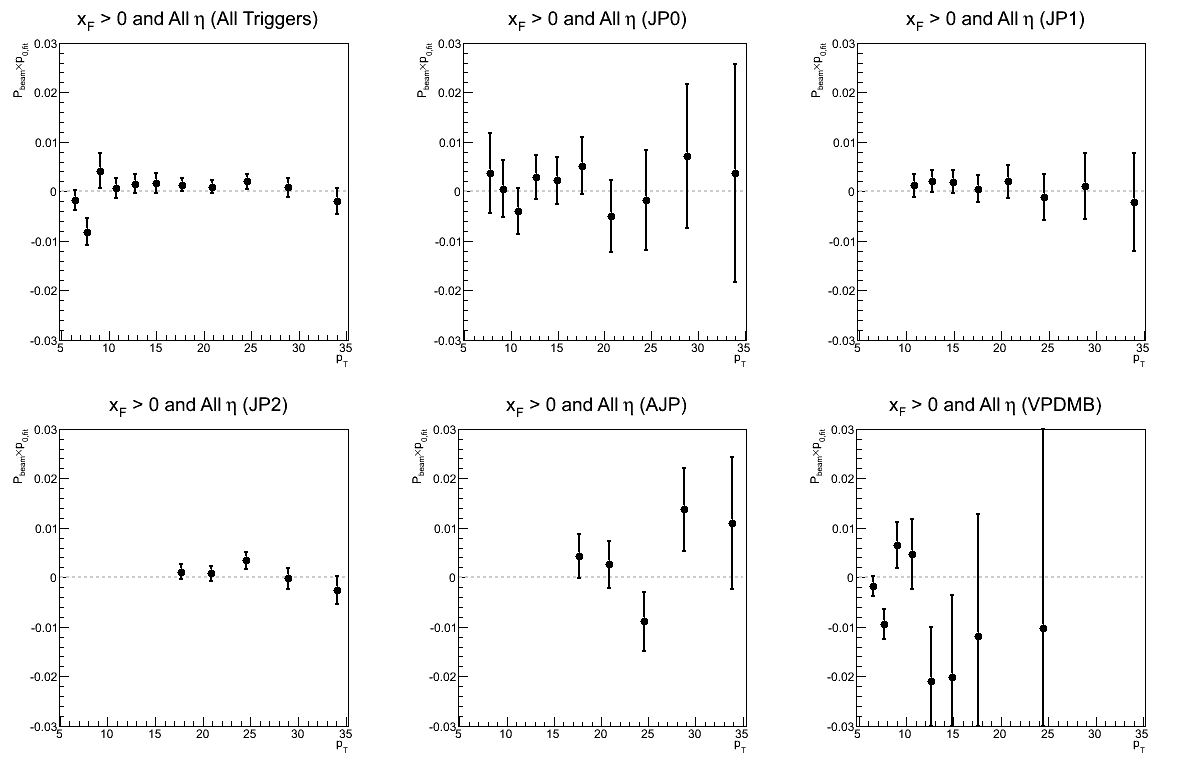Figure 9: p₀ for Collins Asymmetry as a Function of z

Triggers
charge > 0	charge < 0

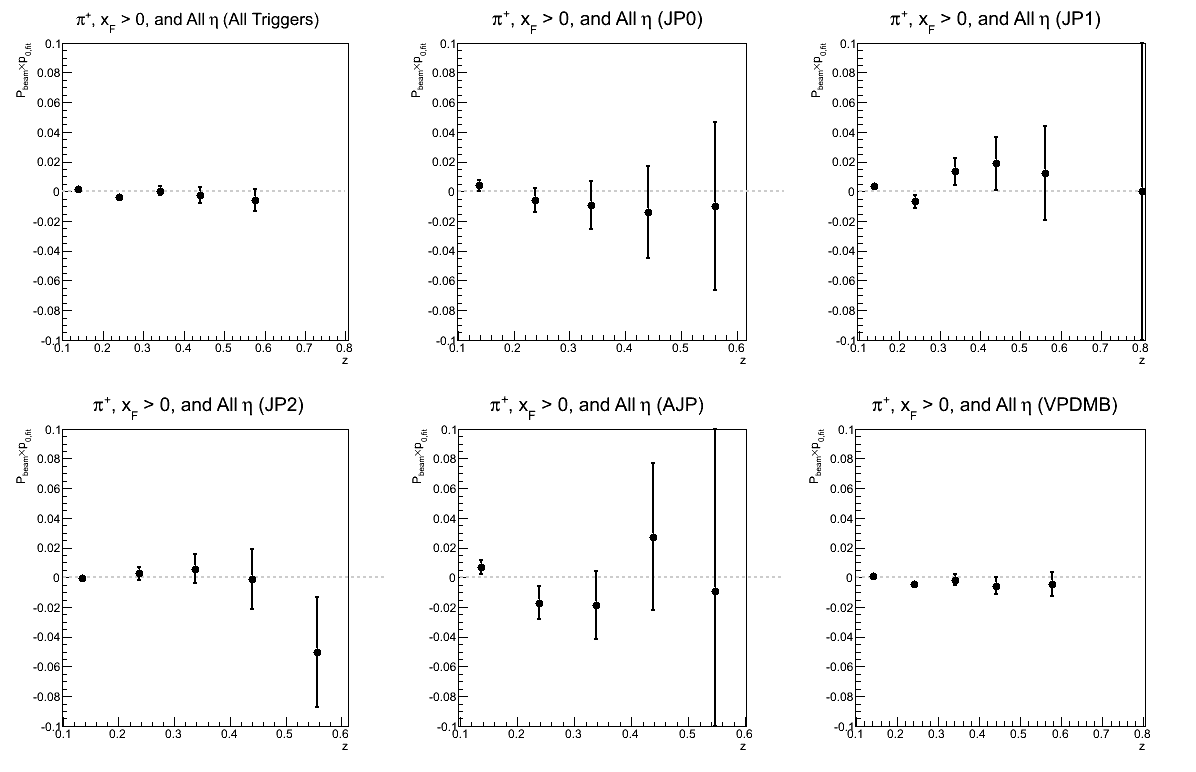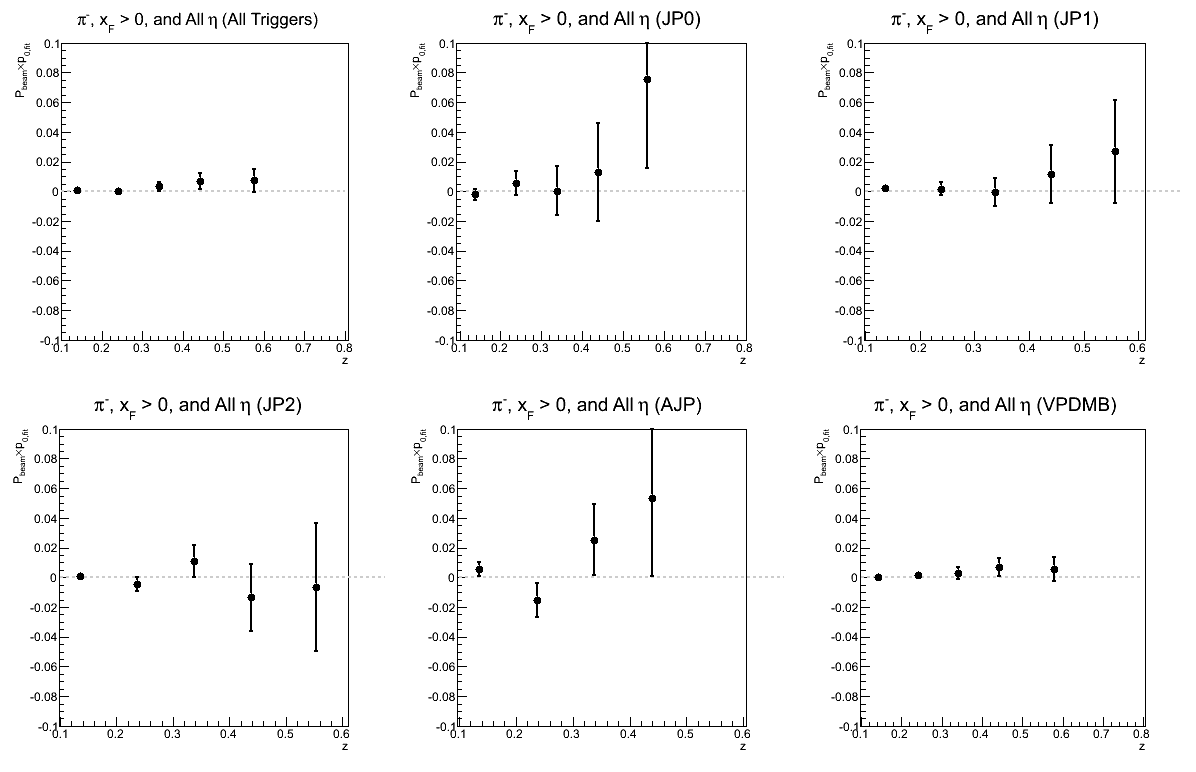Figure 10: p₀ for Collins Asymmetry as a Function of j_T

Triggers
charge > 0	charge < 0

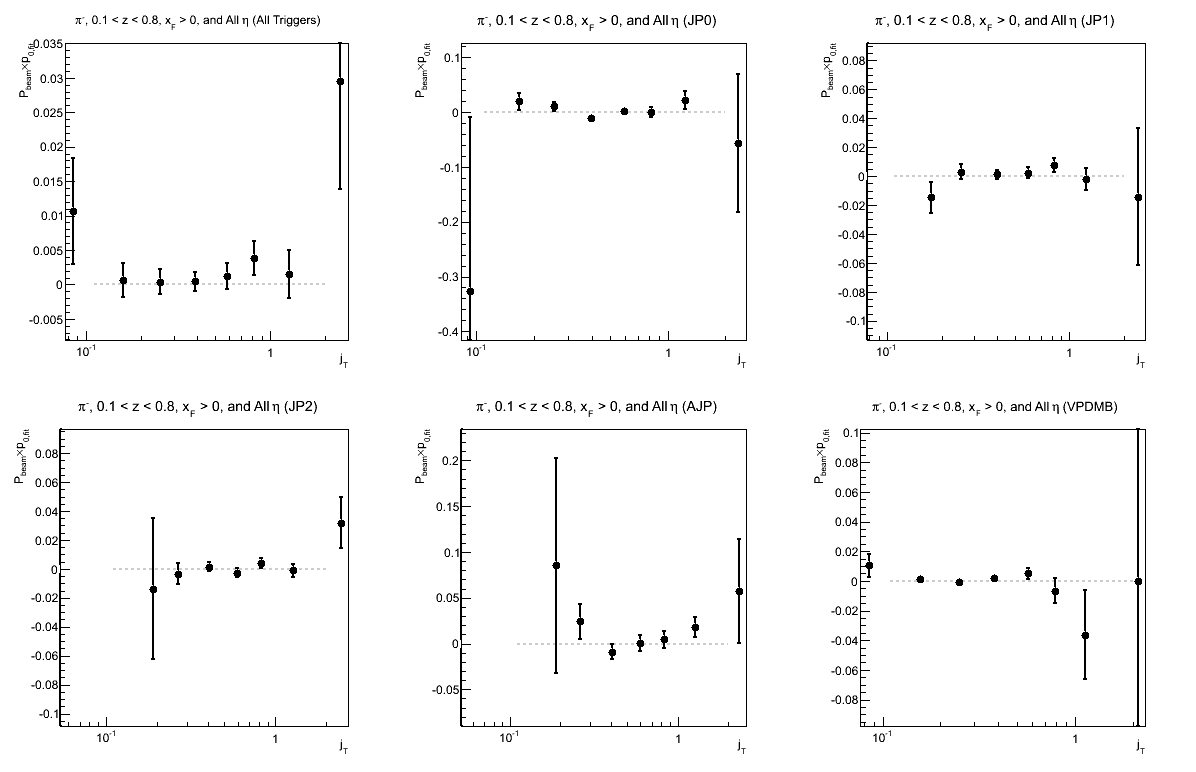Figure 11: p₀ for Collins-like Asymmetry as a Function of z

Triggers
charge > 0	charge < 0

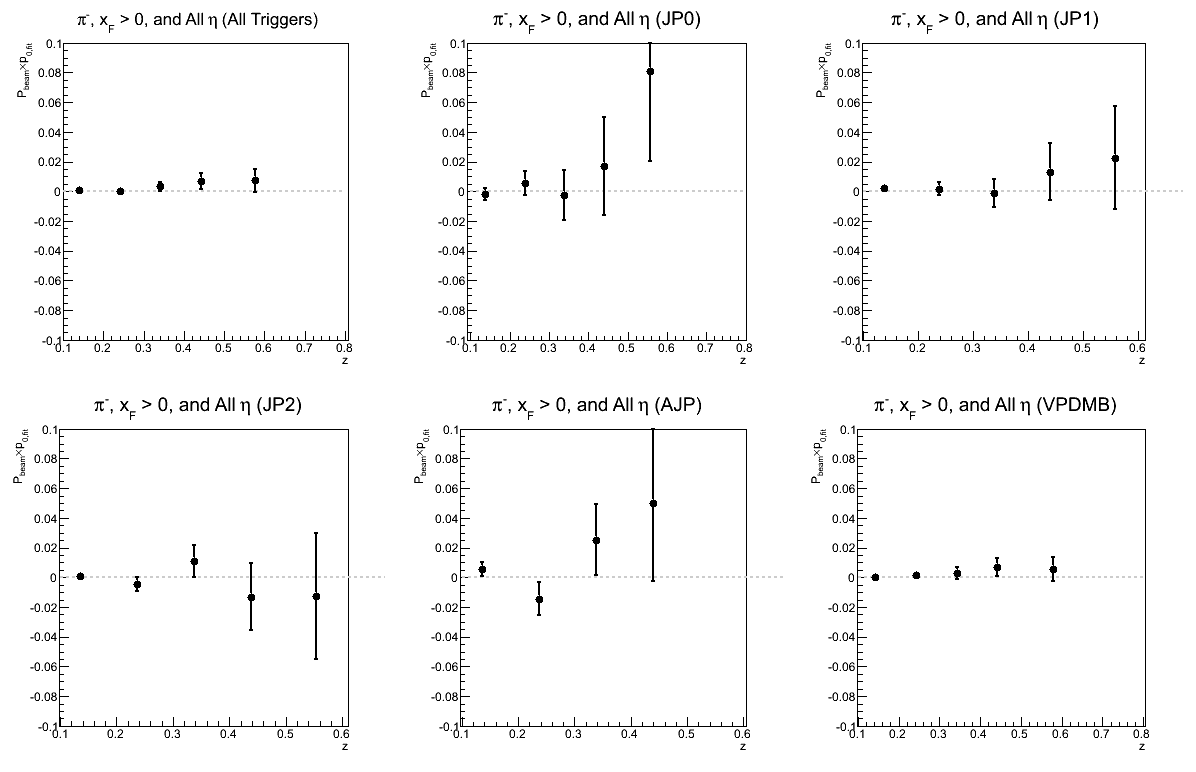Figure 12: p₀ for Collins-like Asymmetry as a Function of j_T

Triggers
charge > 0	charge < 0

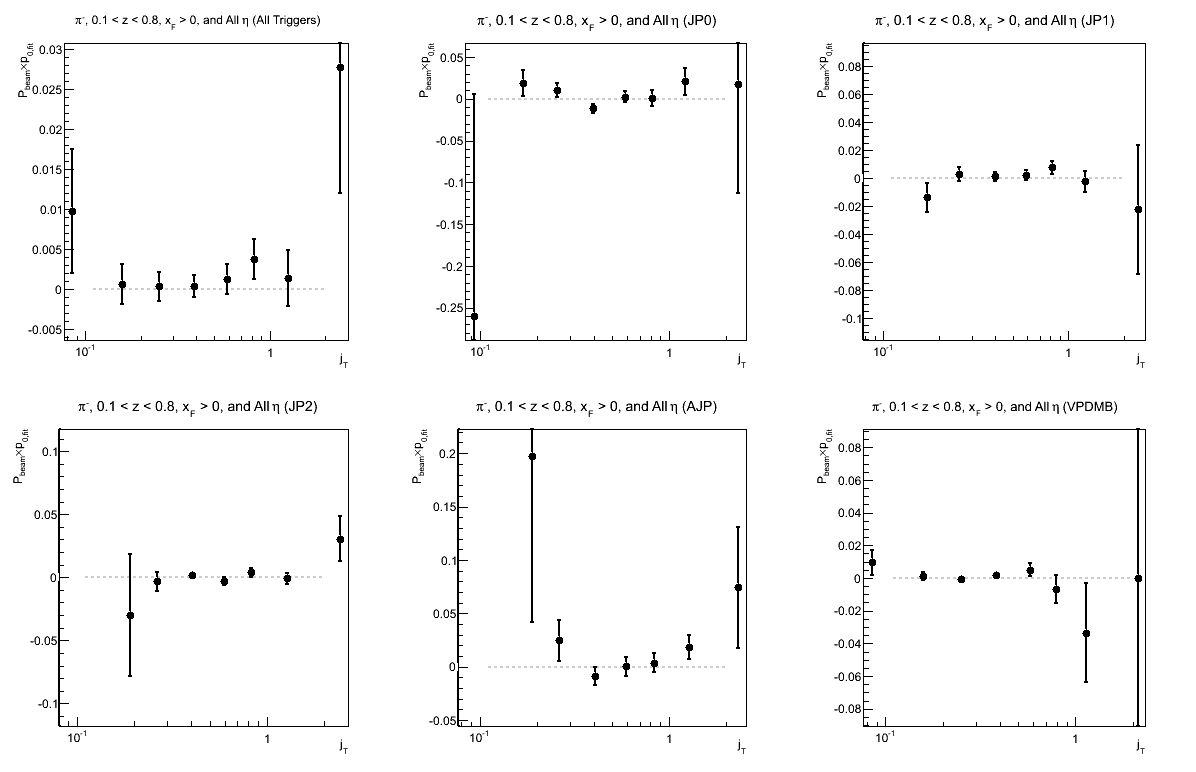An additional useful test is to examine the χ² distribution of the fits. Carl has suggested this, and I intend to do it. I will post the figures when I have them ready.