I have begun to look at transverse-spin jet asymmetries from the Run-11 500 GeV dataset. In this update I look at the Sivers asymmetry in bins of η_jet, Collins asymmetries as a function of z and j_T, and the Collins-like asymmetries for which we may have sensitivity. These data reflect about 1/3 of the full dataset. I currently don't have disc space for more jet trees than this. The analysis, here, utilizes the cross-ratio formalism as used in my Run-8 two-particle asymmetry analysis and the on-going Run-6 Collins analysis by Renee, Kevin, and Rob. I also look at some statistical cross-checks of my analysis. The cuts are described in earlier blog posts, and I will summarize them, here. Note that all asymmetries are shown prior to polarization correction.

Cuts and Kinematics

This update focuses on the 12-point branch running the anti-k_T algorithm with a radius of 0.6 and minimum p_T = 5 GeV/c. Tracks are required to satisfy a hit ratio of 0.51, p_T-dependent DCA, and 0.2 < p_T < 200 GeV/c. Towers have an E_T cut of 0.2 GeV.

I have restricted myself to the following triggers: JP0, JP1, JP2*L2JetHigh, AJP, and VPDMB. VPDMB should provide an interesting data-driven check of trigger bias for JP0. I have required the jet match to a valid trigger patch except in the case of VPDMB, where I simply require the VPDMB trigger fired.

In addition to the trigger-patch matching, I also implement the following definitions:

• VPDMB
  • VPDMB trigger fired and p_{T, jet} > 5.0 GeV
• JP0
  • JP0 trigger fired and p_{T, jet} > 7.1 GeV
• JP1
  • JP1 trigger fired, JP0 trigger did not fire, and p_{T, jet} > 9.9 GeV
• JP2
  • JP2 trigger fired, JP1 trigger did not fire, JP0 trigger did not fire, and p_{T, jet} > 16.3 GeV
• AJP
  • AJP trigger fired, JP2 trigger did not fire, JP1 trigger did not fire, JP0 trigger did not fire, and p_{T, jet} > 16.3 GeV

I have not restricted myself to a fiducial volume in η. This may be necessary in the future, however, there is some expectation that the analyzing powers increase with increasing η. Therefore, I would like to consider looking at jets as far forward as possible, given detector realities.

For the Collins asymmetries I have tried to restrict myself to pions utilizing the same -1 < n_σ(π) < 2 range as the Run-6 Preliminary result. Note, I do not restrict myself to pions for the Sivers asymmetries. I simply look at the jets regardless of the hadrons inside.

Figure 1

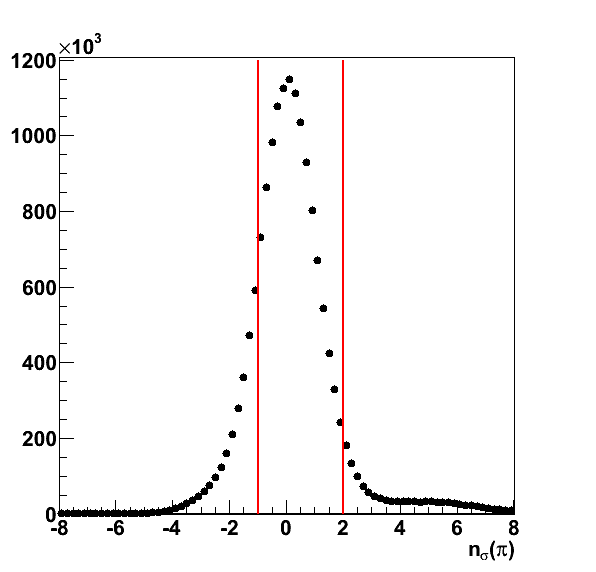
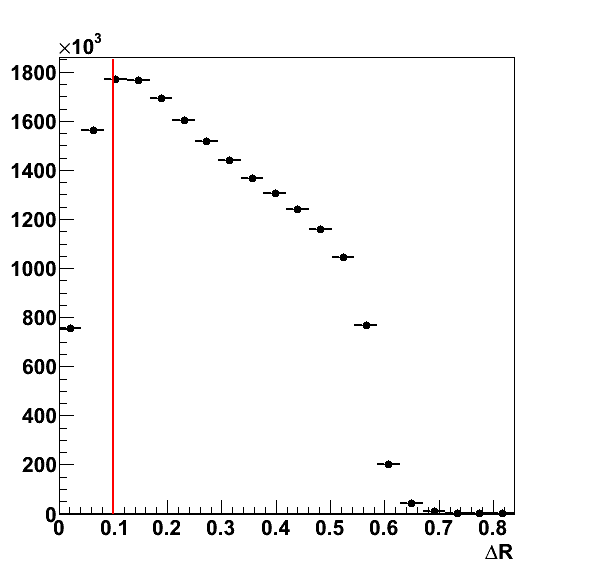
There is also TOF information available; however, at this point, I have not attempted to use it. For the full run, this may be advantageous. To ensure that φ_h is well-determined, I have implemented a cut of ΔR > 0.1.

Figure 2

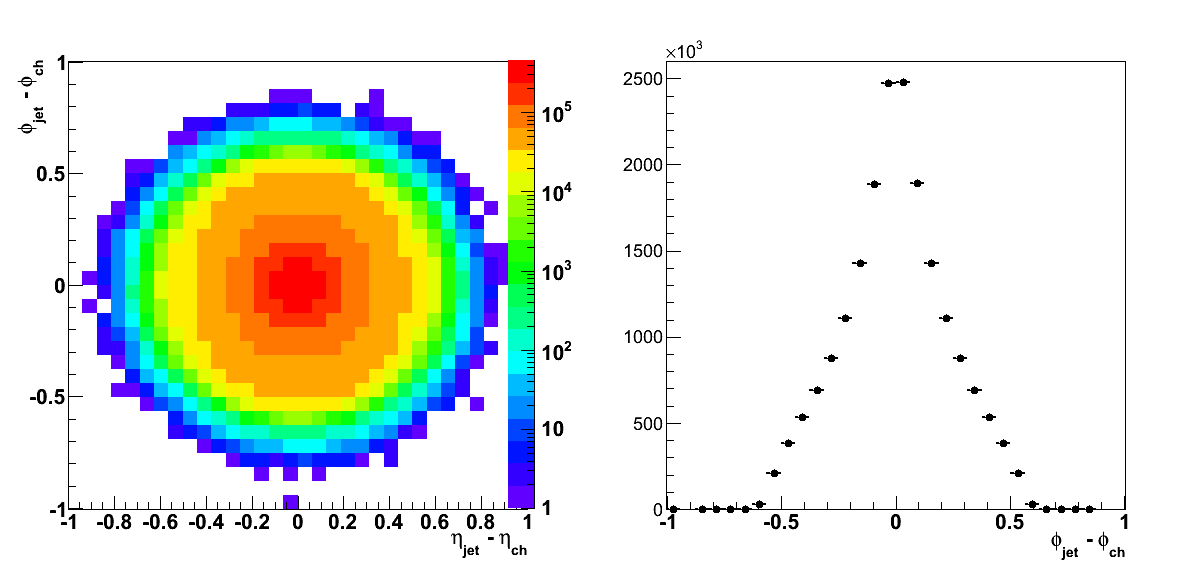
Finally, I have calculated asymmetries in j_T for two ranges of z: 0.1 < z < 0.8 and 0.4 < z < 0.8. Smaller z gets bogged down by stuff at the low end of the fragmentation chain, while higher z gets close to exclusive production and heavy trigger bias.

Figure 3

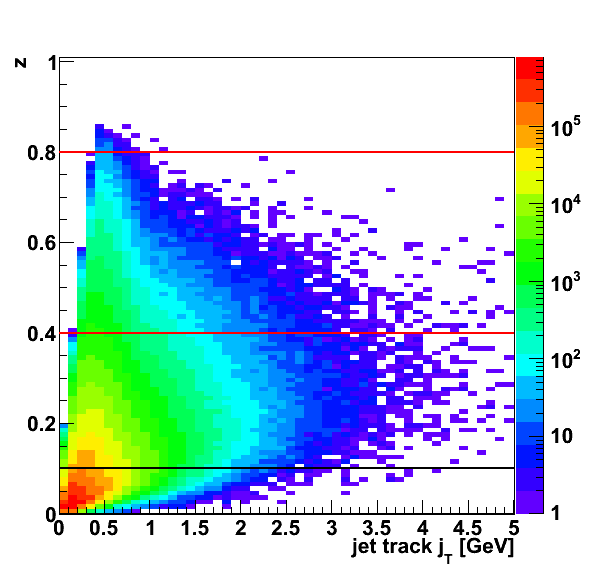
Run-11 triggers push the j_T reach much lower than Run-6, and I don't have many events at higher j_T. I will evaluate Collins asymmetries in j_T for two ranges of z: 0.1 < z 0.8 and 0.4 < z < 0.8 as denoted by the horizontal lines.

Figure 4

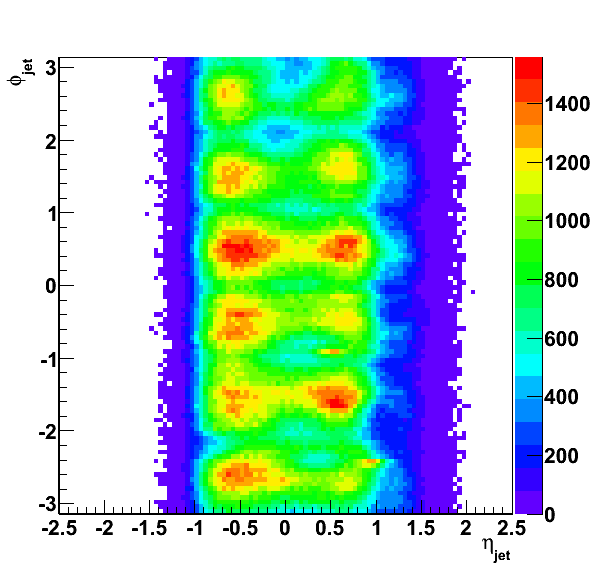
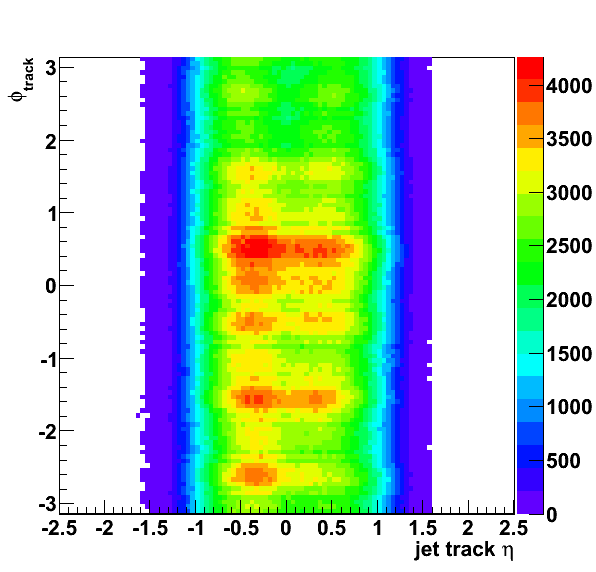
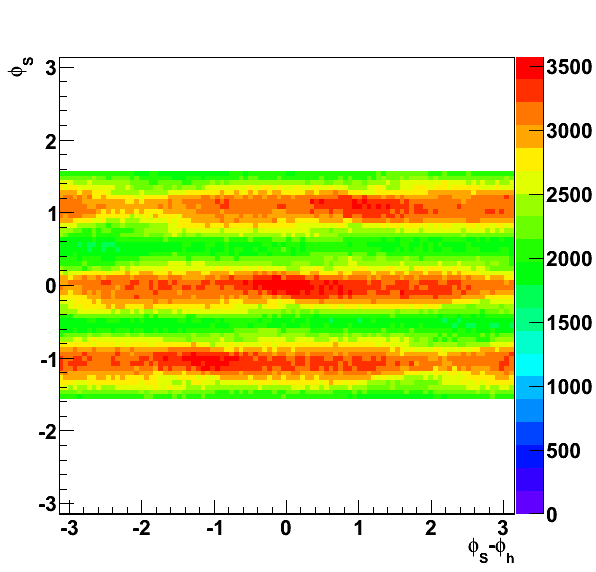
Asymmetries

Asymmetries, again, are shown before correcting for polarization. Note the axis is labeled "P_beam×A_N."

Sivers Asymmetries

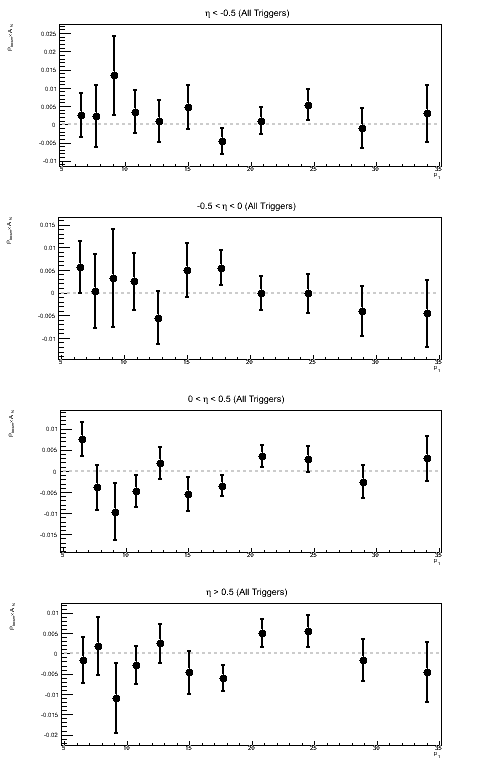
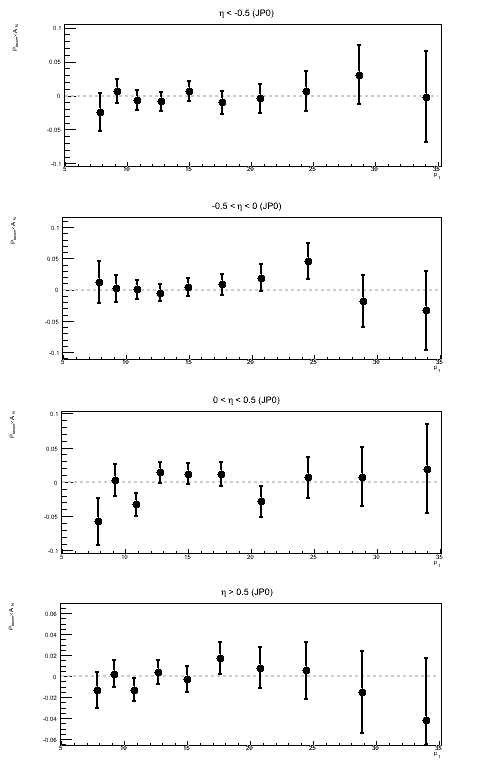
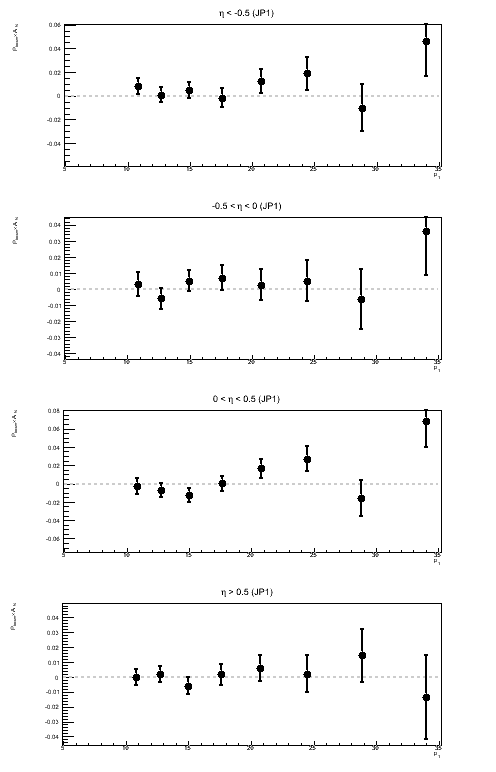
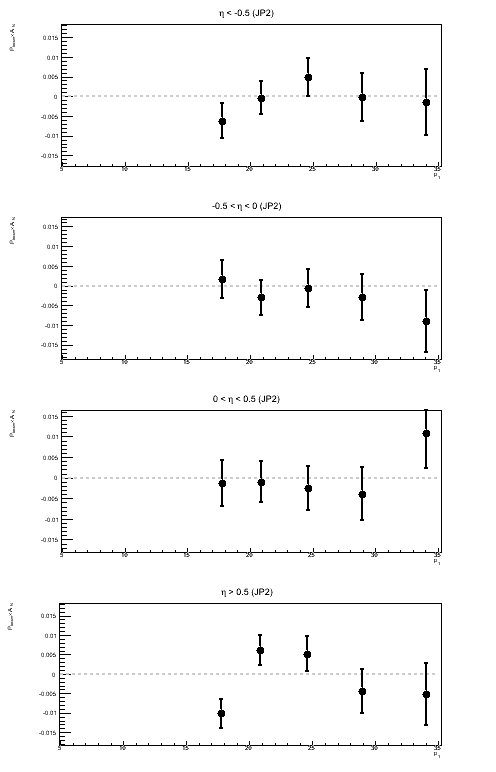
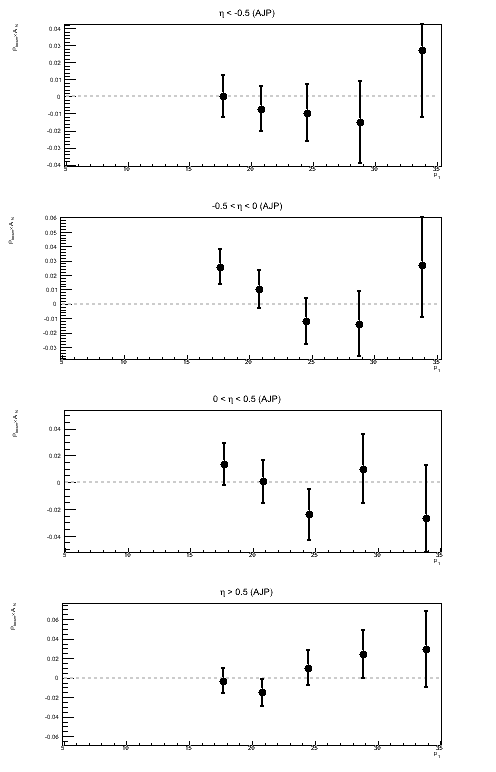
Figure 5: Sivers Asymmetry in Bins of η_jet

All Triggers	JP0	JP1
JP2	AJP	VPDMB

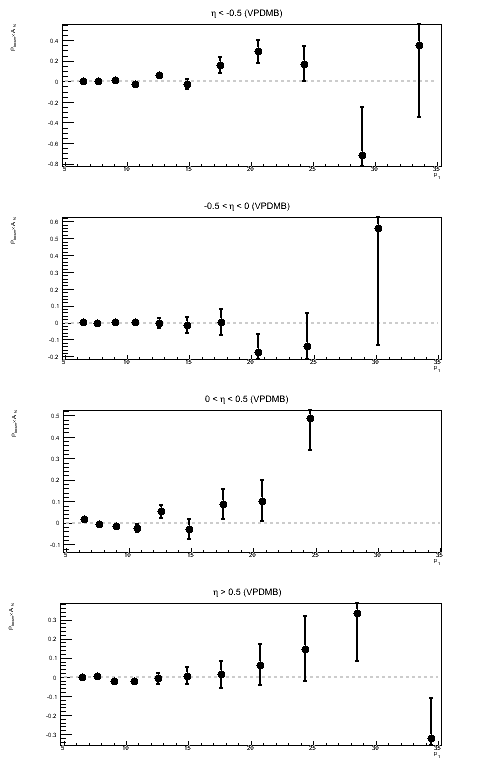Above, I show the Sivers asymmetry as a function of jet p_T for different bins of η_jet. Naïvely, I would assume a real Sivers effect would increase as one moves forward in η and exhibit something like a 1/p_T-dependence. I do not see anything resembling a 1/p_T-dependence. I am also wary of concluding anything from JP1 and VPDM at rather high p_T. As a follow-up to this, it is worth looking at the actual sin(φ_S) fits to see if the fit itself is believable.

Collins Asymmetries

To bin for the Collins asymmetries my code includes the following for z and j_T bins:

  const double zbins[nzbins+1] = { 0., 0.05, 0.1, 0.2, 0.3, 0.4, 0.5, 0.8, 1. };
  const double jtbins[njtbins+1] = { 0., 0.1, 0.2, 0.3, 0.5, 0.7, 1., 2., 10. };

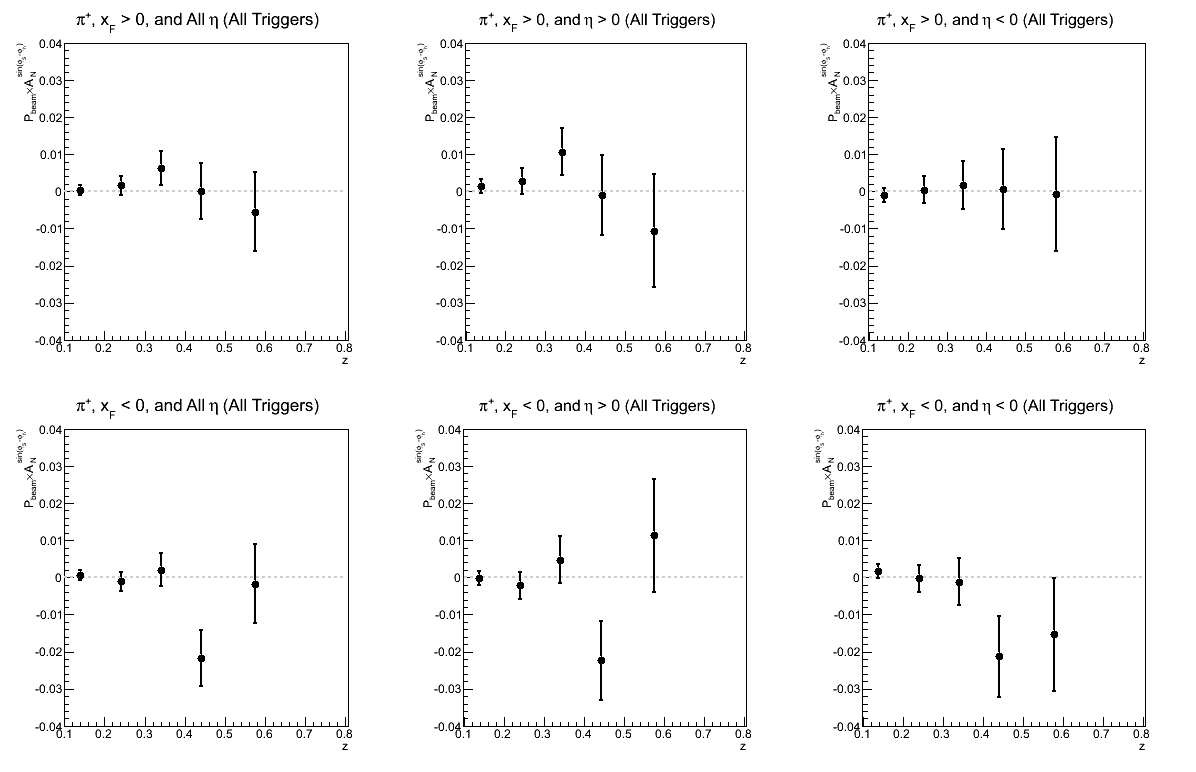
Figure 6: Collins Asymmetry as a Function of z

Triggers
charge > 0	charge < 0
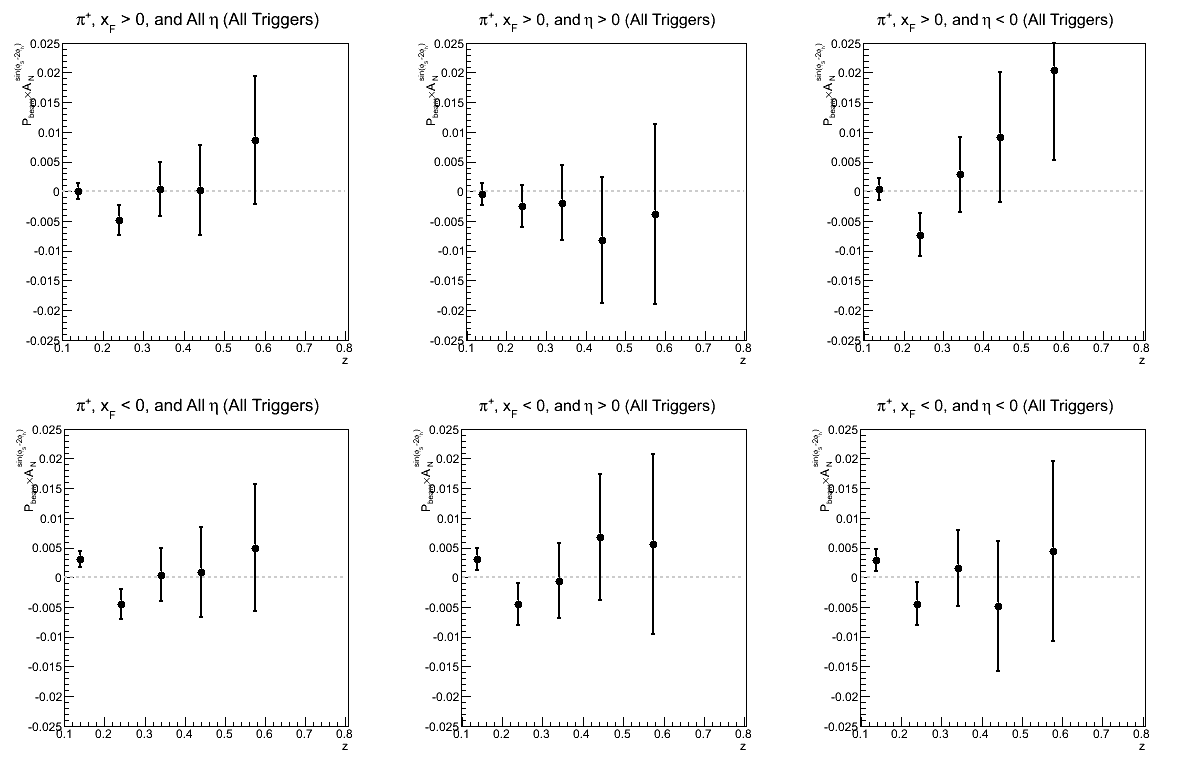
Comparison of Hemispheres and xF
charge > 0	charge < 0

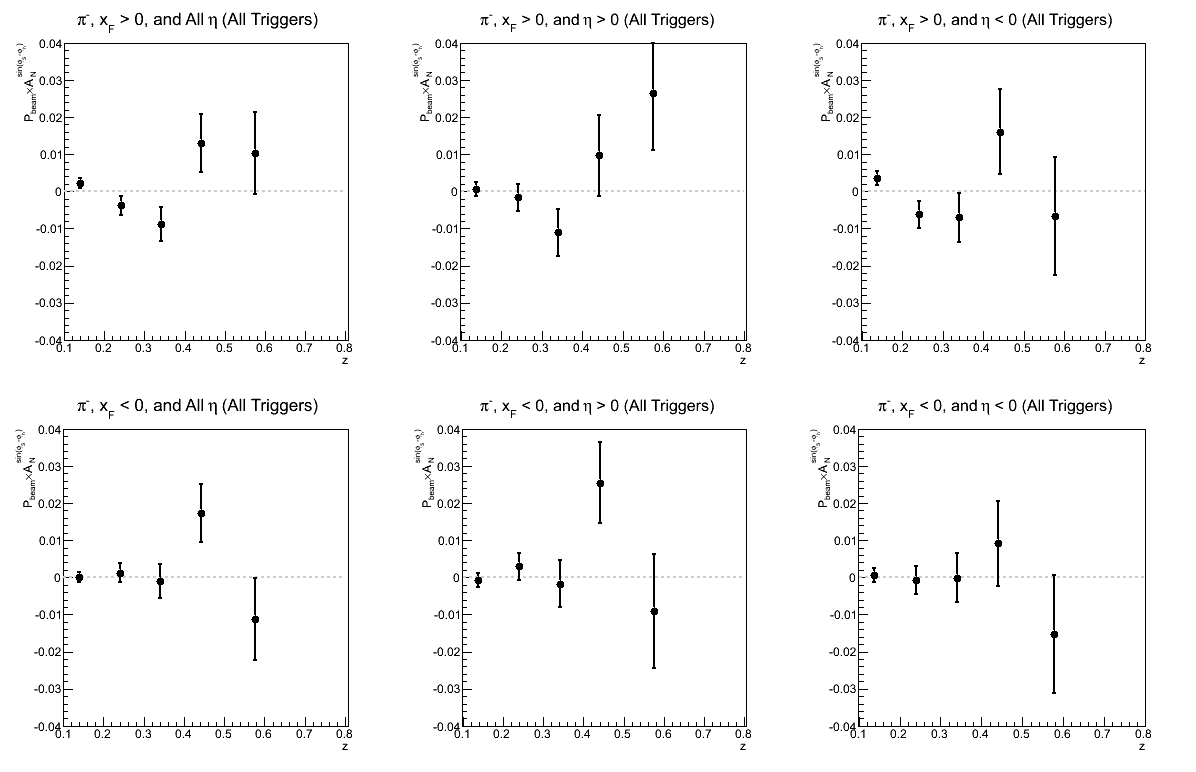While not necessarily optimal for one's eyes, I have kept the vertical scales the same to try to give a sense of which triggers are contributing and where. There does seem to be a hint of charge-sign dependence to the asymmetries in z, but I will definitely need more statistics before daring to state conclusions so firmly.

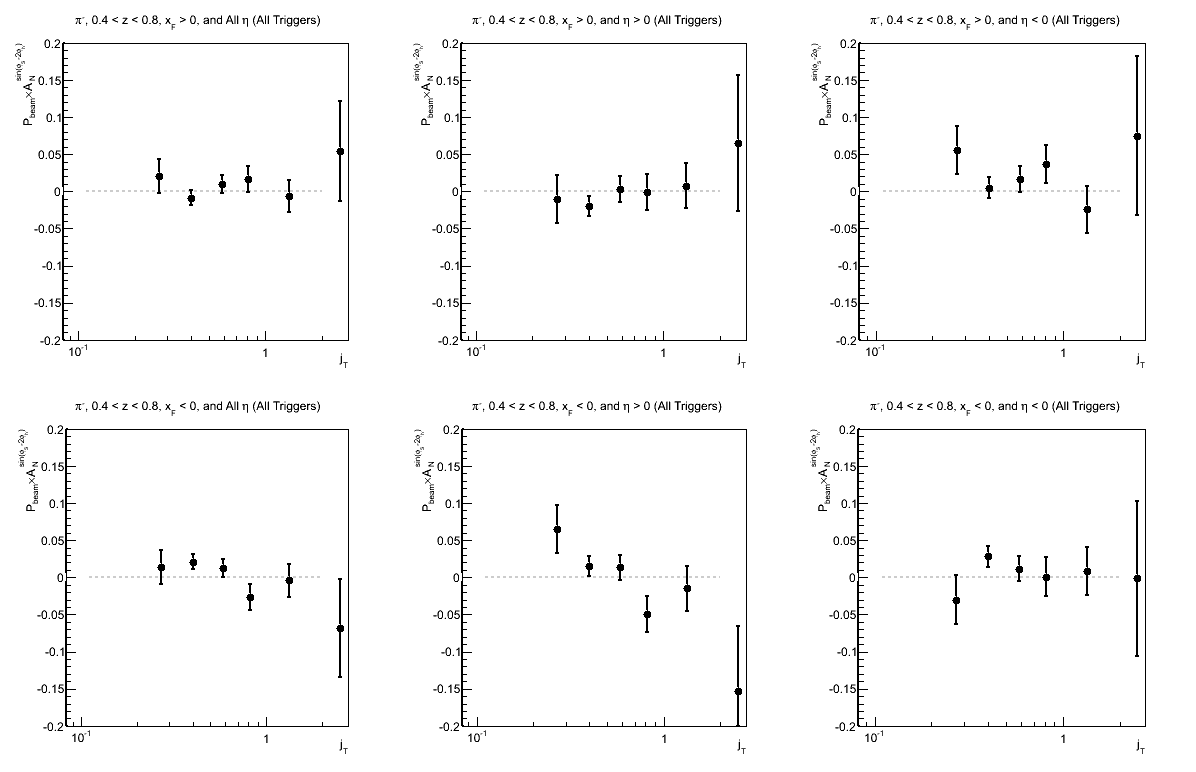
Figure 7: Collins Asymmetry as a Function of j_T (0.1 < z < 0.8)

Triggers
charge > 0	charge < 0
Comparison of Hemispheres and xF
charge > 0	charge < 0

Again, we see hints of charge-sign dependence; but more statistics are needed for sensitivity to what appears to be a rather small effect, if any.

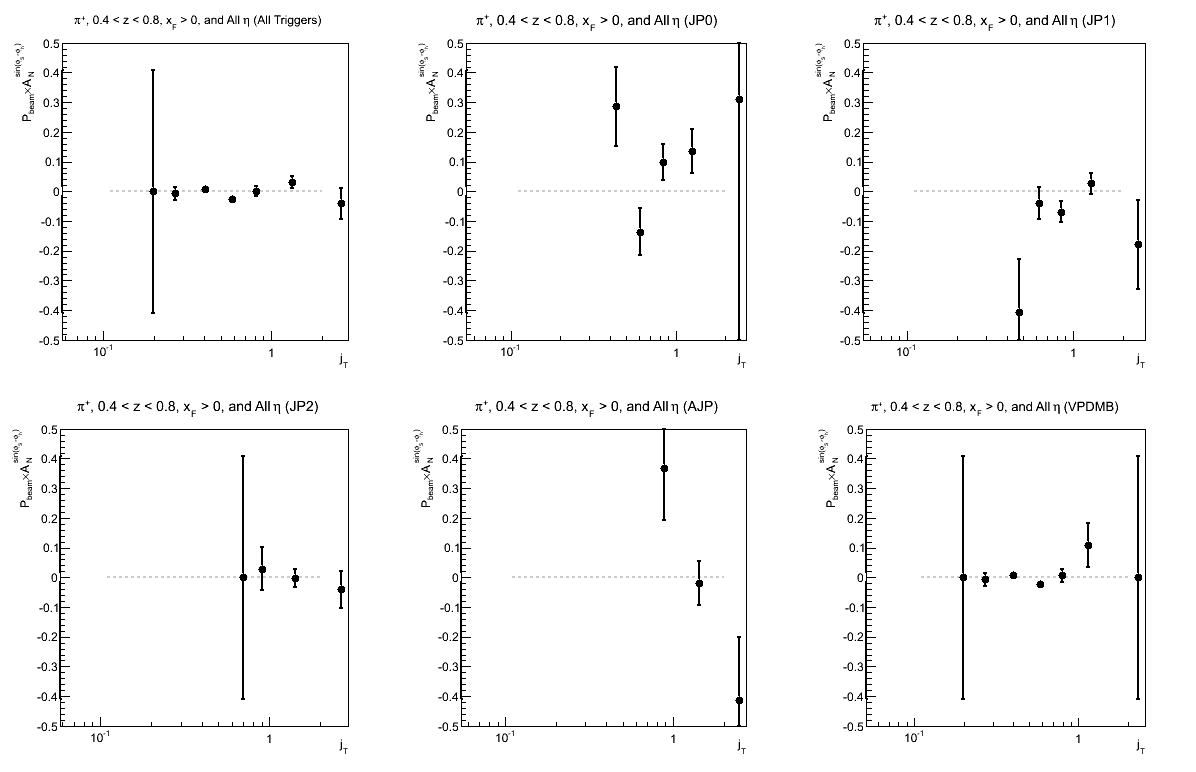
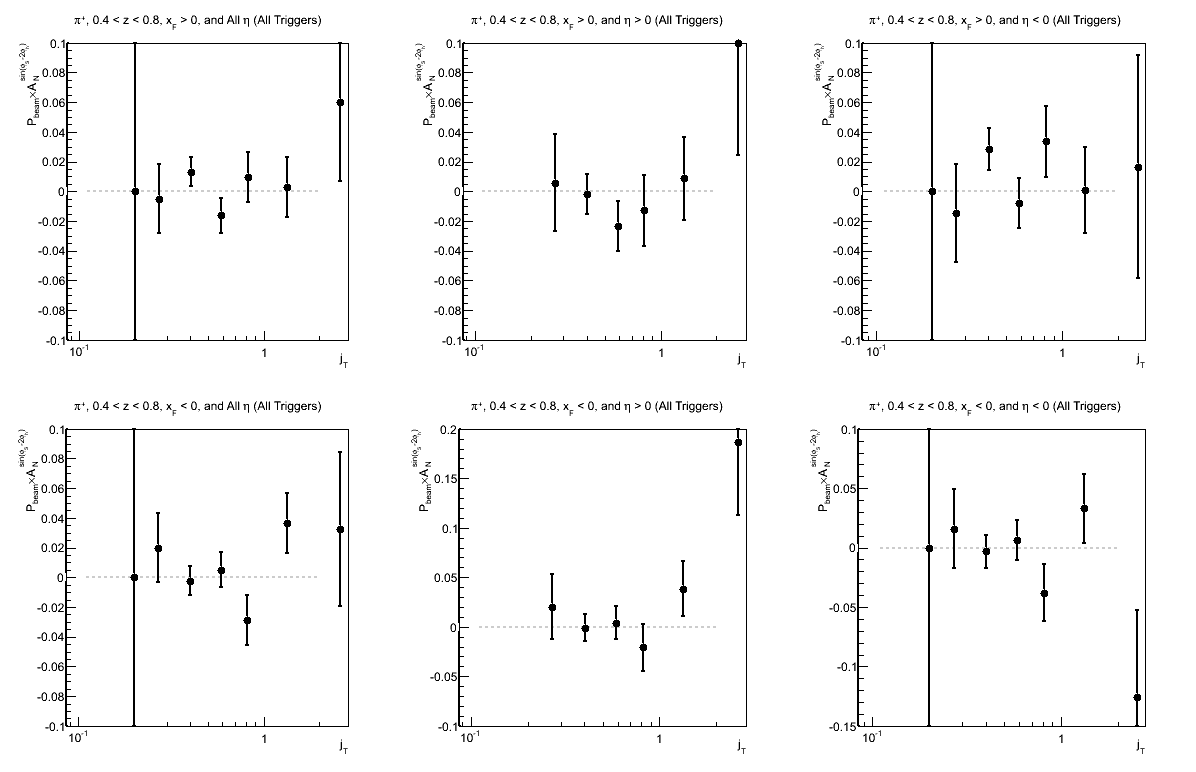
Figure 8: Collins Asymmetry as a Function of j_T (0.4 < z < 0.8)

Triggers
charge > 0	charge < 0
Comparison of Hemispheres and xF
charge > 0	charge < 0

Again, I have so few statistics in the high-z region that it is difficult to draw conclusions.

Collins-like Asymmetries

I have also looked at the sin(φ_S-2φ_h) or "Collins-like" asymmetry. The bins are the same as for the Collins asymmetry.

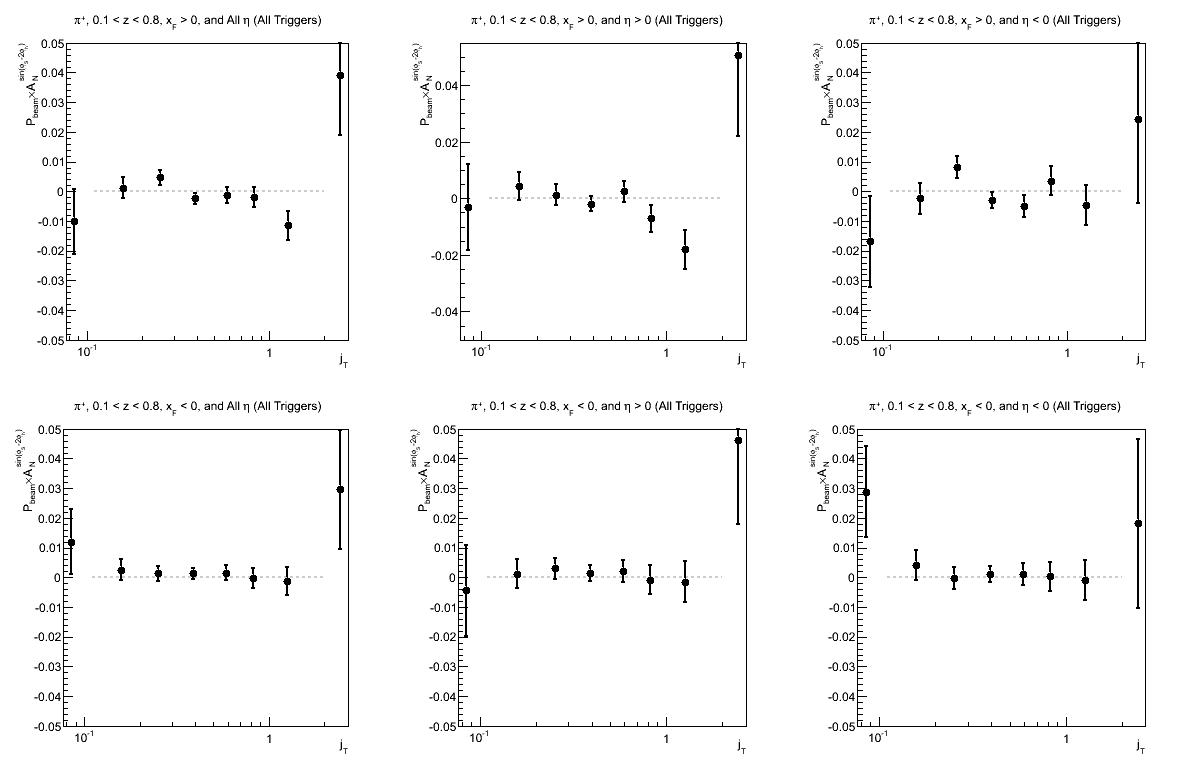
Figure 9: Collins-like Asymmetry as a Function of z

Triggers
charge > 0	charge < 0
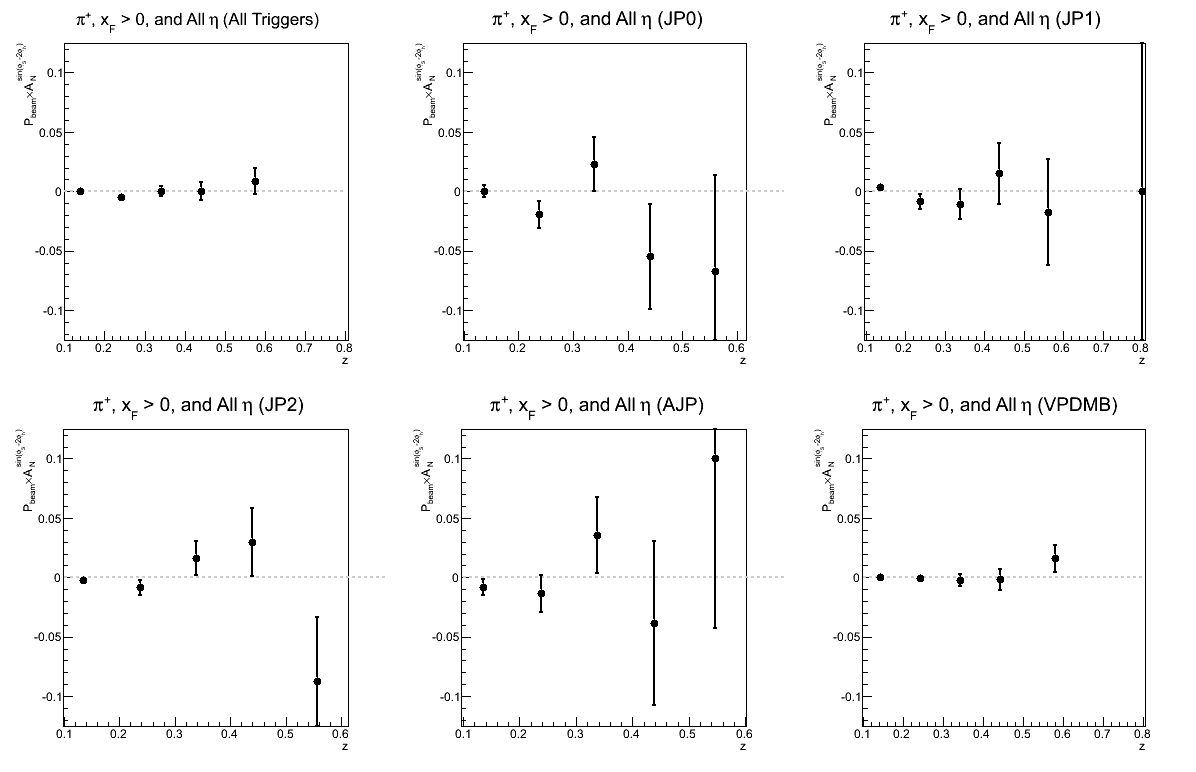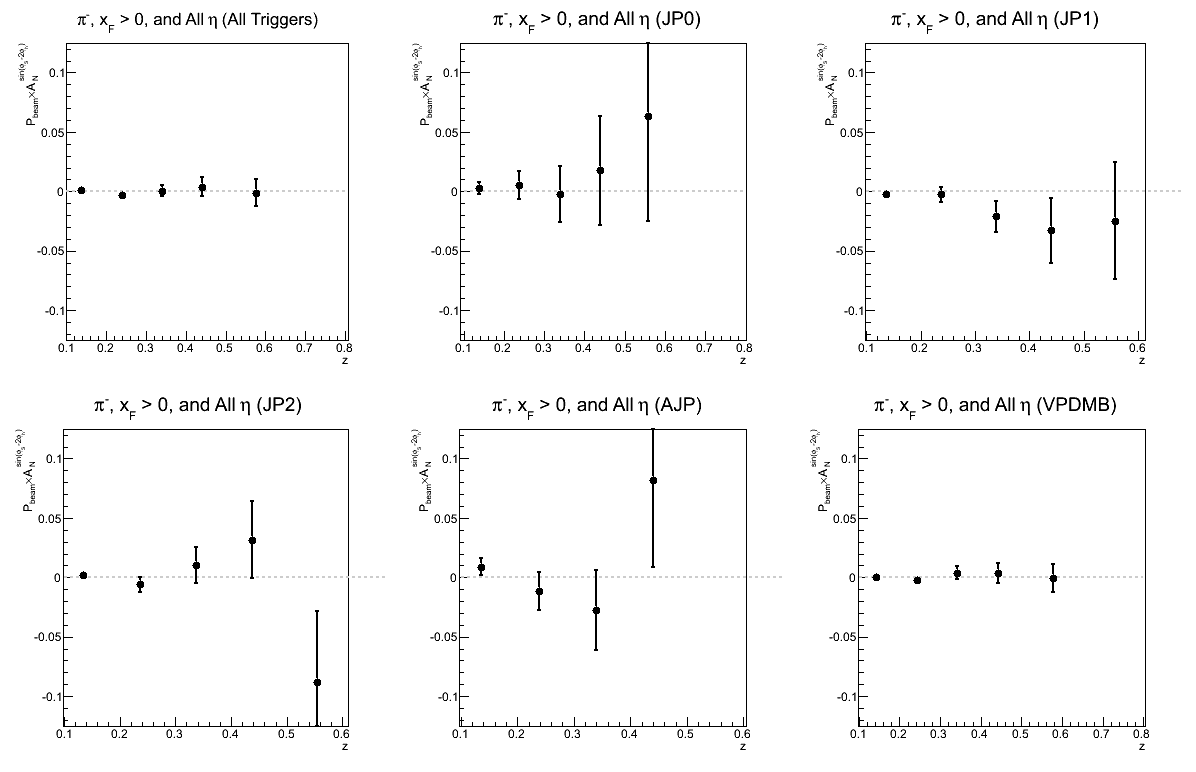Comparison of Hemispheres and xF
charge > 0	charge < 0

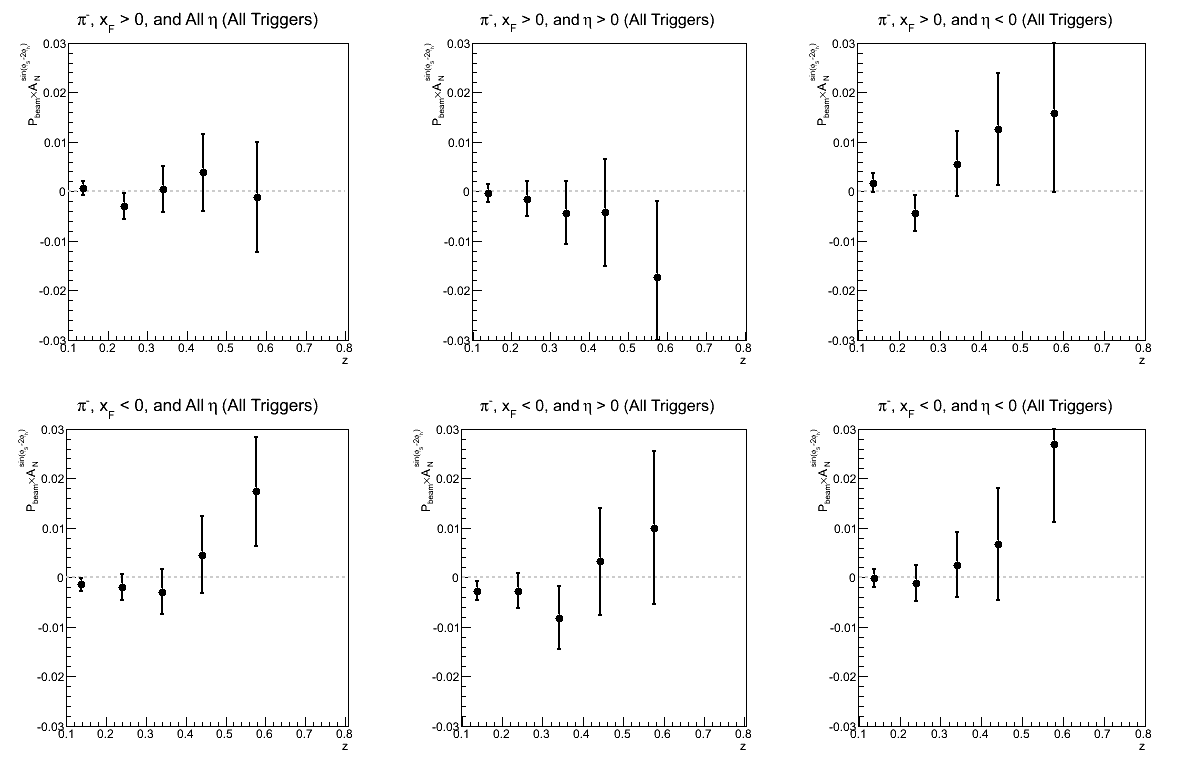Figure 10: Collins-like Asymmetry as a Function of j_T (0.1 < z < 0.8)

Triggers
charge > 0	charge < 0
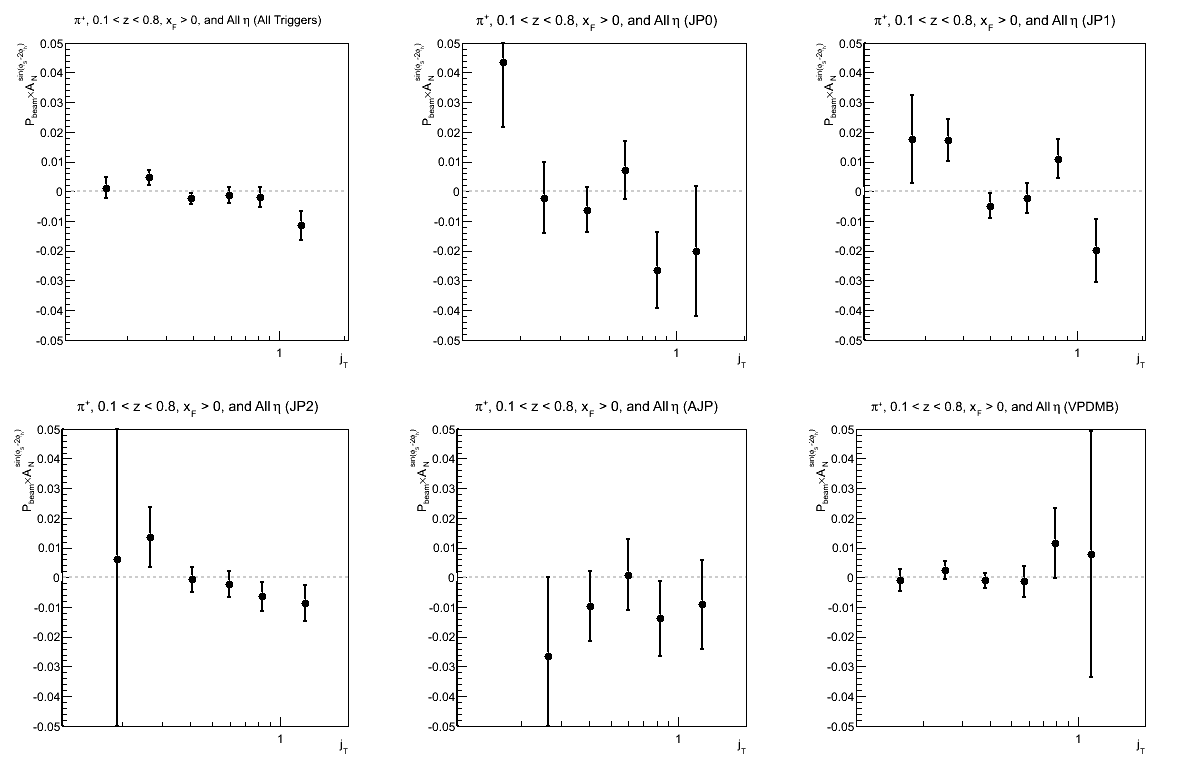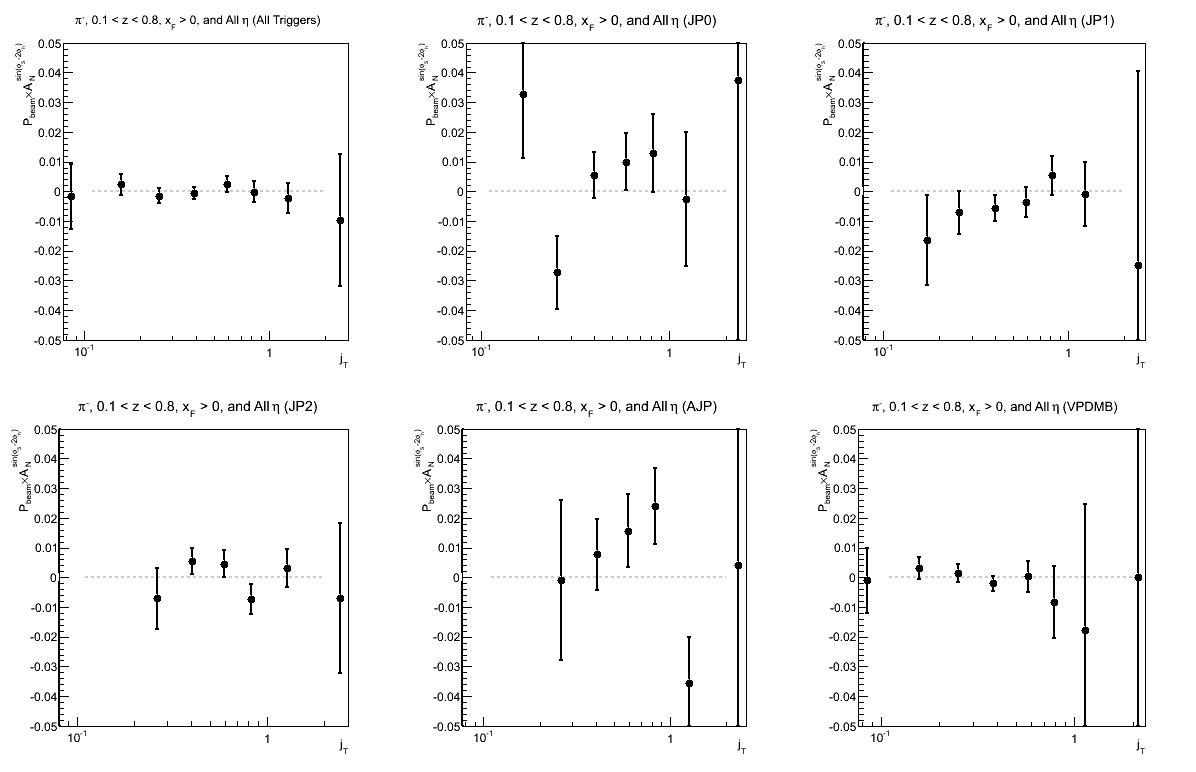Comparison of Hemispheres and xF
charge > 0	charge < 0

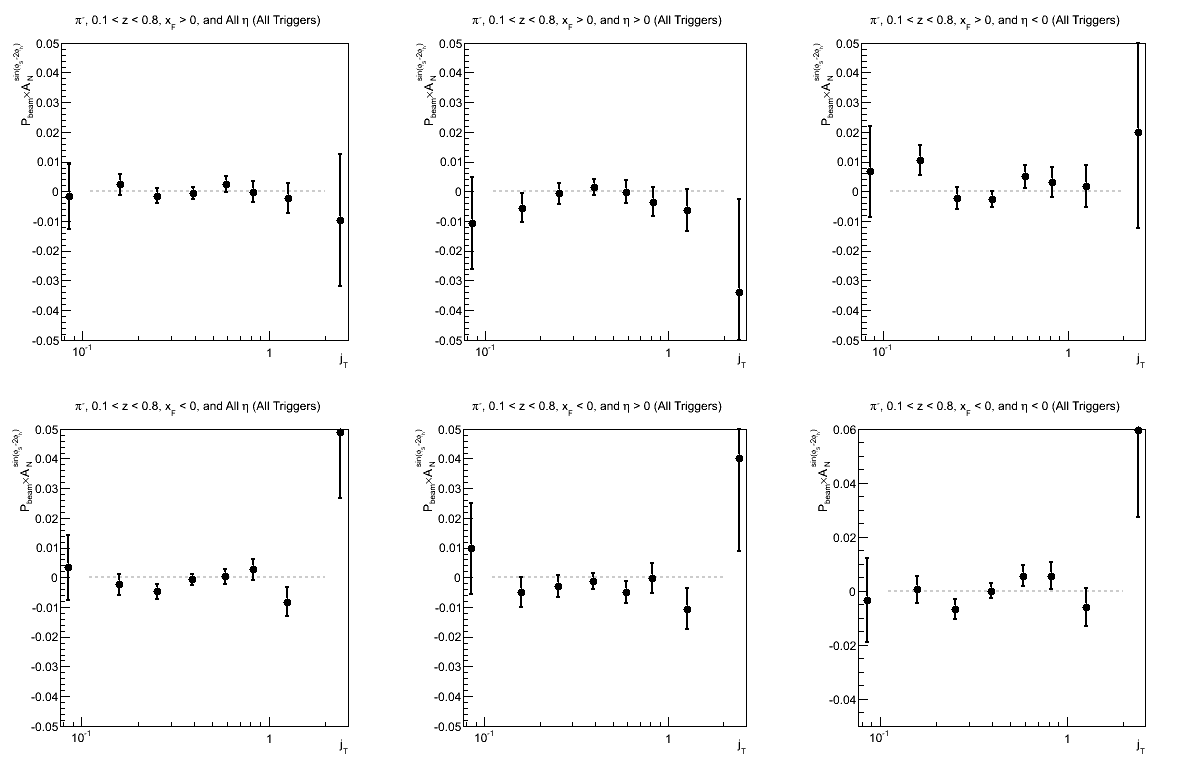Figure 11: Collins-like Asymmetry as a Function of j_T (0.4 < z < 0.8)

Triggers
charge > 0	charge < 0
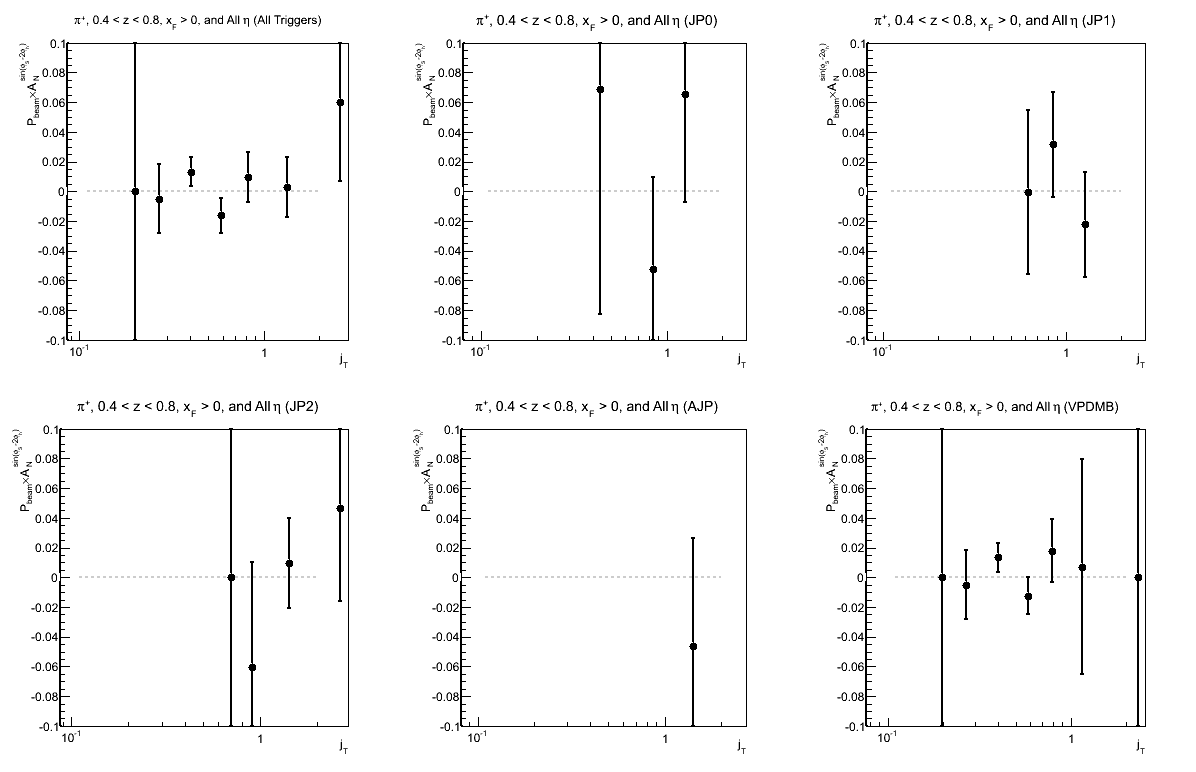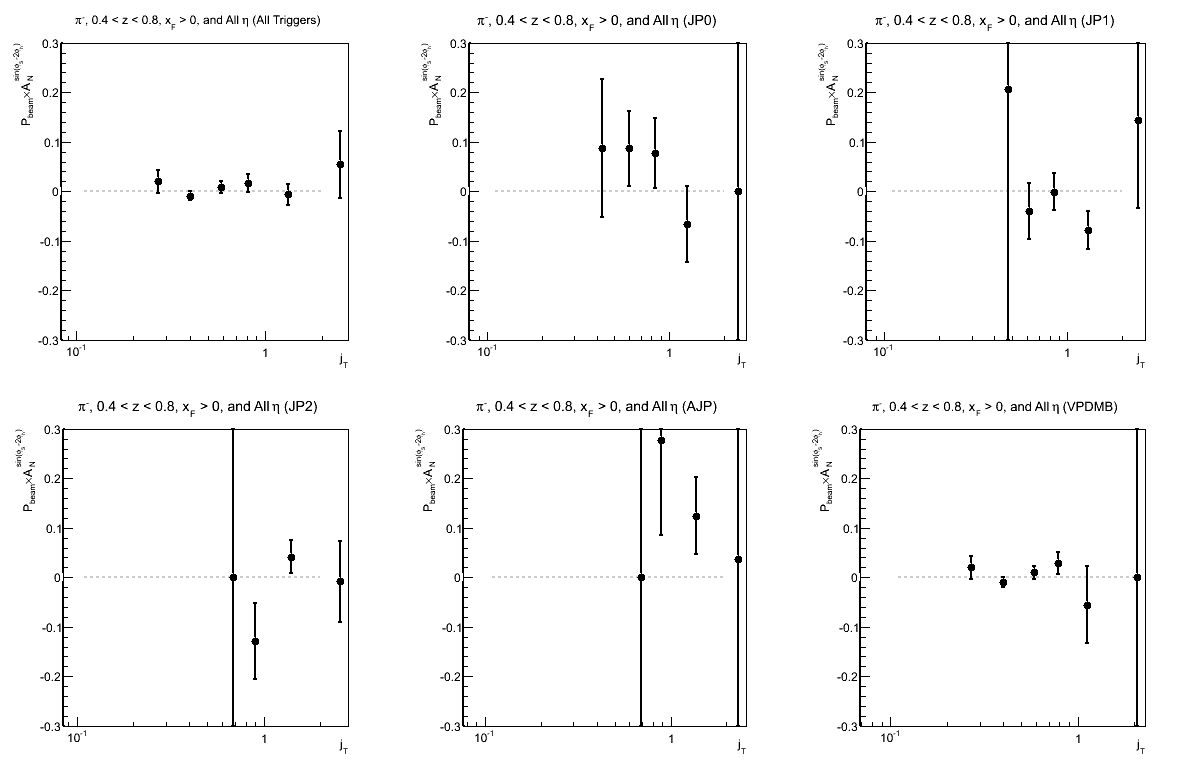Comparison of Hemispheres and xF
charge > 0	charge < 0

Statistical Cross-checks

p₀ From Fits

In principle, the p₀'s from my fits should be the same. Thus, a good cross-check is to see if the p₀'s are consistent within statistical uncertainties.

Figure 12: p₀ for Sivers Asymmetry as a Function of p_T

Triggers

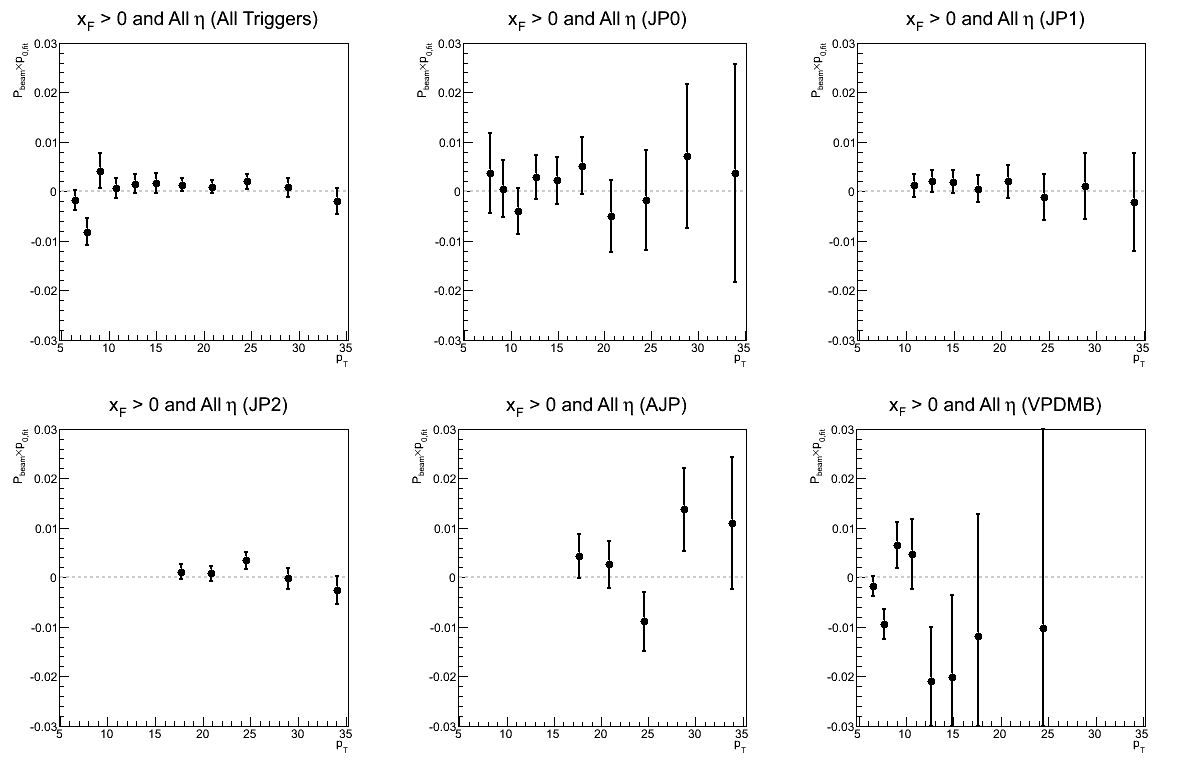Figure 13: p₀ for Collins Asymmetry as a Function of z

Triggers
charge > 0	charge < 0

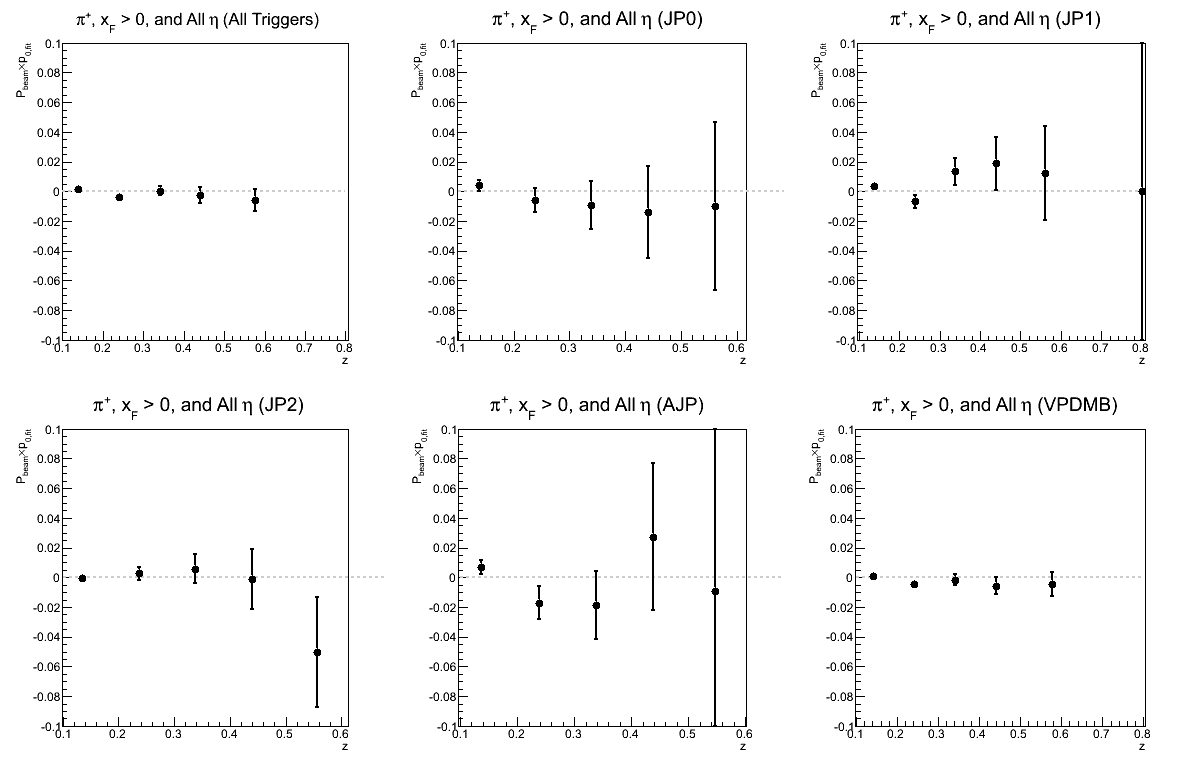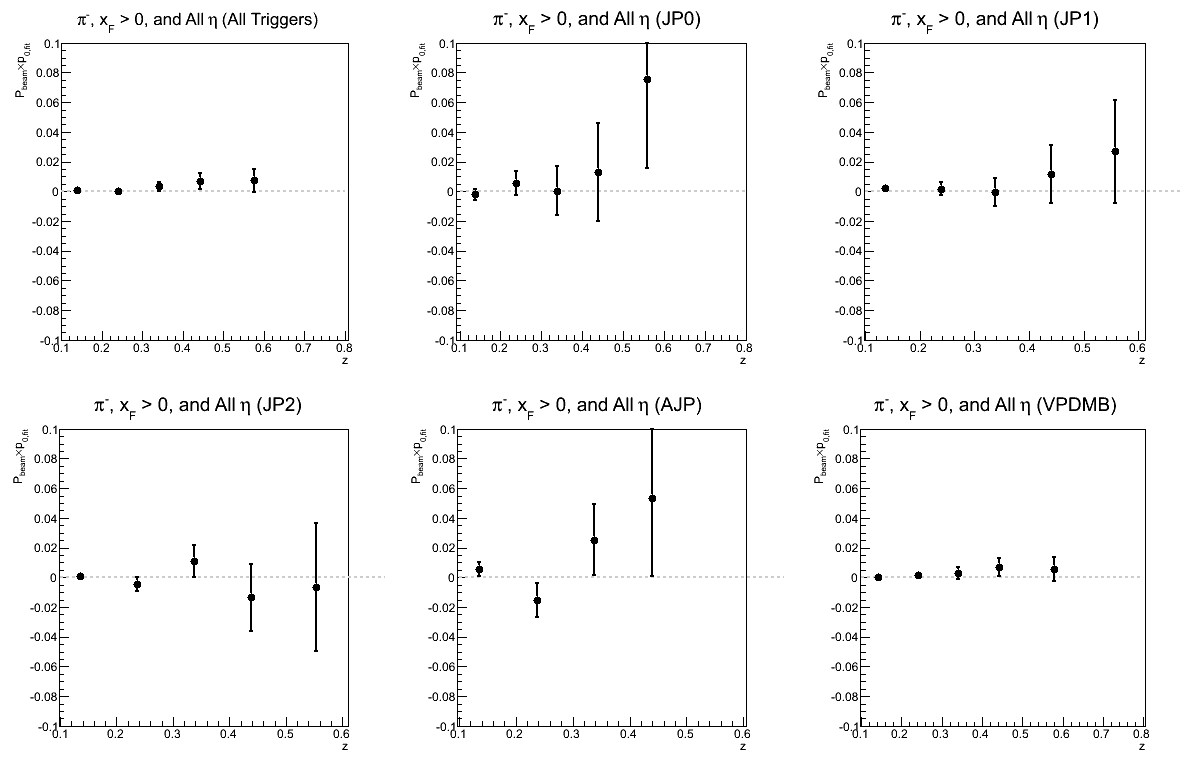Figure 14: p₀ for Collins Asymmetry as a Function of j_T

Triggers
charge > 0	charge < 0

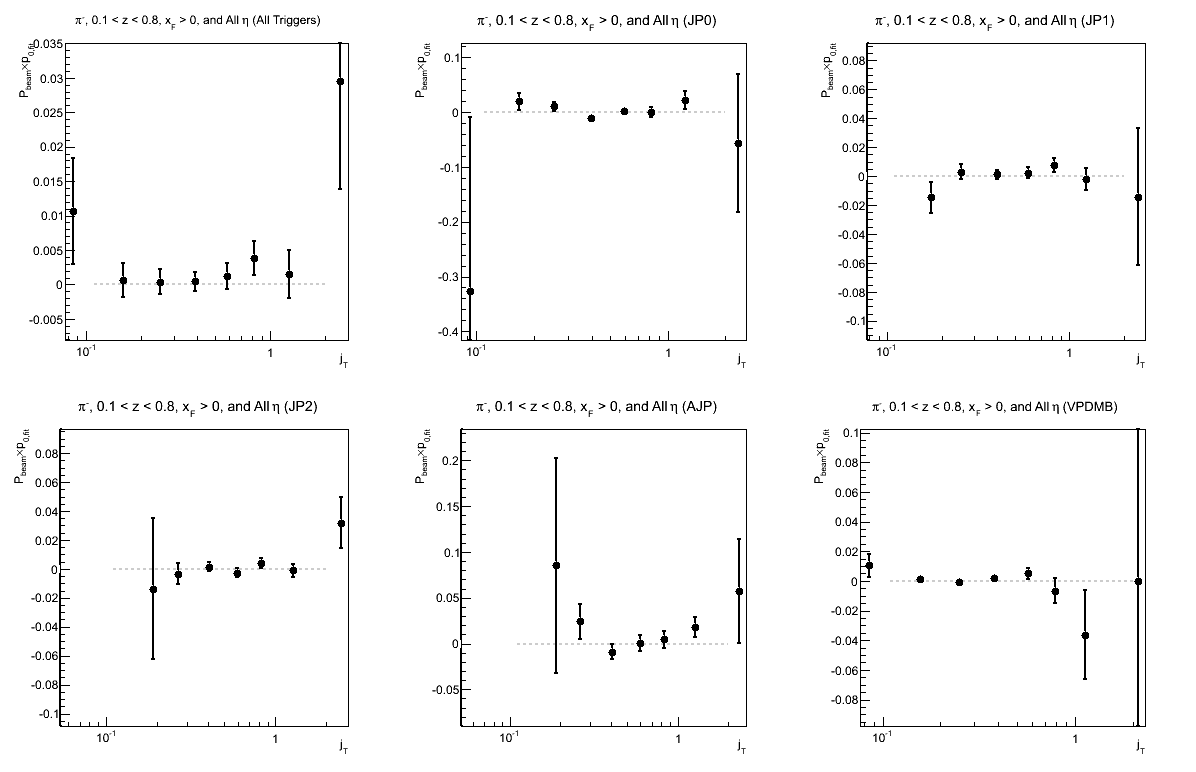Figure 15: p₀ for Collins-like Asymmetry as a Function of z

Triggers
charge > 0	charge < 0

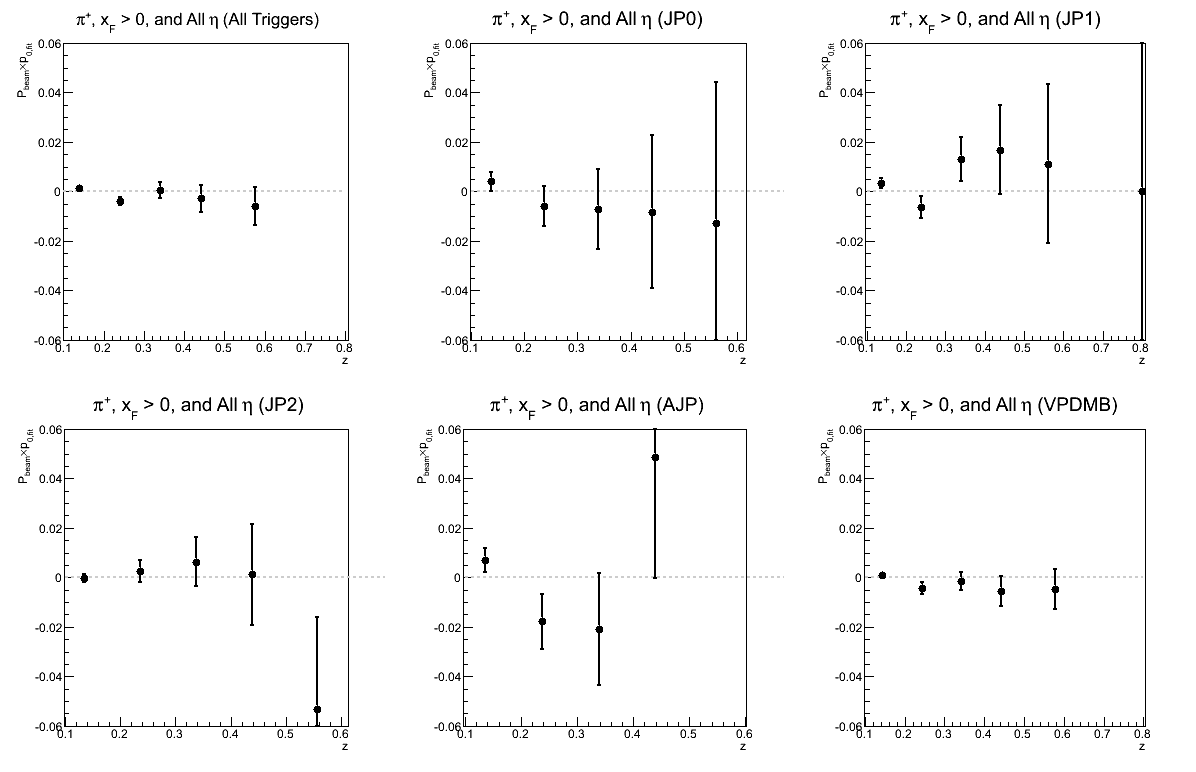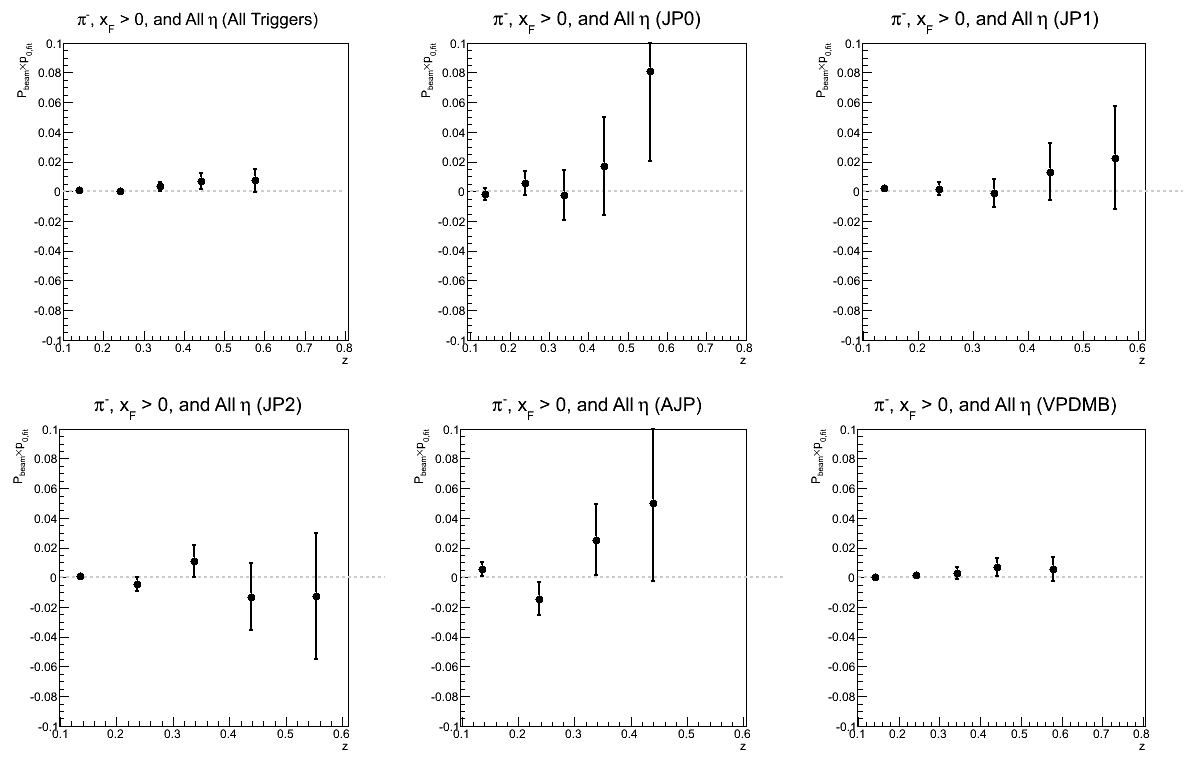Figure 16: p₀ for Collins-like Asymmetry as a Function of j_T

Triggers
charge > 0	charge < 0

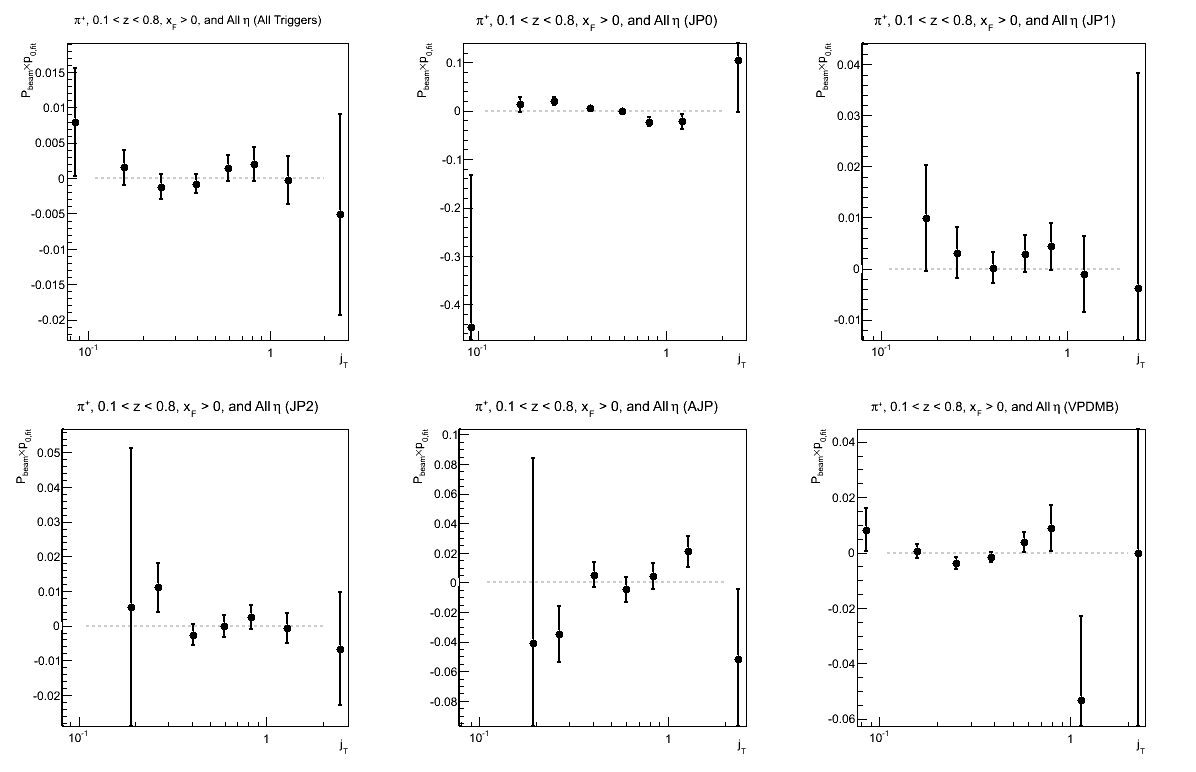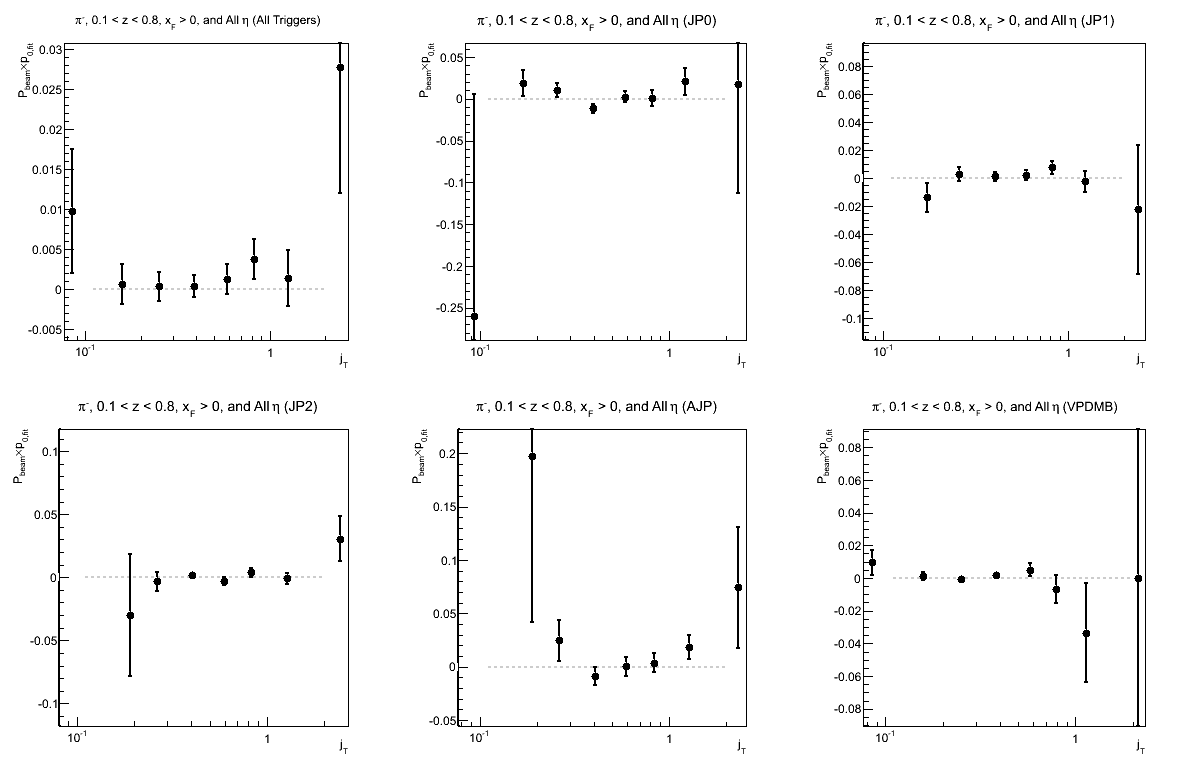An additional useful test is to examine the χ² distribution of the fits. Carl has suggested this, and I intend to do it. I will post the figures when I have them ready.