It was obvious that I had some wrong intuition about the χ² distributions in my last post. Carl set me straight, pointing out that the average of the χ² distribution should equal the number of degrees of freedom, rather than peak at the number of degrees of freedom. After some homework, I have redone the χ² studies. First, I have rebinned the χ² histograms to even out some of the fluctuations. I then coded up the exact distribution (as seen in Bevington Appendix C-4) and fit the histograms with the χ² function for the appropriate degrees of freedom. I let an over-all scale factor float for the fit. The results are shown below.

χ² Distributions

Figure 1

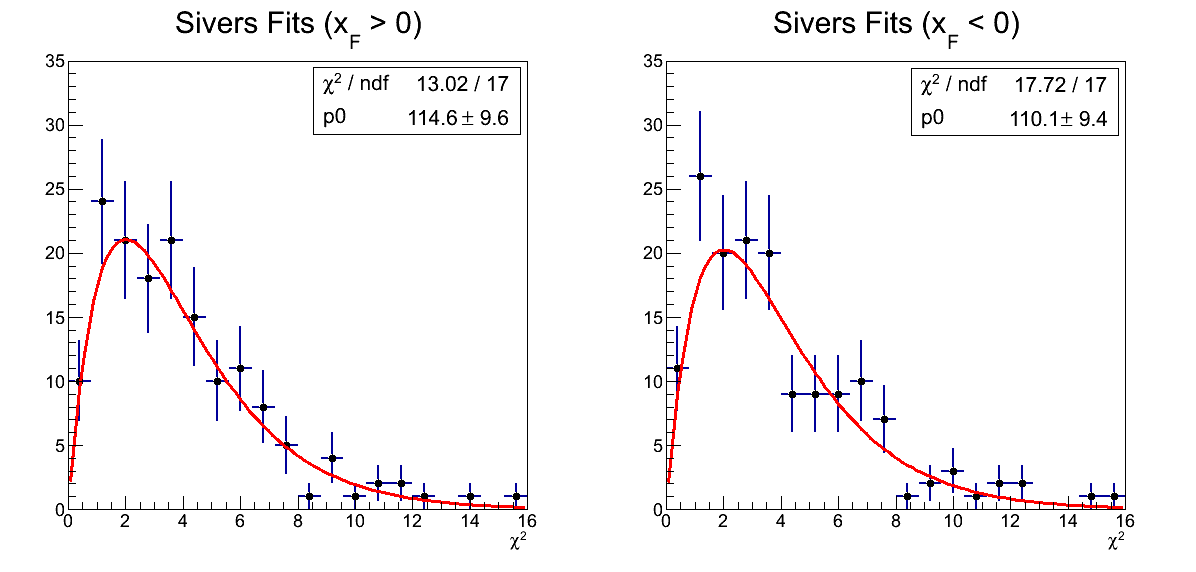
Now, the distributions actually look pretty good to my eyes. As Carl points out, the expected distribution is quite asymmetric for small values of ν.

Figure 2

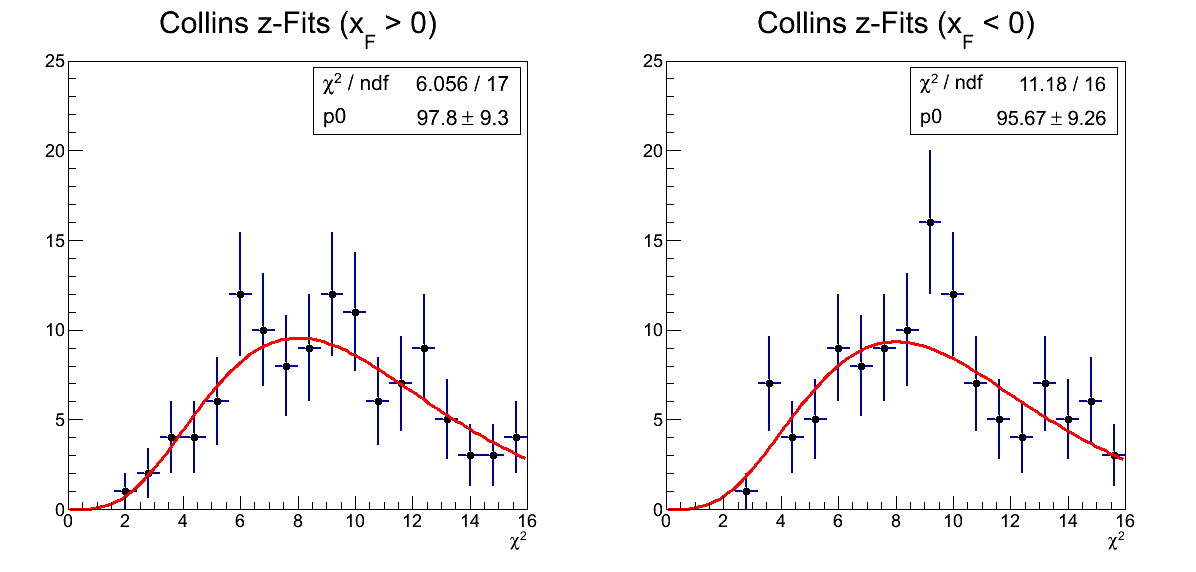
The previous distributions showed rather sizable fluctuations, so I have rebinned these distributions considerably. The result is, again, quite good.

Figure 3

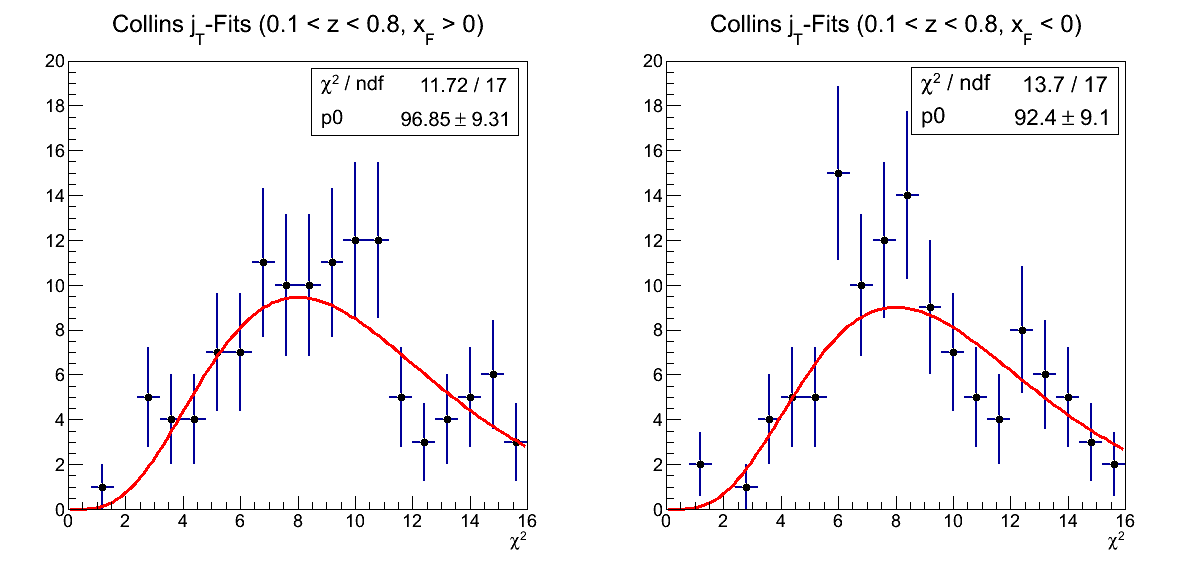
As with the Collins fits as a function of z, the fits as a function of j_T are entirely sensible.

Figure 4

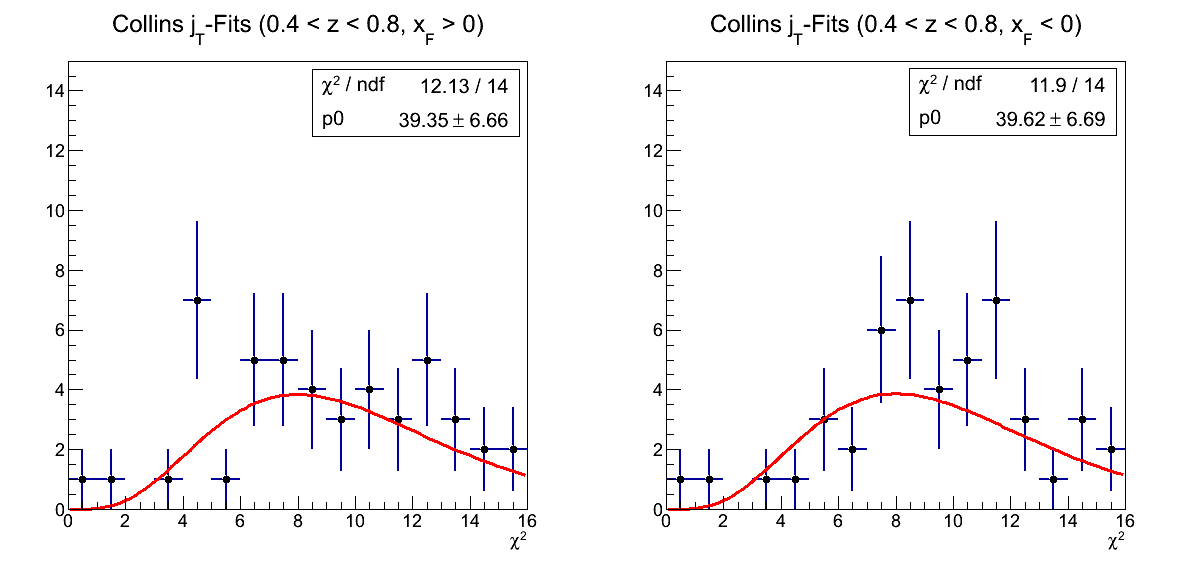
The high-z asymmetries have very few statistics, however, rebinning sufficiently removes the flutuations that one gets a decent picture of the χ². Again, it's completely sane.

Figure 5

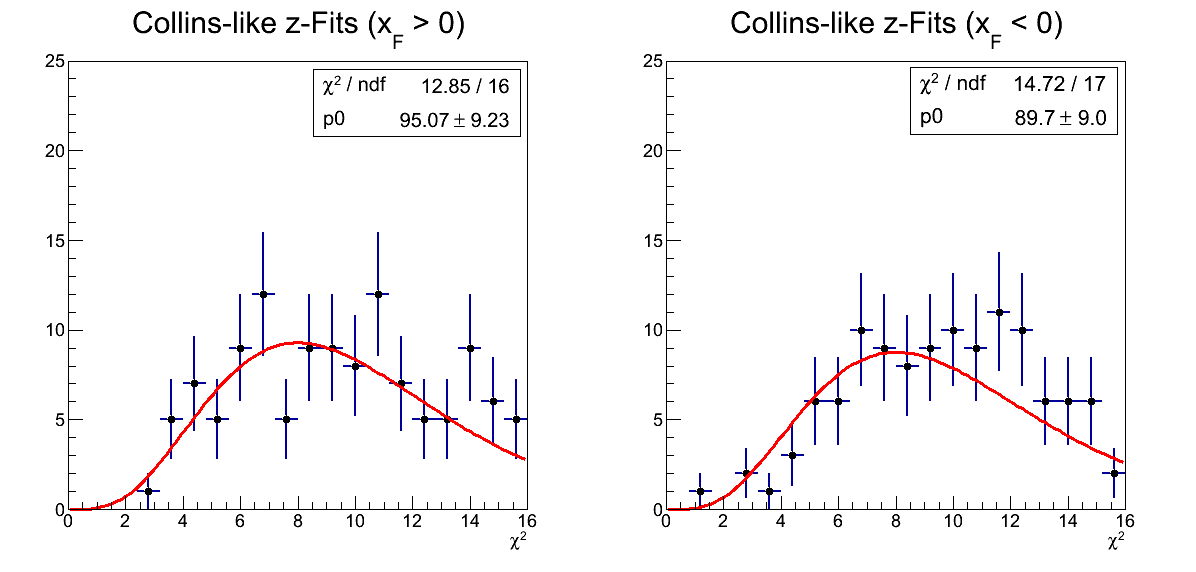
The story is much the same for Collins-like.

Figure 6

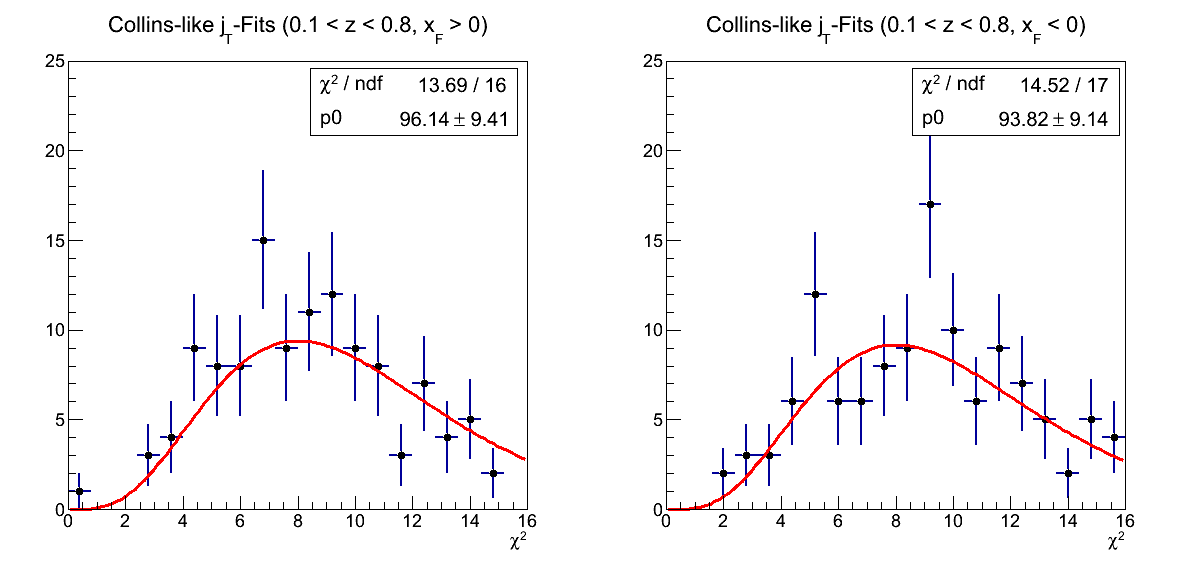
Figure 7

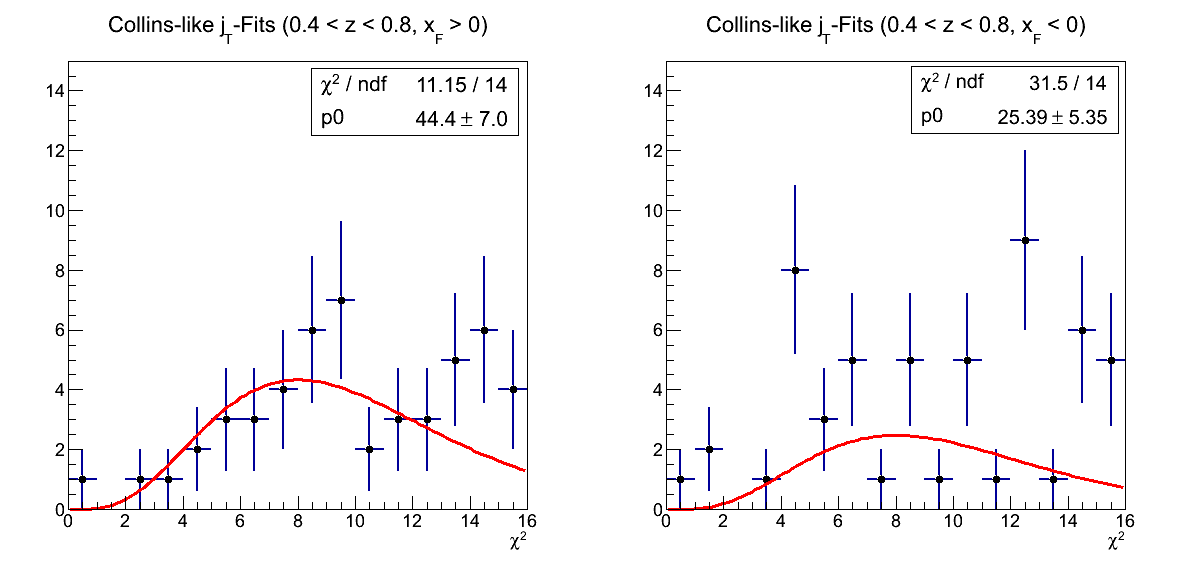
Finally, the x_F < 0 high-z Collins-like looks nuts, but I suspect it's a result of fewer statistics. Perhaps, it's just an outlier in what appears to be an otherwise perfectly sane statistical cross-check.