- drach09's home page
- Posts
- 2022
- 2020
- June (1)
- 2019
- 2018
- 2017
- 2016
- 2015
- 2014
- December (13)
- November (2)
- October (5)
- September (2)
- August (8)
- July (9)
- June (7)
- May (5)
- April (4)
- March (4)
- February (1)
- January (2)
- 2013
- December (2)
- November (8)
- October (5)
- September (12)
- August (5)
- July (2)
- June (3)
- May (4)
- April (8)
- March (10)
- February (9)
- January (11)
- 2012
- 2011
- October (1)
- My blog
- Post new blog entry
- All blogs
Run-11 Transverse Jets: First Look at Sivers Polarization Correction (Full Statistics)
I have finally applied polarization-correction to the Sivers asymmetries for the "all triggers" sample. I utilized a weighted-average techniqe as follows:
- Calculate raw asymmetries in pT-bins separately for the different fills
- Correct the raw asymmetries for each fill by dividing by the polarization for the appropriate fill
- For each pT-bin, calculate the weighted mean:
Note, for these calculations I have left out the polarization uncertainty. I have also performed the calculations under the assumption
and found no significant difference. One reason for excluding the uncertainty is that it includes a systematic piece correlated across all bins. It is trivial to include the polarization uncertainty in the calculation, so I am certainly open to suggestions.
With these asymmetries I have implemented a requirement that I require at least six non-zero φS bins for the calculation. Since I, now, perform the calculation separately for each fill, this will sacrifice a few events from my previous update, which sums over the fills prior to calculating the asymmetries. Additionally, I have only considered fills deemed "physics" on the CNI webpage. This excludes a few fills considered in my previous update. All told, the loss of data is quite minimal.
Figure 1: Polarization-corrected Sivers Asymmetry (All Triggers)
.png)
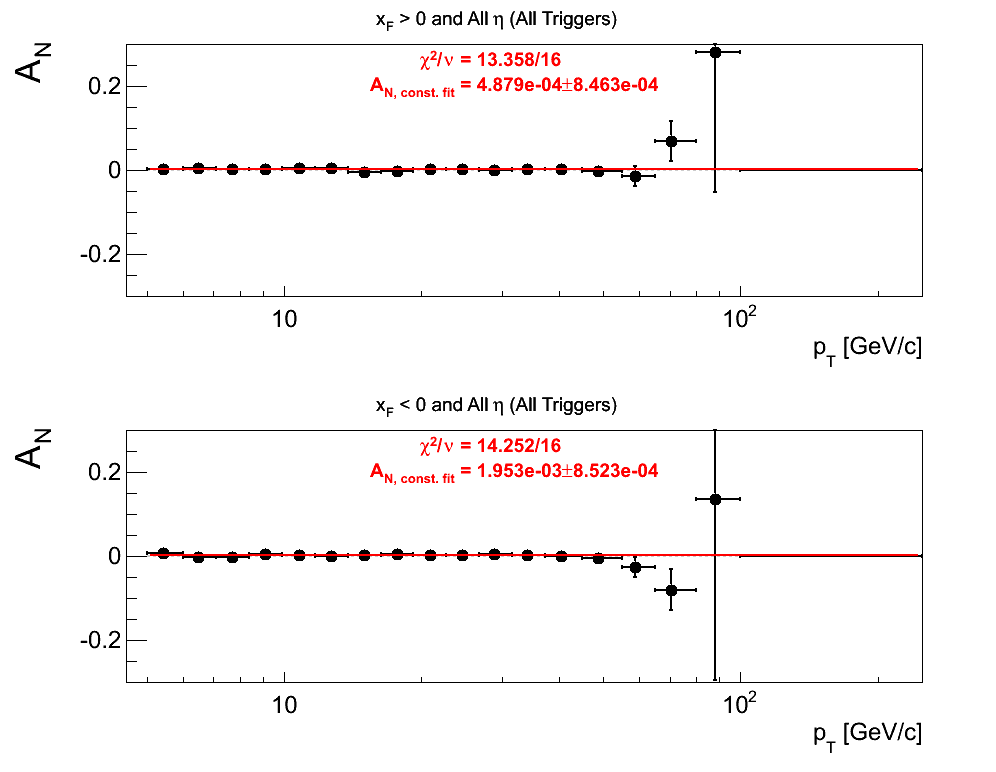
In Fig. 1 I show the Sivers asymmetries summing over triggers and eta bins. On the right I post a zoomed-out version, and on the left I zoom in to show the most significant bins. Qualitatively, the situation looks much like my previous update. As before, the lowest bin of xF < 0 appears to be a bit high (2.57σ).
Figure 2: Polarization-corrected Sivers Asymmetry in η-bins (All Triggers)
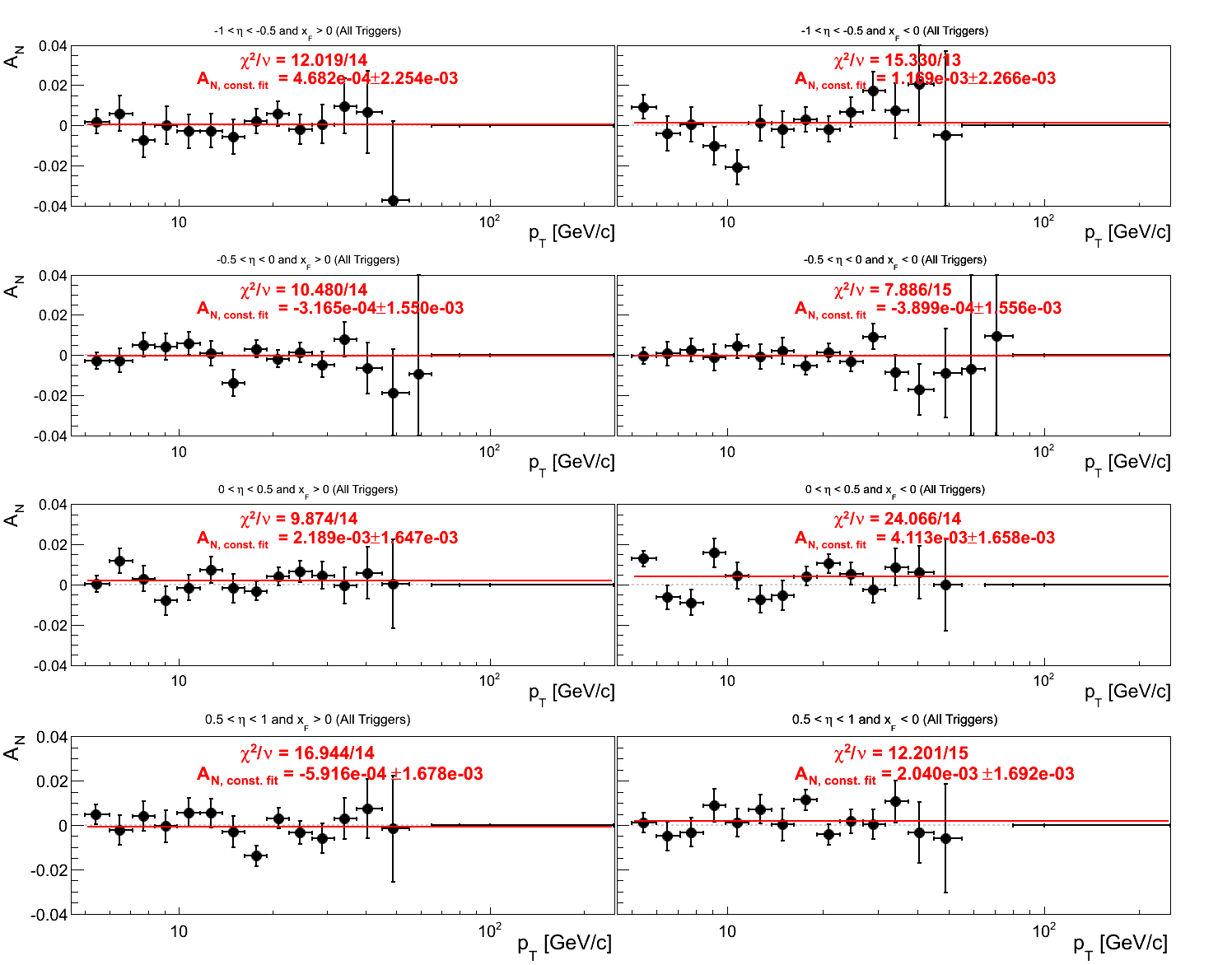
In Fig. 2 I show the asymmetries binned in η. Again, the fluctuations for the lowest bin of xF < 0 appear to derive from the 0 < η < 0.5 bin where there exists a 2.48σ offset from zero and χ2/ν = 24.066/14 (2.00σ).
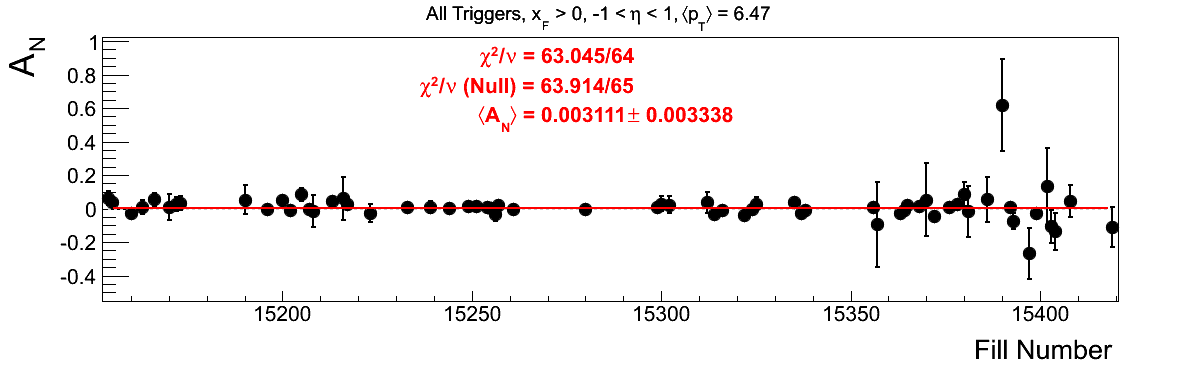
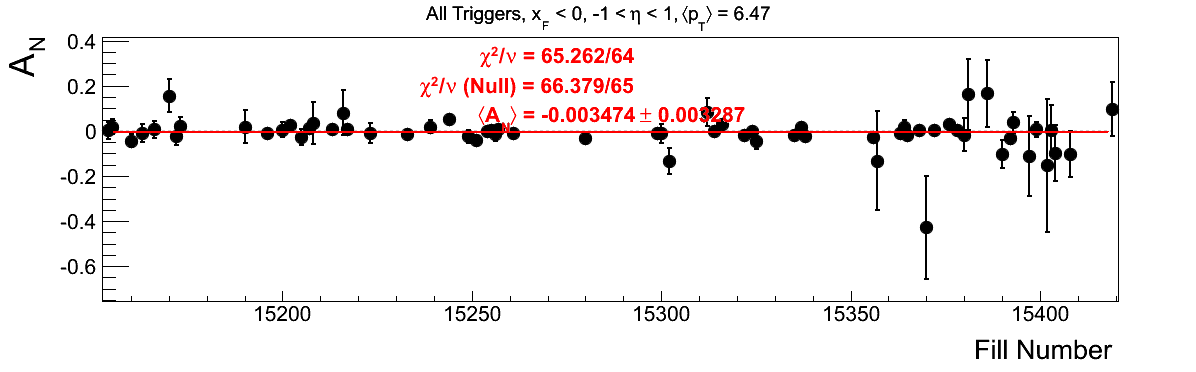
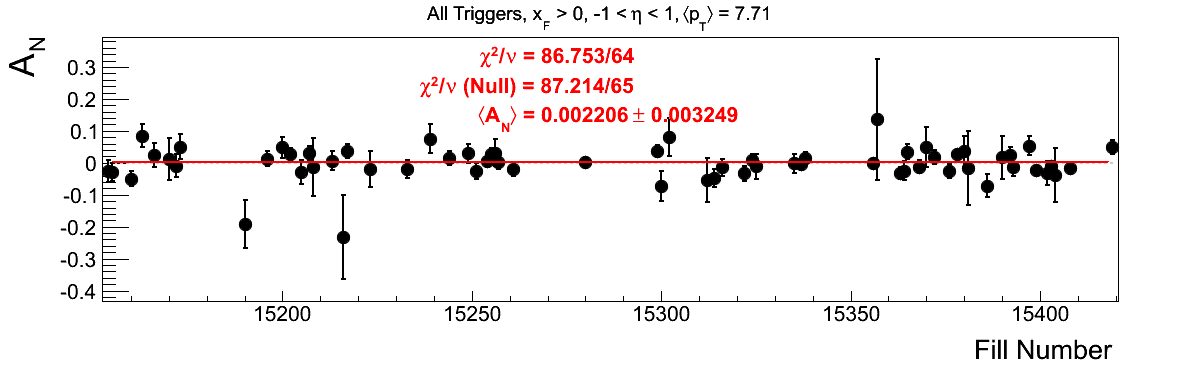
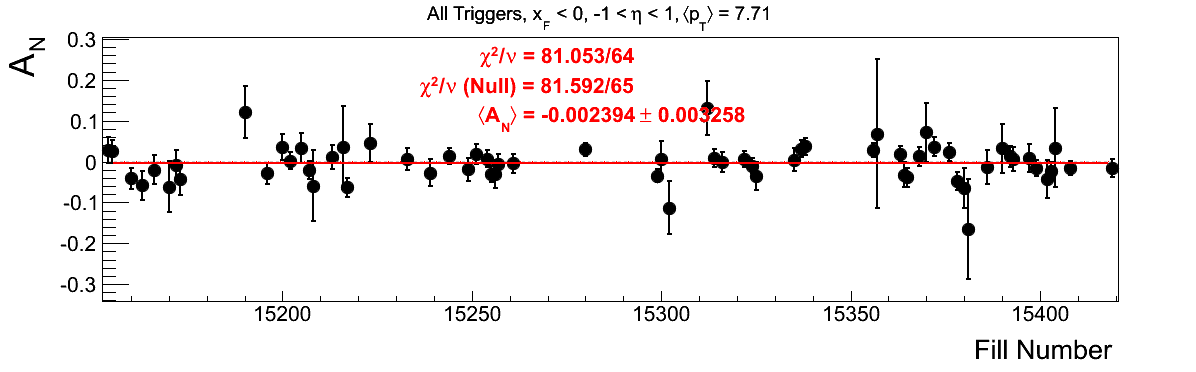
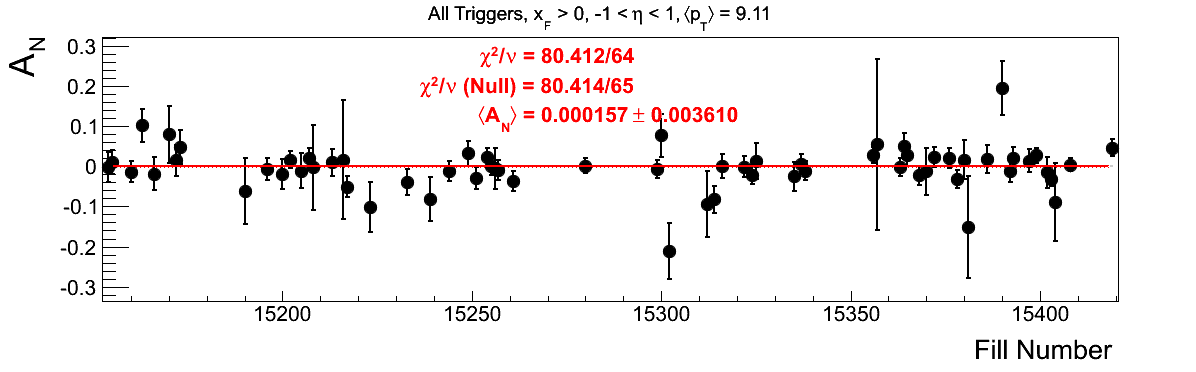
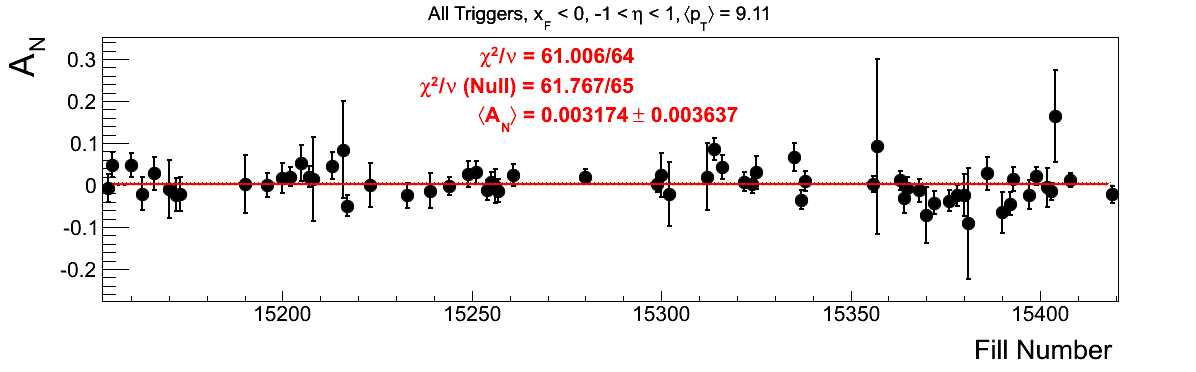
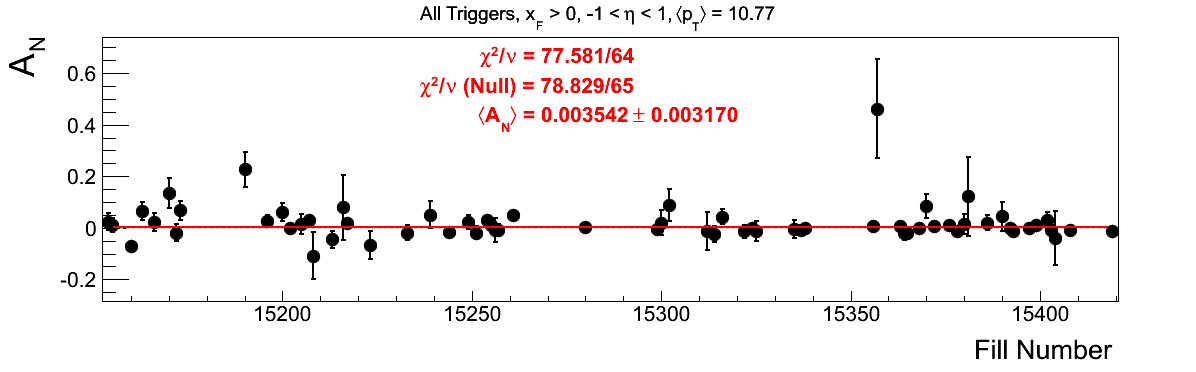
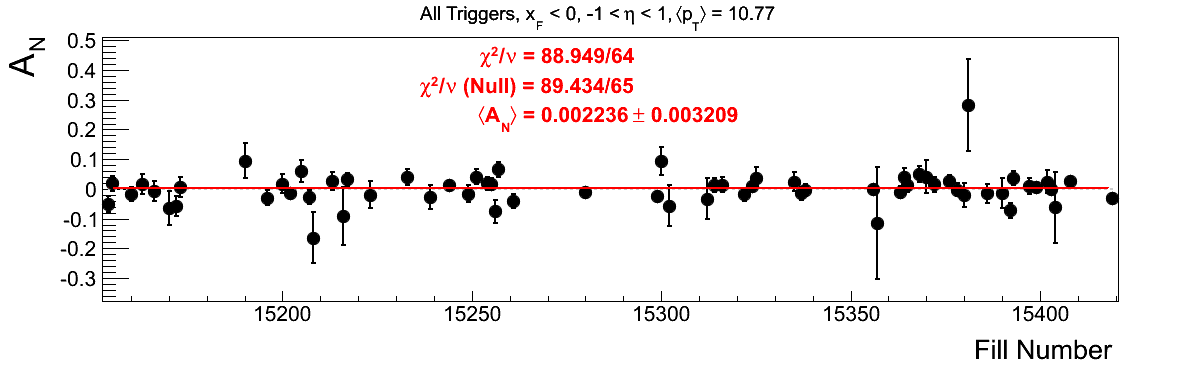
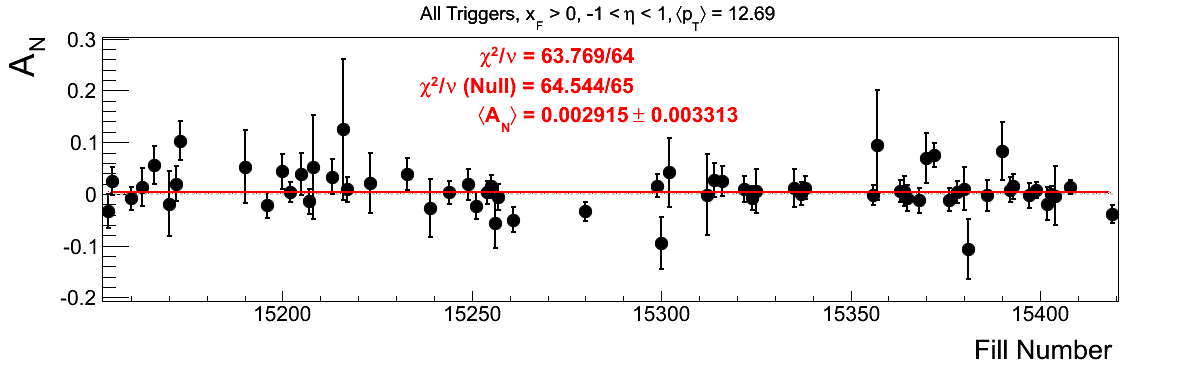
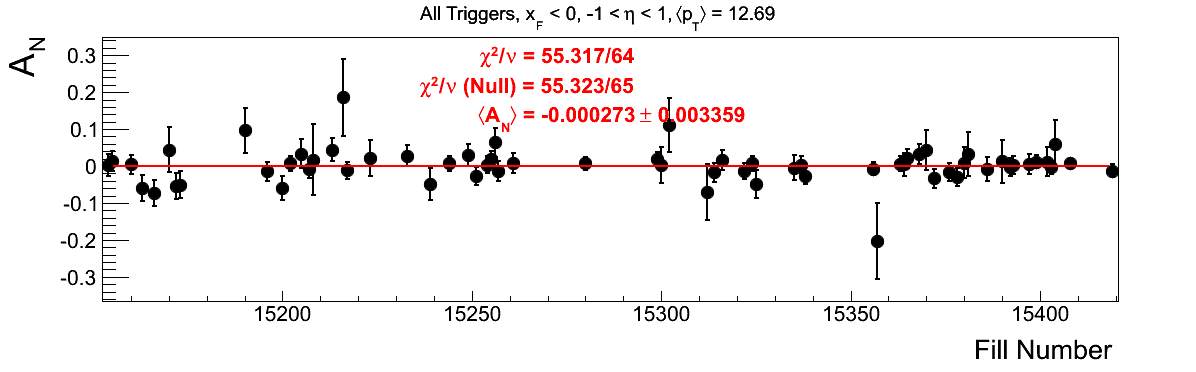
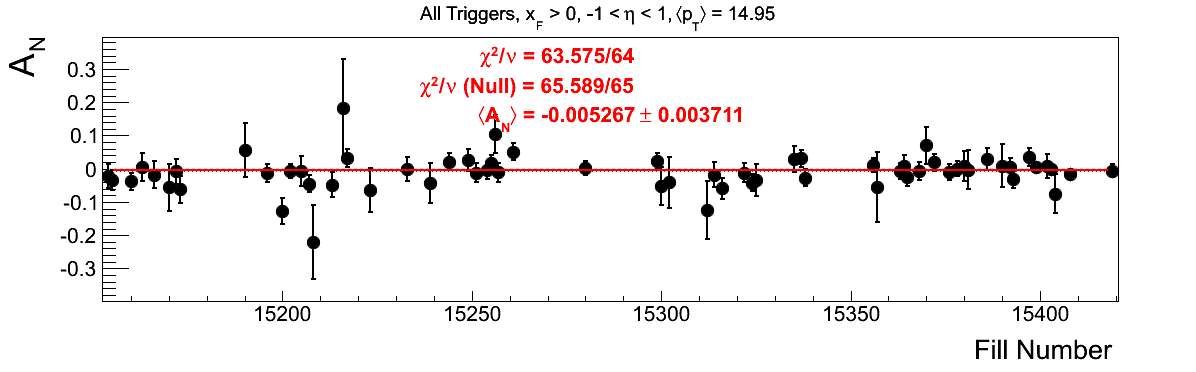
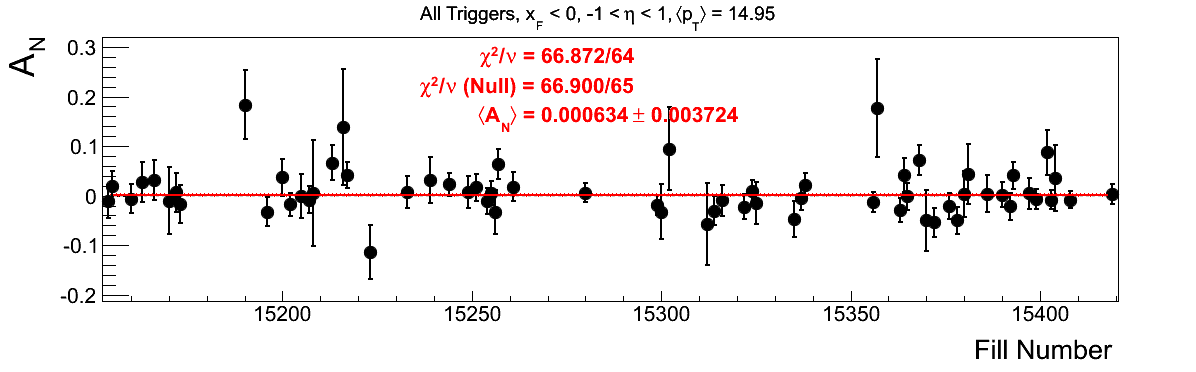
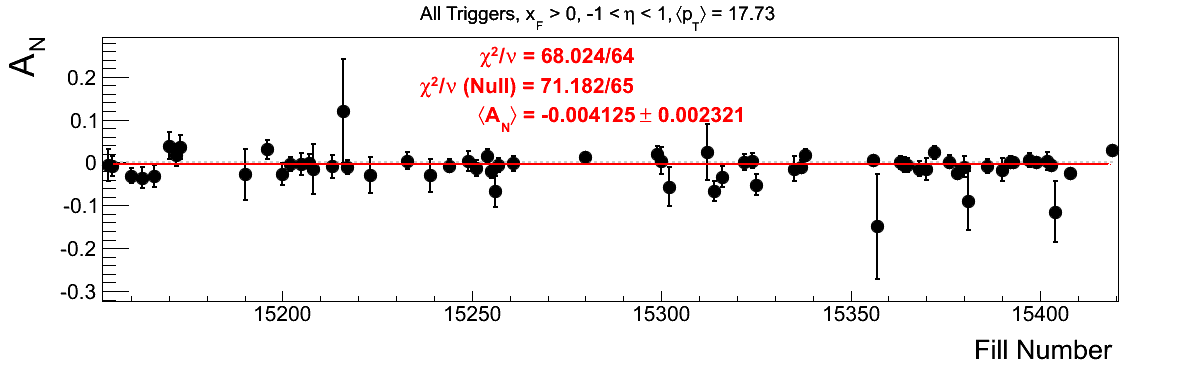
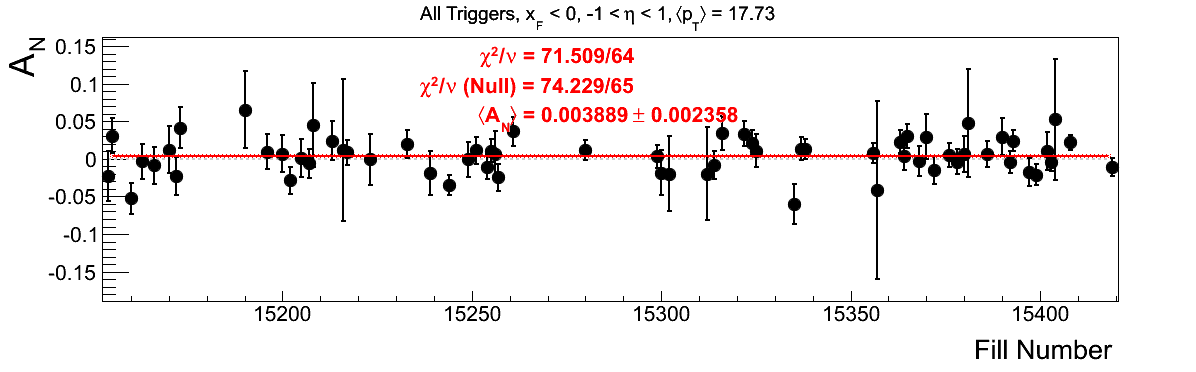
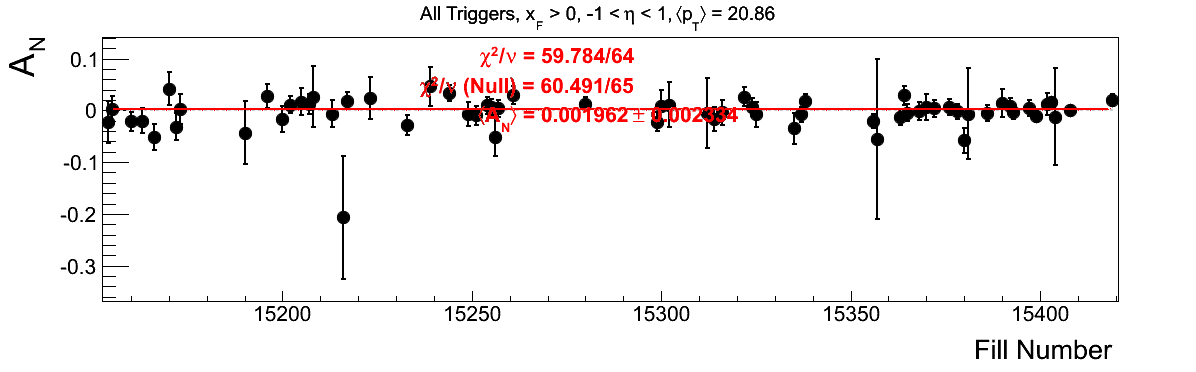
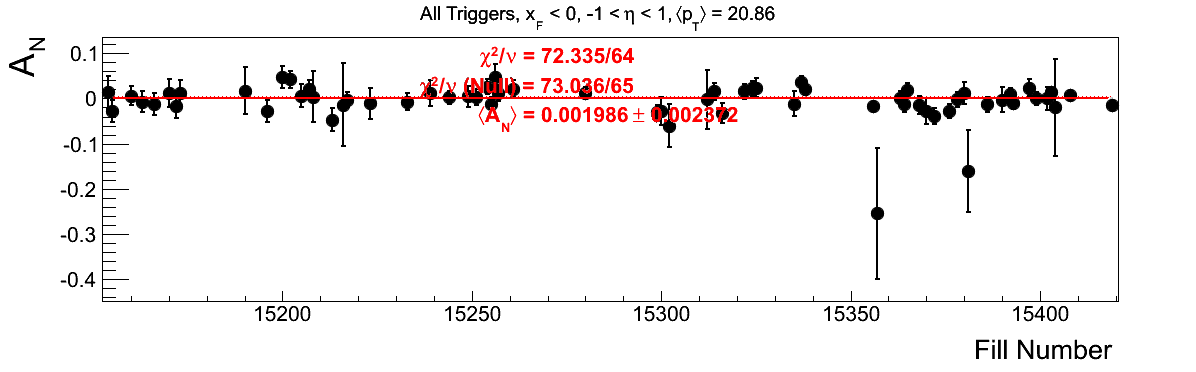
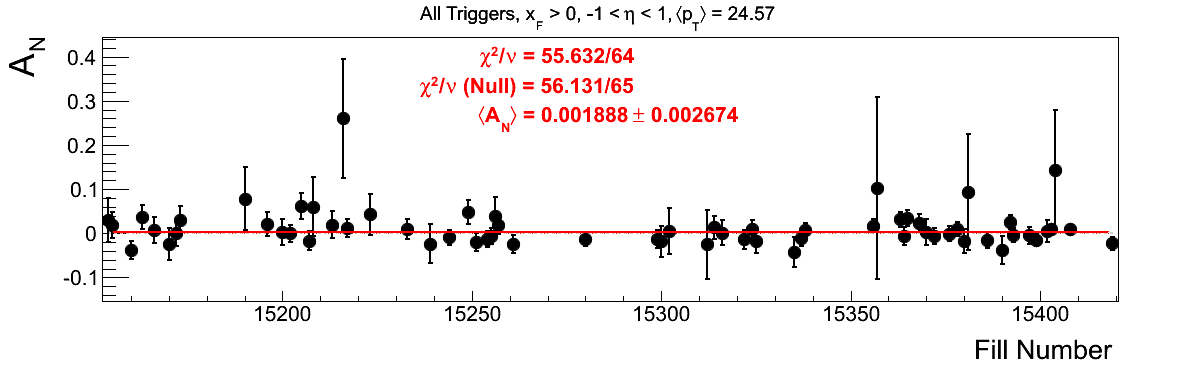
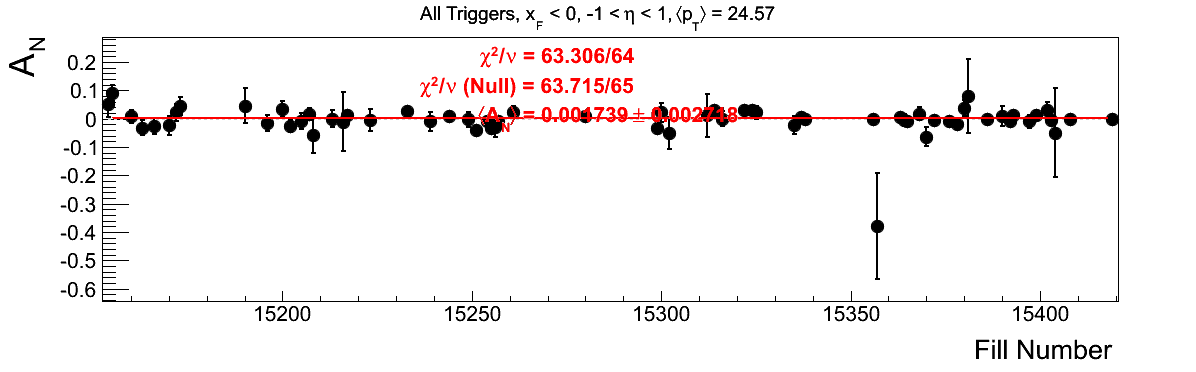
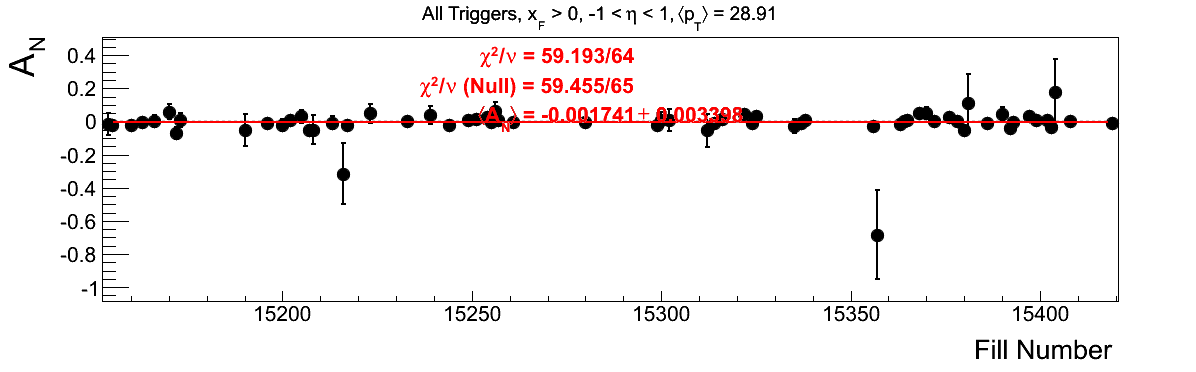
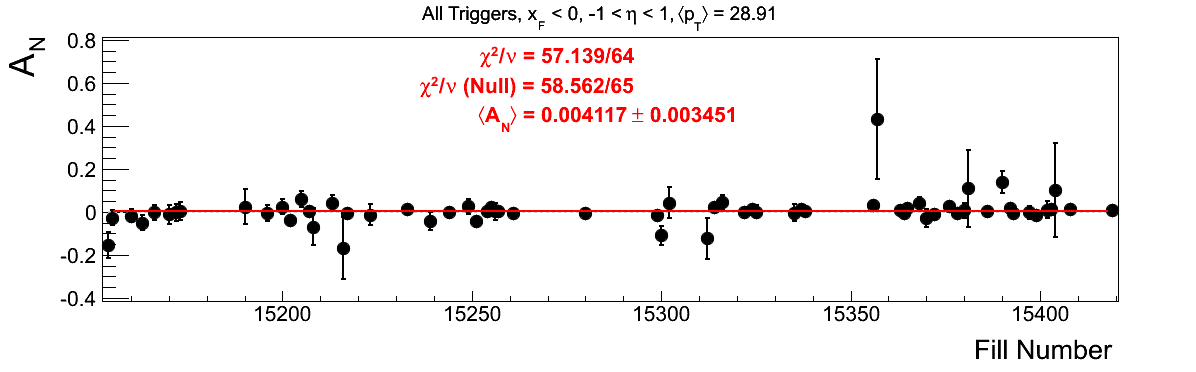
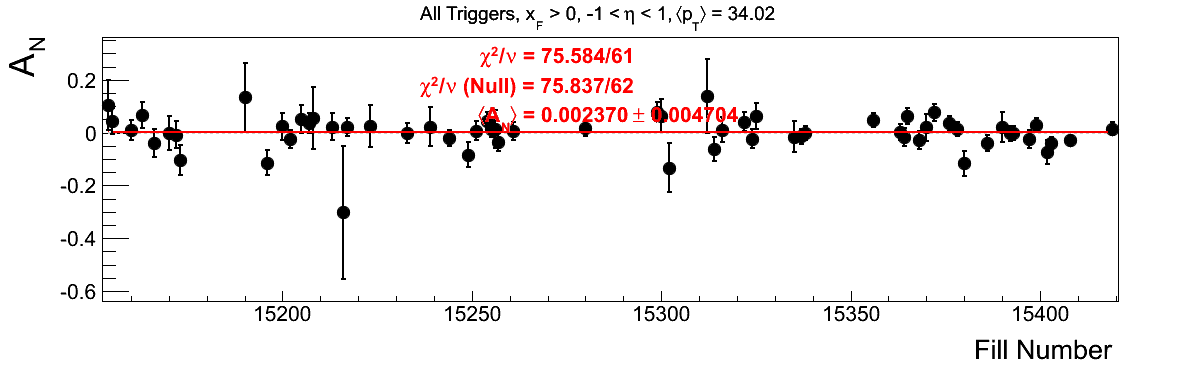
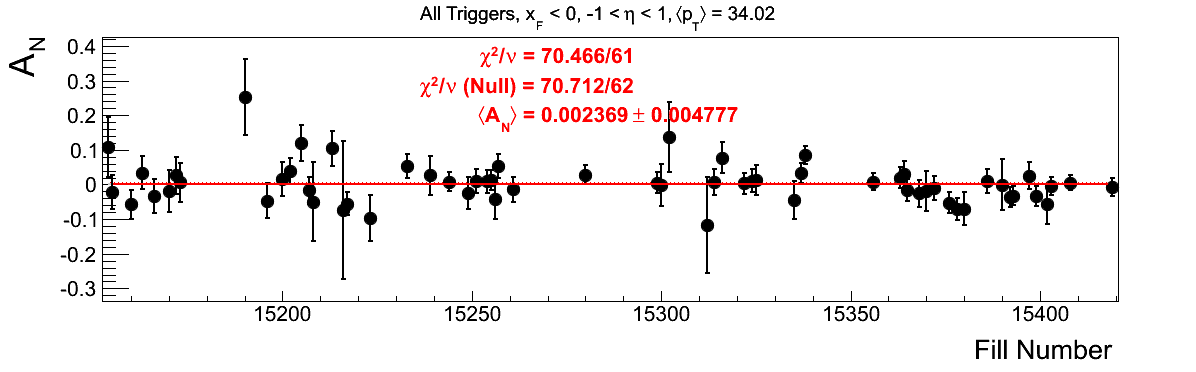
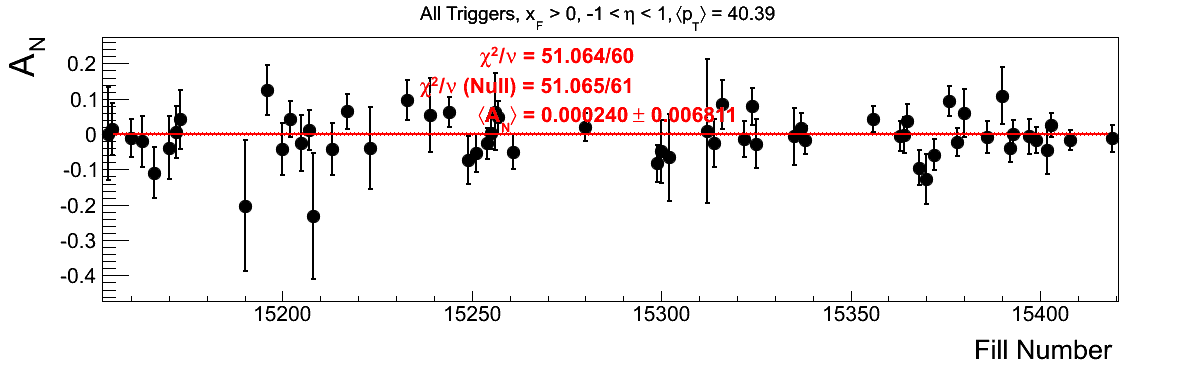
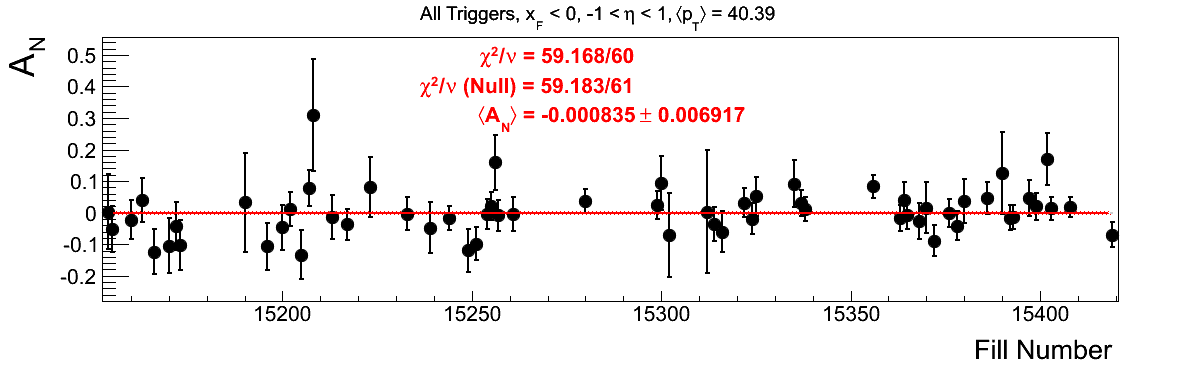
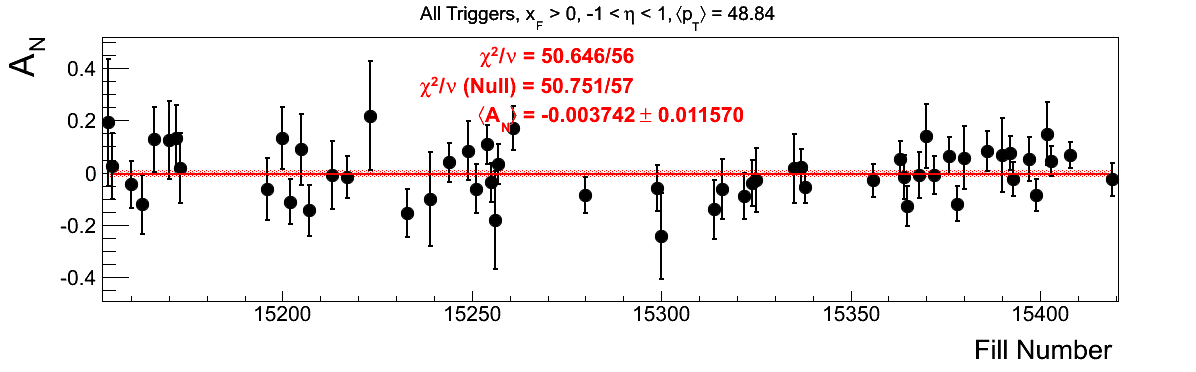
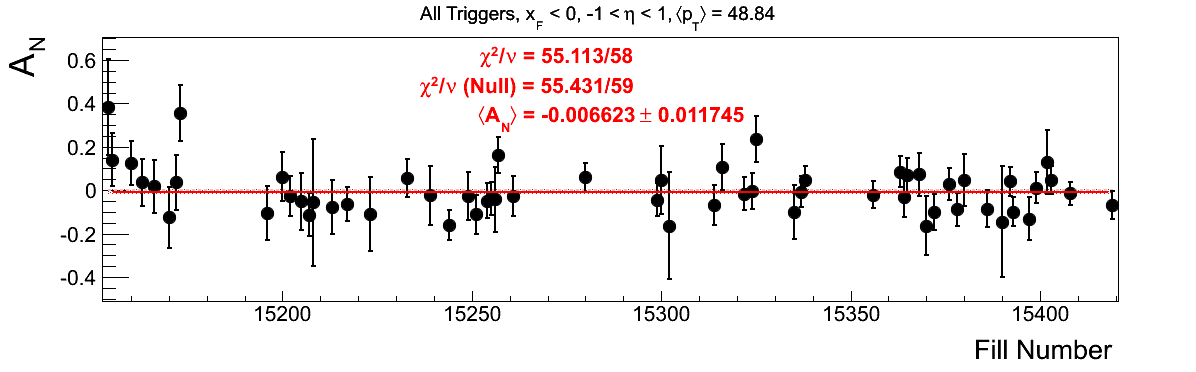
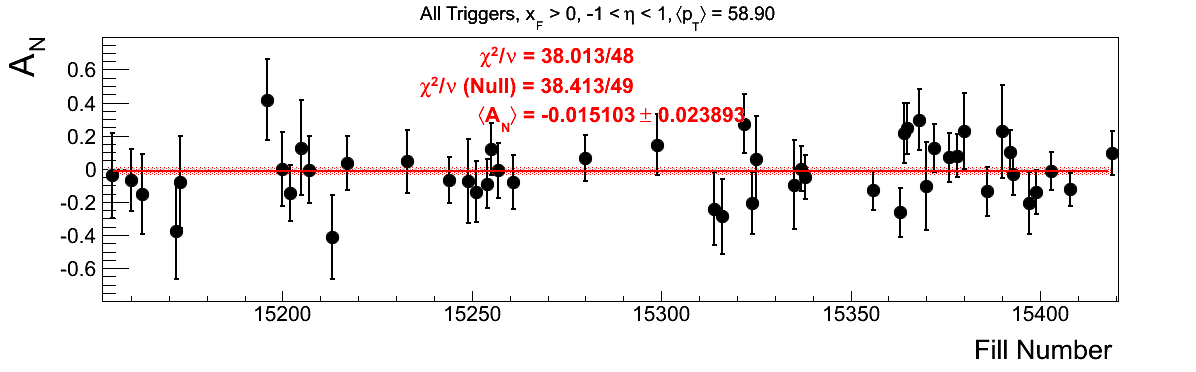
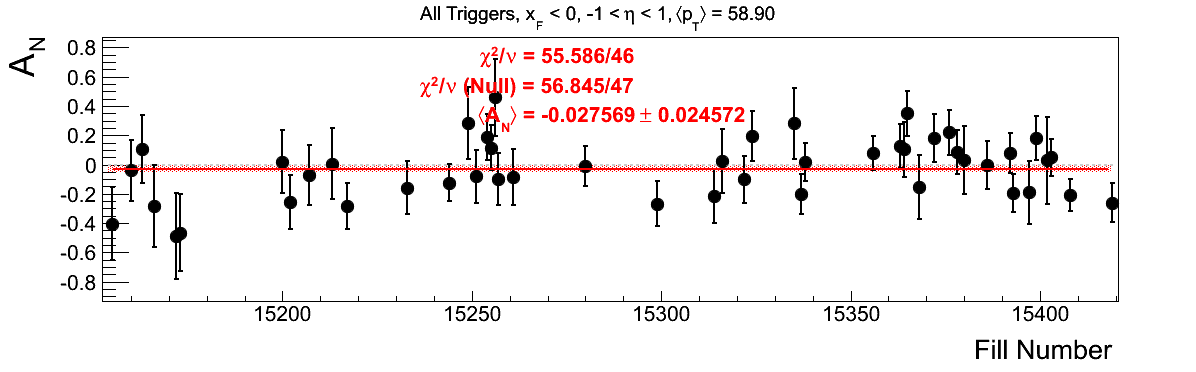
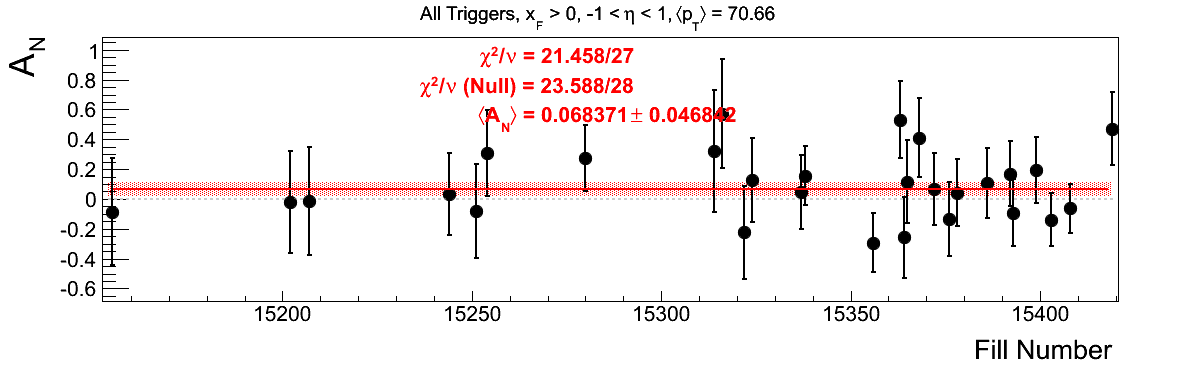
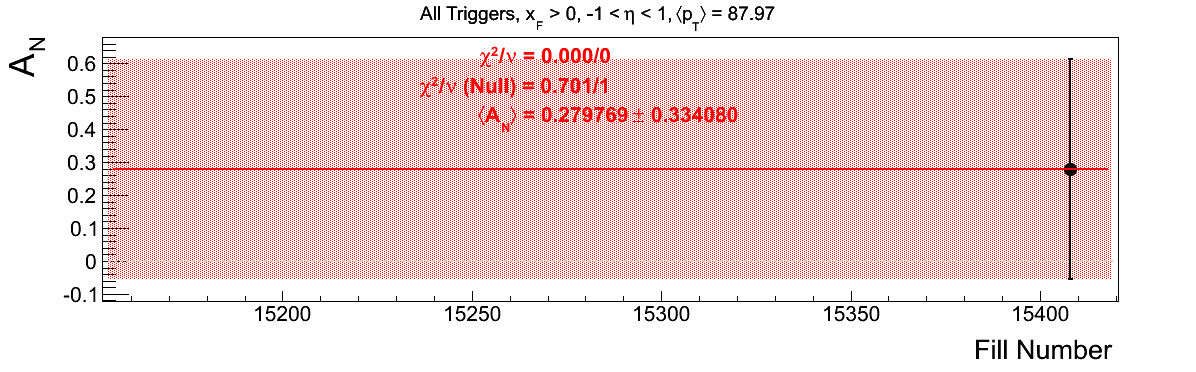
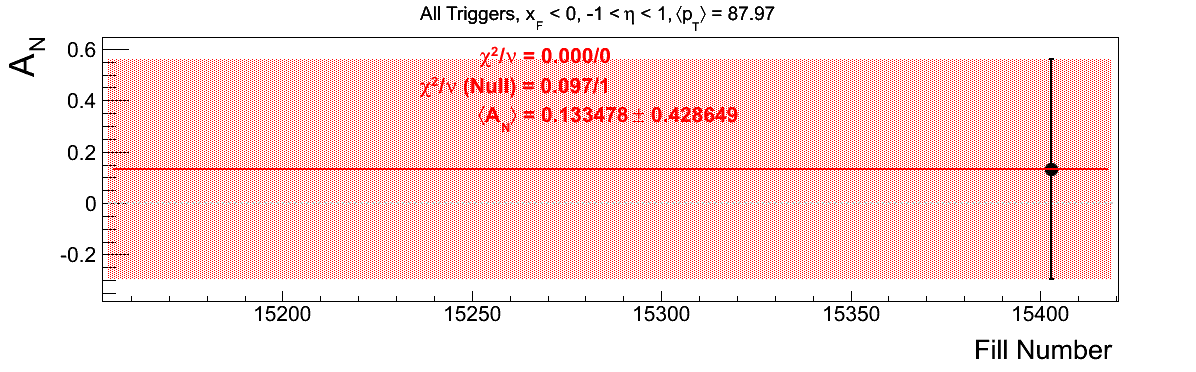
Bin-by-bin Asymmetries
In Fig. 3 I show the individual asymmetry calculations for the bins of Fig. 1. I note that for the lowest bin of xF < 0 the fit quality is not very good (2.5σ). It appeasr that a good portion of this may come from the early fills. It may be worth digging into these fills a bit deeper.
Figure 3: Bin-by-bin Asymmetry Calculation
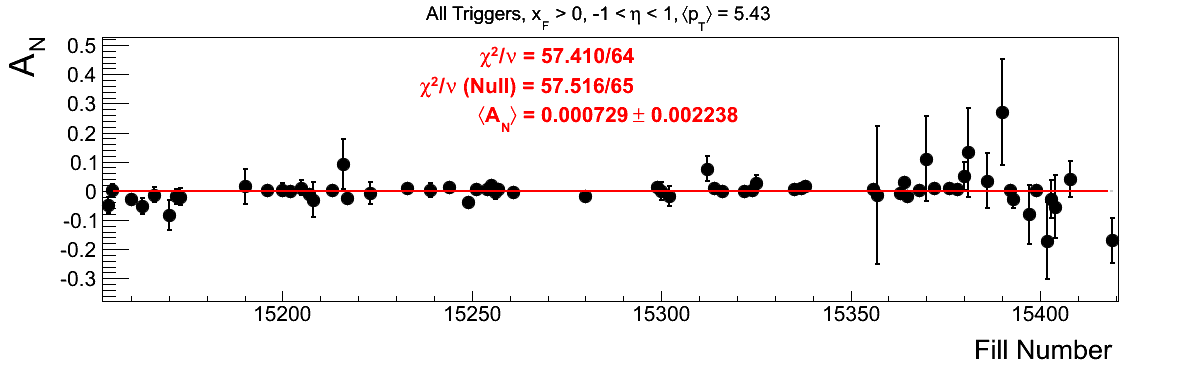
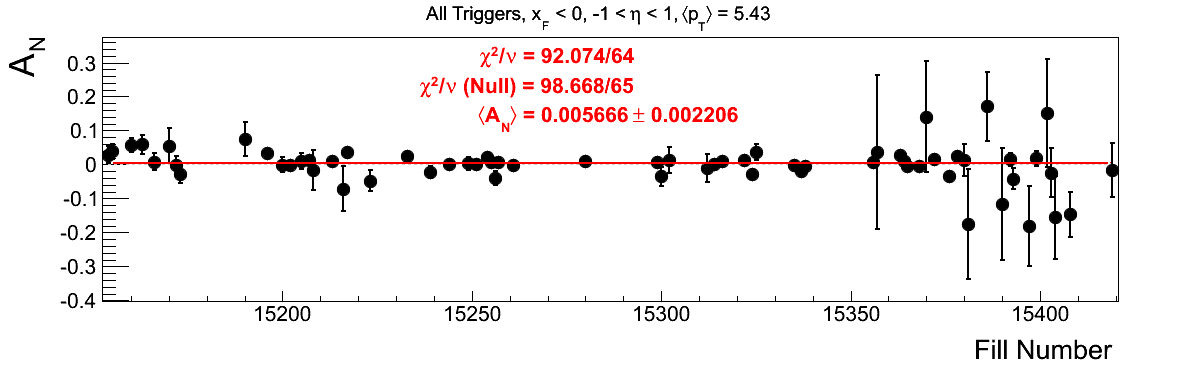

- drach09's blog
- Login or register to post comments
