Following up on a previous update, I now show the sate of the Collins analysis after integrating the full statistics. As before, this should in no way be considered final. Very few cuts have been implemented at this point, and hopefully this analysis will motivate a sensible set.

As before, each plot is fitted with a constant. For negative x_F and for p₀ distributions, this is a sensible expectation. One hopes to see a signal for positive x_F, and comparing to a constant may illuminate such a variation.

NOTE: Asymmetries are not corrected for polarization and error bars are statistical only.

Figure 1: Angular Coverage

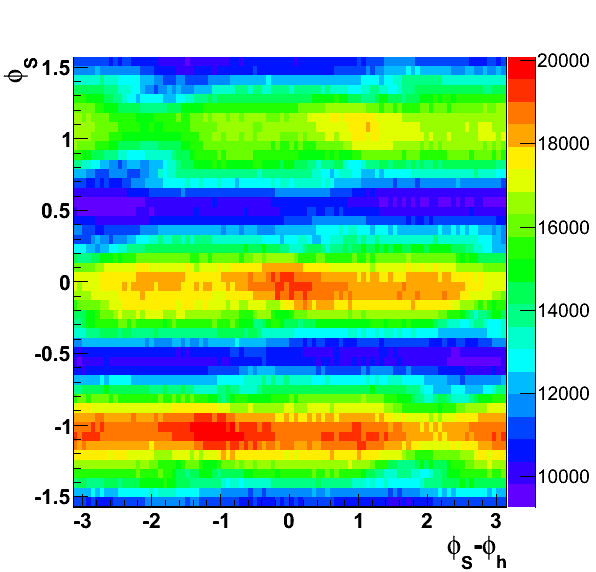
It is worth examining the angular coverage of φ_S vs. φ_S-φ_h. One can see the coverage is rather similar to what one sees for the Collins-like angle.

Hemisphere Dependence

One useful check is to examine the asymmetries in the two hemispheres. All things being equal, the answers should be the same. However, I have not implemented a fiducial volume cut (e.g. |η| < 1), so the acceptance is different for the two hemispheres. Likely, I will need to implement such a cut in the near future.

Figure 2: Asymmetry (π⁺)

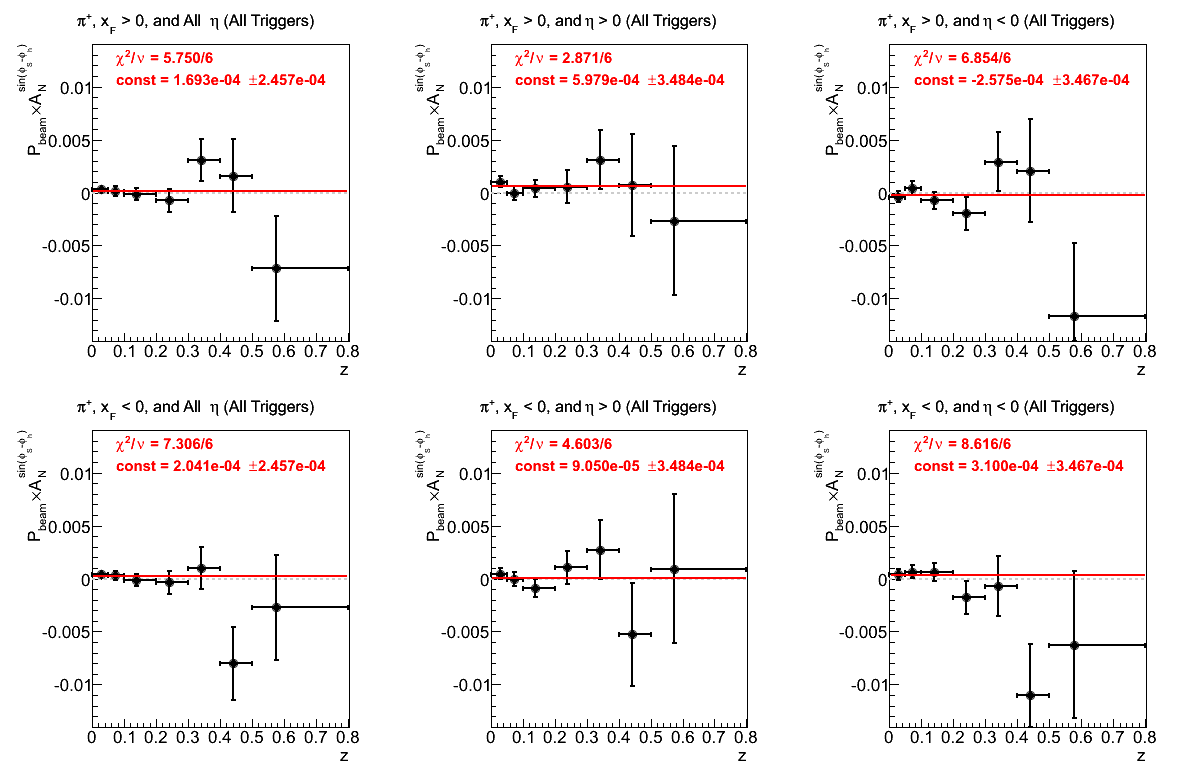
The constant fits for both negative and positive x_F are consistent with zero. For positive x_F and η > 0, 5 of 7 points appear above the horizontal. However, the offset is not terribly significant (1.72σ), nor is the effect reproduced in η < 0.

Figure 3: Asymmetry (π^-)

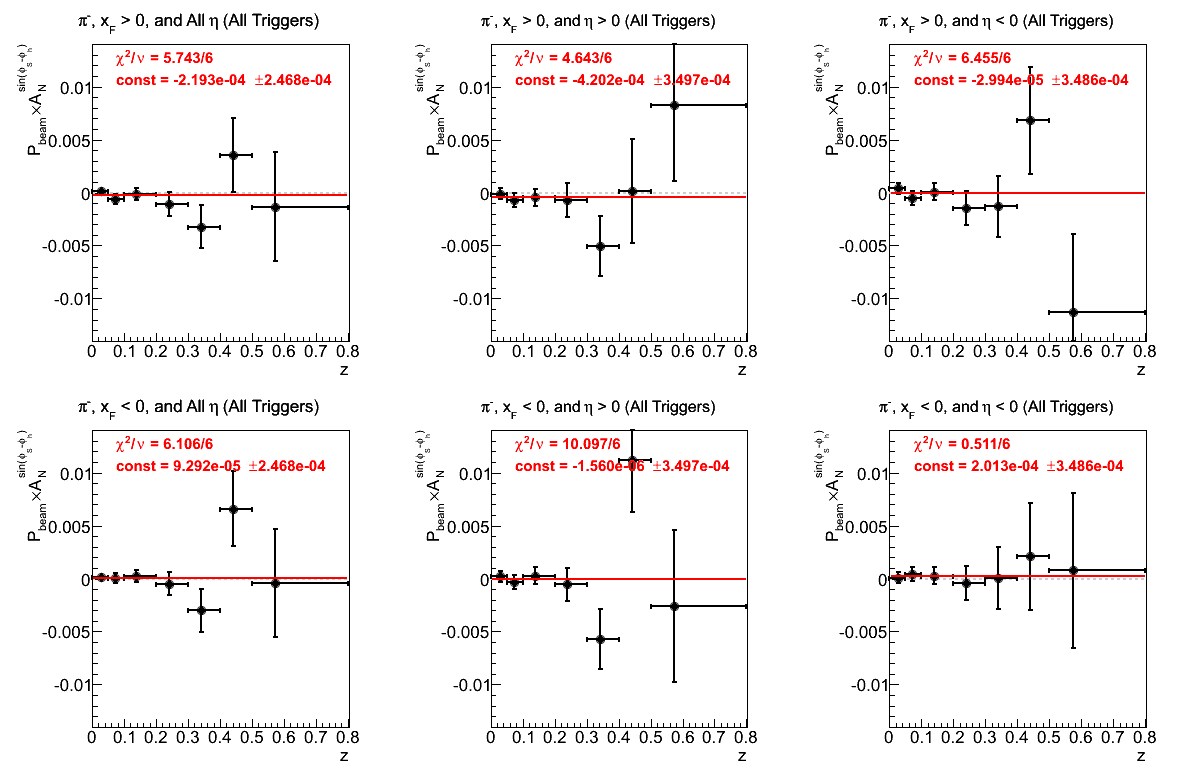
As in Fig. 3, the fits for both negative and positive x_F are consistent with zero. Again, with η > 0, there appears to be a hint of a negative effect, however, the statistical signficance is quite small (1.2σ). It is also not reproduced in η < 0. The fit for negative x_F and η > 0 is not good at all. We could, again, be seeing systematic effects from pusing the edges of detector acceptance or trigger thresholds. It will be important to review a set of appropriate cuts.

Figure 4: p₀ from Fit (π⁺)

One finds fits consistent with zero for positive and negative x_F. However, for negative x_F, there appears to be a fair amount of structure in both hemispheres. Something similar was observed for Collins-like, perhaps, suggesting systematic effects. On the other hand, when broken down into hemispheres, the constant fit is quite reasonable.

Figure 5: p₀ from Fit (π^-)

The fits for positive x_F are quite reasonable. While the fits for negative x_F are also consistent with zero the fit for η > 0 is not good at all.

Trigger Dependence

It is also useful to examine the calculations for the different triggers. One may expect consistent answers in overlap regions. Wide variations may signal systematic effects.

x_F > 0

Figure 6: Asymmetry (π⁺)

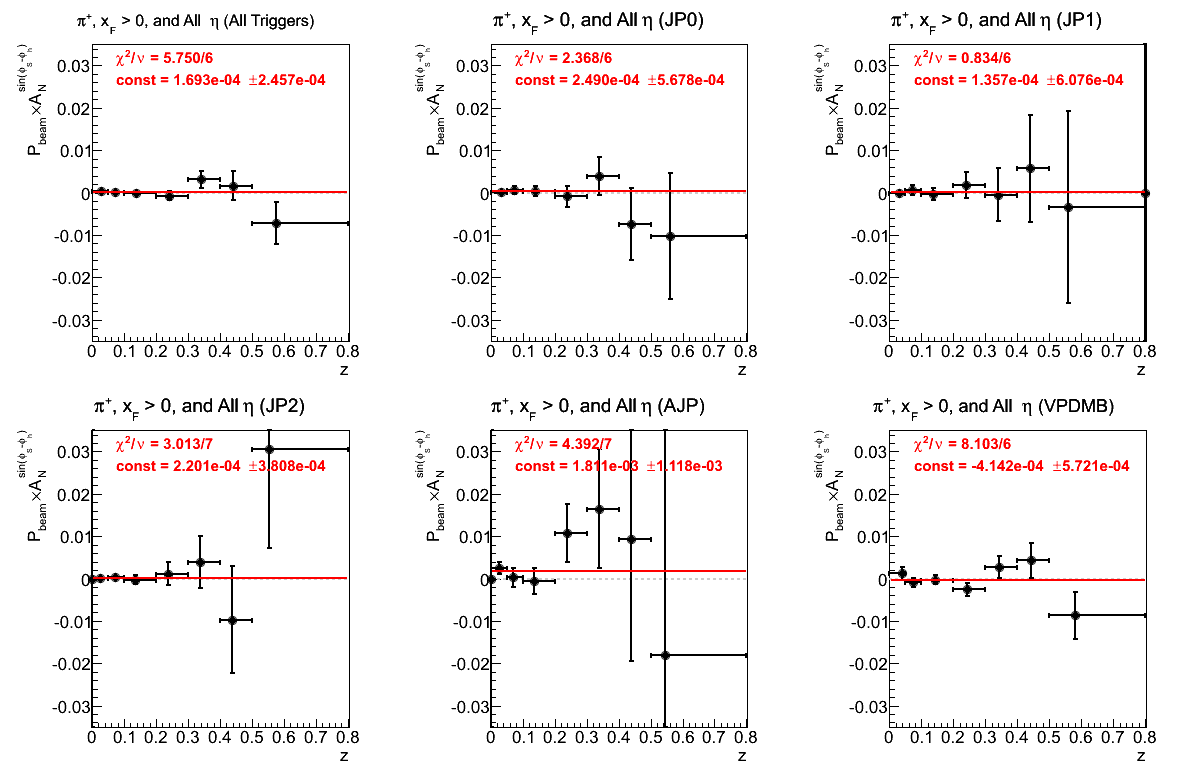
In general, the fits are sensible across the various trigger contributions. The fit for JP1 is ridiculous. The fit for VPDMB is not great, but by no means a show-stopper.

Figure 7: Asymmetry (π^-)

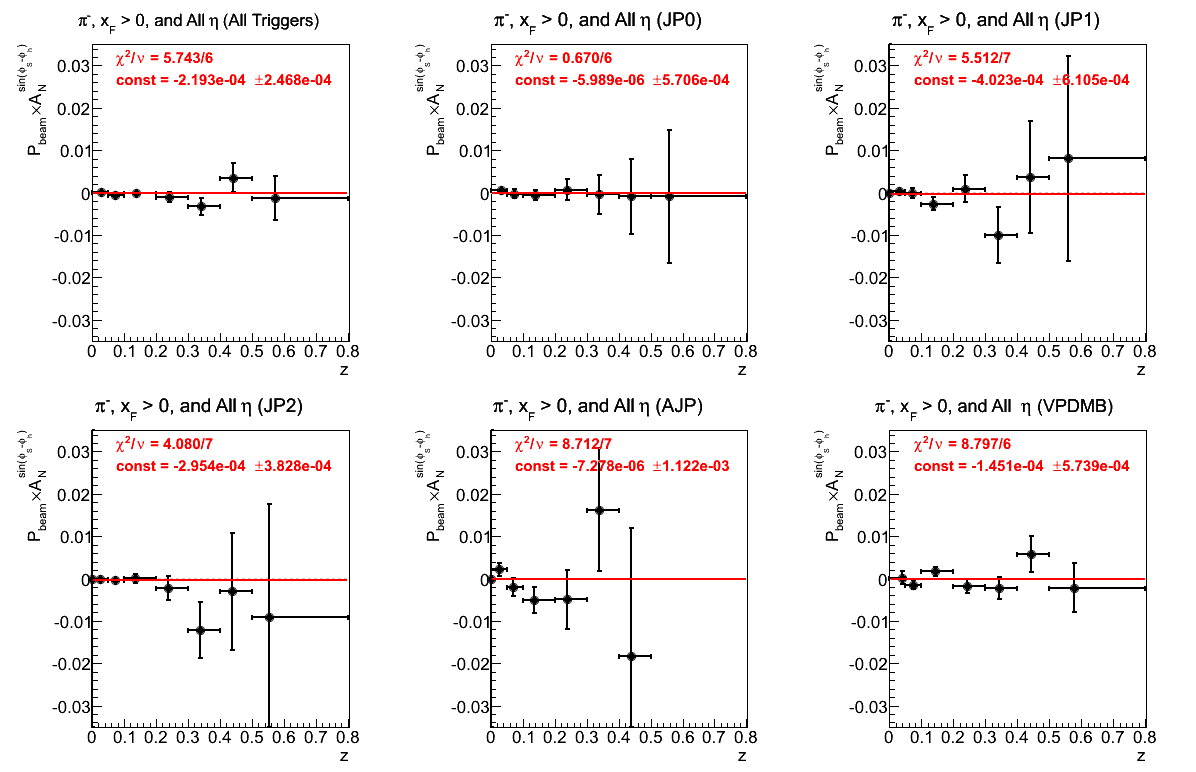
While, the fits are across-the-board consistent with zero, they also appear to be systematically below the horizontal. Again, the fit for VPDMB--and, here also, AJP--are not great, but not inconceivable.

Figure 8: p₀ (π⁺)

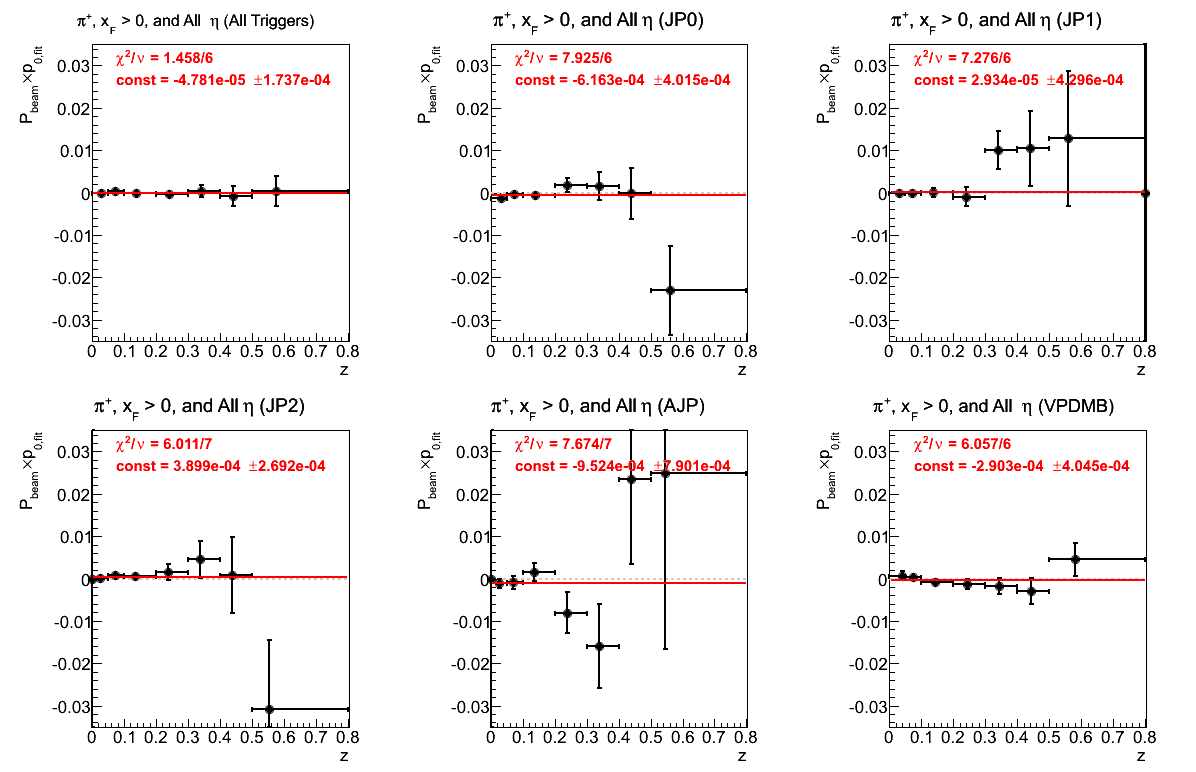
The fits appear to be conistent with zero across the various trigger contributions. The fit quality is not great when broken down into the various contributions but perhaps not alarming.

Figure 9: p₀ (π^-)

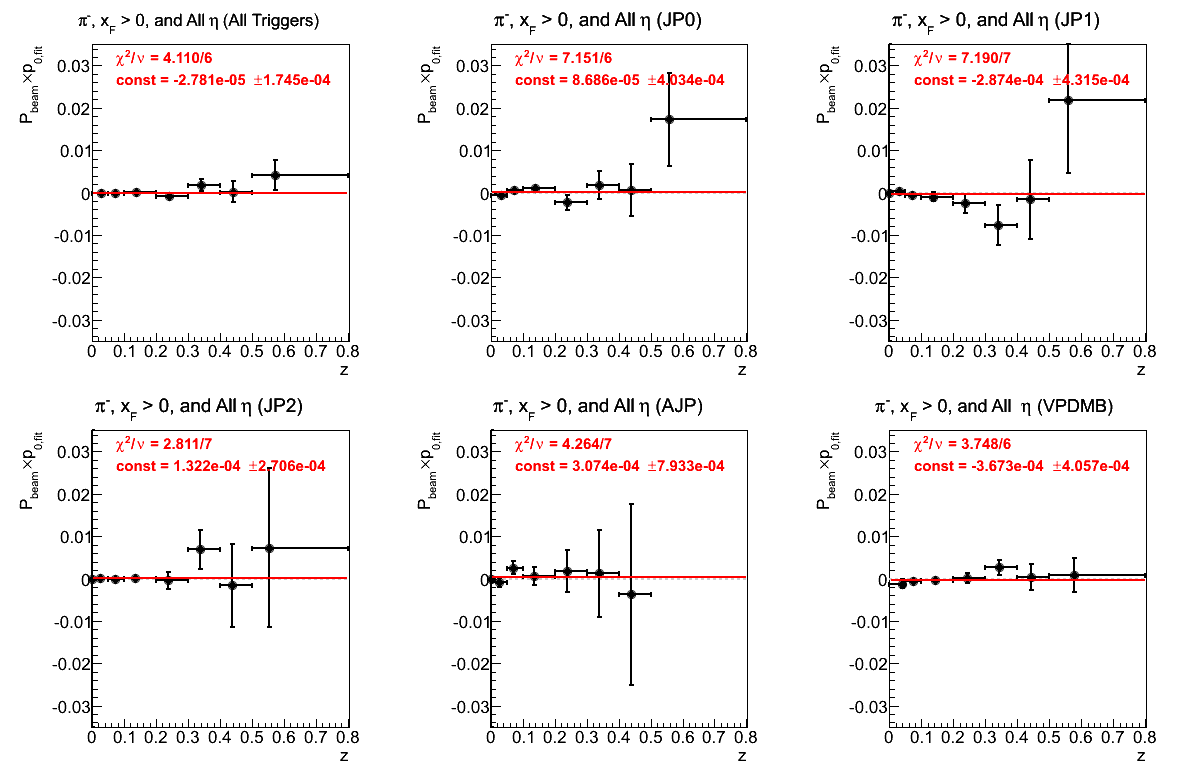
The fits for π^- are a bit more well behaved.

x_F < 0

Figure 10: Asymmetry (π⁺)

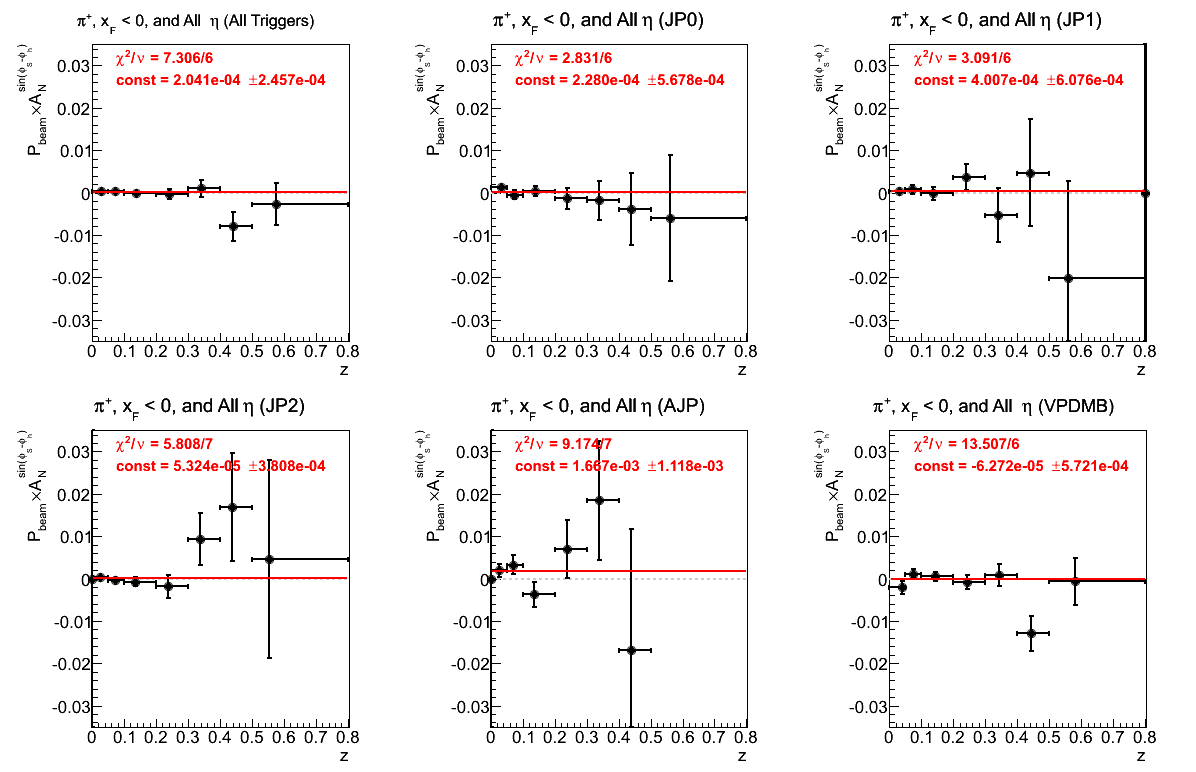
In general things seem as expected. However, the fit for VPDMB is terrible.

Figure 11: Asymmetry (π^-)

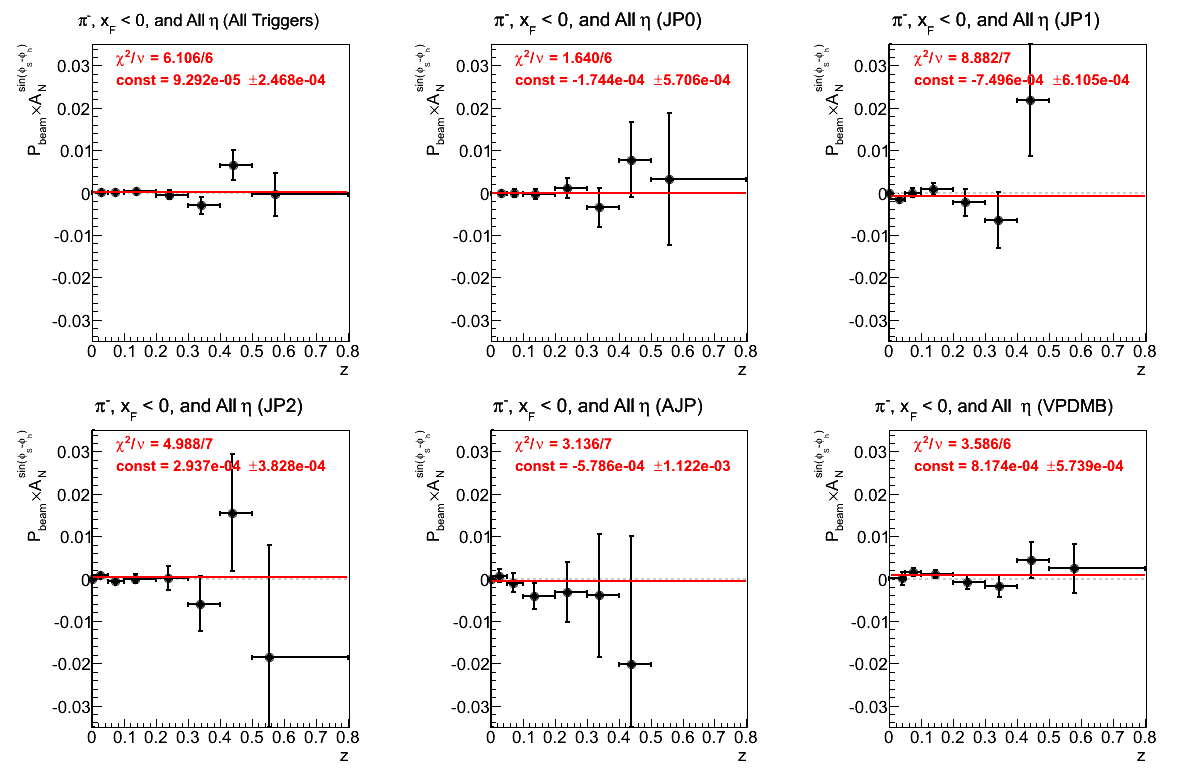
Once again, the π^- distributions are more well behaved than π⁺.

Figure 12: p₀ (π⁺)

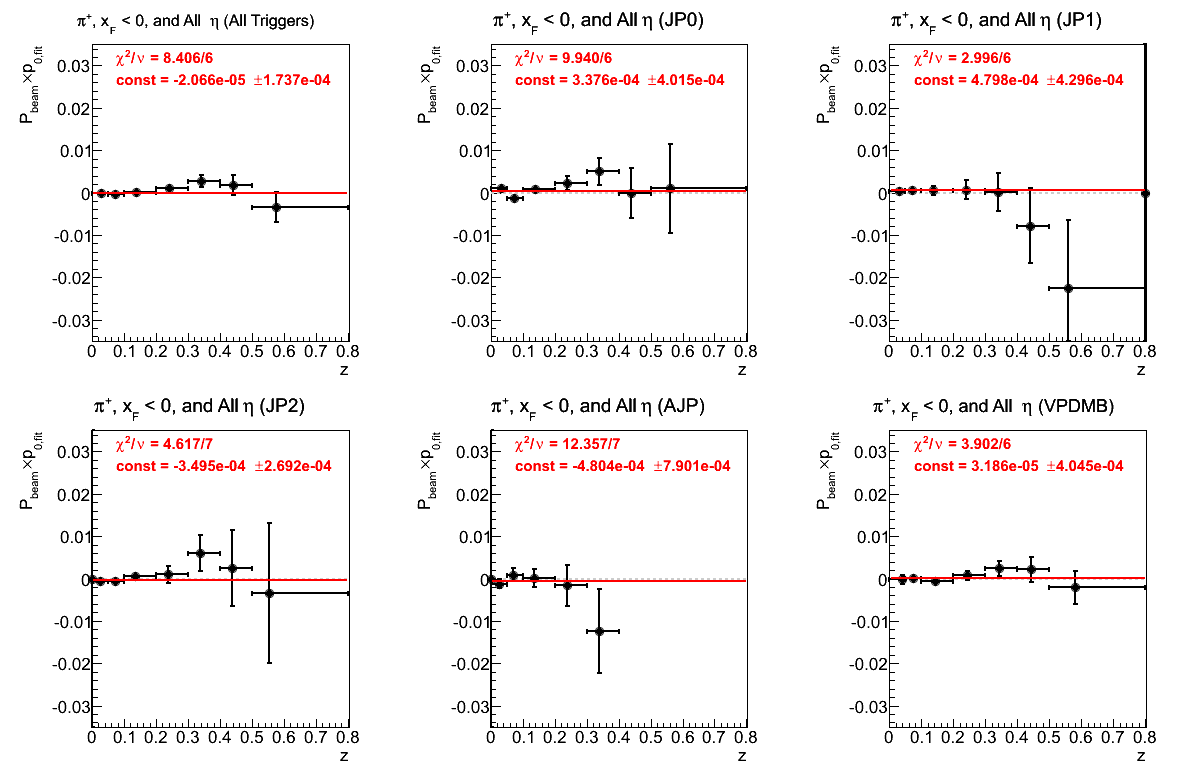
The fits for JP0 and AJP are not very good. Otherwise, the the fits seem reasonable, with slight offsets in JP1 and JP2.

Figure 13: p₀ (π^-)

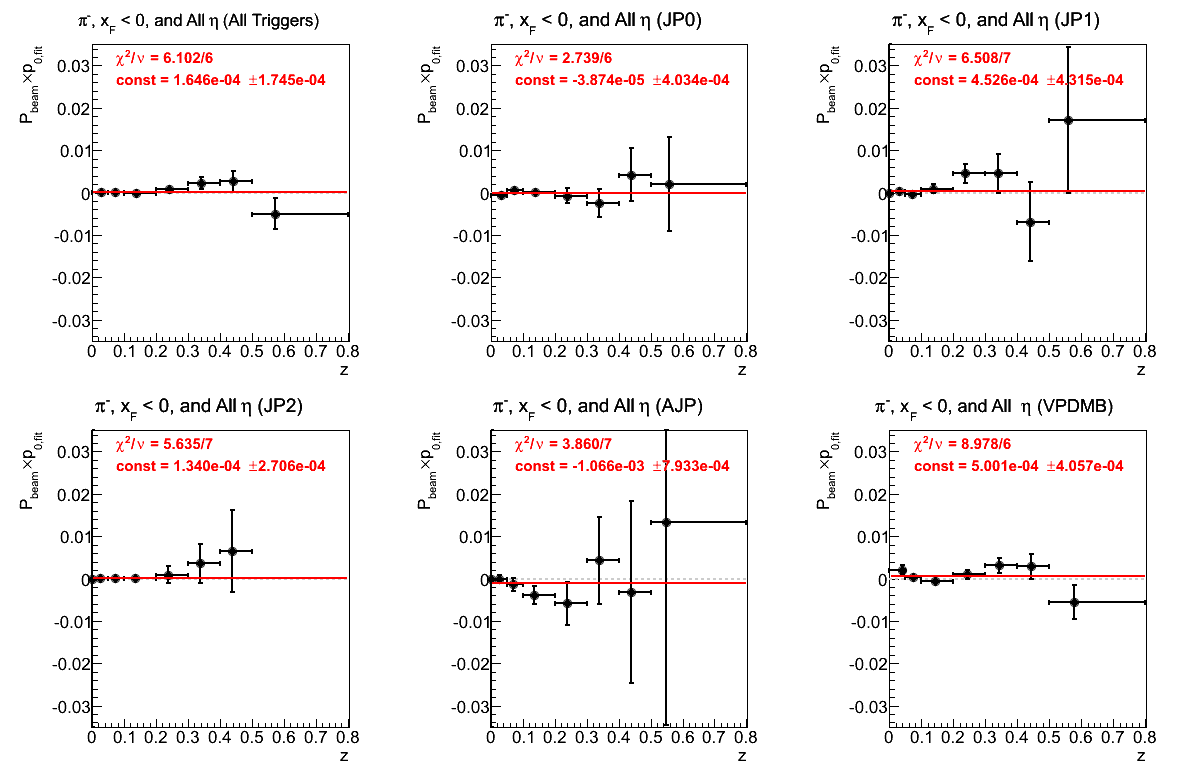
Again, the fit for VPDMB is not great. Otherwise, the fits are not terribly frightening.

Further Statistical Cross-checks

Figure 14: χ²-Distribution for Collins-like Fits

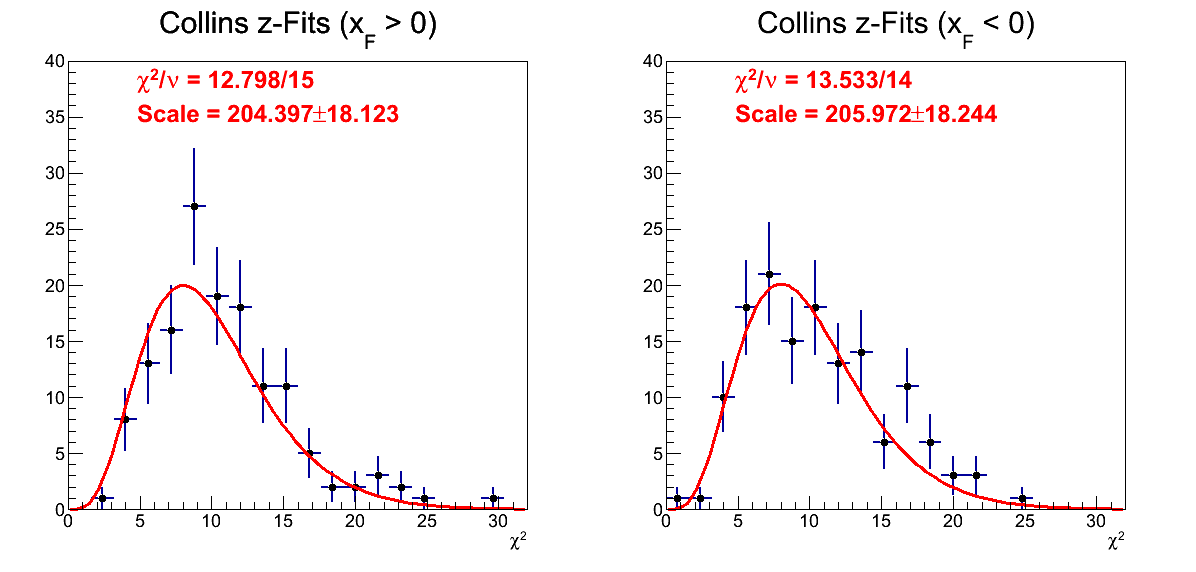
Figure 14 shows the χ² distribution for the Collins fits (p₀+p₁×sin(φ_S-φ_h)). In red is plotted the expected distribution. On top, the distribution is forced to have ν = 10; and the agreement with expectation is quite good. On bottom, the fit allows ν to float. The fits are of fine quality, and ν is found to be close to the expected value (2.02σ for positive x_F and 1.54σ for negative x_F).

Distribution of Constant Fits

Figure 15: Asymmetry Fits

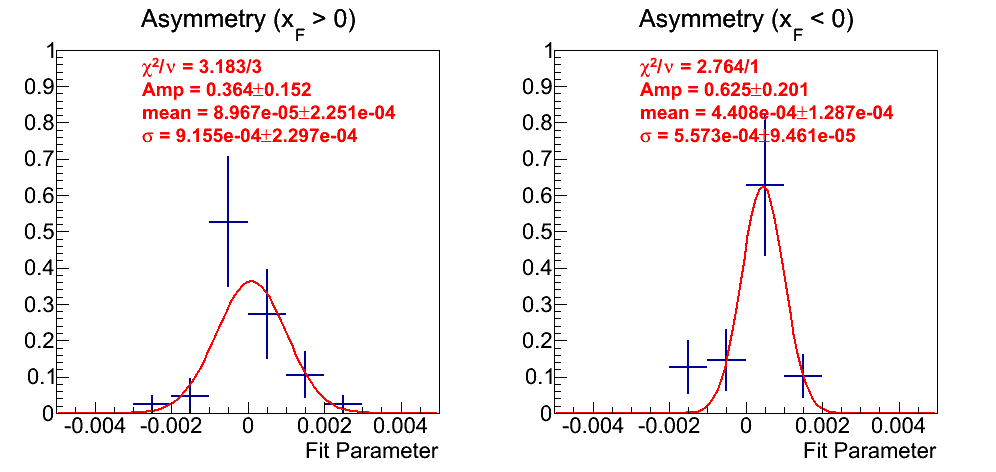
In Fig. 15 I show the distribution of constant fits to the asymmetries weighting the entries by 1/uncertainty. There simply are not many fits, thus, it is difficult to glean much information. The distributions are fit with a Gaussian. The fits are not completely crazy. owever, the mean for negative x_F is significantly offset from zero.

Figure 16: p₀ Fits

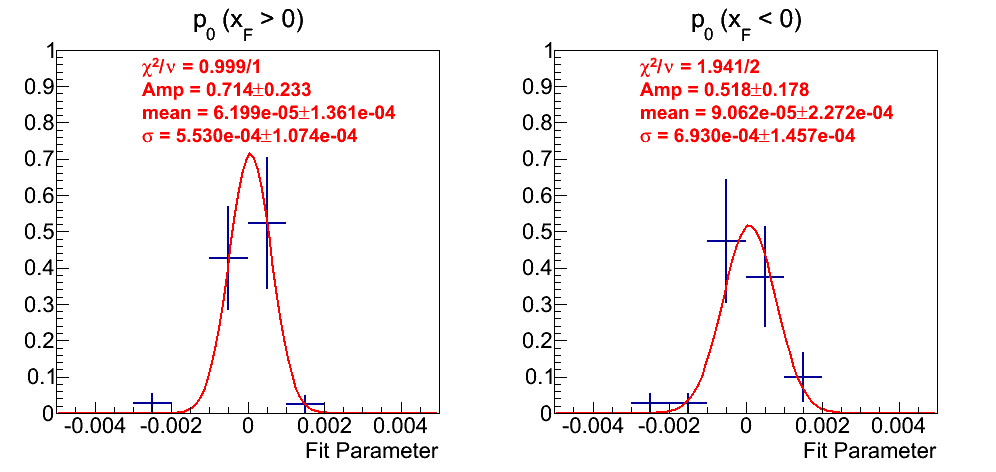
In Fig. 16, I show the weighted distribution for fits to the p₀'s. Again, there are not many fits from which to draw, but the distribution is quite nice. The fits appear quite Gaussian with means consistent with zero and similar widths.

Reduced χ² of Constant Fits

With such a low number of fits with varying degrees of freedom, it is impossible to perform a χ² study of the constant fits. However, we can examine the reduced χ²'s for some information.

Figure 17: Asymmetry Fits

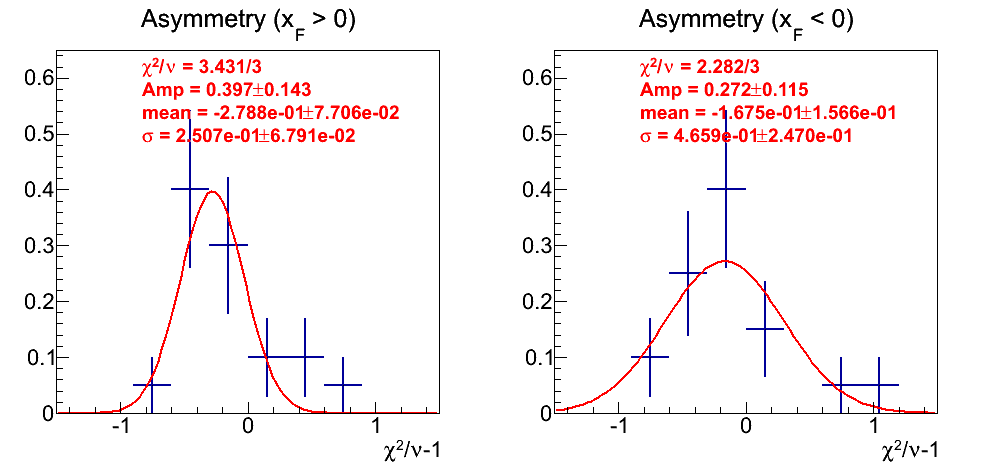
The asymmetry fits seem shifted negatively. Of course, the uncertainties on the mean and width are sizable.

Figure 18: p₀ Fits

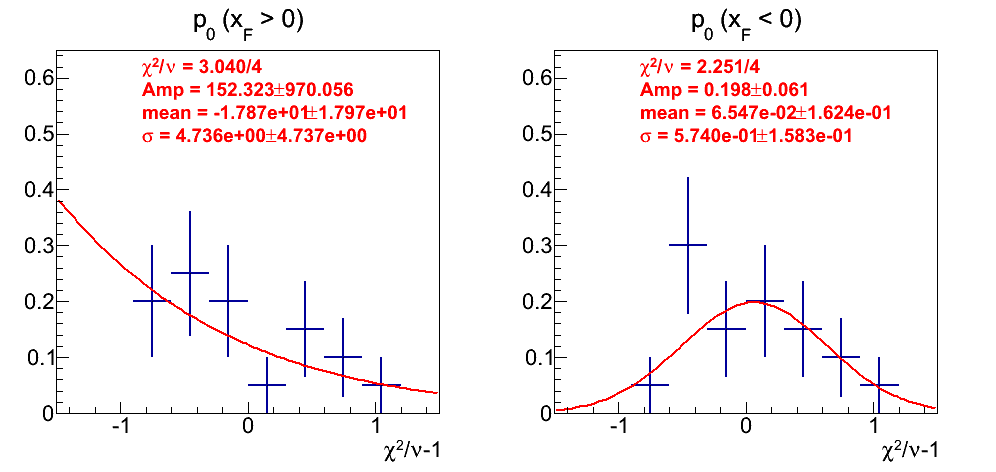
Positive x_F is fairly scattered, and the fit is meaningless. For negative x_F, the distribution is not bad.

η Dependence

The distributions in Fig. 15- Fig. 18 are taken from fits to the various triggers in different hemispheres. In Fig. 19-Fig. 28 I show the results of these fits.

π⁺

Figure 19: JP0 Triggers

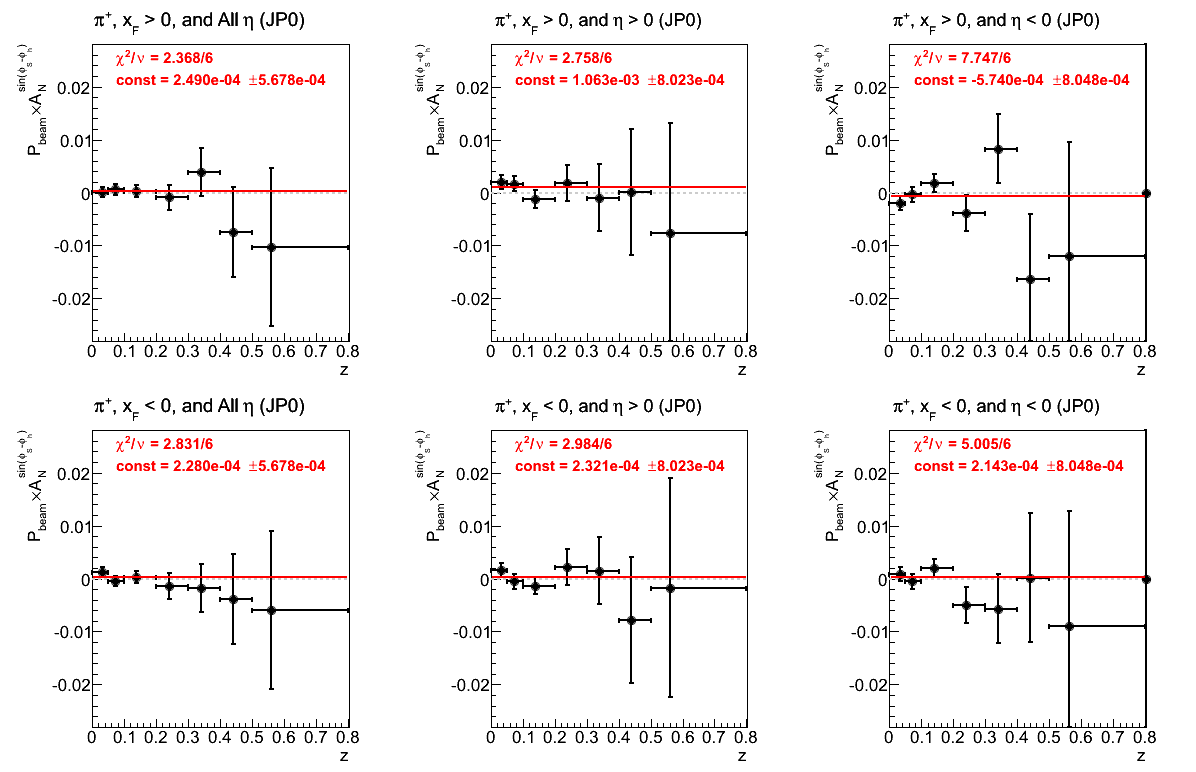
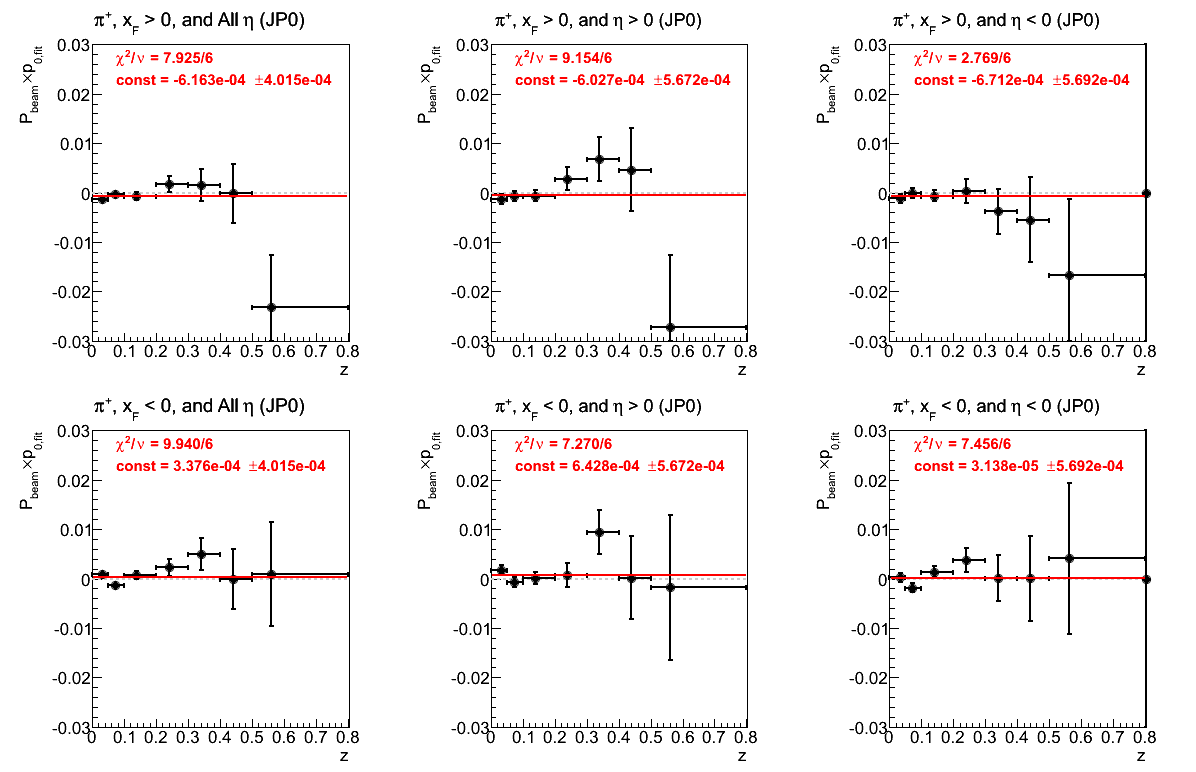
Figure 20: JP1 Triggers

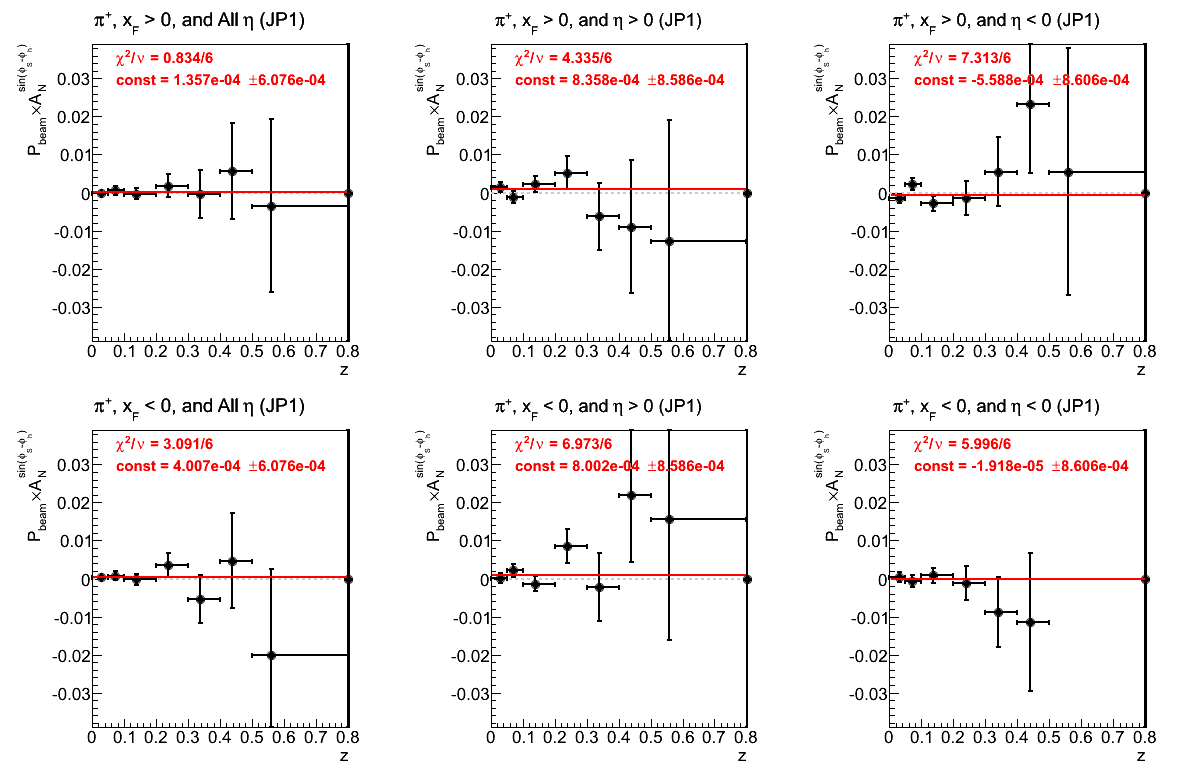
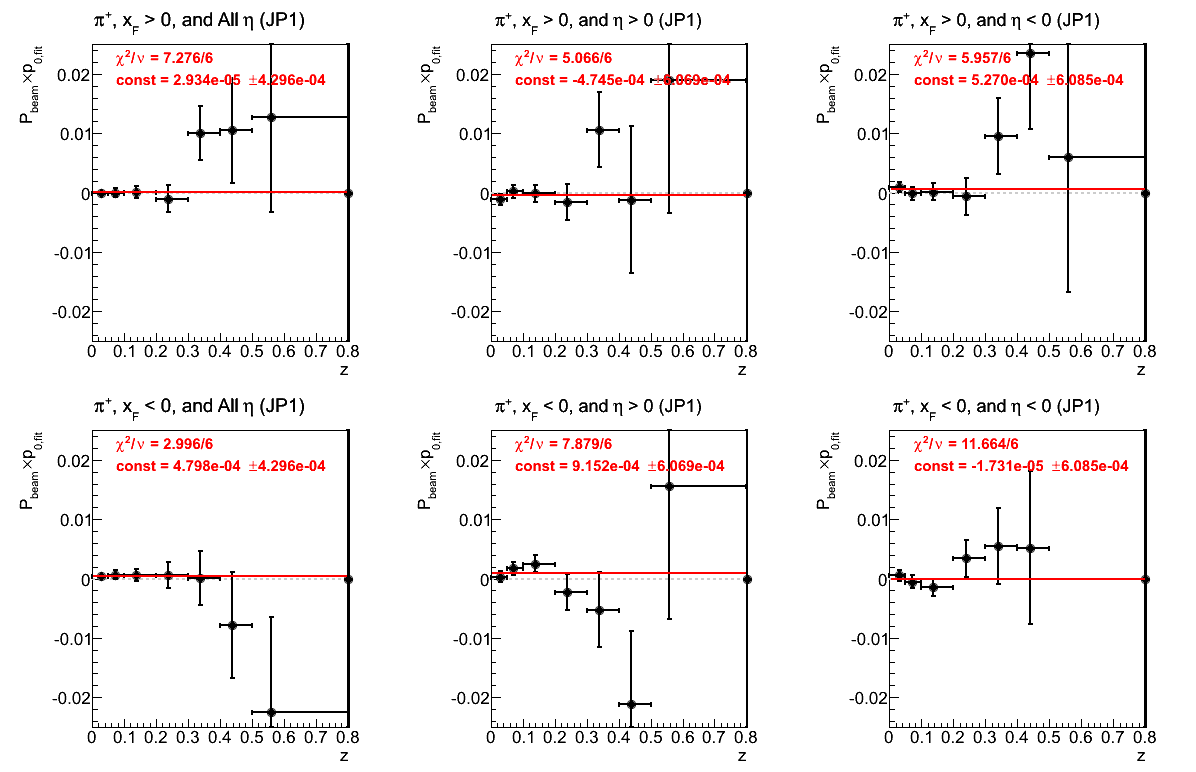
Figure 21: JP2 Triggers

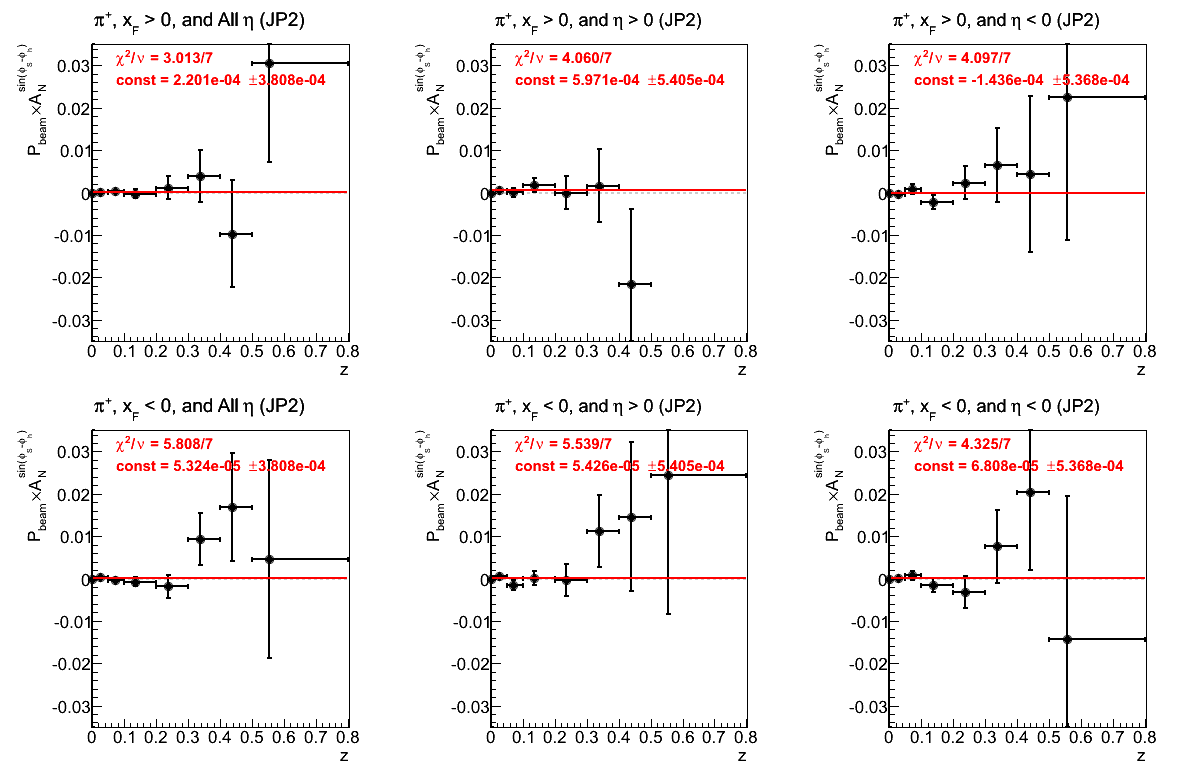
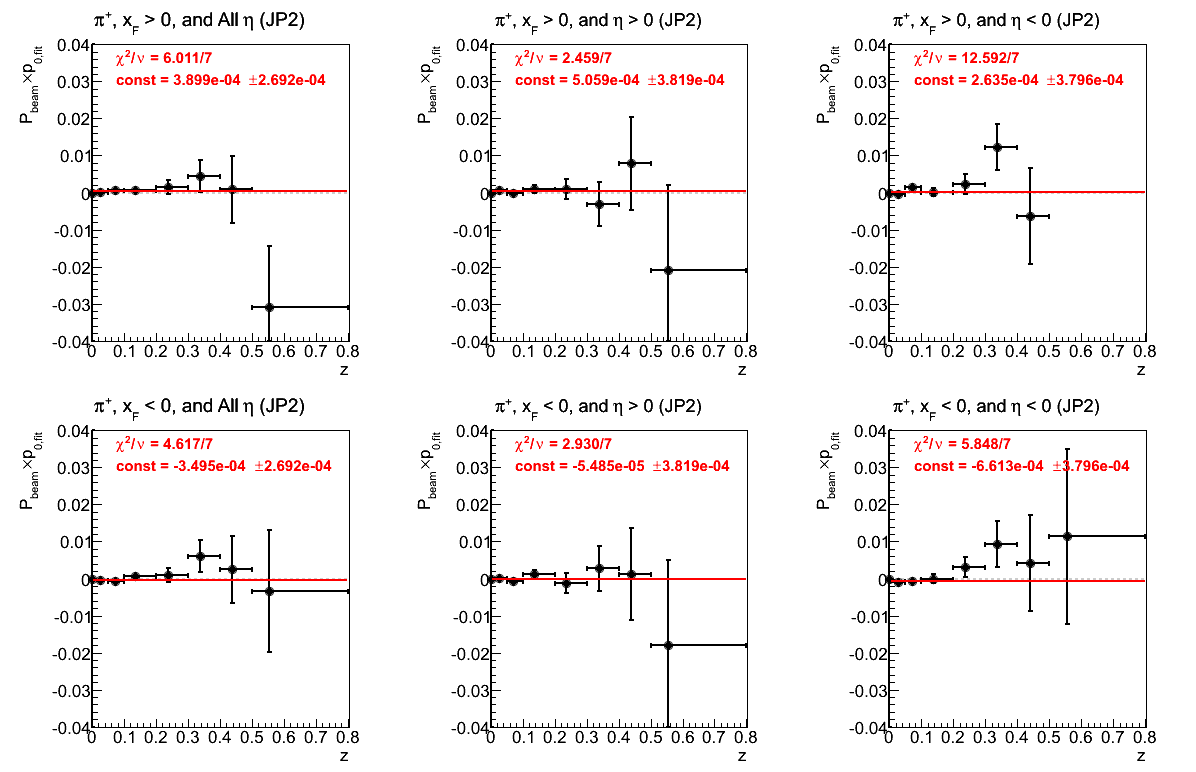
Figure 22: AJP Triggers

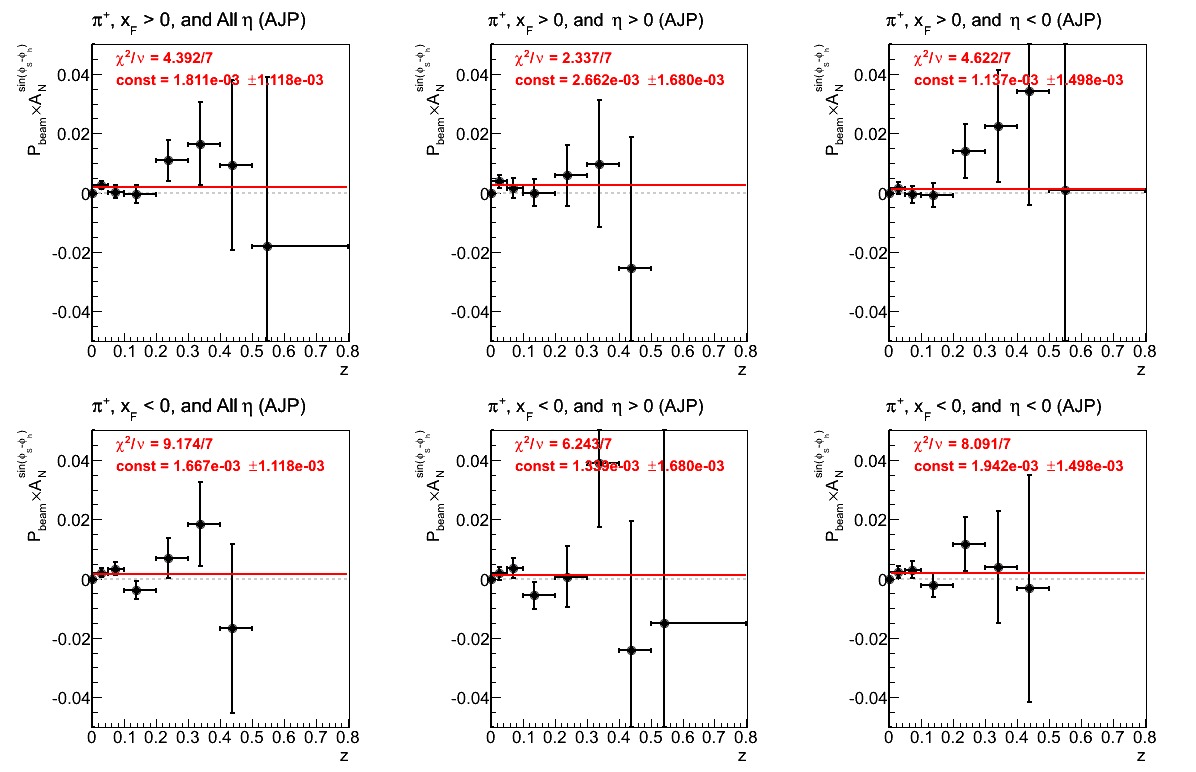
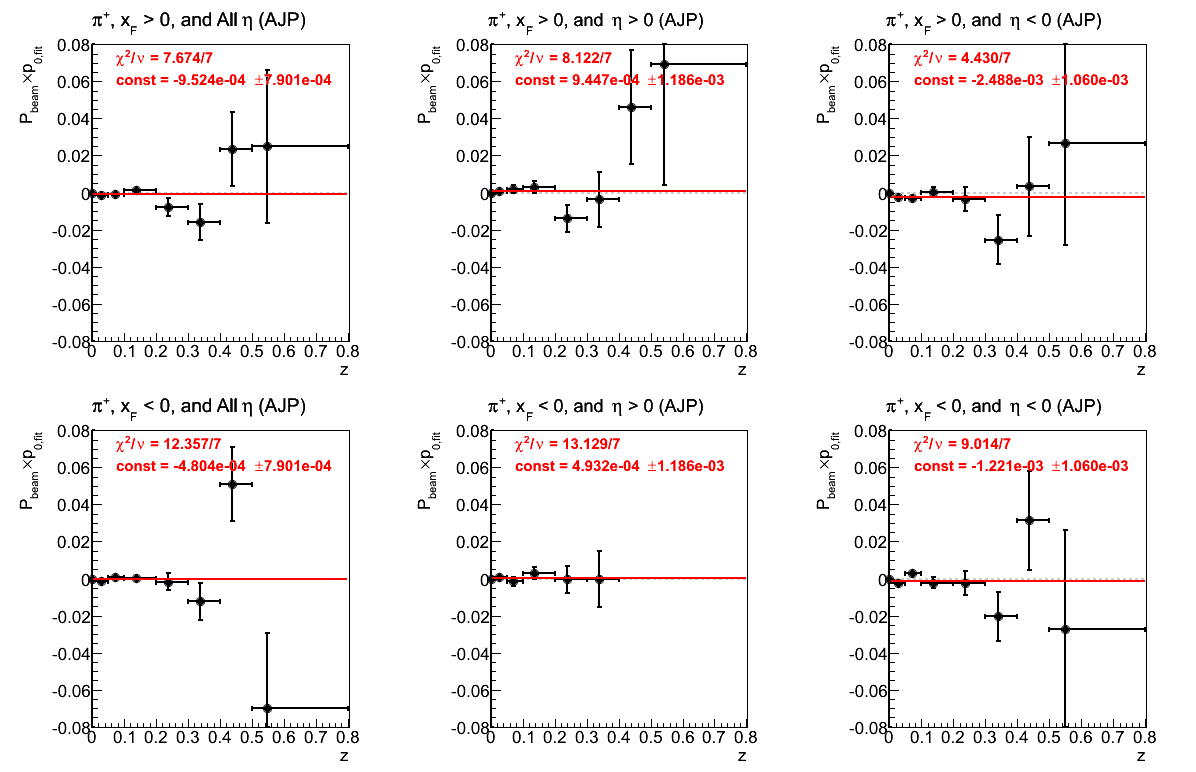
Figure 23: VPDMB Triggers

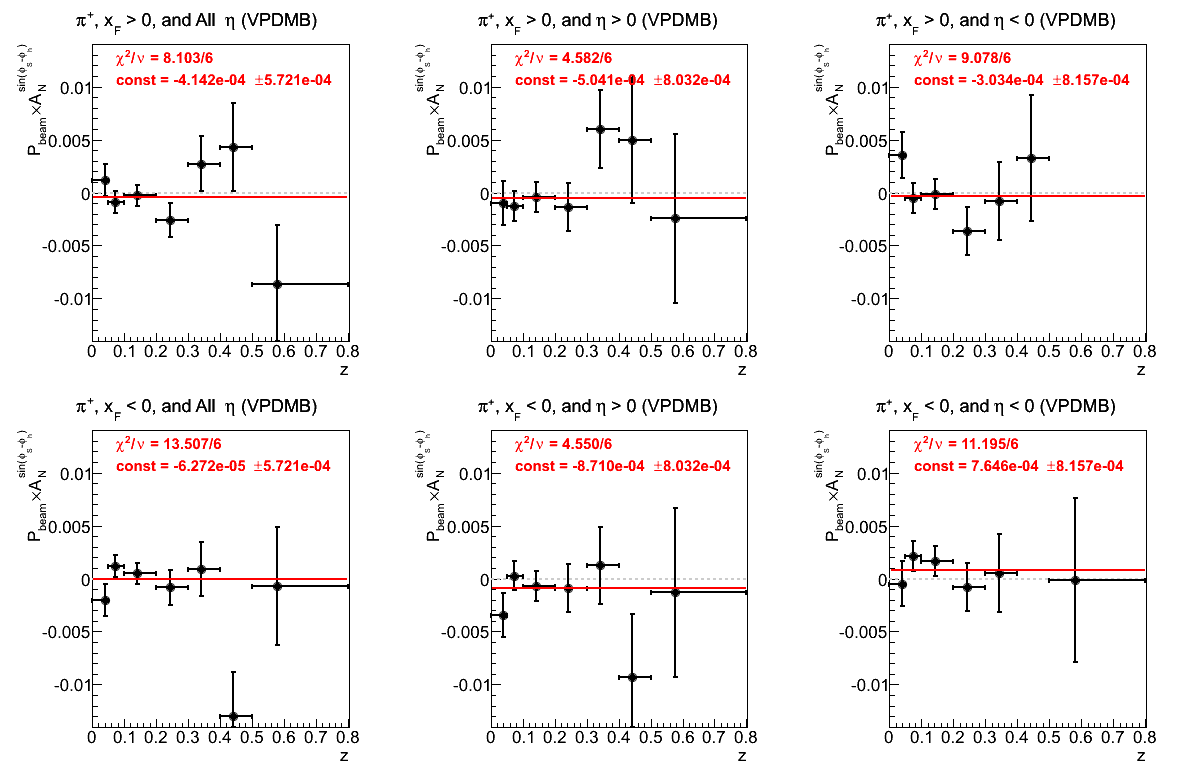
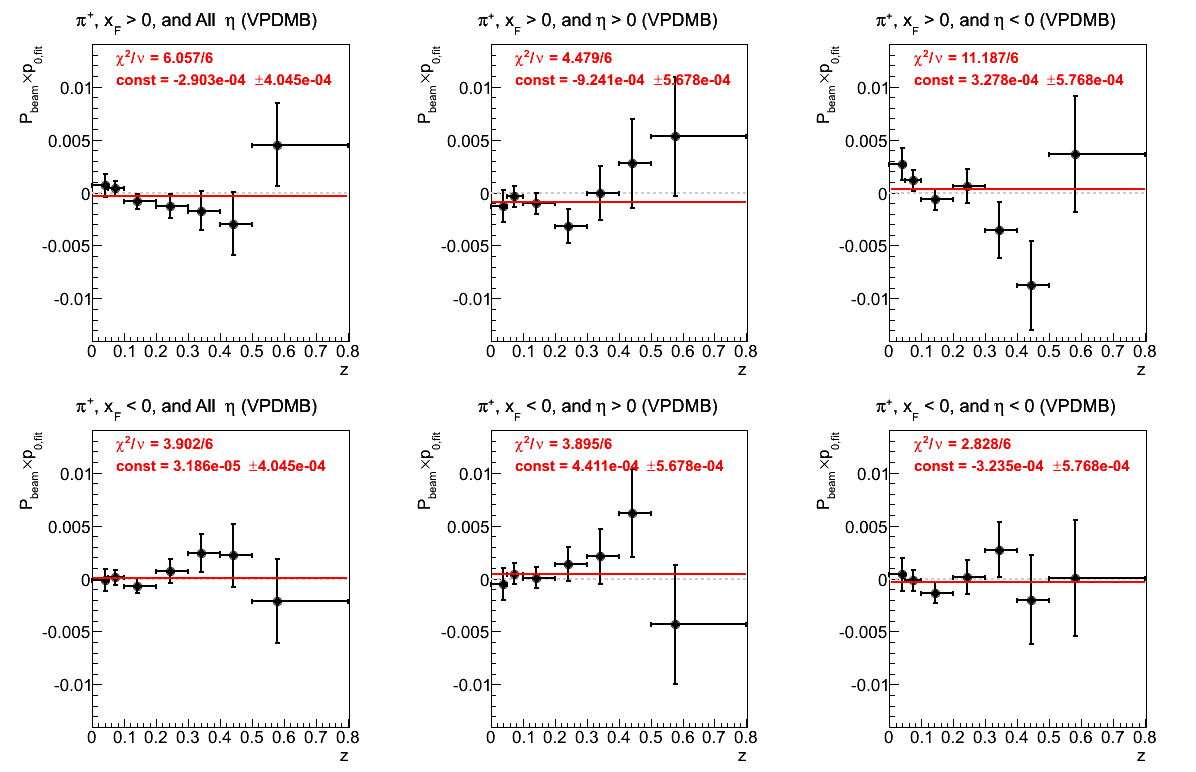
π^-

Figure 24: JP0 Triggers

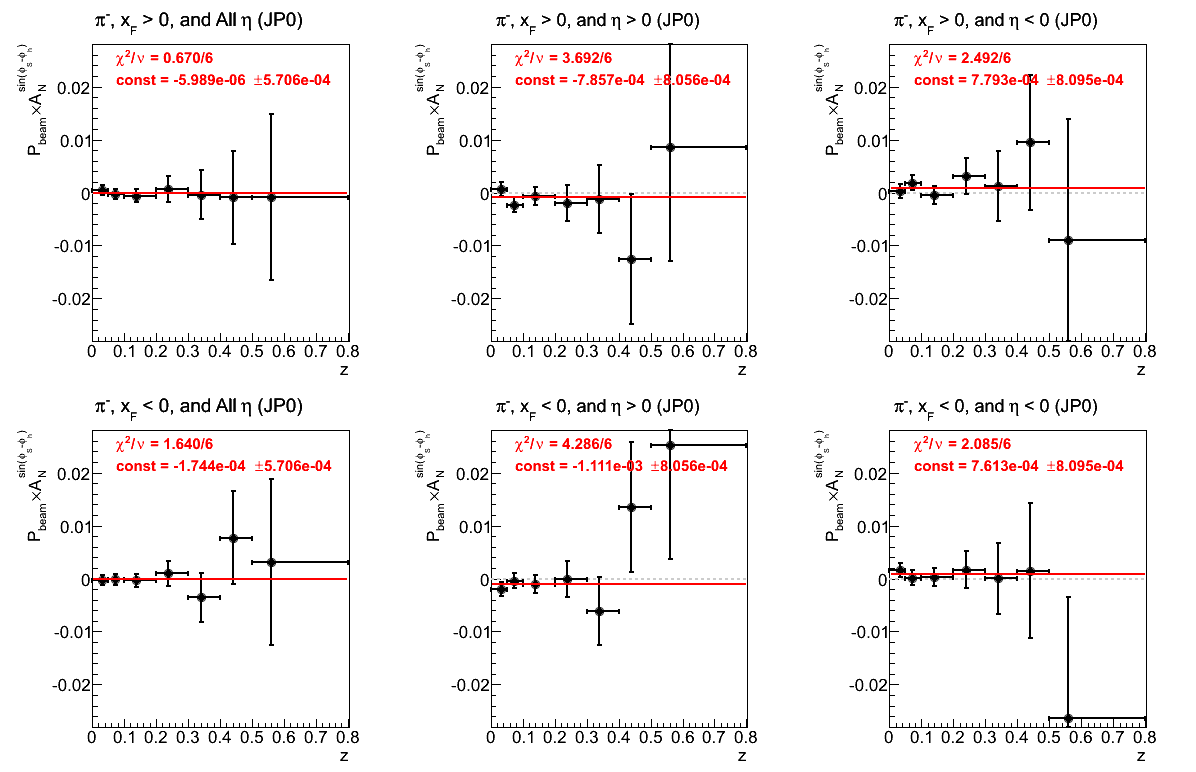
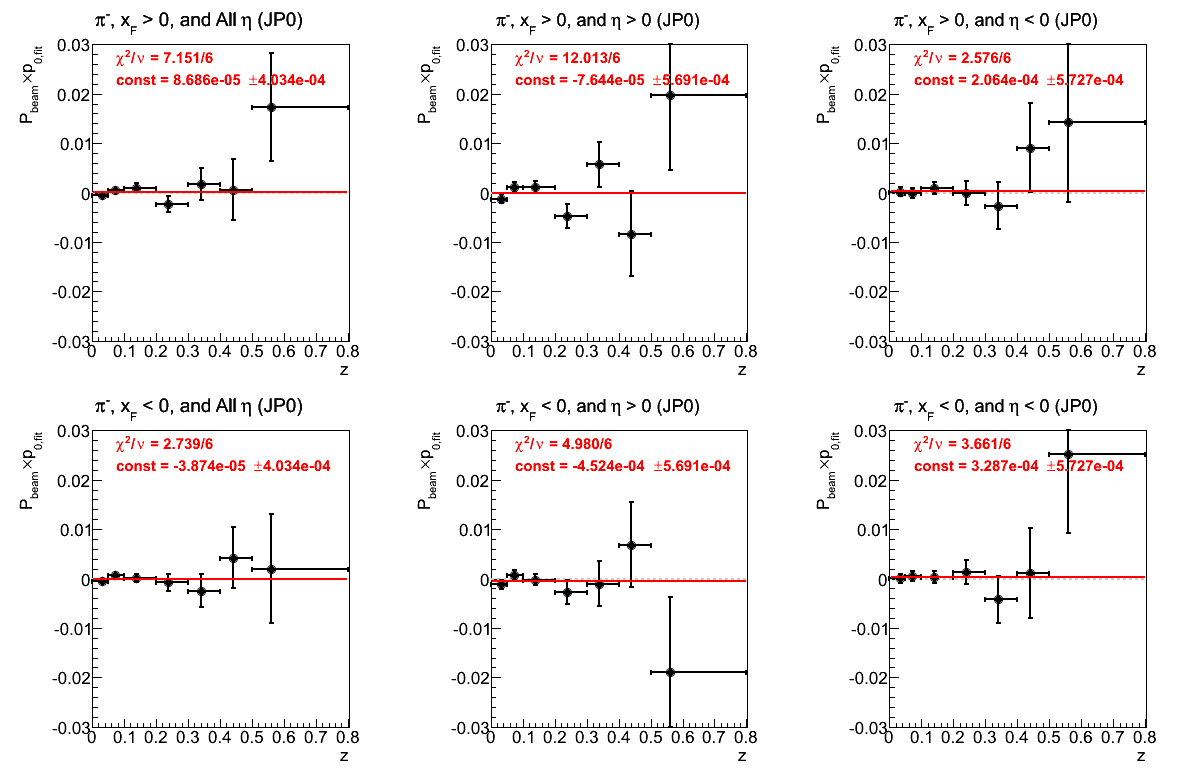
Figure 25: JP1 Triggers

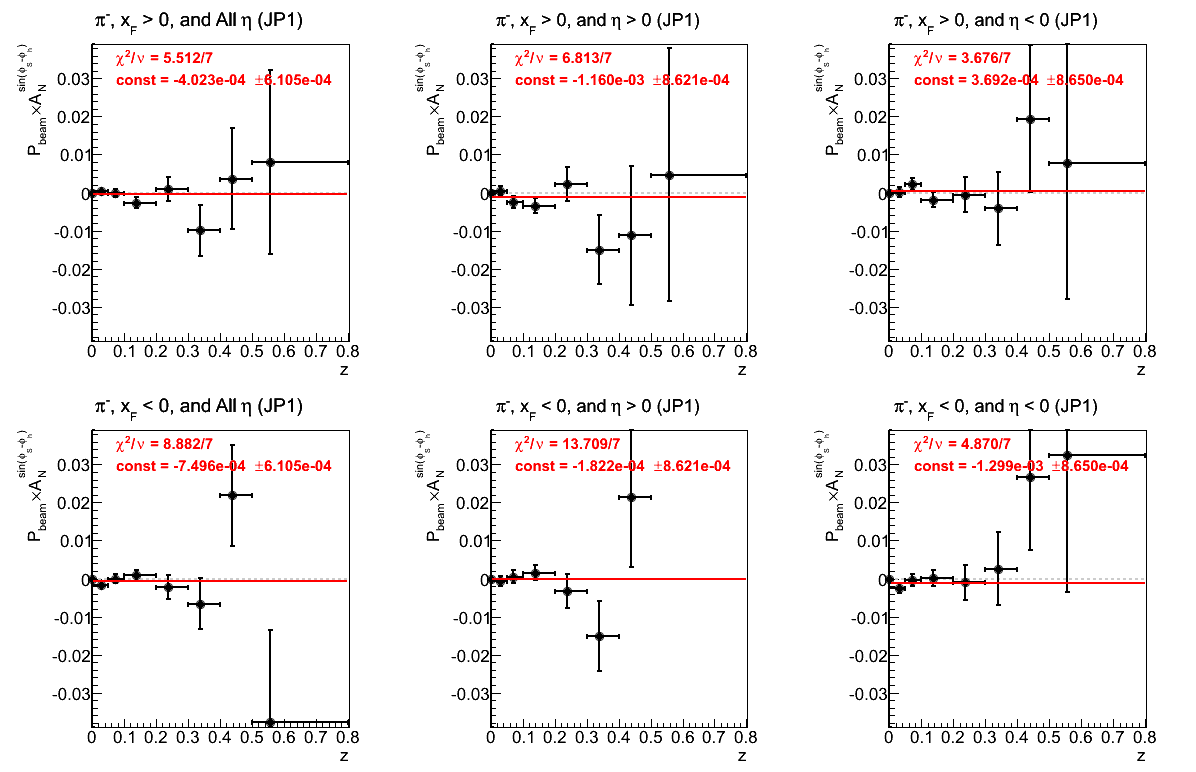
Figure 26: JP2 Triggers

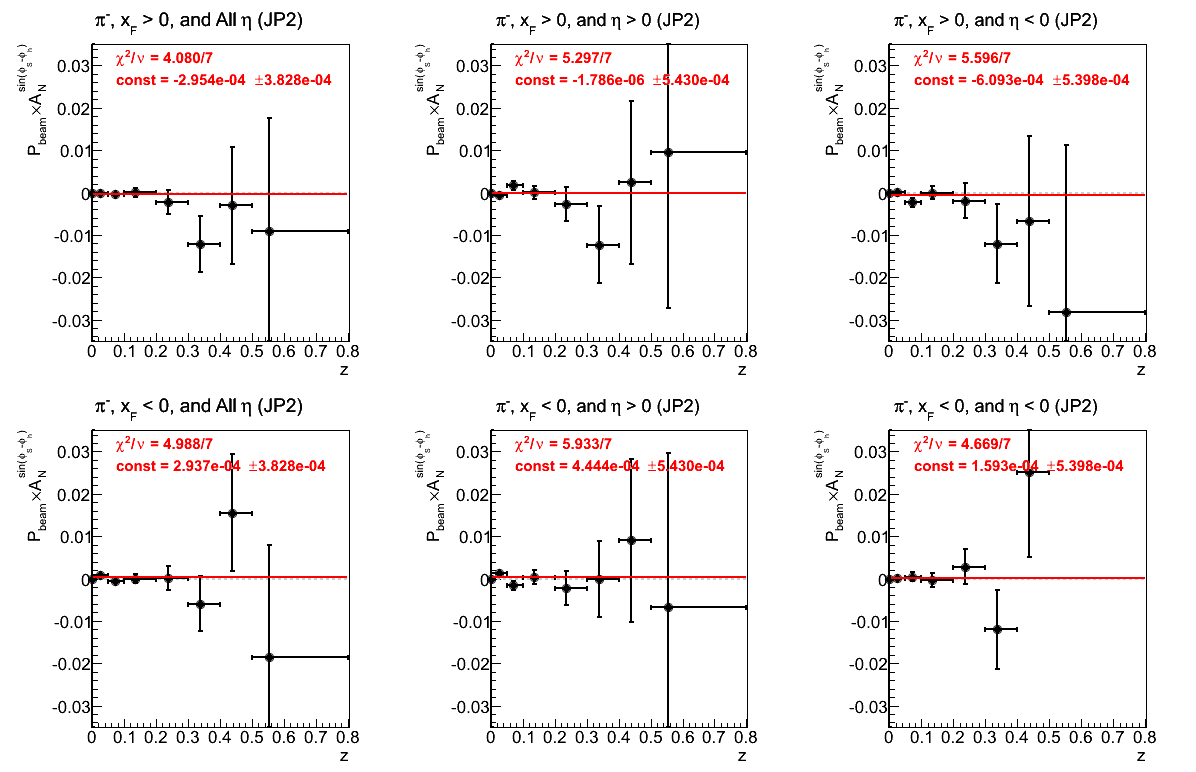
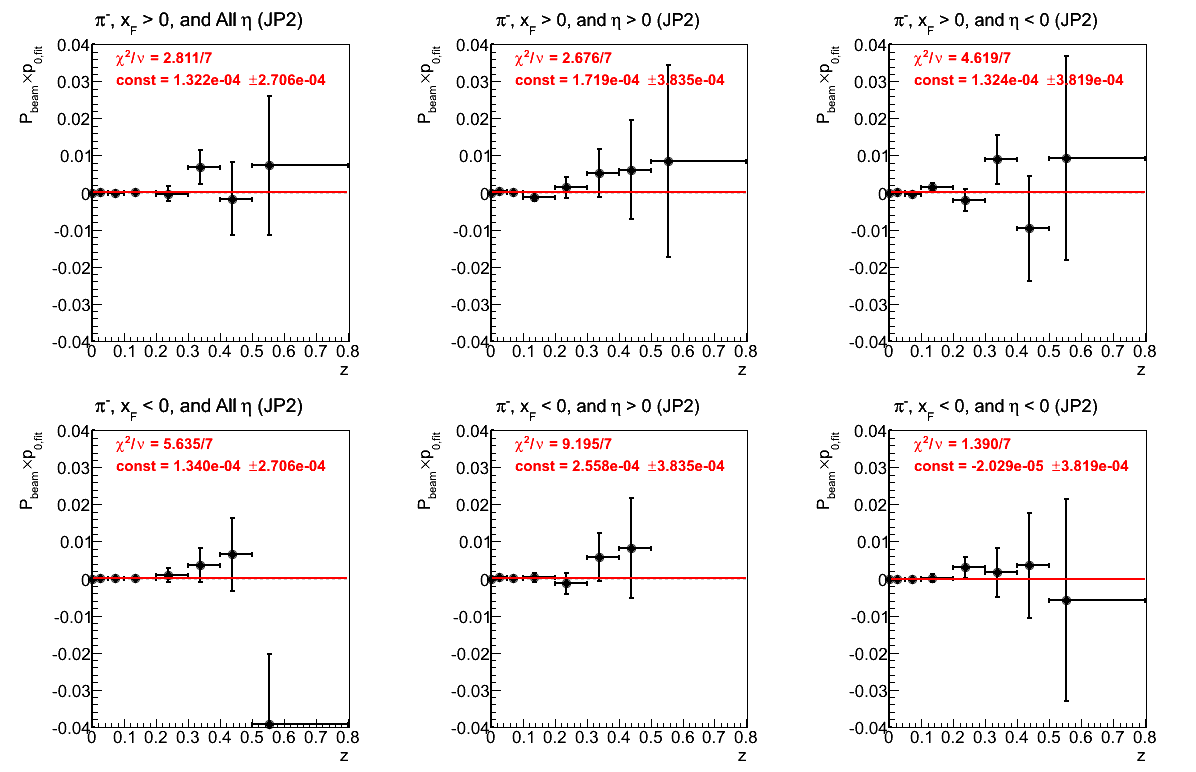
Figure 27: AJP Triggers

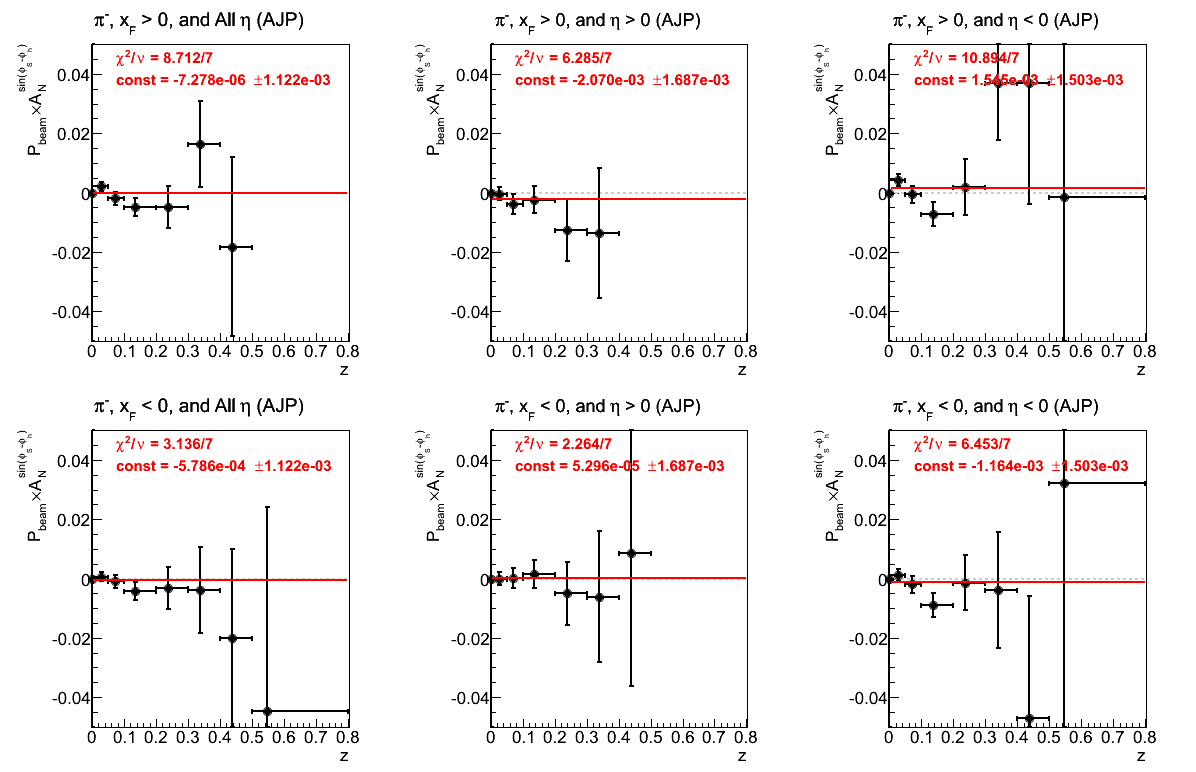
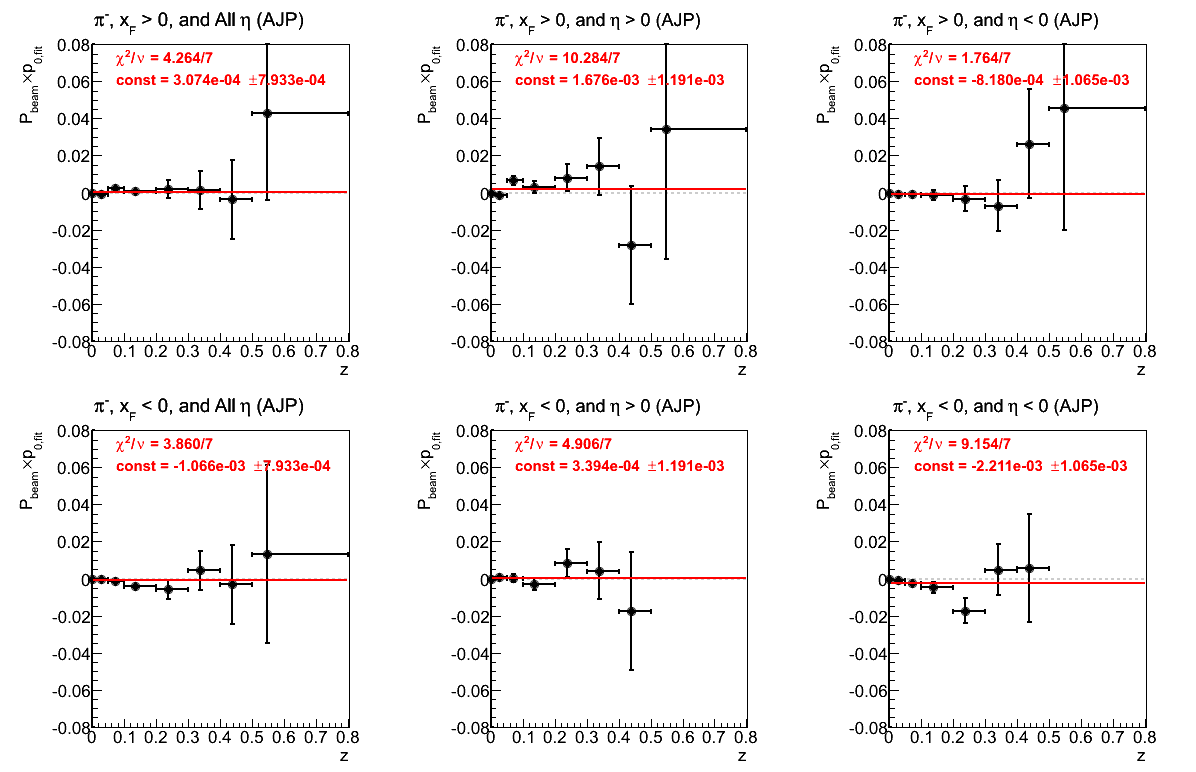
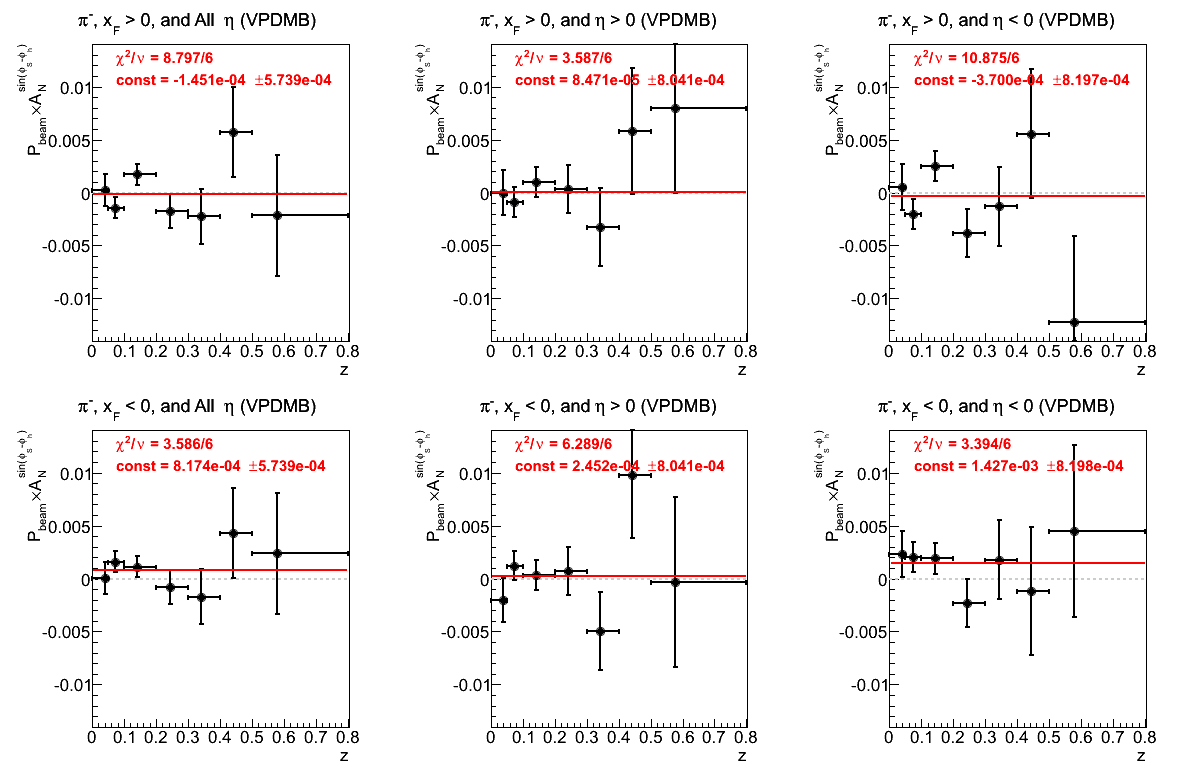
Figure 28: VPDMB Triggers