- drach09's home page
- Posts
- 2022
- 2020
- June (1)
- 2019
- 2018
- 2017
- 2016
- 2015
- 2014
- December (13)
- November (2)
- October (5)
- September (2)
- August (8)
- July (9)
- June (7)
- May (5)
- April (4)
- March (4)
- February (1)
- January (2)
- 2013
- December (2)
- November (8)
- October (5)
- September (12)
- August (5)
- July (2)
- June (3)
- May (4)
- April (8)
- March (10)
- February (9)
- January (11)
- 2012
- 2011
- October (1)
- My blog
- Post new blog entry
- All blogs
Run-11 Transverse Jets: First Look at Collins vs. Track Relative Transverse Momentum (Full Statistics)
Following up on previous updates, I now show the sate of the Collins vs. jT analysis after integrating the full statistics. As before, this should in no way be considered final. Very few cuts have been implemented at this point, and hopefully this analysis will motivate a sensible set.
As before, each plot is fit with a constant. For negative xF and for p0 distributions, this is a sensible expectation. One may hope to see a signal for positive xF, and comparing to a constant may illuminate such a variation.
NOTE: Asymmetries are not corrected for polarization and error bars are statistical only.
Figure 1: Angular Coverage
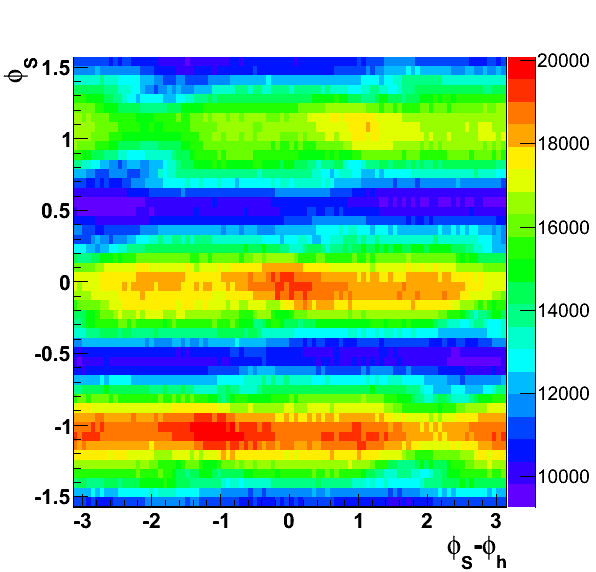
As a reminder, I show the angular coverage of φS vs. φS-φh. One can see the coverage is rather similar to what one sees for the Collins-like angle.
Hemisphere Dependence
One useful check is to examine the asymmetries in the two hemispheres. All things being equal, the answers should be the same. However, I have not implemented a fiducial volume cut (e.g. |η| < 1), so the acceptance is different for the two hemispheres. Likely, I will need to implement such a cut in the near future.
Figure 2: Asymmetry (π+)
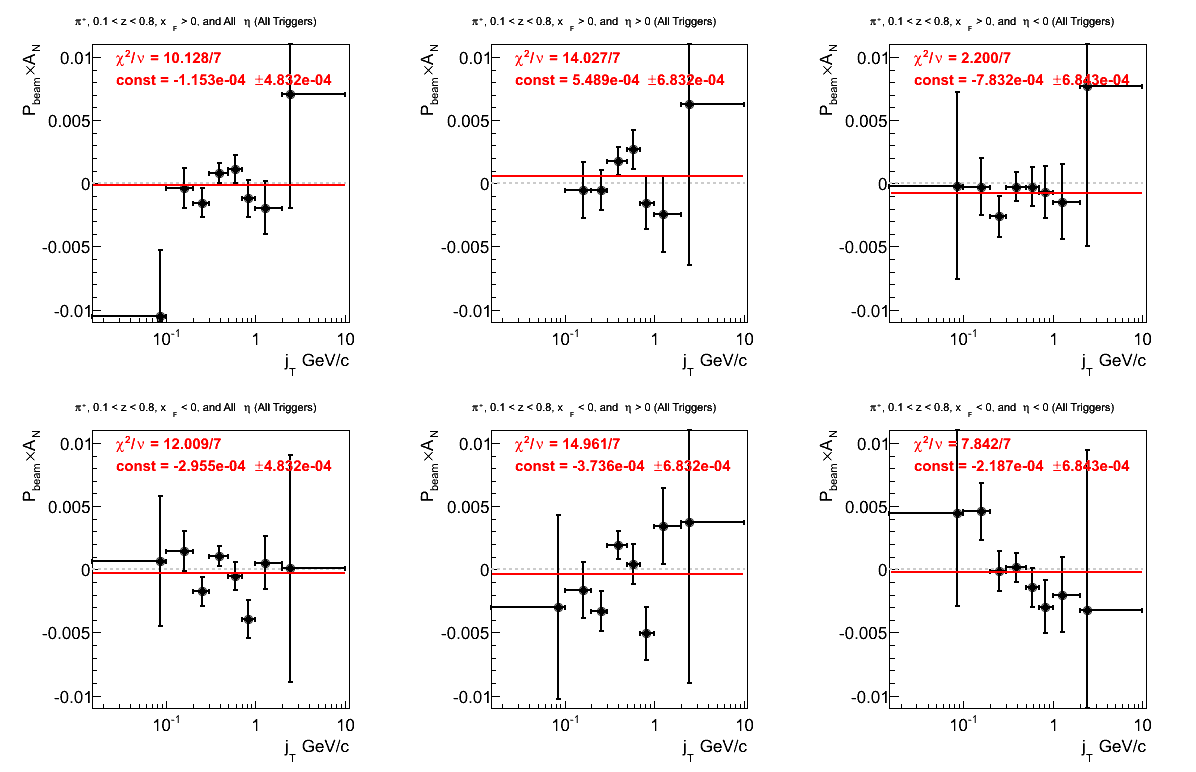
None of the fits are particularly good. While we don't necessarily expect constant behavior for positive xF, the fits for negative xF are espeically troubling.
Figure 3: Asymmetry (π-)
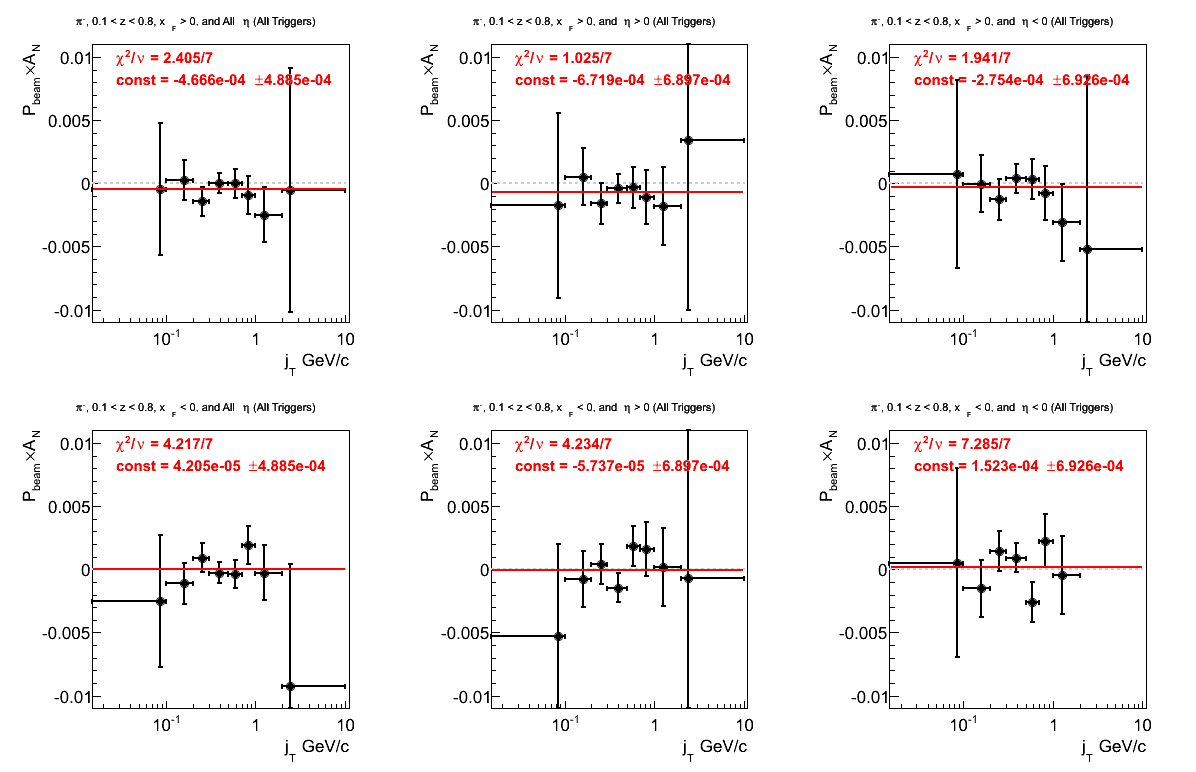
The fits for Fig. 3 are significantly better than those for Fig. 2. No signal appears to be present, however, that may not be entirely suprising.
Figure 4: p0 from Fit (π+)
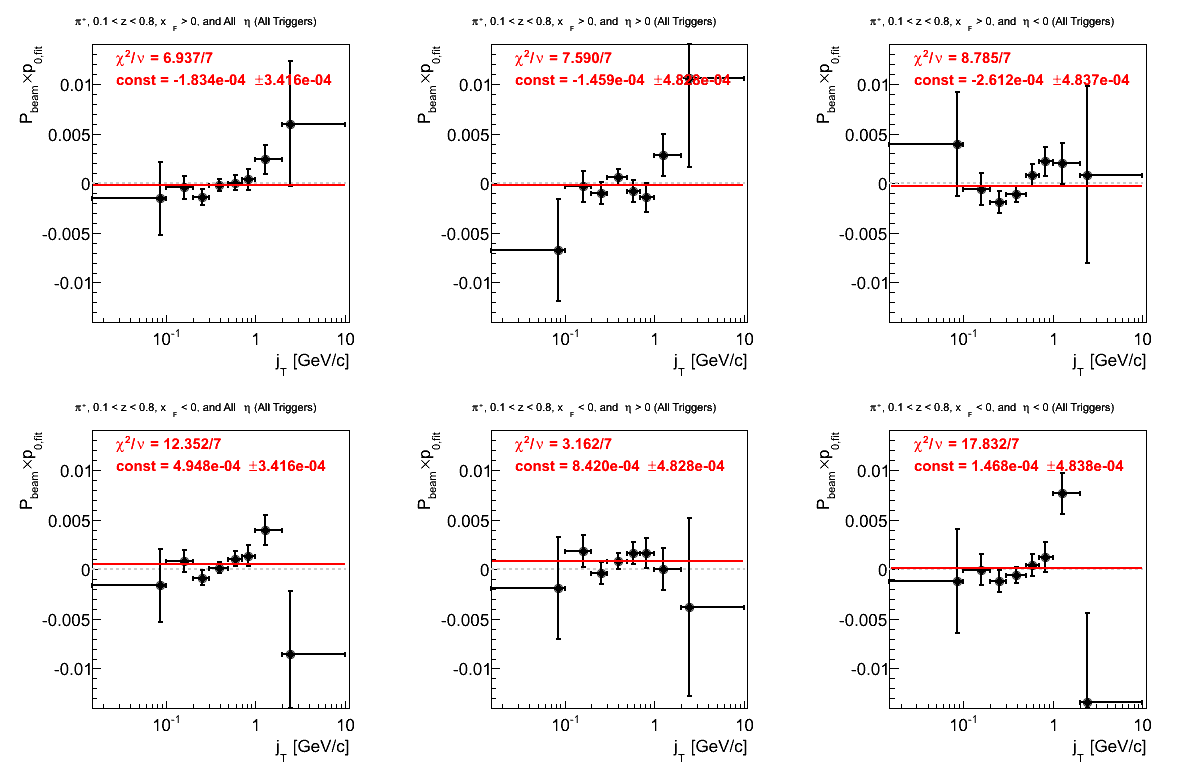
Again, the fits for negative xF are troubling. In this case, it appears the culprit is the negative hemisphere. The positive hemisphere shows a bit of an offset from zero (1.74σ).
Figure 5: p0 from Fit (π-)
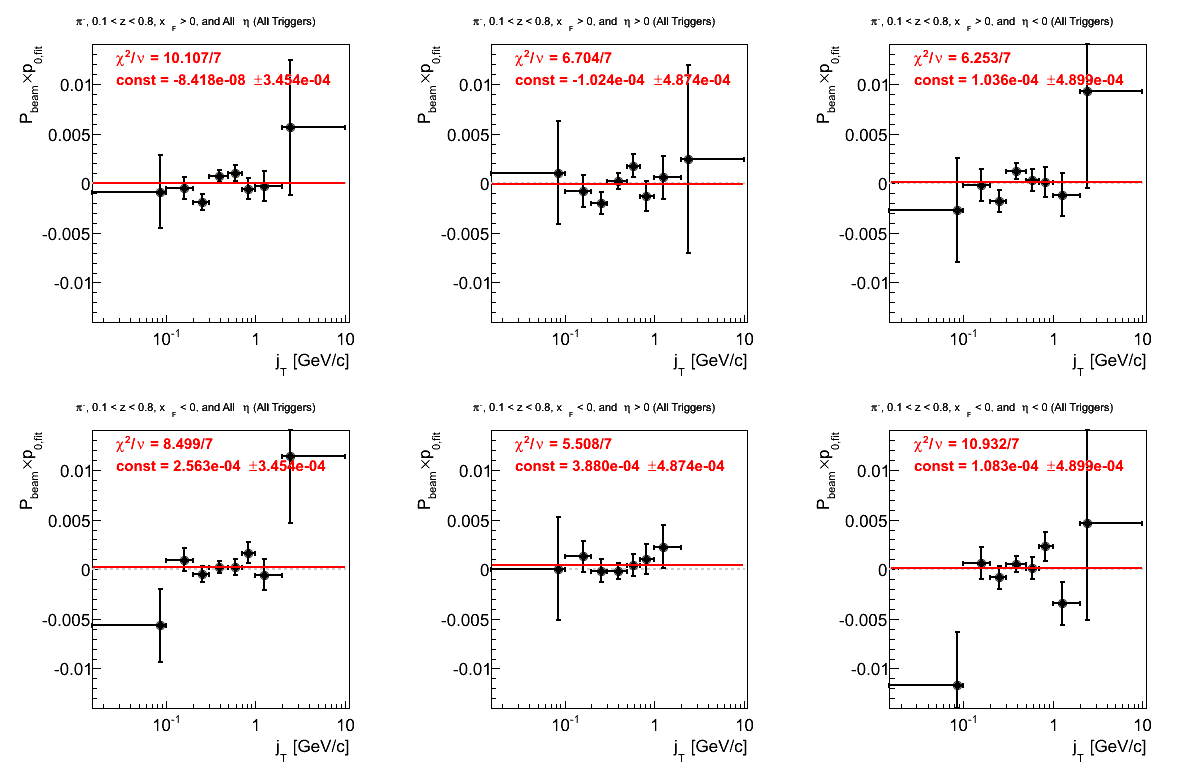
The individual fits for positive xF seem fine, however, the combined fit is a bit worse than one would hope. On the other hand, the combined fit for negative xF is decent, while the fit for the negative hemisphere is quite bad.
Trigger Dependence
It is also useful to examine the calculations for the different triggers. One may expect consistent answers in overlap regions. Wide variations may signal systematic effects.
xF > 0
Figure 6: Asymmetry (π+)
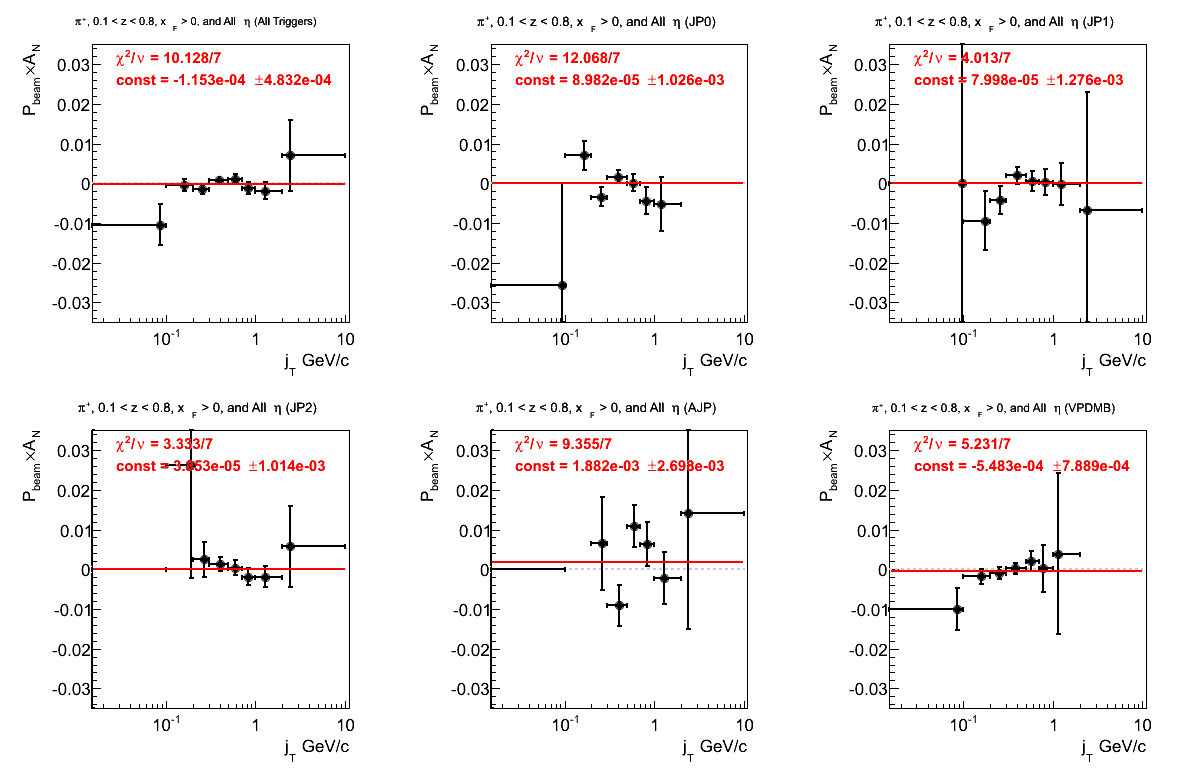
It is difficult to discern a signal trend from these data.
Figure 7: Asymmetry (π-)
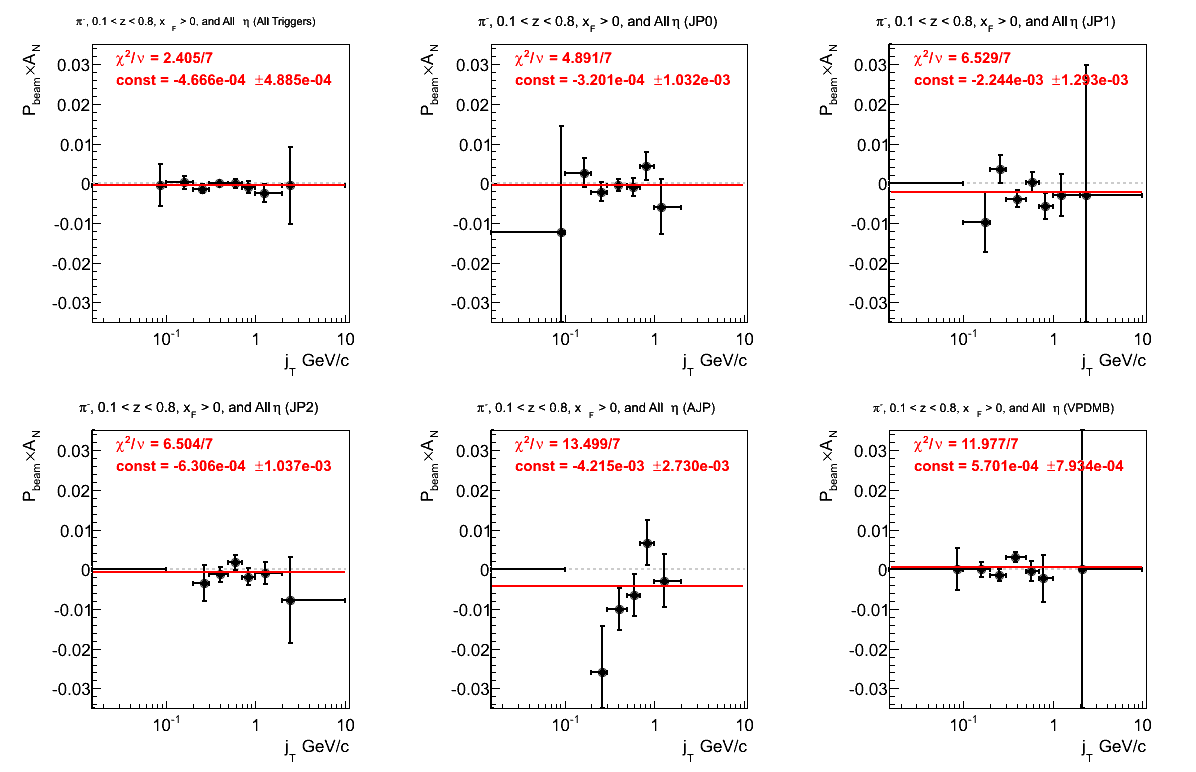
Again, discerning a signal is difficult. Perhaps, one might imagine a bit of a bias toward negative values, but by no means would I say anything conclusive at this stage.
Figure 8: p0 (π+)
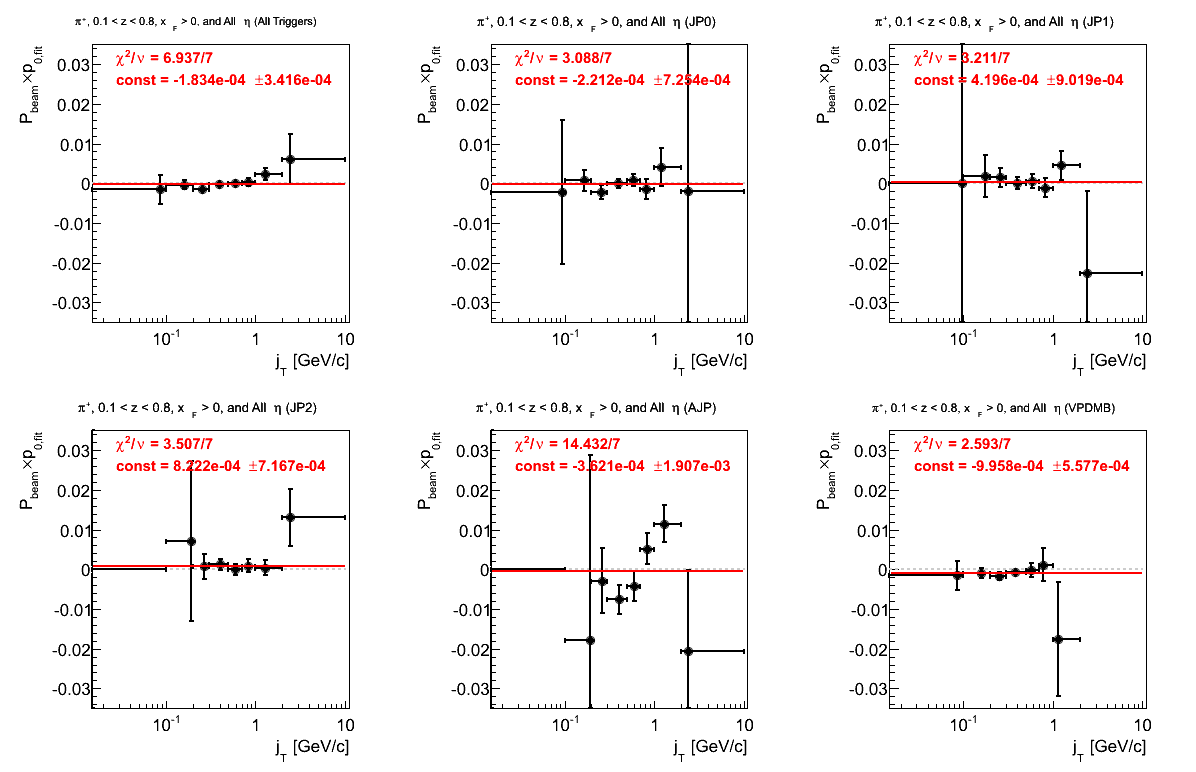
Aside from AJP, the fits are not terrible. There is a bit of an offset in VPDMB but not a large effect (1.79σ).
Figure 9: p0 (π-)
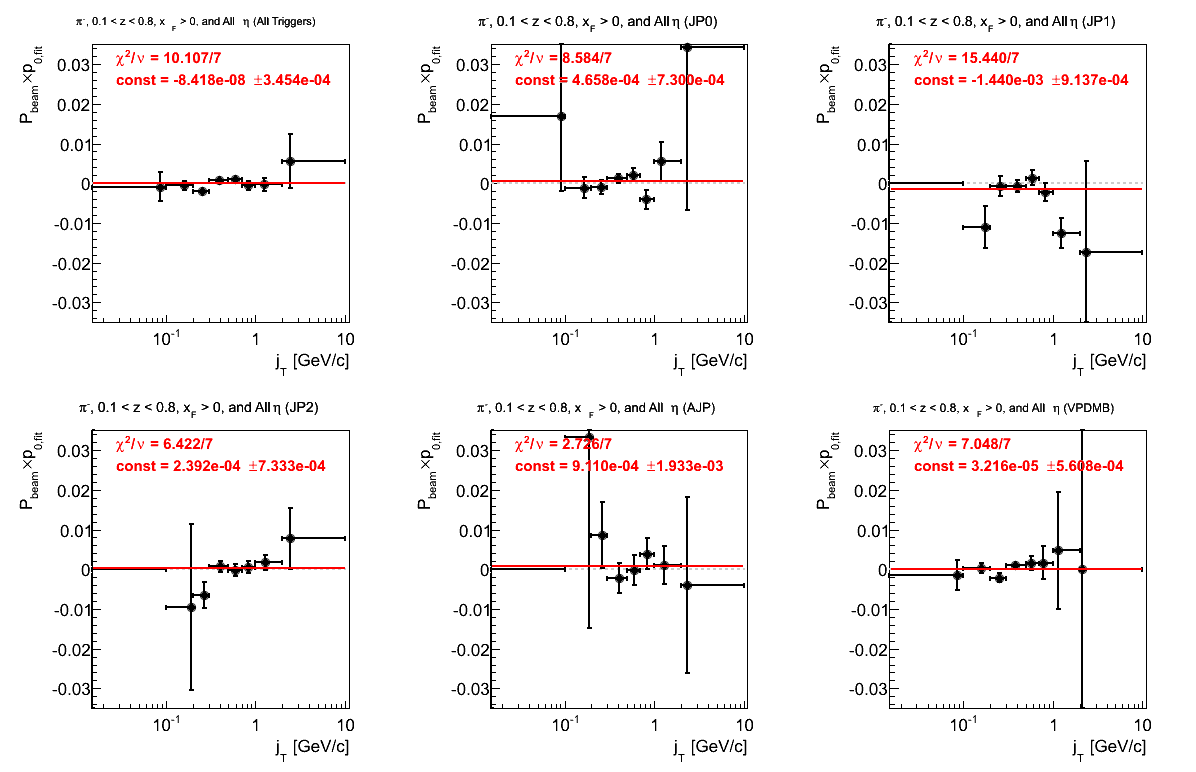
Here, the fit quality seems limited by JP1.
xF < 0
Figure 10: Asymmetry (π+)
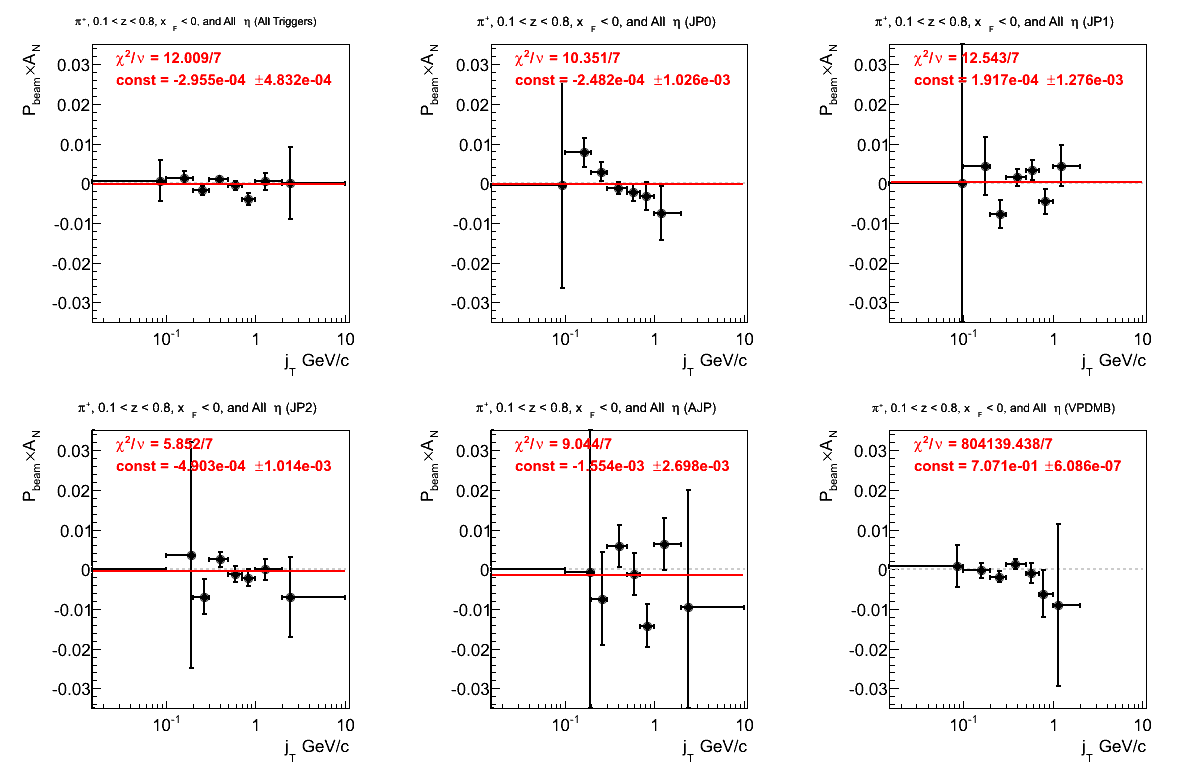
Obviously, something is amiss with VPDMB. Overall, the fit quality is not good.
Figure 11: Asymmetry (π-)
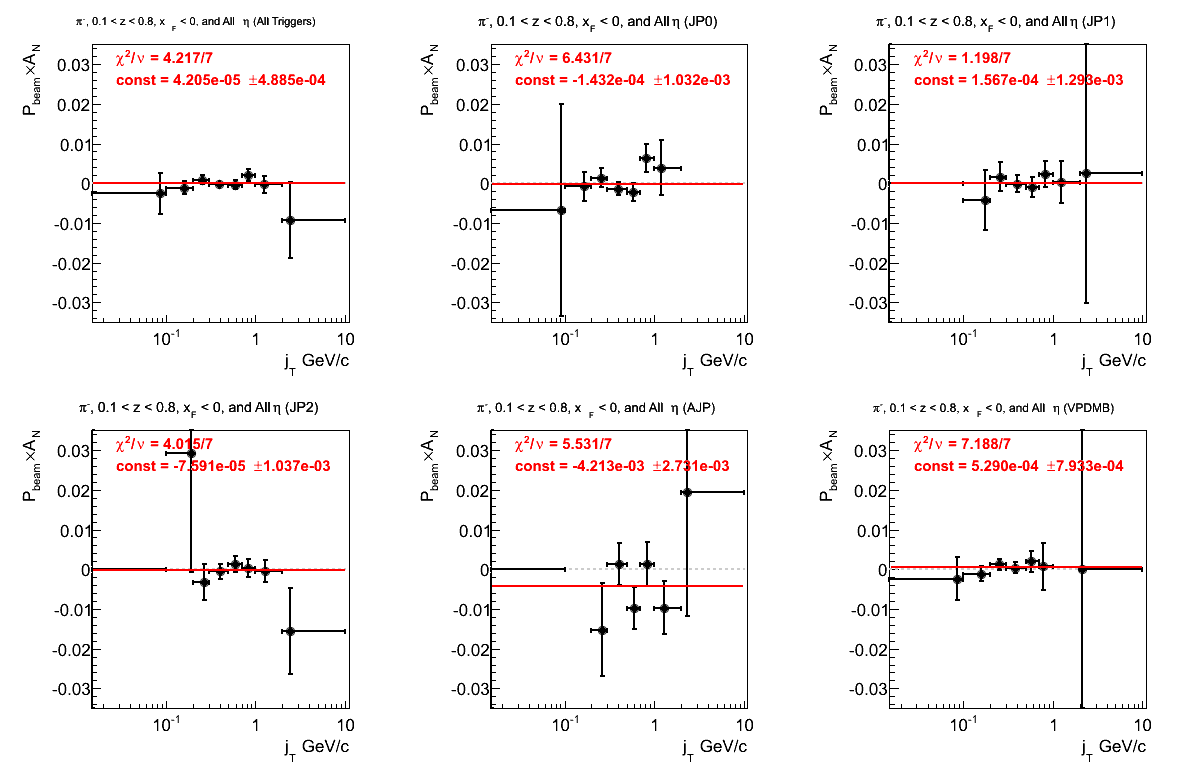
The fits for Fig. 11 are not bad. AJP shows a 1.54σ offset.
Figure 12: p0 (π+)
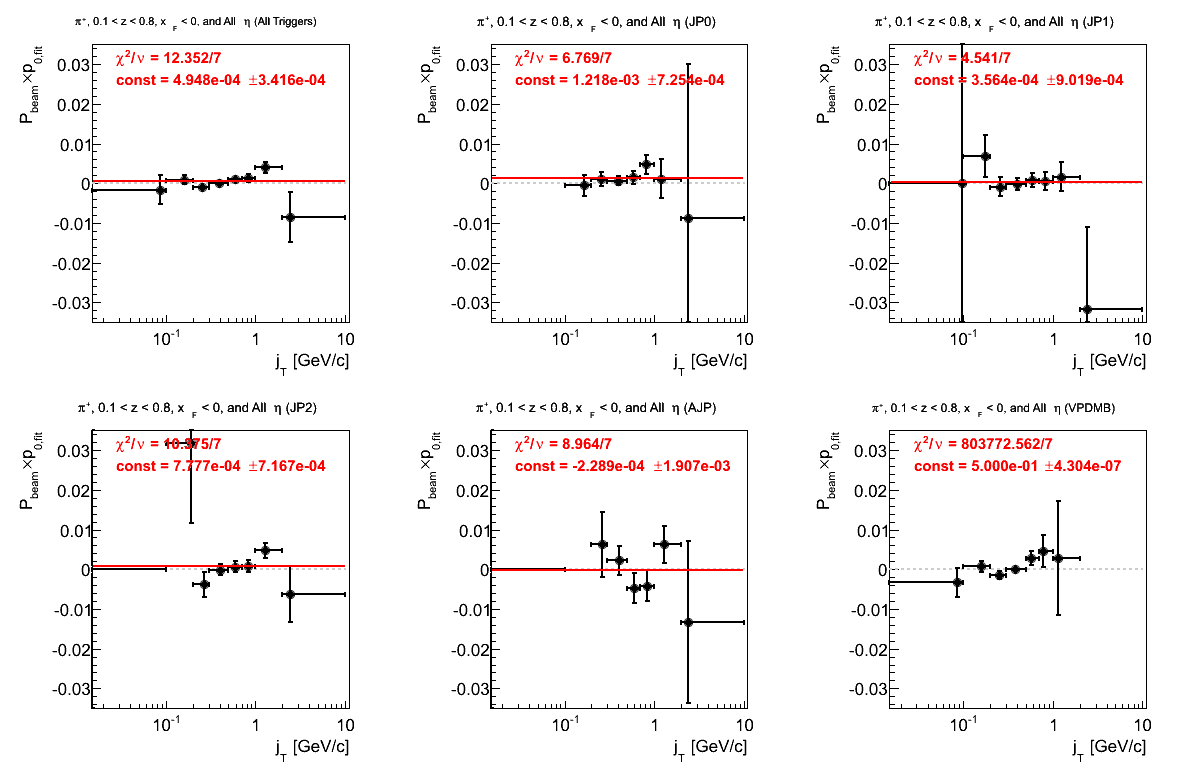
Again, something is not right with VPDMB. The fits for JP2 and AJP are not great.
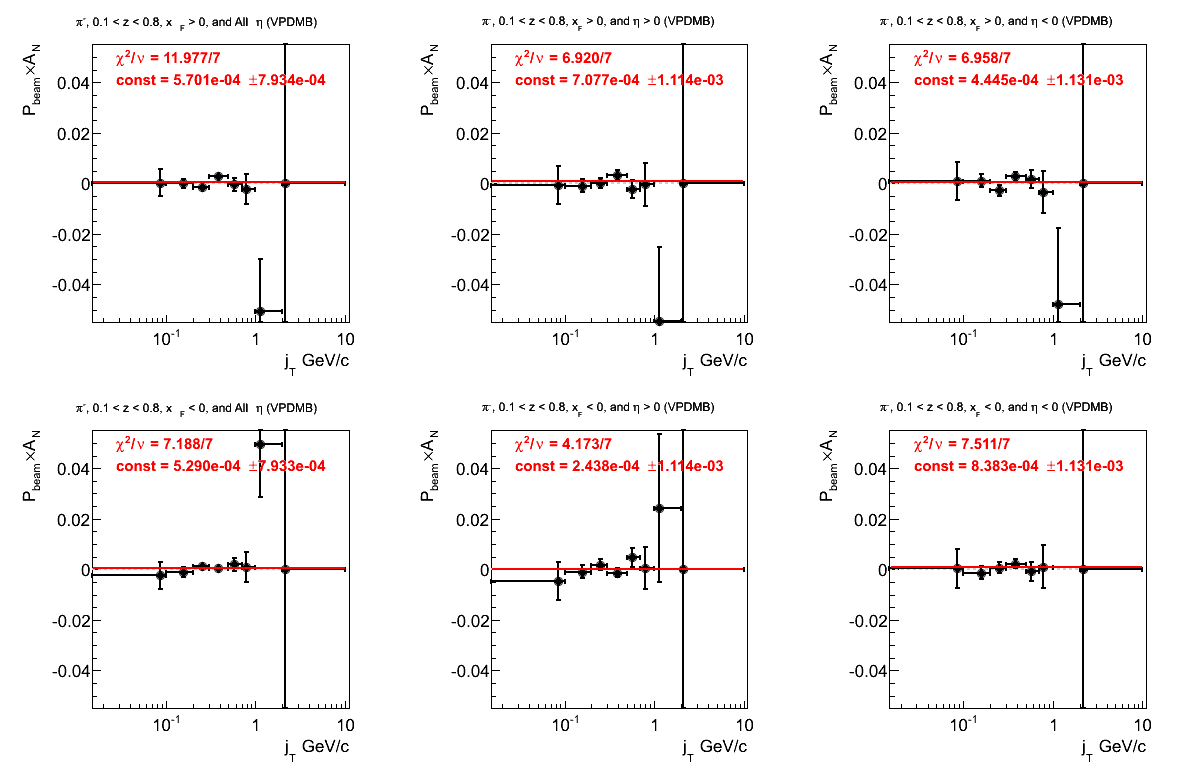
Figure 13: p0 (π-)
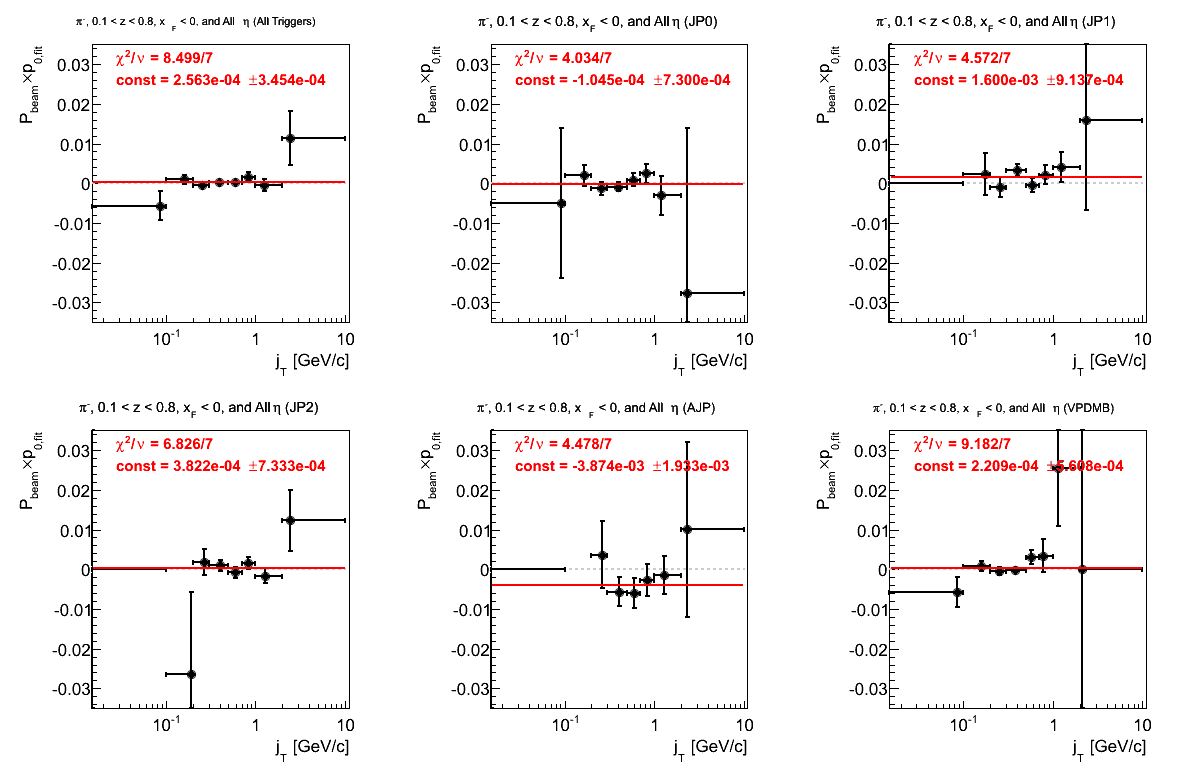
The fit for VPDMB is not great. There is also a 2σ offset in AJP.
Further Statistical Cross-checks
Figure 14: χ2-Distribution for Collins-like Fits
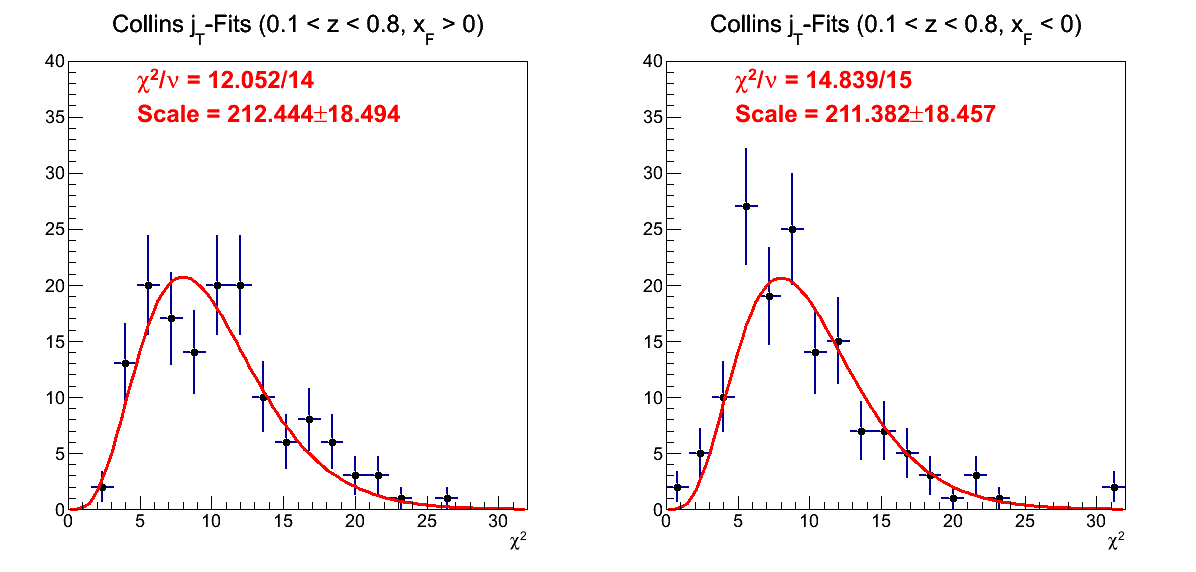
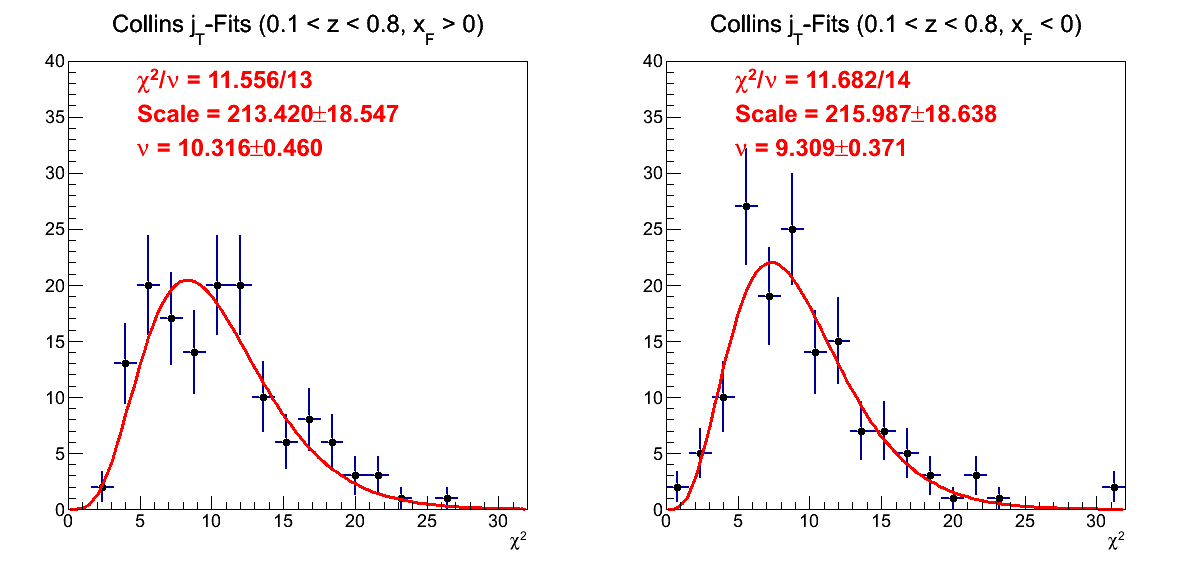
Figure 14 shows the χ2 distribution for the Collins fits (p0+p1×sin(φS-φh)). In red is plotted the expected distribution. On top, the distribution is forced to have ν = 10; and the agreement with expectation is quite good. On bottom, the fit allows ν to float. The fits are of fine quality, and ν is found to be close to the expected value (< 1σ for positive xF and 1.86σ for negative xF).
Distribution of Constant Fits
Figure 15: Asymmetry Fits
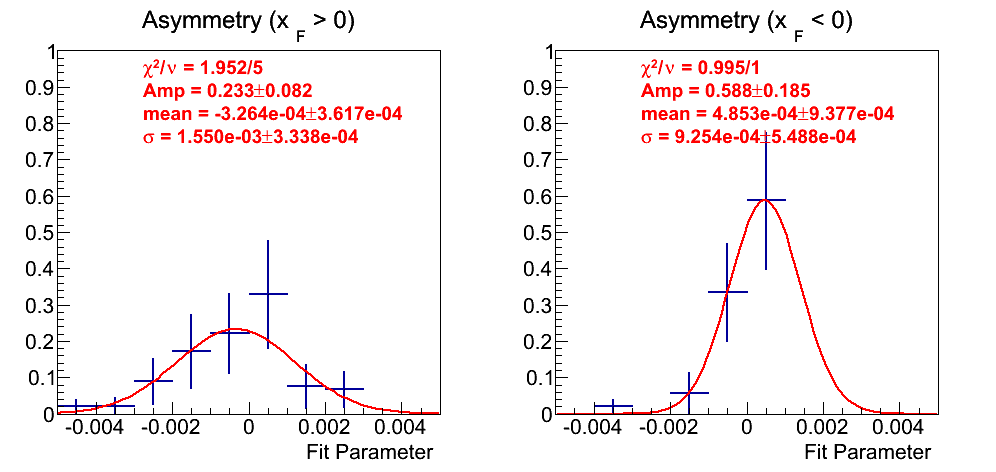
In Fig. 15 I show the distribution of constant fits to the asymmetries weighting the entries by 1/uncertainty. There simply are not many fits, thus, it is difficult to glean much information. The distributions are fit with a Gaussian. Thes fits show means consistent with zero and similar widths.
Figure 16: p0 Fits
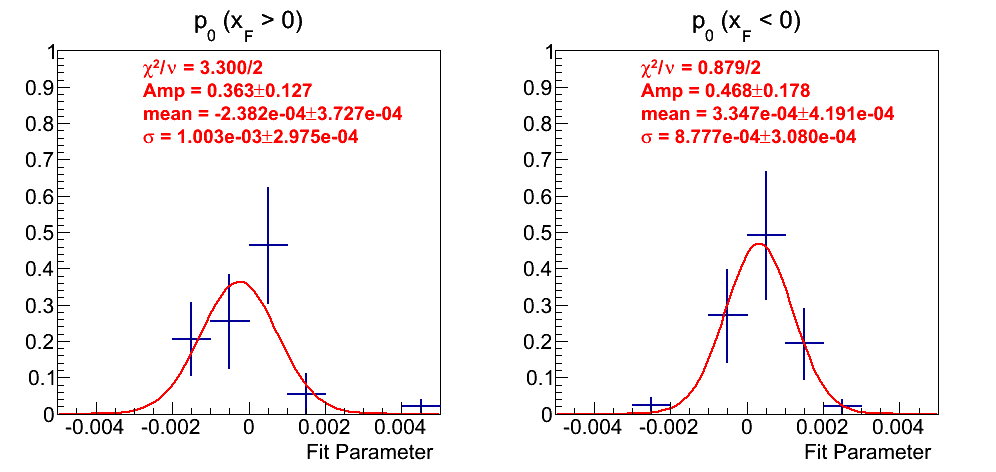
In Fig. 16, I show the weighted distribution for fits to the p0's. Again, there are not many fits from which to draw. The fits appear decently Gaussian with means consistent with zero and similar widths.
Reduced χ2 of Constant Fits
With such a low number of fits with varying degrees of freedom, it is impossible to perform a χ2 study of the constant fits. However, we can examine the reduced χ2's for some information. The distribution for the asymmetries was simply too scattered for this study, so it has been excluded.
Figure 17: p0 Fits
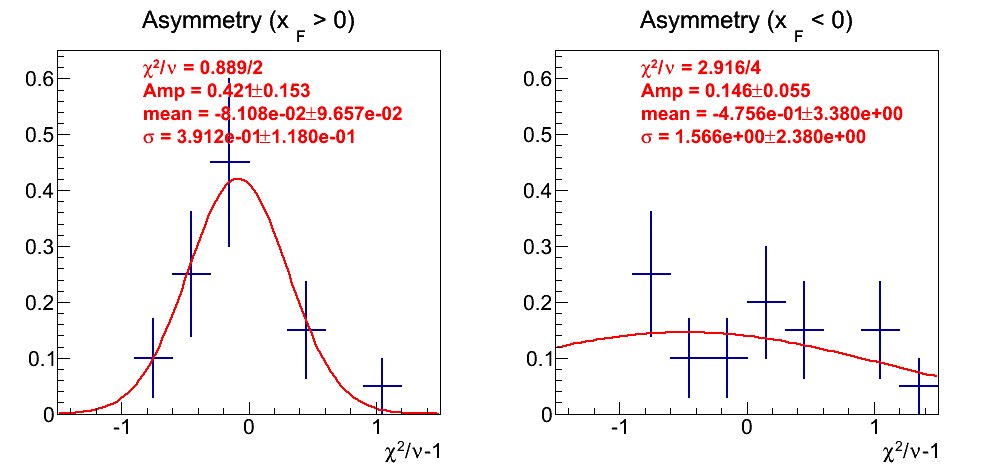
The distribution for negative xF is not very informative. The uncertainties in positive xF are large, but the fitted mean is consistent with zero.
Figure 18: p0 Fits
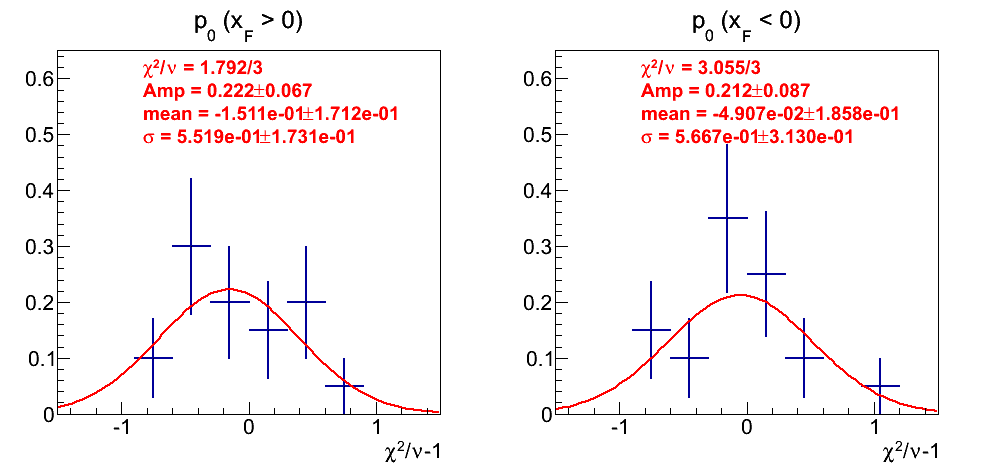
The distribution of fits to p0's is somewhat better than the asymmetries. The uncertainties are large, but the fitted means are consistent with zero and the widths are consistent.
η Dependence
The distributions in Fig. 15- Fig. 18 are taken from fits to the various triggers in different hemispheres. In Fig. 19-Fig. 28 I show the results of these fits.
π+
Figure 19: JP0 Triggers
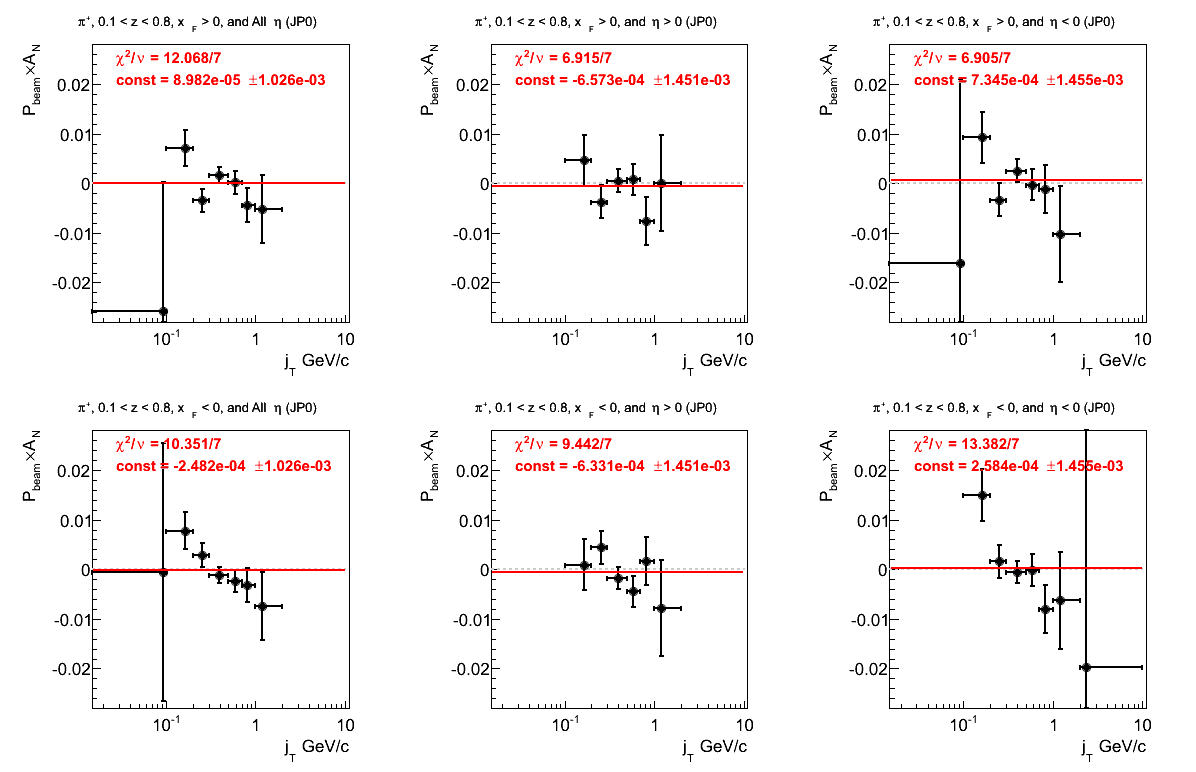
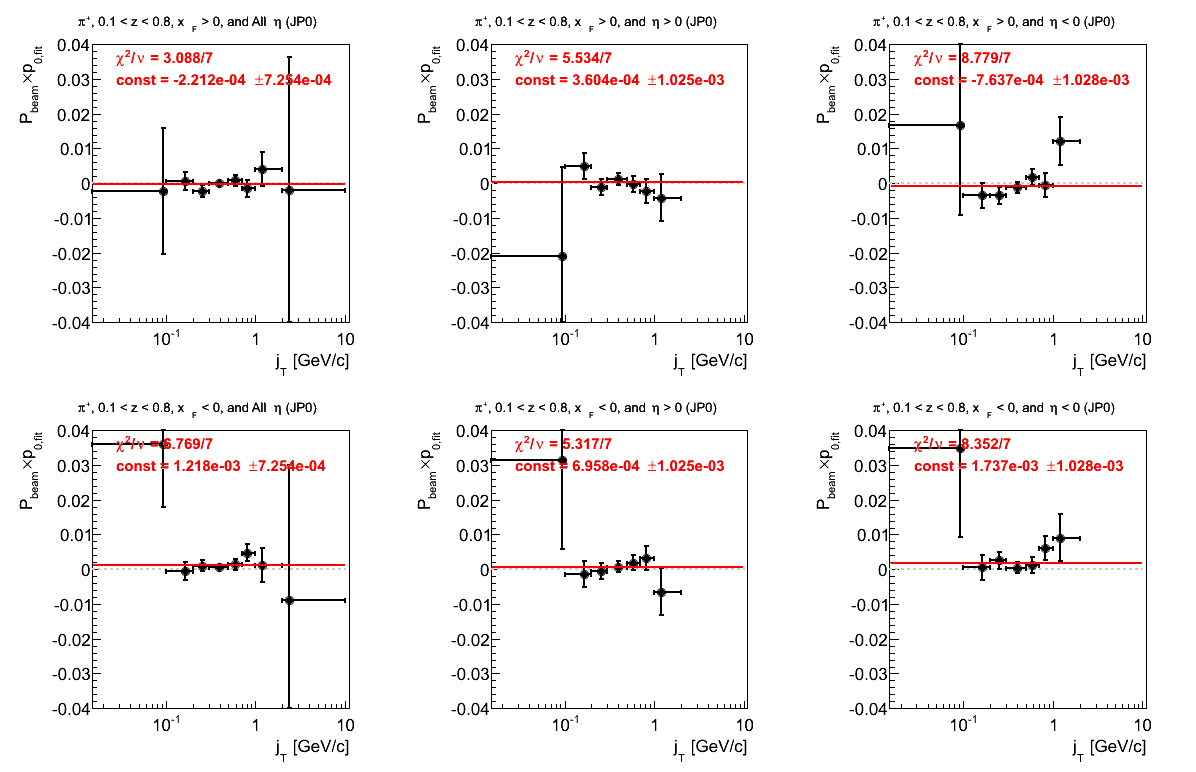
Figure 20: JP1 Triggers
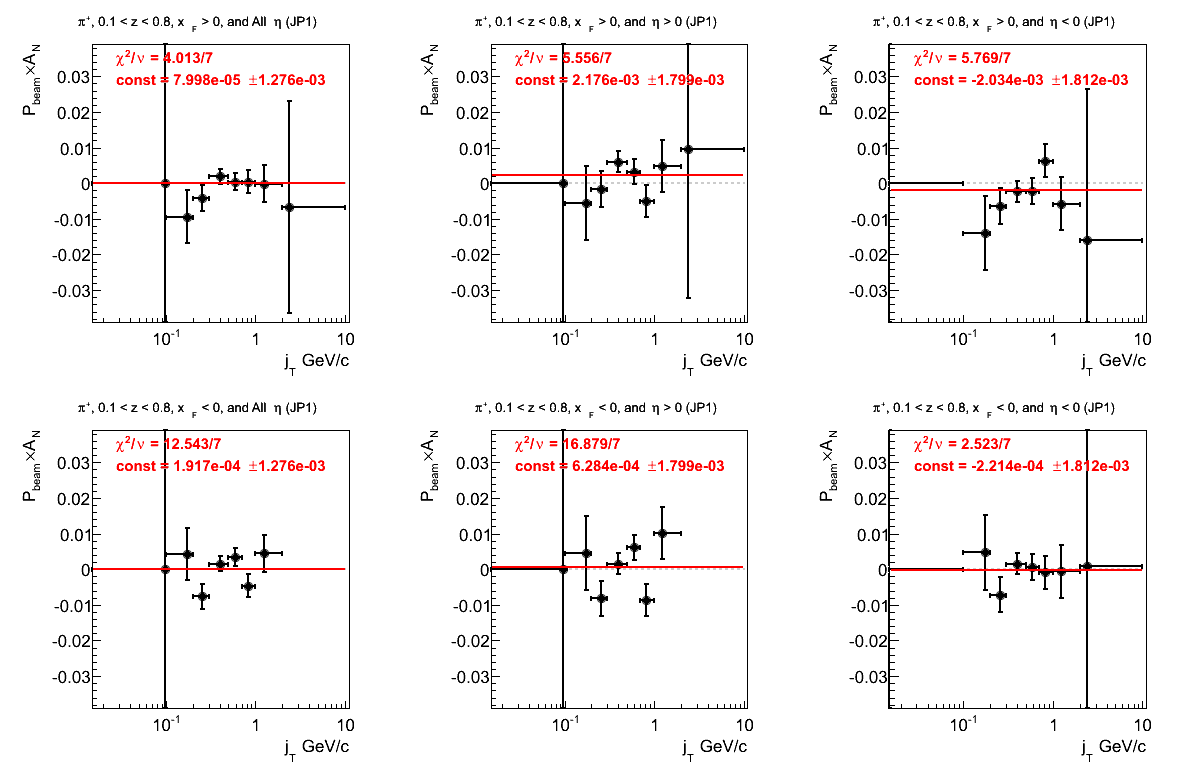
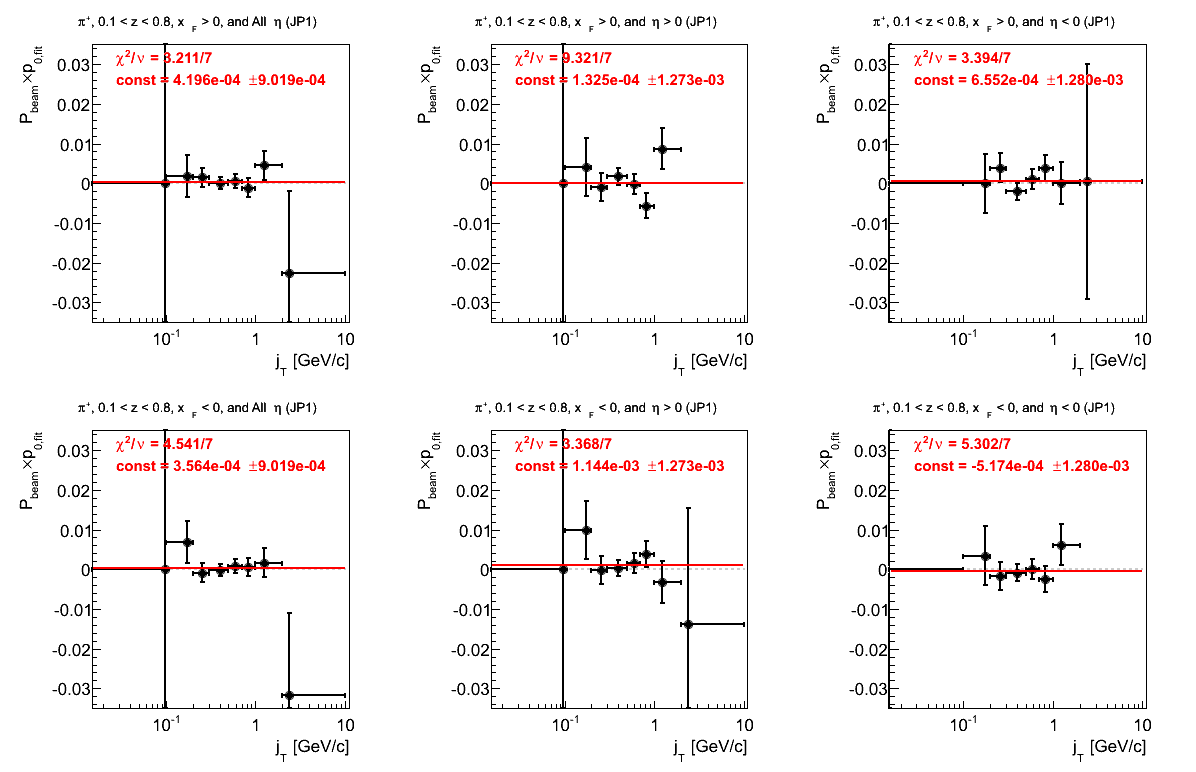
Figure 21: JP2 Triggers
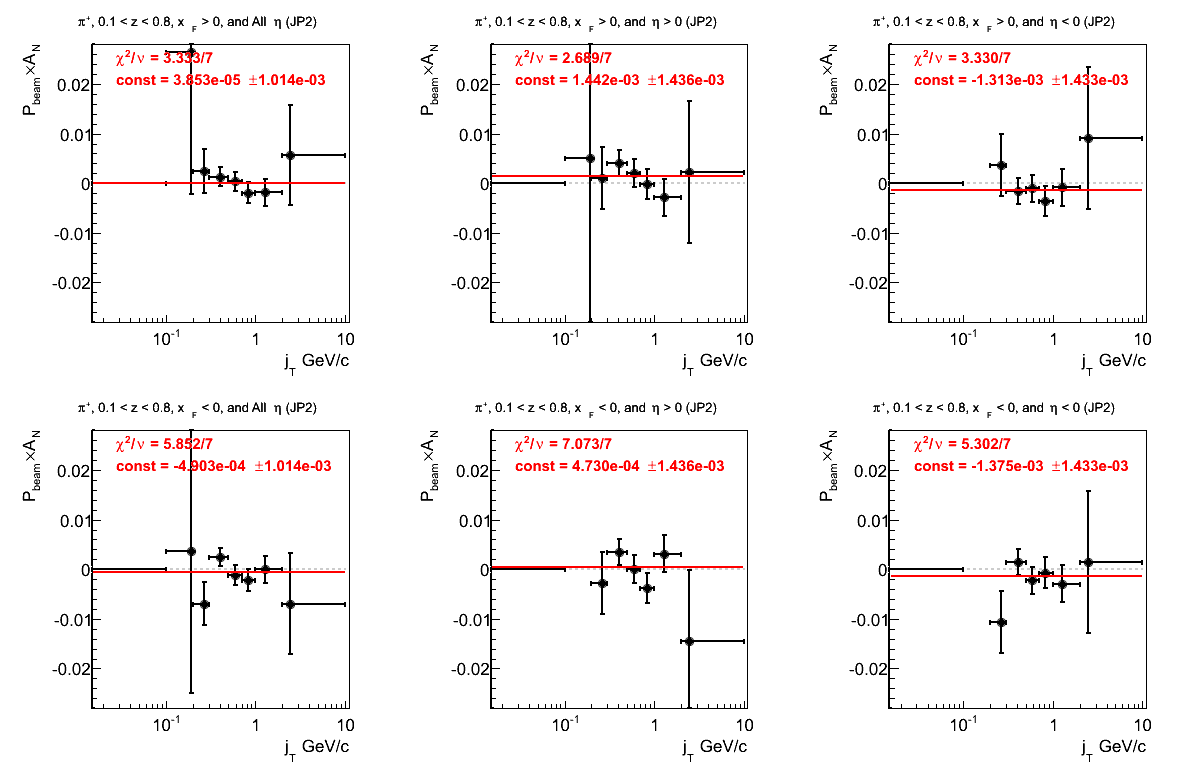
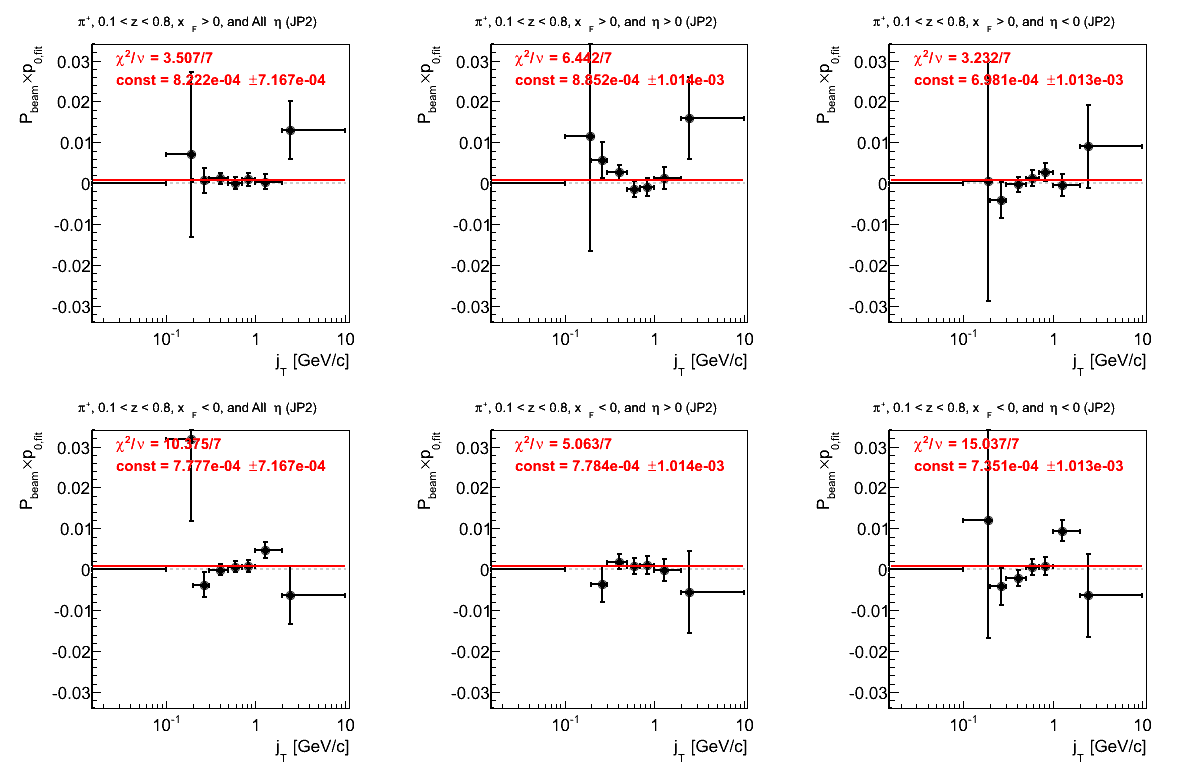
Figure 22: AJP Triggers
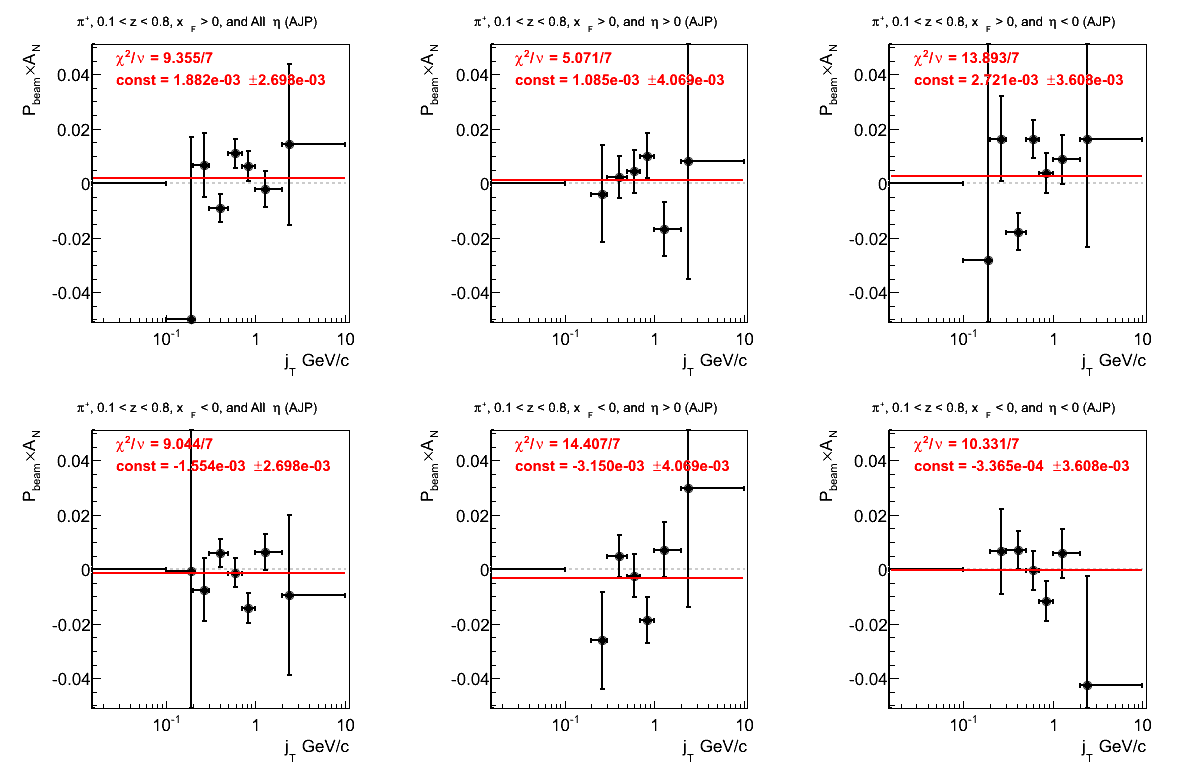
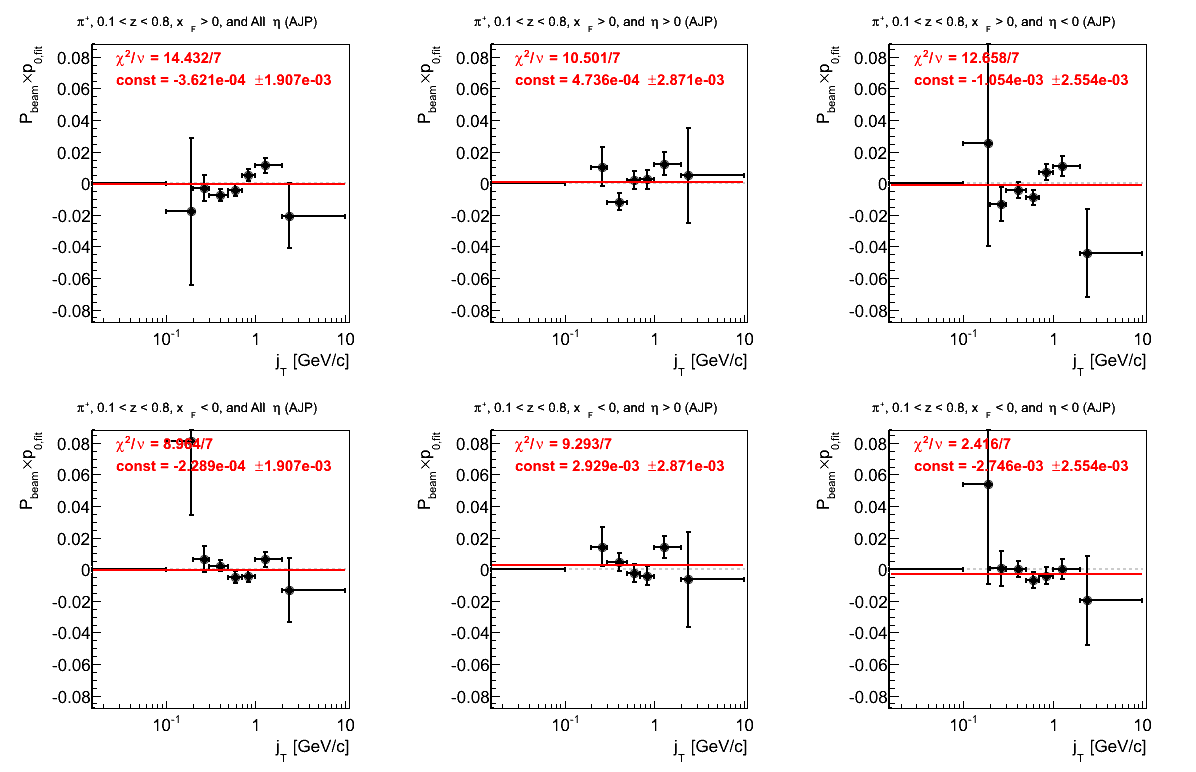
Figure 23: VPDMB Triggers
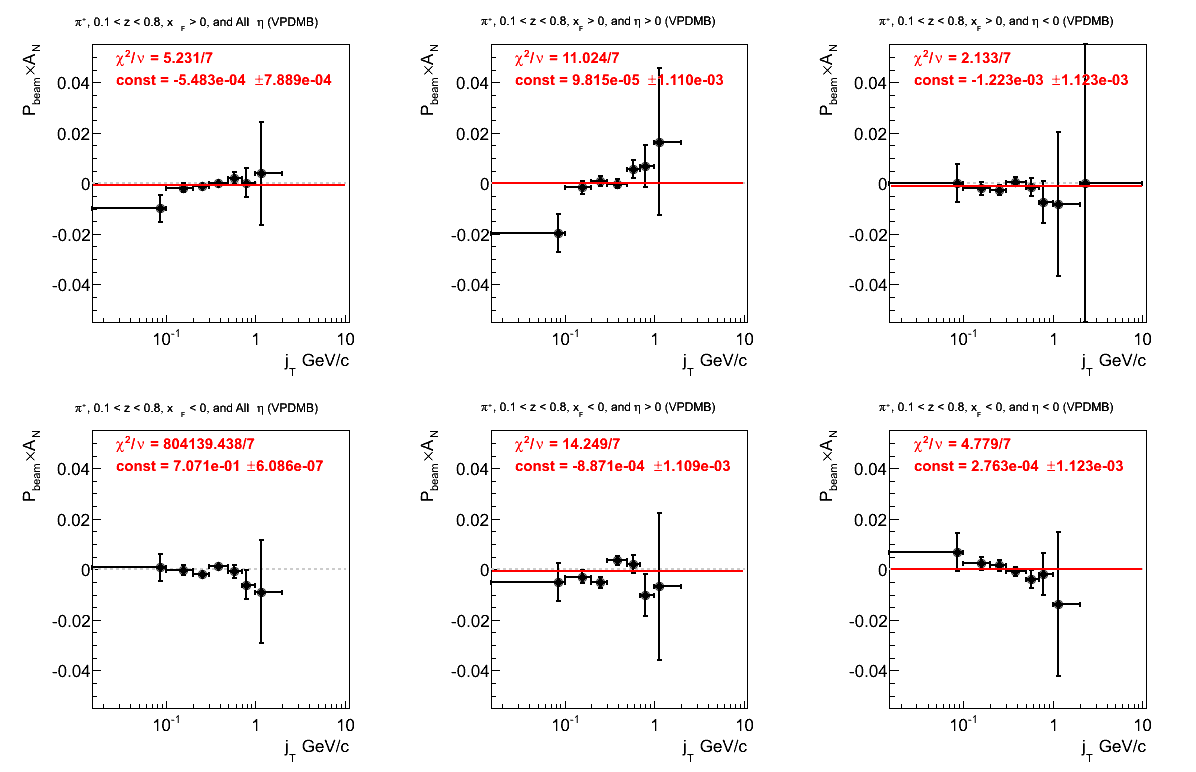
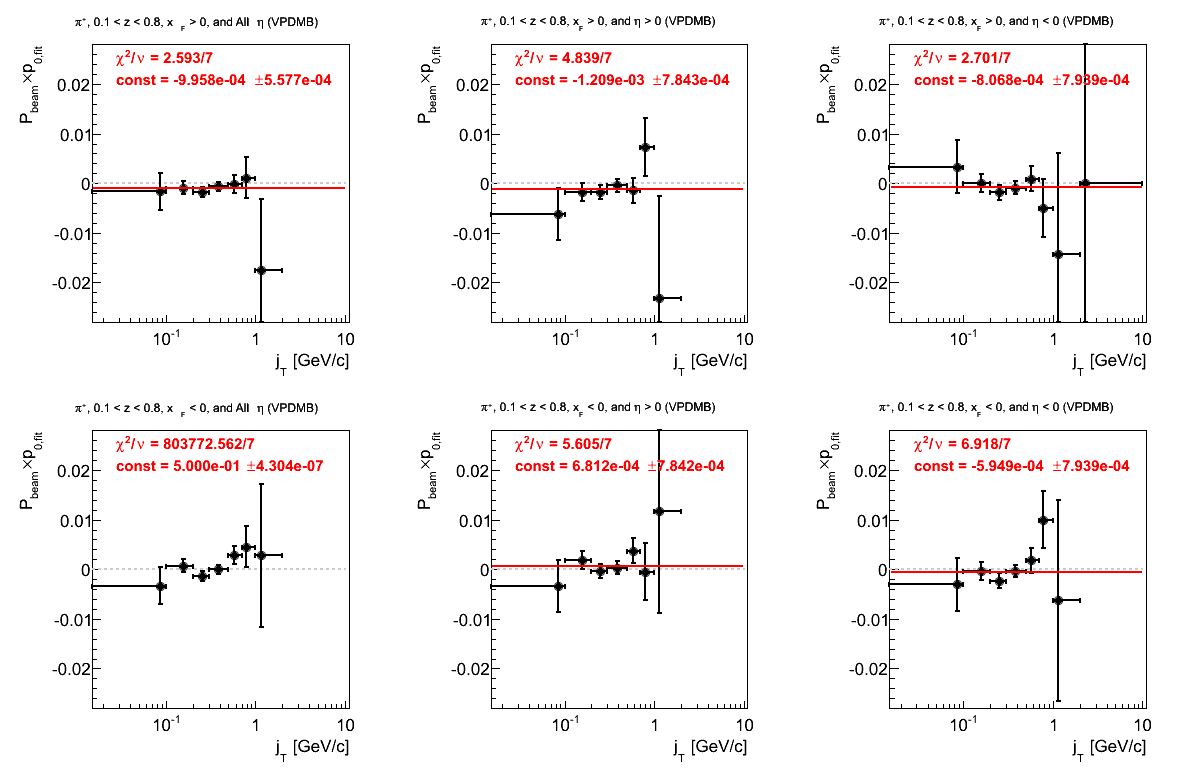
π-
Figure 24: JP0 Triggers
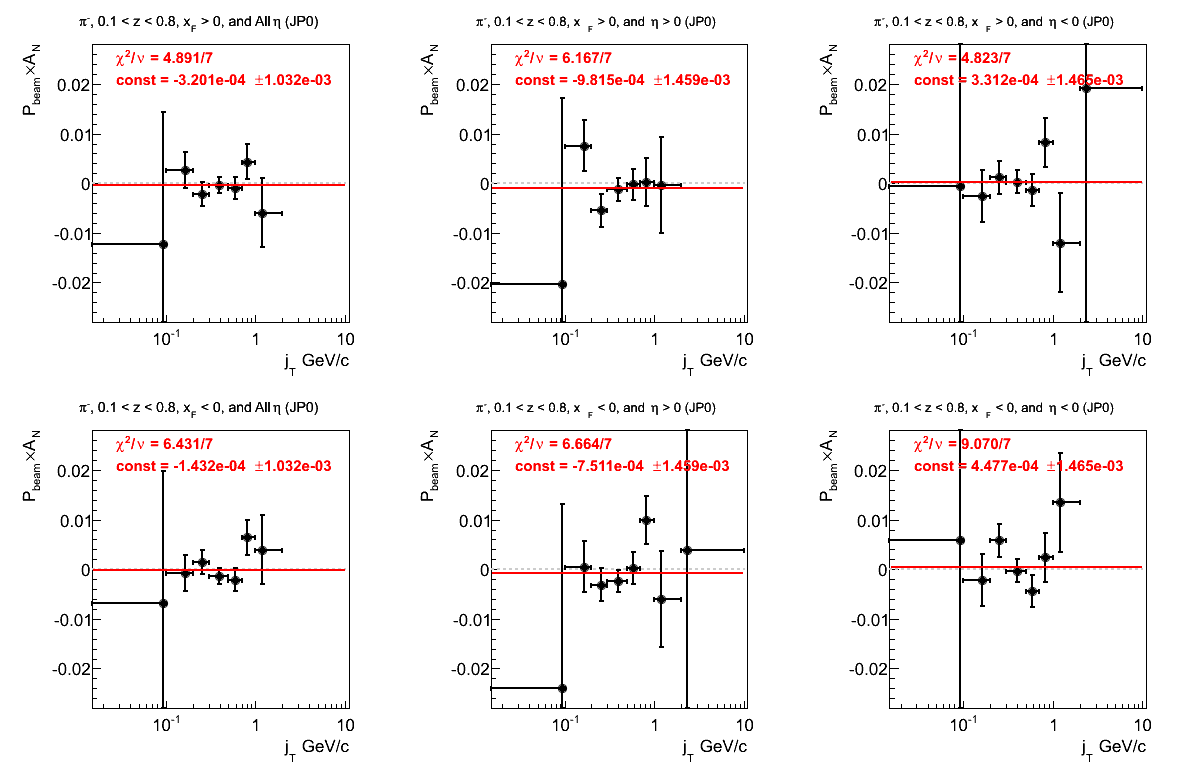

Figure 25: JP1 Triggers
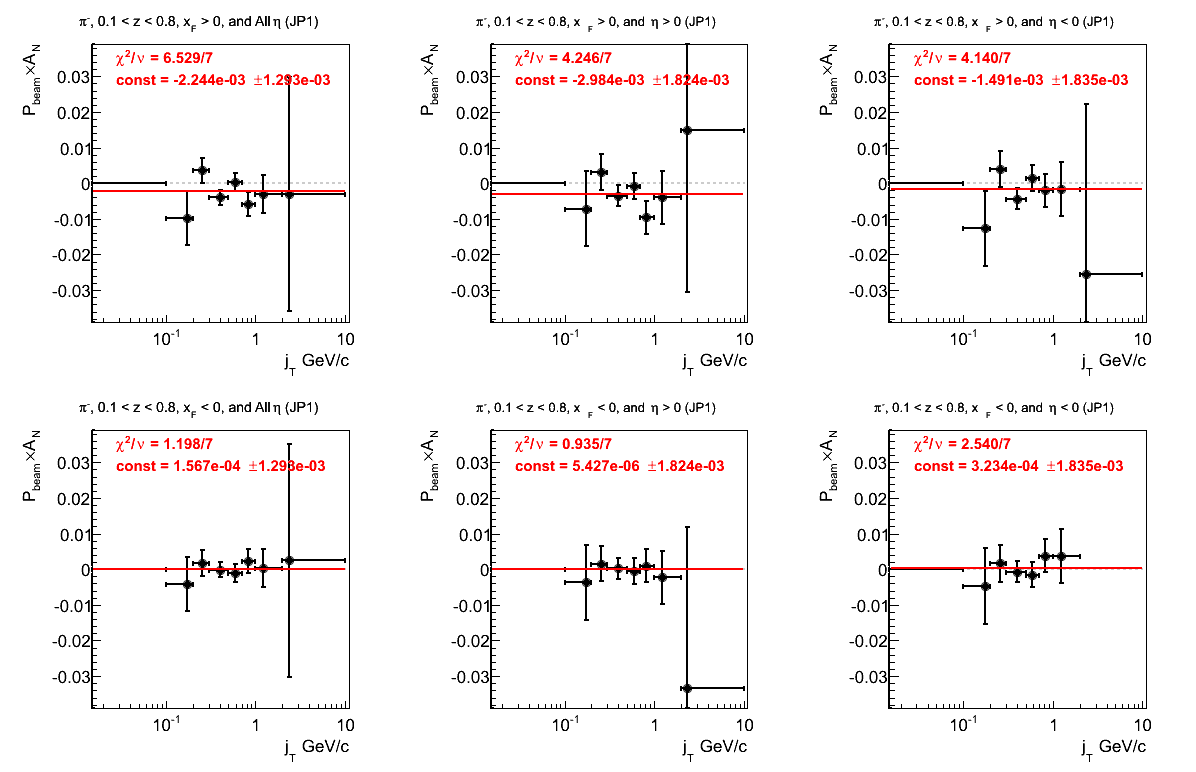
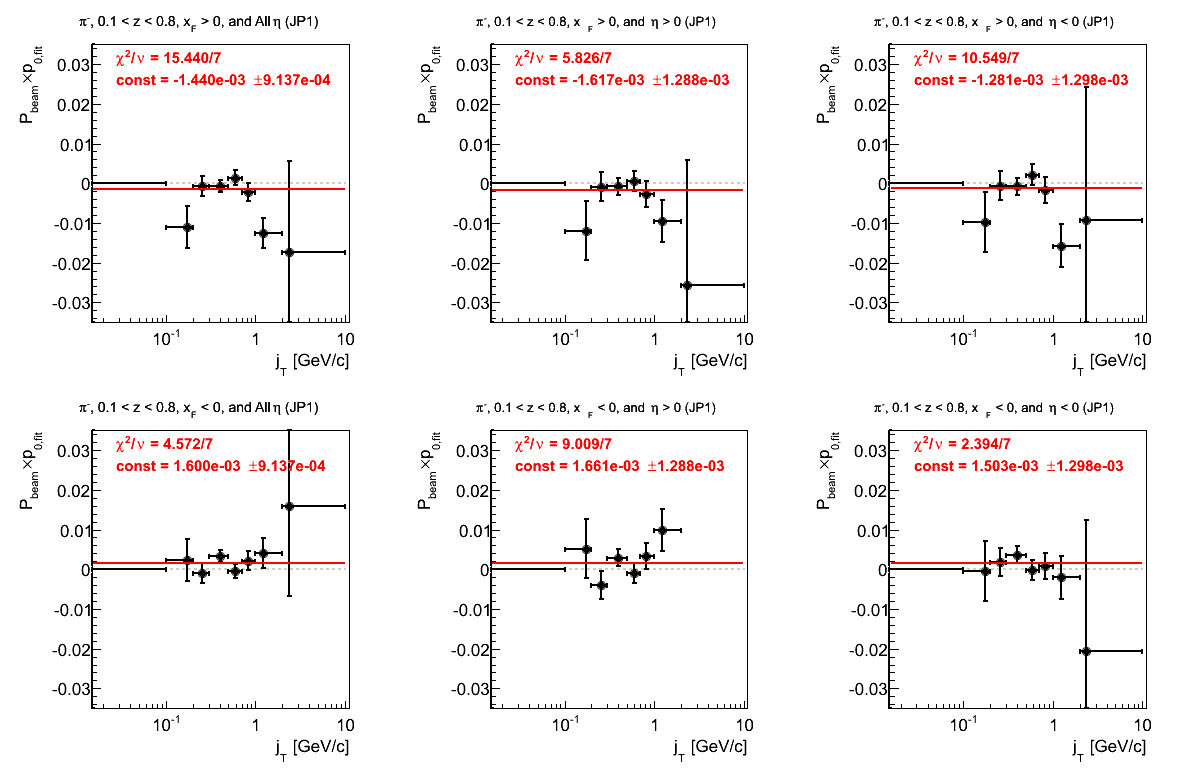
Figure 26: JP2 Triggers
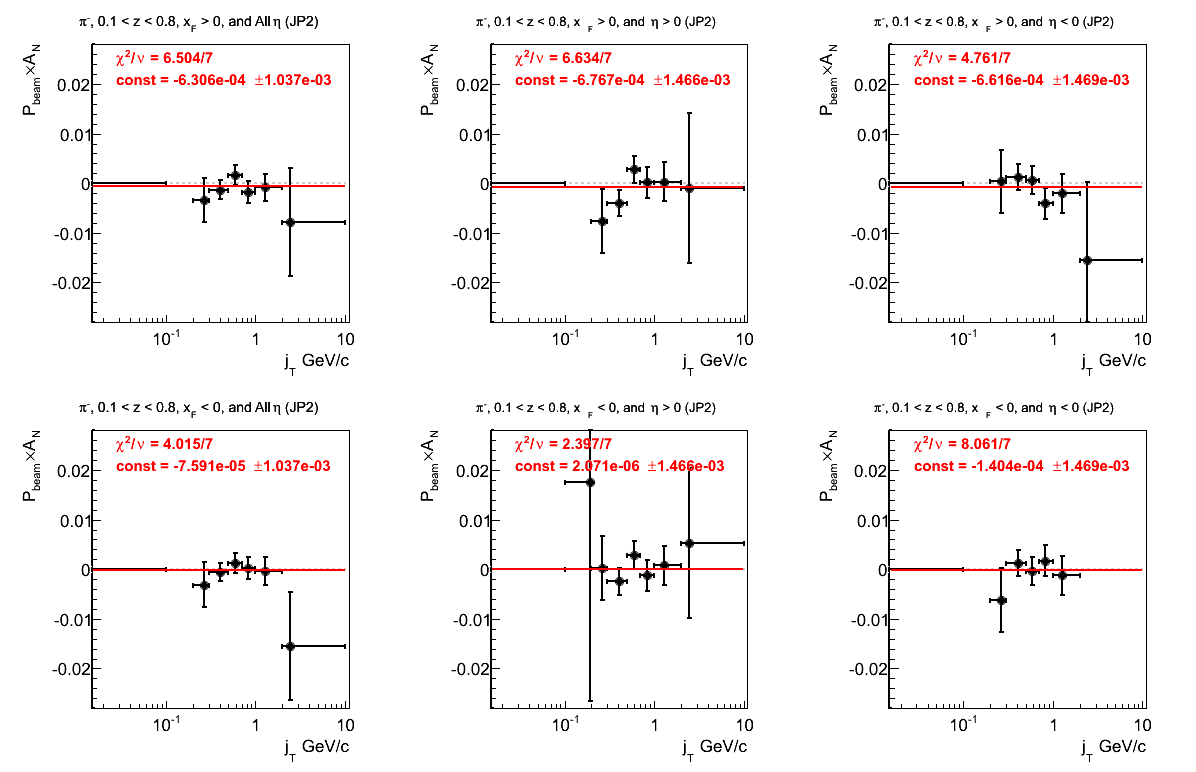

Figure 27: AJP Triggers
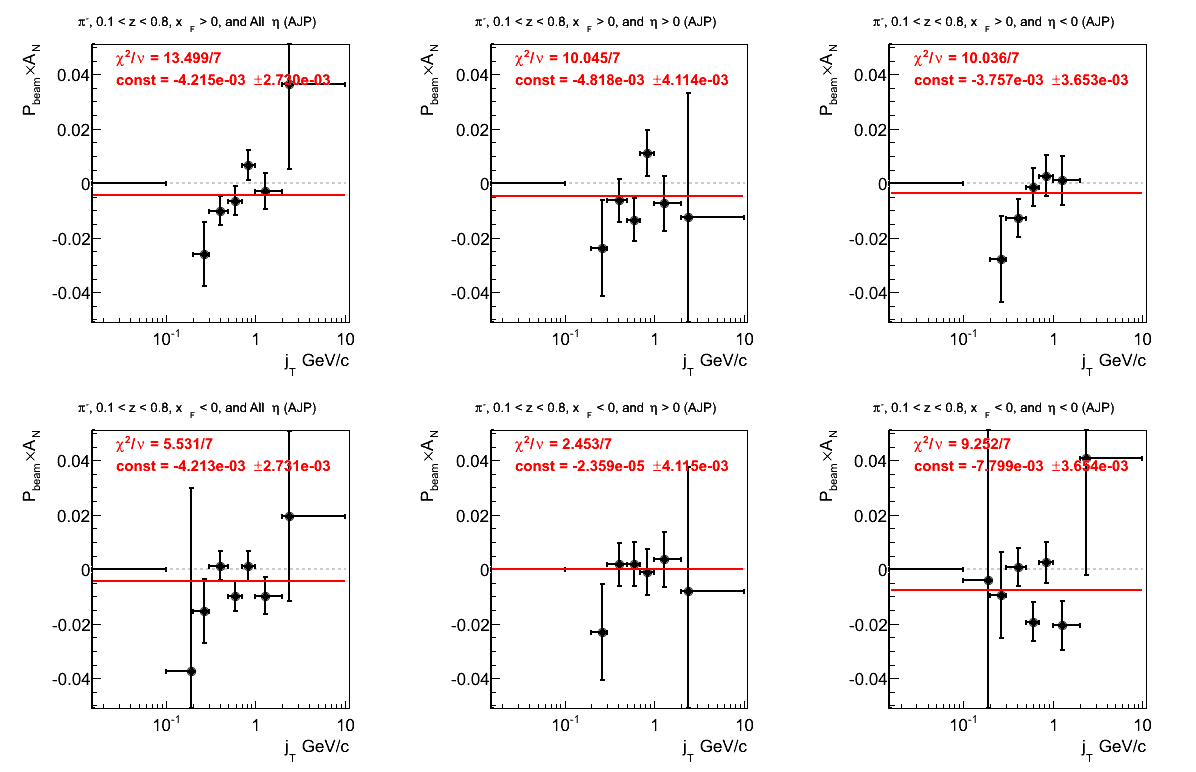

Figure 28: VPDMB Triggers
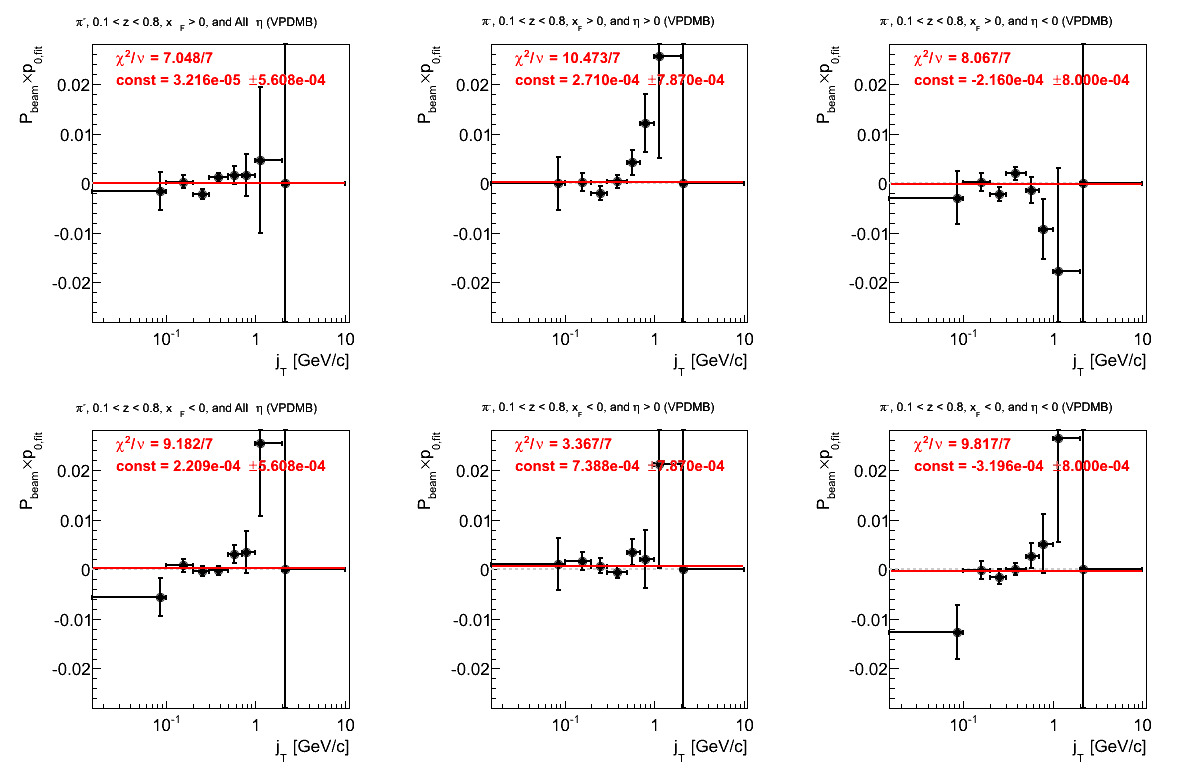
- drach09's blog
- Login or register to post comments
