During the spin meeting it was suggested I post some supporting plots to aide in the consideration of preliminary approval for the latest A_N results. Particularly, there is some concern that the systematics for the highest-x_F bins are properly handled, as it is somewhat surprising that shrinking the mass window can change the central values as much as those bins reflect. We feel that taking the full difference between the points for the two windows is a conservative way to handle the systematic for preliminary approval. However, we also would like to continue to investigate ways to reduce our uncertainties, here in particular, as we move toward final results for publication.

Asymmetry Calculation

Asymmetries are calculated utilizing the form

A_N = ( A_{N, raw} - (1-f_sig)×A_{N, bg} ) / f_sig

Here, I will try to illuminate in detail each of these portions of the calculation.

Signal Fractions

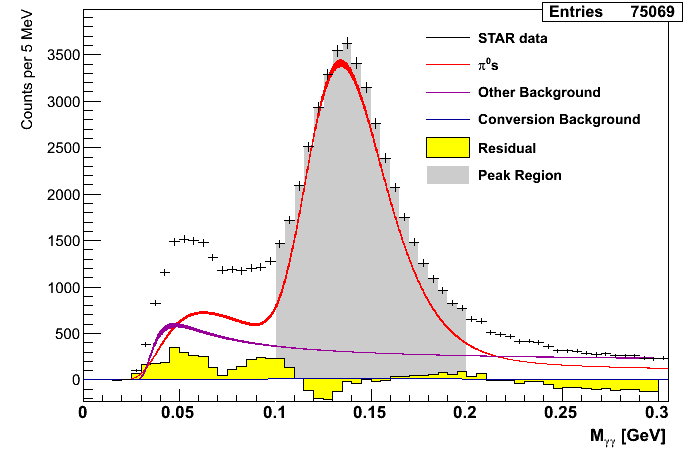
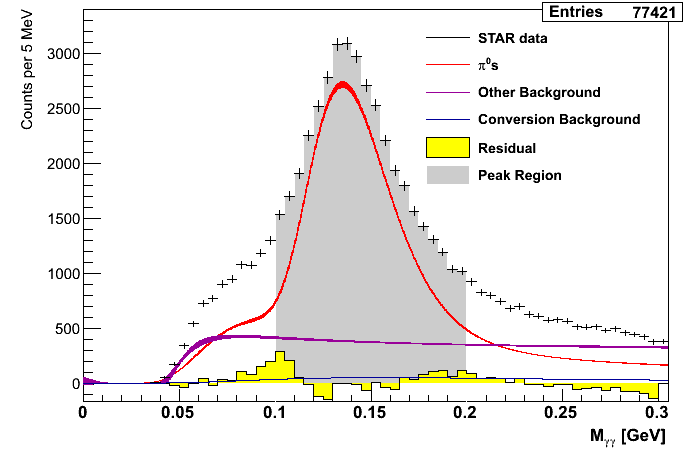
The signal fractions are calculated by fitting mass distributions with functional forms based on Pythia. The mass distributions are fit over the range of 0 < m_γγ < 0.3 GeV/c² and the yields for central values and systematics are integrated over different windows of invariant mass.

Figure 1: Mass Distributions (x_F-bins)

0.06 < xF < 0.13	0.13 < xF < 0.20	0.20 < xF < 0.27

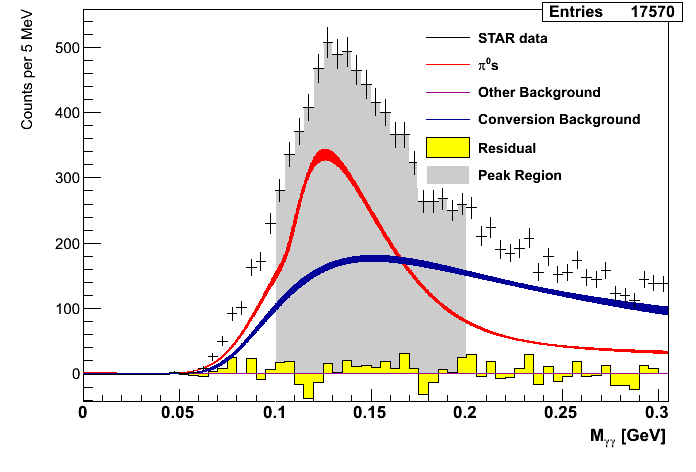In general, the fits tend to find a substantial portion of the mass distributions to be from pions. The residuals suggest the fits tend to undershoot the distributions a bit at lower mass, outside of the peak.

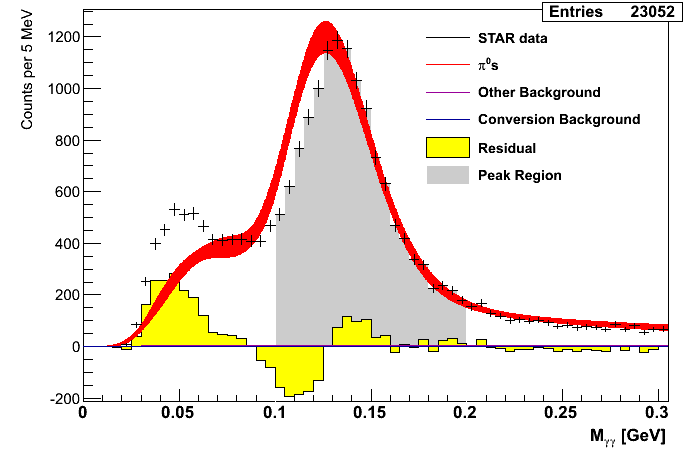
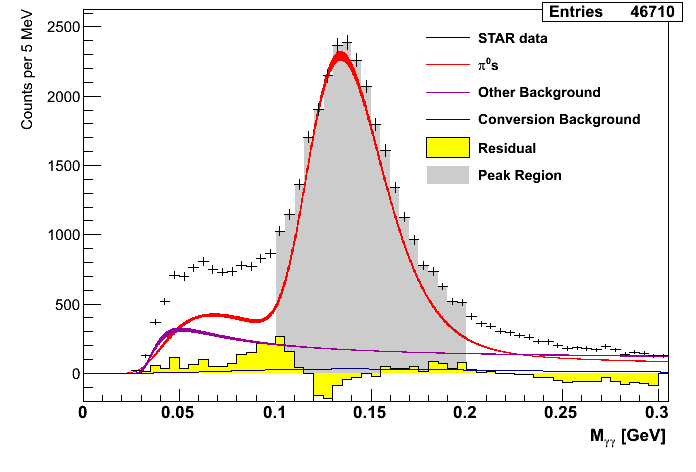
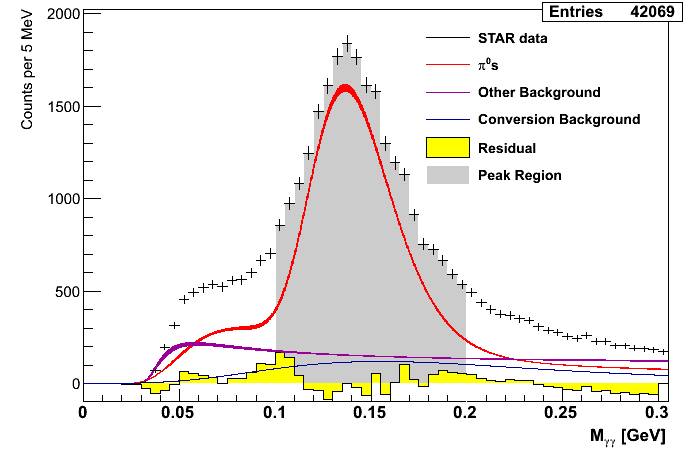
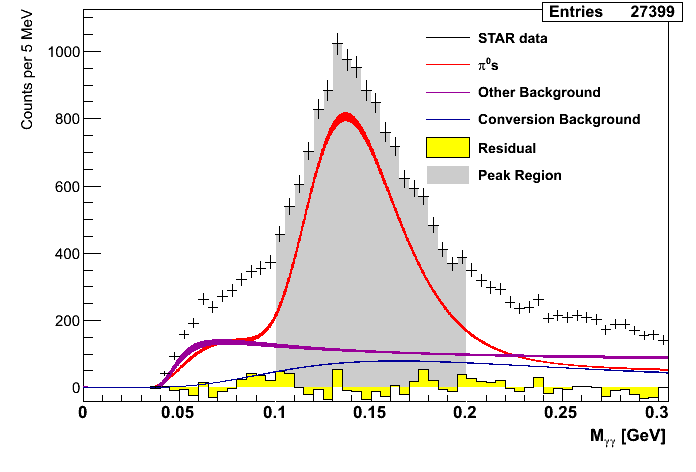
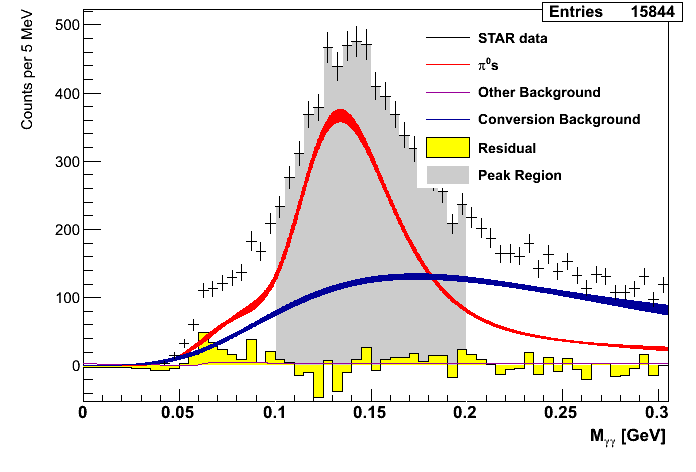
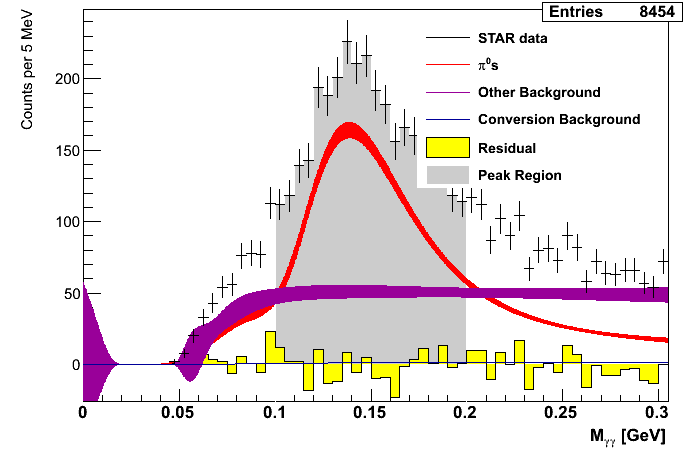
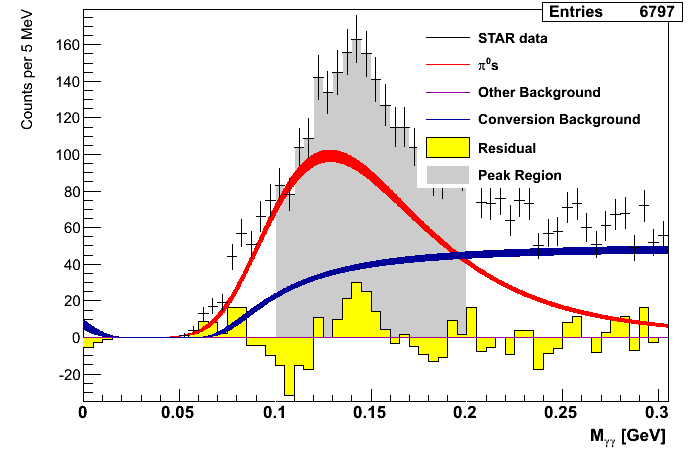
Figure 2: Mass Distributions (p_T-bins)

0.0 < pT < 4.0 GeV/c	4.0 < pT < 5.0 GeV/c	5.0 < pT < 6.0 GeV/c
6.0 < pT < 7.0 GeV/c	7.0 < pT < 8.0 GeV/c	8.0 < pT < 9.0 GeV/c
9.0 < pT < 10.0 GeV/c	10.0 < pT < 12.0 GeV/c	12.0 < pT < 16.0 GeV/c

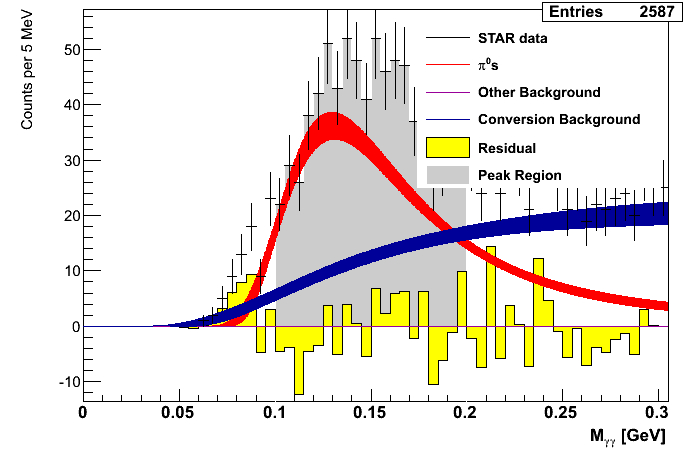While the fit for the lowest p_T bin is not very good, the remaining bins seem to find decent agreemtent between data and simulation.

Figure 3: Calculated Signal Fractions

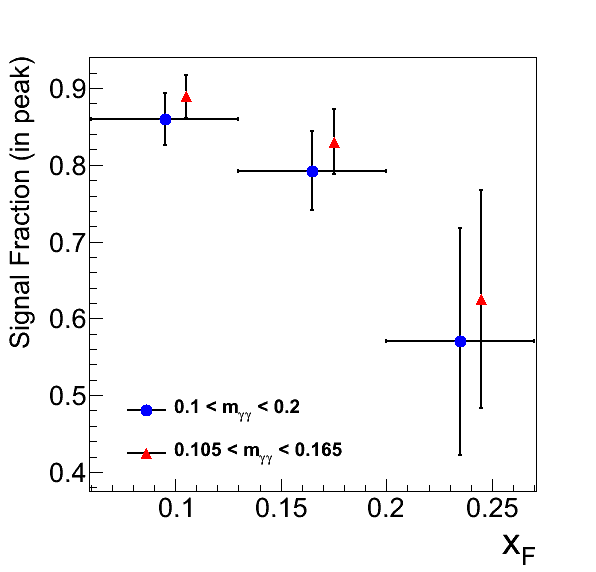
In Fig. 3 I plot the calculated signal fractions with their corresponding error for the relevant xF and pT bins. The uncertainties, which can be rather sizable, contain contributions from the parameter fits as well as the residuals. The horizontal bars denote the bin sizes. The blue points are plotted at the bin centers, whie the red points are offset slightly for clarity. The red points are systematically higher than the blue points, consistent with expectation.

Alternative Signal Fraction

Prior to Steve's latest improvements to the mass-fitting procedure, e.g. extending the fit range down to 0, I performed an alternative calculation of the signal fraction as a systematic check on our signal fraction calculation. The reasoning was that while the Monte Carlo provided physics-driven motivation for the background shapes, there was clear breakdown of the fitting below 0.1 GeV/c². So, a way to estimate our sensitivity to these low-mass discrepancies was to use a data-driven background shape to fit the distribution below the signal range. Comparing the asymmetries from each method could help us set a systematic uncertainty on the signal fraction.

Since our methodology has improved to include the full fit range, as well as more correctly propagate the uncertainties from the fitting, it no longer seems necessary to include the alternative signal fraction method in the calculation. However, it may still provide a useful check on our methodology; so, I include it here for consideration.

Figure 4: Mass Distributions (x_F-bins)

In Fig. 4 I show the mass distributions in x_F-bins fit with a Gaussian + 3^rd-order polynomial (pol3). One can see the fit quality is not very good. Additionally, the fit ranges vary. The motivation at the time was to fit the background below the signal range, since the fit agreement for the functional form fits was rather good in and above the signal range.

Figure 5: Mass Distributions (p_T-bins)

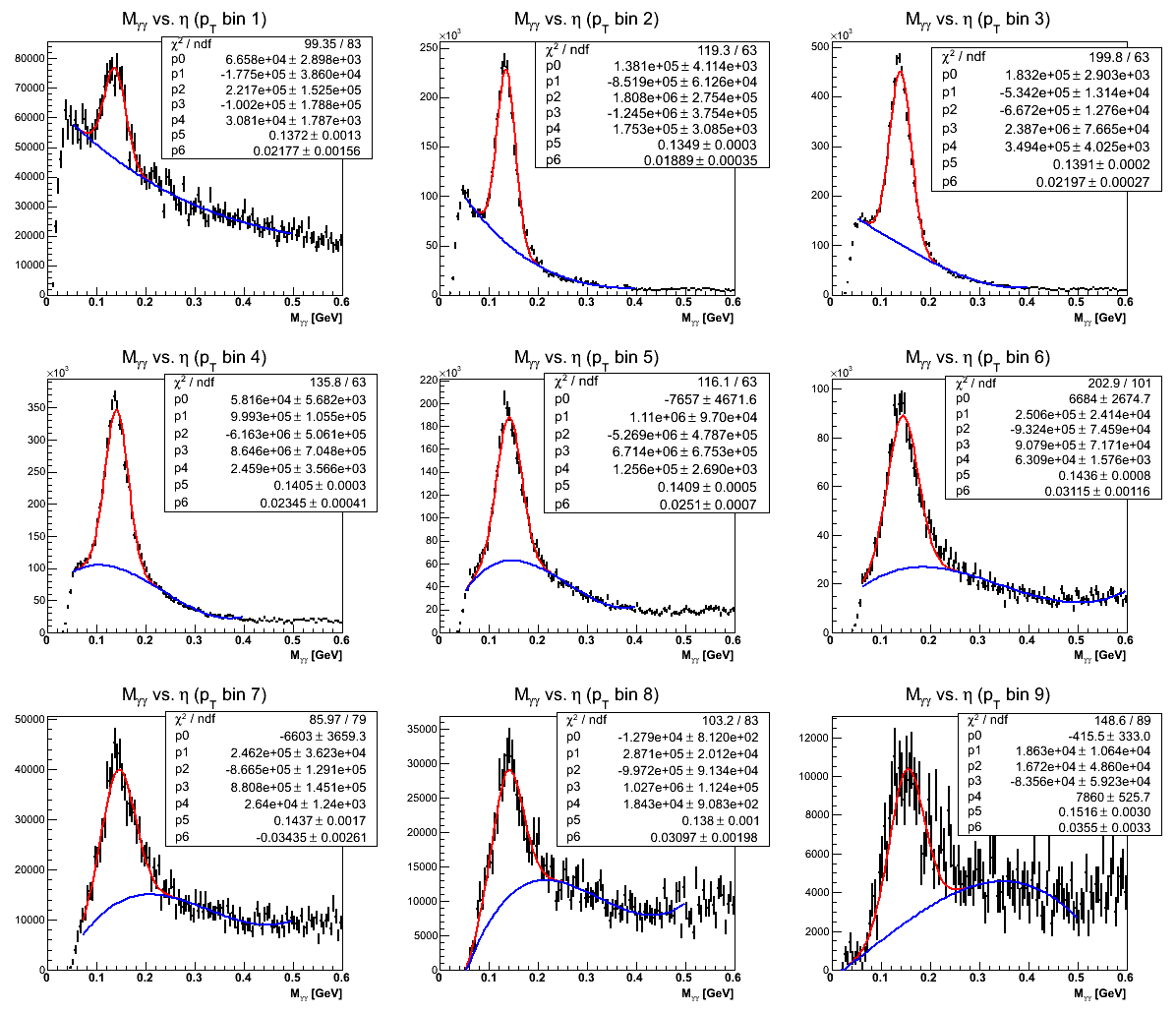
The fit quality for the p_T-bins seems a bit better, but this is most likely due to larger uncertainties. Again, the motivation was to provide fits that modeled the background below the peak. Note that I include the fit for the first p_T-bin, but it will not appear in the analysis.

Figure 6: Calculated Signal Fractions

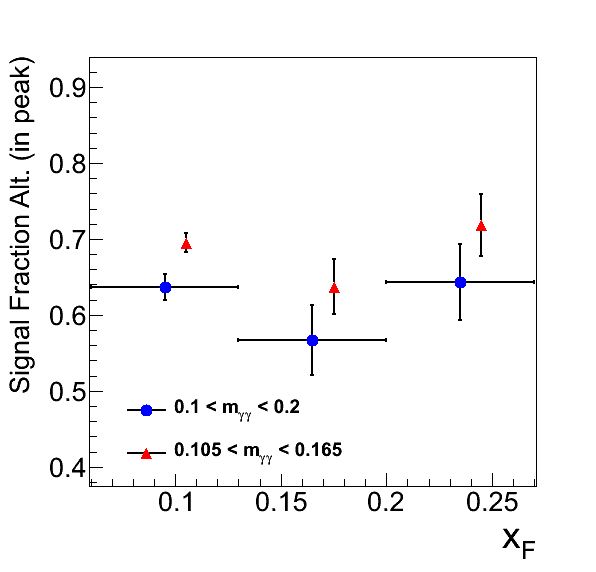
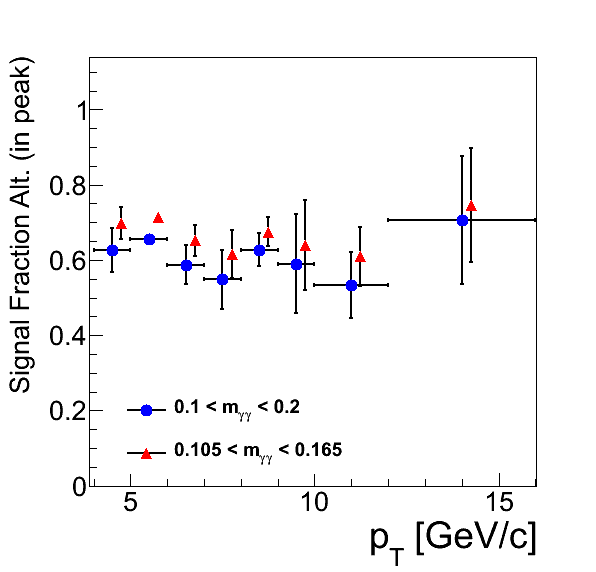
Figure 6 shows the calculated signal fractions for the alternative fitting procedure. One can see that they diverge quite largely in some bins from the functional form fits. In spite of this, the variation in the calculated asymmetries is relatively small compared to our precision.

Raw Asymmetries

x_F Bins

Figure 7: x_F > 0

1 < mγγ < 2 GeV/c2	1.05 < mγγ < 1.65 GeV/c2
0.06 < xF < 0.13
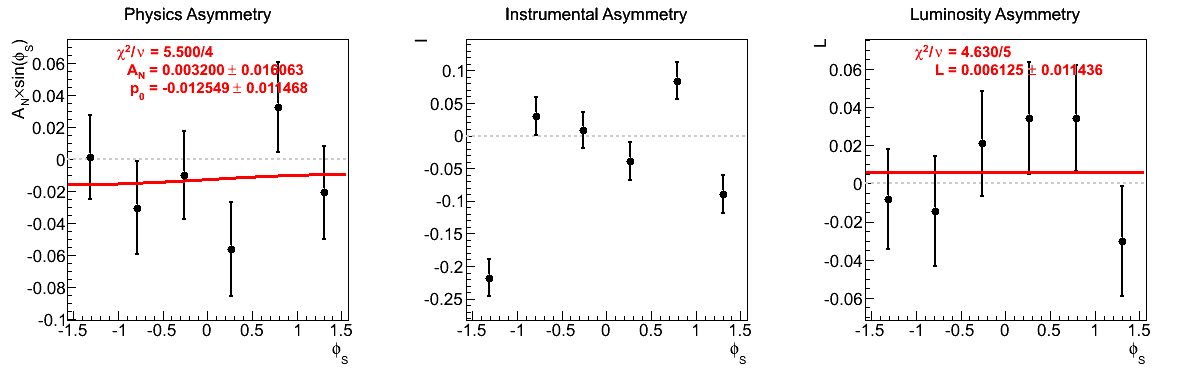0.13 < xF < 0.20
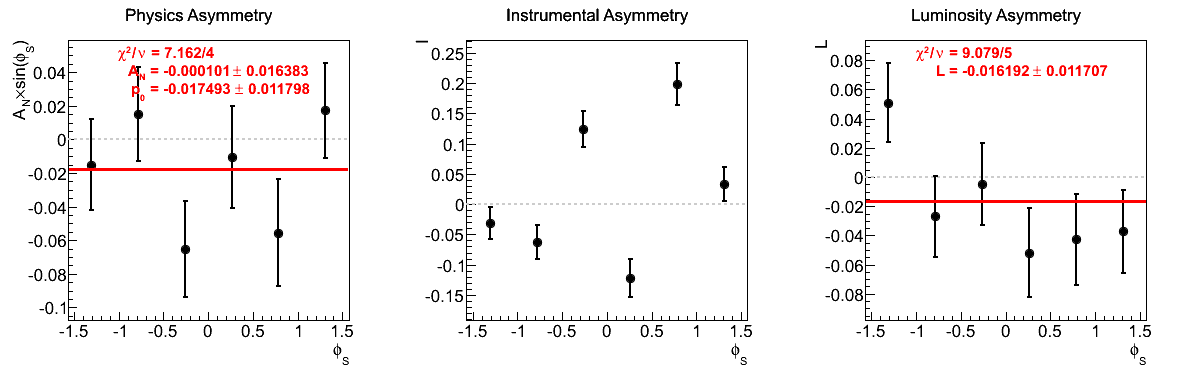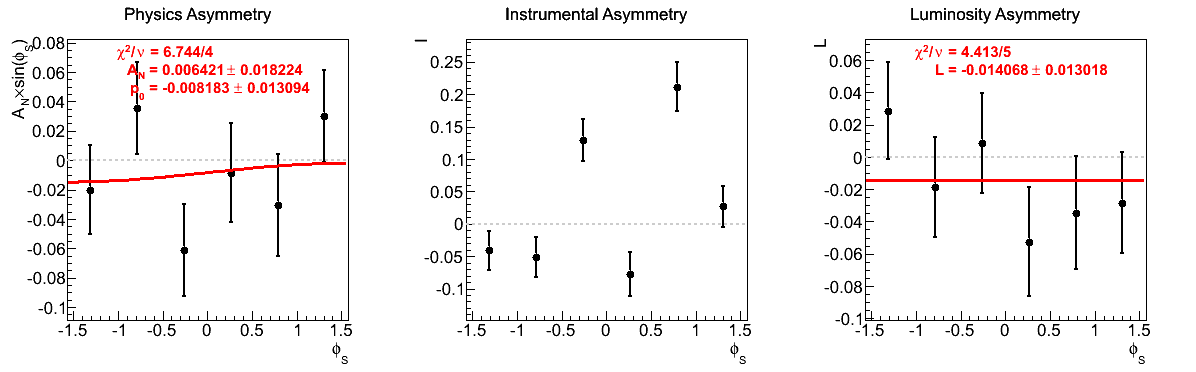0.20 < xF < 0.27

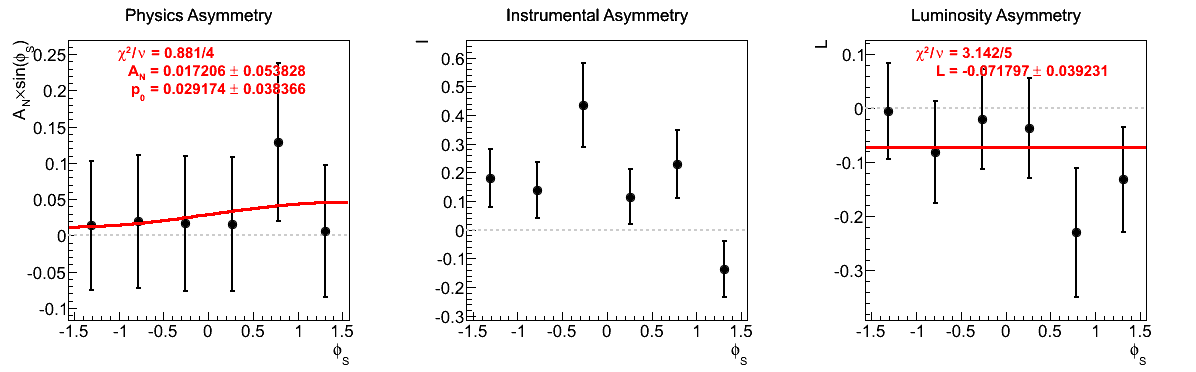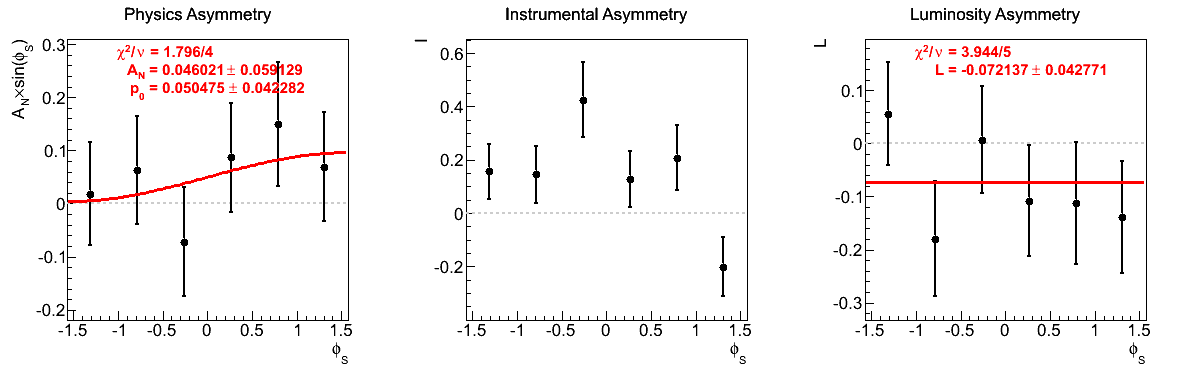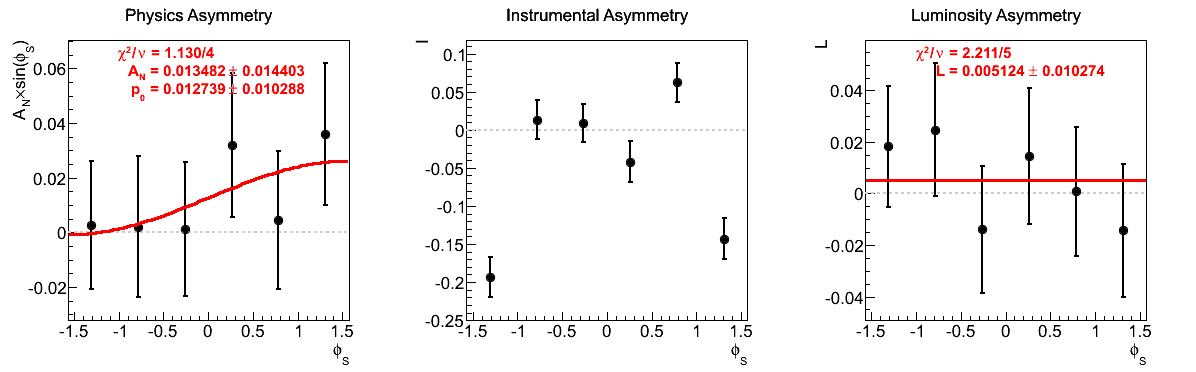
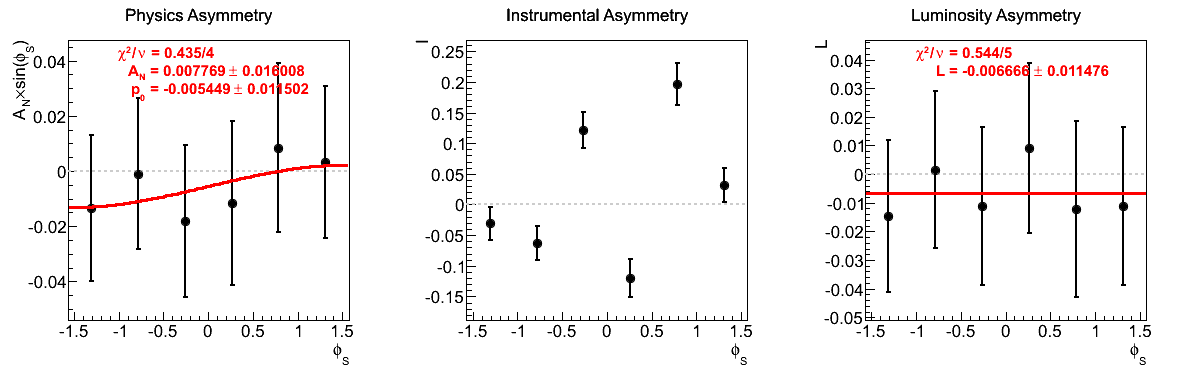
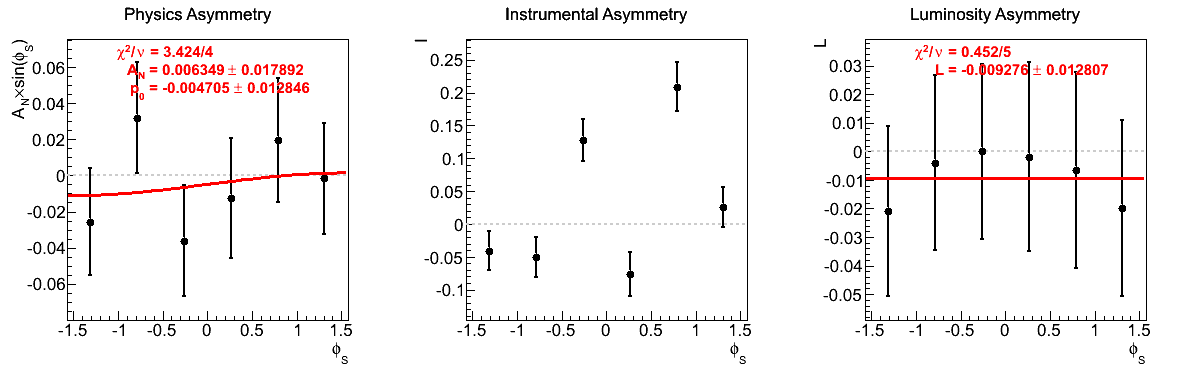
Figure 8: x_F < 0

1 < mγγ < 2 GeV/c2	1.05 < mγγ < 1.65 GeV/c2
0.06 < xF < 0.13
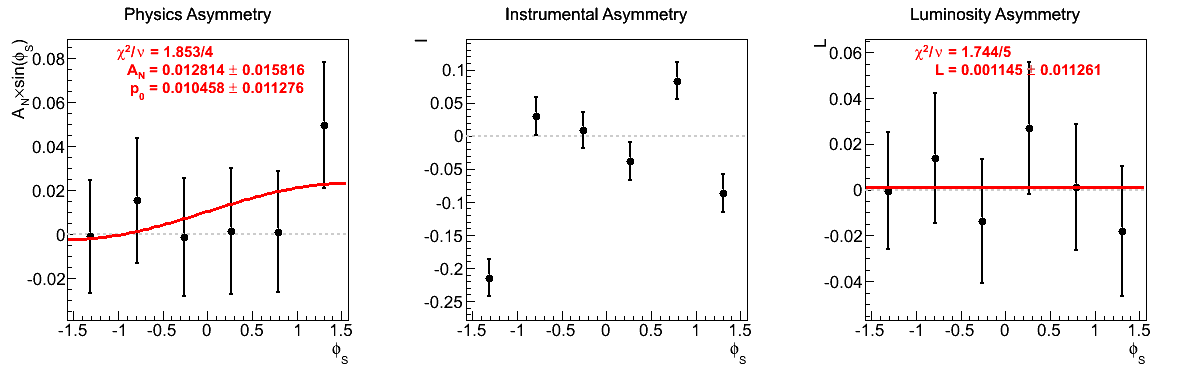0.13 < xF < 0.20
0.20 < xF < 0.27

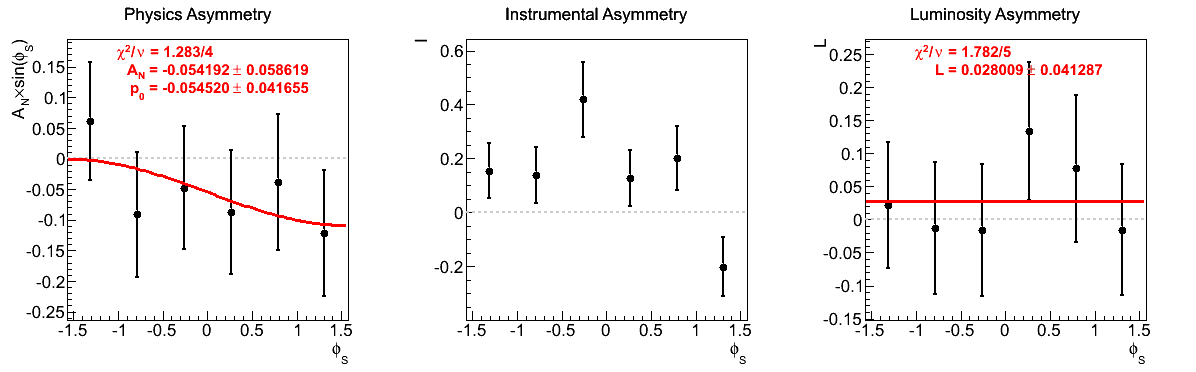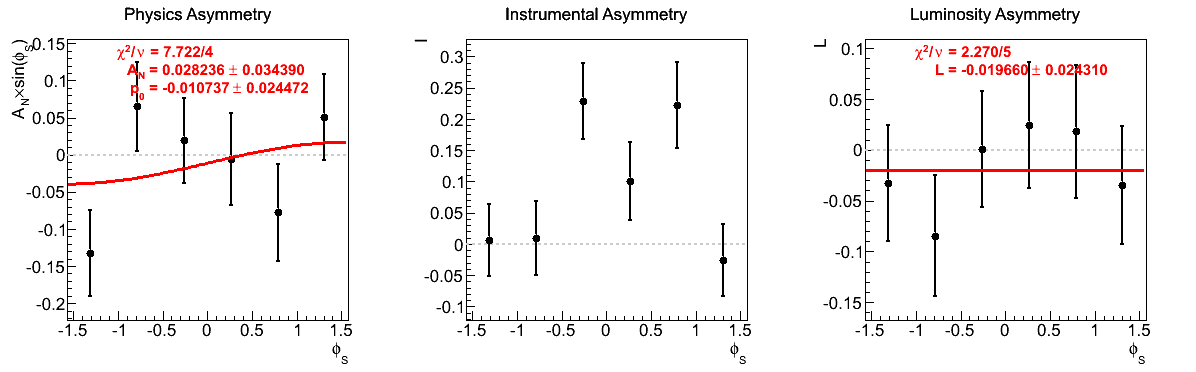
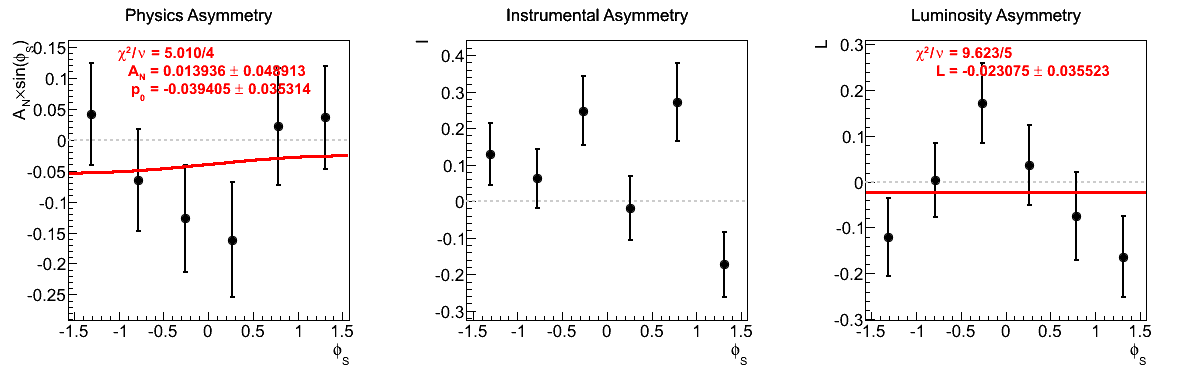
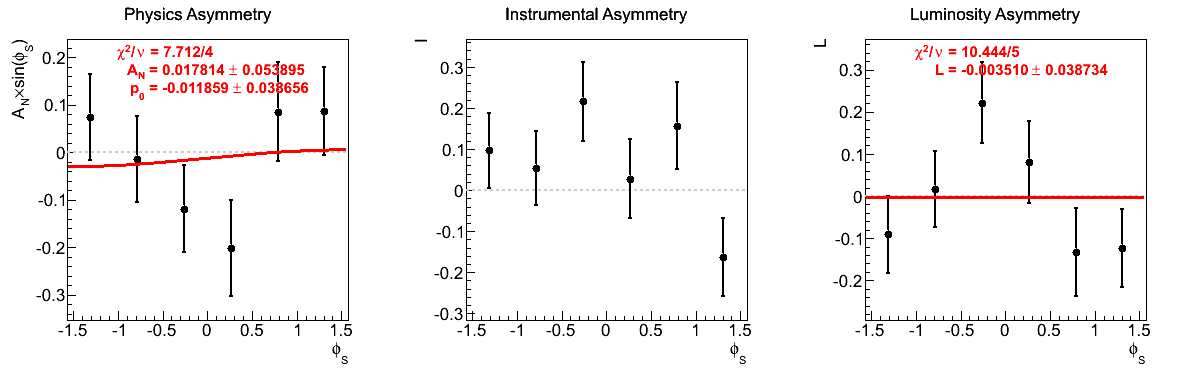
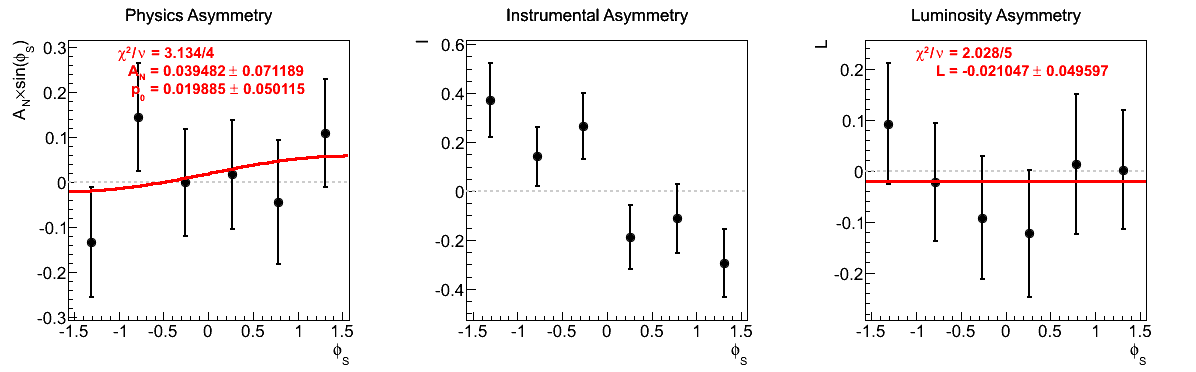
The largest issue that seemed to arise during the spin call concerned the highest x_F bin for x_F < 0. Looking at the corresponding figures (last row of Fig. 5), one sees very little qualitative change between the two mass-window versions of instrumental asymmetries or luminosity asymmetries. However, there does seem to be some shifting of the central values for the physics asymmetry. For instance, the first φ-bin is shifted to the other side of the horizontal. Additionally, the fourth φ-bin is shifted away from the horizontal in the tight mass window. These, and the other shifts, appear to be sufficient to flip the slign of the fit. As the events are highly correlated between the two samples, this is a bit unexpected. One should note, of course, that the uncertainties are enormous on these points (~10%).

p_T Bins

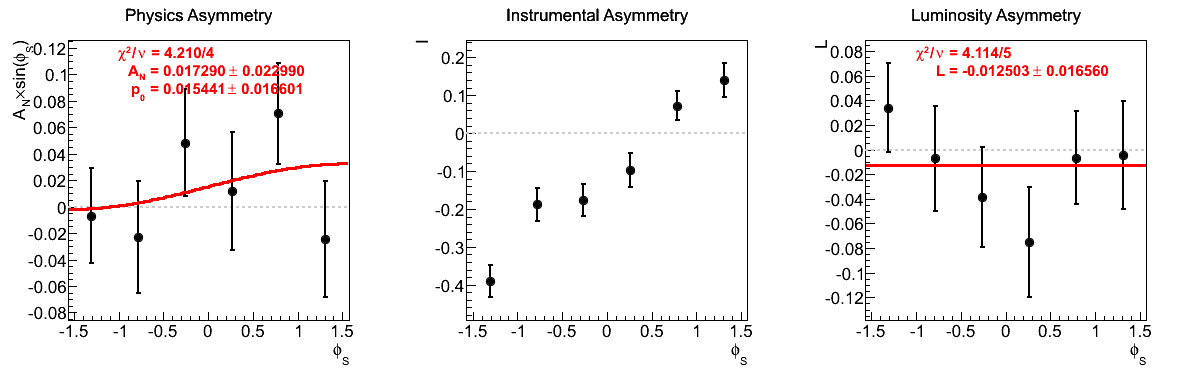
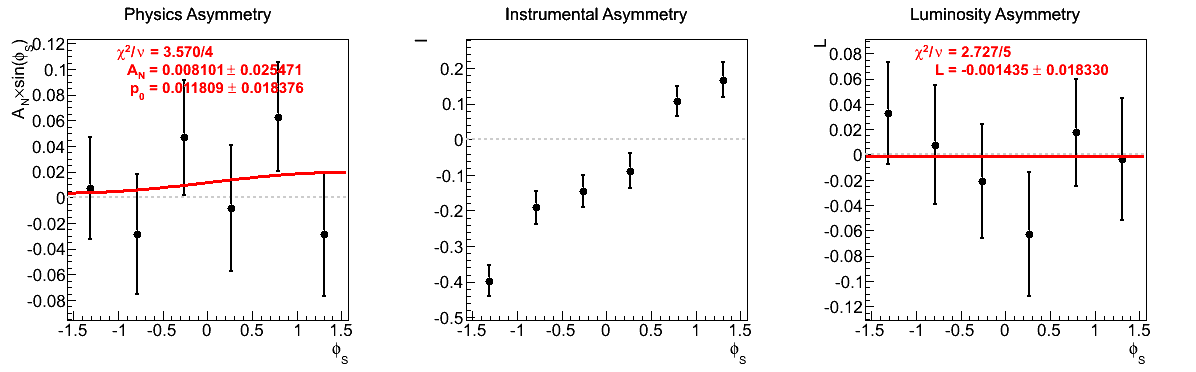
Figure 9: x_F > 0

1 < mγγ < 2 GeV/c2	1.05 < mγγ < 1.65 GeV/c2
4 < pT < 5 GeV/c
5 < pT < 6 GeV/c
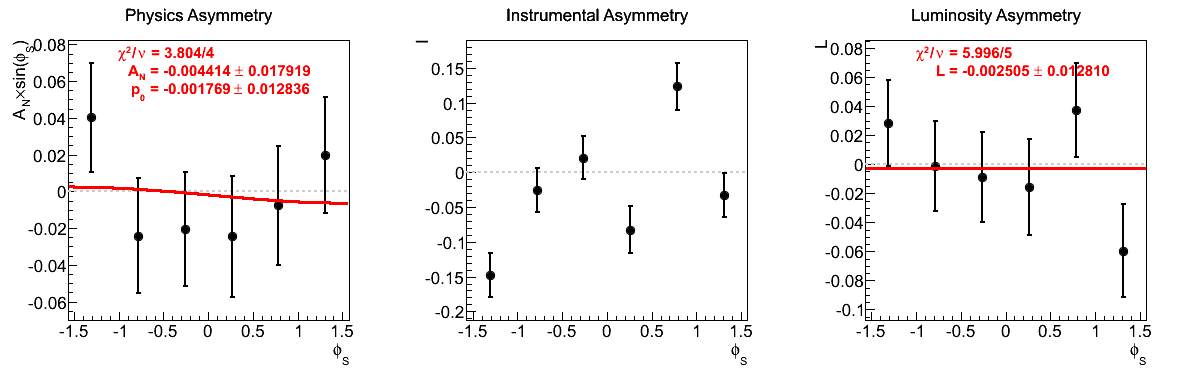6 < pT < 7 GeV/c
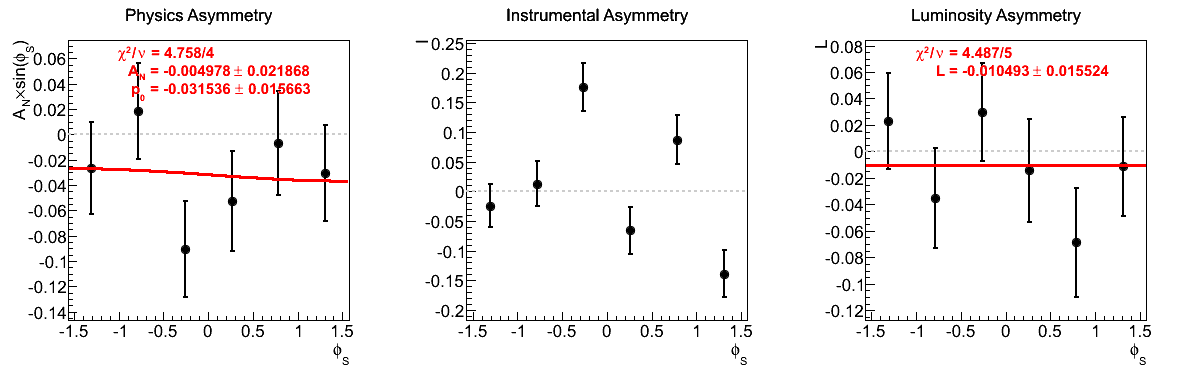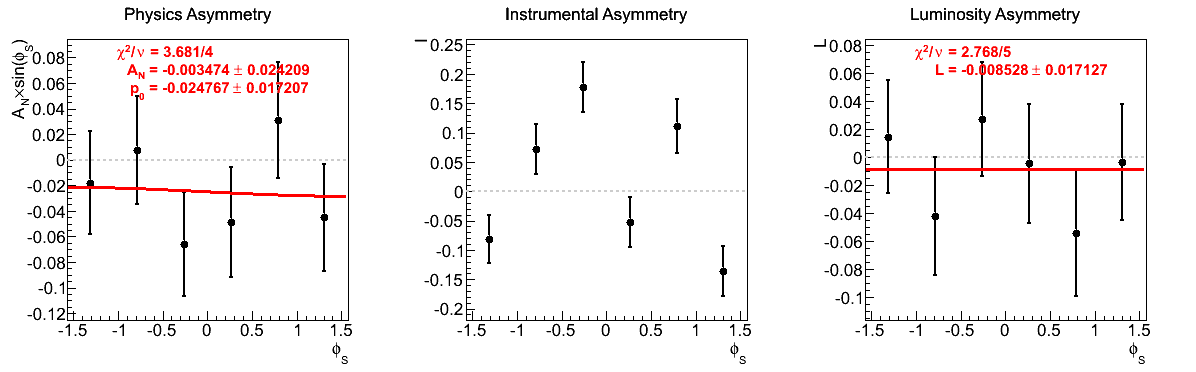7 < pT < 8 GeV/c
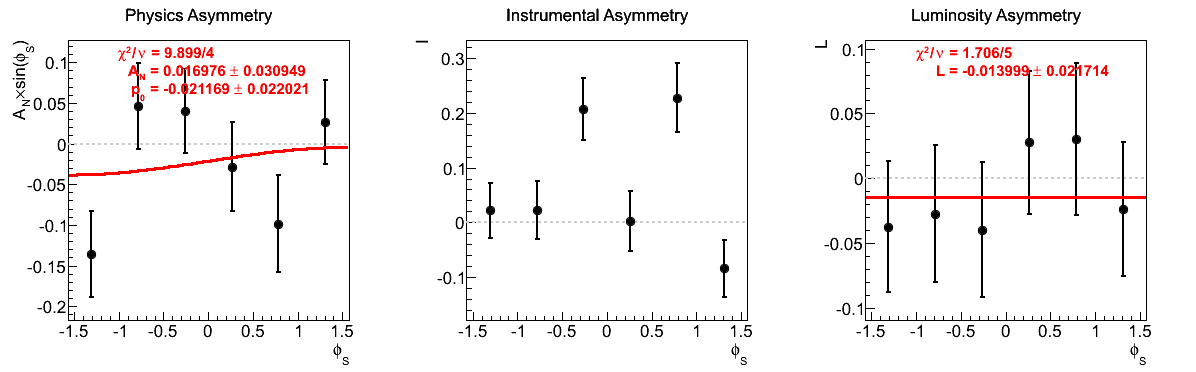8 < pT < 9 GeV/c
9 < pT < 10 GeV/c
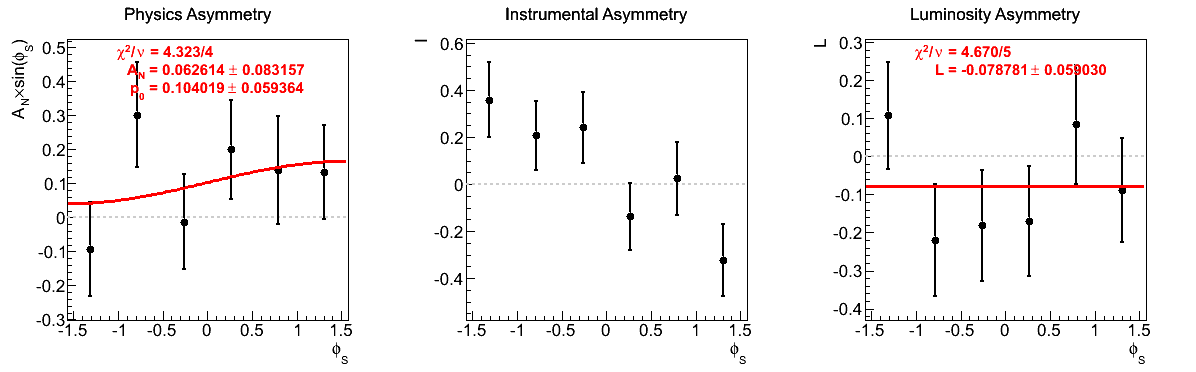10 < pT < 12 GeV/c
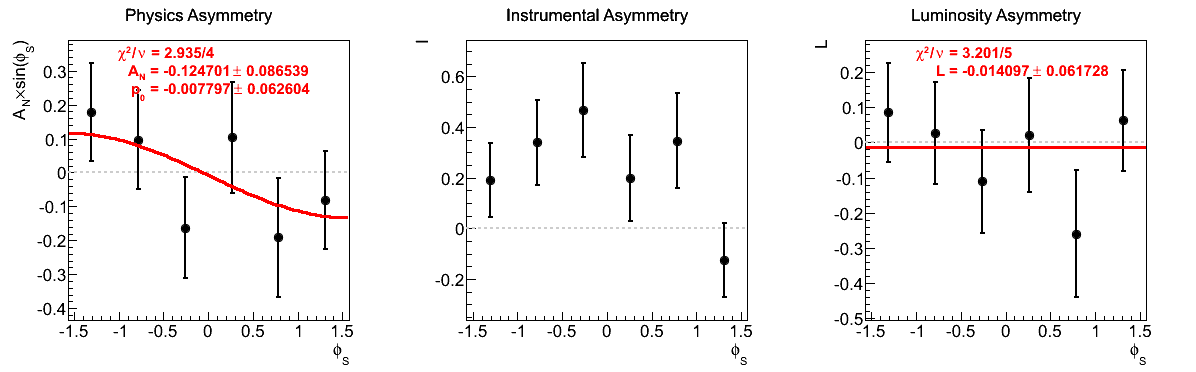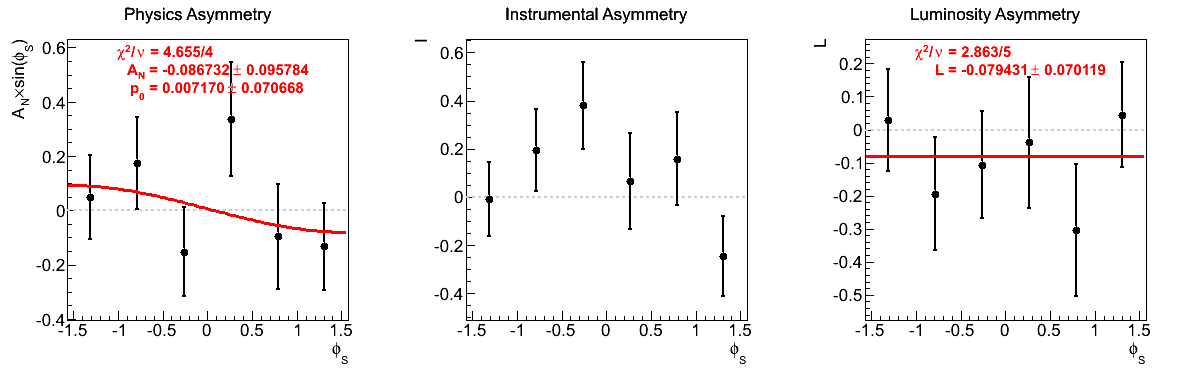12 < pT < 16 GeV/c

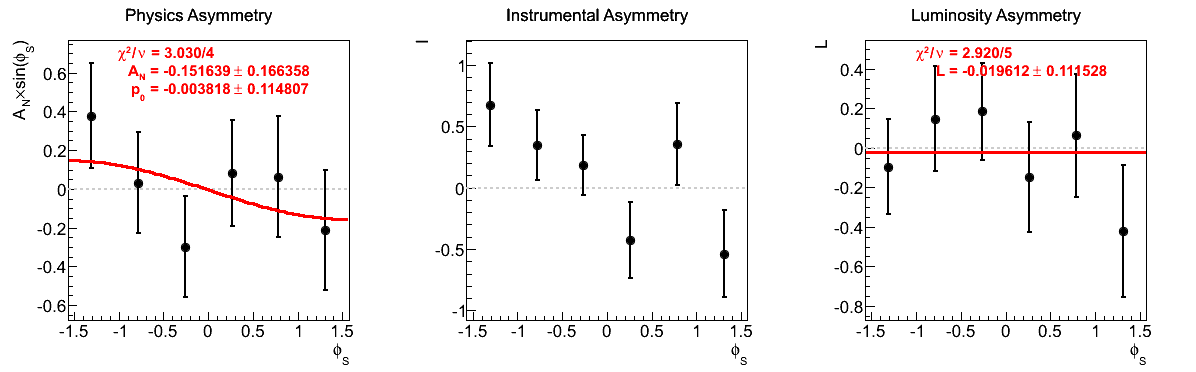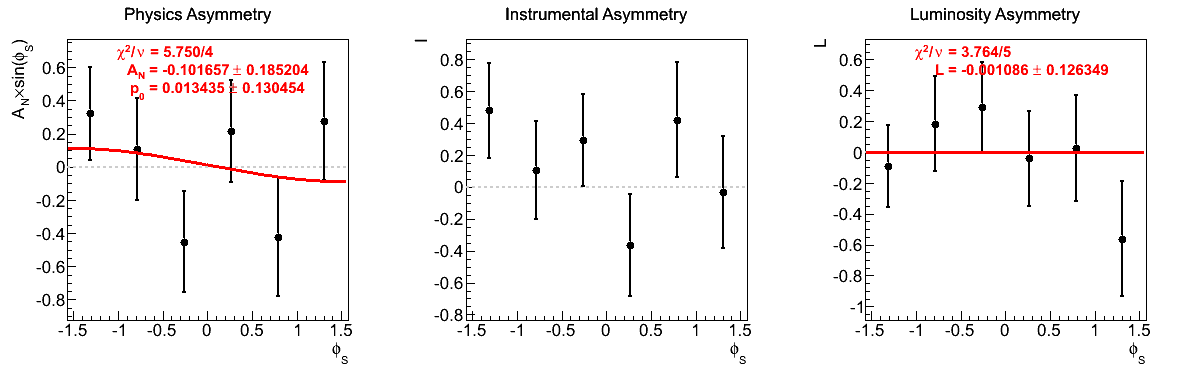The fits appear to be far more stable in p_T bins than x_F-bins. Albeit, the x_F > 0 asymmetries in x_F bins appear to be fairly stable, themselves.

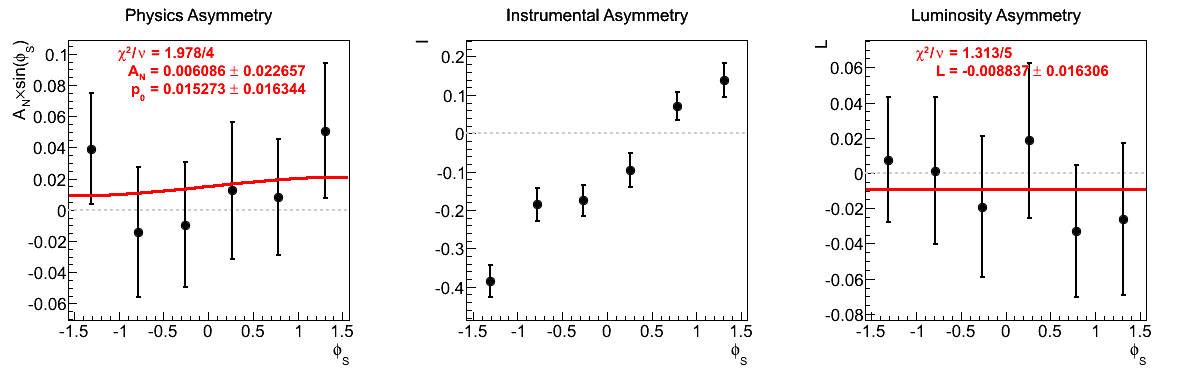
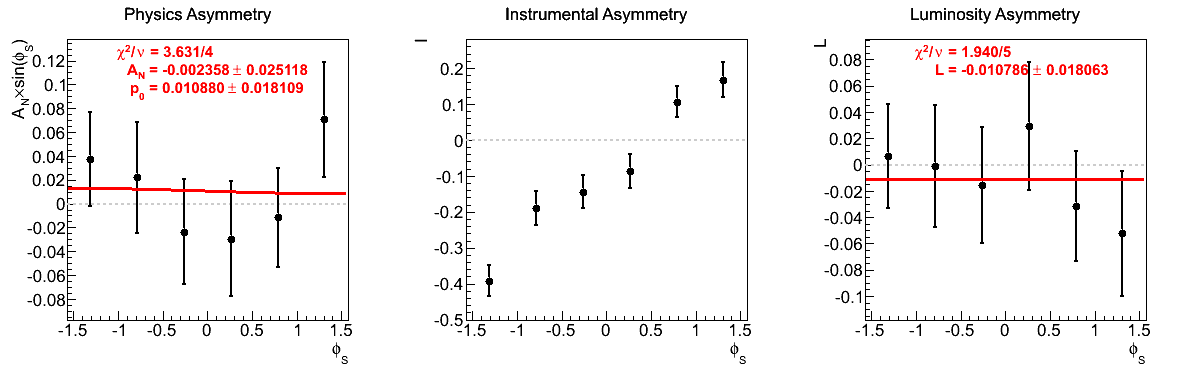
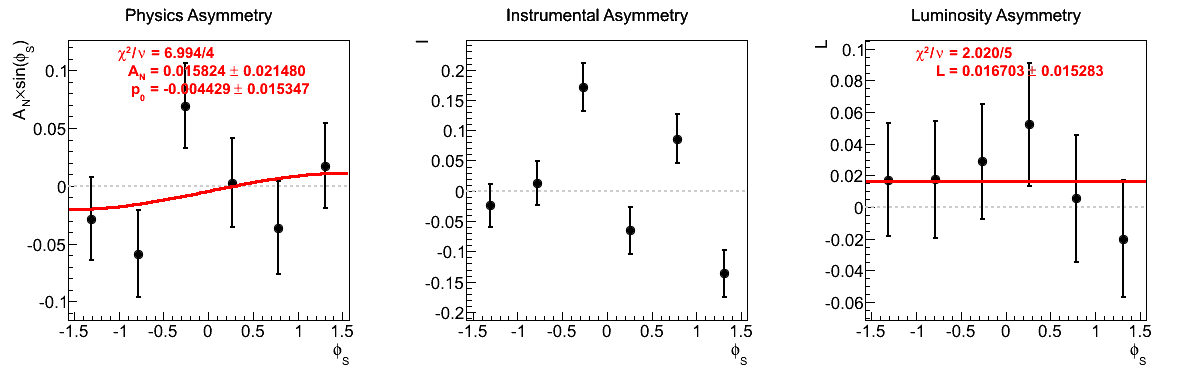
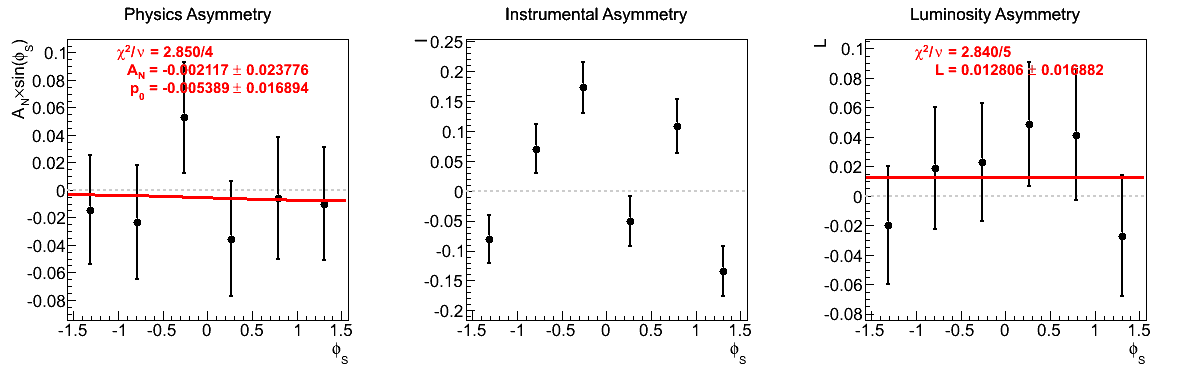
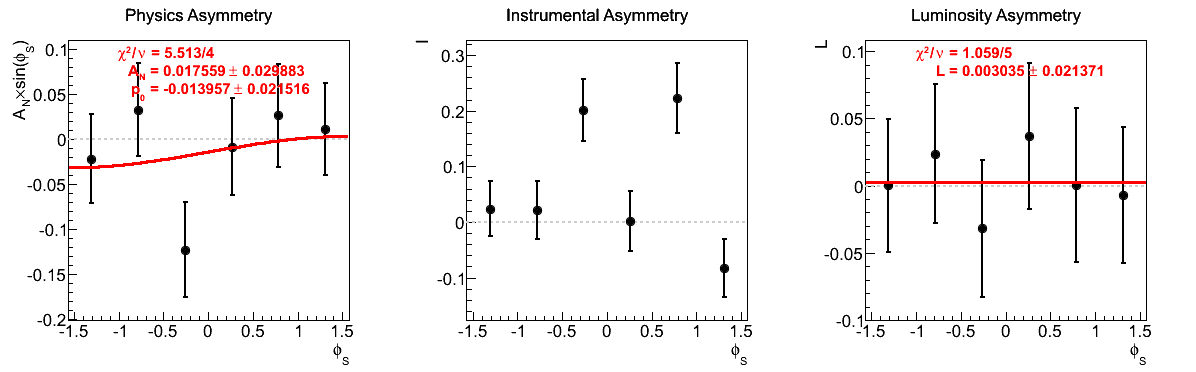
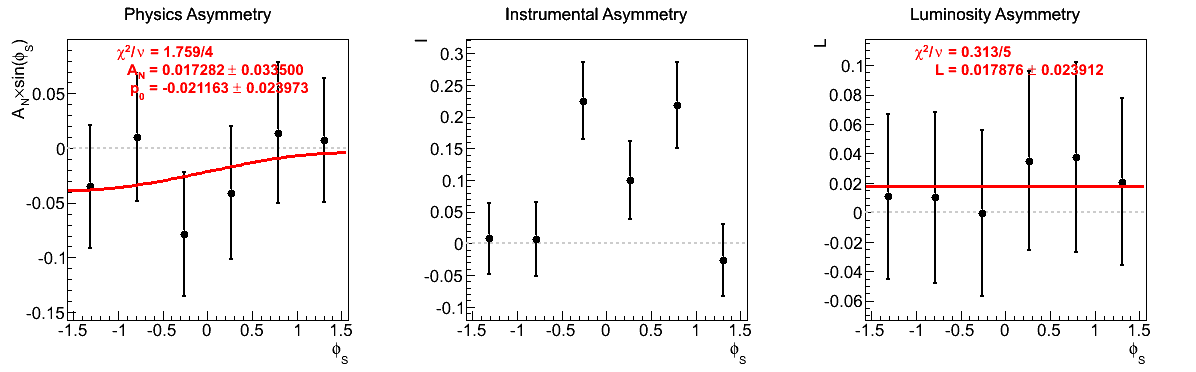
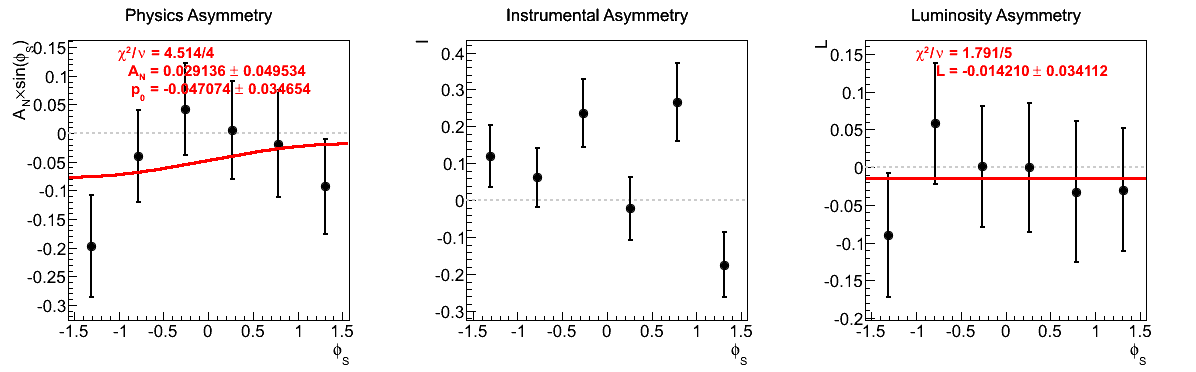
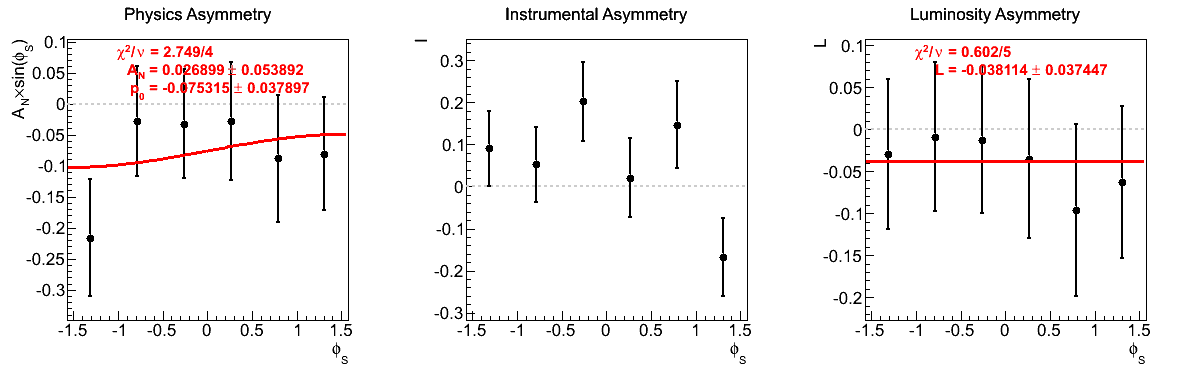
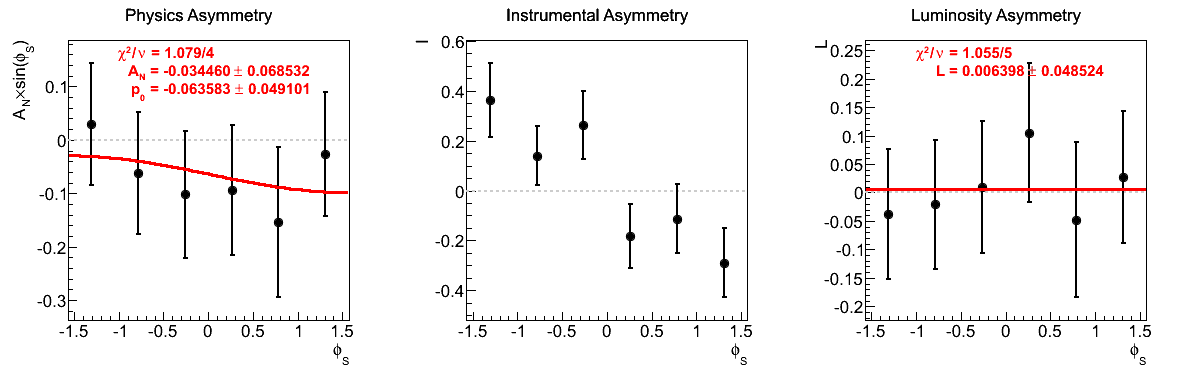
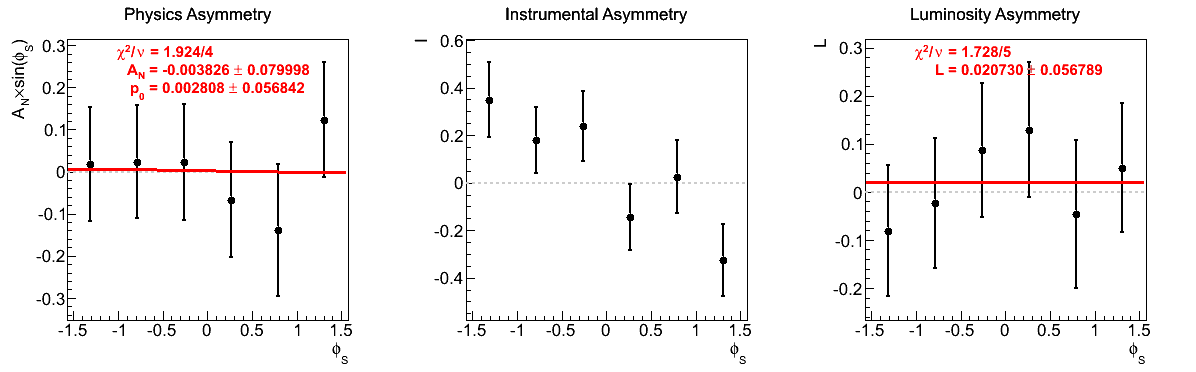
Figure 10: x_F < 0

1 < mγγ < 2 GeV/c2	1.05 < mγγ < 1.65 GeV/c2
4 < pT < 5 GeV/c
5 < pT < 6 GeV/c
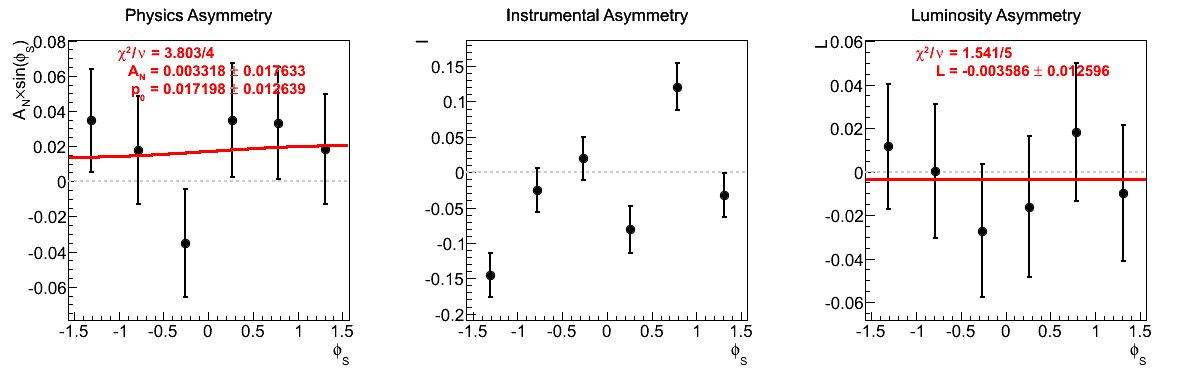6 < pT < 7 GeV/c
7 < pT < 8 GeV/c
8 < pT < 9 GeV/c
9 < pT < 10 GeV/c
10 < pT < 12 GeV/c
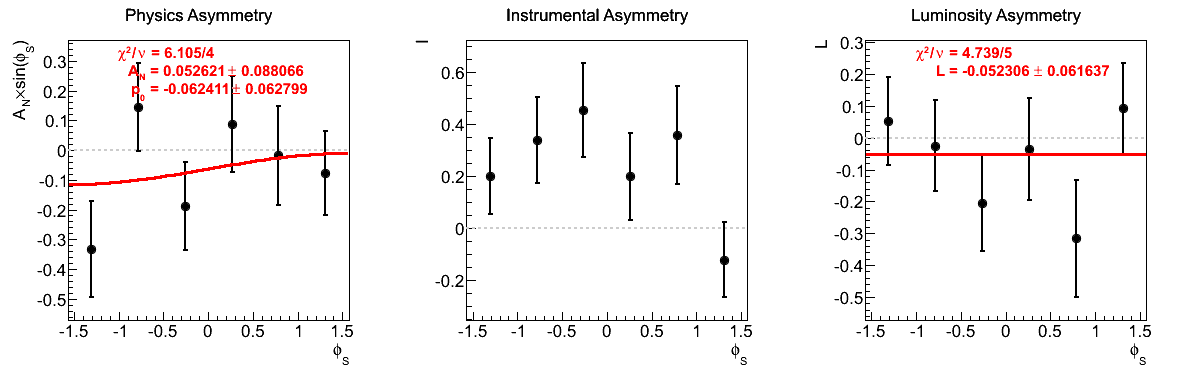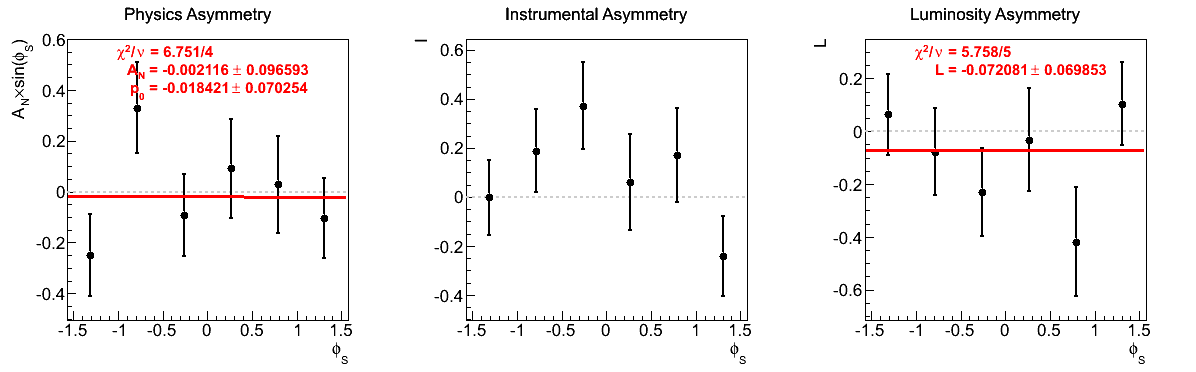12 < pT < 16 GeV/c

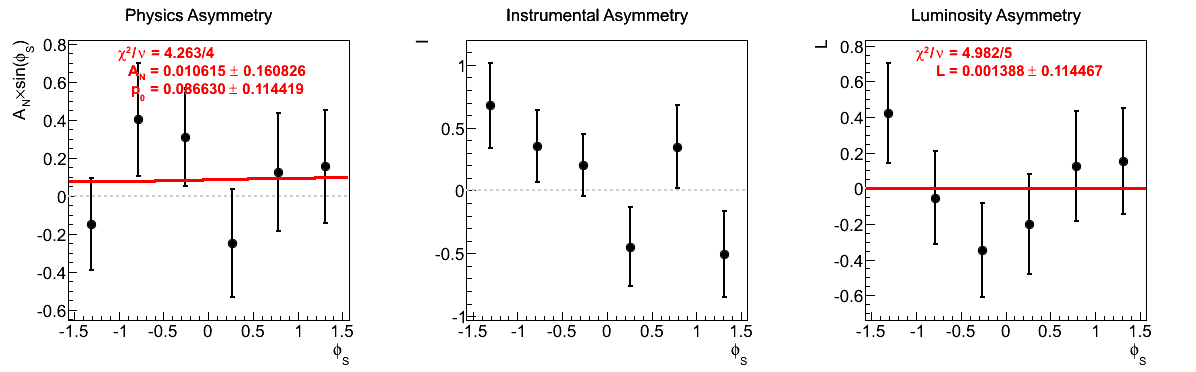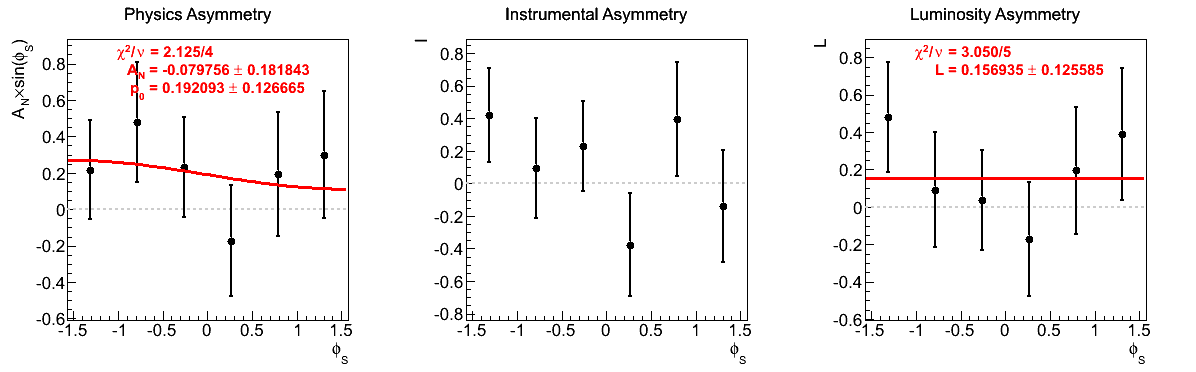One notes that in the highest p_T bin there is some shifting of central values, sufficient to flip the sign of the extracted asymmetry. Again, the first bin appears to shift to the other side of the horizontal. The change, however, is not on the order of the statistical uncertainties (again, keeping in mind that the events are highly correlated).

Spin-sorted Mass Peaks

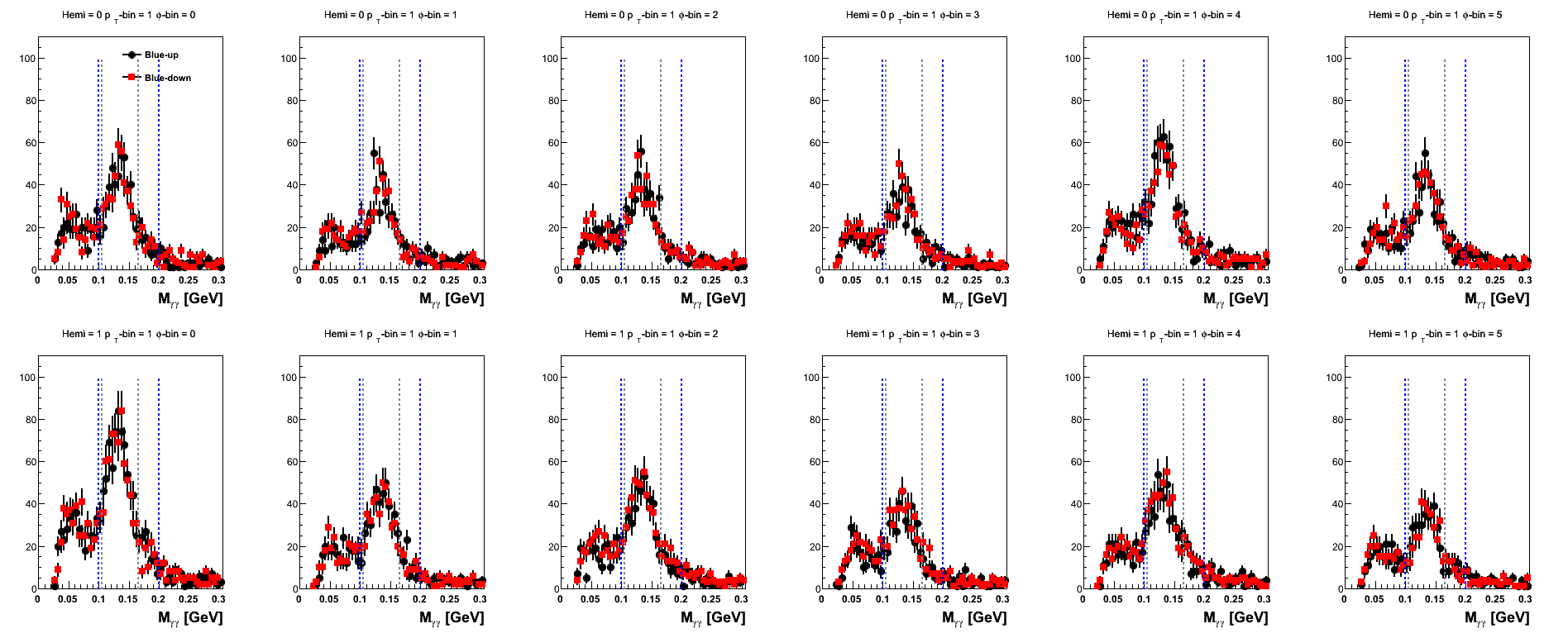
It is also useful to examine the mass peaks from Fig. 1 and Fig. 2, now, sorted into spin states. It is from these distributions, integrated over the appropriate invariant mass range, that we get the raw asymmetries. The following plots are shown with the spins sorted for blue beam spin states and yellow beam spin states, separately. The distributions are shown separated into hemispheres (first row shows "up" hemisphere, second row shows "down" hemisphere) and φ-bins. On the figures is denoted the nominal mass window in royal blue and the tighter window used for the systematic estimation in gray.

Figure 11: Blue Beam Sorted (x_F-bins)

0.06 < xF < 0.13
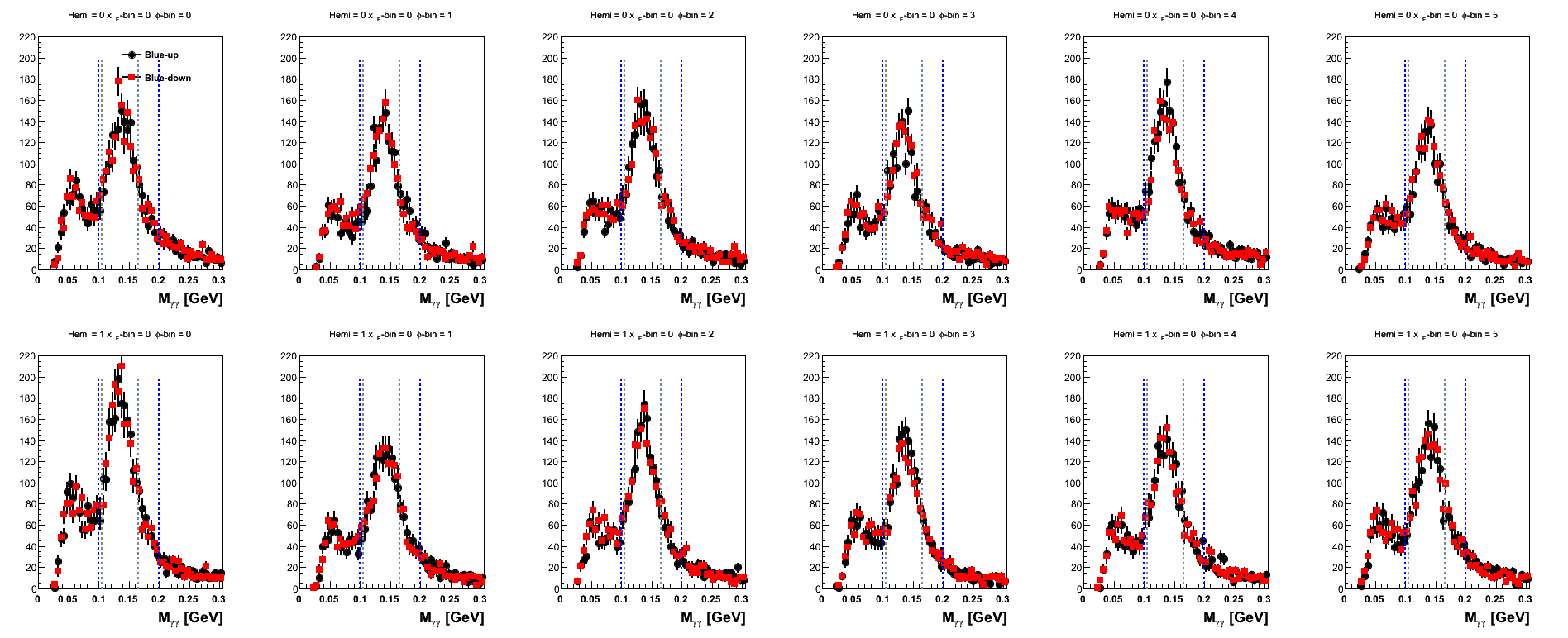0.13 < xF < 0.20
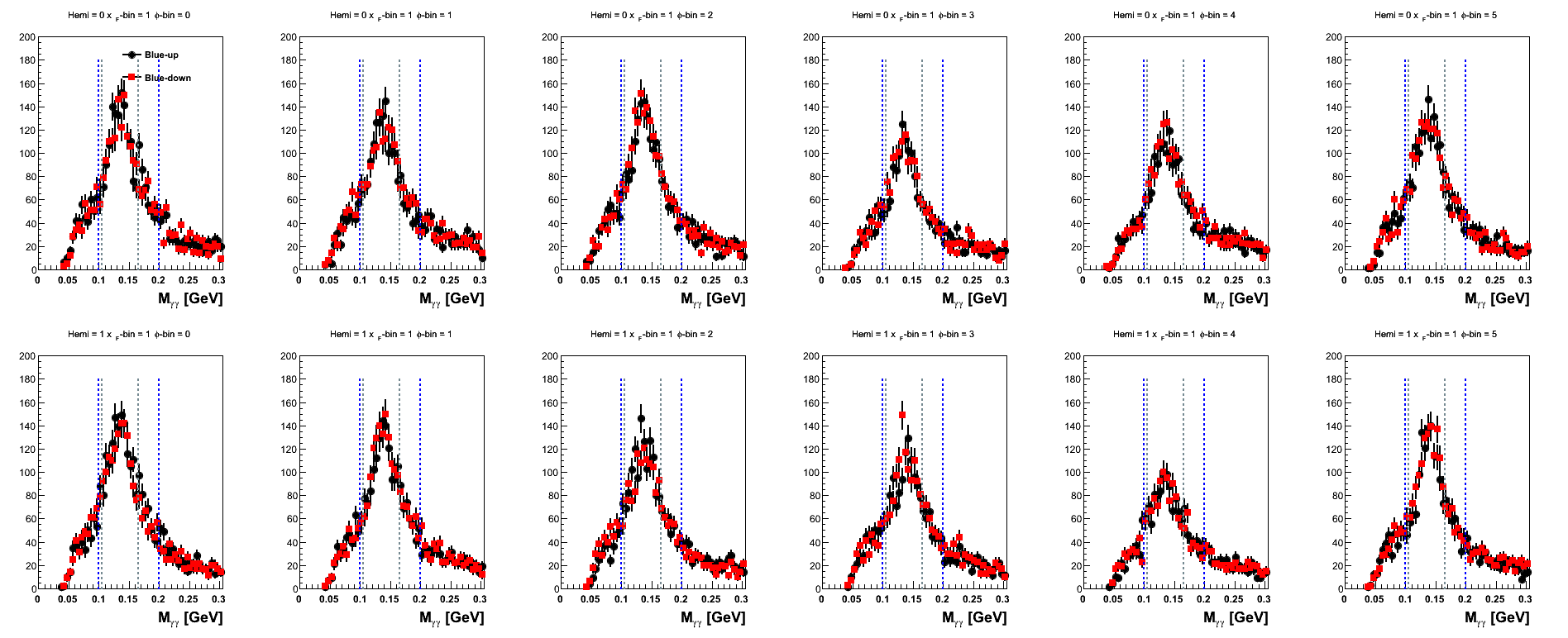0.20 < xF < 0.27

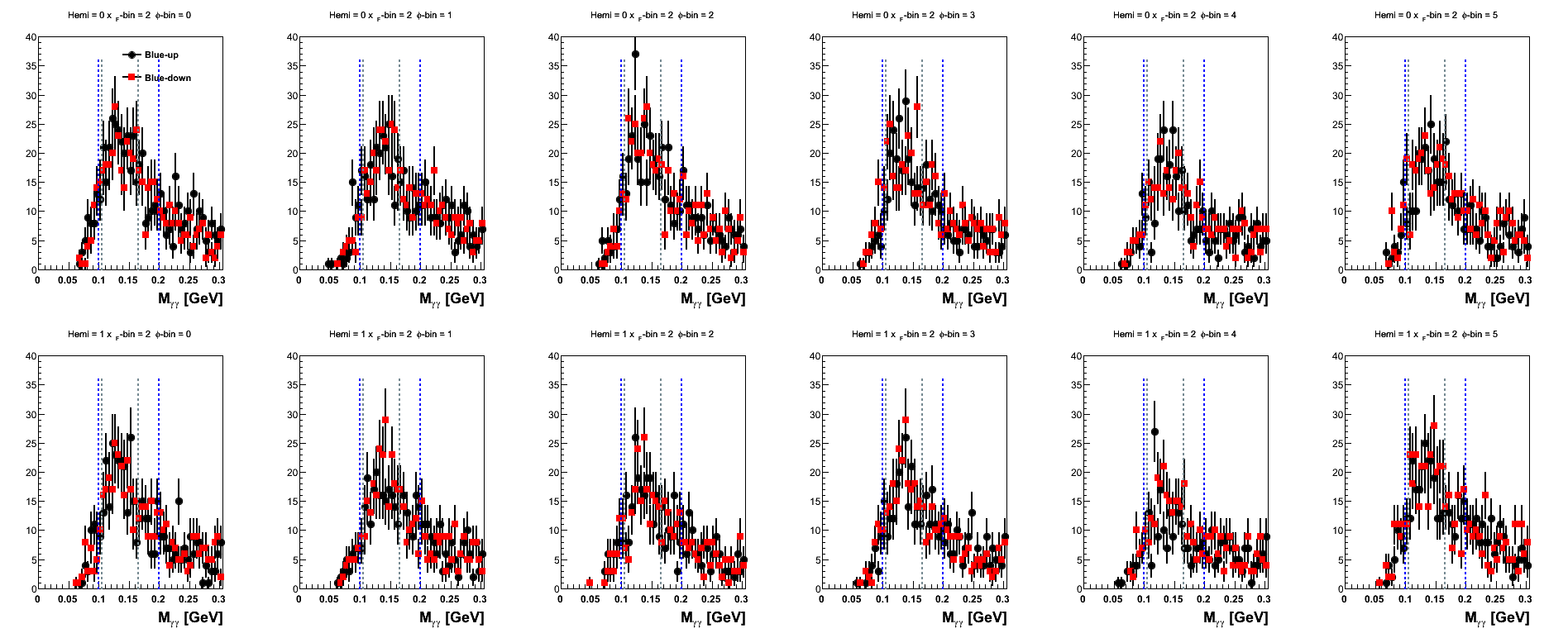One can see that the mass distributions are rather similar in shape between the spins states. For x_F > 0.2, one sees that the statistics begin to drop off quite significantly.

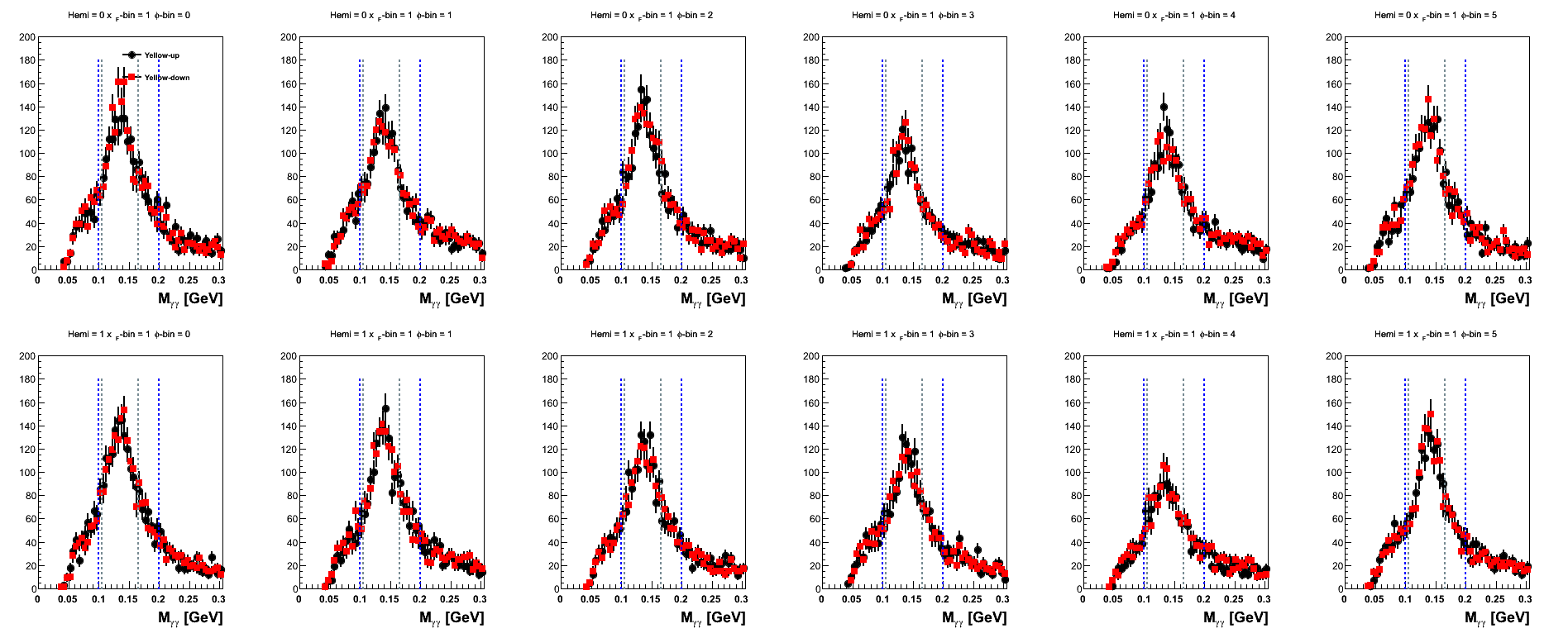
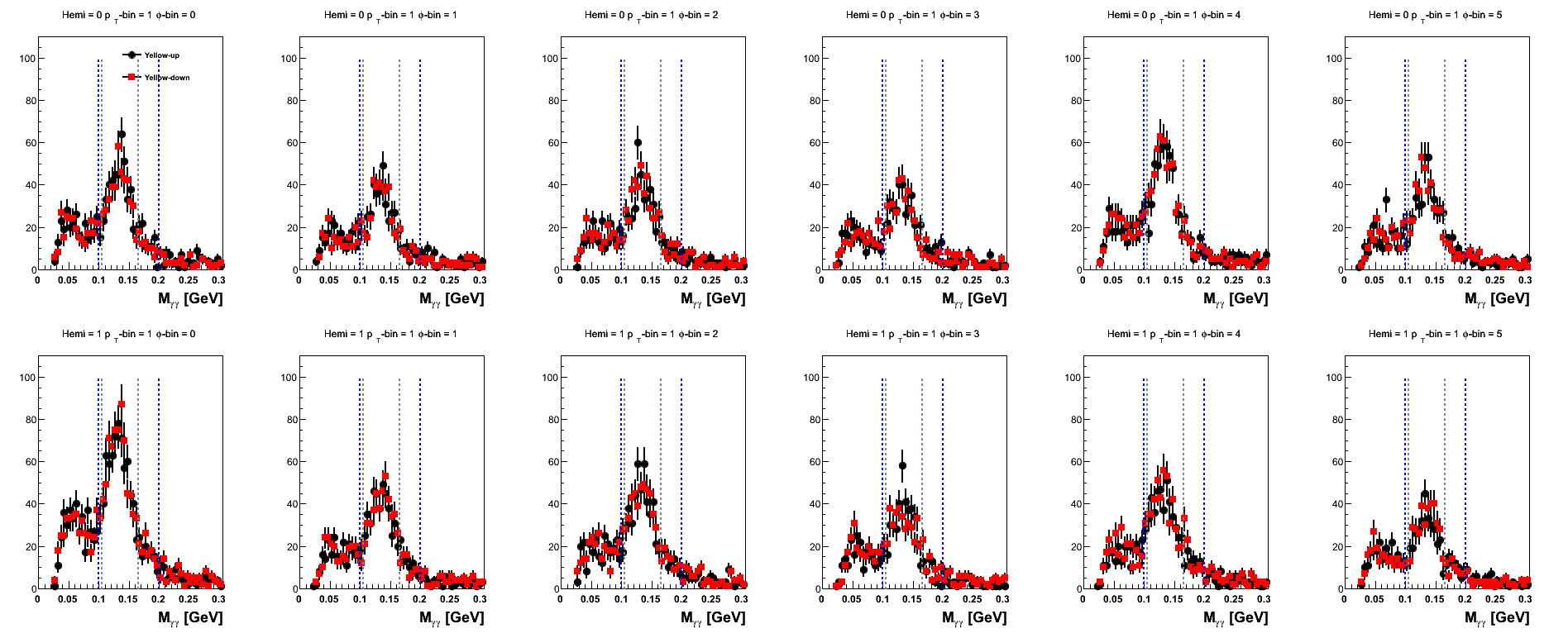
Figure 12: Yellow Beam Sorted (x_F-bins)

0.06 < xF < 0.13
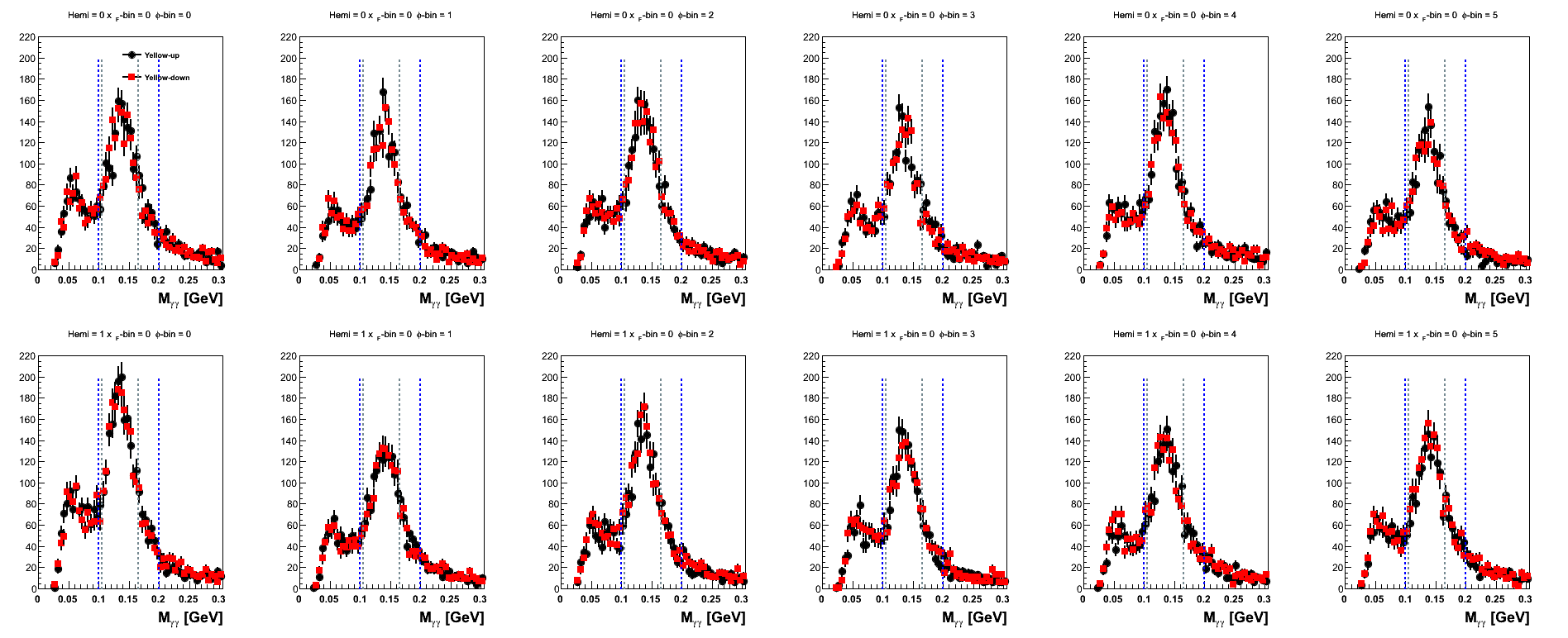0.13 < xF < 0.20
0.20 < xF < 0.27

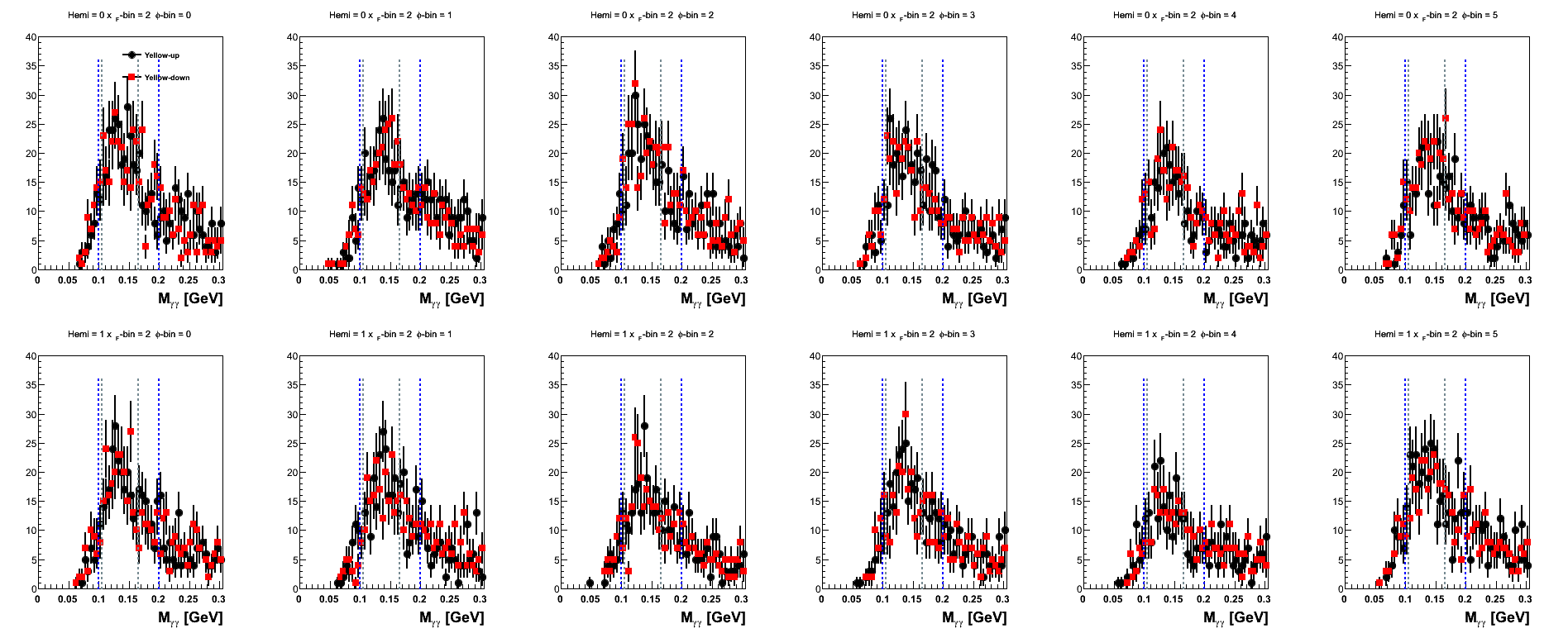Again, one sees that statistics are quite low for the highest x_F-bin. Let us consider for a moment the first φ-bin as an example. One has for the relevant blue beam yields with the nominal mass window

N^↑_up = 350

N^↓_up = 349

N^↑_down = 311

N^↓_down = 314.

For the alternative mass window one finds

N^↑_up = 252

N^↓_up = 240

N^↑_down = 224

N^↓_down = 218.

So, on average, the stricter mass window reduces the yield by 29.5%. The spin-down yields appear reduced by 31% while the spin-up yields appear reduced by 28%. For the relevant yellow beam yields one finds for the nominal mass window

N^↑_up = 345

N^↓_up = 354

N^↑_down = 320

N^↓_down = 305

and for the alternative mass window

N^↑_up = 253

N^↓_up = 239

N^↑_down = 218

N^↓_down = 224.

Thus, for the yellow beam, N^↓_up and N^↑_down are reduced by 32%; and N^↑_up and N^↓_down are reduced by 27%. One can see from Fig. 8 that for the highest x_F bin the blue beam spin-down points tend to sit higher than the spin-up points in the high-mass band (0.165 < m_γγ < 0.2 GeV/c²) excluded by the tight cut. Also, one can see from Fig. 9 that for the highest x_F bin the lower hemisphere spin-up points tend to sit below the spin-down points in the high-mass band. Additionally, one can see that the upper hemisphere spin down points fluctuate a bit within the high mass band region. Evidently, these conspire to produce the following raw cross-ratios: for the nominal window ε_blue = 0.3% and ε_yellow = -1.8%; for the systematic window ε_blue = 0.5% and ε_yellow = 2.1%. Given the qualitative properties of the mass distributions at these kinematics, it is difficult for me to rule out statistics as the culprit, though I am always open to other suggestions.

Figure 13: Raw Asymmetries for 0.165 < m_γγ < 0.2 GeV/c²

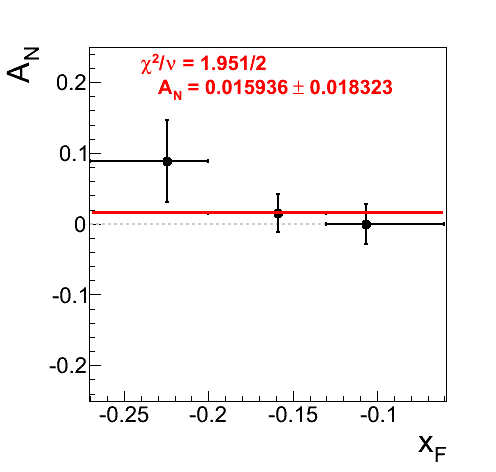
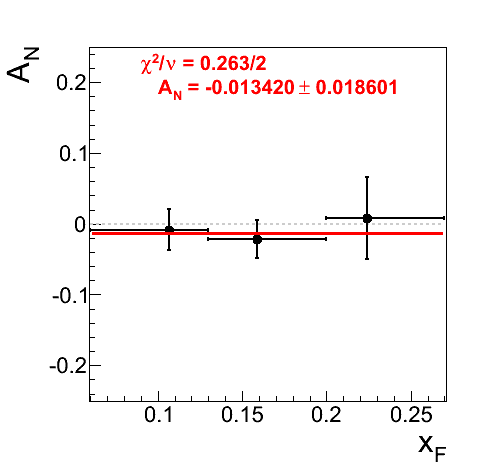
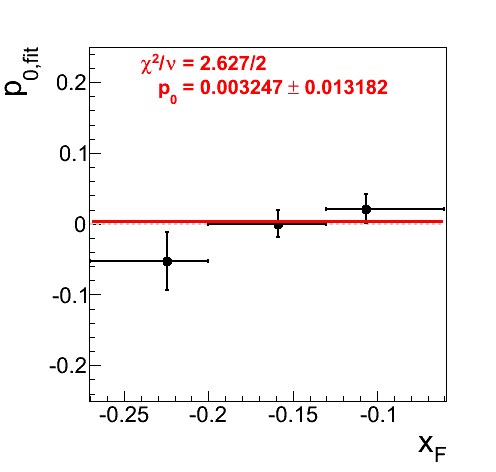
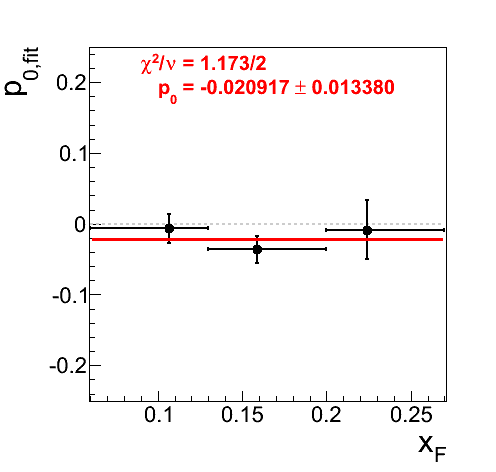
When one isolates the raw, i.e. not corrected for signal-fraction, asymmetries for the high mass band, one sees that there is not a statistically significant dependence on x_F. Further, there is indeed a large (~8.9%) asymmetry in the highest bin for x_F < 0, however, the effect is only 1.54σ. The p₀'s are tiny and perfectly consistent with zero.

Figure 14: Asymmetries Using Standard Signal Fraction Values for 0.165 < m_γγ < 0.2 GeV/c²

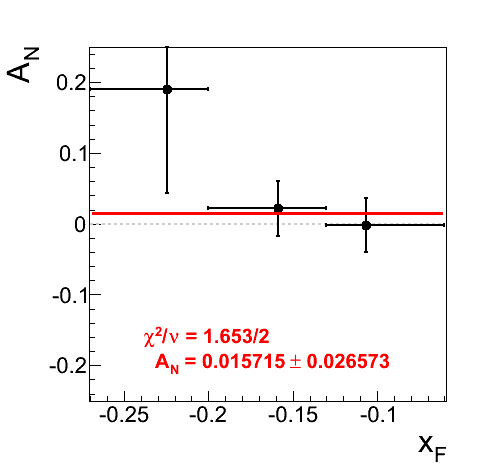
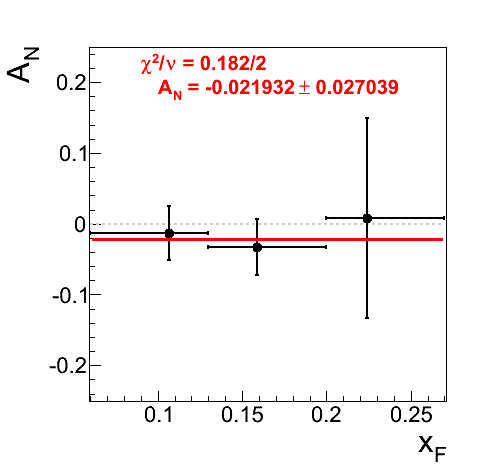
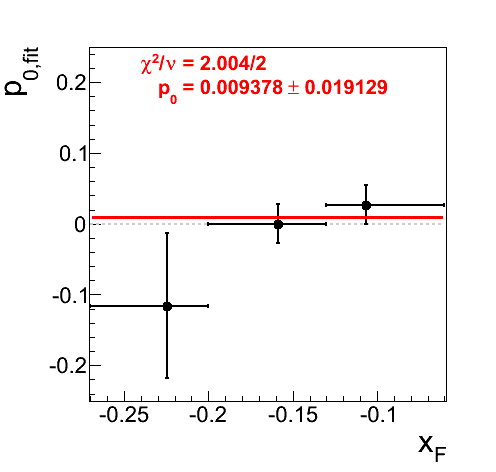
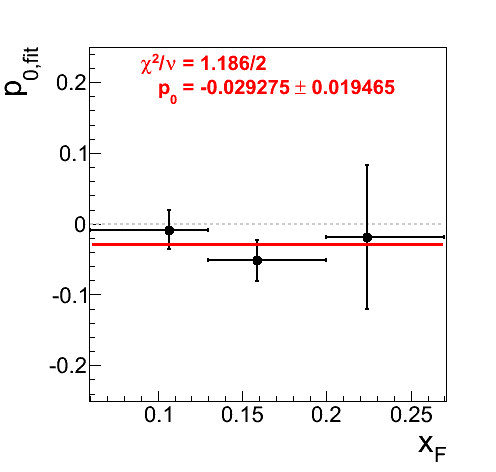
In Fig. 14 I have calculated the asymmetry for pions using the standard background correction procedure. One can see that the highest bin for x_F < 0 contains a large asymmetry (19.1%) with large error (14.7%). The effect is 1.3σ.

Figure 15: Asymmetry Comparison for x_F < 0

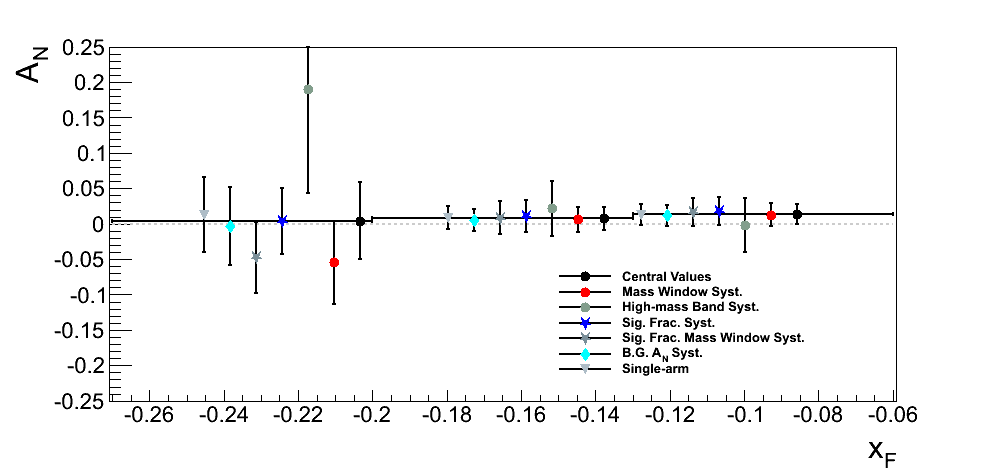
In Fig. 15 I post the asymmetry comparison between some various calculations. This is quite similar to the version I showed during the PWG (also posted below), except that it now includes the high-mass band asymmetries from Fig. 14 and tight-window asymmetries using the alternative signal fraction calculations. One can see that the variation between the "Mass Window" and "High-mass Band" asymmetries (using independent datasets) are not statistically significant. The variation in the highest bin is 1.55σ.

Figure 16: Blue Beam Sorted (p_T-bins)

4 < pT < 5 GeV/c
5 < pT < 6 GeV/c
6 < pT < 7 GeV/c
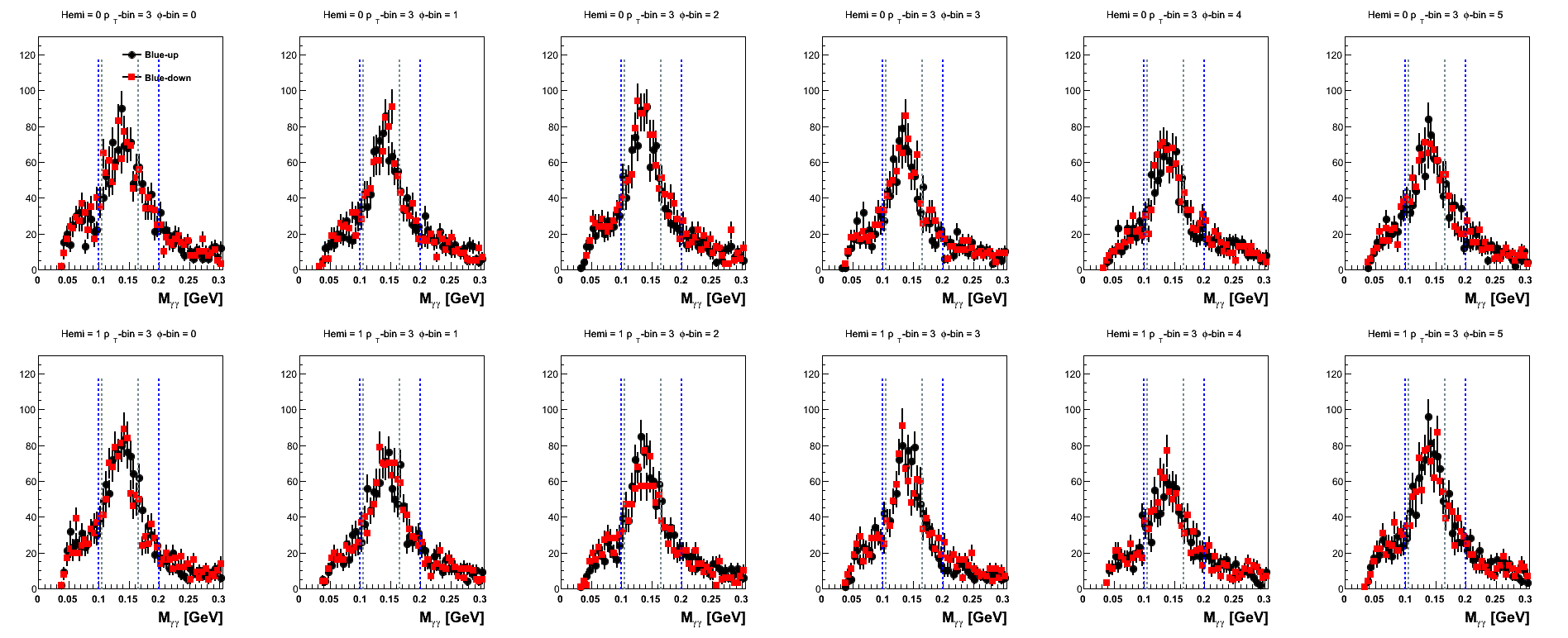7 < pT < 8 GeV/c
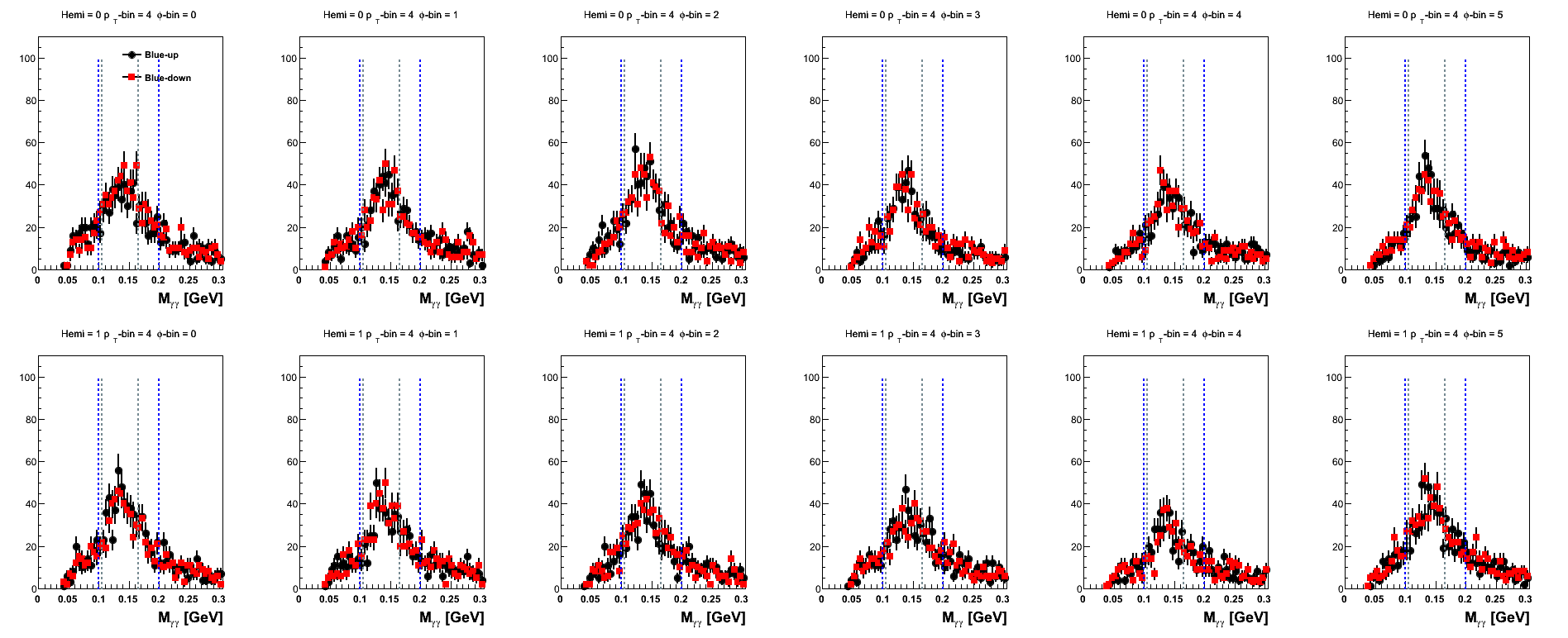8 < pT < 9 GeV/c
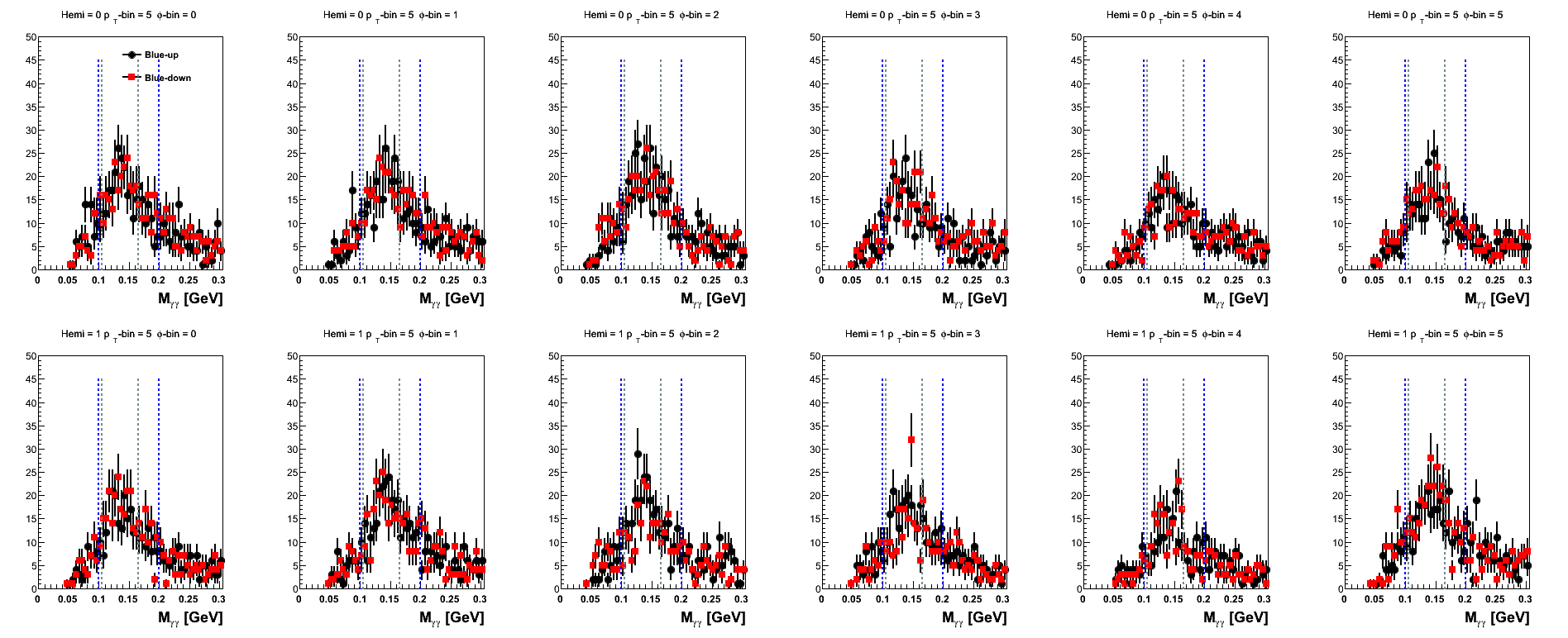9 < pT < 10 GeV/c
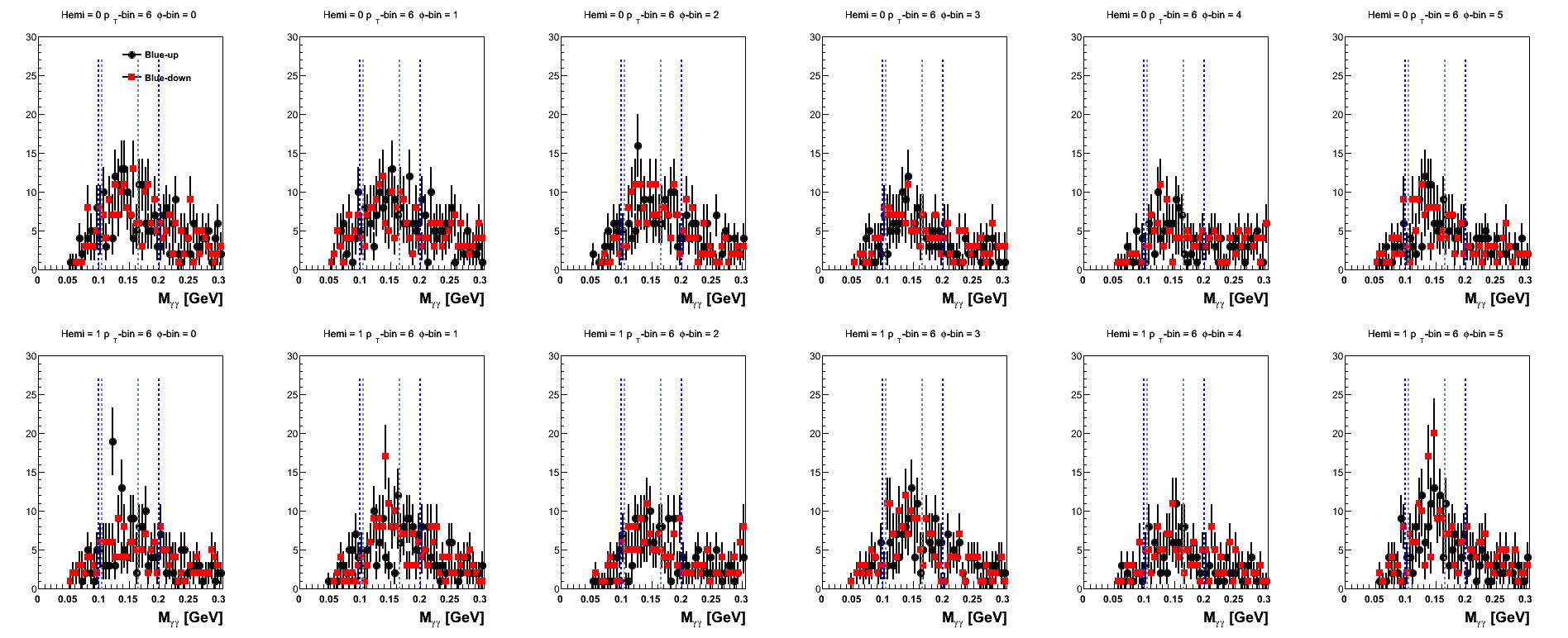10 < pT < 12 GeV/c
12 < pT < 16 GeV/c

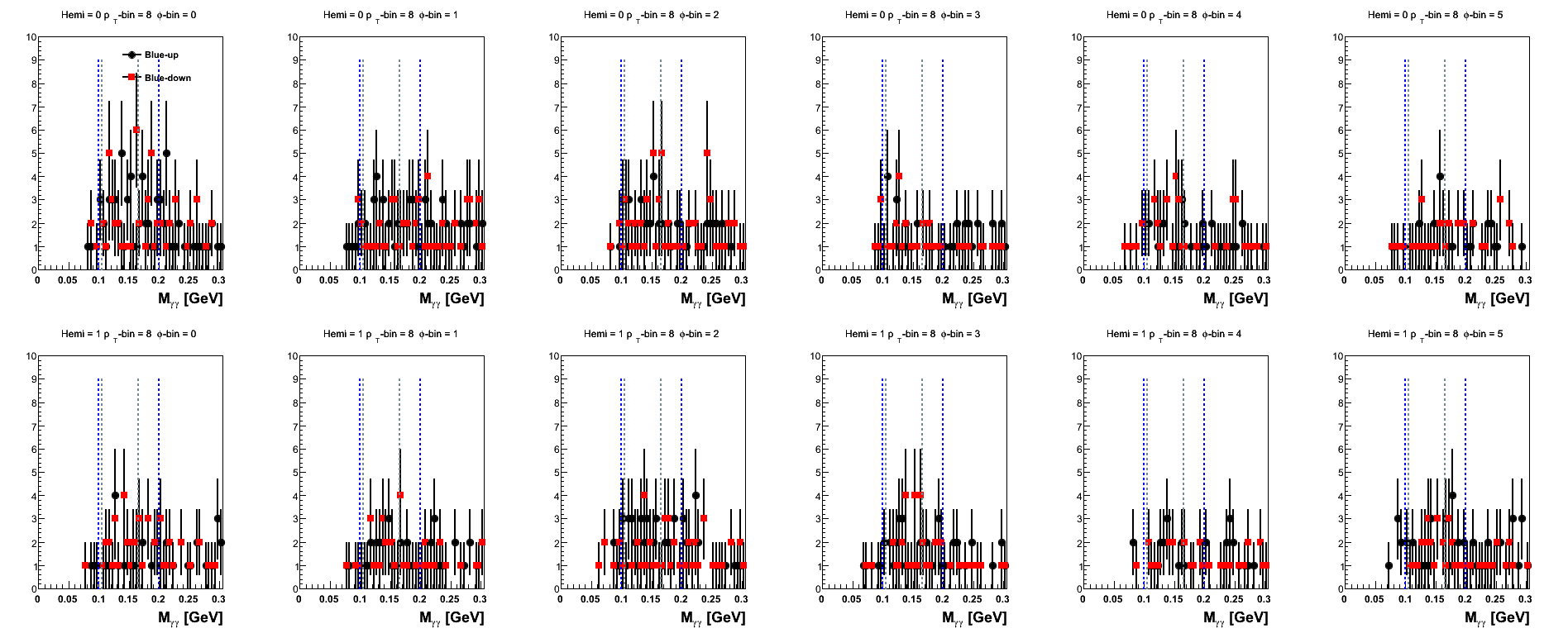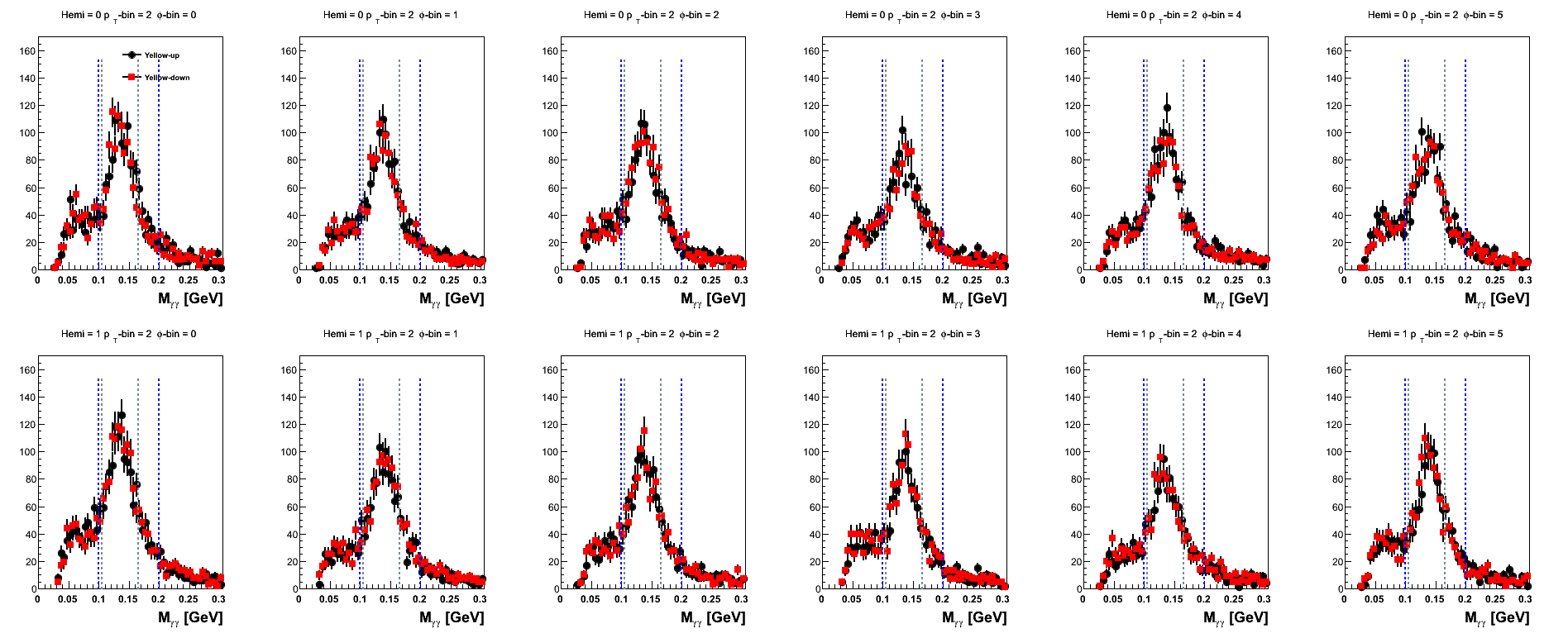
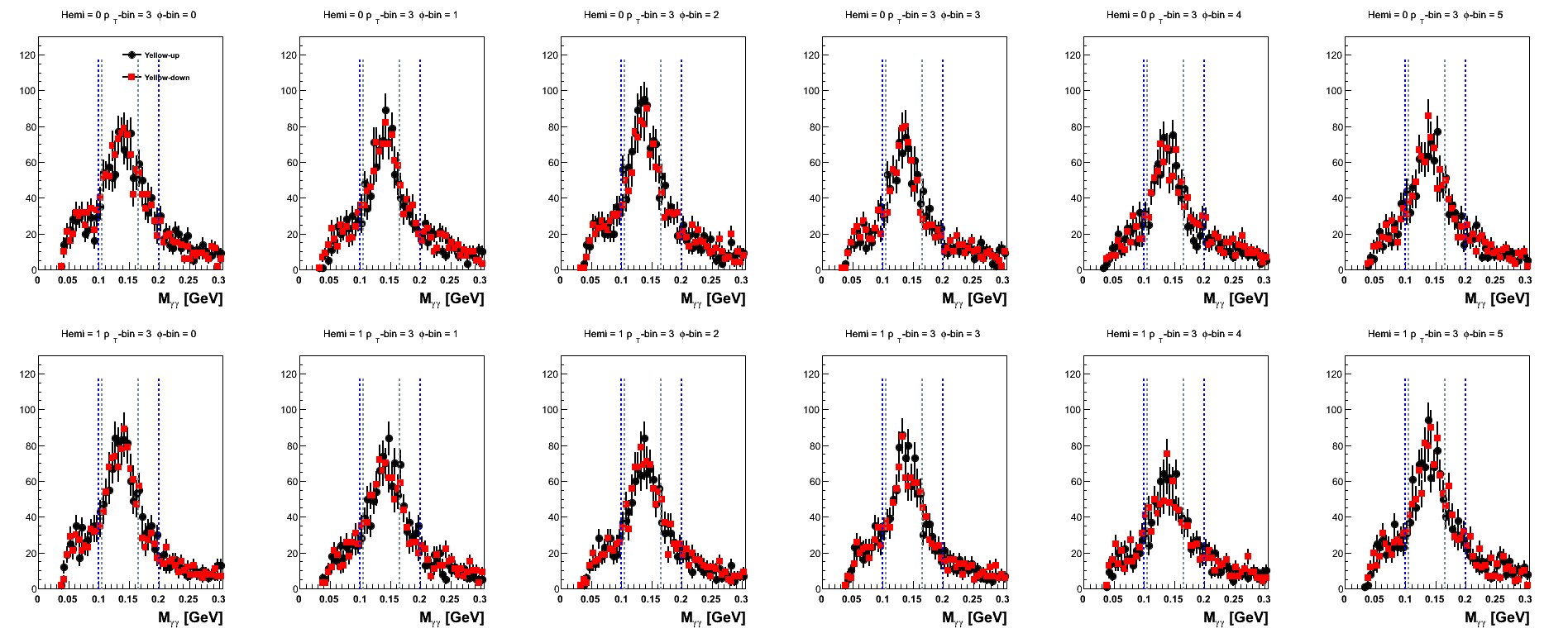
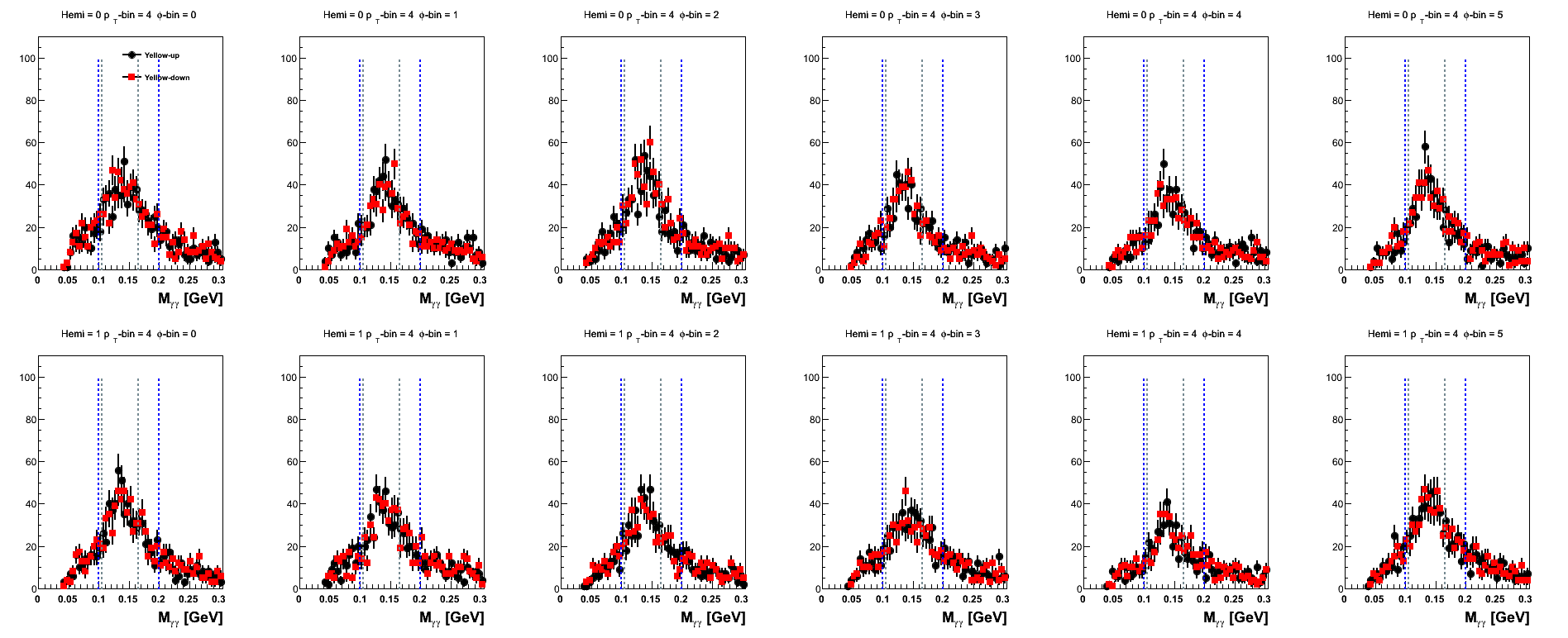
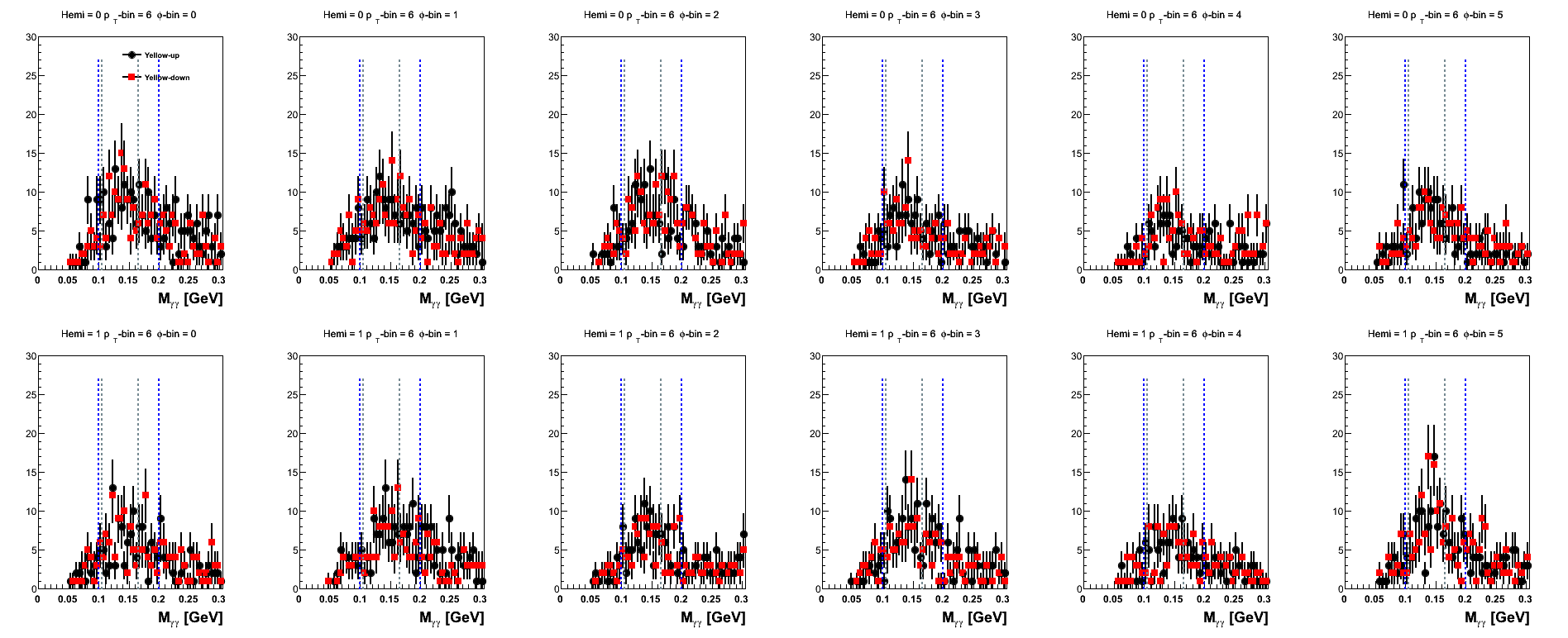
Figure 17: Yellow Beam Sorted (p_T-bins)

4 < pT < 5 GeV/c
5 < pT < 6 GeV/c
6 < pT < 7 GeV/c
7 < pT < 8 GeV/c
8 < pT < 9 GeV/c
9 < pT < 10 GeV/c
10 < pT < 12 GeV/c
12 < pT < 16 GeV/c

The mass distributions for p_T-bins are posted here, mainly, for the sake of completeness. One notes that the high-p_T bins are rather sparsely populated when sepating into spin-states and φ-bins.

Background Asymmetry

The final piece of the formula is A_N for the background events. There are various ways to estimate the background contribution. Our original intent was to extract the asymmetries from signal yields calculated from the phi-binned mass plots. This would effectively separate the signal and background asymmetries up front. However, the requires a good deal more Monte Carlo than we have. Our alternative approach is to estimate the background asymmetry by calculating A_N as a function of invariant mass. Under these circumstances it is difficult to bin in x_F and p_T, thus, we simply calculate the asymmetries for mass distributions integrated over the kinematic variables.

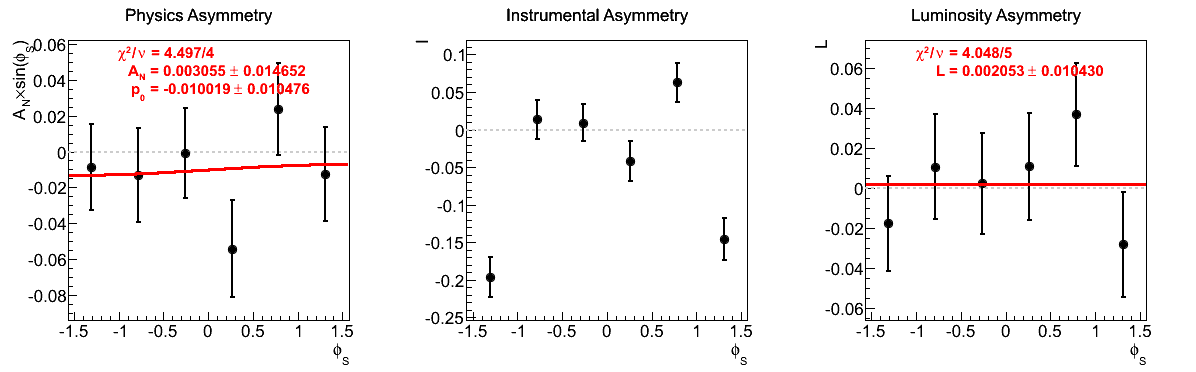
Figure 18

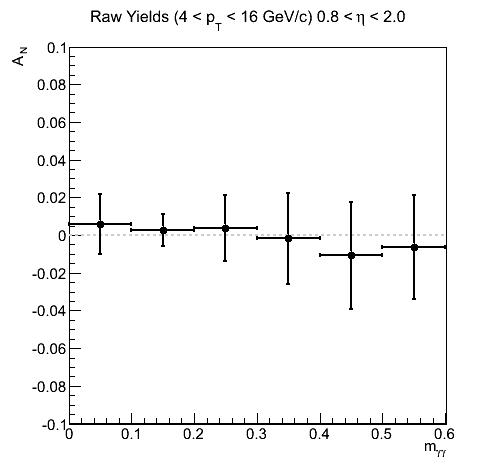
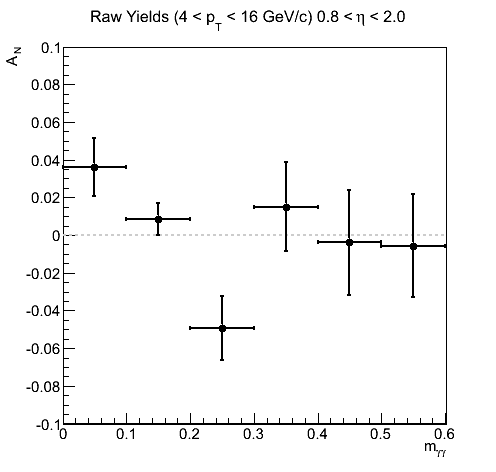
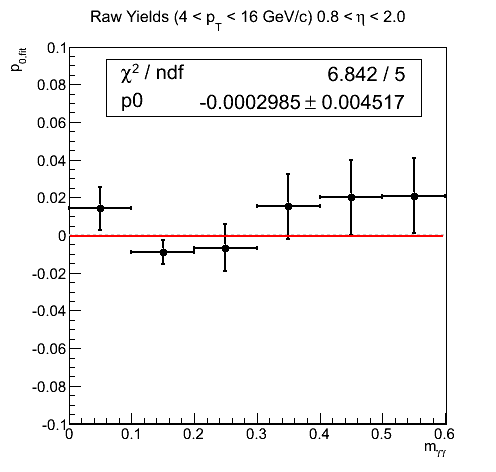
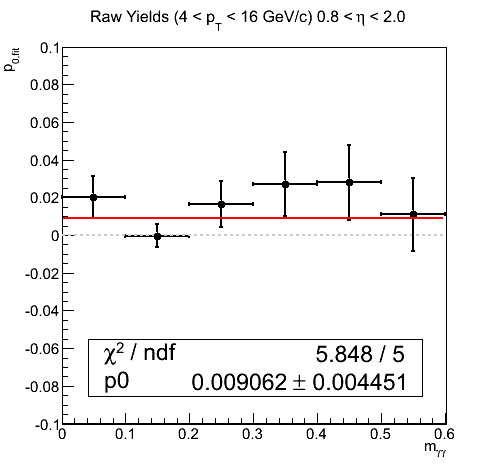
One can see that in the signal region, the asymmetries and p₀'s are rather quite small and not inconsistent with zero. Outside of these regions, however, there are some fluctuations in x_F < 0. Thus, we have adopted the following approach. For our central values, we assume for the background asymmetry the average of A_N for 0 < m_γγ < 0.1 GeV/c² and 2 < m_γγ < 0.3 GeV/c² for blue (turns out to be 0.005±0.012) and 0 for yellow. For systematics we calculate the asymmetry with a different value for the background asymmetry and take the difference between this and the previous version. For the yellow beam asymmetries, the behavior around the signal region appears rather linear. One might assume the background may contain positive asymmetry for the lower half of the signal region and a negative asymmetry for the upper half. Indeed, when one averages the values for the two neighboring bins one gets an answer rather close to zero. Thus, we have taken a value of 1%, comparable to the uncertainty on the two-bin average (1.2%), for an alternative background asymmetry. We apply this to both blue and yellow beam asymmetry calculations in estimating the systematic uncertainty due to the background asymmetry.

Summary of Various Studies

I included the following figures in my update to the PWG; and I post them, here, as well. They summarize various studies undertake to estimate our sensitivity to systematic errors. Namely, they compare our central-value calculation to calculations utilizing a different background asymmetry, calculations utilizing a different signal fraction estimation, calculations utilizing a different mass window, and calculations utilizing the yield-difference asymmetry formulation [i.e. fitting a sine-function to (N^↑-N^↓)/(N^↑+N^↓) binned in φ].

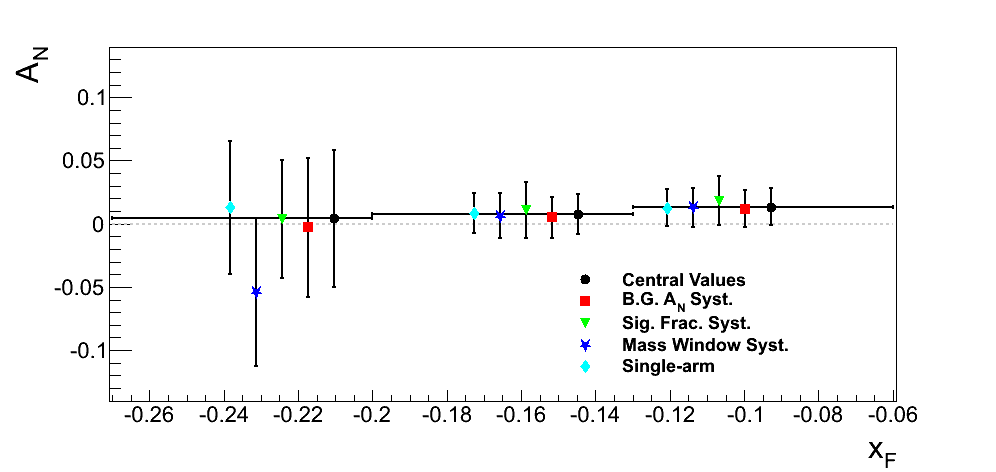
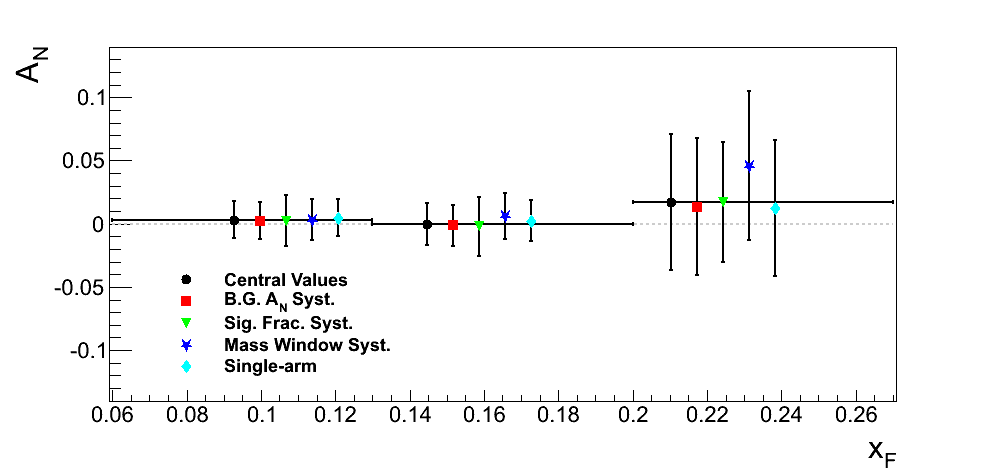
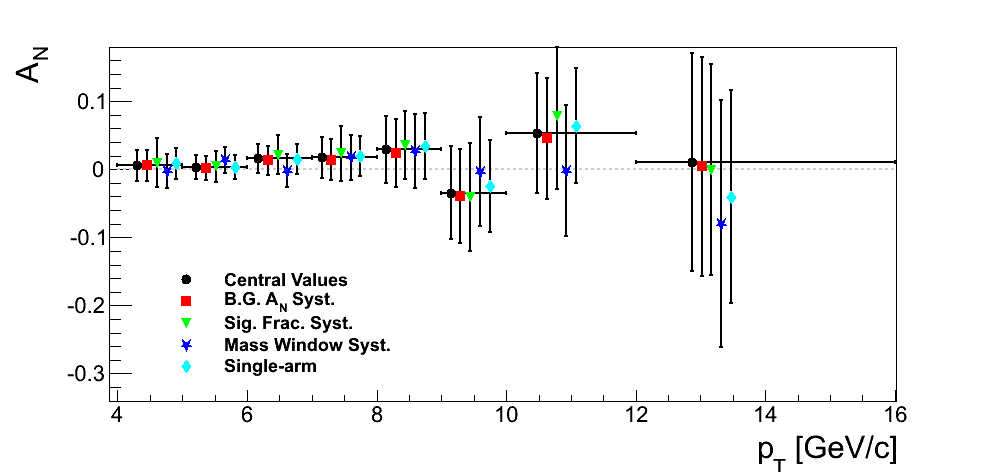
Figure 19

xF < 0	xF > 0

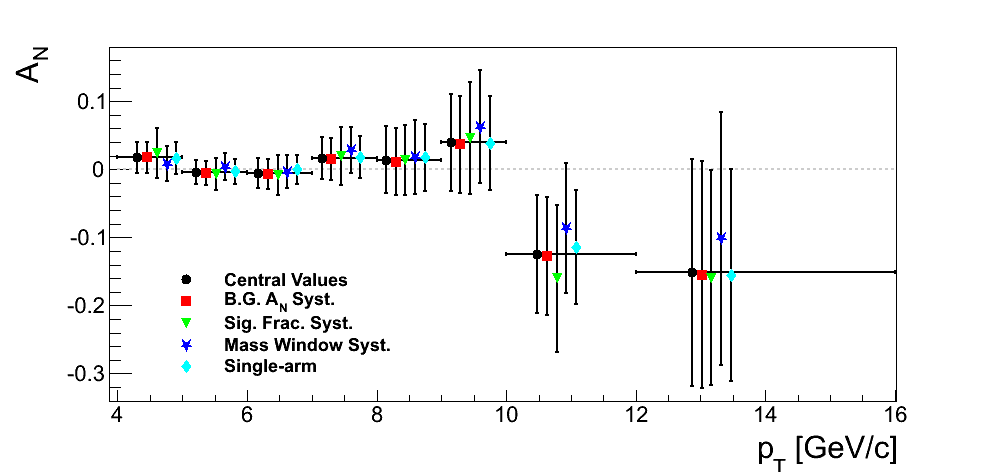Note that while we are not completely insensitive to various methodologies, our sensitivity is not significant given our level of precision. We have chosen to include as our systematic uncertainties differences due to the alternative background asymmetry and the alternative mass window added in quadrature. For our final result, we will continue to investigate the variations due to the mass window, as this tends to be our leading systematic.