We are investigating the use of Omnifold for the hadron-in-jet FF analysis. To set a baseline for comparison, I will run a quick unfolding study with RooUnfold. Omnifold is an iterative Baysian approach, so I will utilize the Baysian unfolding method in the RooUnfold package. For this first study, we will do a simple 1-D unfolding of the jet p_T. I will use the Run-11 embedding sample, as I've used previously. For what Omnifold calls the "synthetic," i.e., the simulation sample, I will use the nominal partonic p_T weights. For the "natural," i.e., the "data" sample, I've done a functional reweighting based on the partonic p_T.

Figure 1: The Migration Matrix

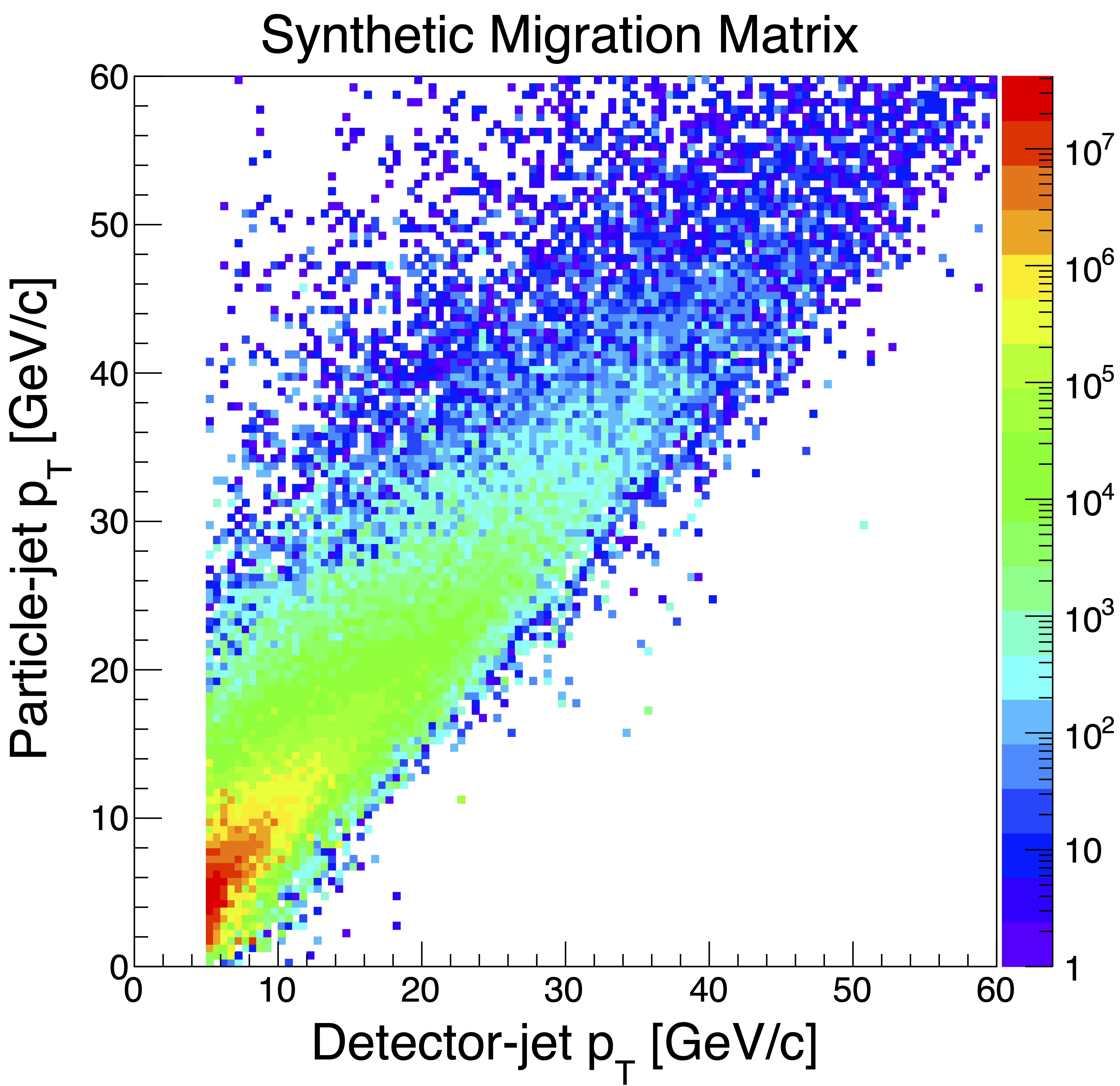
Figure 1 presents the migration matrix from the "synthetic" distribution, i.e., using the nominal partonic weights. This is passed to RooUnfold to create the "response" function.

Figure 2: Unfolding Results

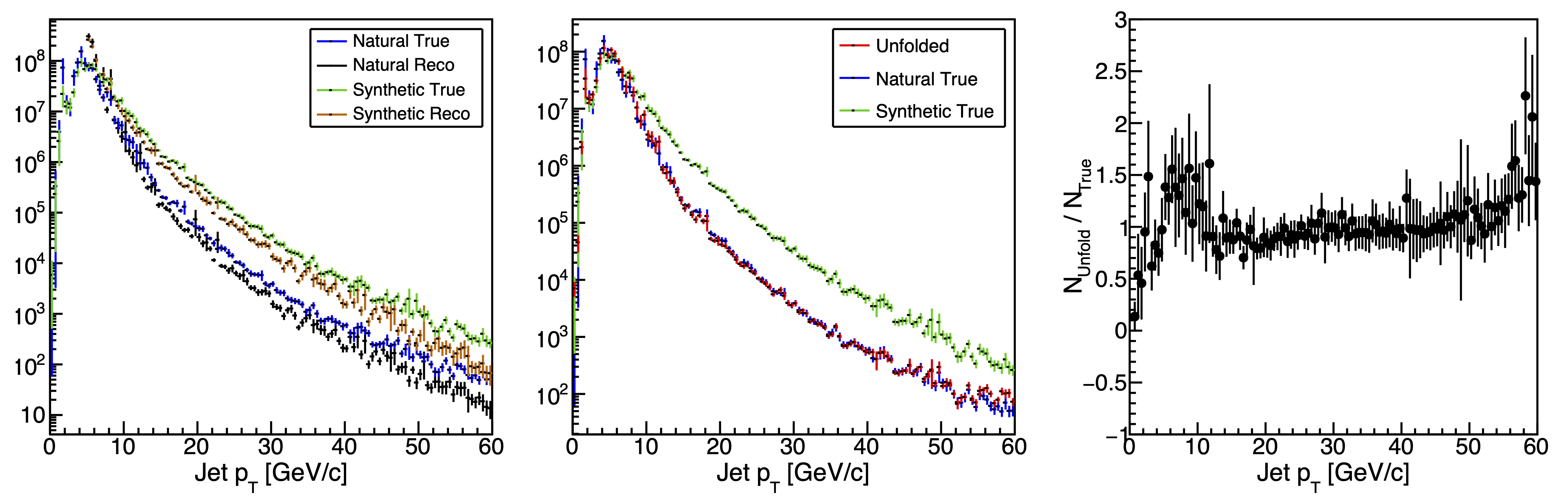
Figure 2 presents the unfolding results after 3 iterations. On the far left, I present the true and reconstructed distributions for the "natural" and "synthetic" samples. The synthetic has been normalized so that the two distributions have the same integral (total weight). In the middle panel, I compare the unfolded distribution to the natural and synthetic true distributions. On the right-hand panel, I present the ratio of the unfolded and natural true distributions. The uncertainties are likely not properly calculated, so don't take them too seriously. There is a bit of a wiggle around the detector-jet pT cutoff. Outside of that the match between the distributions is within a few 10s of percent.

This serves as a decent baseline for comparison to the machine-learning methods, e.g., Omnifold, which may ultimately provide some unique advantages.

Test with Vastly Different Initial Weights

Iterative Baysian unfolding is supposed to work well even for crazy initial weights, so I thought I'd try it out to ensure I am not biasing my result with an initialization that is "too good." In this pass, I initialize all the partonic p_T weights to 1. The results are shown below.

Figure 3: Migration Matrix with Unity Initial Weights

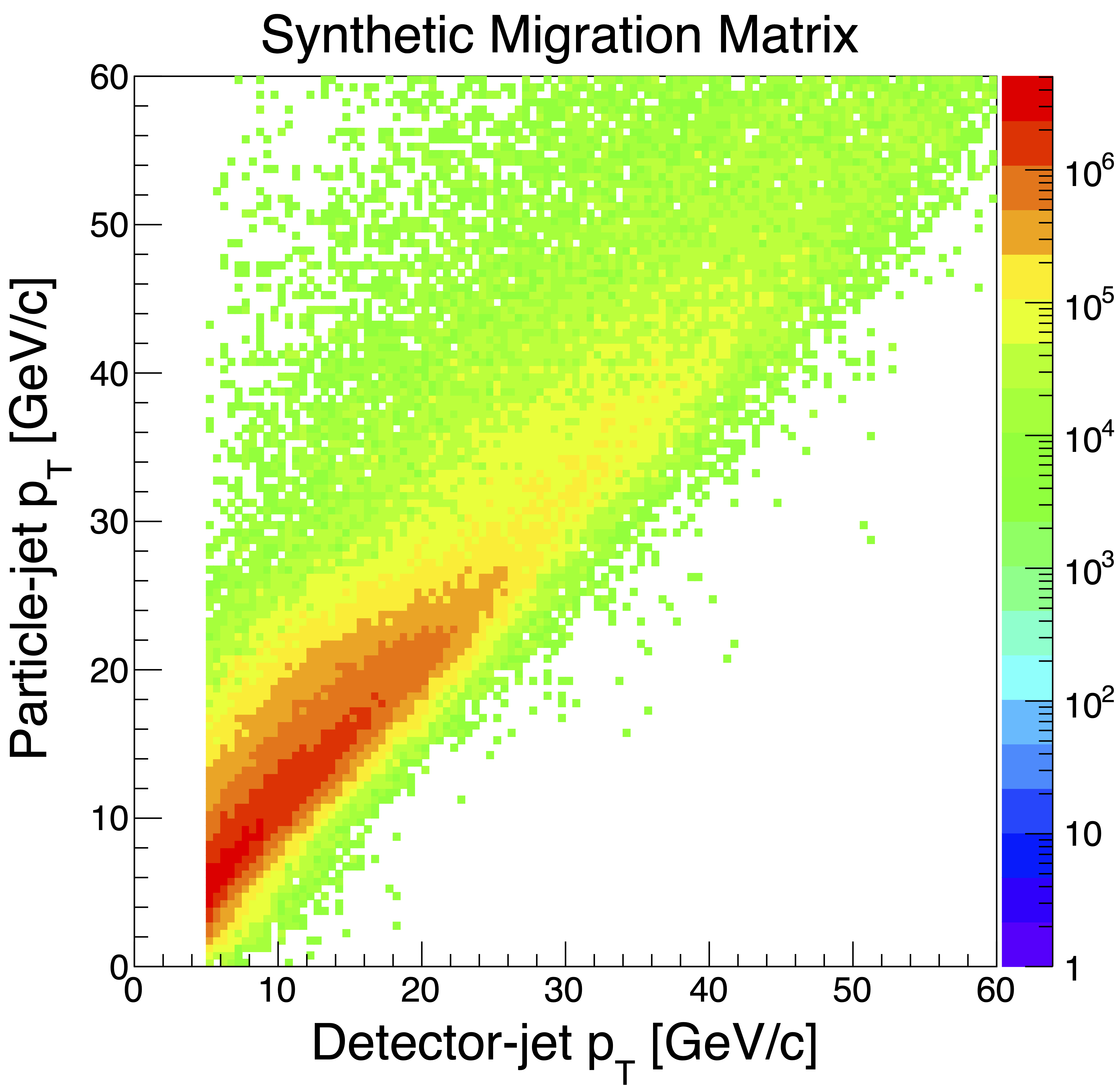
In this case, the migration matrix is essentially unchanged, save the event weights are different. Therefore, again, the response of the detector to a particular particle jet is the same between the natural and synthetic. It is only the event probabilities that are different. In principle, the procedure should work for different underlying physics assumptions between synthetic and natural.

Figure 4: Unfolding Results with Unity Initial Weights

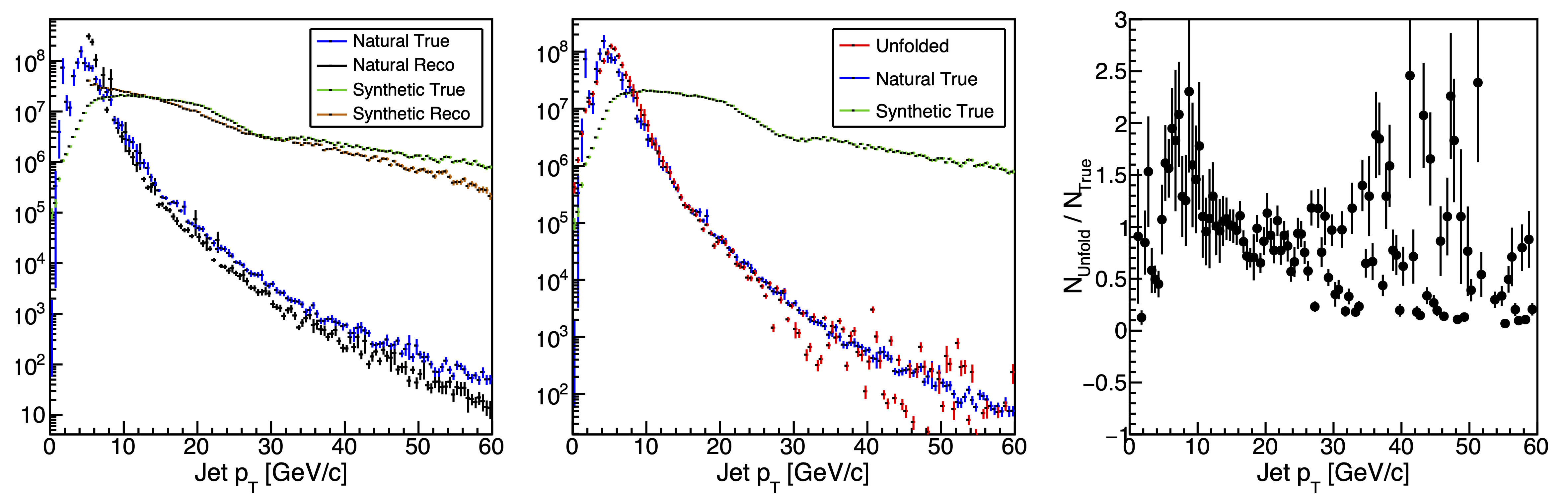
One can see on the far left that the synthetic jet spectrum is vastly different than the natural, now. However, after only three iterations, the unfolded spectrum (middle) matches the true natural distribution relatively well. The right-hand figure shows the ratio between the two. While the binning is rather fine for the available statistics, the scatter is clearly around unity, and quite good in the region of high statistics. This suggest to me that the procedure works well even when the initial assumption about the physics is quite wrong.