NOTE: We have not yet declared victory concerning the data-embedding discrepancies. However, if the PYTHIA-NLO disagreement is real and not, e.g., the result of inconsistently handling the L-W points, Carl has suggested that the culprit may be the primordial k_T PYTHIA parameter. As a quick check, I have generated another 3M PYTHIA events with the "Perugia 0" tune. However, I force the kT parameter [PARP(91)] to be 1 GeV rather than the default of 2 GeV.

Again, I normalize to the PYSTAT cross section (34.97 mb) divided by the number of generated events (3e6). There appears reason to believe this value is not entirely correct, perhaps, off by around 50-60% when comparing to NLO.

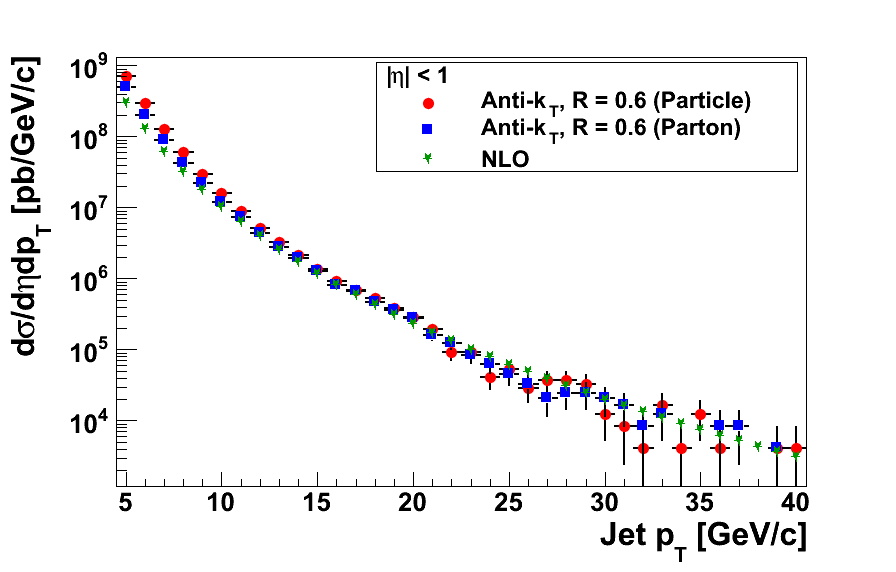
Figure 1

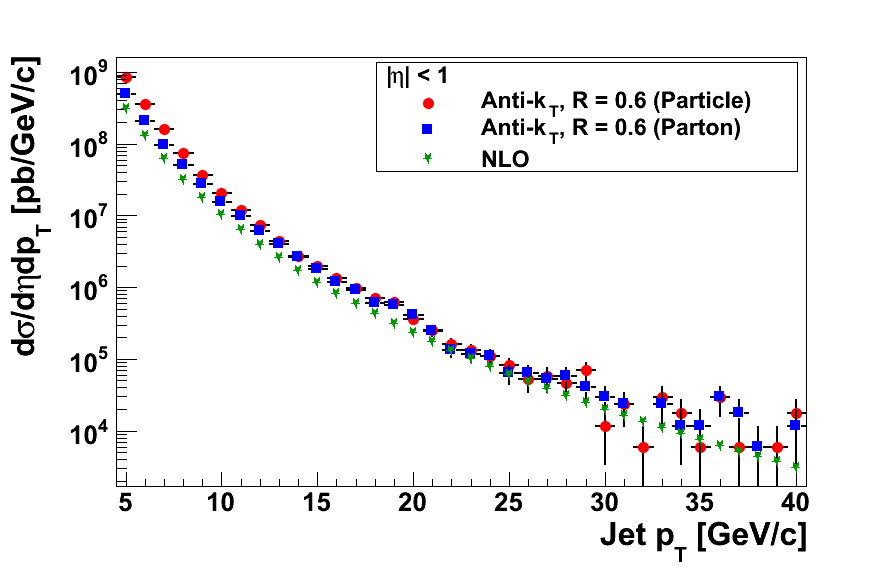
In Fig. 1 I show the PYTHIA cross sections compared to NLO where I now use primordial k_T = 1 GeV. There still appears to be a constant offset of PYTHIA relative to NLO of around 50-60%. However, the low-p_T enhancement in parton jets is all but gone. There is still an enhancement in particle jets, but it is somewhat reduced.

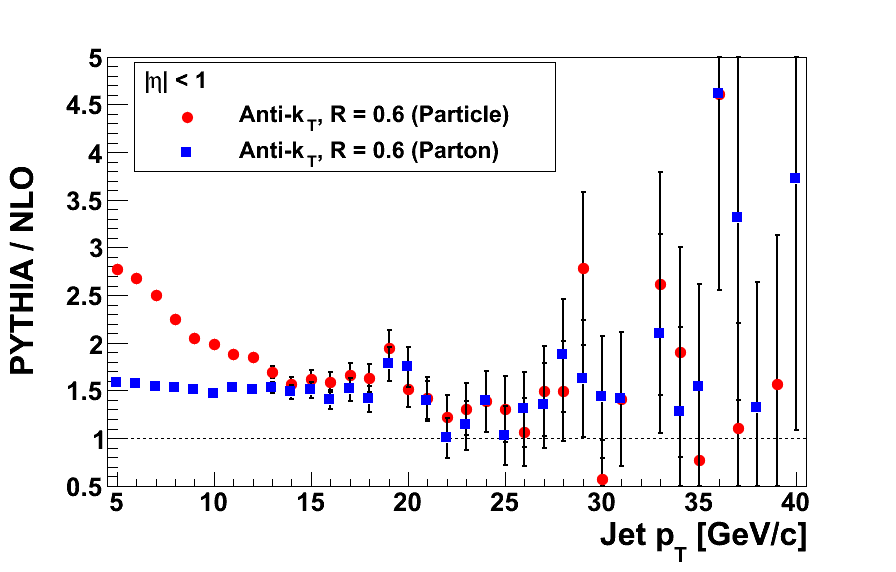
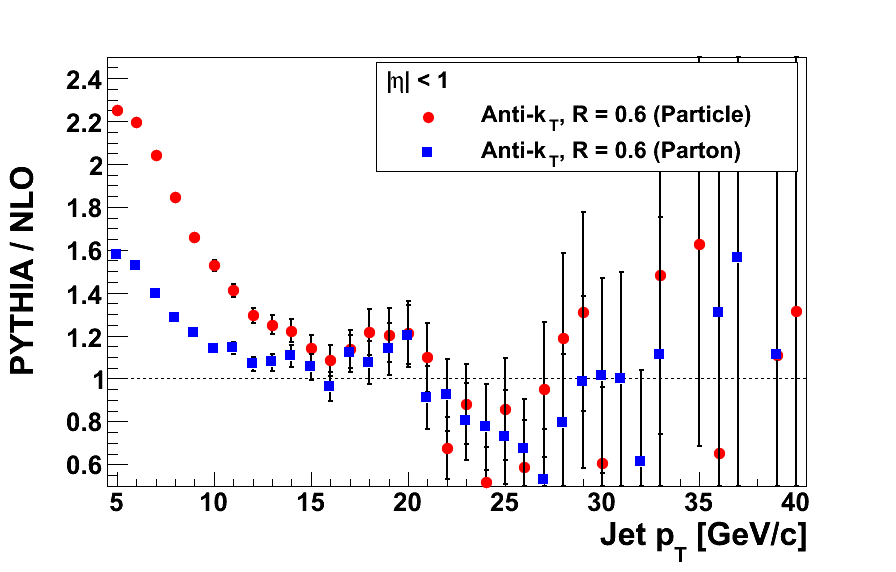
Figure 2

Primordial kT = 1 GeV	Primordial kT = 2 GeV

In Fig. 2 I compare directly the ratios of PYTHIA-to-NLO for the case of primordial k_T = 1 GeV and the case of primordial k_T = 2 GeV. Indeed, the difference is quite dramatic in parton jets while not as dramatic in particle jets.

As we saw, there is clearly a constant offset in the comparison of PYTHIA to NLO. It is known that the low partonic p_T cross sections are overstated in PYTHIA, and thusfar I have normalized to the PYSTAT cross sections without attempting to correct for this effect. As a first-order correction, I divide by the fudge factor calculated for the highest partonic p_T bin (75-∞ GeV/c) in the embedding sample. Specifically, this factor is 1.415.

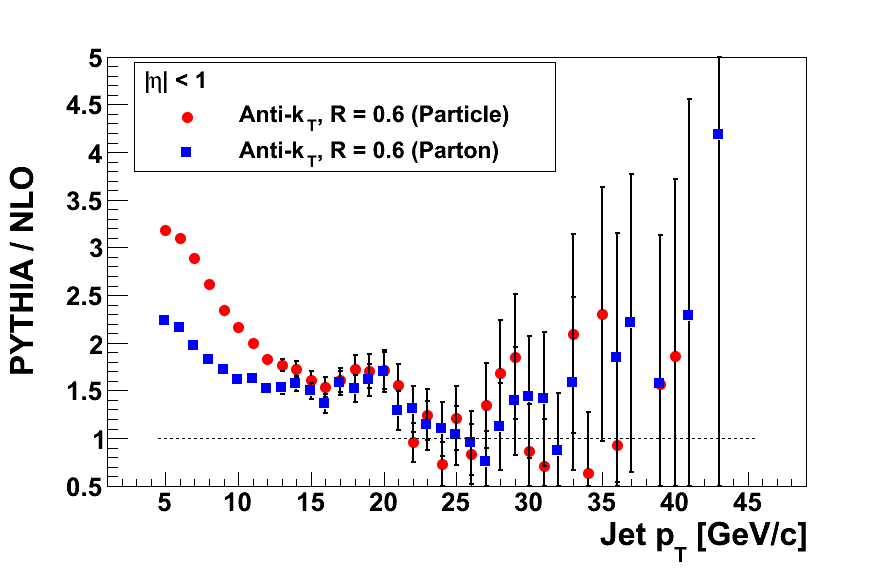
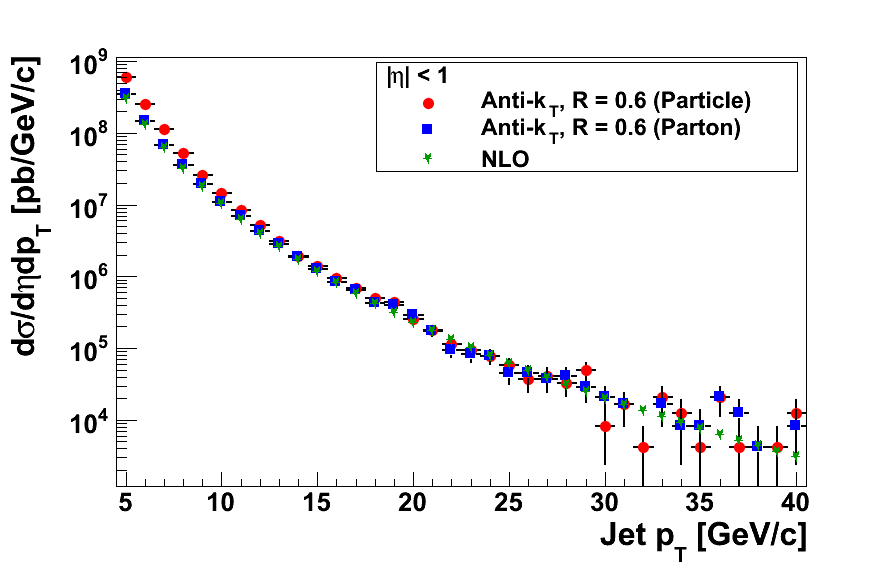
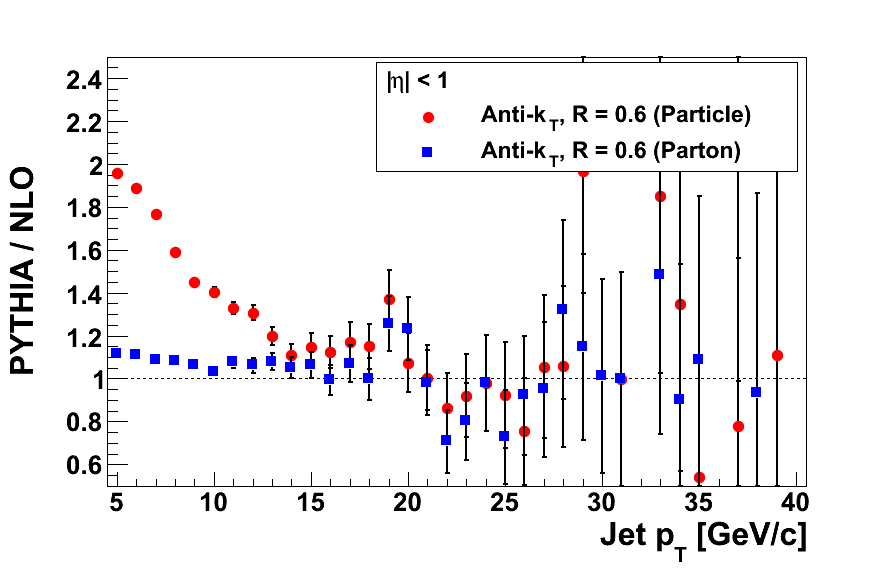
Figure 3

Primordial kT = 1 GeV	Primordial kT = 2 GeV

Dividing by the high-p_T fudge factor significantly improves the apparent offsets in both samples of varying primordial k_T. I should note that in the study with the embedding sample, I noted a near-constant offset of 1.64. Dividing by this factor appears to overcorrect.