Howard Wieman's calculations:


In his calculation of expected space charge (local copy) in 200 GeV AuAu collisions in STAR, Howard concludes that, for the TPC, the generated space charge is as follows:


At a luminosity...
ℒ = 90 x 10²⁶ / cm²sec
...we expect...
ρ = ρ(z,r)
ρ(0, 50 cm) = 1.9 x 10^-14 C/cm³

So...
ρ / ℒ = ~2.1 x 10^-42 C sec/cm


_________________


My calculations from the SpaceCharge distortion corrections:


C-AD reports that during Run 11 200 GeV AuAu operations, their delivered ℒ_peak was ~50 x 10²⁶ / cm²sec.

For distortion corrections, we use the modeled average charge density over the full TPC volume...

<ρ_SC> ≡ ∭_{{full TPC volume}} ρ(z,r,phi) r dr dz dφ / ∭_{{full TPC volume}} r dr dz dφ
= 2π ∬_∀z,r ρ(z,r) r dr dz / 2π ∬_∀z,r r dr dz
= ∬_∀z,r ρ(z,r) r dr dz / ∬_∀z,r r dr dz

Using our shape of...
ρ(z,r) = C (z_GG - |z|) [(3191/r² +122.5/r - 0.395) / 15823]
...where z_GG = 208.707 cm, C is an overall magnitude coefficient, and z and r go over [0, 208.707 cm] and [47.9 cm, 200.0 cm] respectively (the calculation is per TPC half). The z and r integrals can be separated...

<ρ_SC> = C ∫_∀z (z_GG - |z|) dz ∫_∀r [(3191/r² +122.5/r - 0.395) / 15823] r dr / ∫_∀z dz ∫_∀r r dr
= C (21779.3 * 0.99513) / (208.707 * 18852.8)
= C * 0.005508

...and...
ρ(0, 50 cm) = C * 0.04394

So we can write the relationship...
ρ(0, 50 cm) = 7.977 * <ρ_SC>

In Run 11 200 GeV AuAu operations, we determined the following expression from the calibration...
<ρ_SC>/ϵ₀ = (4.091 x 10^-8 V/cm²) (zdcsum - 16320 Hz)
...where zdcsum is the sum of the singles scaler rates from the east and west ZDCs.

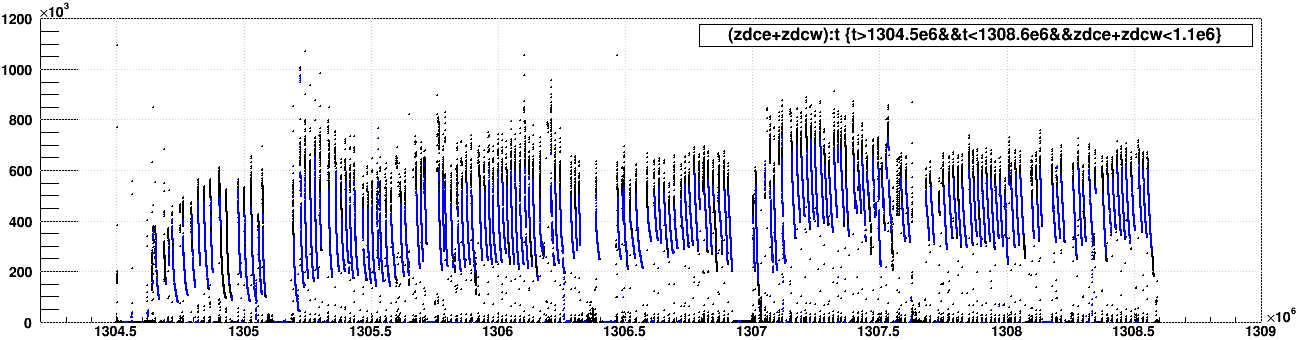
Plotting the Run 11 200 GeV AuAu scaler rates (click on the below image for a larger version), I see that the maximum observed zdcsum rate is in the neighborhood of 1 MHz, but it's not simple to decide what this number should be. We want to match the occasion(s) that C-AD used to determine ℒ_peak, but the maxima vary from fill-to-fill, often below 1 MHz, and sometimes above it. This number is probably best taken with an error on the order of 10%.


Using the above calibrated equation, the observed <ρ_SC,peak> was ~0.040 ϵ₀ V/cm². Plugging in ϵ₀ = 8.854 x 10^-14 F/cm, we have <ρ_SC,peak> = 3.54 x 10^-15 C/cm³.

Thus, I calculate an observed value for:
ρ(0, 50 cm)_peak / ℒ_peak = (<ρ_SC,peak> * 7.977) / ℒ_peak
ρ / ℒ = ~5.7 x 10^-42 C sec/cm


__________________


My calculations from the cathode currents:


I made a calculation of the cathode current expected from space charge in Run 13 510 GeV pp operations, with the conclusion that, while agreeing to within an order of magnitude, the current due to space charge ion neutralization should be larger than what was observed by a factor of at least 2x.


__________________


Summary:


That means we see nearly 3x (~2.7 to be slightly more precise, but should be taken with ~10% error anyhow) the space charge per 200 GeV AuAu collision than Howard calculated. It's valuable to note that for Run 11 we had no inner silicon, so there wasn't some additional source of background to radically change the charged track production.

If it's really all due to a contaminant carrying the ionic charge instead of methane, then it's moving 3 times more slowly than the 250 cm/sec that Howard used for his calculations.

Yuri Fisyak suggests that Howard's input is flawed for two reasons:

1. Howard uses a dN/dη for primary tracks only. We've historically seen global track multiplicities about twice as high as primary track multiplicities per event, and global tracks are more relevant to the calculation.
2. Even with global tracks, there are many TPC hits that are not included on reconstructed tracks. These are likely due to tracks which we simply do not reconstruct well, such as very low pT secondaries.

It seems rather plausible that the two of these could combine to give a multipicative factor to Howard's calculation of near ~3x, accounting for all observed discrepancy.


__________________


-Gene