New Analysis of Run 6 Eta Signal

The PSU software used to analyze the FPD/FMS data has been reorganized in the year since the transverse spin analysis of Run 6 Eta production was presented. We do not believe that any changes in the reconstruction algorithm have occurred with this reorganization.  Looking at a few runs reconstructed a year ago and reanalyzed now seem to bear out this assumption.

The East FPD data from the Run 6 transverse proton data set has been reanalyzed with the latest PSU software. This reanalysis will soon be compared with analysis of new simulation of the East FPD. 

• The analysis was done with calibration associated with SPIN 08 presentations.
• There is not any non-linear (energy dependent) gain correction applied to the data.
• The data are selected to have two photons within the FPD (no FPD fiducial cut).
• There is a photon energy sharing cut (Z<.8) used for all data shown here.
• A "centercut" is applied to data, selecting data with a 2 photon momentum in the psuedo-rapidity and azimuthal angle  range:
                          sqrt( (Y+3.65)² + tan(phi)²)<0.15 
• The "Eta" signal is defined to have invariant mass .45 GeV < M12 < .65 GeV.

 
Eta Mass Distributions

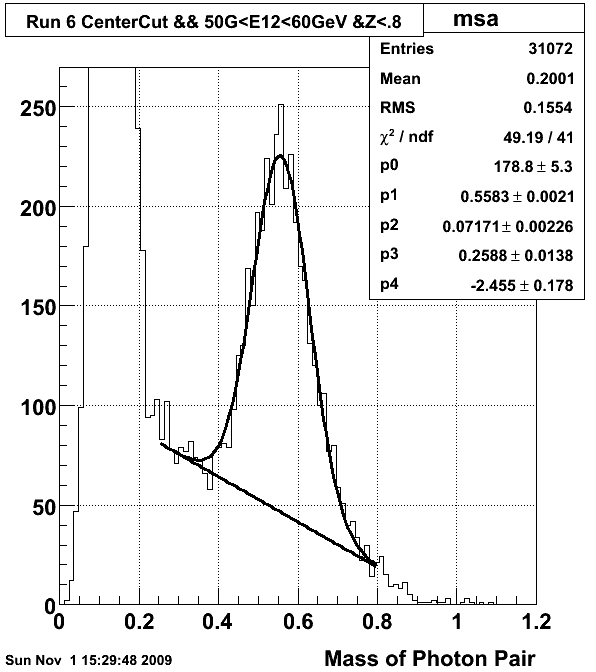
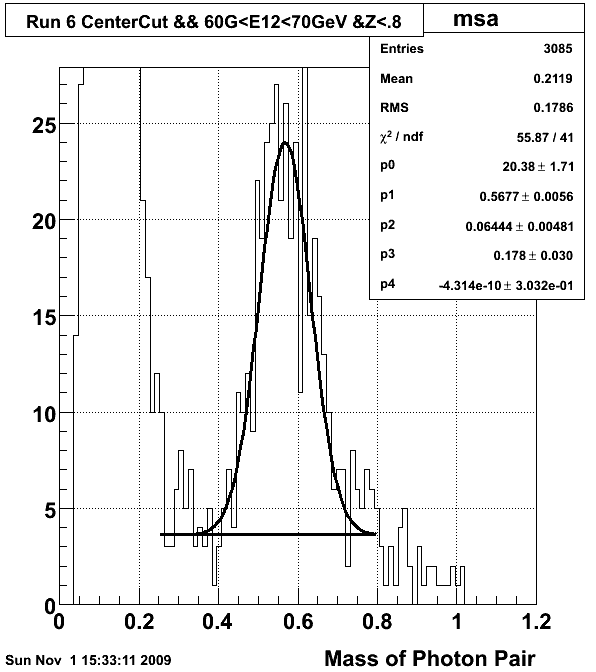
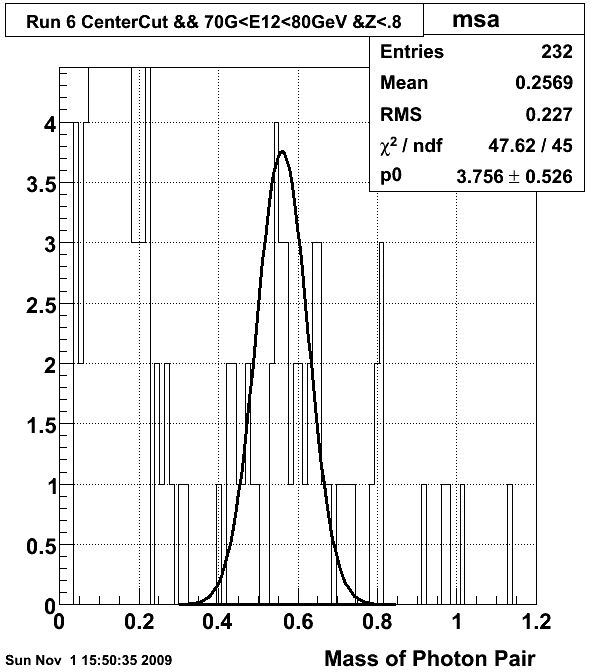
The following three figures show fits to Eta mass peaks for the cuts indicated

1. 50 GeV< E12< 60 GeV (5 parameter fit)
   
   • Fitted Mass = 0.558 GeV +/- .002 GeV
   • Fitted Width = .0717 GeV +/- .0023
   • Fitted Background/Signal @ peak = 25.88 % +/- 1.38%
   • chi2/dof = 49.2/41
2.  60 GeV < E12 < 70 GeV (5 parameter fit) 
   • Fitted Mass = 0.568 GeV +/- .006 GeV
   • Fitted Width = .064 GeV +/- .0048
   • Fitted Background/Signal @ peak = 17.8 % +/- 3%
   • chi2/dof = 55.8/41
3. 70 GeV < E12 < 80 GeV (1 parameter fit) 
   • Mass Fixed = 0.56 GeV
   • Width Fixed = .065 GeV
   • Background Fixed = 0%
   • chi2/dof = 47.6/45

 

 

 

 
Eta Energy Distributions

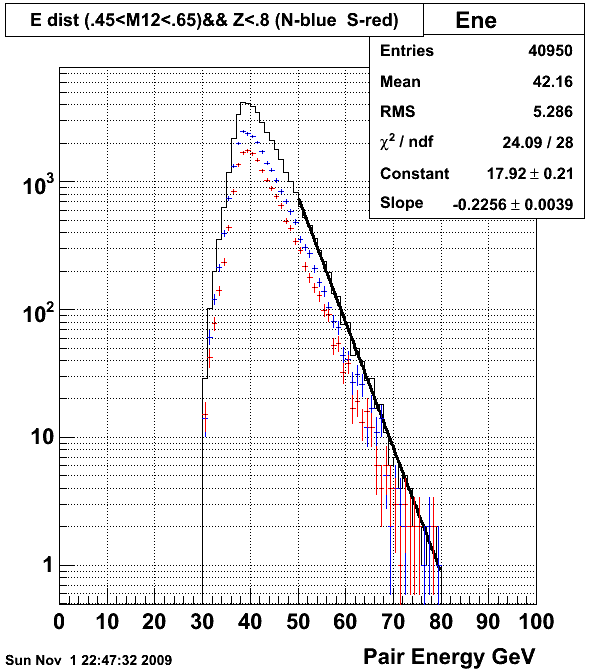
The following plot shows the energy distribution for events that satisfy 

 

• There is a photon energy sharing cut (Z<.8) used for all data shown here.
• A "centercut" is applied to data, selecting data with a 2 photon momentum in the psuedo-rapidity and azimuthal angle  range:
                          sqrt( (Y+3.65)² + tan(phi)²)<0.15 
• The "Eta" signal is defined to have invariant mass .45 GeV < M12 < .65 GeV.

The black curve represents the sum of the blue (FPD East-North) and red (FPD East-South) event distributions.

Although this is not corrected for acceptance, the fit to exponential is consistent with the prediction of

invariant cross section proportional to (1-x)⁵/pt⁶ , which predicts an exponential slope of -(5+6)/50 for energies in the neighborhood of 50 GeV.

• Fitted slope = -0.226 +/- .004 GeV^-1

 

 

 

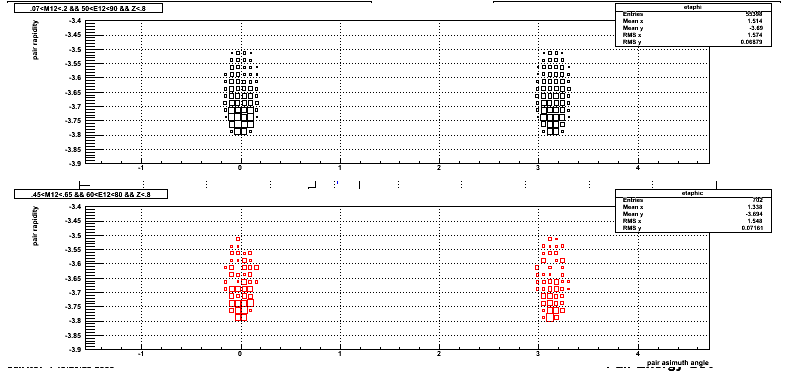
Pseudo-Rapidity and Phi dependence within Center Cut for two photon events in Pi and Eta mass region.

 

The top (black)  of the following plot represents the Pseudo-Rapidity vs Phi distribution for events in the pion mass region (.07 GeV < Mass< 0.2 GeV) and (50 GeV < Energy < 90 GeV).

The Bottom (red) represents the Pseudo-Rapidity vs Phi distribution for events in the Eta mass region (.45 GeV < Mass< 0.65 GeV) and (60 GeV < Energy < 80 GeV).

 

 

 
Analysis of Eta's in (70 GeV< Energy <80 GeV) with (.45 GeV<Mass<.65 GeV) bin.

 Number of Events

• North (Yellow up)              9  Events        
• South (Yelllow down)       14 Events
• North (Yellow down)         6  Events
• South (Yellow up)              1 Event 

AN=(1/polarization) (9+14 - 6 -1)/(9+14+6+1)= (1/0.6) (23 - 7)/(23+7) =  89%

Cross Ratio AN= 1.07

 

Binomial(M,N,p) = probability of observing M events in N tries where the probability of success is p

 

If the asymmetry  is AN = 0 and we observe 30 events with 0 to 7 counts of one spin, the probability is?

 

Sum_{j=0,7} Binomial(j,30,0.5) =  .0026

Sum_{j=23,30} Binomial(j,30,0.5) = .0026

So probability = 0.005 = 0.5 %

 

 

If the asymmetry is AN = 0.3 (Pol=.6) and we observe 30 events with 0 to 7 counts of one spin , what is the probability?

p=.5-(AN*Pol)/2= .5 -(0.3*0.6)/2=.41

 

Sum_{j=0,7} Binomial(j,30,.41) =  .034

Sum_{j=23,30} Binomial(j,30,.41) = 0.

So probability = 0.034 = 3.4 %

 

 

If the asymmetry is  AN = 0.4 (Pol=.6) and we observe 30 events with 0 to 7 counts of one spin?

p=.5 - (AN*Pol)/2= .5 - (0.5*0.6)/2=.38

 

Sum_{j=0,7} Binomial(j,30,.38) =  .068

Sum_{j=23,30} Binomial(j,30,.38) = 0.

So probability = 0.068 = 6.8 %