I ran some Pythia simulation together with GSTAR for FMS and here are some of the results. The basic settings for the study are:

1. Pythia 6.222 + GSTAR.

2. Event is triggered by Esum > 40 GeV in any qt card of FMS small cells.

3. Simulated event vertexZ has Gaussian distribution of 0 +- 60 cm.

4. Digitization effect is included. Pedestal adc values ([0,1]) are simulated by uniform distribution

5. Energy deposition generated in Geant is fed to Yiqun's code for reconstruction.

Fig1. Reconstructed Pi0 energy distribution. Pi0 is from two-photon event where each photon is associated with a Geant track. The two-peak structure confirms the trigger condition that was set.

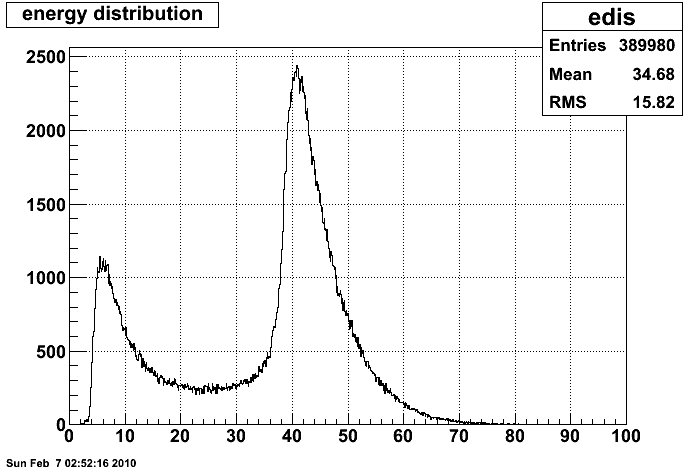
Fig 2. Distribution of the distance between a reconstructed "photon" and an associated Geant track (a track which does not decay, not necessarily a photon). If a reconstructed photon can be associated with a simulated track, the distance between them is 0.78 cell size on average.

Fig. 3.

Invariant mass distribution for reconstructed two-photon event in different energy regions. No associated Geant track is required for the two photons. This is similar to real data analysis, in which we don't know whether a reconstructed photon is real or not. From the figure we can see that the fitted mass increase with energy, even though the peak seems to be very good at high energy.

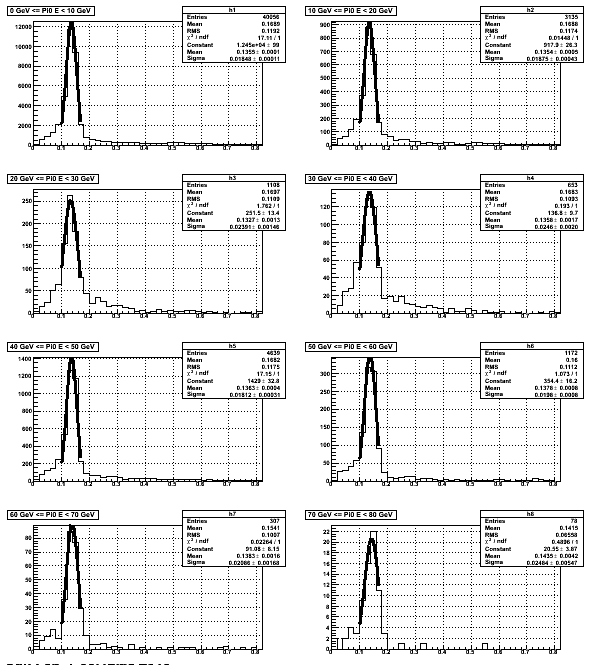
Fig4. Invariant mass distribution of two-photon event, where each of the photons is required to have an associated Geant photon, and the reconstructed Pi0 is required to have an associated Geant Pi0. By doing this association, we are mostly sure that we are reconstructing "real" Pi0. Contrary to the figure above, the Pi0 invariant mass shown in the figure below almost doesn't change as a function of energy.

This indicates that  unknow background shape is one very important reason for the mass shift we are seeing in real data. Energy region such as 40~60 GeV, where real Pi0 yield is dominant over background, might be the best place for calibration.