So, Carl asked... will using Matt’s dijet filtered simulation sample cause bias in my unfolding matrix.

I’ve given this question some thought.

The unfolding process is meant to account for effects of detection and reconstruction, and the iterative method is designed to remove any influence caused by the particular initially thrown distribution. (In fact, it should converge even if a flat distribution is initially thrown.)

So, with the problem of the thrown distribution under control, what Carl was suggesting is that somehow the presence of a second jet would change the measurement of the first jet. This seems unlikely, but it's not impossible to dream up a scenario where it would.  For example, if all the BEMC PMTs were fed by the same under-specced power source, then the power dip caused by one set of towers would alter the gain on the other, and vice versa. And that this effect is properly simulated.

Matt's dijet pythia filter was used make sure that the simulated events would pass a 7 and 10 GeV dijet cut, which, for this blog entry will be called the “normal cut”.

Since I don’t have a sample size as large as Matt’s for inclusive jets, what I did to investigate this question was to make a sub-sample from Matt’s Monte Carlo set with a 7 and 17 GeV dijet cut -- called here the “dijet supercut”.  The supercut removes >90% of the dijet events.

I calculated the unfolding matrix using the normal cut and the supercut, and compared them.

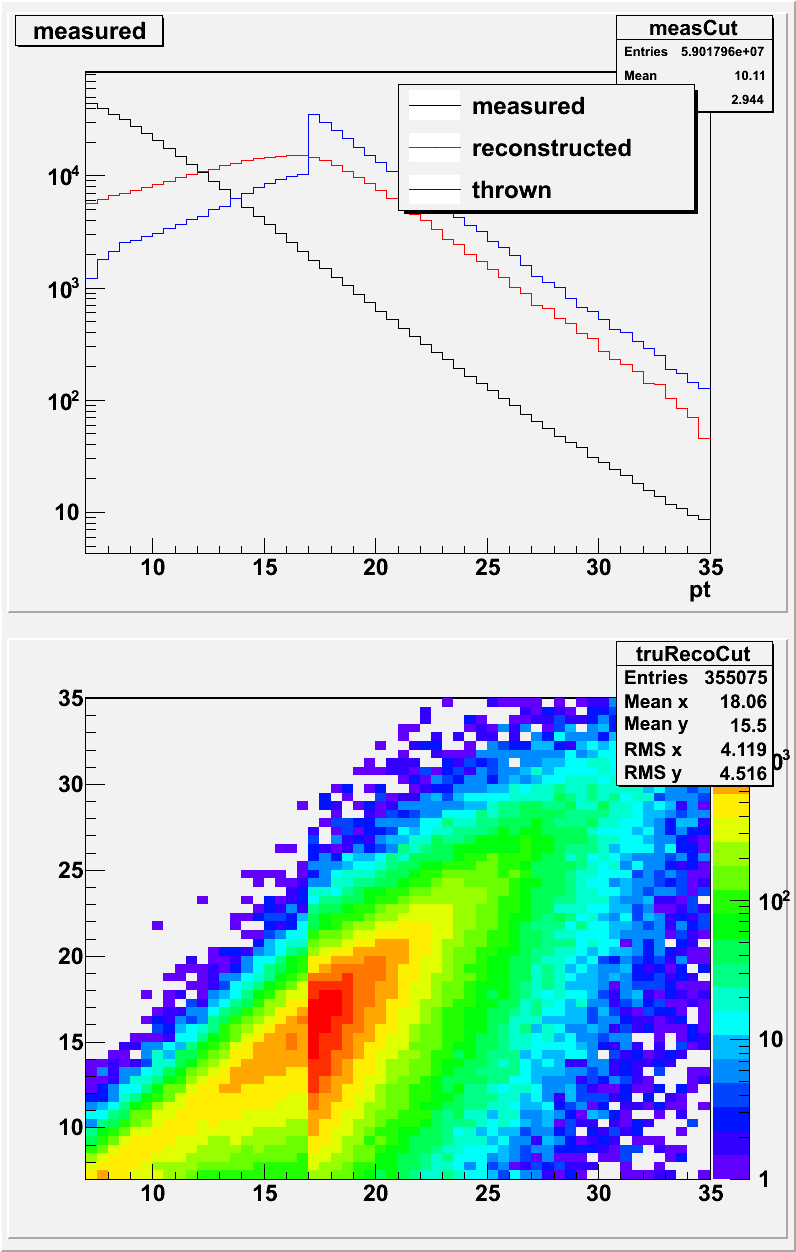
This figure shows: (bottom panel) the distribution of reconstructed events at a given jet p_t (y) vs. thrown jet p_t;

(upper panel) a) in red, the reconstructed distribution (vertical projection of the 2d histogram).

b) in blue, the reconstructed distribution (horizontal projection of the 2d histogram) and c) in black, the actual measured jet p_t distribution.

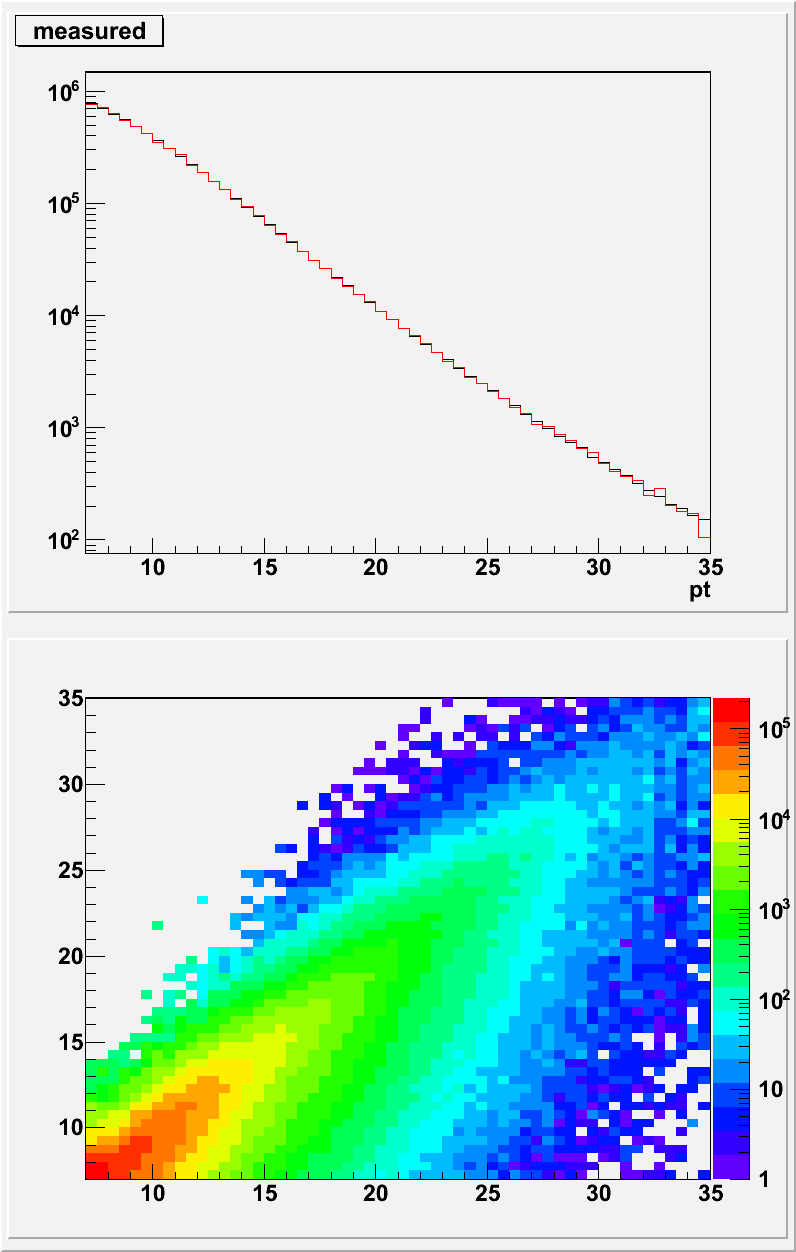
After iterative unfolding, the superCut sample falls smoothly on both axes, and looks similar to the distribution for the normal sample. (see previous blog entry)

The most different area is the tail of the low-pt jets that were reconstructed high. (The blue band should continue over the top there.)  My best guess is this comes from mostly from the paucity of events thrown below 17 GeV.

But how different is it? 

The important metric is: for any reconstructed jet pt, does p(true|reco) give the same range for both normal cut and super-cut?

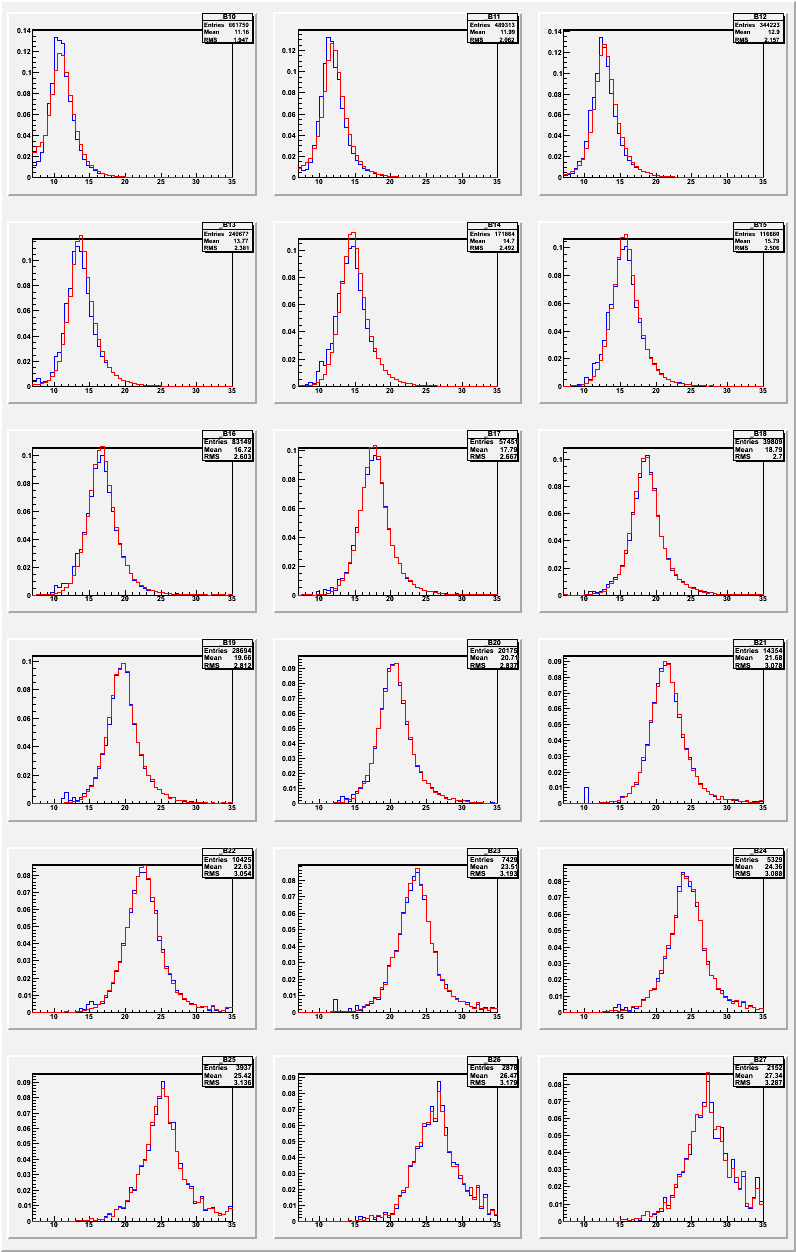
Figure 3 is a series of true distributions for given reconstructed jet pt (10<reconstructed pt<11 in top left up to 27<reconstructed pt<28 in bottom right ). They are integral-normalized to unity , so the vertical axis measures probability, while the x horizontal axis is thrown jet p_t.

As you can see, the agreement between dijet (in blue), and supercut (in red) is not great for the lower bins, but is spot on for the higher ones.

The worst example is the 13 GeV bin shown below with gaussian fits to both distributions.

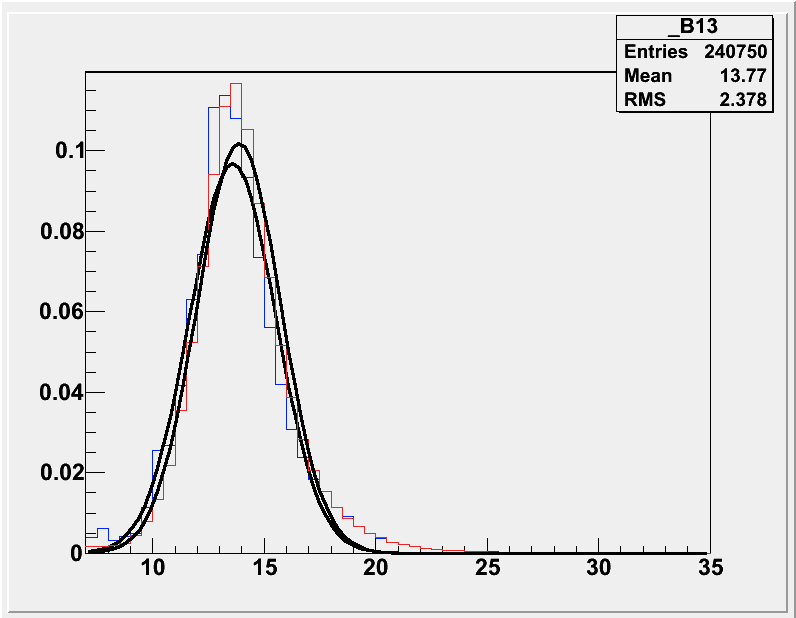
In this bin, the cut sample is fit to a gaussian with mean 13.86 +/- 2.0 GeV, while the superset sample is fit to a gaussian with mean 13.59 +/- 2.1 GeV. So there is in fact a bias of 0.27 GeV (+/- 2.9)

In terms of my analysis, this would mean that in the 0.45<z<0.65 bin, events with a ~13.5 GeV jet will experience a bias in z of 0.01, or a net ~5% bin migration effect under one unfolding matrix compared to the other.

If this is an unacceptable bias, the conclusion to draw is that a simulation sample using the 7&17 superCut should not be used to unfold jets under 17 GeV. By analogy, Matt's 7&10 sample should not be used to unfold jets under 10 GeV.  So I think that my analysis should include a jet cut at 10 GeV.

Part 2: why not unfold directly in Z?

This is a reasonable question, and it would probably work fine.  But it's theoretically dicey. Consider the following hypothetical (fictitious) situation:

A 12 GeV jet is unfolded to 11-15, while a 24 GeV jet unfolds to 19-25

So a 6 GeV pion opposite the 12 GeV jet would unfold from z=0.5 to 0.4-0.55, and a 12 GeV pion opposite the 24 GeV jet would unfold from z=0.5 to 0.48 - 0.63

So if we have just one unfolding matrix for z, it will be dominated by the lower energy situation, and higher energy events at the same z will experience this bias in the form of incorrect unfolding.