Where are the photons? - A slightly different way to look at the photon yield

Recently, I came to an unfortunate conclusion that there seems to be much less photons in the data than what I expected. But this estimate was made after I performed various background subtraction schemes, which could of course be wrong. Here, I look at the same issue from a slightly different angle.

First, I use the weighted simulation as usual, design to match the xF slope of the data that is softer than what we get in Pythia 6.222 + Cherenkov. I did make some technical improvements on this front, so now I have a distribution that is good from ~30GeV and up instead of working with two sets of simulations with different Pythia filter thresholds.  

Fig. 1. Two cluster event energy distribution, data (dark blue) and weighted simulation (red)

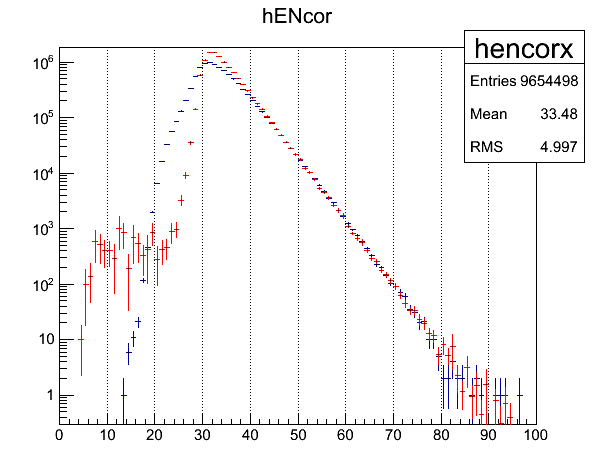
Energy weitghing was done on the true energy of hadrons as well, so as not to bias particle content. In addition to the slope matching, I also corrected for the eta over-production in Pythia for all eta decay photons.  

Now we look at the sigma max distribution, and compare simulation to data. The normalization was done for each panel, so that the number of events above sigMax>0.6 is equal in both data and simulation. The purpose here is to compare the relative peak sizes between 1 and 2 photon peaks.  This is NOT a statement about the absolute yield in the simulation. 

For now, only pi0 and eta decays have been included. The reason is that we know how many of these things are in this region, and this is the bare minimum in terms of the number of single photon events we should observe. So we exclude things with greater uncertainty, like the hadrons (response uncertain), and misc. decays and direct photons (x-section uncertain). 

Fig. 2. Cluster sigma max distribution for 1 cluster events, 8 GeV bins from 40 to 80 GeV. Simulation includes only pi0 and eta decays. (no direct photons, hadrons, and any other decays) 

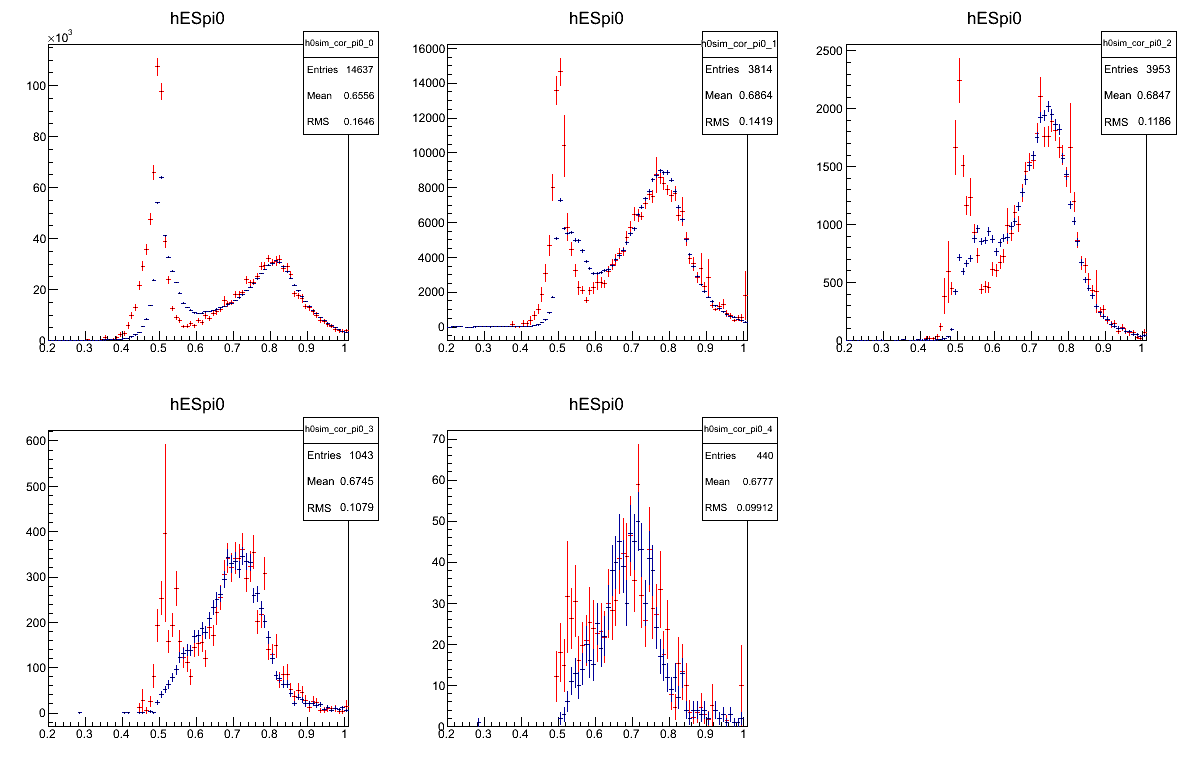
So apparently, we don't even have enough single photons to account for the pi0 and eta decay. HOWEVER, this is not the whole story. Turns out, the probability of getting a 1 cluster event, which is plotted above, is much higher in the data than in the simulation. In other words, the cluster finder works better in the simulation in terms of identifying a valley and breaking a connected cluster of energy into two.  

Fig. 3. Number of 2 cluster events / number of 1 cluster events

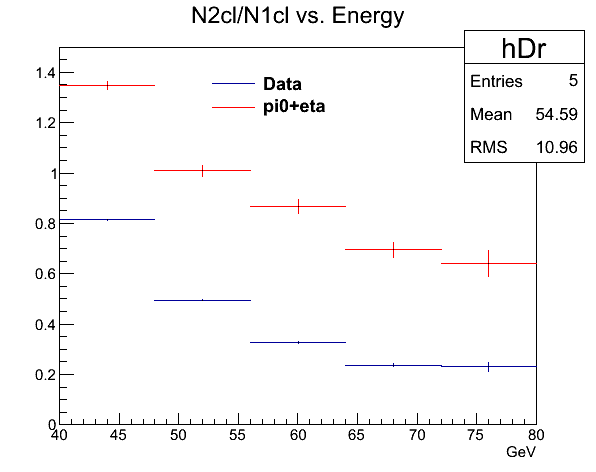
So essentially,  the tw photon peak in the data is enhanced compared to the simulation, as the two cluster events would show up as a part of the two photon peak if the cluster finder failed to break them apart. 

Now I count the number of 1 photon events vs 2 photons, taking this into account. In addition, instead of doing a sharp cut at a particular sigma max value to determine the photon content of a cluster as it has been done, I tried fitting. The 1 photon peak gets two gaussians, as it tends to have funkier shape, and the 2 photon peak gets one. Obviously this is quite crude. Also, I know exactly how much of it is really single photons in the simulation, but I am ignoring that information and using the same method both in data and simulation.  The difference between the fit result, and the straight up counting up to the valley, is used as the error. 

Fig. 4. Data sigma max fits

Fig. 5. Simulation sigma max fits

After counting 1 and 2 photons based on the simga max distribution for 1 cluster events, I add the 2 cluster events to the 2 photon count. (2 cluster events are completely dominated by single photon clusters)

Now I look at the ratio between 1 and 2 photon events. The idea is that the 2 photon events are mostly produced by processes that will also produce 1 photon events in the FPD, like pi0 and eta. And this is mostly dominated by the aceptance effect, which should really be well simulated. So, this already dictates the minimum ratio of 1ph / 2ph,  and then the question is if we have enough single photons beyong that level for the direct photon signal. 

Fig. 6. Number of 1 photon events / number of 2 photon events

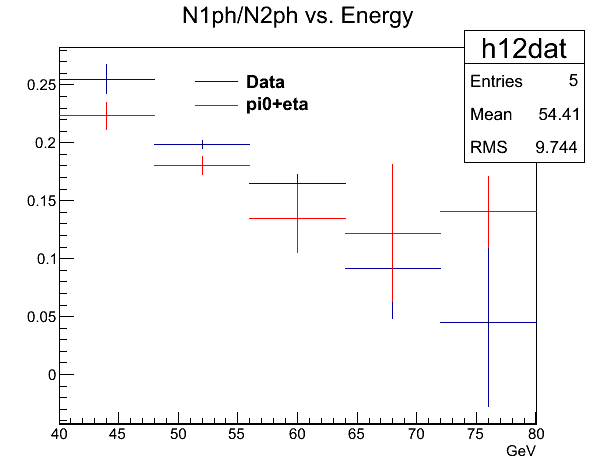
So it seems that, from this point of view, we have somewhat more than enough single photons to account for the pi0 and eta below 65GeV, but maybe not beyond that. But still, this looks ok. 

Fig. 6a. Now we add hadrons to the pi0 and eta

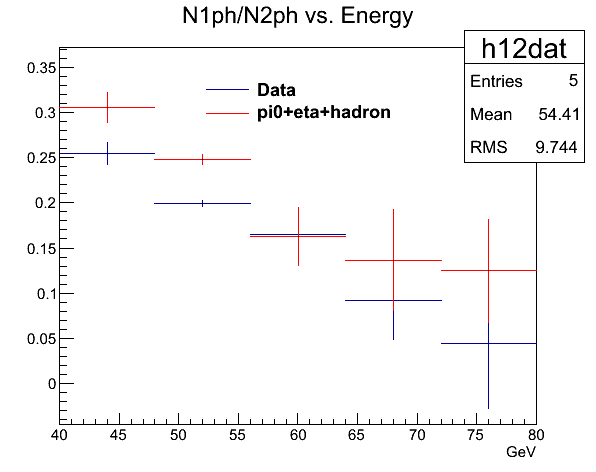
Once the hadron signal (hadrons showing up as a photon) is added, the simulation single photon level overshoots the data, especially at the low energy end. I emphasize that we don't know for sure if this level of strength for the hadronic response is really right.

Fig. 6b. Instead of hadrons, we add direct photons. 

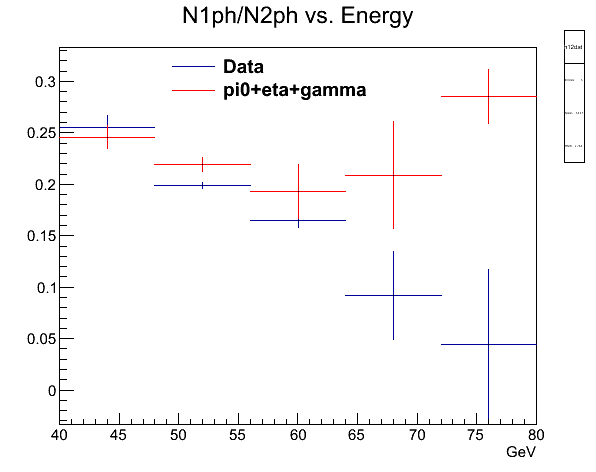
If we look at pi0 + eta + direct photons and compare it to the data, the biggest change occurs at the high energy end, where we expect the prompt photon cross-section to become significant.  

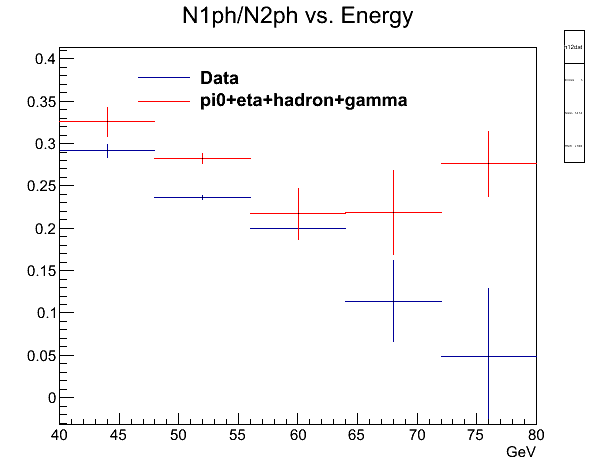
Fig. 6c. With both hadrons and direct photons

Once I include pi0, eta, hadrons, and prompt phtons, the lack of single photons in the data is very clear. 

Finally, I varied the relative energy scale between 1 and 2 photon events. I have estimated the uncertainty here to be about 1%, coming mostly from the energy dependent gain shift, and the possible bias in the reconstruction. So I increased the 1 photon gain by 2% relative to the 2 photon events to see if I get enough single photons. 2% is obviously very generous.

Fig. 6d. Data 1 photon gain increased by 2%

So it seems very unlikley that this apparent photon difficiency is coming from the miscalibration of 1 photon gain.