What does the BBC min bias condition buy us?

 

Traditionally, we've always imposed the BBC min bias condition in all of our analysis. This consists of both sides BBC having more than certain amount of charge, and being in some time interval. This is done in order to ensure that we reject junky events. What constitue junky events is not trivial. We would of course like to reject beam background. We would also like to reject diffractive events for most of our analysis. It is not clear how we would treat the beam remnant (underlying) events, or if there is anything we can do about them. 

For this study, I am using a Pythia only simulation. The version used is 6.4, with tuneA, except that the width of the intrinsic kT is set at 1GeV. I believe this is the default value in ver 6.2, which is what we've all been using. Pretty much all of the 2->2 sub-processes are enabled, including diffractive and photo-productions. I put a minimum pT cut of 1GeV to speed up the generation, which should not be an issue for hard scattered, high energy events that we are interested in. I'm not so sure about the potential bias this condition inevitably brings in to the beam remnant type events. 

Since there is no detector simulation, what I do is I look at the pi0s with eta between 3.2 and 4.0 to represent the signal in the FPD/FMS. At the same time, I count the number of charged tracks with E > 1GeV in the eta range of 3.3 and 5, to represent the signal in the inner BBC tiles. The latter is especially crude, but that will have to do for now.

 

First, we look at the diffractive events. 

 

Fig. 1. BBC Ntrack distribution for non-diffractive (based on subprocess ID) events.

 

Fig. 2. BBC Ntrack distribution for diffractive (based on subprocess ID) events.

 

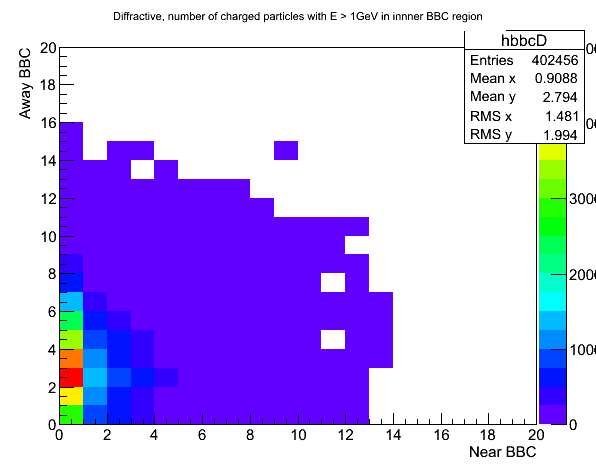
So clearly, the BBC coincidence condition will do a good job in sorting out the diffractive events, as we would expect. 

However, should we really be worried about the diffractive events at the high xF region that we are most interested in?

 

Fig. 3. Energy distribution for diffractive (red) and non-diffractive (dark blue) events.

 

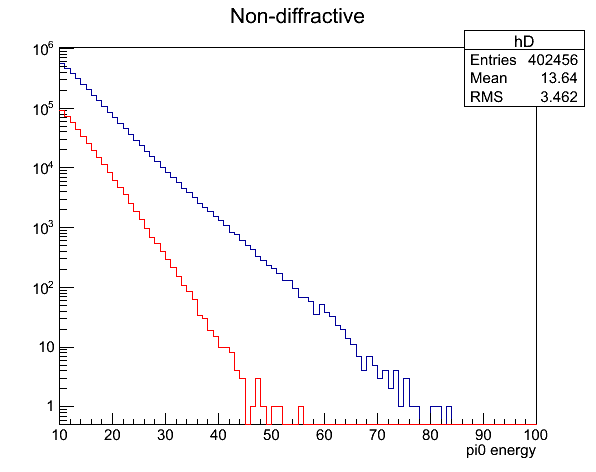
At 40 GeV, which is the lowest energy that out anlysis cover, the diffrative events are roughly two orders of magnitude suppressed compared to non-diffractive events. It only gets better from that point on. 

 

If we apply a cut similar to our half-BBC condition, that is we demand that the away side to have more than certain number of tracks to pass the cut, then we throw away most of the diffractive events, and some of the non-diffractive events. At high energy, there are no diffractive events, so here we look at the fraction of non-diffractive events taht we lose by imposing this cut. 

 

Fig. 4. Fraction of non-diffractive events that fail the "away-side or both" BBC condition. Blue: 3 track or less is fail. Red: 4 track or less is fail. 

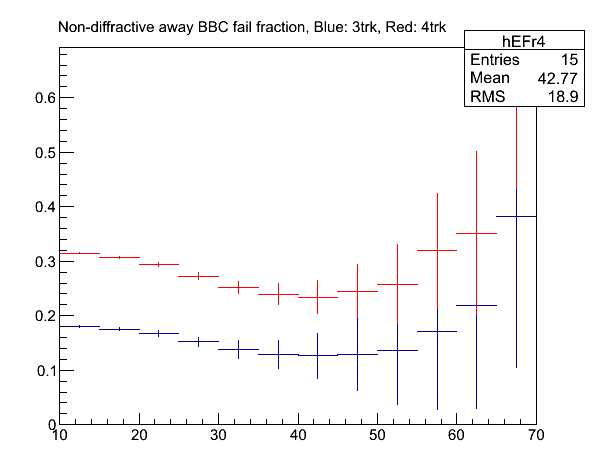
So we are throwing away 20~30% of the non-diffractive events, and the energy dependence is failry weak. 

 

Fig. 4a. COMPARISON: Fraction of events that fail "west or both" BBC condition in the data (red). (disregard the histogram title)

 

 

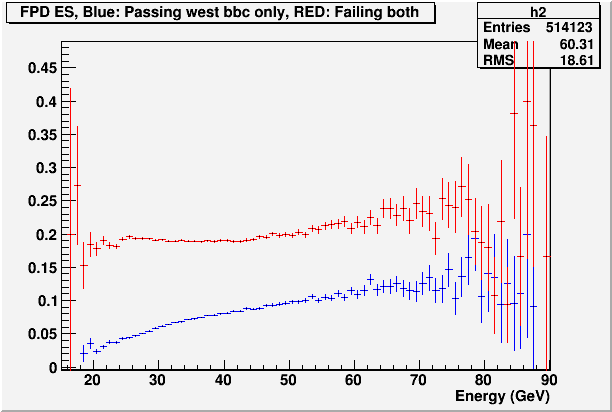
Simulation suggests that by imposing BBC condition, we will lose 20~30% of perfectly good events, and that the ratio will not have a significant energy dependence. The data is consistent with this picture. If what we sort out through the BBC condition was a different kind of physics, such as diffractive and/or beam background, it is difficult (while not impossible) to imagine how this fraction can be so energy-independent.  

 

 

Now we look at the hard scattering vs. beam remnant events.

 

First, we have to distinguish these two types of events from the Pythia event record. I actually do not know a definitive way of doing this, as everything is connected to strings that make it hard to trace its parentage. The most reliable method I've found so far is to compare the momentum of the final state parton coming out of the hard scattering (after final state radiation) to the momentum of the observed pi0. 

 

Fig. 5. pZ ratio vs pT ratio, final state/pi0 for Epi0 > 30 GeV.

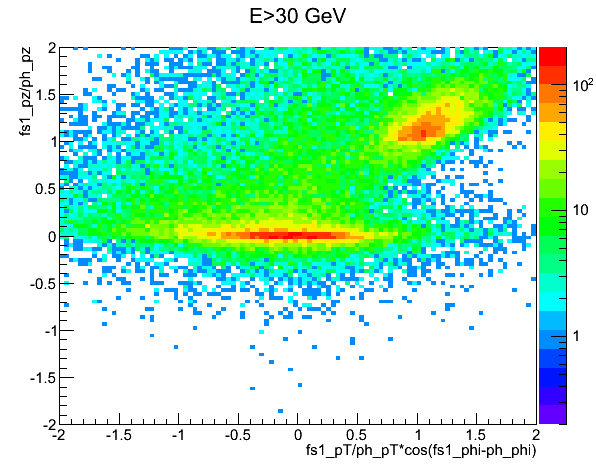
The blob at the top right indicates hard scattering events. They are the ones where the the pZ of the final state parton was similar to or greater than that of the pi0, and the component of the parton pT that is in the direction of pi0 was also similar to or greater than that of the pi0.  The rest is likely beam remnant. (I am selecting the final state parton with more positive pZ, as I am simulating the forward region on the west side)

 

Fig. 6. Same as above, but for Epi0 > 50 GeV.

 

At 50 GeV, the story does not change. The structure is basically the same as the case with Epi0>30GeV. So I apply a cut at 0.5 on both axes to sort out the hard scattering events. 

 

Fig. 7. Energy spectrum for hard scattering (dark blue) and beam remnant (red)

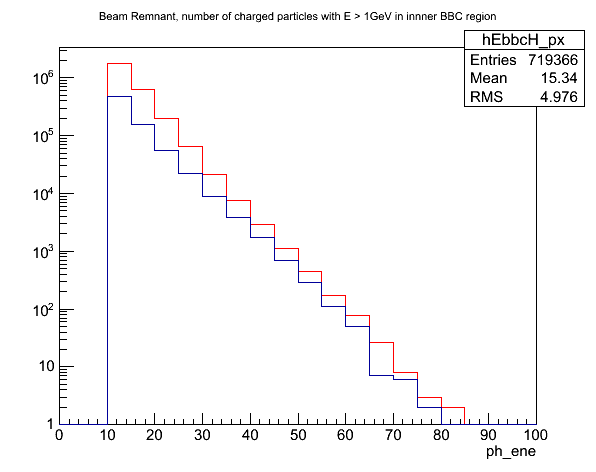
Apparently, Pythia 6.4 thinks we are dominated by beam remnant events. The exponential slope is ~0.18 for the hard scattering, and ~0.22 for the beam remnant, so not drastically different. 

 

So do these events have different BBC signature?

 

Fig. 8. BBC Ntrack distribution, hard scattering.

 

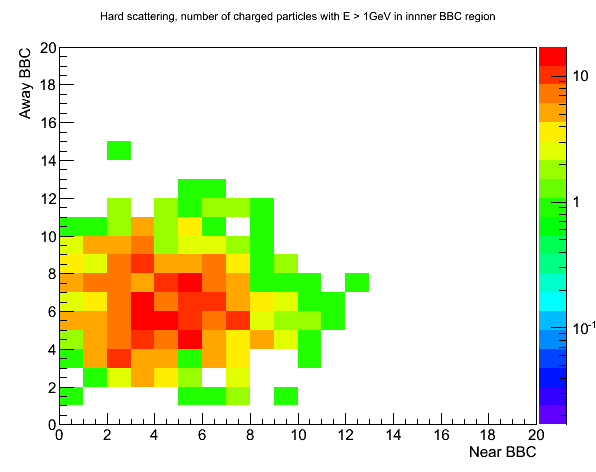
Fig. 9. BBC Ntrack distribution, beam remnant.

 

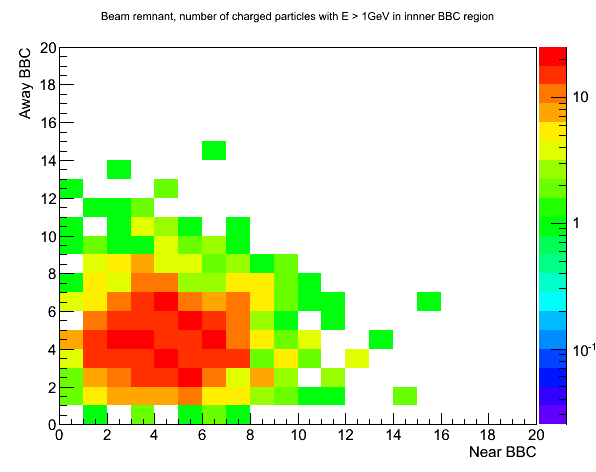
The beam remnant events do tend to throw somewhat smaller number of charged tracks through the away side BBC. But the difference is fairly small compared to the hard scattering events. 

Now if we apply the same BBC condition as before with threshold at "3 tracks or less fails", then we lose the following fraction of events for the two types of physics. 

 

Fig. 10. Fraction of events lost due to the BBC condition.

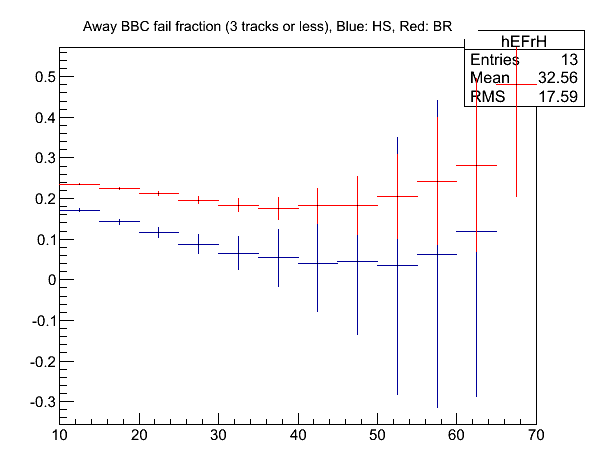
So it does suppress the beam remnant more than the hard scattering, but only mildly so without any serious energy dependence.  

 

Finally,  following is the result of the analysis with (lower) and without (upper) BBC condition.

NOTE: Efficiency correction currently does not include BBC efficiency, which, according to figure 4, can be 20~30%. So the BBC-condition cross-section is about 20~30% lower than it should be. 

NOTE: I am now using the RooUnfold package to do the unfolding. This is more relaible compared to the method I devised. I no longer have the statistical and systematic errors separated, and the error bars include both. 

 

Fig. 11. Upper: Without BBC Condition, Lower: With BBC condition

 

Fig. 12. Ratio of cross-sections for pi0 and eta, (No bbc condition) / (West or both bbc condition)

 

Again, due to the lack of BBC efficiency correction, we would expect the no-BBC cross-section to be 20~30% higher than the one with BBC condition. The above plots show that the observed cross-section with and without BBC condition is consisten with each other. I have removed the luminosity uncertainty from the errors, as it is common to both. We see no evidence that the beam background is significant.  

 

CONCLUSIONS

1. BBC condition does sort out diffractive events well, but Pythia 6.4 thinks diffraction dies out much faster as a function of xF. It's two OoM down from non-diffractive at 40GeV, and the gap widens as you go higher. Therefore, at face value, we do not need to worry about diffractive physics at the xF we are interested in.