Kernel-Component Comparisons:
FIG.1 The toy-model simulations of $2\Delta\gamma_{112}$, $\Delta_{R2}$ and $\Delta'_{\rm SBF}\equiv(\frac{\pi^4}{64M^2}\Delta_{\rm SBF}+\frac{8}{3}v_2\Delta\delta)$ as function of the input $a_1^2$. The open markers represent the  pure-signal scenario without resonances, and the solid markers denote the scenario with resonance decays. In comparison, the linear function of $4a^2_1$ is also added.

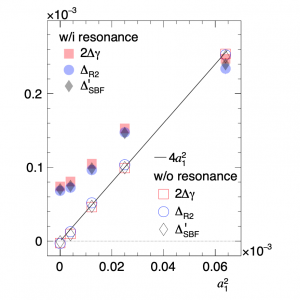
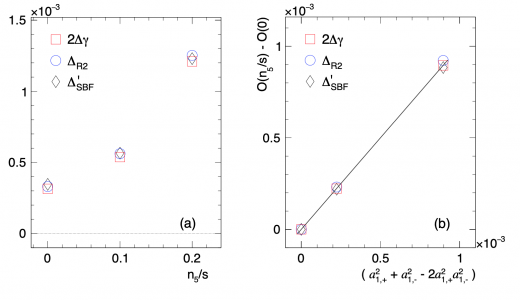
FIG.2  (a) The EBE-AVFD simulations of $2\Delta\gamma_{112}$, $\Delta_{R2}$ and $\Delta'_{\rm SBF}\equiv(\frac{\pi^4}{64M^2}\Delta_{\rm SBF}+\frac{8}{3}v_2\Delta\delta)$ as function of $n_5/s$ in 30-40\% Au+Au collisions at 200 GeV. (b) The same results with the subtraction of the pure-background case vs $(a_{1,+}^2 + a_{1,-}^2 - 2a_{1,+}a_{1,-})$. In comparison, a linear function of $y=x$ is drawn to verify the relation in Eq: O(n_{5}/s) - O(0) =  a_{1,+}^2 + a_{1,-}^2 - 2a_{1,+}a_{1,-}.

Sensitivity study for isobaric collisions:

TABLE I: The $a_{1,\pm}$ values calculated for the EBE-AVFD events of 30-40\% isobaric collisions at $\sqrt{s_{\rm NN}} = 200$ GeV.



FIG.3 EBE-AVFD calculations of  $\gamma_{112}^{\rm OS(SS)}$ (a) and $\Delta \gamma_{112}$ (b) as functions of $n_{5}/s$ for 30-40\% isobaric collisions at $\sqrt{s_{\rm NN}} = 200$ GeV, together with the ratio of   $\Delta \gamma_{112}$ (c) between Ru+Ru and Zr+Zr. In panel (c), the $2^{\rm nd}$-order-polynomial fit function illustrates the rising trend starting from (0, 1). 

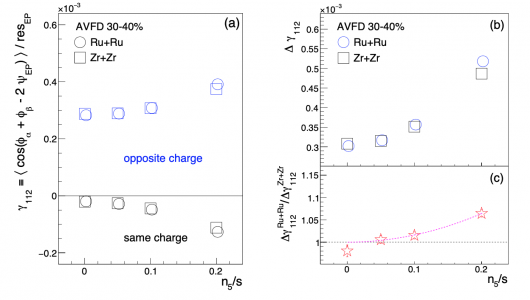
FIG.4 EBE-AVFD calculations of  $v_2$ (a) and $\kappa_{112}$ (c) as functions of $n_{5}/s$ for 30-40\% isobaric collisions at $\sqrt{s_{\rm NN}} = 200$ GeV, together with the ratios of $v_2$ (b) and $\kappa_{112}$ (d) between Ru+Ru and Zr+Zr. In panels (d), the $2^{\rm nd}$-order-polynomial fit function illustrates the rising trend starting from (0, 1). 

 

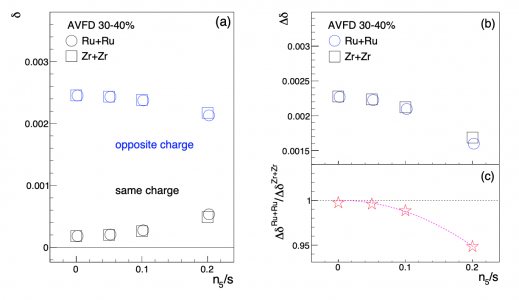
FIG.5   EBE-AVFD calculations of  $v_2$ (a) and $\kappa_{112}$ (c) as functions of $n_{5}/s$ for 30-40\% isobaric collisions at $\sqrt{s_{\rm NN}} = 200$ GeV, together with the ratios of $v_2$ (b) and $\kappa_{112}$ (d) between Ru+Ru and Zr+Zr. In panels (d), the $2^{\rm nd}$-order-polynomial fit function illustrates the rising trend starting from (0, 1).

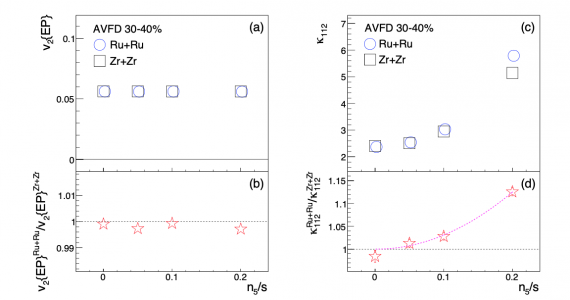
FIG.6  Distributions of $R(\Delta S_2^{''})$ from EBE-AVFD events of 30-40\% Ru+Ru (a) and Zr+Zr (b) at 200 GeV with different $n_{5}/s$ inputs.  Panel (c) lists  $\sigma^{-1}_{R2}$ vs $n_{5}/s$, extracted from panels (a) and (b), and the $\sigma^{-1}_{R2}$ ratios between Ru+Ru and Zr+Zr are shown in panel (d), where the $2^{\rm nd}$-order-polynomial fit function shows the rising trend starting from (0, 1).

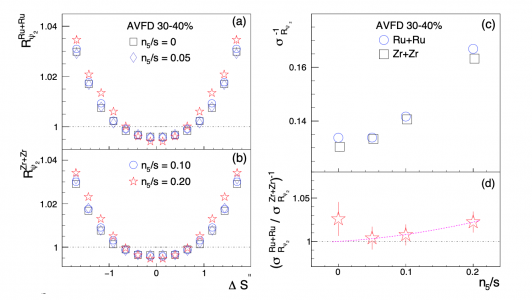
FIG.7 $r_{\mathrm{lab}}$ (a) and $R_{\mathrm{B}}$ (c) as  function of $n_{5}/s$ from the EBE-AVFD model for 30-40\% Ru+Ru and Zr+Zr collisions at $\sqrt{s_{\rm NN}} =200$ GeV, with their ratios between Ru+Ru and Zr+Zr in panels (b) and (d), respectively. In panel (b), the $2^{\rm nd}$-order-polynomial fit function demonstrates the rising trend starting from (0, 1).

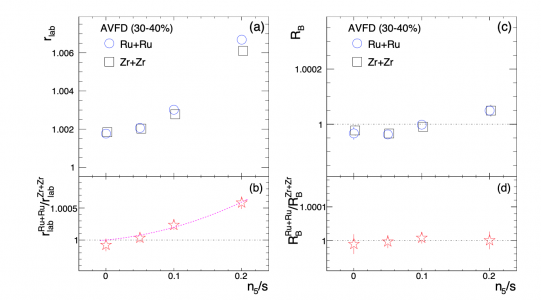
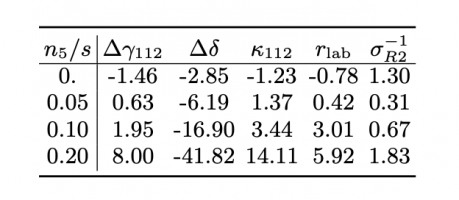
TABLE II: The statistical significance of $(O^{\rm Ru+Ru}/O^{\rm Zr+Zr} -1)$ for different experimental observables. Contrary to other observables, the $\Delta\delta$ ratio expects negative  significance values due to the CME signal.

Summary: