The direction of the beam in STAR FXT
Updated on Wed, 2020-07-08 17:05. Originally created by lisa on 2020-07-08 10:50.
Executive Summary:
Whatever the internal coordinates (east-west, up-down, whatever boost frame) that an experiment (STAR/PHENIX/HADES/...) uses, the plots in collision-center-of-mass frame must be identical, modulo acceptance effects.
.png)
Then, to find the rapidity of a particle in the collision center-of-mass frame, just use the normal, standard formula:
 Equation 1
Equation 1
In the STAR internal coordinate system
IMPORTANT: This is how your picoDsts are formatted. For StPicoTrack::dcaPoint(), StPicoTrack::gMom(), StPicoEvent::primaryVertex(), StBbcGeom::TileCenter(), StEpdGeom::TileCenter() etc...
As any experimentalist knows, once you have decided upon a coordinate system, it is important to maintain it consistently. And as anybody experienced in STAR (and its many sign quirks and previous errors) knows, you should be extra careful to be consistent in STAR.
Answers: No. And no.
It's not a problem in collider mode, and it's not a problem in fixed-target mode. In the earlier fixed-target days, the experiments set up their internal coordinate systems (and event reconstruction and analysis software) such that the beam traveled in the +z direction. And that's fine. But the internal coordinate system does not matter, so STAR's internal system is fine, too.
Question: But wait, if the beam has negative rapidity, won't that mess things up? Won't you get negative proton v1 at large positive rapidity?
Answer: No. Not if you simply consistently use STAR coordinates (as you should always do) and equation 1 (as you should always do). Don't overcomplicate things.
The (physics-motivated) convention that works for ALL experiments in BOTH collider and fixed-target modes is: "proton v1 is positive at large positive rapidity." NOT "proton v1 is positive in direction of 'the' beam rapidity."
Example:
For the first STAR FXT paper, sqrt(sNN)=4.5 GeV, and in internal coordinates, y'beam=-3.04. So,
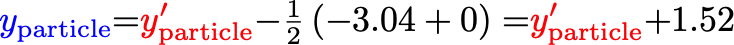
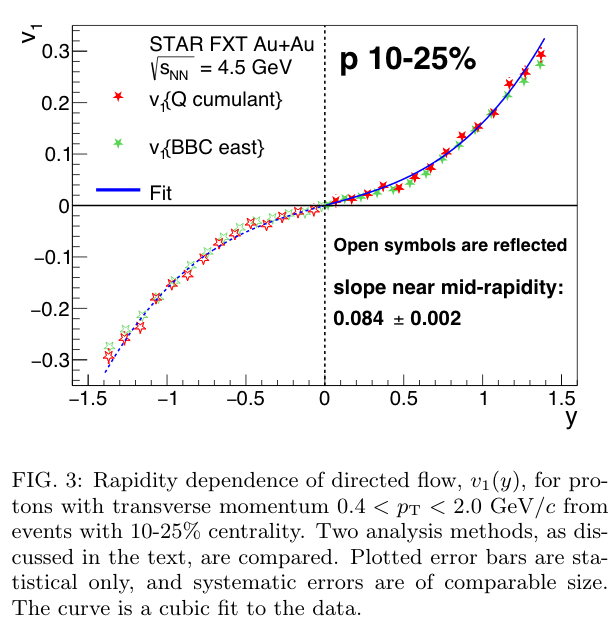
and simply using STAR coordinates and the simple equation 1, we get the "right sign" of v1, etc, as seen below, in figures taken from the first STAR FXT paper.

Why should you listen to me?
Executive Summary:
On this page, I argue that it is a pointless and bad idea to try to redefine East (yellow beam direction) as the "positive z direction" in STAR for FXT running.
This is a simple discussion intended to help reduce the rather surprising level of confusion developing in discussions on FXT measurements in STAR. If it seems lengthy, it is only because each issue is fully discussed.General considerations:
The physics of a system does not depend on the frame (boosts) or coordinate system (rotations, translations) in which it is measured. Every experiment has its own internal measurement frame/system, but when publishing physics results, it only makes sense to use collision-center-of-mass frame, i.e. the frame in which total momentum is zero.Whatever the internal coordinates (east-west, up-down, whatever boost frame) that an experiment (STAR/PHENIX/HADES/...) uses, the plots in collision-center-of-mass frame must be identical, modulo acceptance effects.
Transforming rapidity from the internal system to the center-of-mass system.
I will use super-explicit notation here:.png)
Then, to find the rapidity of a particle in the collision center-of-mass frame, just use the normal, standard formula:
STAR's internal system:
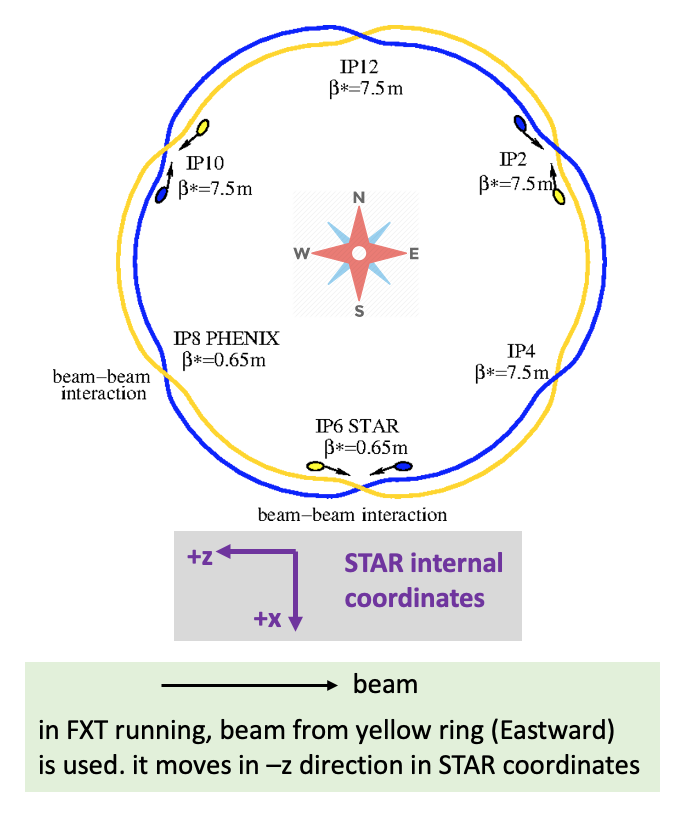
Experiments are built out of physical detectors, which are oriented in the physical world, where "up, down, North, South, East, West" are the relevant coordinates. Event reconstruction software takes signals from the detectors and converts such that the analyzers are presented with data in an internal (x,y,z) system. Every experiment has its own system.In the STAR internal coordinate system
- South (North) is +x (-x)
- Up (down) is +y (-y)
- West (East) is +z (-z)
IMPORTANT: This is how your picoDsts are formatted. For StPicoTrack::dcaPoint(), StPicoTrack::gMom(), StPicoEvent::primaryVertex(), StBbcGeom::TileCenter(), StEpdGeom::TileCenter() etc...
As any experimentalist knows, once you have decided upon a coordinate system, it is important to maintain it consistently. And as anybody experienced in STAR (and its many sign quirks and previous errors) knows, you should be extra careful to be consistent in STAR.
STAR in FXT mode:
In the WAH (where the STAR detector is located), beams from the Yellow (Blue) rings travel East (West). In FXT running, we use Yellow beam, traveling East, which travels in the negative z direction in STAR internal coordinates. Hence, in STAR internal coordinates, the beam has negative rapidity in FXT mode.
Discussion - is it a problem for the beam to have negative rapidity in STAR internal coordinates? How about in collision-center-of-mass coordinates?
Answers: No. And no.
It's not a problem in collider mode, and it's not a problem in fixed-target mode. In the earlier fixed-target days, the experiments set up their internal coordinate systems (and event reconstruction and analysis software) such that the beam traveled in the +z direction. And that's fine. But the internal coordinate system does not matter, so STAR's internal system is fine, too.
Question: But wait, if the beam has negative rapidity, won't that mess things up? Won't you get negative proton v1 at large positive rapidity?
Answer: No. Not if you simply consistently use STAR coordinates (as you should always do) and equation 1 (as you should always do). Don't overcomplicate things.
The (physics-motivated) convention that works for ALL experiments in BOTH collider and fixed-target modes is: "proton v1 is positive at large positive rapidity." NOT "proton v1 is positive in direction of 'the' beam rapidity."
Example:
For the first STAR FXT paper, sqrt(sNN)=4.5 GeV, and in internal coordinates, y'beam=-3.04. So,
and simply using STAR coordinates and the simple equation 1, we get the "right sign" of v1, etc, as seen below, in figures taken from the first STAR FXT paper.


Summary
- We should and do present our physics results in the collision-center-of-mass frame, using equation 1 as always.
- It is always wise to maintain a consistent coordinate system in a complex analysis, and it is especially important to do so in STAR, where you may be using the STAR coordinate system in parts of your analysis even without realizing it. (There is much conversion from detector to x,y,z in the reconstruction software.)
- There is no reason to "redefine" the Yellow ring beam to be moving in the positive direction. It will only lead to mistakes, and "z --> -z" will produce left-handed coordinate systems. Yes, one can be super-careful and catch mistakes, but one adds potential chaos for no gain. In fact, it is a bad idea.
- STAR has made sign errors in the past. This happens more easily than you think.
Why should you listen to me?
- I got my PhD doing several fixed target measurements, including design, detector construction, and analysis. I got tenure based on a fixed-target experiment. I know fixed-target measurements through and through, and there is no reason to define 'the' beam as moving in the positive direction.
- I have done many analyses where the sign of the first-order plane matters crucially, including (1) directed flow; (2) azimuthally-sensitive HBT; (3) global polarization.
- I have written STAR event-reconstruction software over the course of years, and I have built a first-order-plane sign-dependent detector in STAR. I know how important it is to stay consistent.
»
- lisa's blog
- Login or register to post comments
