EP resolution and the eta dependence of directed flow in Au+Au collisions
Updated on Sat, 2018-06-02 06:32. Originally created by lisa on 2018-05-30 05:20.
Executive summary:
In the 27 GeV Au+Au collisions, the directed flow for charged particles switches sign within the acceptance of the EPD. This means that, for example, in a given event, the inner rings (which measure spectators, defined as positive v1) show excess signal to the right while the outer rings (measuring forward-going participants, with negative v1) show excess signal to the left.
This physics-driven partial cancellation of the EP[1] signal severely degrades our EP[1] resolution, if we naively weight all rings/tiles equally. This explains the terrible EP resolution that I have reported previously. Ring-dependent (actually, eta-dependent, since the primary vertex fluctuates) should be used. ShinIchi Esumi also discussed this in a post last week.
In this post, I quantify the v1 correlation between the rings for mid-central collisions occurring near the center of the TPC, and make some initial attempts at ring weights to improve EP[1] resolution.
I find, in concurrence with ShinIchi's post, that the innermost rings have the highest sensitivity to EP[1]. Signals from the other rings are correlated with these innermost rings (even if that correlation is negative), so we need to explore how best to combine all information.
Flow/antiflow of spectators/participants and the correlation between EPD rings
At sqrt(s)=27 GeV, the rapidity of the beam is ybeam=3.4. Massless participant particles would have pseudorapidity eta (which is what the EPD measures) of 3.4. Massive participants (nucleons) will be found at higher eta, the exact value depending on pT. Using a straight-line approximation (ignoring magnetic field), a proton originating at the center of STAR with pT=0.3 GeV/c at y=3.4 will wind up at eta=4.6, in our inner rings. At this energy, our inner rings legitimately measure participant protons.
In the outer rings, eta~2-3, we are looking at forward participants, which can (depending on species and pT) have directed flow in the opposite direction from the spectators.
We can quantify this correlation/anticorrelation as the average (over events) cosine between the EP[1] for ring i versus EP[1] for ring j. In formulae:
.png)
As usual, the weight for tile k, Wk, depends on the calibrated ADC value (aka "nMIP"), a threshold and a maximum ("MAX") value, according to:
Here, I study mid-central (roughly 10%-40%) collisions, since they have the largest directed flow, and collisions near the center of the TPC (|Vz|<30 cm), to suppress fluctuations that smear the relationship between eta and ring number. I'm looping over about 1.7M Au+Au events with no trigger cut (should improve that, but the events are very dominantly minbias, especially with such a RefMult cut).
Here is the correlation between rings. The ring-specific EP[1] angles are not flattened; therefore I am looking at the East side, which is less affected by material at high eta.
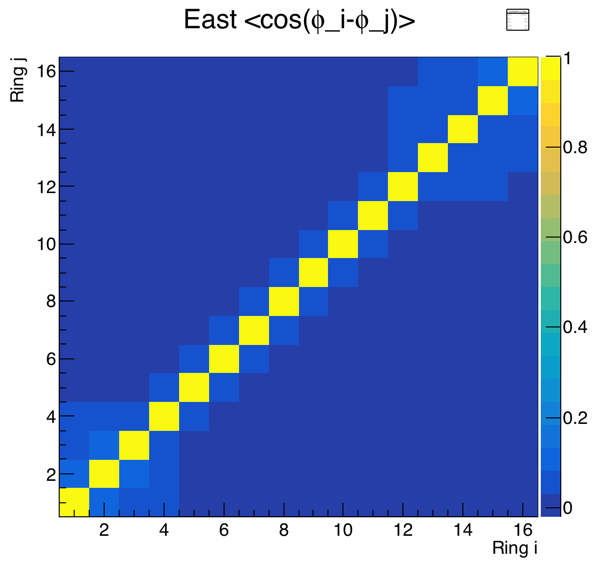
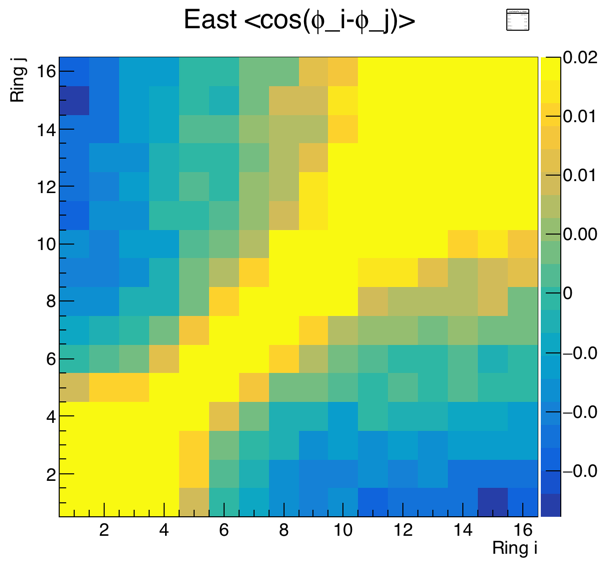
Figure 1 - Correlation C1i,j between ring-dependent first-order event plane angles, for mid-central Au+Au collisions at 27 GeV. The left and right plots show the same data, but in different z-ranges. By definition, C1i,j=1 when i=j, so diagonal components of the matrix are unity. Only by zooming in is the detailed off-diagonal structure clear.
It is instructive to examine the matrix explicitly. See table 1.
Table 1 - Correlation matrix C1i,j. The diagonal elements are trivially unity. Negative matrix elements are identified with yellow background.
Update 2 June 2018 - Hey, I found a really cool option that will put the numbers directly on the plot! Thought I'd share:
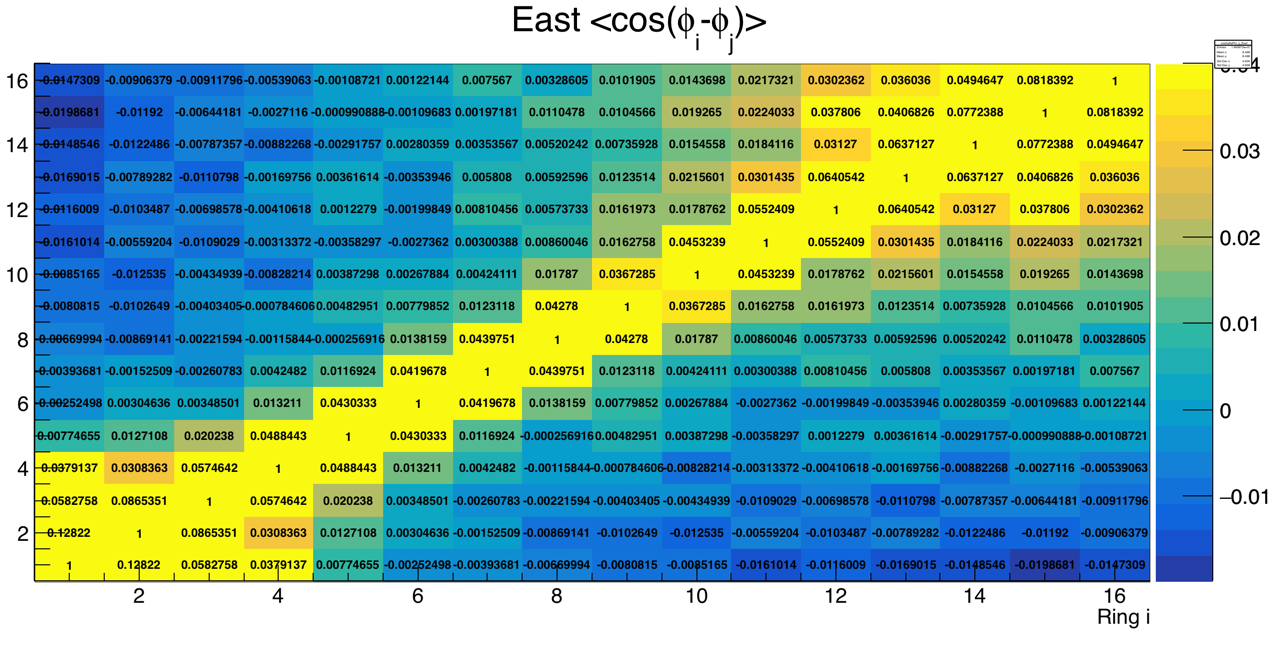
Figure 1.5 - This plot contains the same info as the plots above and the table, but it's cool you can do both at once in root, with these commands:
Some notes on the matrix:
Below, I investigate some options. It is not clear to me how to "optimize" this in a mechanical way, though there must be a way.
Exploring EP[1] resolution using ring weights.
I will find the EP[1] on East and West wheels using the following formula, which incorporates "ring weights" Zr.
.png)
Then, as usual, I flatten (shifting method) each side, and estimate the (total, or "full event") EP[1] resolution according to the correlation between East and West.
EP[1] resolution treating all rings equally, Zr=1 for all r.
This is the "default" method, which actually worked pretty well for the Zr+Zr/Ru+Ru at 200 GeV! It does not work so well for the Au+Au at 27 GeV....
.png)
Figure 2 - First-order event plane study for mid-central collisions. Here we use all rings with equal weight. Pad 1: EP[1] resolution. (Note that only the 10-20%, 20-30% and 30-40% bins are studied, so all others are zero.) Pad 2: EP in East versus West, for flattened (shifted) event planes. Pads 3 and 4: Raw (red) and shifted (blue) EP resolution for East and West wheels, respectively. Pad 5: ignore. Pad 6: RefMult distribution. We are using the third, fourth and fifth bins from the right.
In BES-I for the 27 GeV collisions with the BBC, we had EP[1] resolutions up to 0.35!! The performance above is much worse!! (Note that I have not tried using the BBC for this year's data.) Furthermore, there is no visible East-versus-West correlation in Pad 2 of figure 2. This looks terrible.
EP[1] resolution using only rings 1-5 (Z1-5=1, Z6-16=0)
This just uses the BBC acceptance. It is a LOT better:
.png)
Figure 3 - Same as figure 2 except here we use only EPD rings 1-5.
Now the East-West correlation is VERY obvious in pad 2 of figure 3. The EP[1] resolution has gone to 0.4, which is better than the 0.35 we had with the BBC in BES-I, but...... yay? We want to do better. Surely the outer rings (which are clearly anti-correlated with the inner ones) can provide some information to improve things...
EP[1] resolution using only rings 10-16 (Z1-9=0, Z10-16=1)
Here, we use only the outer rings. These are nominally eta=2.1-2.7.
.png)
Figure 4. Same as figure 2, except using only the outer rings, 10-16.
Well, even just using these outer rings, we can determine the EP[1] better than with treating all rings equally. And hey, you can even see a correlation between East and West in pad 2 in figure 4. (Unfortunately, one fluctuating pixel is kind of screwing up the autoscale in z.) So, presumably this information can be "combined" somehow with the inner rings to squeeze out some more resolution....
EP[1] resolution using rings 1-5 with positive unity weight and 10-16 with negative unity weight (Z1-5=+1, Z10-16=-1, Z6-9=0)
Here, we acknowledge the negative correlation between the inner and outer rings, and try to use it to our advantage.
.png)
Figure 5 - Same as figure 2, but using positive weight for the inner and negative weight for outer tiles. See text for details.
Huh. Well, I expected better. This is (a little bit) worse than simply ignoring the outer rings. That's not mathematically impossible. While the outer rings are anti-correlated on the average, the dispersion might be so large as to simply smear things too much. Nevertheless, I was expecting better.
EP[1] resolution using rings 1-4 with positive unity weight and 13-16 with negative unity weight (Z1-4=+1, Z13-16=-1, Z5-12=0)
The idea here is the same as the previous case, except I look more inner and more outer...
.png)
Figure 6 - Same as figure 2, but using positive weight for the inner and negative weight for outer tiles. See text for details.
Well.... we did get some tiny bit of improvement.
EP[1] resolution using only rings 1-2 (Z1-2=1, Z3-16=0)
Completely ignoring all other rings except 1 and 2, which are treated equally. This seems a bit extreme, right? Well, if you mean extremely good, then yes!
.png)
Figure 7 - Same as figure 2, but only using rings 1-2. Note that pad #1 has a different scale than in figures 2-6.
Wow, that is a real improvement even over using just 1-5. Note that I had to increase the scale on the y-axis of the resolution plot! We are now at 0.45.
EP[1] resolution using only ring 1 (Z1=1, Z2-16=0)
Well, shoot. If restricting everything to rings 1 and 2 is surprisingly good, then what happens if we ONLY use ring 1? (This means using only 12 out of the 372 tiles on a wheel.....)
.png)
Figure 8 - Same as figure 2, but only using ring 1.. Note that pad #1 has a different scale than in figures 2-6.
So, using rings 1 & 2 is better than using ring 1 alone, even if only a little. Gee, nice to know that we should look at more than 3% of our tiles.....
Outlook:
These weights (and other methods?) need a lot more study. We really do have to beat 0.35. Can we get to 0.6?
In the 27 GeV Au+Au collisions, the directed flow for charged particles switches sign within the acceptance of the EPD. This means that, for example, in a given event, the inner rings (which measure spectators, defined as positive v1) show excess signal to the right while the outer rings (measuring forward-going participants, with negative v1) show excess signal to the left.
This physics-driven partial cancellation of the EP[1] signal severely degrades our EP[1] resolution, if we naively weight all rings/tiles equally. This explains the terrible EP resolution that I have reported previously. Ring-dependent (actually, eta-dependent, since the primary vertex fluctuates) should be used. ShinIchi Esumi also discussed this in a post last week.
In this post, I quantify the v1 correlation between the rings for mid-central collisions occurring near the center of the TPC, and make some initial attempts at ring weights to improve EP[1] resolution.
I find, in concurrence with ShinIchi's post, that the innermost rings have the highest sensitivity to EP[1]. Signals from the other rings are correlated with these innermost rings (even if that correlation is negative), so we need to explore how best to combine all information.
Flow/antiflow of spectators/participants and the correlation between EPD rings
At sqrt(s)=27 GeV, the rapidity of the beam is ybeam=3.4. Massless participant particles would have pseudorapidity eta (which is what the EPD measures) of 3.4. Massive participants (nucleons) will be found at higher eta, the exact value depending on pT. Using a straight-line approximation (ignoring magnetic field), a proton originating at the center of STAR with pT=0.3 GeV/c at y=3.4 will wind up at eta=4.6, in our inner rings. At this energy, our inner rings legitimately measure participant protons.
In the outer rings, eta~2-3, we are looking at forward participants, which can (depending on species and pT) have directed flow in the opposite direction from the spectators.
We can quantify this correlation/anticorrelation as the average (over events) cosine between the EP[1] for ring i versus EP[1] for ring j. In formulae:
.png)
As usual, the weight for tile k, Wk, depends on the calibrated ADC value (aka "nMIP"), a threshold and a maximum ("MAX") value, according to:
In this study, threshold=0.3 and MAX=2. These are reasonable values, but can be played with.Wk = 0 if nMIP<threshold [this is to cut out noise and out-of-time light]
Wk = MAX if nMIP>MAX [this is to suppress the noise effects of Landau fluctuations]
Wk = nMIP otherwise
Here, I study mid-central (roughly 10%-40%) collisions, since they have the largest directed flow, and collisions near the center of the TPC (|Vz|<30 cm), to suppress fluctuations that smear the relationship between eta and ring number. I'm looping over about 1.7M Au+Au events with no trigger cut (should improve that, but the events are very dominantly minbias, especially with such a RefMult cut).
Here is the correlation between rings. The ring-specific EP[1] angles are not flattened; therefore I am looking at the East side, which is less affected by material at high eta.


Figure 1 - Correlation C1i,j between ring-dependent first-order event plane angles, for mid-central Au+Au collisions at 27 GeV. The left and right plots show the same data, but in different z-ranges. By definition, C1i,j=1 when i=j, so diagonal components of the matrix are unity. Only by zooming in is the detailed off-diagonal structure clear.
It is instructive to examine the matrix explicitly. See table 1.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
| 1 | 1.00e+00 | 1.30e-01 | 6.02e-02 | 3.54e-02 | 9.78e-03 | -6.42e-04 | -3.67e-03 | -7.67e-03 | -9.27e-03 | -9.13e-03 | -1.34e-02 | -1.11e-02 | -1.27e-02 | -1.15e-02 | -1.88e-02 | -1.46e-02 |
| 2 | 1.30e-01 | 1.00e+00 | 9.07e-02 | 3.24e-02 | 1.42e-02 | 2.09e-03 | -2.64e-03 | -7.69e-03 | -1.01e-02 | -1.10e-02 | -8.53e-03 | -1.09e-02 | -8.37e-03 | -1.18e-02 | -1.18e-02 | -1.14e-02 |
| 3 | 6.02e-02 | 9.07e-02 | 1.00e+00 | 6.05e-02 | 1.60e-02 | 3.79e-03 | -6.59e-04 | -2.82e-03 | -9.12e-03 | -6.13e-03 | -8.95e-03 | -6.54e-03 | -9.13e-03 | -6.28e-03 | -6.58e-03 | -6.96e-03 |
| 4 | 3.54e-02 | 3.24e-02 | 6.05e-02 | 1.00e+00 | 4.92e-02 | 1.14e-02 | 4.44e-03 | -2.52e-03 | -2.75e-03 | -6.03e-03 | -1.11e-03 | -2.75e-03 | -1.69e-03 | -5.18e-03 | -5.07e-03 | -7.11e-03 |
| 5 | 9.78e-03 | 1.42e-02 | 1.60e-02 | 4.92e-02 | 1.00e+00 | 4.61e-02 | 1.24e-02 | 3.20e-03 | 3.78e-03 | 6.59e-04 | 2.09e-04 | 1.24e-03 | 3.27e-04 | 6.73e-04 | 5.09e-04 | -1.29e-03 |
| 6 | -6.42e-04 | 2.09e-03 | 3.79e-03 | 1.14e-02 | 4.61e-02 | 1.00e+00 | 4.23e-02 | 1.52e-02 | 7.94e-03 | 4.21e-03 | 2.09e-03 | 2.28e-04 | 4.07e-04 | 1.61e-03 | -1.41e-03 | -5.89e-04 |
| 7 | -3.67e-03 | -2.64e-03 | -6.59e-04 | 4.44e-03 | 1.24e-02 | 4.23e-02 | 1.00e+00 | 4.27e-02 | 1.55e-02 | 6.62e-03 | 4.71e-03 | 5.38e-03 | 3.20e-03 | 5.13e-03 | 2.80e-03 | 3.51e-03 |
| 8 | -7.67e-03 | -7.69e-03 | -2.82e-03 | -2.52e-03 | 3.20e-03 | 1.52e-02 | 4.27e-02 | 1.00e+00 | 4.39e-02 | 1.89e-02 | 9.30e-03 | 7.00e-03 | 6.45e-03 | 8.22e-03 | 9.67e-03 | 3.96e-03 |
| 9 | -9.27e-03 | -1.01e-02 | -9.12e-03 | -2.75e-03 | 3.78e-03 | 7.94e-03 | 1.55e-02 | 4.39e-02 | 1.00e+00 | 3.97e-02 | 1.73e-02 | 1.63e-02 | 1.20e-02 | 8.07e-03 | 8.90e-03 | 1.05e-02 |
| 10 | -9.13e-03 | -1.10e-02 | -6.13e-03 | -6.03e-03 | 6.59e-04 | 4.21e-03 | 6.62e-03 | 1.89e-02 | 3.97e-02 | 1.00e+00 | 4.64e-02 | 2.18e-02 | 1.97e-02 | 1.43e-02 | 1.61e-02 | 1.36e-02 |
| 11 | -1.34e-02 | -8.53e-03 | -8.95e-03 | -1.11e-03 | 2.09e-04 | 2.09e-03 | 4.71e-03 | 9.30e-03 | 1.73e-02 | 4.64e-02 | 1.00e+00 | 5.65e-02 | 2.89e-02 | 2.05e-02 | 2.14e-02 | 2.46e-02 |
| 12 | -1.11e-02 | -1.09e-02 | -6.54e-03 | -2.75e-03 | 1.24e-03 | 2.28e-04 | 5.38e-03 | 7.00e-03 | 1.63e-02 | 2.18e-02 | 5.65e-02 | 1.00e+00 | 6.26e-02 | 3.29e-02 | 3.62e-02 | 3.07e-02 |
| 13 | -1.27e-02 | -8.37e-03 | -9.13e-03 | -1.69e-03 | 3.27e-04 | 4.07e-04 | 3.20e-03 | 6.45e-03 | 1.20e-02 | 1.97e-02 | 2.89e-02 | 6.26e-02 | 1.00e+00 | 6.35e-02 | 4.08e-02 | 3.71e-02 |
| 14 | -1.15e-02 | -1.18e-02 | -6.28e-03 | -5.18e-03 | 6.73e-04 | 1.61e-03 | 5.13e-03 | 8.22e-03 | 8.07e-03 | 1.43e-02 | 2.05e-02 | 3.29e-02 | 6.35e-02 | 1.00e+00 | 8.02e-02 | 4.91e-02 |
| 15 | -1.88e-02 | -1.18e-02 | -6.58e-03 | -5.07e-03 | 5.09e-04 | -1.41e-03 | 2.80e-03 | 9.67e-03 | 8.90e-03 | 1.61e-02 | 2.14e-02 | 3.62e-02 | 4.08e-02 | 8.02e-02 | 1.00e+00 | 8.57e-02 |
| 16 | -1.46e-02 | -1.14e-02 | -6.96e-03 | -7.11e-03 | -1.29e-03 | -5.89e-04 | 3.51e-03 | 3.96e-03 | 1.05e-02 | 1.36e-02 | 2.46e-02 | 3.07e-02 | 3.71e-02 | 4.91e-02 | 8.57e-02 | 1.00e+00 |
Table 1 - Correlation matrix C1i,j. The diagonal elements are trivially unity. Negative matrix elements are identified with yellow background.
Update 2 June 2018 - Hey, I found a really cool option that will put the numbers directly on the plot! Thought I'd share:

Figure 1.5 - This plot contains the same info as the plots above and the table, but it's cool you can do both at once in root, with these commands:
cosDeltaPhi_ij_East->Draw("colz")
cosDeltaPhi_ij_East->Draw("text,same")
Some notes on the matrix:
- Each ring is correlated with its two closest neighboring rings at the level of a few percent.
- The correlation in the inner five rings (rings 1-5) is particularly strong and extends through the entire group.
- The large-eta rings (say 12-16) are relatively well correlated with each other and negatively correlated with the inner (say 1-5) rings. This is the flow/antiflow effect of spectators/participants.
- The intermediate rings (say 6-11) are a transition region, where the correlation with the two other groups is weak.
Below, I investigate some options. It is not clear to me how to "optimize" this in a mechanical way, though there must be a way.
Exploring EP[1] resolution using ring weights.
I will find the EP[1] on East and West wheels using the following formula, which incorporates "ring weights" Zr.
.png)
Then, as usual, I flatten (shifting method) each side, and estimate the (total, or "full event") EP[1] resolution according to the correlation between East and West.
EP[1] resolution treating all rings equally, Zr=1 for all r.
This is the "default" method, which actually worked pretty well for the Zr+Zr/Ru+Ru at 200 GeV! It does not work so well for the Au+Au at 27 GeV....
.png)
Figure 2 - First-order event plane study for mid-central collisions. Here we use all rings with equal weight. Pad 1: EP[1] resolution. (Note that only the 10-20%, 20-30% and 30-40% bins are studied, so all others are zero.) Pad 2: EP in East versus West, for flattened (shifted) event planes. Pads 3 and 4: Raw (red) and shifted (blue) EP resolution for East and West wheels, respectively. Pad 5: ignore. Pad 6: RefMult distribution. We are using the third, fourth and fifth bins from the right.
In BES-I for the 27 GeV collisions with the BBC, we had EP[1] resolutions up to 0.35!! The performance above is much worse!! (Note that I have not tried using the BBC for this year's data.) Furthermore, there is no visible East-versus-West correlation in Pad 2 of figure 2. This looks terrible.
EP[1] resolution using only rings 1-5 (Z1-5=1, Z6-16=0)
This just uses the BBC acceptance. It is a LOT better:
.png)
Figure 3 - Same as figure 2 except here we use only EPD rings 1-5.
Now the East-West correlation is VERY obvious in pad 2 of figure 3. The EP[1] resolution has gone to 0.4, which is better than the 0.35 we had with the BBC in BES-I, but...... yay? We want to do better. Surely the outer rings (which are clearly anti-correlated with the inner ones) can provide some information to improve things...
EP[1] resolution using only rings 10-16 (Z1-9=0, Z10-16=1)
Here, we use only the outer rings. These are nominally eta=2.1-2.7.
.png)
Figure 4. Same as figure 2, except using only the outer rings, 10-16.
Well, even just using these outer rings, we can determine the EP[1] better than with treating all rings equally. And hey, you can even see a correlation between East and West in pad 2 in figure 4. (Unfortunately, one fluctuating pixel is kind of screwing up the autoscale in z.) So, presumably this information can be "combined" somehow with the inner rings to squeeze out some more resolution....
EP[1] resolution using rings 1-5 with positive unity weight and 10-16 with negative unity weight (Z1-5=+1, Z10-16=-1, Z6-9=0)
Here, we acknowledge the negative correlation between the inner and outer rings, and try to use it to our advantage.
.png)
Figure 5 - Same as figure 2, but using positive weight for the inner and negative weight for outer tiles. See text for details.
Huh. Well, I expected better. This is (a little bit) worse than simply ignoring the outer rings. That's not mathematically impossible. While the outer rings are anti-correlated on the average, the dispersion might be so large as to simply smear things too much. Nevertheless, I was expecting better.
EP[1] resolution using rings 1-4 with positive unity weight and 13-16 with negative unity weight (Z1-4=+1, Z13-16=-1, Z5-12=0)
The idea here is the same as the previous case, except I look more inner and more outer...
.png)
Figure 6 - Same as figure 2, but using positive weight for the inner and negative weight for outer tiles. See text for details.
Well.... we did get some tiny bit of improvement.
EP[1] resolution using only rings 1-2 (Z1-2=1, Z3-16=0)
Completely ignoring all other rings except 1 and 2, which are treated equally. This seems a bit extreme, right? Well, if you mean extremely good, then yes!
.png)
Figure 7 - Same as figure 2, but only using rings 1-2. Note that pad #1 has a different scale than in figures 2-6.
Wow, that is a real improvement even over using just 1-5. Note that I had to increase the scale on the y-axis of the resolution plot! We are now at 0.45.
EP[1] resolution using only ring 1 (Z1=1, Z2-16=0)
Well, shoot. If restricting everything to rings 1 and 2 is surprisingly good, then what happens if we ONLY use ring 1? (This means using only 12 out of the 372 tiles on a wheel.....)
.png)
Figure 8 - Same as figure 2, but only using ring 1.. Note that pad #1 has a different scale than in figures 2-6.
So, using rings 1 & 2 is better than using ring 1 alone, even if only a little. Gee, nice to know that we should look at more than 3% of our tiles.....
Outlook:
These weights (and other methods?) need a lot more study. We really do have to beat 0.35. Can we get to 0.6?
»
- lisa's blog
- Login or register to post comments
