Executive summary:

The geometric efficiency (i.e. the fraction of area that is occupied by scintillator) is not 100%, due to regions occupied by optically-isolating epoxy, and due to gaps between supersectors.  Because these structures (glue and gaps) have fixed scale independent of radius, while the scintillating tile size grows with radius, the geometric efficiency is lowest for the inner rings.

According to the "nominal geometry" encoded by StEpdGeom, the geometric efficiency for the four innermost rings (which cover the BBC) is on average 92%; it grows to about 98% at the outer edge.

These numbers do not explain Xiaoyu's results, in which she sees BBC tiles fire about 20-25% of the time when the EPD tiles in front of them see nothing.  According to the calculations presented here, we would expect the BBC tiles to fire 8% of the time.

Taken at face value, this suggests that the "nominal geometric inefficiency," associated with glue and gaps, accounts for only half of the true inefficiency.  Since it does not account for the central channel or WLS channel grooves (which are relatively speaking a larger fraction of the area, for the small tiles), this may not be shocking.  I may do a more detailed analysis at some point, but do not plan on one right now.

---

The glue gaps and gaps between supersectors are encoded in the StEpdGeom object found in the StRoot/StEpdUtil/ package on CVS.  The BBC geometry is found there as well.  A nice macro to visualize these is StRoot/StEpdUtil/Macros/SeeBoth.C.



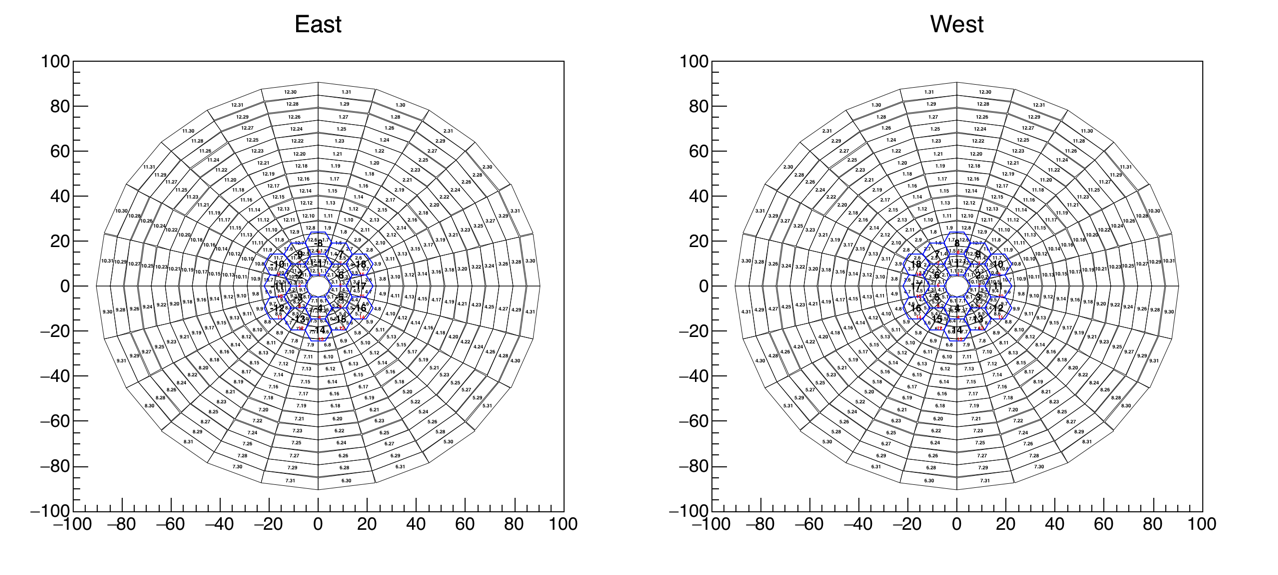
Figure 1 - The geometry of the EPD and BBC, as encoded into the StEpdGeom and SetBbcGeom classes.  Tile numbers are written in tiny text.


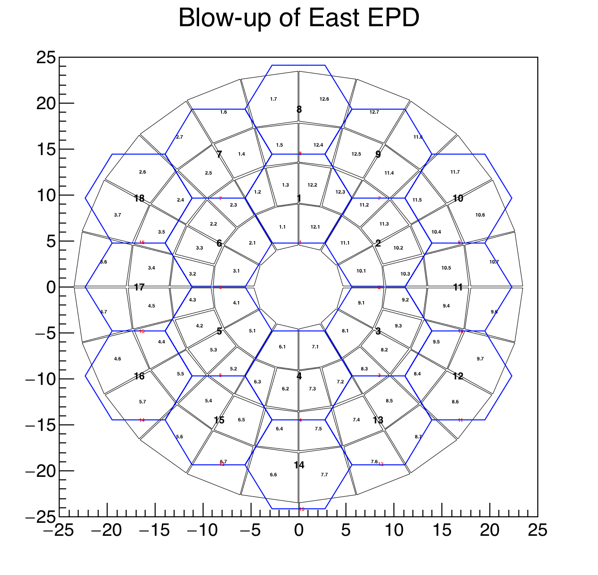
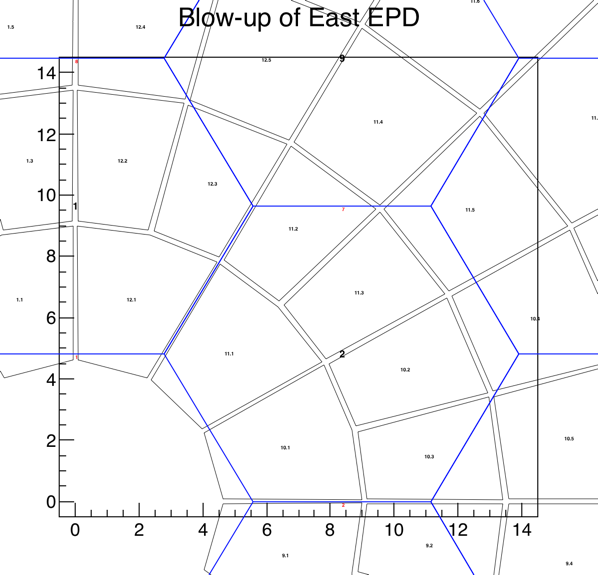
Figures 2-3: Zooming in on the region where the inner BBC tiles are.  The gaps become clearer here.  Note that gaps between the BBC tiles are NOT included, as detailed information on their inner structure is not available.

The nominal geometry encoded in StEpdGeom is certainly not absolutely correct.  I would trust the gap widths to about 10%.  Furthermore, the "central channel" where the tiles become progressively thinner (hence producing less light) is not included, nor are the WLS fiber grooves, for which light conversion will be reduced.  For these reasons, using the StEpdGeom geometry is likely to produce a somewhat higher estimate of geometric efficiency than reality.

With these caveats, I have sampled the space (just thrown random points in the area, and used the nice StEpdGeom->IsInTile() method to see the fraction of times it lands on a tile.  This provides the geometric efficiency, shown below as a function of radius:


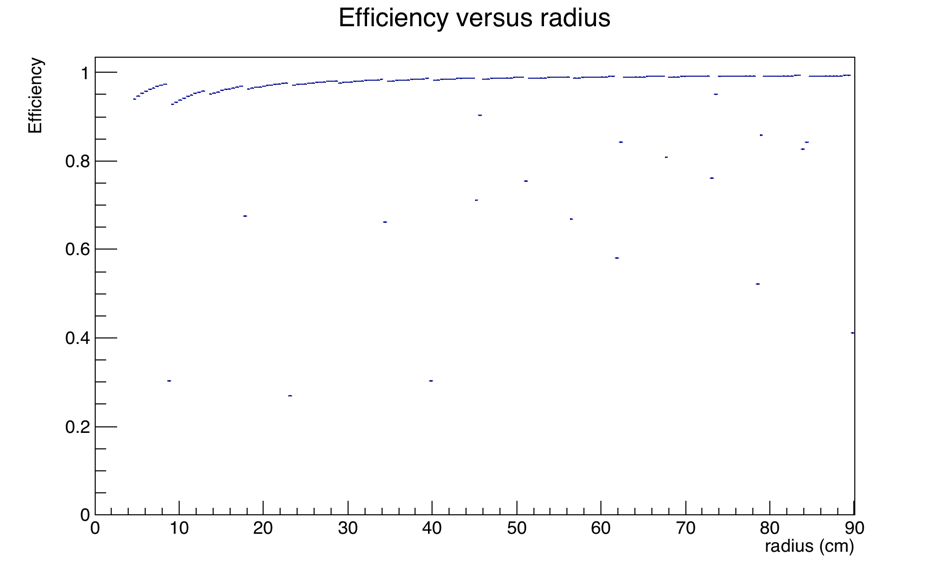
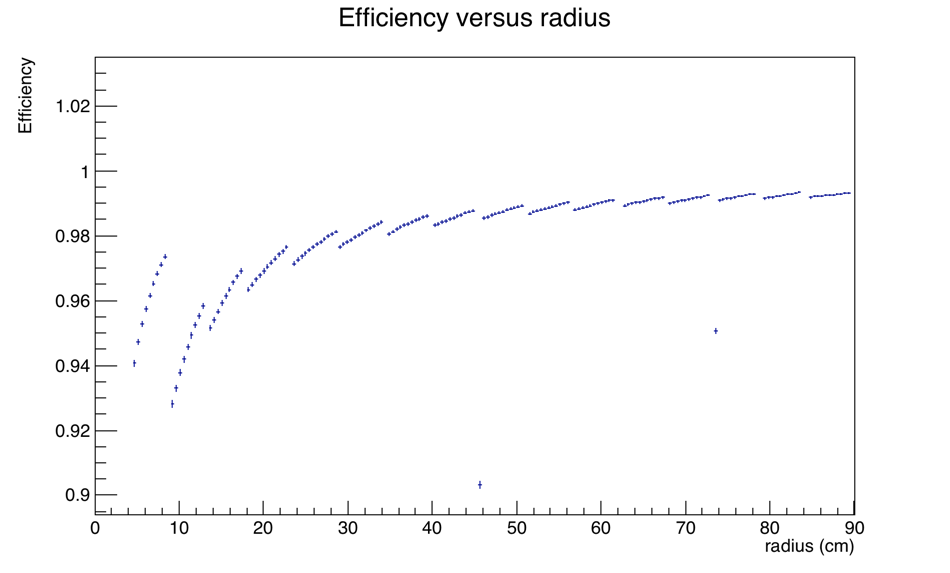
Figures 4-5 - Geometric efficiency as a function of radius, over the entire device.  The 16-ring structure is obvious.  The efficiency grows with radius in general, as the ratio of tile size to gap size increases.  The region associated with ring 1 (TT01) has higher efficiency than the region associated with ring 2 (TT02 and TT03), because that ring has only 12 tiles, rather than 24, hence fewer gaps.  There are radii that have zero efficiency due to "transverse gaps." 


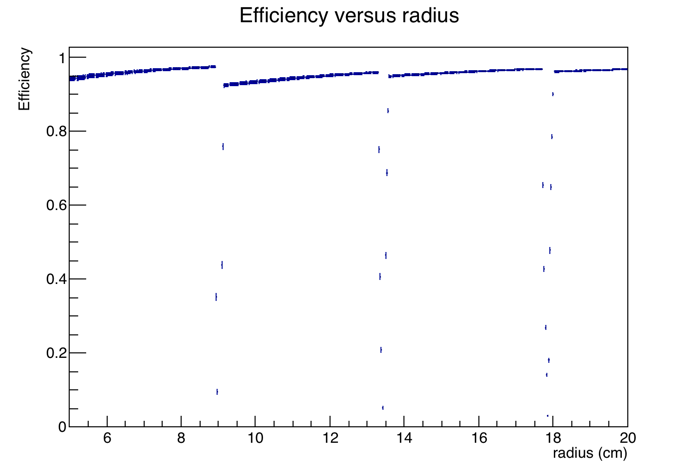
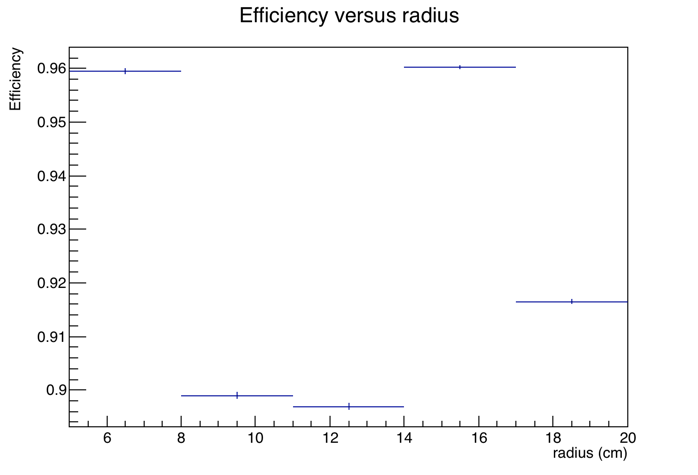
Figures 6-7:  Zoom in on region that covers the BBC.  Geometric efficiency, according to nominal geometry encoded in StEpdGeom, is about 92%.

The results shown in figures 4-7, above, would indicate that, when no EPD tiles that sit in front of a BBC tile see any particle, that BBC tile would see a particle about 8% of the time.  We would therefore expect a "suppression factor" (in Xiaoyu's language) of 1/0.08=12.5.  She sees a significantly lower factor, ~5.