Unfolding dN/deta with RooUnfold
0) dN/dη measurement with unfolding
Let us suppose we measure Ni hits in each EPD ring, and we would like to restore the original dN/dη from this.
This is basically an unfolding problem, as
f(x) = ∫ R(x,y) g(y) dy
with:
x: EPD hit identifier (ring number or corresponding eta)
y: eta of primary track causing EPD hit
f(x): measured signal in the EPD
g(y): true dN/dη
We measure f(x), somehow (with simulations) determine R(x,y), and would like to restore g(y).
There is one caveat: in regular unfolding problems, one hit in g(y) only causes one or zero hit in f(x). But here we have multiple hits in f(x) from the same hit in g(y), this is like having >100% efficiency for some of the tracks.
As it appears to me this can not be handled in this method, as we cannot tell if for track1->hit1, track2->hit2, track1 and track2 were the same, as both cases (track1=track2 and track1=/=track2) just give an entry to R(x,y) the same way.
We'll come back to this later.
There are many methods for unfolding, probably one mathematically very advanced (i.e. convergence properies formally proven) is this one:
A. Laszlo, A Robust Iterative Unfolding Method for Signal Processing, J. Phys. A39 (2006) 13621-13640 [arXiv:math-ph/0601017]
A. Laszlo, A Linear Iterative Unfolding Method, J.Phys.Conf.Ser. 368 (2012) 012043 [arXiv:1111.3387]
but this is somewhat non-standard, and anyway refers to iterative Bayesian unfolding by d’Agostini and others:
G. D’Agostini, A Multidimensional unfolding method based on Bayes' theorem, Nucl. Instr. Meth. A362 (1995) 487
This is also implemented in RooUnfold and widely used, as I heard, so let us work with RooUnfold. See details about it here:
statisticalmethods.web.cern.ch/StatisticalMethods/unfolding/RooUnfold_01-Methods/
hepunx.rl.ac.uk/~adye/software/unfold/htmldoc/RooUnfold.html
Let us now determine R(x,y) from the simulations as:
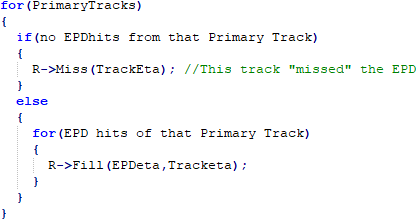
Once again note that here we cannot differentiate two (EPDeta,Tracketa) pairs if they came from the same track or not. So if we use this method, then we have to deal with this later, probably in form of a correction.
Let us see how we can get the dN/dη from this.
1) Unfolding a square matrix
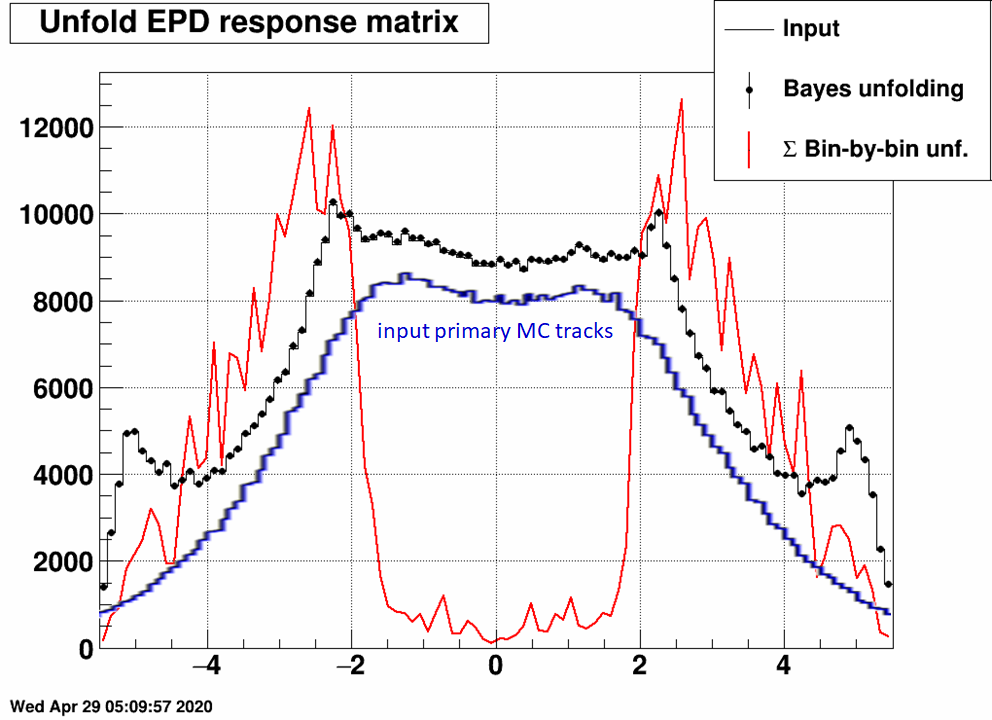
If we define equal amount of bins in the "truth" and the "response", then this is our matrix and the related EPD distribution as well as the "truth" (which has a higher integral than the response or the truth, as many tracks don't leave a hit at all):
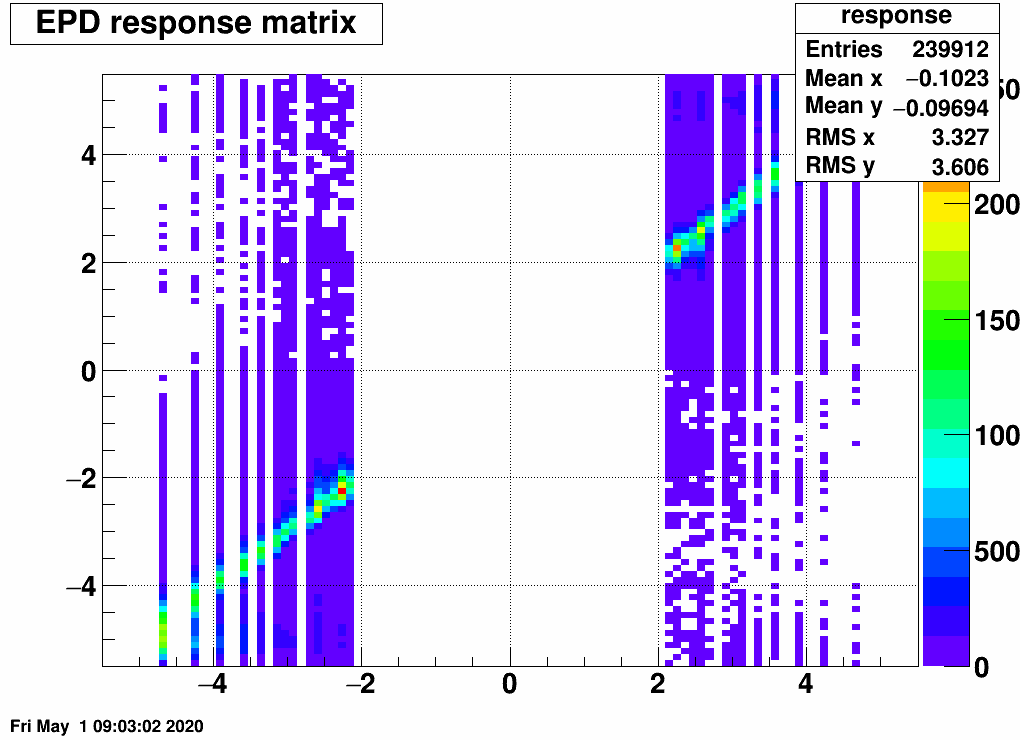
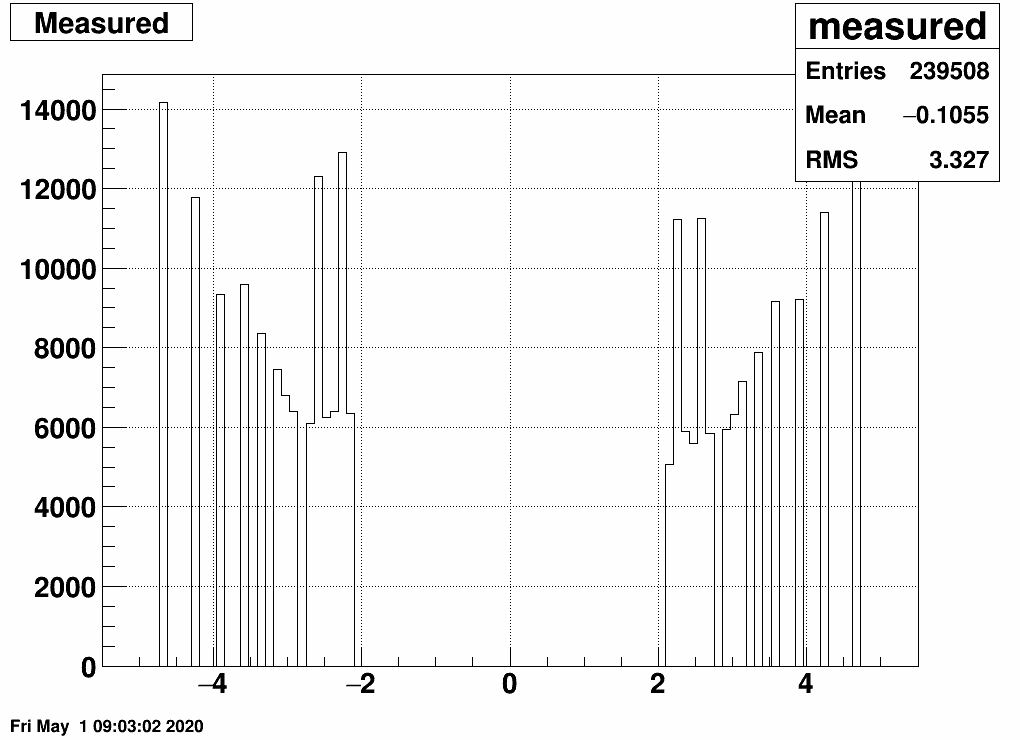
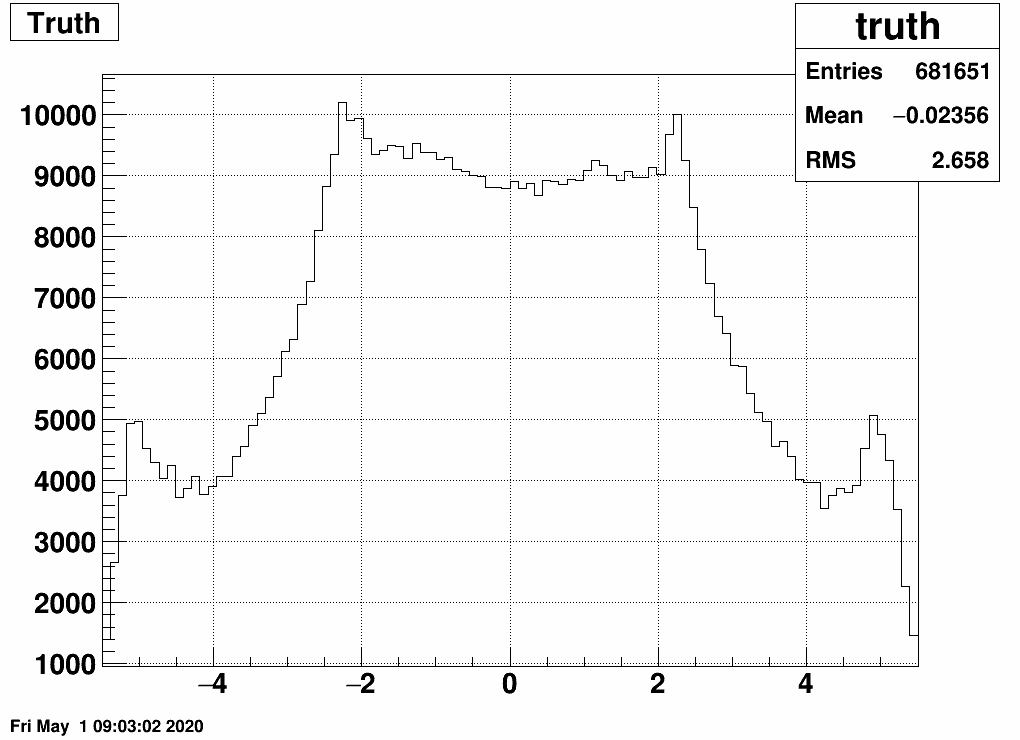
Note the "peaked" bins in the EPD response: here two EPD rings belong to the same eta bin - not fortunate. We will deal with this (and other things) in the next section.
Now the conventional "matrix inverse" type of unfolding does not work, as there are empty columns in the response matrix.
Instead Bayes type of iterative unfolding may be utilized. Here is the result:
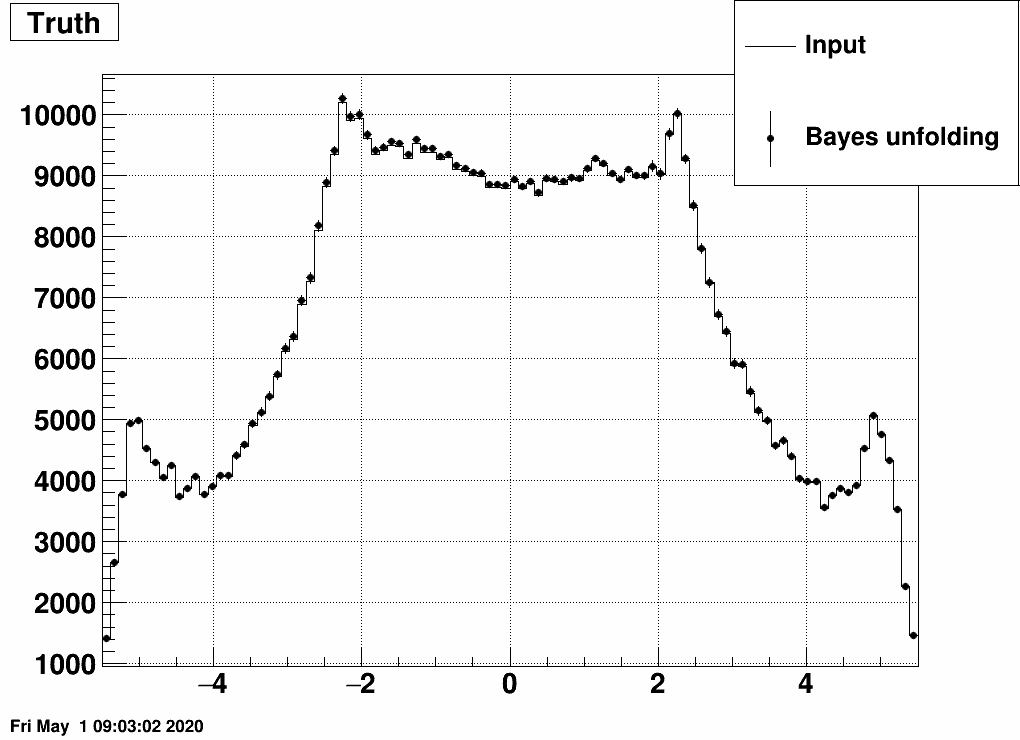
This looks a bit strange, how the input (dN/dη) is exactly reproduced. (Note also that the shape is not the usual dN/dη as there is multiple counting here, many of the primaries leave multiple hits, and this dN/dη is a "summed" result: one entry for each EPD hit). This may be due to the fact that we fed EXACTLY the same measurement as on which the response matrix was trained on.
Let us do two tests.
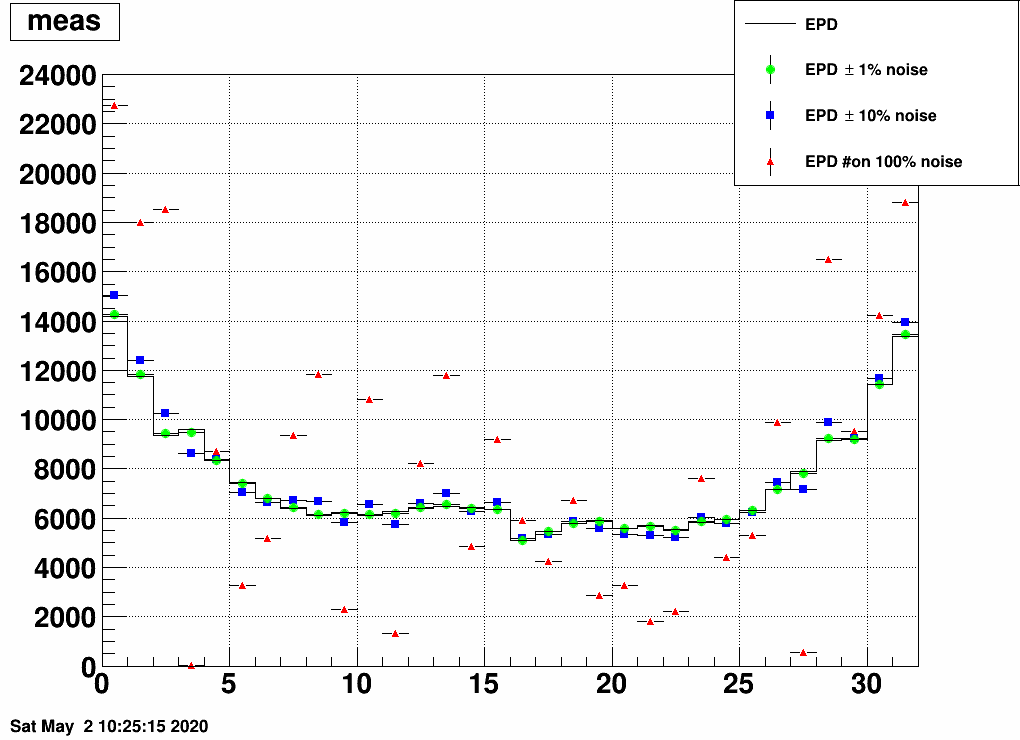
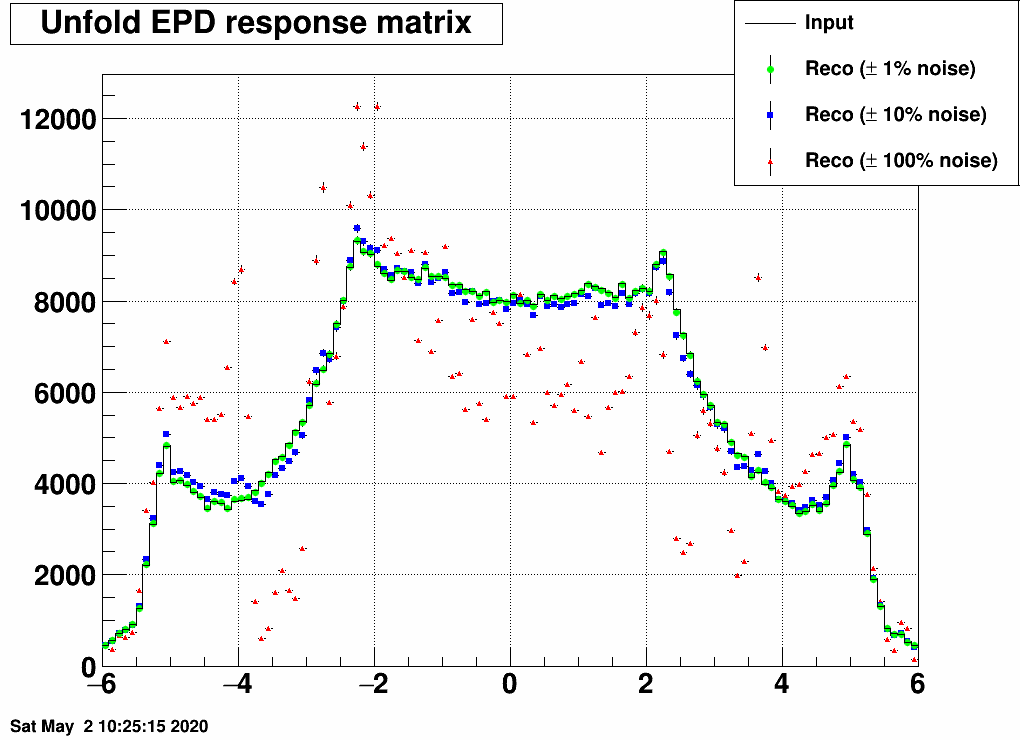
a) Add random noise to the EPD distribution. See these distorted "measured samples" and their unfolded images here:
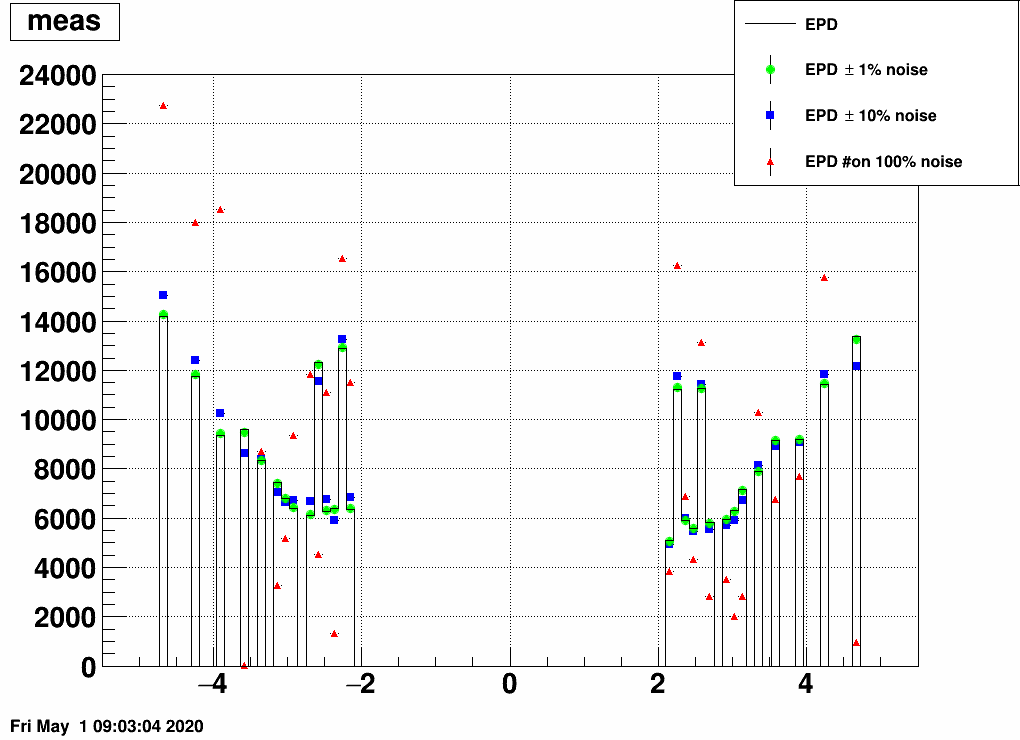
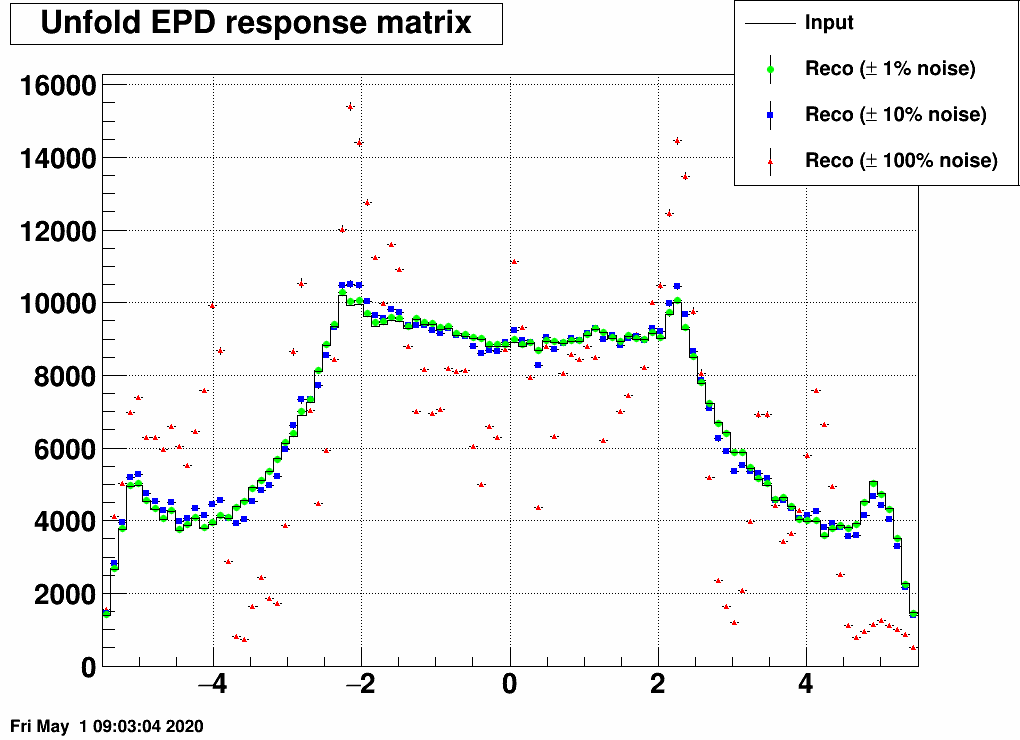
Note that even 10% noise allows the unfolding to be quite good.
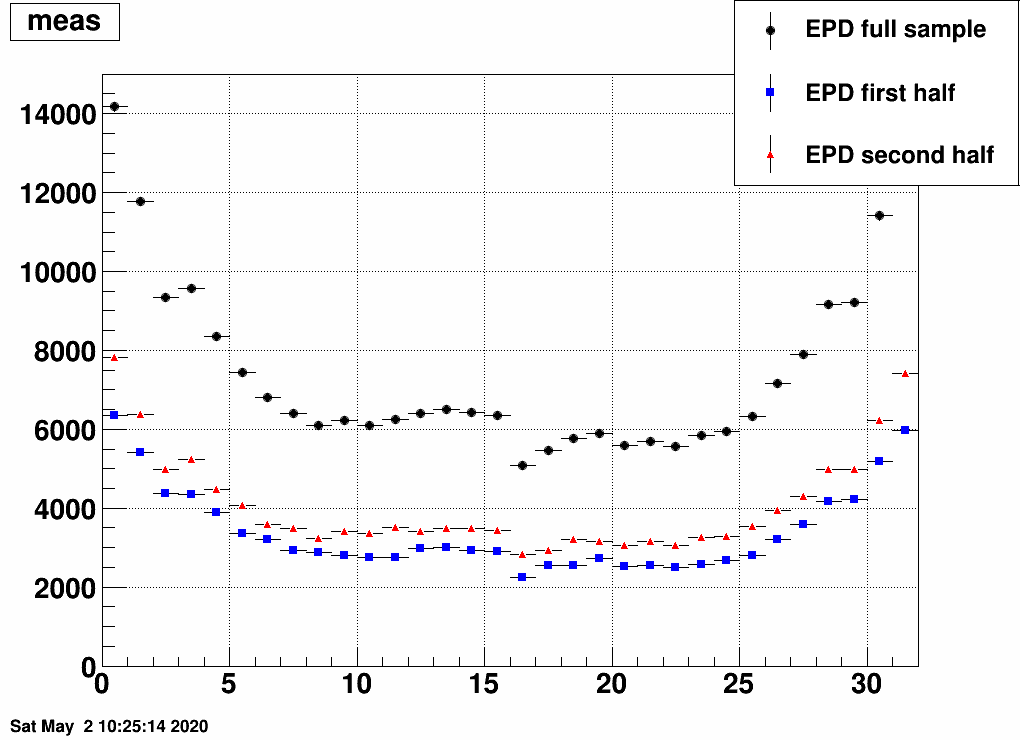
b) Separate the simulated data into two samples, and unfold sample 1 with a response trained on sample 2, and vice versa:
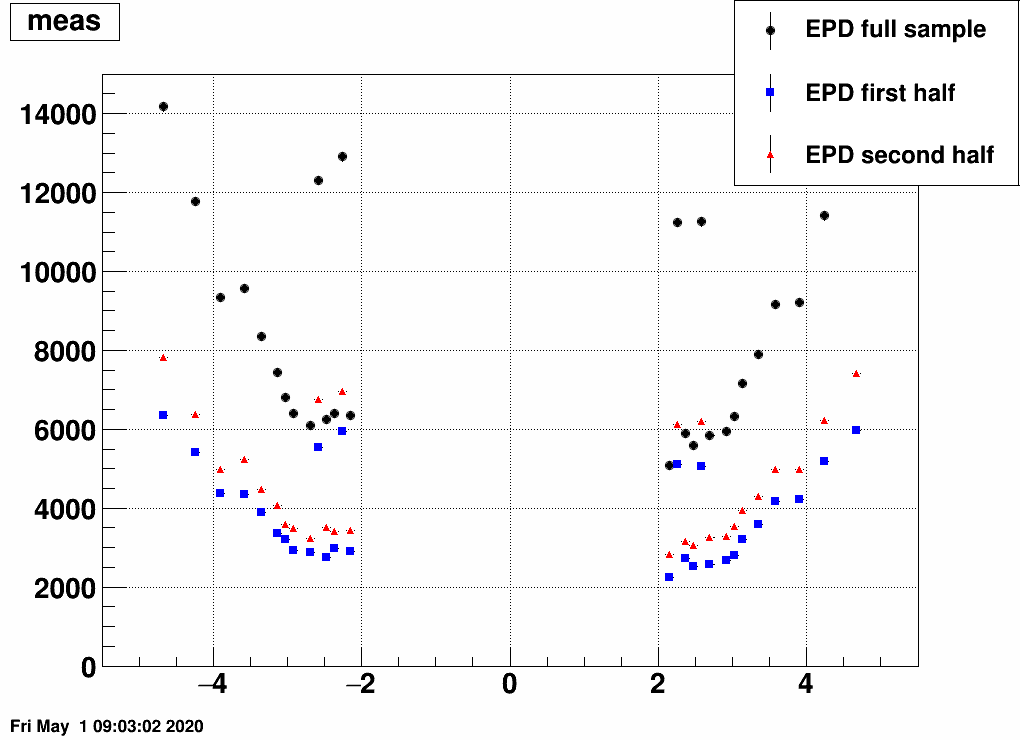
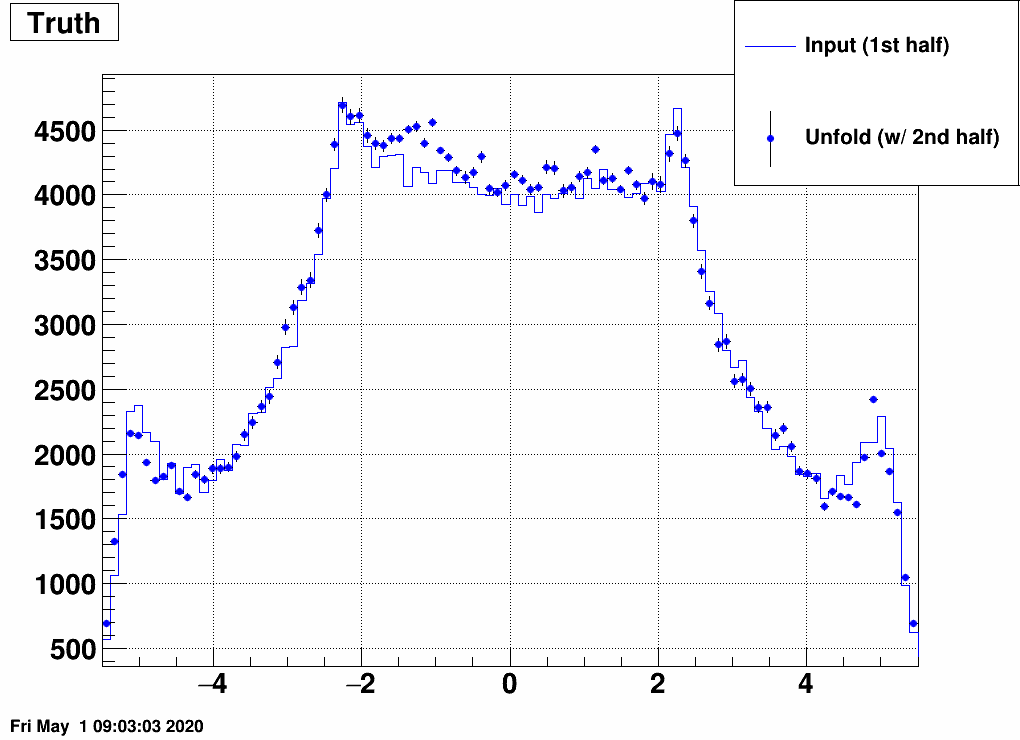
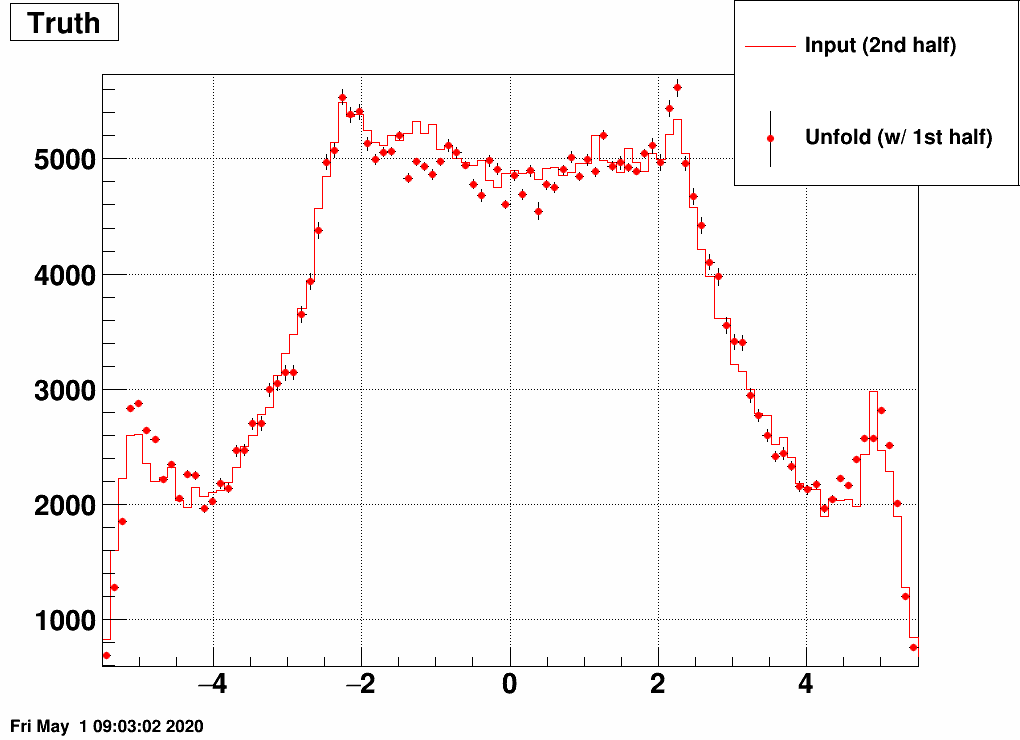
This still also works, although it is a bit strange how unfolding result 1 is similar to input 2 and vice versa. Note the magnitude however, that that's obtained correctly from the unfolding.
Furthermore, one can check what happens if one unfolds the EPD eta bins one-by-one:
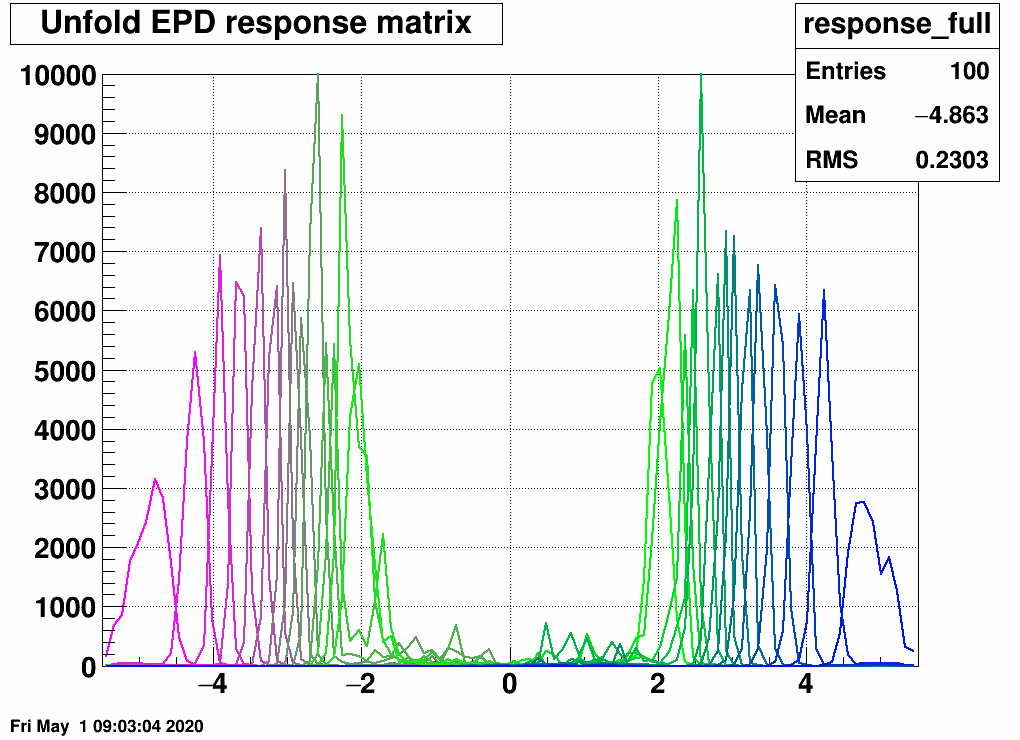
this is sort of close to what one expects, and note that the sum of these is close to empty in the midrapidity bins:
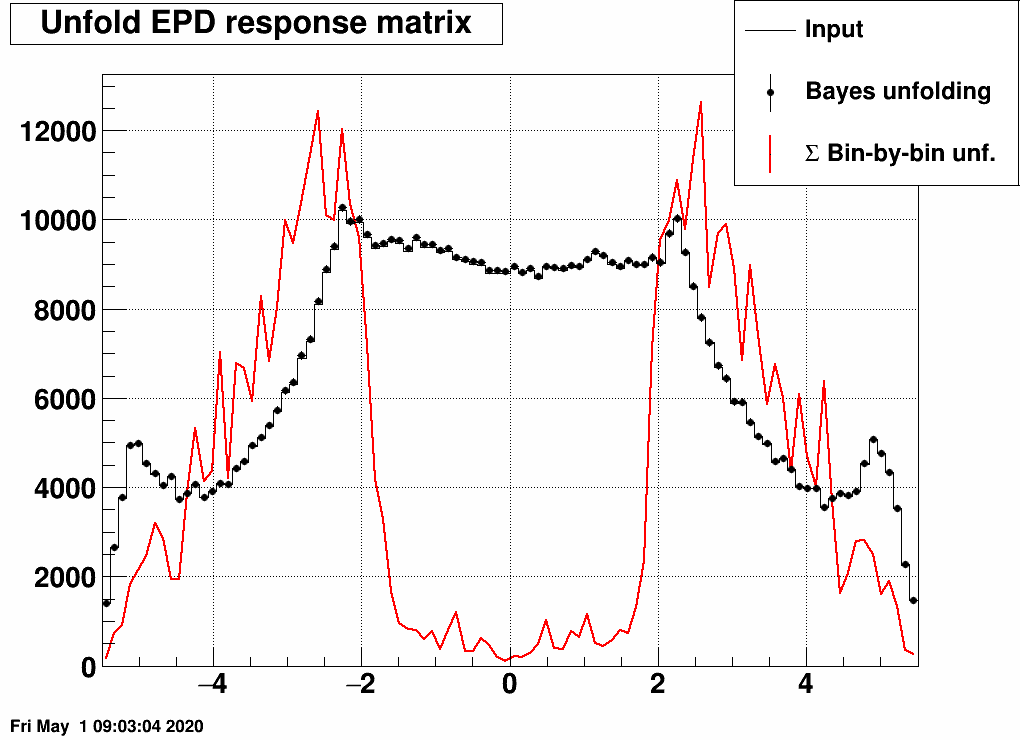
Just to visualize where is the "really true" dN/dη, which comes from Hijing:
The difference between the "really true" input and the input used here is caused by the multiple hits from many of the primary tracks. In fact this difference could be used as a correction to the unfolded dN/dη.
2) Unfolding a non-square matrix
We could in fact define a non-square matrix, with EPD Ring number in the measurement and some sort of eta bin in the input ("truth"). So instead of
R->Fill(EPDeta,Tracketa)
we do
R->Fill(RingNumber,EtaBin)
but for now, EtaBin is really just eta - but in the end, uneven binning in eta would also be possible.
In any case, this way we get rid of the zeros. The response matrix is then this:
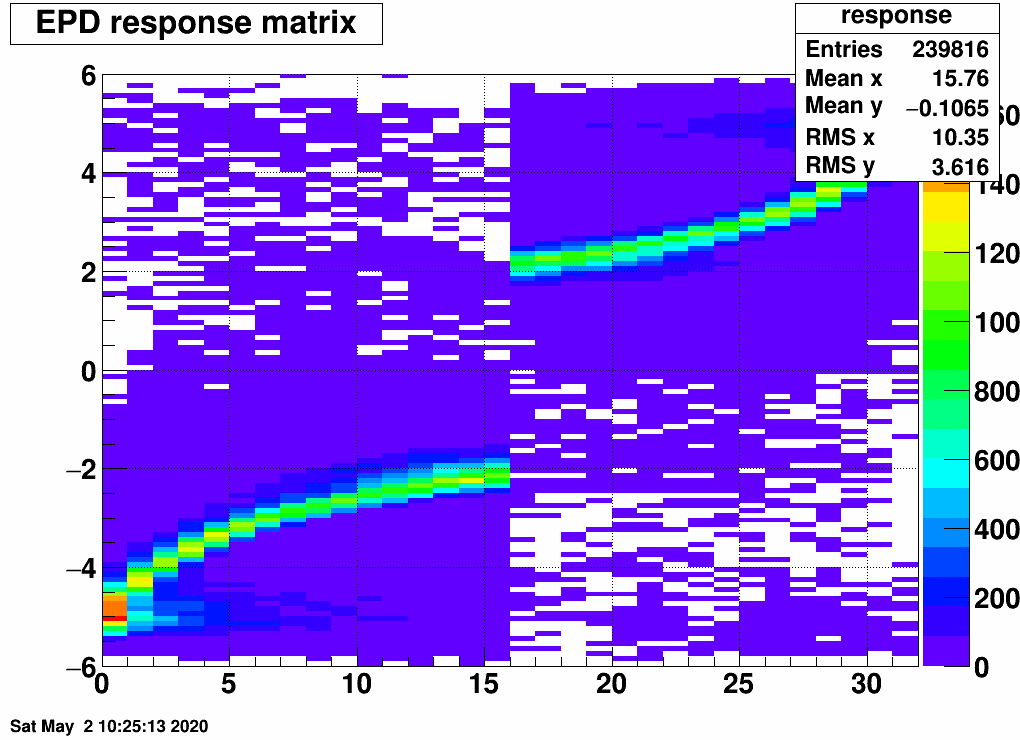
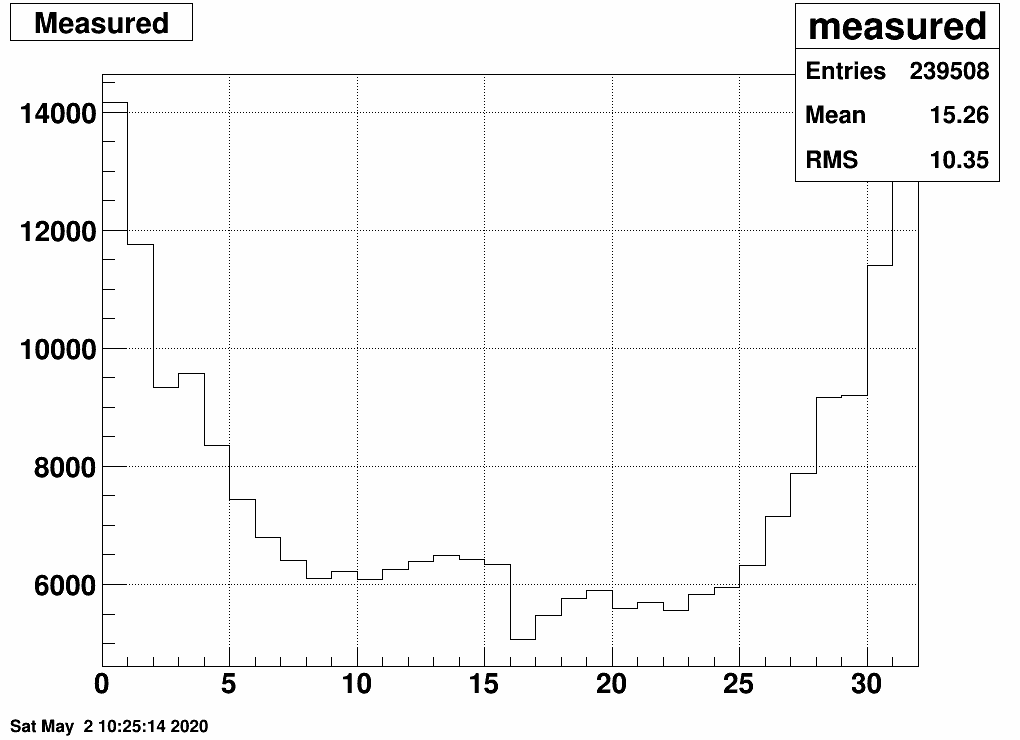
Here is the EPD distribution from ring to ring (0..15 for side<0, 16..31 for side>0)
Unfolding this is possible via matrix inverse (as we do not have empty rows or columns), but also Bayes unfolding (as before), and one gets these from the two methods:
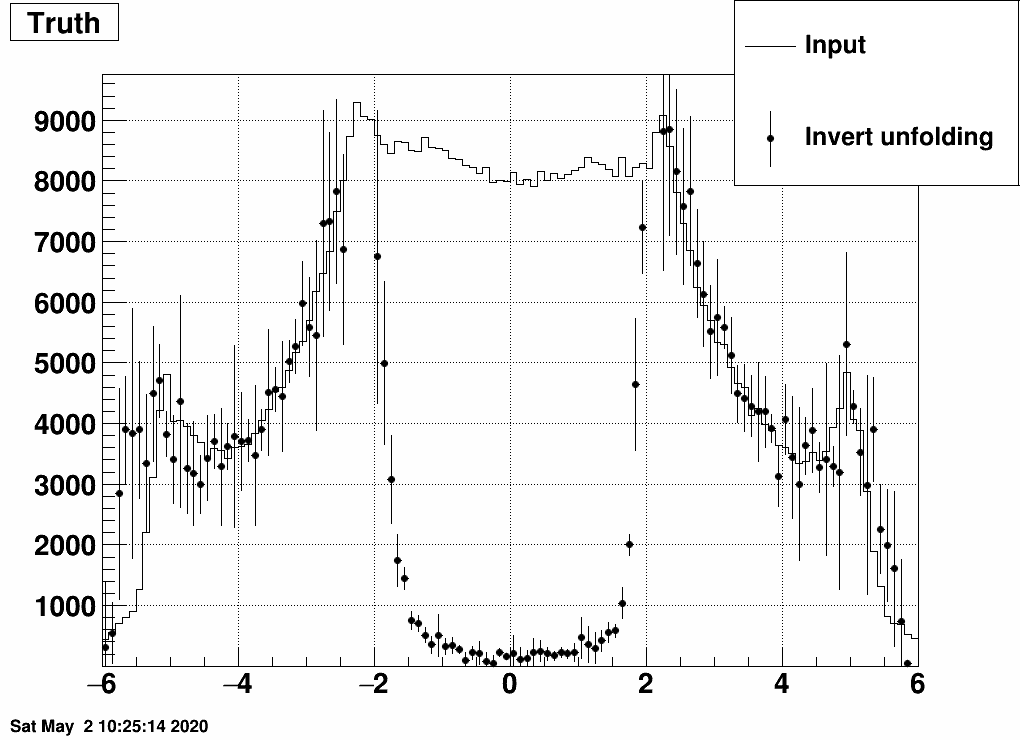
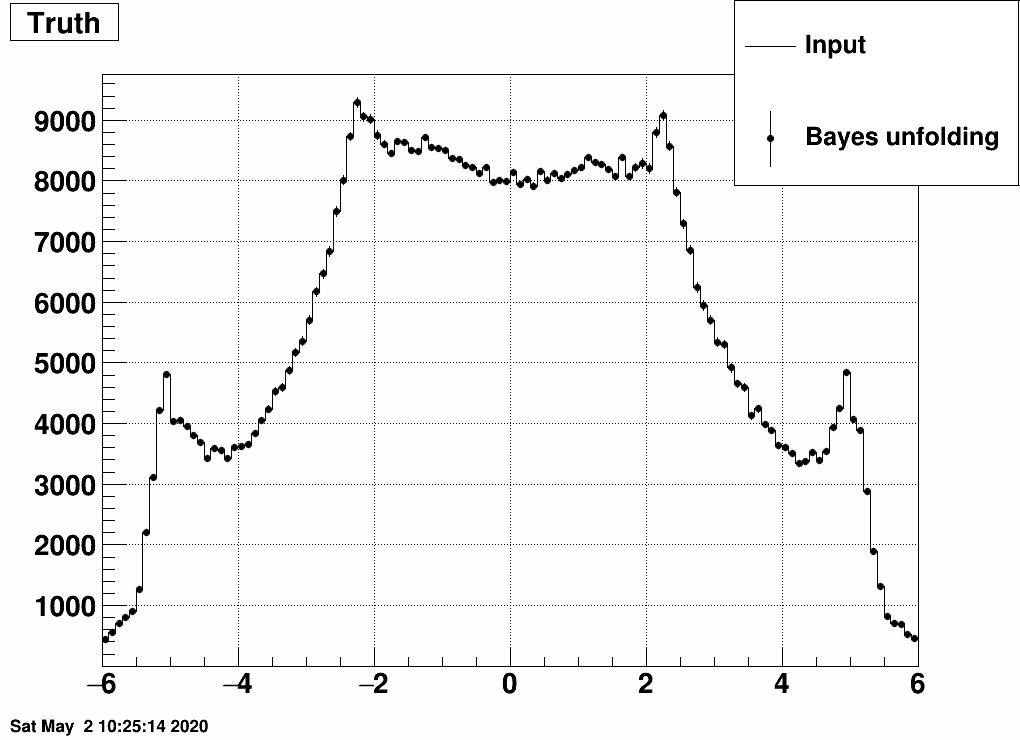
Here we see that the midrapidity region is not reproduced by inverse unfolding, probably due to the fact that very little amount of info is available from there, i.e. midrapidity primary tracks don't leave many hits in the EPD.
Bayes unfolding still works however. It even looks like a bit of magic is going on here, the level of reproduction is so high. Let us hence again do the two test: adding noise and using statistically separate samples.
Here is the result with random noise added to the EPD distribution before unfolding:
And here is the test with two statistically independent samples:
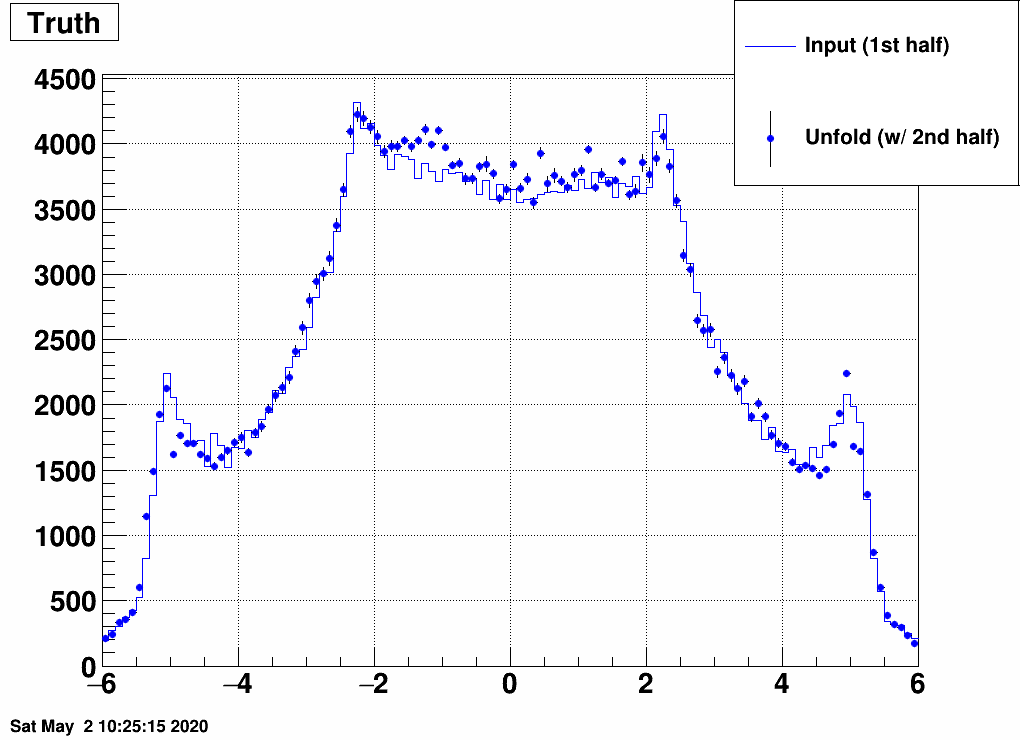
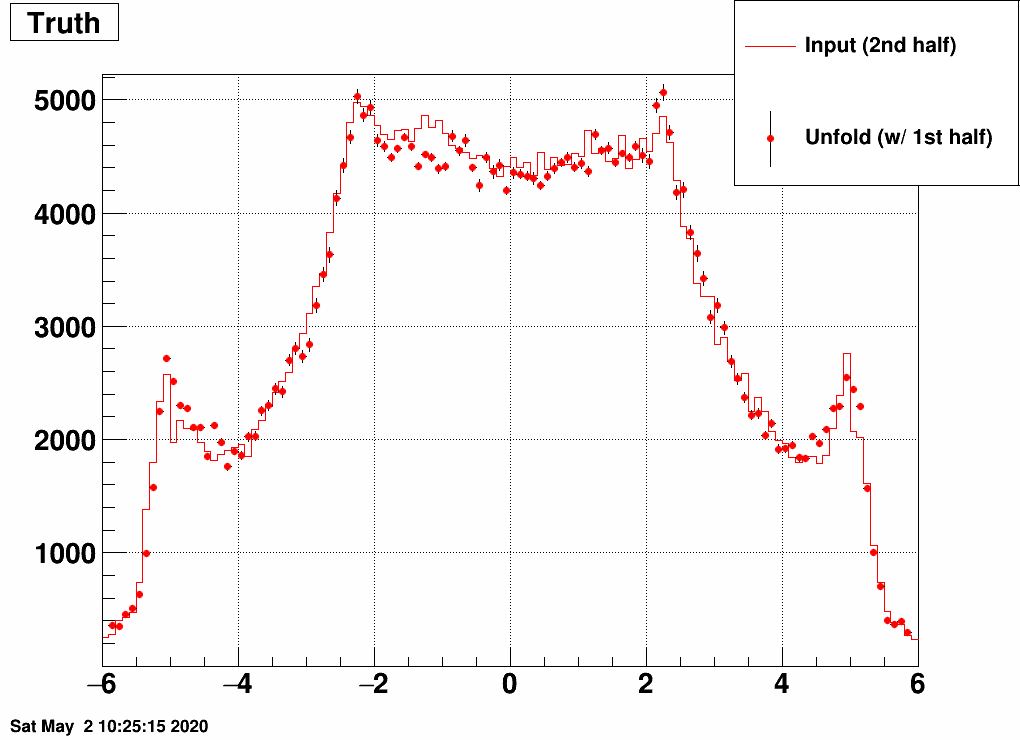
So with the checks so far, nothing was found that would devfinitely invalidate using this. This does not mean we are done of course...
Note that after unfolding, an η-by-η correction on dN/dη has to be applied, to account for having multiple hits from single primary tracks.
Here is a comparison of dN/dη with multiple counting vs single counting and the resulting efficiency plot:
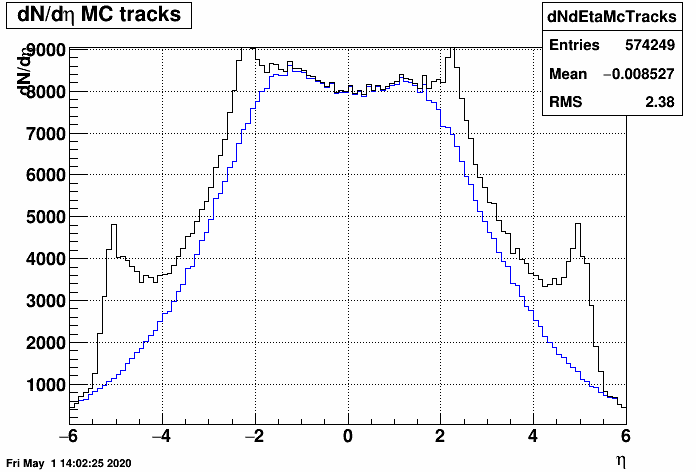
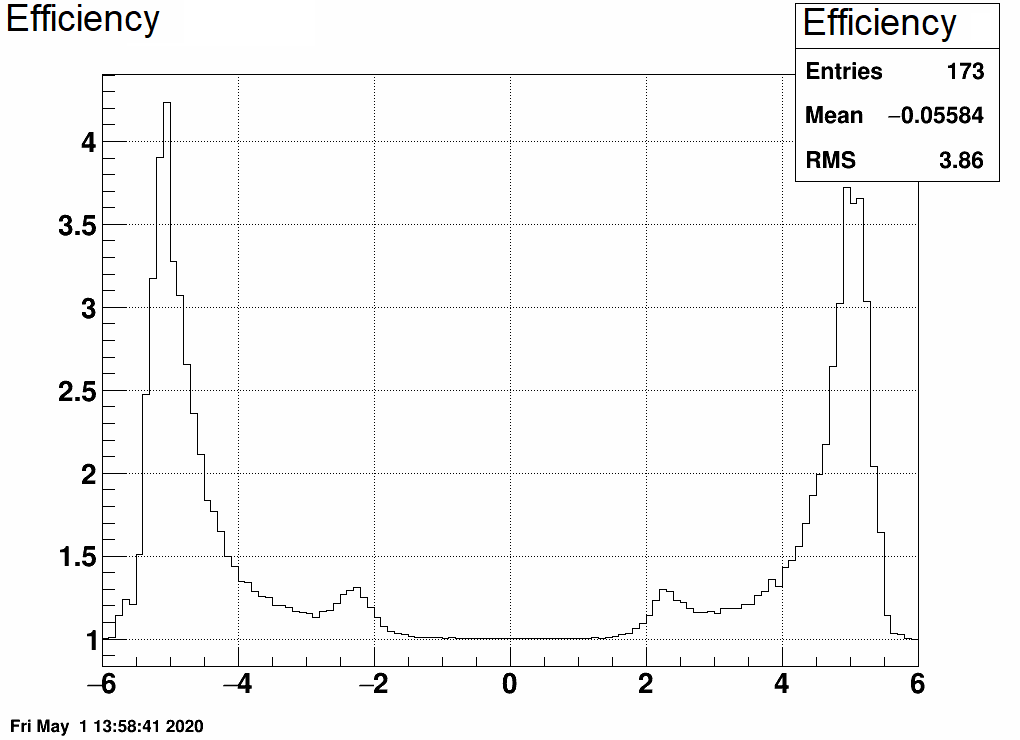
- mcsanad's blog
- Login or register to post comments
