Home » Groups » STAR Protected

Correction factor in the continum limit :

Updated on Sat, 2010-01-02 03:12. Originally created by mriganka on 2010-01-02 01:28.

Earlier way of calculating and problem for wide pT hard bins :

drupal.star.bnl.gov/STAR/blog/mriganka/2009/sep/10/calculation-correction-factor-kt-with-star-simulated-datasets-dijets

This is the page where the star simulated data has been  used for calulating <Zt>  <\hat(xh)>-1 .  The simulatd

datasets contain pt-hard bins in the ranges :  3-4, 4-5, 5-7, 7-9, 9-11, 11-15, 15-25,  25-35 GeV/c. It has been shown

earlier that mixing the bins (7-9, 9-11, 11-15, 15-25,  25-35) are sufficient for reproducing triggered neutral cluster

pt distributions which correspons to HT2 data. 

 The correction factor (" f ") for all the bins are summed up by making correspondig cross section weightage as follows : 

      pt hard bins       x-sections <Zt><\hat(xh)>-1
    pT,hard  1           x1                f1
    pT,hard  2
           x2
                f2
     
     

 

     f     =  (f1 *x1 + f2 *x2 + f3*x3 + .......  ) / (x1 + x2 + x3 + ....)

It is obvious that the f1 distibution can not extend above the maximum value of pT,hard  1.

Therefore while making weighatage we found a jump  in the value of  " f " for using the pT

bins of a wide ranges while going to high pT ranges.

 

The method describes here for transfrom this discontinutiy to a continious limit.

 1.   " f "  distributions for different pT hard bins are fitted with  exponetial distributions.

2.   The parameters,  the constant (par[0])  and the slope (par[1])   changes for different pT-had bins.

3. The par[0] and par[1] as a function of <pT (hard scattered partons)>  has been extracted. The function

     used here is polinomial of degree 2.

4,  x-section as a function of <pT (hard scattered partons)>  has also been fitted with expo[0]+expo[2]+expo[3]

     and seems to be rasonable in the <pT, trigger> for  for pT, trigger bins we are looking for.

5. Hence f     =  (f1 *x1 + f2 *x2 + f3*x3 + .......  ) / (x1 + x2 + x3 + ....) has been calculated for fine pT-hard bins.

 

   FIG : 1 : <Zt>,  <\hat(xh)>-1 and "f" for various  pT hard bins :

 

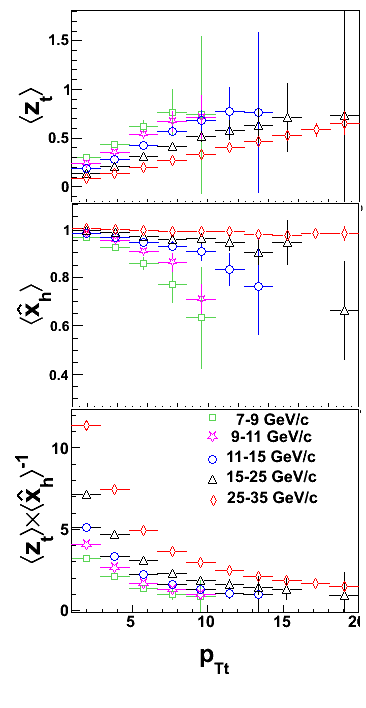
FIG. 2 :  expo fitting (region of interest in x-axis  6-20)

 

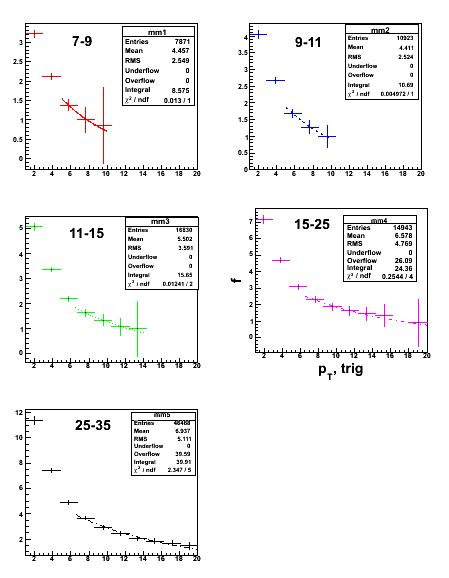
FIG. 2 :  x section as <pT (hard scattered partons)>

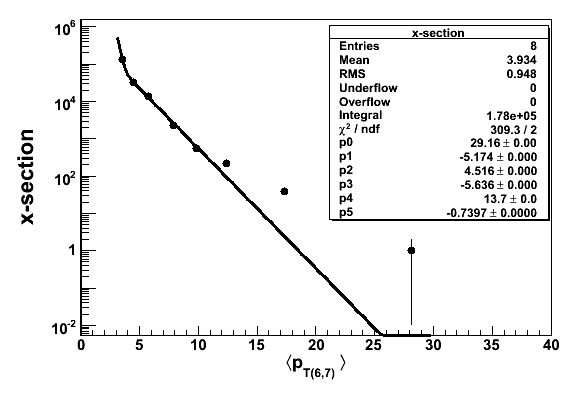
FIG. 4 :  par[0] and par[1] as a function of <pT (hard scattered partons)>

 

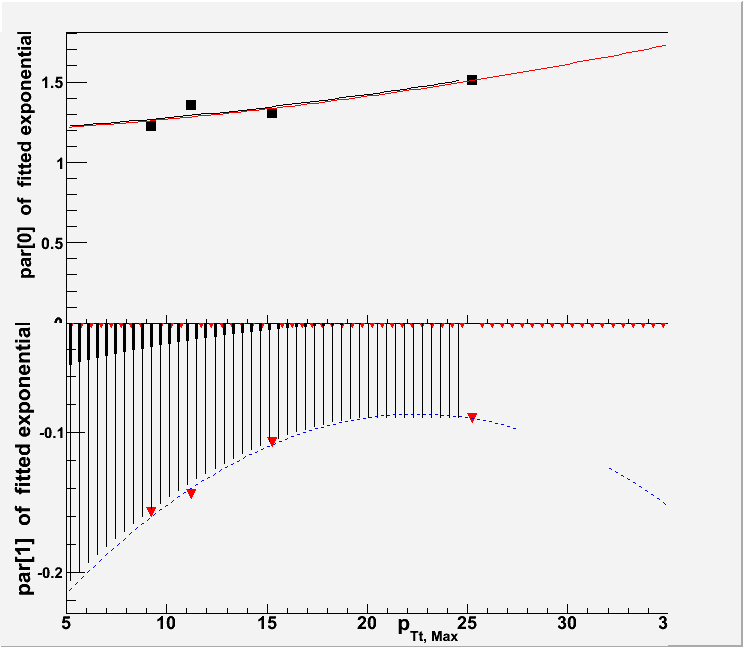
FIG : 5 the final value if  " f " is shown in thick dotted black line.

 

 

 

Groups: