Home » Blogs » pokhrel's blog

Dihadron azimuthal correlation asymmetry and unpolarized cross section: Paper Proposal Draft

Updated on Mon, 2024-06-10 10:57. Originally created by pokhrel on 2023-05-23 10:31.

 

Target Journal: Physics Review D 

Title:
   Measurement of Transverse Spin Dependent $\pi^+\pi^-$ Azimuthal Correlation Asymmetry in $p^\uparrow p$ and $\pi^+\pi^-$ Cross-Section in $pp$ Collisions at $\sqrt{s} = 200$ GeV at STAR

Abstract:

  The transversity distribution function,  $h_1^{q}(x)$, encapsulates the transverse spin structure of the proton at the leading twist, where $x$ represents the longitudinal momentum fraction carried by the quark $q$. In polarized proton-proton ($p^\uparrow p$) collisions, measurement of the dihadron azimuthal correlation asymmetry, $A_{UT}$, probes $h_1^{q}(x)$ coupled with the chiral-odd interference fragmentation function (IFF). The IFF needs to be extracted independently. The leading source of uncertainty in the $h_1^{q}(x)$ is from the unpolarized dihadron FF (DiFF), for which the unpolarized dihadron cross-section is urgently needed from the experiment, specifically from pp. The STAR Collaboration reports the measurement of $\pi^+\pi^-$ $A_{UT}$ using $p^\uparrow p$ data collected at center-of-mass energy ($\sqrt{s}$) of 200 GeV in 2015. Additionally, we report the first unpolarized $\pi^+\pi^-$ cross-section result using $pp$ data at $\sqrt{s} = 200$ GeV collected in 2012. These datasets probe the intermediate $x$ region ($0.1 < x < 0.3$) at $Q^2$ of $\sim 900$ $\rm GeV^2$. The cross-section result provides direct sensitivity to the unpolarized DiFF for gluons for the first time. These observables will improve precision in the global extraction of $h_1^{q}(x)$. Furthermore, comparing these results to the measurements from the SIDIS and $e^+e^-$ directly tests the universality of these observables.  

Dihadron Channel and Azimuthal Correlation Asymmetry (AUT)

Dihadron channel:   pî + p -> π+π- + X (for asymmetry),  p+ p -> π+π- + X (for cross-section)

Polarized (dσUT) and unpolarized (dσUU) dihadron cross-sections:

Azimuthal angles definitions:
Test test

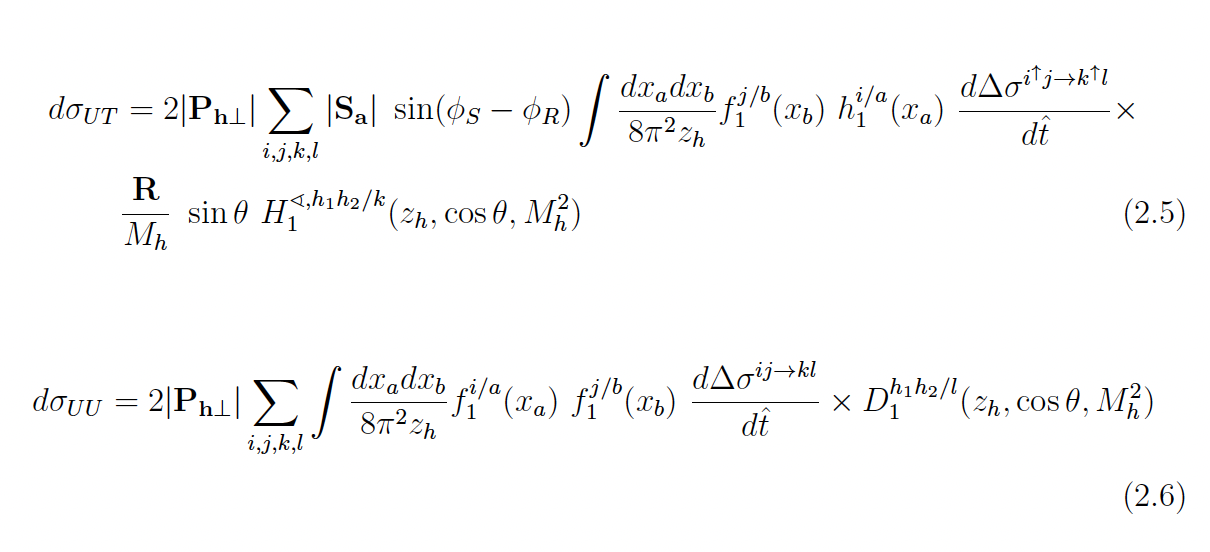
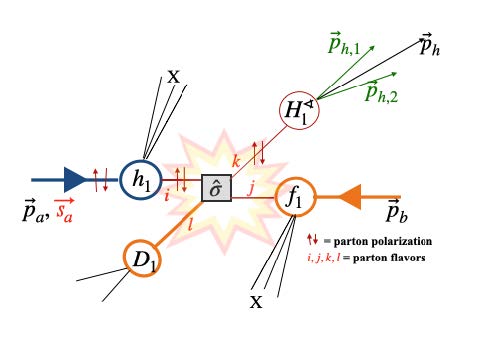
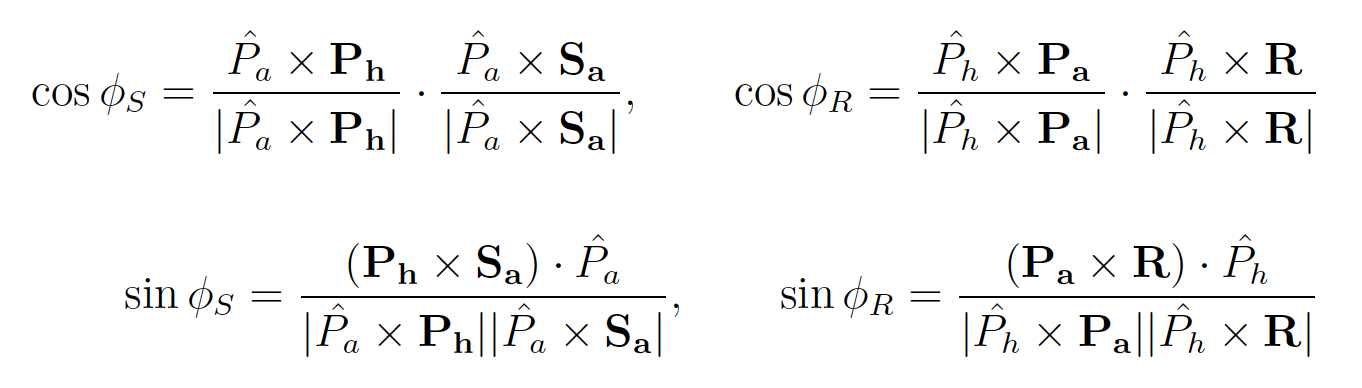
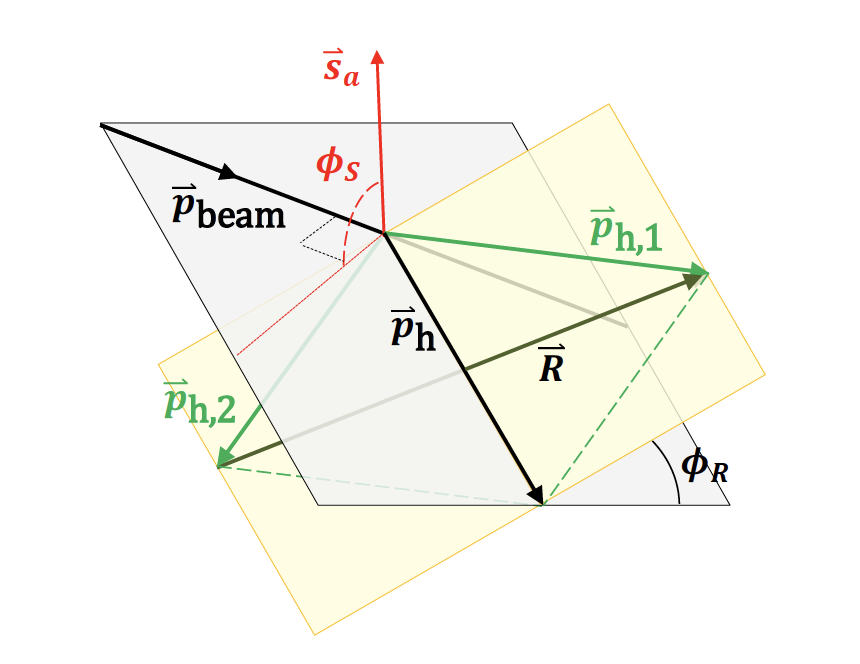
Dihadron azimuthal correlation asymmetry is sensitive to the product of transversity (h1)and IFF (H1):


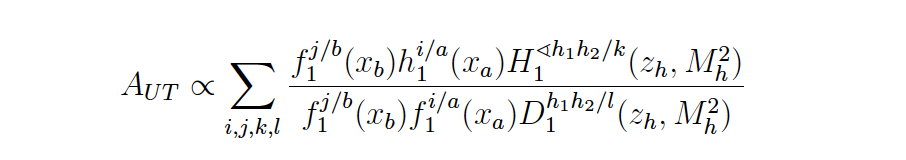
The unpolarized fragmentation function (UFF), D1, appears in the denominator, which is the leading source
of uncertainty in the transversity. Specifically, D1 for gluons is unconstrained. Unpolarized cross-section
measurement (dσUU) from the pp collision provide access to D1 sensitive to the both quark and gluons. 
Thus, the dσUU measurement from pp is crucial constraining transversity.

 AUT Extraction: Cross-Ratio Formula




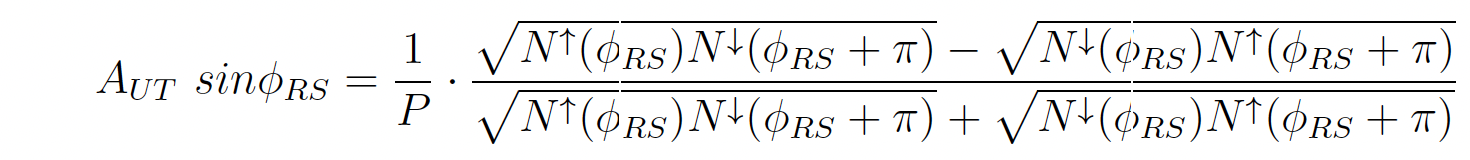
where, N represents the number of π+π- pairs when the spin is up or down. 

Dataset:

  IFF Asymmetry Cross-Section
Run Year 2015 2015
Center-of-mass energy 200 GeV 200 GeV
Polarization transverse transverse
Trigger Set production_pp200trans_2015 pp200_production_2012
Production Library SL16d SL12d
Integrated Luminosity ~ 52 pb-1 ~ 14 pb-1
Triggers JP1, JP2 JP0, JP1, JP2

Dipion selection:

  IFF Asymmetry Cross-Section
Z-Vertex (Vz) |Vz|<60 |Vz|<60
Z-Vertex Ranking (Vz,rank) Vz,rank > 1e6 Vz,rank > 1e6
Track eta |eta|<1 |eta|<1
Track pT 15 > pT > 1.5 GeV/c 15 > pT > 0.5 GeV/c
Track dca dca < 1.0, ( pT > 1.5) dca < 2.0, if pT < 0.5
dca <(2.5 - pT), if 0.5<pT <1.5
dca < 1.0, if pT >= 1.5
Track nHItsFit  nHitsFit > 15 nHitsFit >15
Track nHitsFit/nHitsFitPoss (fitRatio)  fitRatio > 0.51 fitRatio > 0.51
Pion Selection  -1<nSigmaPion<2 -1<nSigmaPion<2
π+π- Cone  cone < 0.7 0.02 < cone < 0.7
π+π- Minv

0.27 < Minv < 4

 0.27 < Minv < 4
π+π- eta (n) |n|<1 |n|<1
π+π- pT 2.5< pT < 15.0  1.0< pT < 15.0 


Results:
AUT extracted in Minv, pT, and eta bins. The eta direction is a surrogate of x, with forward eta region probes higher x, and vice-versa.

Dipion azimuthal correlation asymmetries:

1. AUT vs Minv, multi-binning in pT and eta

Figure 1: AUT vs Minv in forward (eta > 0 )(red) and backward (eta < 0) (blue) pseudorapidity
regions in five pT bins. The average pT increases from left to right and from top to bottom, the value
of which is shown on the top right corner of each panel. Higher asymmetries are observed in forward
region and the signals are more prominent in higher pT bins. Forward asymmetries peak around
Minv ≈ 0.8 GeV/c2, close to the rho-meson mass (Minv  ≈ 0.775 GeV/c2 ). Backward asymmetries are
relatively small, which are mostly from unpolarized beam. Systematic uncertainty includes the particle
identification and trigger bias combined.

2. AUT vs Eta, integrated pT and Minv

Figure 2: AUT vs Eta  integrated over Minv and pT (top panel). < x >, average of x1 and x2, and < z >,
average of z1 and z2, in the same eta bins from simulation (bottom panel). x increases from 0.1 to 0.22
from negative to positive eta regions. z shows slight dependence in forward and backward pseudorapidity
region separately, but overall, it is averaged out to be  ≈ 0.46. Forward asymmetries are large, where we
have access to higher x. Small backward asymmetries, which is mainly from the unpolarized beam, corresponds
to the lower x region. Systematic uncertainty includes the particle identification and trigger bias combined.

3. AUT vs pT multi-binning in Minv and eta

Figure 3: AUT vs pT in forward (eta > 0 )(red) and backward (eta < 0) (blue) regions in five Minv bins. The average Minv
increases from left to right and  from top to bottom, the value of which is shown on the top left corner of each panel.
Higher asymmetries are observed in forward region and the signals are more prominent in Minv bins close to
Minv ≈ 0.775 GeV/c2. Backward asymmetries are small, but non-zero, at higher pT, which is mostly from the unpolarized
beam. Systematic uncertainty includes particle identification and trigger bias combined.

4. AUT vs Minv, integrated pT (Below figure will be updated as a two panel plot, including eta < 0 result in the bottom panel)



Figure 4: (Top Panel) STAR AUT vs Minv in  eta > 0 region integrated over pT, compared with the theory at √s = 200 GeV.
The uncertainty band of the theory curve is obtained with the bootstrap method based on 600 replicas at 90%
confidence level (Radici et. al.). 

Unpolarized dipion cross-section 

Test test

Figure 5: Top panel: the measured (shown in red), PYTHIA (shown in black), and JAM (shown in blue) cross-sections.
Bottom panel: total relative systematic error (green band), statistical error (red band), shown on the left axis , and
relative difference of the PYTHIA and JAM DiFF prediction to the measured cross-section  (Ratio) is shown in the right axis.   

 Other relevant figures:


==>> Reference to this figure (originally drawn by Anslem Vossen) or draw new

Figure 6: DiFF kinematics



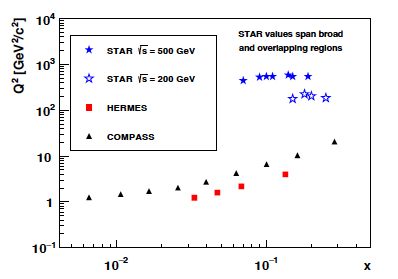
==>> Reference Plot ( Alternative figure would be the x distribution from the simulation, probably in
asymmetry binning . For example, x distribution in Mass, pT, and Eta bins. x-distribution
with varying cone.)

Figure 7: (Figure from STAR 500 GeV paper) Similar figure showing STAR kinematic coverage

==>> In addition to this, process dependent distribution from the Pythia in Mass
bins would be more impactful. 

Figure 8: Data and embedding comparison for π^+π^- invariant mass (this is important for
the cross section part as this measurement heavily relies on the embedding) 

         (figure 9/10 not ready!)

Figure 9/10: PID studies for IFF and cross-section (data-driven approach). There will be two
figures, one for each part, as the origin of the systematic uncertainties are different in the IFF
and cross section analysis. 

----------------------------------------------------
Further analysis:
----------------------------------------------------
IFF Analysis

  1. Particle Identification  (PID) and Systematic uncertainty associated with the PID
    PID with the dE/dx calibration method (similar as in the Collins analysis).
    PID systematic uncertainty is expected to be small.


  2. Systematic uncertainty from the background (underlying events) contribution
    (Study found that the contribution is small (< 1%) )

IFF Systematic Checks:

  1. Consistency check between Blue and Yellow beam asymmetry (tested)
  2. Cosine modulation should result zero(diluted) asymmetry
  3. Random spin ordering should result in zero(diluted) asymmetry
  4. Randomizing vector R should result in diluted asymmetry (tested)

Unpolarized Cross-Section Measurement

  1. Data-driven PID correction (same as in the IFF analysis)
  2. Systematic uncertainty revisit 

----------------------------------------------------
----------------------------------------------------

Conclusion:

1. IFF asymmetries are statistically precise, which are in good agreement with previous STAR
measurements and the model calculation.
2. The unpolarized dipion cross section result, which is in good agreement with the JAM prediction,
will constrain the unpolarized fragmentation functions. 
3. These high precision measurements will provide a foundation for the transversity extraction with
greater precision than previously possible. 
4. These measurements will also tests universality between different processes: SIDIS, e^+e^-, and pp.

Relevant presentations and links
Please refer to the preliminary request page.
Paper proposal presentation: Link
Cone Optimization Studies

Analysis Note
 Please refer to the analysis note for the analysis details in the attachment: Analysis Note

Code location
    
     IFF Code Location
     Cross Section Code Location

»