Going back through the code I'm using has resolved the mismatch I saw last week in the ratio of BHT3coin to BHT3.  With that fixed, I can more confidently post plots showing the stability of the BHT3coin luminosity as a function of the opening angle used.

My last update showed that all the excess luminosity seemed to be coming from the early part of the run (fig. 1).  This did indeed turn out to be because of the altered BHT3 trigger there.  When I correctly applied the trigger condition in my software, the issue resolved itself (fig. 2).

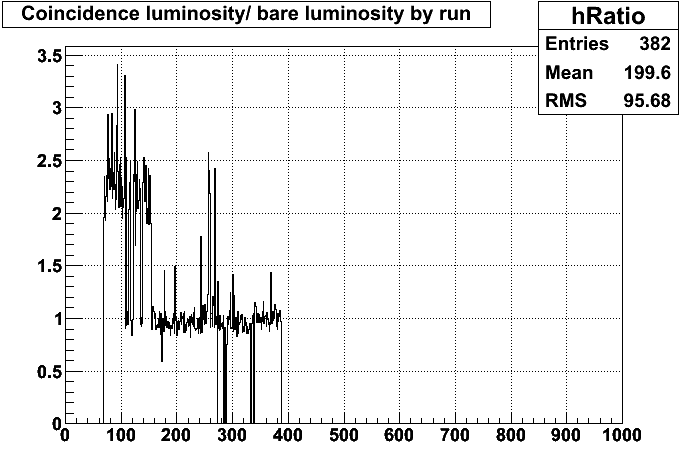
Figure 1, ratio of BHT3coin(5) luminosity to BHT3(aps) luminosity as of last week.  The gross features of the ratio corresponds to the difference between the number of L2Wrandom events and the number of those events that would have passed the BHT3 production trigger.

Figure 2, the same ratio with the L0 condition applied in software.  With this correction, the only differences remaining are shifts due to the change in number of abort gap events used in the background calculation, and any systematic shift from the different calculation of the BHT3coin(5) cross section.

The BHT3coin trigger has two parameters that can be chosen - the number of towers opposite the high tower to be included in the away sum (called opening angle), and the threshold requirement of the away sum (called threshold).  I chose the threshold based on a study of the vernier scans where each choice of opening angle seemed to have a natural shift between being insensitive to beam position and having the expected structure.  Each choice of opening angle then yields a different BHT3coin cross section.  I note the different BHT3coin variants with a number in parentheses.  The opening angles (in trigger patches) are twice this value.  Applying these conditions in the data, I've plotted them against one another (fig 3).  I intend to use BHT3coin(5) as a good middle ground.  

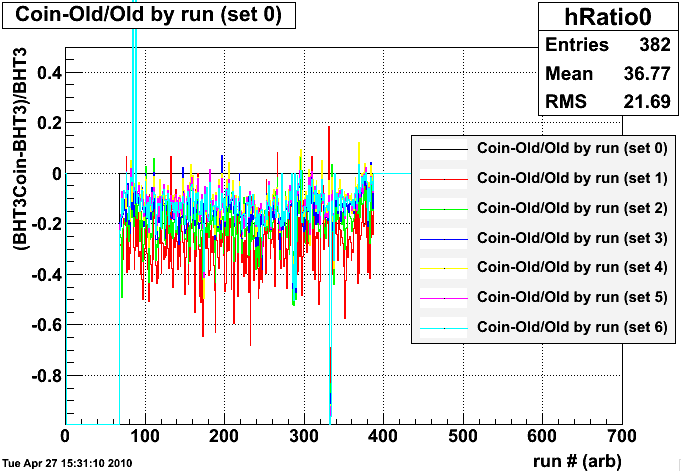
Figure 3, variation in the number of events passing each BHT3coin choice, normalized to the number passing the original BHT3(aps) condition.  Note that BHT3coin(0) (black) has an opening angle of zero and a threshold of -1, so it is exactly the same as BHT3(aps).  Others tend to trend slowly downward.

Integrating over all runs for each of the 16 choices of opening angle (0 through 30 in multiples of 2), I can plot the integrated luminosities (fig 4).  This plot shows that the coincidence requirement is stable for any reasonable choice of opening angle.

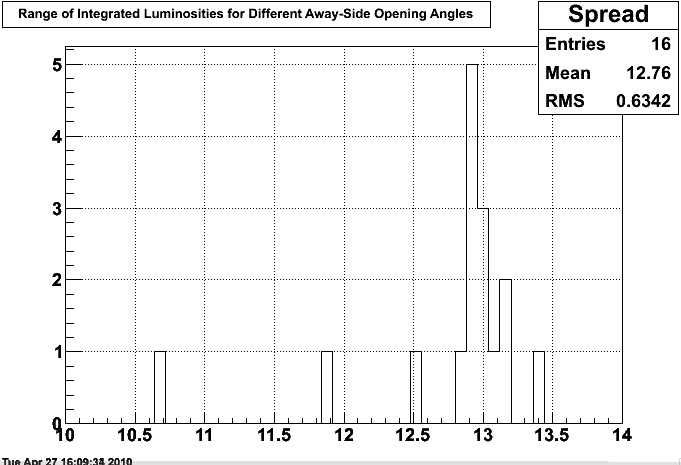
Figure 4, histogram showing the luminosities coming from each choice of opening angle.  The leftmost is BHT3coin(1), where the off-center nature of the awayside calculation is important.  The rightmost is BHT3coin(15) where the away side includes the entire barrel.  Removing these, the remainder has a mean of 12.84 and RMS 0.31.

Selecting an opening angle of 5 (corresponding to 10 trigger patches roughly centered opposite the highest trigger patch) yields an integrated luminosity of 12.88pb^-1 (shown vs day in fig 5).  This is a 6% decrease from the value quoted at APS, and has significantly smaller error bars.

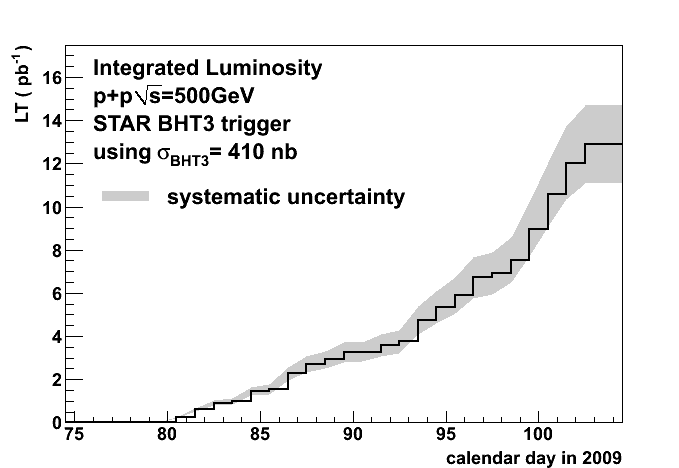
Figure 5, integrated luminosity vs calendar day in 2009 using the BHT3coin(5) requirement.  This result is in agreement with the value presented at APS.

The next steps are to investigate the JP1 discrepancy by comparing also to the ZDC.  After that, I still need to revisit the error analysis.