I probably won't be able to get to the morning meeting tomorrow, so here's the update:

I currently measure a single efficiency term by looking at the embedding data and dividing the number of final W events found by the number thrown (initial criterion is that the decay lepton falls in detector eta -1<eta<1 in the geant record).  This is done in bins of eta as well as instantaneous luminosity, and results in the following plot.

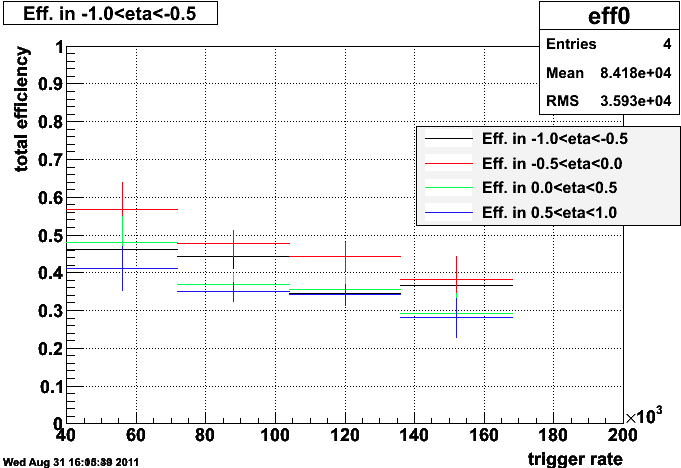
We see the expected behavior where the efficiency decreases as the amount of pile-up in the detector increases.  Additionally, we see that the efficiency seems to decrease as we move to higher eta.  I don't fully understand this effect, but I suspect it is a result of the additional veto power of the endcap, which will reject QCD background as well as W events with inconvenient underlying events.  (The problem is that this is at odds with the information seen later on, which shows a more symmetric effect from the endcap.)

Originally, I wanted to fit the line above apply these efficiencies run-by-run, using the equation of the line to get the efficiency at the luminosity of each run.  Limited statistics makes that impossible, but I can instead compute the average instantaneous luminosity of the entire dataset and use the efficiency associated with that.  

To get the raw W yield, I follow the procedure from the various published and proposed STAR W papers, but divided into eta bins.  The following plot shows the breakdown of each eta bin.  Black is the output pt spectrum from the cuts, red is the missing endcap (the difference between the yield in the opposite eta bin with and without the endcap included), green is the data-driven QCD background, and blue is the remaining yield.

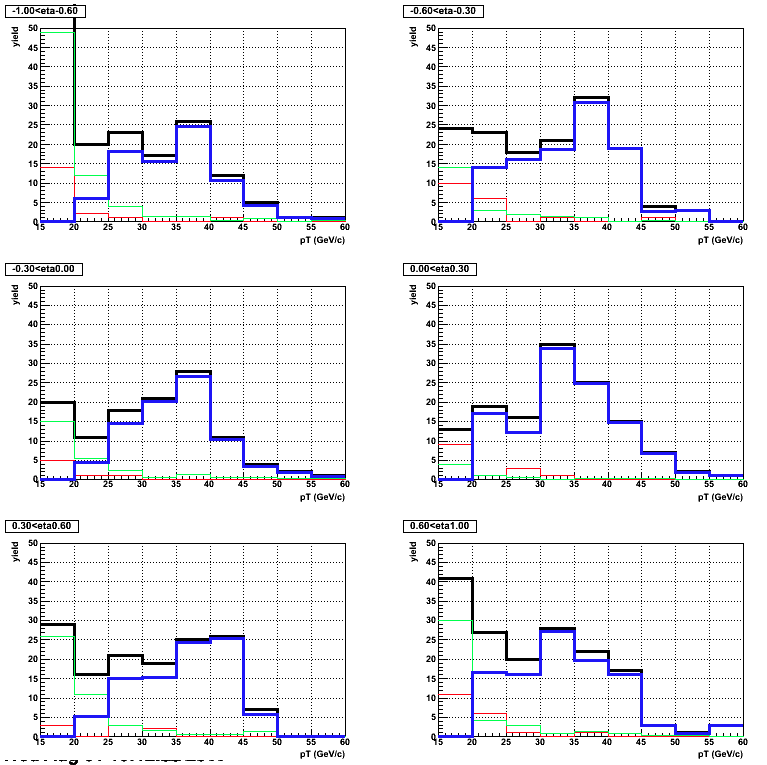
I would expect the red to be a larger effect far from the existing endcap, but it seems that that's not the case.

Applying the efficiency from above, we get the corrected 'true' yield as a function of eta: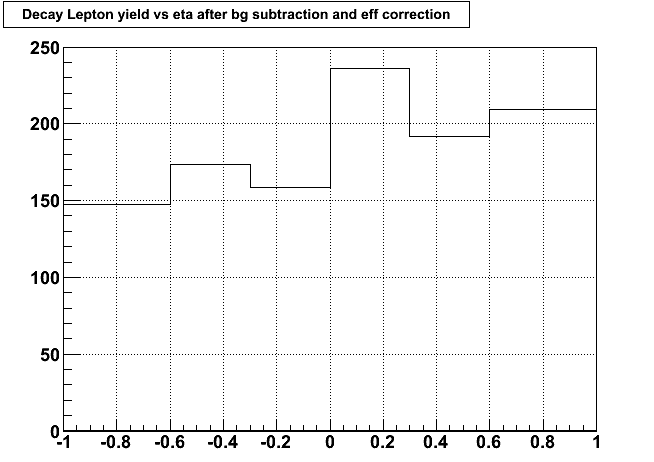

The error bars aren't yet included. The main sources will be efficiency uncertainty from gain variation and the luminosity distribution, and pre-efficiency yield uncertainty from background QCD variation.  This plot does not separate charge sign.  In a future iteration I'll separate the two charges and treat each independently.