I have currently divided the systematic uncertainty for the eta-dependent W cross section into three groups which will be treated as uncorrelated for purposes of the final value:

1) Background uncertainty - pending.  The smaller statistics of the eta bins encourage me to use fewer bins, which makes this diverge from the official analysis - I can't easily vary the cut-off point.

2)Total reco efficiency uncertainty - pending.  This is made up of four systematics pieces:  Tower gain uncertainty, Jet scale uncertainty, and luminosity dependence (as well as statistical uncertainties from the MC itself)

a) Energy scale uncertainty - essentially done. Using a nonlinear gain term produces very small uncertainties in the reconstruction efficiencies.  I still need to check that the results 'make sense' since the method is not entirely straightforward.  I haven't decided whether or not to split the fit by eta bin.

b) Jet energy scale uncertainty - pending.  Easy, but I wanted to finish the overall energy scale first so I could add linearly.  I intend to compare the efficiency (at nominal, nominal+sigma, and nominal-sigma) for the two extreme subtraction schemes.  I expect this to be a relatively small contribution

c) luminosity dependence - essentially done.  I scale the MC to match the luminosity distribution in the data, and also the z distribution in the data.  Since the efficiency I calculate uses the exact distribution found in the data, the uncertainty should only be from statistical fluctuations.

d) status table dependence - pending.  I still need to check how the status tables are handled by default before I can manually reset them.  This should be straightforward, comparing efficiency with the most-functioning and fewest-functioning towers tables as a way to bracket any other choices.

3) integrated luminosity uncertainty - essentially done.

Most of my work lately has been on 2a.  I follow Justin's overall approach of using a maximum likelihood, comparing the simulated W peak to the background-subtracted W yield in data.

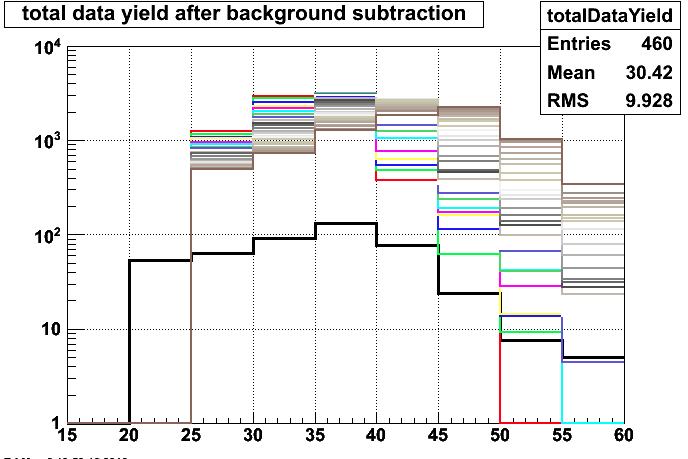
Figure 1.  The solid black line shows the W- yield in data.  The other lines show the simulated yields (shape normalized to the sampled distribution of Z and instantaneous luminosity, but not set to a specific cross section) for various assumptions of the nonlinear term in the gain.  

These histograms are compared using a log likelihood system and the large number approximation of that.  The result (figure 2) shows the optimal value of this term and the fit to that.  

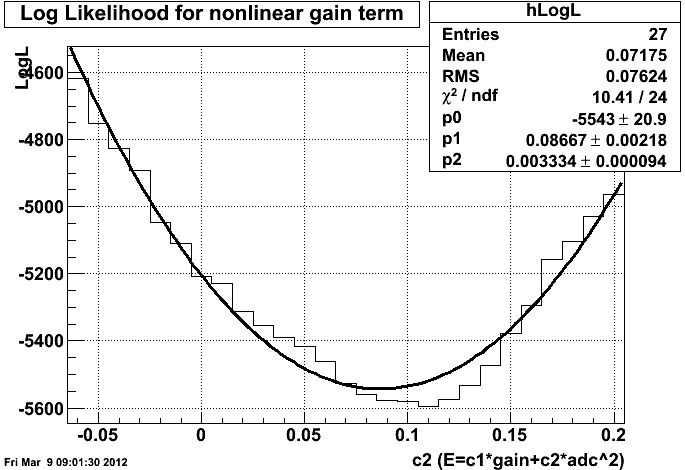
Fig 2.  This shows the negative log likelihood of all choices of the c2 term between -0.06 and +0.20.  The optimum occurs at 0.11, which is taken as the nominal value.  The fit doesn't quite capture the shape of the curve, so the sigma (p2) defined by it is not a good choice.  I am extending the range of this parameter to give more room to fit on the right hand side of the figure, but for the moment I am taking the uncertainty to be the difference between the fit's optimum and the true optimum of the plot.  

Taking the nominal, nominal+sigma, and nominal-sigma values from this optimization, I compute the efficiencies for each.  They turn out to be essentially indistinguishable.

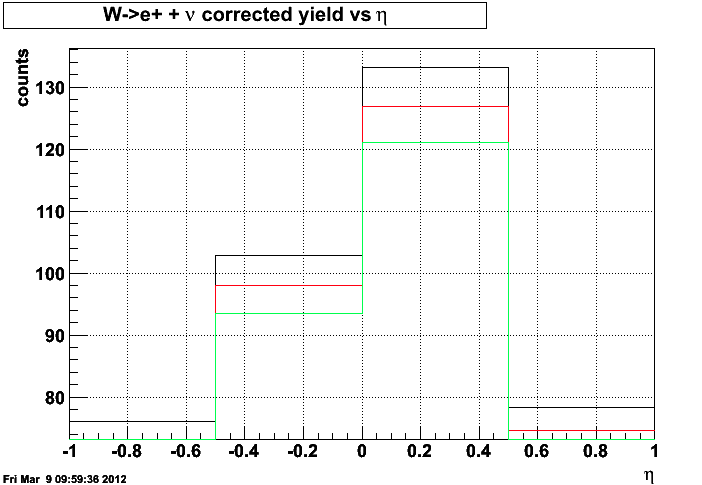
Fig 3.  This shows the W yield corrected for efficiency for the nominal (black) and the high and low nonlinear terms.  I have manually shifted them by 5% each so that they are drawn separately.  They lie essentially on top of each other.

What still needs to be done for gain uncertainty:

I need to add in the uncertainty in the linear term in the gain to each of these extreme conditions to fully contain the gain uncertainties.  I still want to extend the fit further to the left (which should be done by this weekend).  I will also go over the code, since I was expecting a slightly larger shift in the effiiciencies.  

Edit:

Extended fit still shows the same issue.  Since I know the effect on the final uncertainty is negligible, I will quote the large number described above, and move on.