I've used a toy model to determine whether we can unfold an EPD hit distribution, where some number of truth particles split and hit multiple rings.

First to start I picked a distribution for the truth particles:
 TF1* Truth = new TF1("Truth","gaus(0)",2.14,5.09); Truth->SetParameters(1,0,2);

Which gives me this distribution for 100,000 particles:

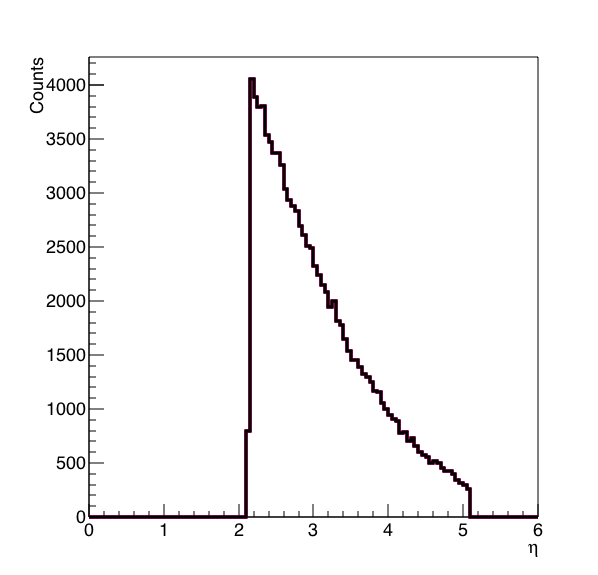
Figure 1: "Truth" distribution vs eta for toy model study.

To establish whether unfolding works at all, I simply start by distributing these particles into the various EPD rings and creating a response matrix from this.
float Epdeta[] = {2.14,2.2,2.27,2.34,2.41,2.50,2.59,2.69,2.81,2.94,3.04,3.08,3.26,3.47,4.03,4.42,5.09};

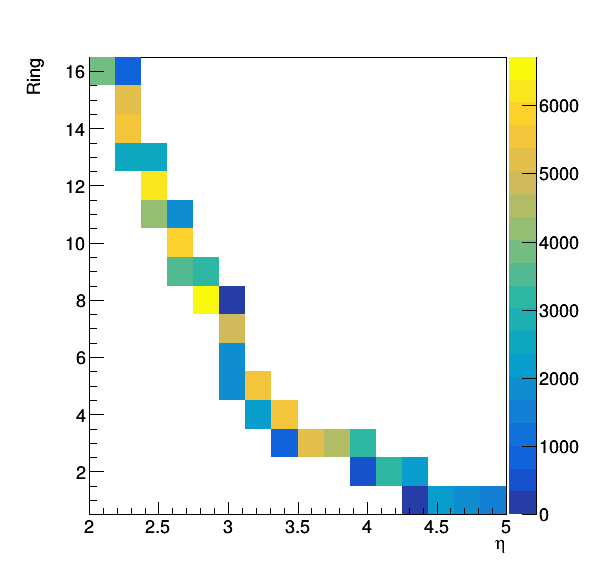
This response matrix looks like:

Figure 2: Response matrix (RM) for the distribution of eta vs Ring #.

To start, I will cheat by using the same data to create the response matrix, and to create the "measured" distribution that I unfold.  In this case, I will use a Bayesian unfolding mechanism via the RooUnfold package.   Additionally, I assumed (as you see above) that I had 16 bins in eta (evenly distributed) vs 16 ring weights - which is encoded via:
RooUnfoldResponse response(16,0.5,16.5,16,2,5);

This yields:

Figure 3: The truth distribution is in black, the unfolded distribution is in green.  We see here that at least with this simplistic assumption, we can multiply by a matrix and then divide by that same matrix via the unfolding process.

Now to add some sort of splitting into the mix.  I will assume the splitting probability is constant through out the distribution here, that the "split" particles always end up in the EPD themselves.  I will calculate the new etas by smearing the "truth" eta with a gaussian.  This procedure would allow more than 1 split as I will simply use a random # generator to determine whether to split or not.  I will force the new values to also be within the epd acceptance (reroll if not).

My hypothesis is that I could treat this the same way as we treat inefficiencies.  In the RM, each split would have its own entry (so one particle hitting 2 rows would have 2 entries, both with the same truth value but different final values).  But I would keep track of the ratio of #entries for a given eta, vs #of particles and scale the final result by this amount.

To start I chose a smearing of sigma = 0.1 and a 5% probability of splitting.  The input distributions (fined binned) and RM are below.

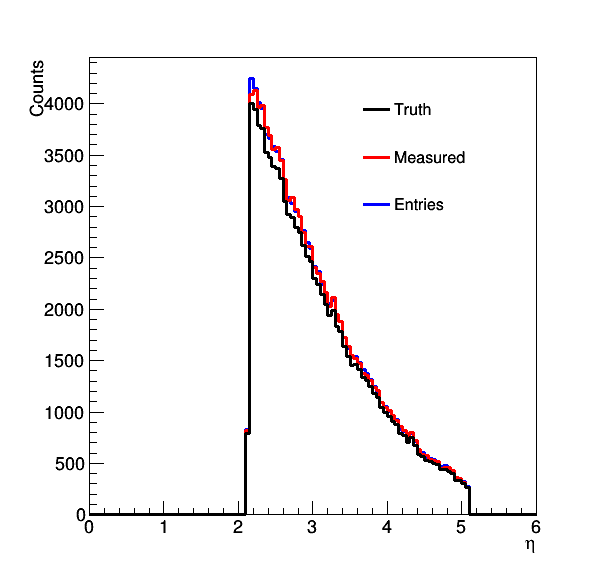
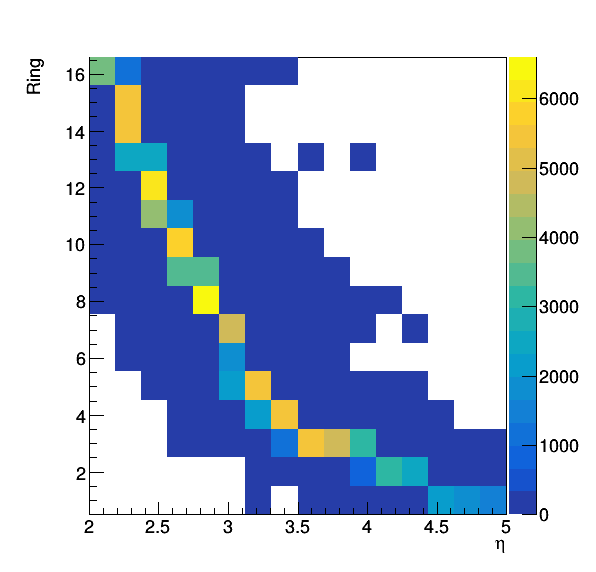
Figure 4: Fine binned distribution of the inputs to the unfolding, the truth is in black, the measured in red, and the blue shows the distribution of truth values with repeated counts for splitting.  This gives the response matrix on the right where we can now see some of the smearing.

When we unfold, we get:

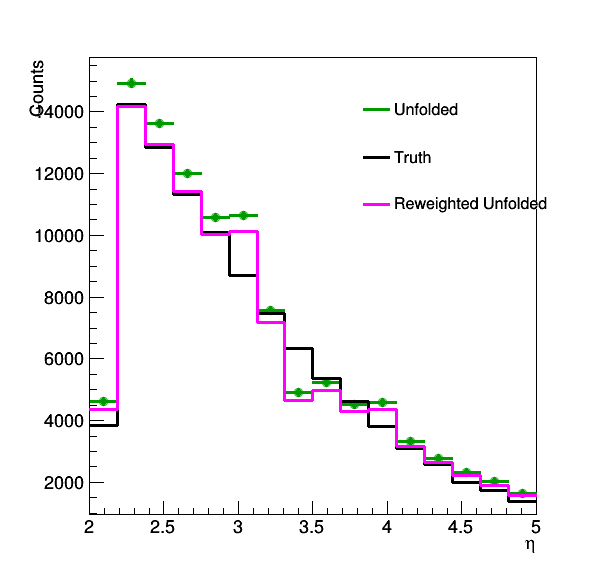
Figure 5: The black distribution is the truth, the green distribution is the unfolded, and the purple is the unfolded reweighted by the number of counts.

In figure 5 it seems the method is working - other than the issue of the two pivot points that one sees at eta ~3 and ~3.5.  The integral is preserved in the unfolding, so a higher bin will cause others to be lower in response.   You can see from the bright point in the RM that this would happen - which indicates to do this properly I would need to normalize the response matrix (which I won't do today).  But as we increase the splitting probability, these two points will be a bit problematic.

Increasing to 50% splitting probability (which means x2) we see:

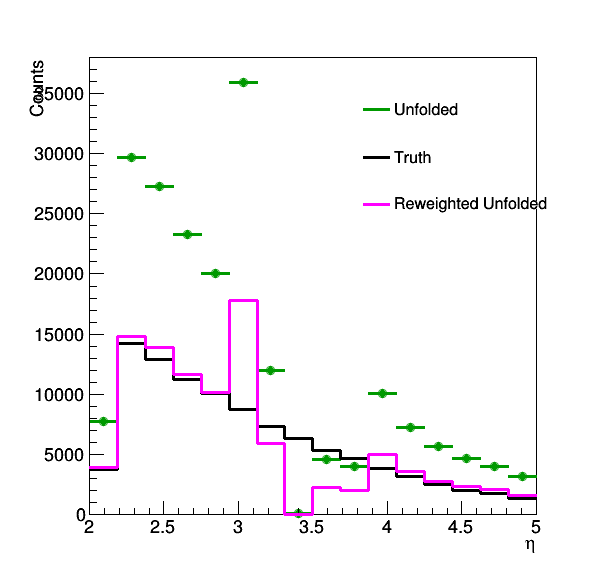
Figure 6: Same distributions but with 50% splitting probability.

Ignoring the problem points (I believe can be fixed by normalizing the RM), we see that the procedure works well for the other values.  Note here I am specifically suppressing the error bars as I would have to carry them through properly and haven't had the time to think about.

Next up - what if the smearing was more extreme?  (i.e. splitting could cause the hits to be even further from their "truth" value)