a) The algorithm receives a 7-bit number (range 0-127) from each of the 5 ring groups from each of the 2 sides (East/West). The largest ring group multiplicity that should ever occur is 96 (e.g if every tile in ring group #5 is hit) and 96 is a 7-bit number.

b) Each of the 10 incoming multiplicity values are turned on/off using their bit in a register (actually 2 registers, one for East and one for West).

c) I add up the masked multiplicities to get separate East and West totals. The sum of 5 7-bit numbers is a 10-bit number so at this point I have 2 10-bit numbers.

d) To calculate the total multiplicity I add together the those 2 10-bit numbers to get an 11-bit number, and then I just select the 8 MSB and ignore the 3 LSB.

e) In parallel I calculate the difference. Calculating the difference between 2 integers using bitwise logic (which is what an FPGA does) is more complicated than summing because it takes an extra step in series. The total time is reduced if you reduce the size of the integers. So, in this case I truncate first and then calculate the difference. I take just the 7 LSB of the 2 10-bit numbers and calculate their difference. When you including the sign bit this makes an 8-bit result.

f) The output is the 8 MSB of the total sum and the 8-bit difference of the truncated sums.

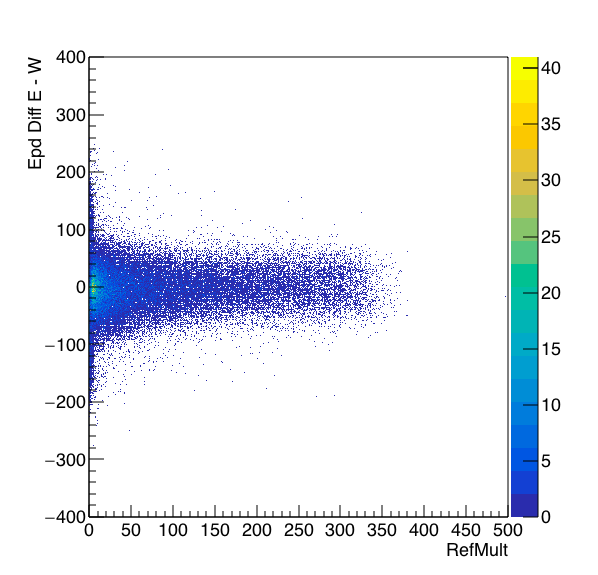
Figure 1: On the left is the EPD tiles above threshold vs Refmult for AuAu 27, the middle is the difference E - W, and the right is the two EPD based quantities plotted together.

So to look at Eleanor's part d, I would need to bitshift the total multiplicity by 3 (744>>3 gives 93).  This looks like:

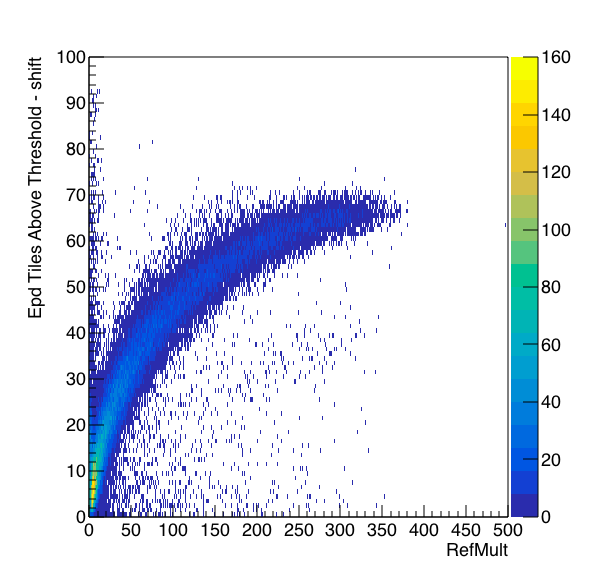
Figure 2: New EPD sum vs RefMult going to a 7 digit #.  Confirmed that the math is correct wrt to the trigger logic.

Then I wanted to find the difference with Eleanor's step e, I looked at an example to make sure I have the math right:

If I have an event  with sum E = 169 and sum W = 147, the 7 lowest significant digits would correspond to 41 and 19.  For this event, the difference is 22 with the full precision and still 22 afterwards.  Confirmed...

Caveat - The calculation is actually East + 128 - West in order to make the result positive definite.

So to return to the example above, the actually calculation would give 41 + 128 - 19 = 150.  I will keep the plots below for my own education.

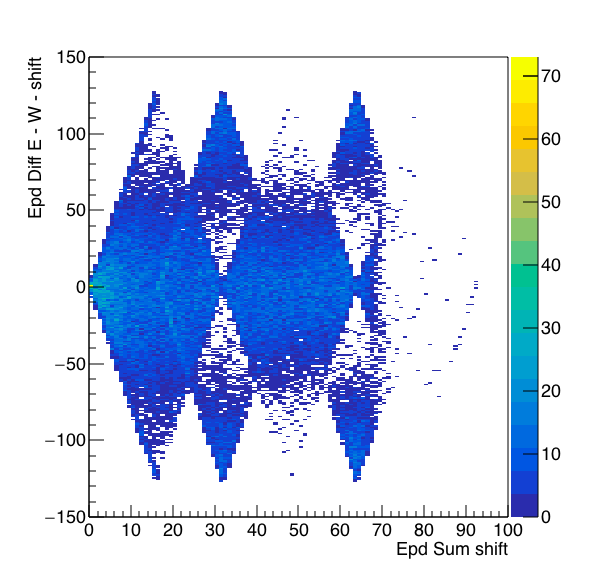
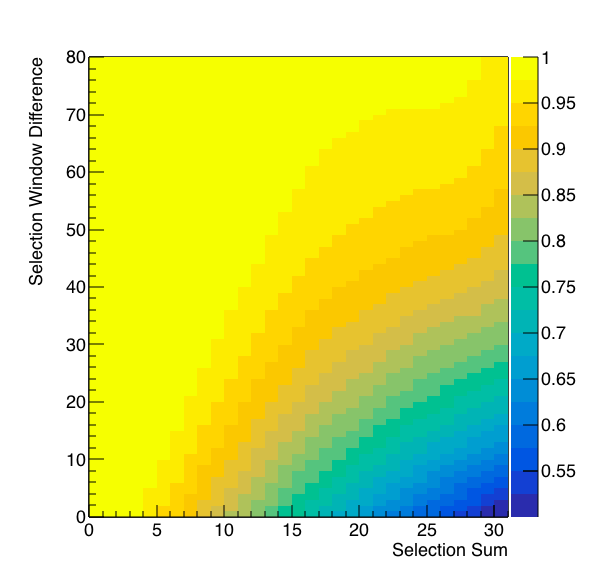
Figure 3: On the left is the application of this algorithm vs RefMult.  On the right is the proposed difference vs sum.

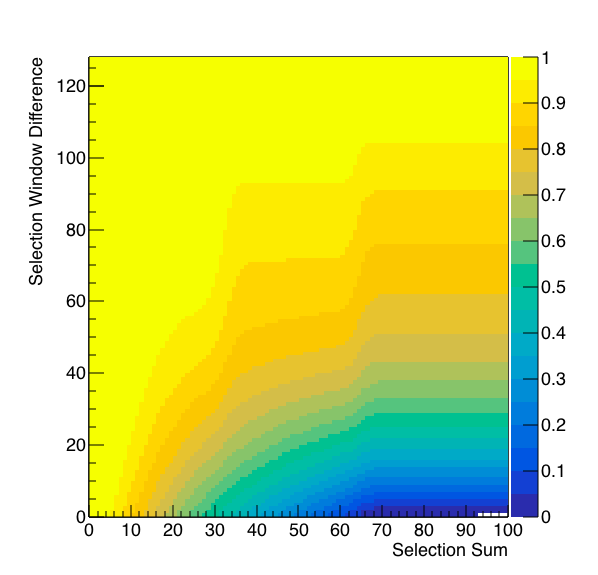
Figure 4: These are a repeat of Figure 3, but with the proper algorithm as how it will functionally look.