My dearest blog, how it must've seemed that I've abandoned you! Fret not, for it was not I who abandoned you but circumstance that created chasm between us. As Ulysses once said in the Odyssey: "There is a time for making speeches, and a time for going to bed" and I'm afraid the latter does not pertain to us at this very moment. This blog post will be lengthier than
normal and serves as an update to what I have done since the last post.

Update

In the last update (I recommend reading it) I stated that I figured out how to draw the correctly weighted pJetPt with the partonic weight but was confounded on  how to save it to a TH1F. With a script that I wrote, I produced the following plot that has t->Draw("pjetPt","partonicWeight") plotted with the histogram that I created. The histogram was created by looping through the number of entries in the TTree, grabbing the weight and pJetPt for that entry in the TTree,  and filling the T1HF with the appropriate pJetPt and partonic weight. 

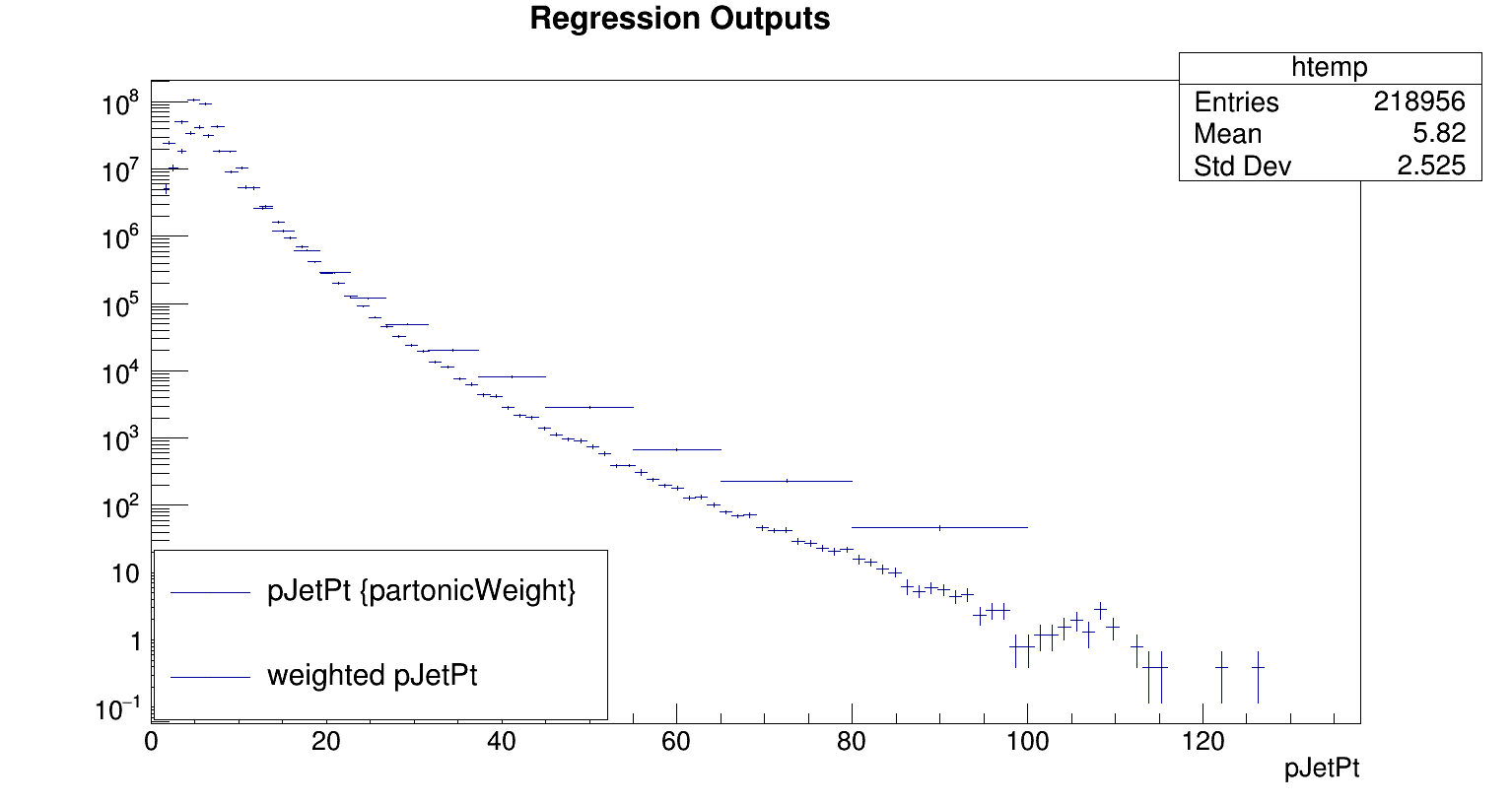
As useful (or not useful) as that may be, it is of no use to the TMVA regression but serves as sanity check. 

My biggest concern for the TMVA regression was giving TMVA the correctly weighted pJetpT distribution. The reason behind this concern goes as follows:

• The regression depends on the target variable (the pJetPt dist. passed in) 
• TMVA will perform a regression based on this target variable. 
• If the target variable is not "correct", it will still perform the regression correctly (based on the method chosen) but won't produce the regression that is sought after. Rather, it will be a regression that is "incorrect".

TMVA has a "Setweightexpression()" in which you can pass event-by-event weights to your input variables. However, I digressed from using this initially due to not knowing if this applied the weight to the target variable, the regression variables, or both. I attempted then to apply the weights myself by calling the the pJetPt and partonicWeight from each entry in the TTree and naively multiplying them together in a loop. KNOWING that this will not yield what I wanted, I still wanted to look at the result. That is seen in the next plot:

pJetPt*partonicWeight 

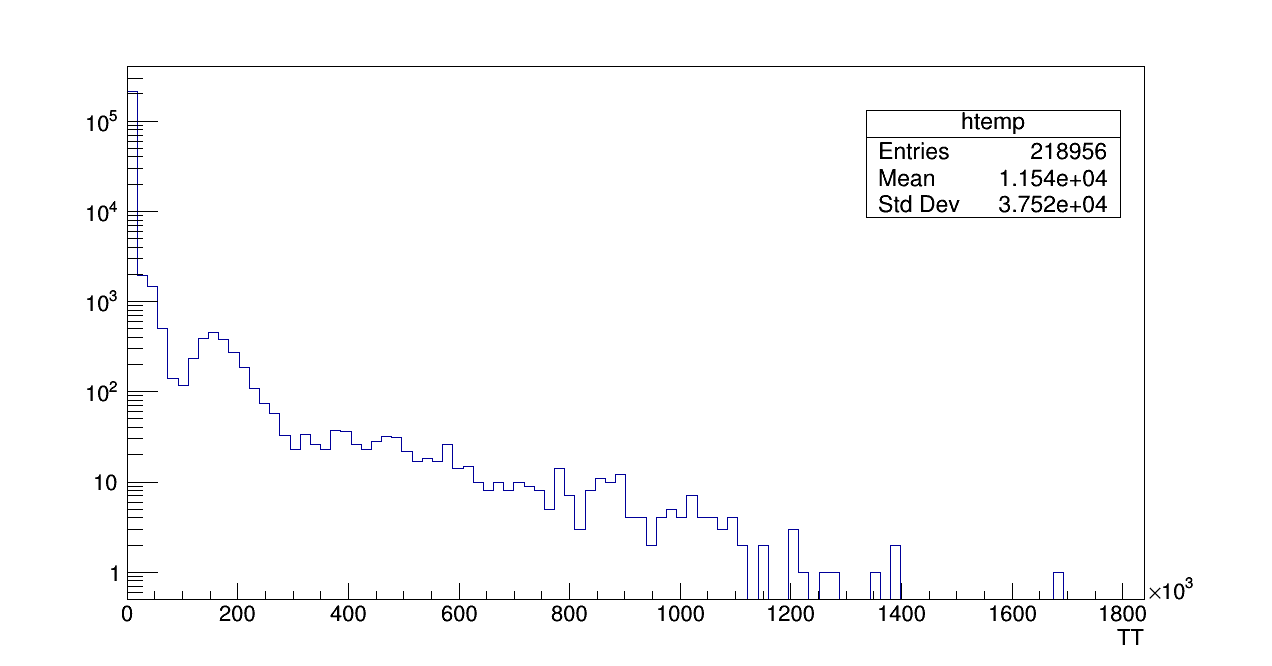
From just a quick glance at this, one can tell this is NOT what one wants.Nonetheless, I learned something from this and moved on. I began investigating the "setweightexpression()" that TMVA has to offer and how it is actually applied. 

SetweightExpression()

I have gleaned that "setweightexpression()" applies the weights to target variable and not the regression variables. This can be seen in the following plot in which I ran the TMVA regression (with only one method: MLP) with and without using the "setweightexpression()" function. The MLP results were grabbed from the TrainTree which accounts for the different number of entries.

Looking at the different regression outputs, the blue (with setweightexpression) plot is clearly different from the green and red. Additionally, one can see that the red (without seweightexpression) follows the same sort of decay that pJetPt does (which is without the weights). I infer that setweightexpression() applies the weights to only the target variable. Comparing the pJetPt with the weights applied and the regression that this method (MLP) produced is seen in the following deviation plot.

Deviation Plot

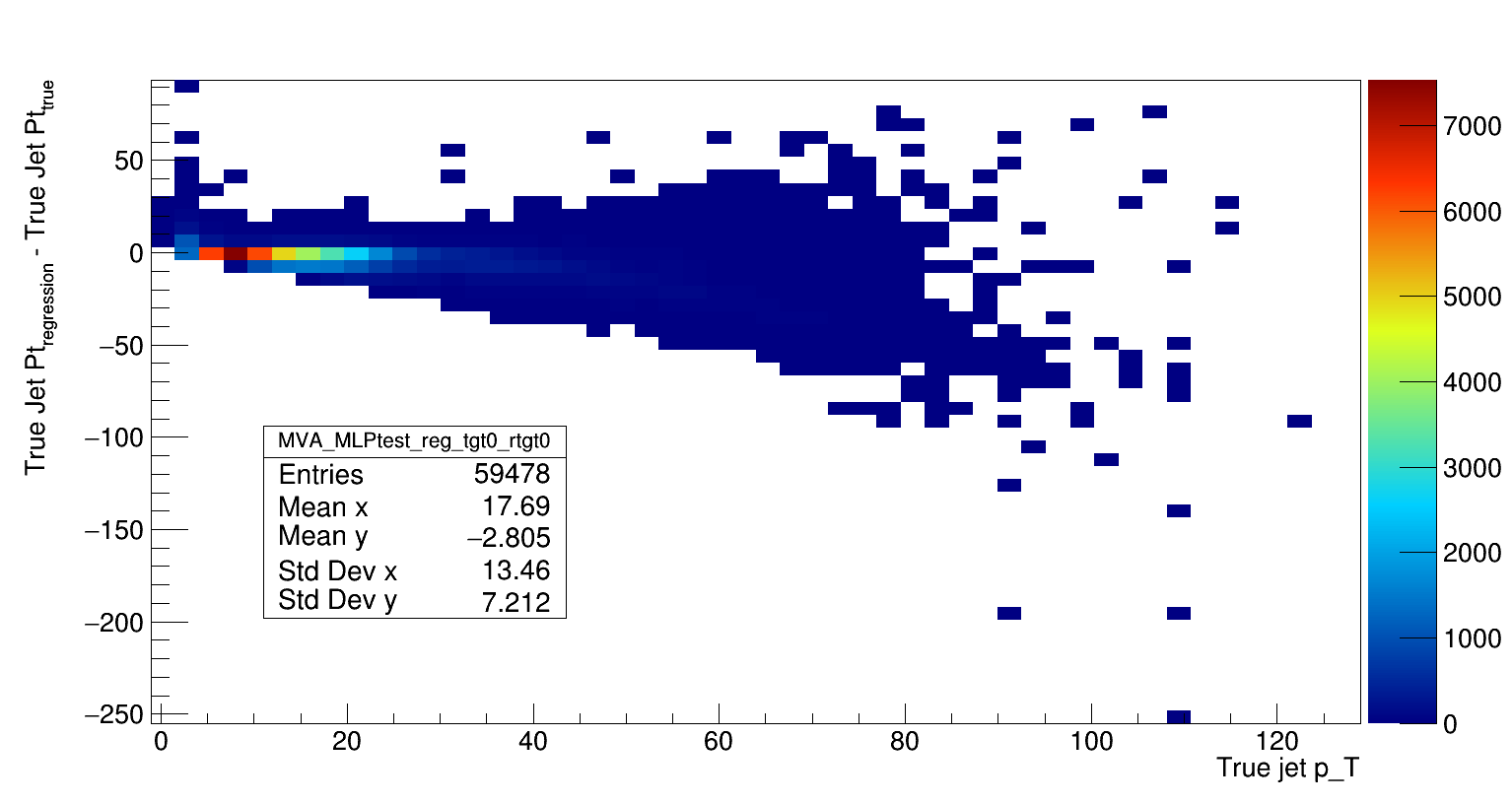
Just utilizing this MLP method, there is large discrepancies between the regression output and the true pJetpT (weighted distribution) at low pT. This is expected due to the larger number of events in this lower pT region. This is not to say that we should cast all worry in the larger pT region away. The primary purpose of this entry was to demonstrate and record how setweightexpression was working to lay rest the set of concerns surrounding this question to make way for another set concerns. The logical step now is to explore the different TMVA methods to reduce the deviation between true and regression pT, parametrize even further the regression to investigate feature importance, and eventually create a regression for what this is intended for: pions-in-jets with pT,jT, and Z.