It was suggested to see the effect of smoothing on the IU algorithm.  However, once one starts by smoothing, a few parts of the standard IU algorithm are less relevant and the smoothing also facilitates some new cuts.  So, instead of just smoothing and then applying the IU algorithm, I have created a new algorithm, the TSIU (Tukey-Smoothed IU Algo).

The Procedure

Note, the following is applied to each layer of each sector in the ESMD.  Paremeters in the following are followed by the default value in parenthesis, e.g. mNumSmoothIters (10).  If the step in the following algorithm was included in either the TSP or standard IU (or both) this is indicated by noting the older algo in square brackets, e.g. [IU].

1. Apply Tukey-smooter with mNumSmoothIters (10) iterations. [TSP]
   
2. Let all strips with energy above threshold, mSeedAbsThres (2 MeV),  be defined as seed strips [IU].  
3. Associate mNumStripsPerSide (3) strips on either side of the seed as part of the cluster. [IU]
4. Require that the cluster meet the following cuts:
   
   1. The number of non-zero strips (before smoothing) is greater than mMinStripsPerCluster (5 strips) [IU]
   2. The total energy in the cluster is greater than mMinEnergyPerCluster (3 MeV) [TSP]
   3. The energy of the strips (after smoothing) monotonically decreases from the seed.
      

Commentary

In general, the above procedure is much more simple than either the IU or TSP algorithms.  For example, the need to sort seeds in order of energy (relevant to deciding whether to drop seeds if they are too close to other seeds) is no longer needed, as the monotonically decreasing requirement automatically makes it is so seeds cannot be in multiple clusters which pass the cuts.  In particluar, this cut forces the clusters to share at most strip, on the outer edge of the clusters.  As of date, if one strip is shared, it is given weight 1 in both clusters (this could be updated in the future).  There is no longer any need for the seed floor procedure.  Also, while it is recognized that most clusters are larger than +/- 3 strips around the seed (7 strips), the smoothing causes the energy and position of the central 7-strips to be more strongly correlated with the energy and position of the entire cluster.  As the central parts of the clusters overlap less often than the tails of the clusters, the central portion of the cluster can be determined more acurately than the energy and position of the entire cluster.

The monotonic-decreasing cut helps reduce much of the false cluster splits.  Some false cluster splitting is still present.  It can be significanly reduced by adjusting the parameters, specifically increasing the number of smoothing iterations and increasing the seed threshold.  However, if one combines all pi0 candidates within a very close (eta, phi) distance (to be discussed in more detail in a future blog), the number of pi0 candidates due to false cluster splits can be greatly reduced.

Parameter Optimization

About 15 variations of the parameters were attempted, in a by-hand steepest decent type of fashion.  The code from this blog was used to determine how many 1-1 pi0s were present, and the code was augmented to seperate based on how closely the reconstructed pT matched the generated pT.  The optimization criterea was to maximize the number of 1-1 pi0s with pT within 1 GeV of the correct value, using the pi0_set1_run1 data set of 2000 pi0s fired at eta = 1.5, phi = 0 and with pT = 10 GeV.  All pi0 candidates within Delta R < 0.04 were recombined into a single pi0 candidate.  Only a minimal set of cuts were considered, the cuts listed as "common to both sets" on this blog.

Type Plots

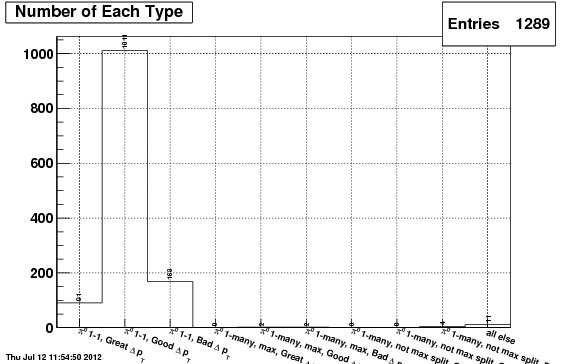
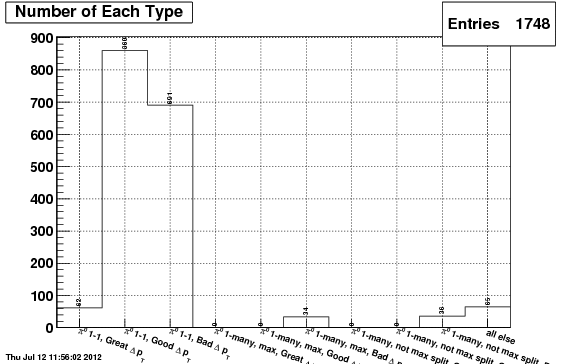
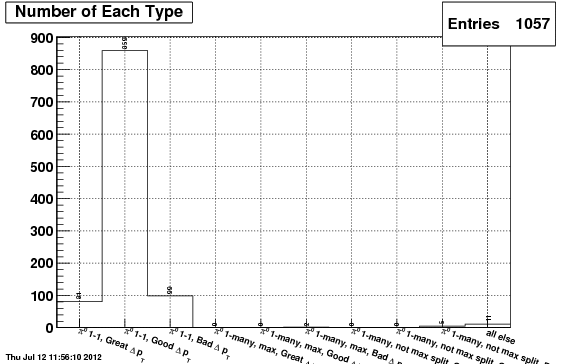
Following is the "candidate type" plot for the winning set of parameters (now denoted as the defaults), as well as for the IU and TSP algorithms for comparison.  

TSIU

IU

TSP

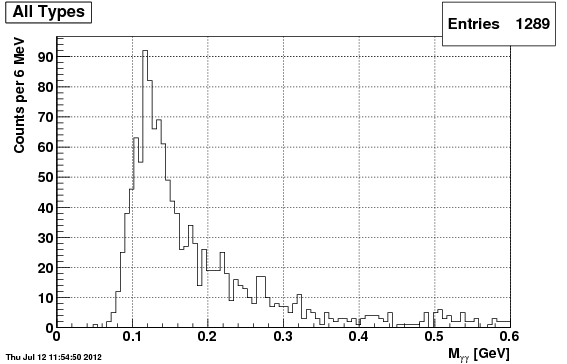
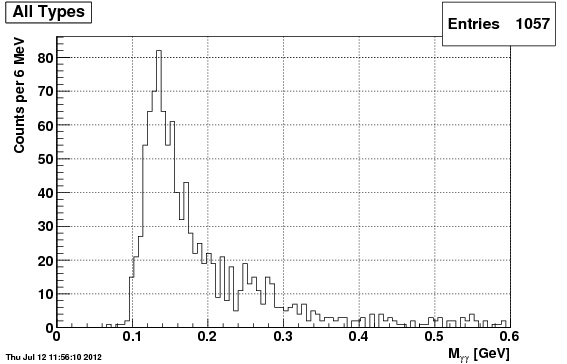
Mass Plots

Following are the mass plots for all pi0 candidates used in the above "type" plots", again in order TSIU, IU, TSP.  Note, in all cases, the plots can be considered nearly entirely signal (based on the above type plots), all originating from the same signal gun.

TSIU

IU

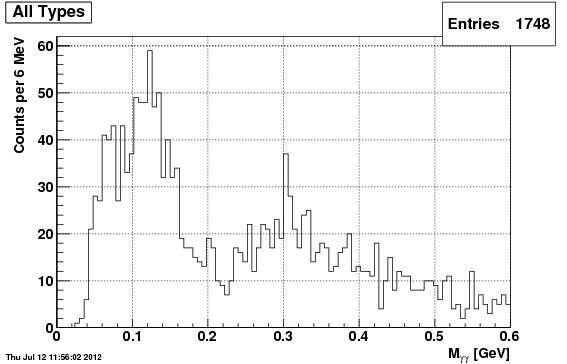
TSP

Conclusions

So far, the TSIU algorithm seems to have the highest efficieny and best signal shape.