In regard to Dave Underwoods post on Jan. 12th, 2012, I plot the Mu vs Mv and several related mass plots.

The following definitions are used.

• is the energy of the candidate
• is the magnitude of the asymmetry in the energy of the two photons
• is the number of strips seperating the two clusters in the plane--set to zero if only one cluster in the plane.  Simular definition for .
• is the mass of the candidate.
• is the asymmetry in the two clusters is the plane, and is set to 0 if there is only one cluster.  is defined simularly.
• is a mass for the plane, but computing and the asymmetry using only the plane.  Simular definition for
• 
• is a mass for the plane, but using the standard and renormalizing so that .  Simular definition for

The following plots were made using the standard IU algorithm on Hal's gamma_set1_run1 (left plots) and pi0_set1_run1 (right plots) MC files.  Note all pi0 candidates from the gamma MC file are from either falsely split pairs or conversions.

Figure 1

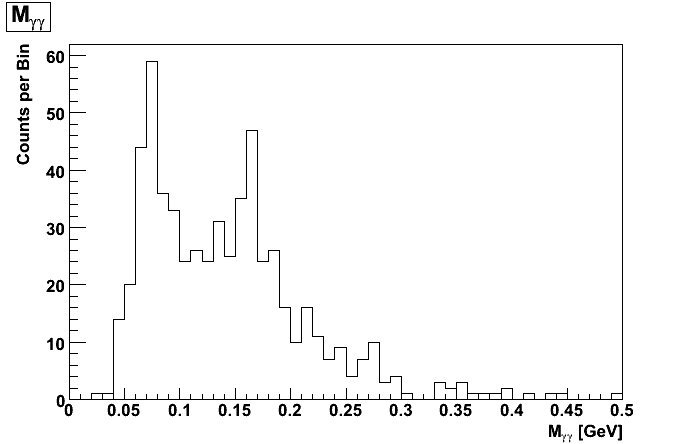
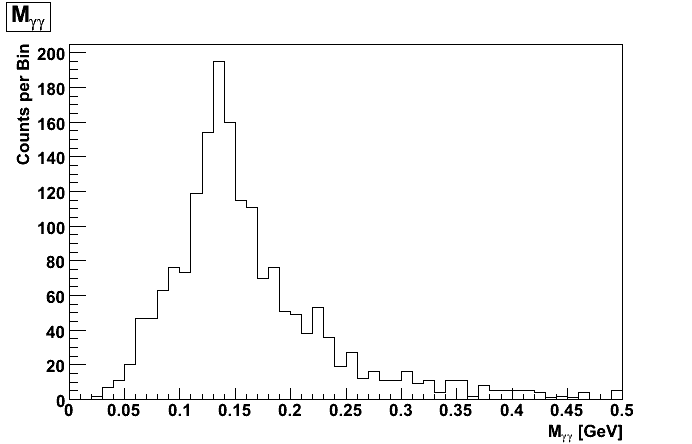
Figure 2

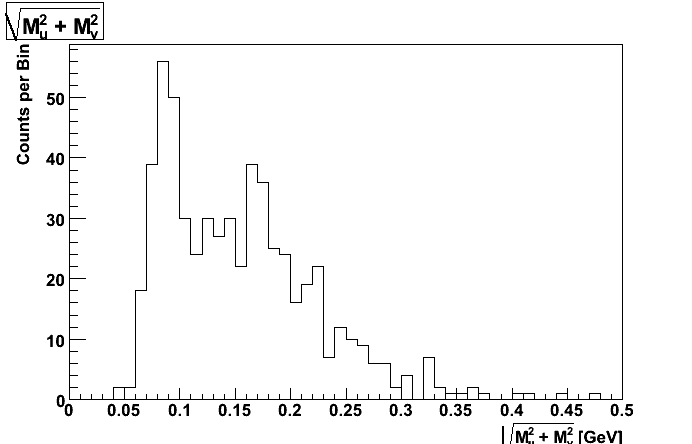
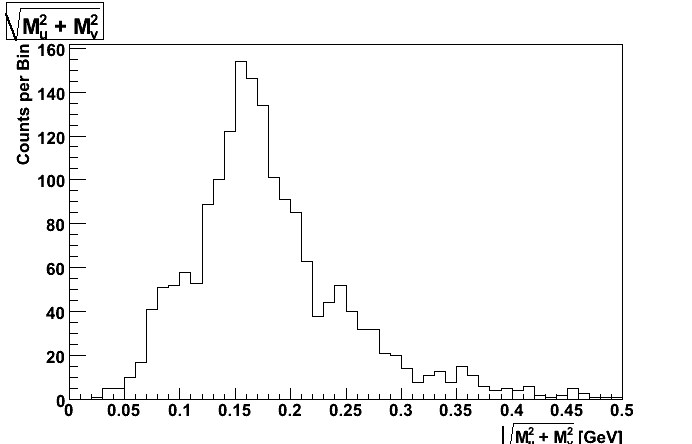
Figure 3

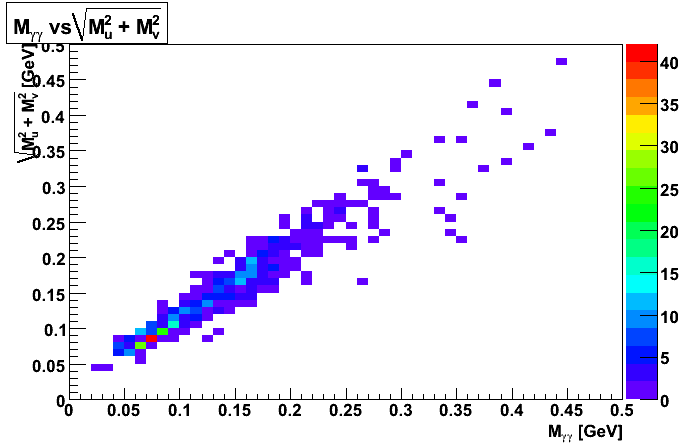
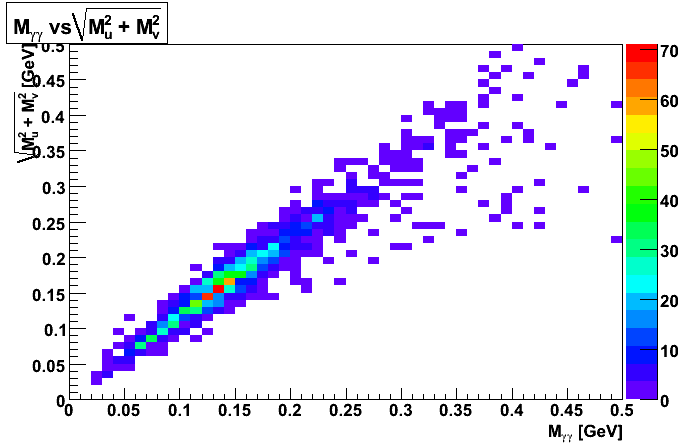
Figure 4

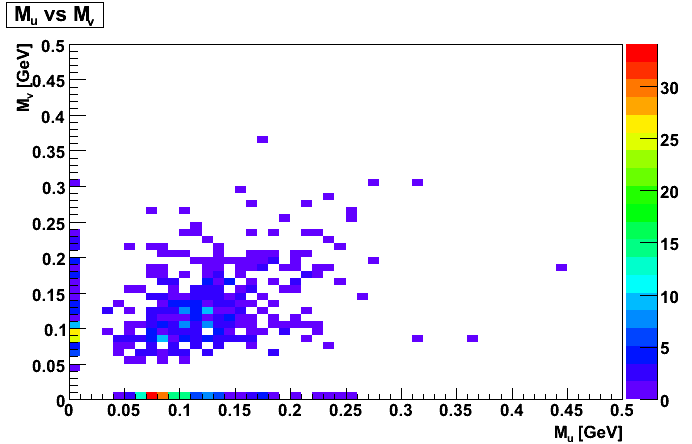
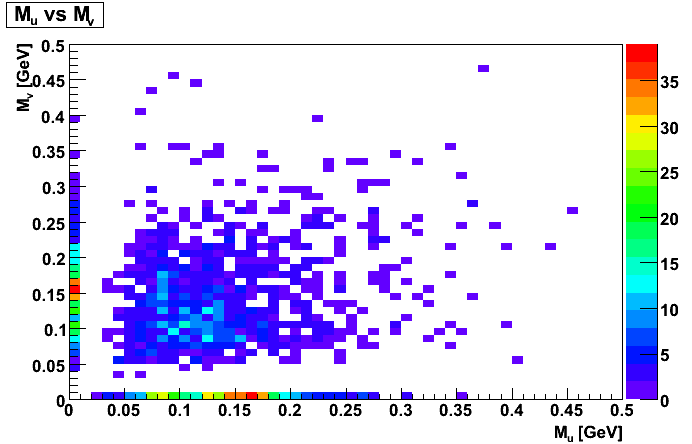
Figure 5

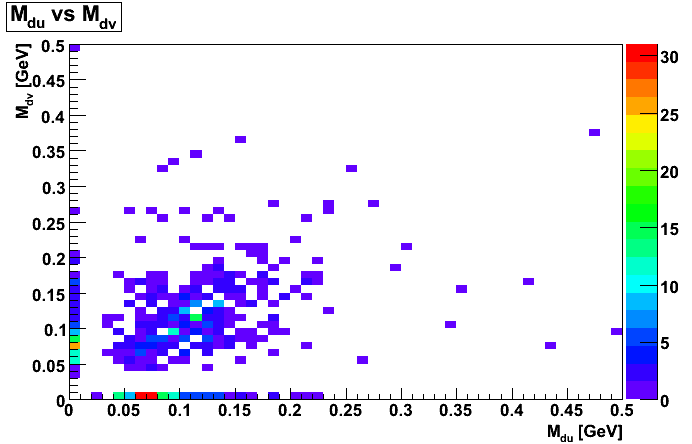
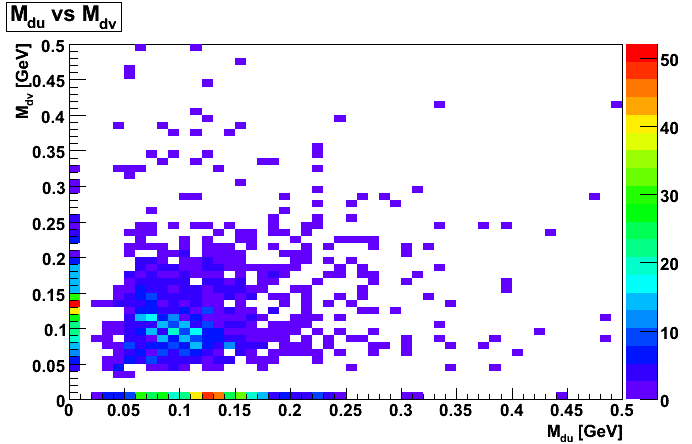
Figure 6

Commentary

The left panel of Figure 4 should be compared with Figure 6 and 7 of Dave's document, and the right panel of Figure 4 should be compared with Figure 8 of Dave's document.  Note: Figure 4 of this document also has falsely split clutsers, which Dave's document does not have.

The gap in du and dv seems to be problematic.   Note: gamma->e+e- conversions generally are near Mu = Mv, and falsely split clusters have Mu or Mv = 0.  Much of the region between is lost due to requiring the clusters to be not too close.  If the SMD strips were narrower or less noisy, then more events would occur with both du and dv not zero, and this method of distinguishing would be more promising--though it still may be useful.  Perhaps an alternate algorithm could also allow for smaller, but non-zero du and dv.   The fact that the central part of the left panel of Figure 4 is more closerly distributed to the line Mu = Mv than the corresponding part of the right panel of Figure 4 implies that using a cut on Mu and Mv may be useful, though with less dramatic results than one may have hoped for based on Dave's blog.