Additive vs Multiplicative
In the Equations of this other blog, it was noted that the effect of pi0s generated outside [n1,n2] and smeared into [n1,n2] can be accounted for in either an additive or multiplicative mannor. Below are the results comparing both. The additive method is then consistent with other publications which do not use "buffer bins", such as arXiv:1103.5704 and arXiv:1204.4161. Note: in pp we can use one MC instead of two, as we do not have to account for radiative effects on the leptons.
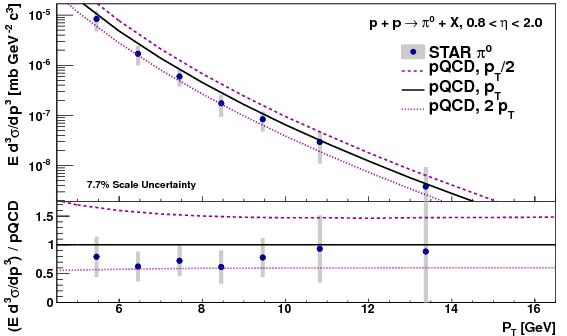

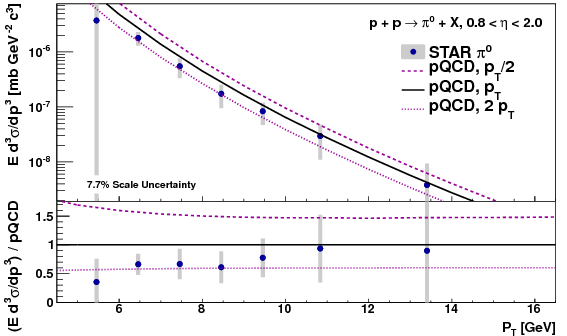
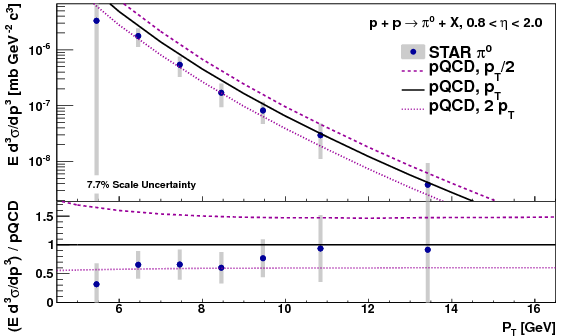
I still trust the option that leaves the 4-5 bin summed with the not-reconstructed bin, i.e. leaving it out of the smearing matrix and having it in the "outside smeared in" background, because the data/MC discrepency has less effect on the sum. The large uncertainty on the 5-6 GeV bin due to half the difference between the whether to include the 4-5 GeV bin in the smearing matrix is probably overkill, but probably fine to leave as is for the sake of being conservative.
So I vote to leave things as we are doing with the possible exception of multiplicative vs. additive removal. We could consider taking the average of the two and half the difference as a further systematic. My inclination is that this is overkill, and I'd mildly suggest not doing it. If others feal it is important, it would be easy to add and I won't be hard to convince on that point.
So the only remaining question is whether to do smo
Unfolding: n1=5-6 GeV, multiplicative

Unfolding: n1=5-6 GeV, additive

Unfolding: n1=4-5 GeV bin, multiplicative

Unfolding: n1=4-5 GeV, additive

Conclusions
When the 4-5 bin is in the smearing matrix and not in the "outside smeared in" catagory (3rd and 4th plot), the results are extremely consistent across all pT bins between multiplicative and additive removal of the "outside smeared in" background. When the 4-5 bin is part of the "outside", data vs. MC discrepancy in the 4-5 GeV bin causes there to be a difference in the multiplicative vs. additive removal for the 5-6 GeV bin. In this case, much of the smearing of "outside" mostly is coming from the 4-5 GeV bin. Other bins show little change. None of this is suprising.I still trust the option that leaves the 4-5 bin summed with the not-reconstructed bin, i.e. leaving it out of the smearing matrix and having it in the "outside smeared in" background, because the data/MC discrepency has less effect on the sum. The large uncertainty on the 5-6 GeV bin due to half the difference between the whether to include the 4-5 GeV bin in the smearing matrix is probably overkill, but probably fine to leave as is for the sake of being conservative.
So I vote to leave things as we are doing with the possible exception of multiplicative vs. additive removal. We could consider taking the average of the two and half the difference as a further systematic. My inclination is that this is overkill, and I'd mildly suggest not doing it. If others feal it is important, it would be easy to add and I won't be hard to convince on that point.
So the only remaining question is whether to do smo
Groups:
- sgliske's blog
- Login or register to post comments
