CSB-H4L and He4L binding energy
Title :
Measurement of H4L and He4L binding ennergy in Au+Au collisions at sqrt{s_{NN}} = 3 GeV
PAs :
Tianhao Shao, Jinhui Chen, Yue-Hang Leung, Yugang Ma, Zhangbu Xu
Targeted journal :
Physics Letters B
Abstract :
Measurements of mass and $\Lambda$ binding energy of \hl and \hel in Au+Au reactions at $\sqrt{s_{_{\rm NN}}}=3$ GeV are presented, with an aim to address the charge-symmetry breaking problem in hypernuclei systems with atomic number A = 4. The $\Lambda$ binding energies are $\rm B_{\Lambda}(^4_{\Lambda}H) = 2.22\pm0.06(stat.) \pm0.14(syst.)$~MeV and $\rm B_{\Lambda}(^4_{\Lambda}He) = 2.38\pm0.13(stat.) \pm0.12(syst.)$~MeV for \hl and \held, respectively. In our results the $\Lambda$ binding-energy difference is $\rm \Delta B_{\Lambda}^4(0_{g.s.}^{+})=0.16\pm0.14(stat.)\pm0.10(syst.)$~MeV for ground states. Combined with the $\gamma$-ray transition energies, the binding-energy difference for excited states is $\rm \Delta B_{\Lambda}^4(1_{exc}^{+})=-0.16\pm0.14(stat.)\pm0.10(syst.)$~MeV, which is negative and comparable to the value of the ground states within uncertainties. Within current uncertainties, these new measurements on the $\Lambda$ binding-energy difference in A = 4 hypernuclei systems are matched by the theoretical calculations that result in $\rm \Delta B_{\Lambda}^4(1_{exc}^{+})\approx -\Delta B_{\Lambda}^4(0_{g.s.}^{+})<0$ and present a new method for the study of charge symmetry breaking using relativistic heavy-ion collision experiments.
Conclusions :
In this paper, we present measurements of the $\Lambda$ binding energies of \hl and \held.~The invariant-mass distributions of \hl and \hel are reconstructed in Au+Au collisions at $\sqrt{s_{\rm NN}}=3$~GeV taken in the fixed-target mode at STAR. The $\Lambda$ binding energies of \hl and \hel in ground states are obtained: $\rm B_{\Lambda}(^4_{\Lambda}H)~=~2.22~\pm~ 0.06(stat.)~\pm~0.14(syst.)$~MeV and $\rm B_{\Lambda}(^4_{\Lambda}He)~=~2.38~\pm~0.13(stat.)~\pm~0.12(syst.)$~MeV. Using the $\gamma$-ray transition energies of the excited states from previous measurements, the $\Lambda$ binding energies in excited states are also extracted. The $\Lambda$ binding-energy differences between the two A = 4 hypernuclei and between their corresponding excited states are calculated as $\rm \Delta B_{\Lambda}^4(0_{g.s.}^{+})~=~0.16~\pm~0.14(stat.)~\pm~0.10(syst.)$~MeV and $\rm \Delta B_{\Lambda}^4(1_{exc}^{+})~=~-0.16~\pm~0.14(stat.)~\pm~0.10(syst.)$~MeV, respectively. Within current uncertainties, our results are consistent with the theoretical calculation of the charge symmetry breaking effect in A = 4 hypernuclei with a positive $\rm \Delta B_{\Lambda}^4(0_{g.s.}^{+})$ and a negative $\rm \Delta B_{\Lambda}^4(1_{exc}^{+})$ of comparable magnitude; however, the statistical uncertainties are large. Our approach provides a new avenue to study the charge symmetry breaking in heavy-ion collision experiments. Higher-statistics data sets and more accurate measurements of $\gamma$-ray transition energies will be able to improve these measurements..
Figure 1. (a): The mean energy loss versus rigidity ($p/q$, where $p$ is the total momentum of the particle and $q$ is its electric charge) in the TPC. The dashed curves represent the expected values calculated by the Bichsel function for each species of particles. (b): The square of the ratio of mass and charge, $m^2/q^2$ versus rigidity in the TOF detector. The dashed curves represent the theoretical values for $\rm ^{3}He$ and $\rm ^{4}He$.
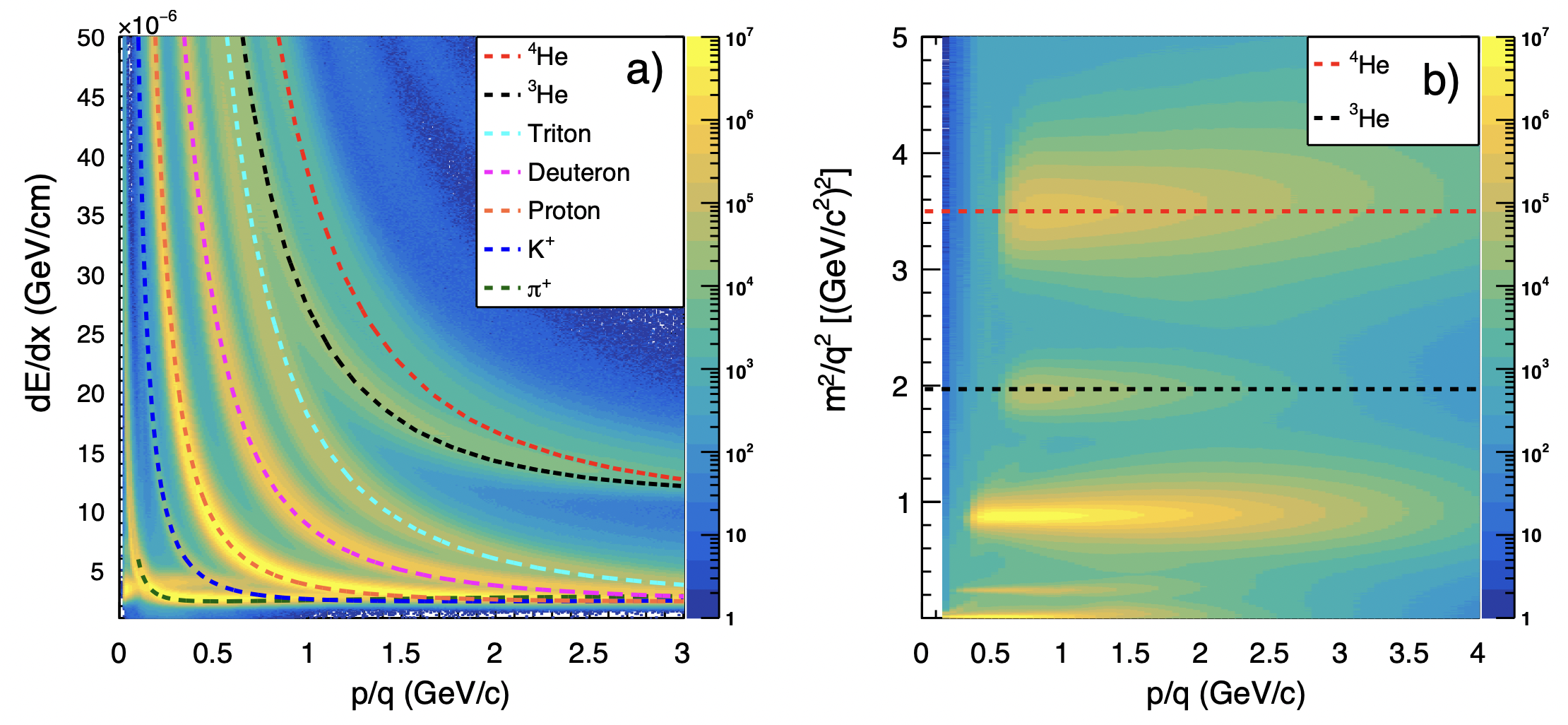
Figure 2. Invariant-mass distributions for \hl (a) and \hel (b) reconstructed with KFParticle and TMVA-BDT. The green histograms represent the rotated backgrounds. The blue dashed curves represent the background fits and are obtained by fitting the invariant-mass distributions outside of the signal regions with double-exponential functions. The black dashed curves are obtained by fitting these distributions across the full range of invariant mass with the background fit result and a Gaussian function. The orange dashed curves represent the signal Gaussian functions.
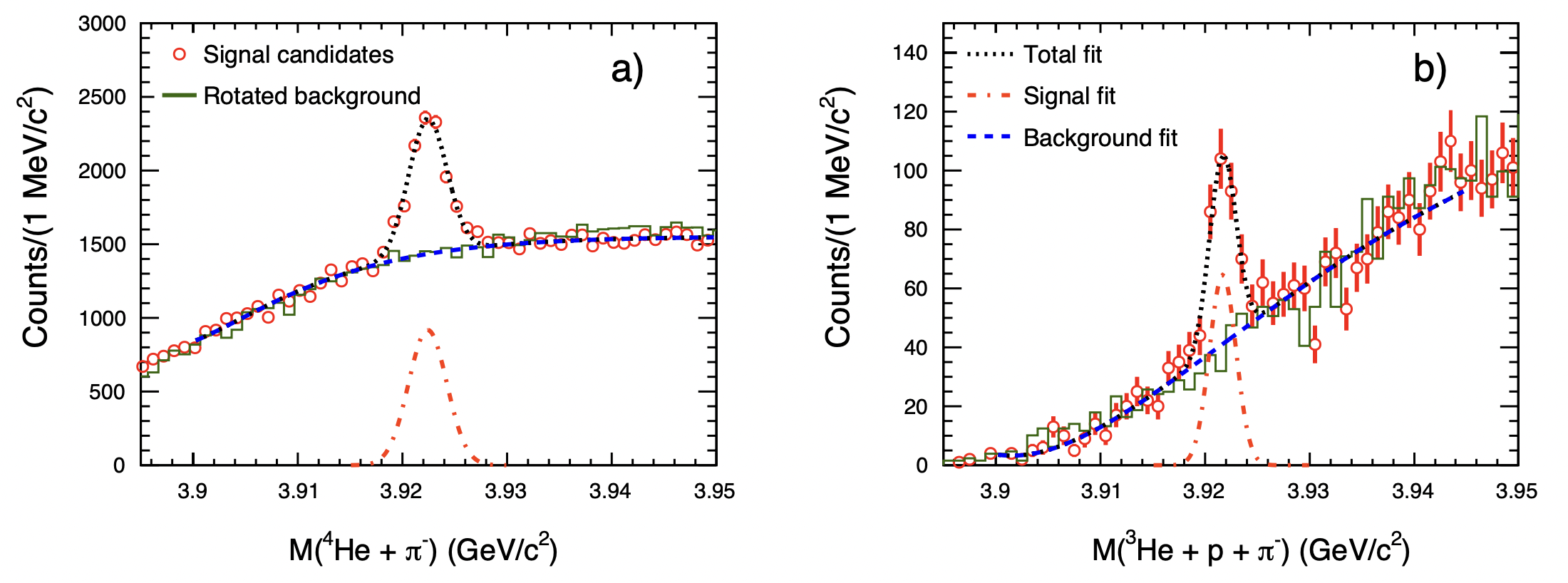
Figure 3. The average difference between the measured momentum and the MC input momentum as a function of the measured momentum for $\rm ^4He$. The red circles represent the energy loss without any corrections and the blue triangles are with energy-loss correction applied on the measured momentum.
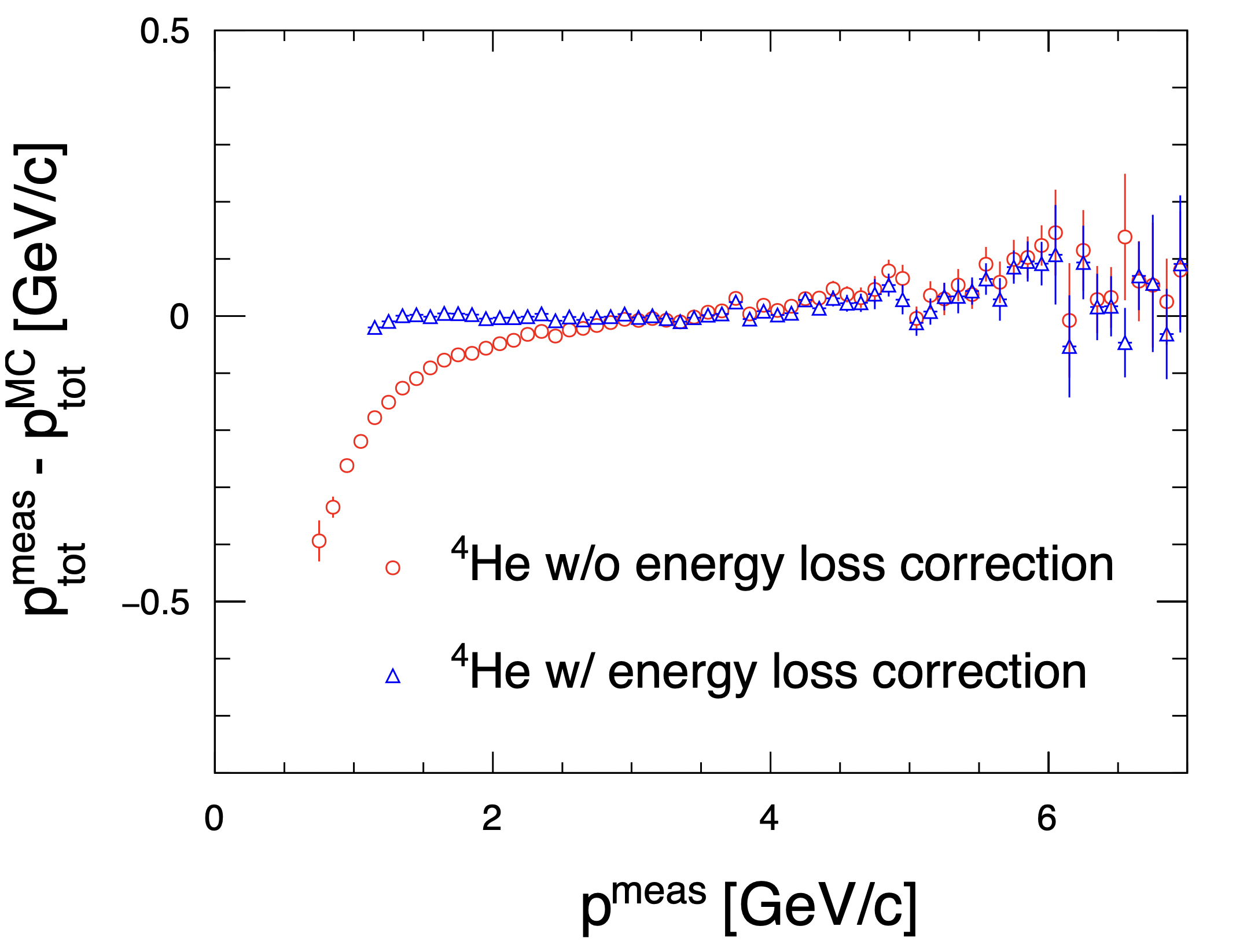
Figure 4. Energy level schemes of \hl and \hel in terms of $\Lambda$ binding energies. The ground-states binding energies are from this analysis. The values for excited states are obtained from the $\gamma$-ray transition energies measured in Refs.
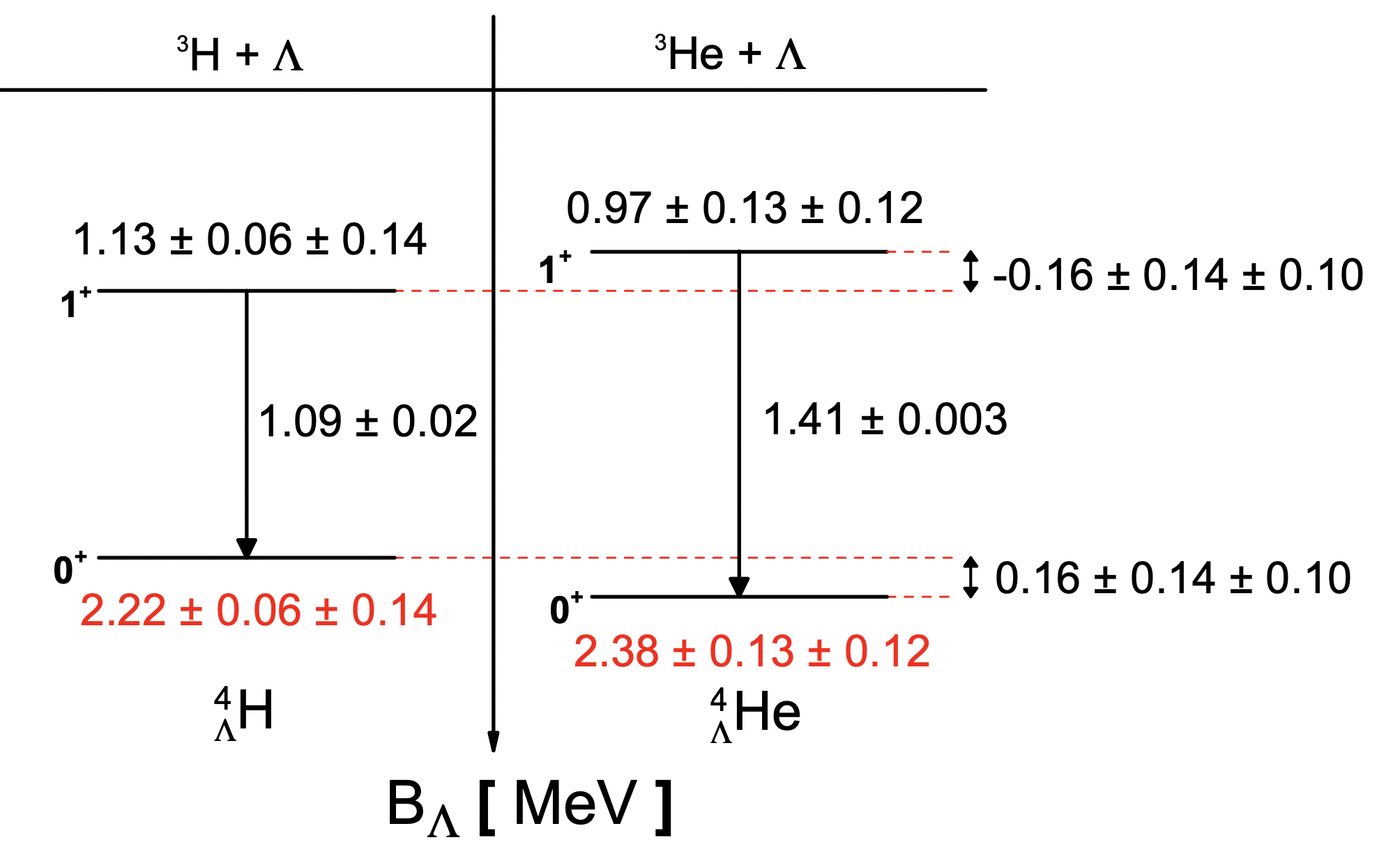
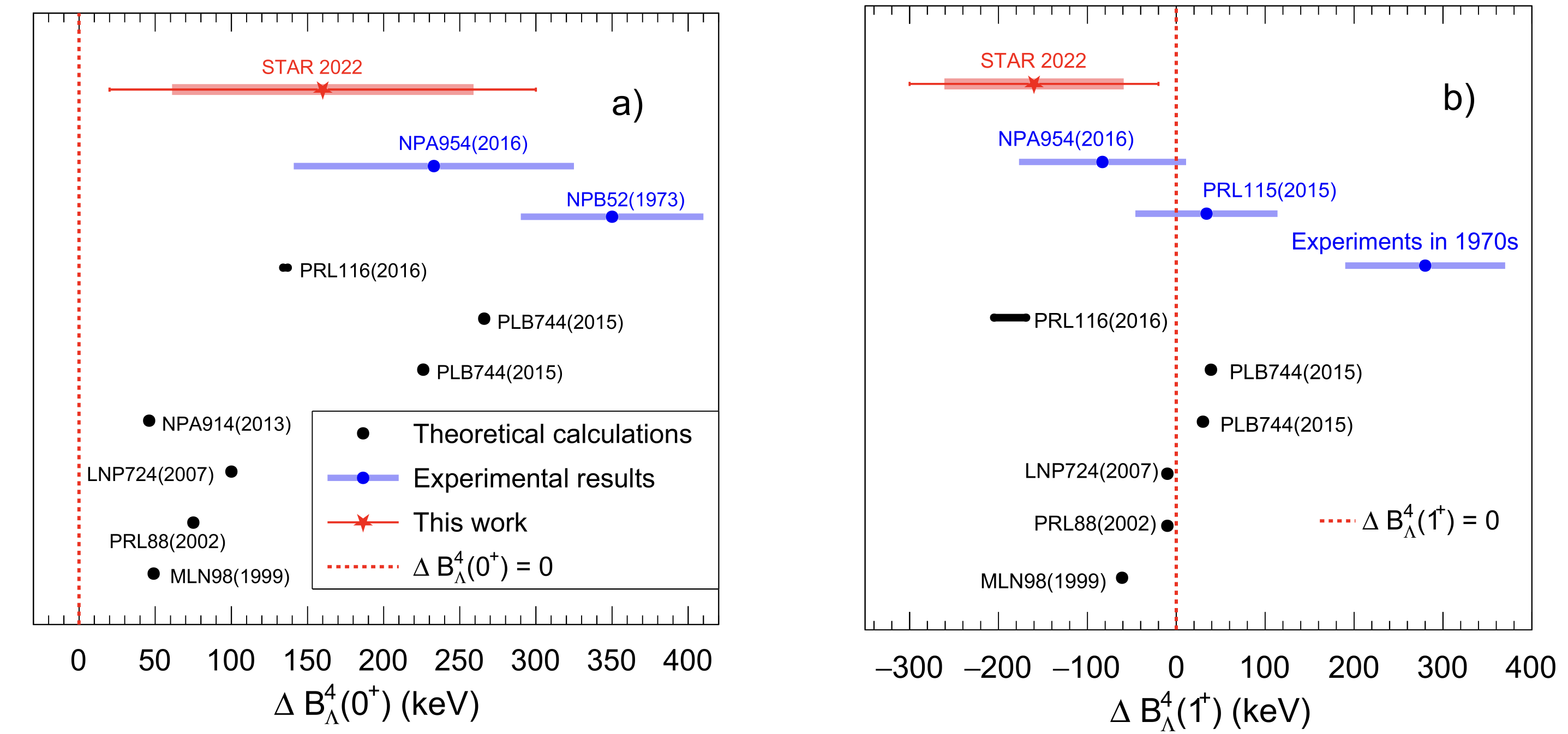
Figure 5. The $\Lambda$ binding-energy differences between \hl and \hel in ground states (a) and in excited states (b) compared with theoretical model calculations (black dots) and previous measurements (blue dots). Solid error bars show statistical uncertainties and boxes show the systematic uncertainties. Red dashed vertical lines are drawn at $\rm \Delta B^4_{\Lambda}(0^+~or~1^+)=0$.
Previous PWG presentations :
drupal.star.bnl.gov/STAR/system/files/H4L-He4L-production-FXT-3p85-v0817.pdf
drupal.star.bnl.gov/STAR/system/files/2020-09-H4L-He4L-production-FXT-3p85.pdf
drupal.star.bnl.gov/STAR/system/files/Tianhao-11-16-H4L-energy-loss-FXT-3p85.pdf
drupal.star.bnl.gov/STAR/system/files/Tianhao_2020-12-He4L-energy-loss-FXT-3GeV.pdf
drupal.star.bnl.gov/STAR/system/files/Tianhao-2021-01-29-Lambda-energy-loss-correction-3GeV.pdf
drupal.star.bnl.gov/STAR/system/files/2021-02-Update-H4L-He4L-binding-energy-FXT-3p85-v2.pdf
drupal.star.bnl.gov/STAR/system/files/Tianhao-2021-03-Update-H4L-He4L-binding-energy-FXT-3p85.pdf
drupal.star.bnl.gov/STAR/system/files/Tianhao-2021-06-Update-CSB-paper-3p85.pdf
https://drupal.star.bnl.gov/STAR/system/files/Tianhao-2022-02-Update-CSB-paper-3p85.pdf
Analysis Note :
CSB_analysis_note
PWGC preview :
PWGC_preview_slides
Paper draft :
Paper_draft_v19
Code for review : /afs/rhic.bnl.gov/star/doc_protected/www/lfsupc/shaoth/gpc_CSB
-->
- shaoth's blog
- Login or register to post comments
