- stevens4's home page
- Posts
- 2014
- 2013
- 2012
- 2011
- December (1)
- November (2)
- October (1)
- September (1)
- August (2)
- July (3)
- June (7)
- May (2)
- April (2)
- March (5)
- February (2)
- January (2)
- 2010
- November (1)
- October (1)
- September (3)
- August (3)
- July (3)
- June (1)
- May (1)
- April (3)
- March (4)
- February (4)
- January (8)
- 2009
- December (4)
- November (3)
- October (4)
- September (5)
- August (1)
- July (2)
- June (2)
- April (1)
- March (1)
- February (2)
- January (1)
- 2008
- My blog
- Post new blog entry
- All blogs
W Trigger Efficiency Study
W Trigger Efficiency Study
There are 3 outstanding issues for the trigger efficiency:
a) Eta dependence of trigger efficiency
b) Phi dependence of trigger efficiency (BEMC module boundries)
c) Lower trigger efficiency in W- sample for lepton ET<35 GeV
Part I: Study eta and phi dependence of trigger efficiency
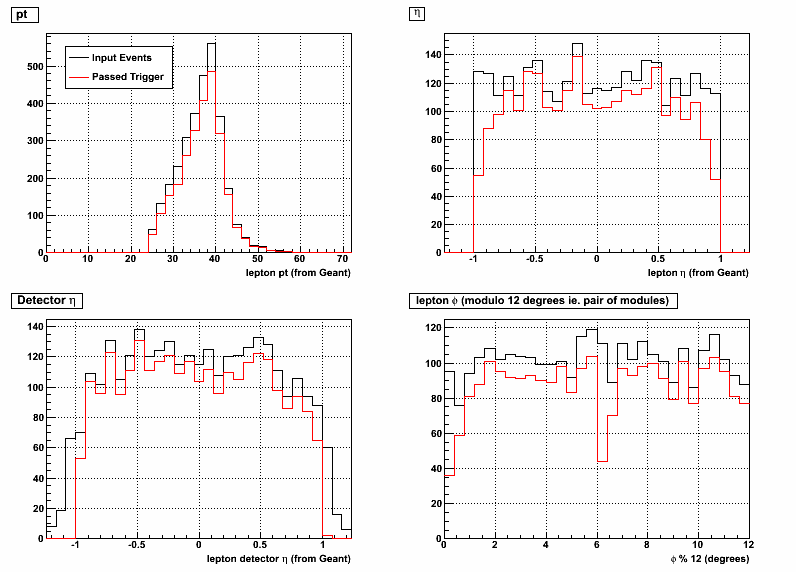
The first 4 figures below show the trigger efficiency as a function of 4 leptonic variables pt, eta, detector eta, and phi (Here detector eta is defined as the psuedorapidity in the STAR reference frame where the lepton track crosses the front of the BEMC). For the phi distribution the barrel has been "wrapped up" to stack all pairs of modules (12 degrees wide) on top of each other to emphasize the inefficiency at the module boundries. In figure 2 and 4 you can see the numerator (Passed Trigger) and denominator (input Events) for the efficiency calculation.
Note: Both the numerator and denominator of the efficiency calculation have the ET>25 and |eta|<1 cut applied.
Figure 1: W+ Trigger Efficiency
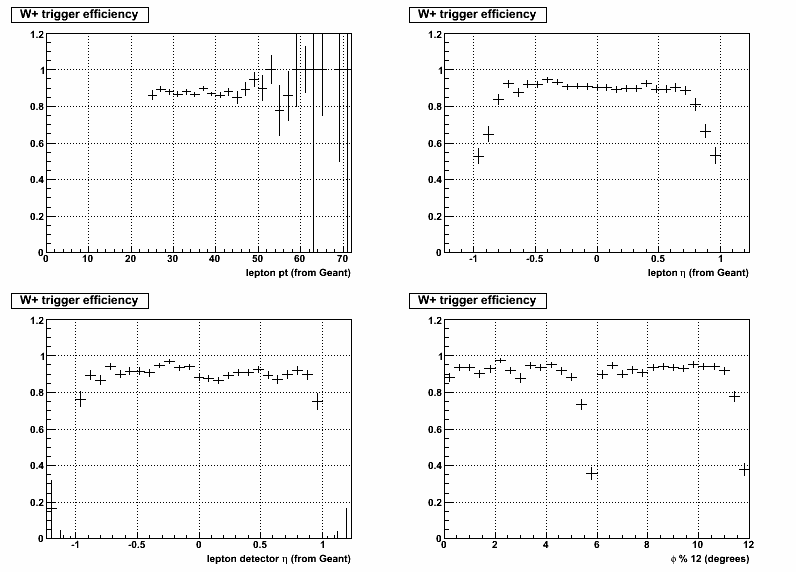
Figure 2: W+ Trigger Efficiency Input Distributions
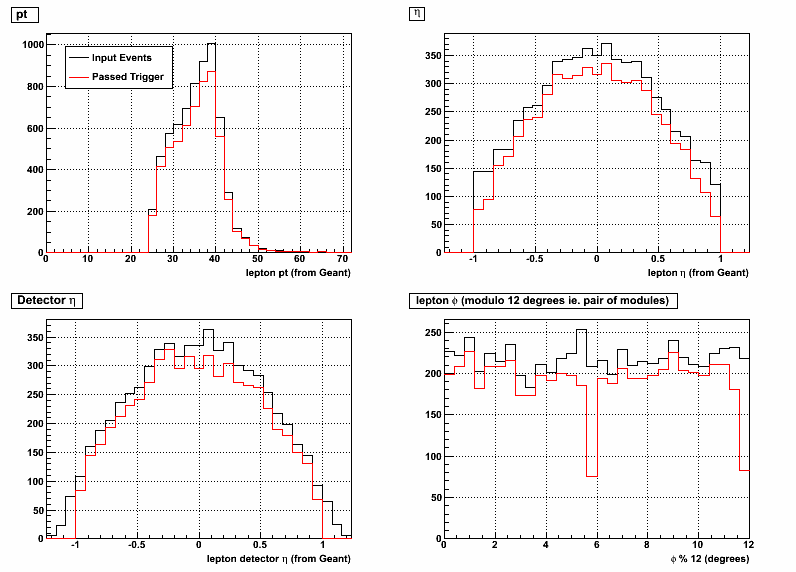
Figure 3: W- Trigger Efficiency
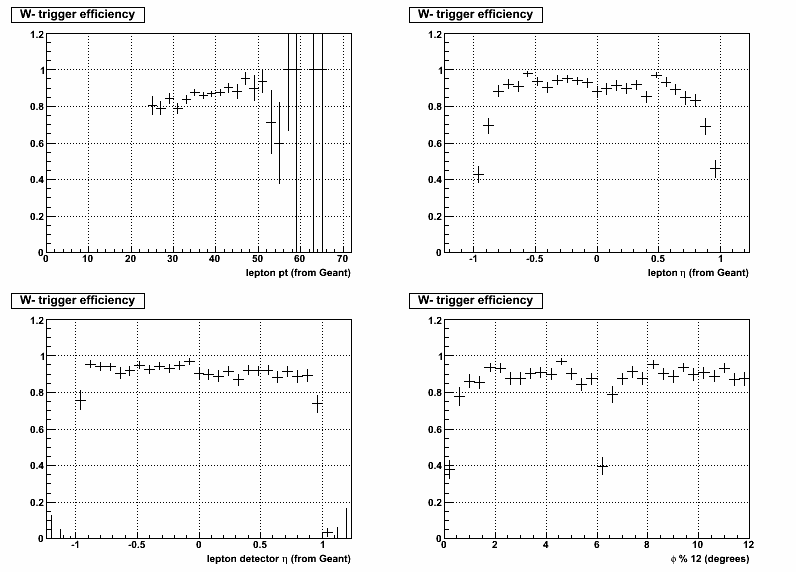
Figure 4: W- Trigger Efficiency Input Distributions
Conclusions:
a) The detector eta dependence of the trigger efficiency is ~flat and doesn't fall off until the last bin. So the eta dependence of the trigger efficiency is a result the leptons falling within |eta|<1 in the event reference frame, but the EM shower falling outside the BEMC detector volume.
b) The phi dependence of the trigger efficiency can be seen clearly at the module boundries.
Part II: Lower Trigger Efficiency for W- at lepton ET ~ [25,35]
Figure 5: W+ detector eta distribution for lepton ET = [25,35]

Figure 6: W- detector eta distribution for lepton ET = [25,35]

Table of events with lepton ET = [25,35]
| Input Events | Pass Trigger | Input Events |detector eta| > 1 | |
| W+ | 2949 | 2578 (87.4% effic) | 90 (3.1% of input events) |
| W- | 1076 | 889 (82.6% effic) | 91 (8.5% of input events) |
Conclusion:
c) From the table above we see that the W- sample has a larger fraction of events with |detector eta| > 1 than the W+ sample. This indicates that the lower efficiency for the W- sample in this ET range is a result of the different eta distributions between the two samples. The difference in the eta distributions in this ET range is shown below for the RHICBOS yields.
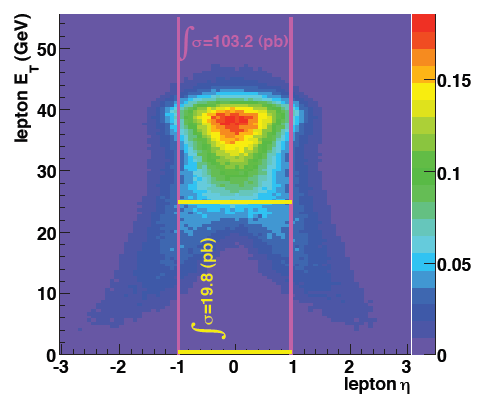
Figure 7: RHICBOS W+ differential cross section lepton ET vs eta


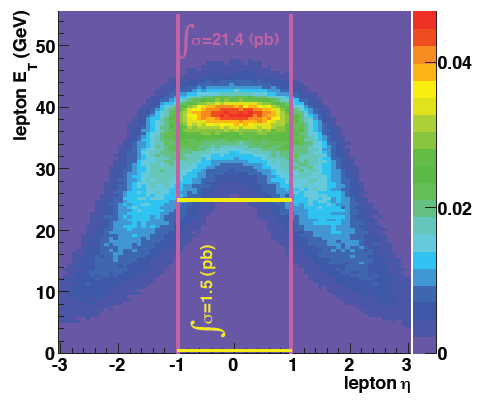
Figure 8: RHICBOS W- differential cross section lepton ET vs eta
In the ET=[23-35] range the W- yield peaks at larger |eta|, where as the W+ yield falls off at larger |eta|. This is qualitatively consistent with what is seen in the MC samples.
- stevens4's blog
- Login or register to post comments