The original algorithm I was using to calculate new voltages and bit shifts was sometimes resulting in bit shifts significantly different from zero, which remained so over numerous iterations. In the original algorithm, I only took account of the starting voltage/bit-shift and the final desired gain. It could then be that the iteration procedure left the bit-shift stuck at a high value, a situation perhaps best demonstrated by an example.

Say on the first iteration a gain factor of 5 was requested (quite common in our early iterations). If the voltage was already high for this cells, the bit shift could end up being increased by 2 or even 3 to achieve the requested gain. If on subsequent iterations a gain factor < 1 was requested, and the voltage was still quite high, the gain reduction might be accommodated solely by voltage reduction without the bit-shift decreasing. To counter this, we introduced conditions such as "if bit-shift > 2 and gain factor < 0.5, decrement bit-shift before calculating voltage". However, these conditions were somewhat ad hoc and made the code rather complicated to follow and maintain. They also still resulted in the bit-shifts accumulating around the boundary of where we imposed the condition (e.g. bit-shift 2 in the above example).

To counter this, I have implemented a new algorithm. Now, whenever a new gain is requested, I calculate the voltage that gives that gain for every bit-shift in the range [-5, +5]. After rejecting (bit-shift, voltage) combinations that cannot achieve that gain, I select the combination that gives the bit-shift with the smallest magnitude. In this way I maximise the number of cells with zero or small bit shift. This differs from the original algorithm in that is more "global", taking account of every possible way to achieve the desired gain, rather than just considering the initial conditions of the cell.

The best way to see the effect is with a picture. Figure 1 shows, for small cells, the bit shift resulting from iteration 14 using the old (black) and new (red) algorithm. The shift towards bit-shifts of zero is clear. The resulting voltage distributions for the small cells are comparable for this iteration, so I don't show them.

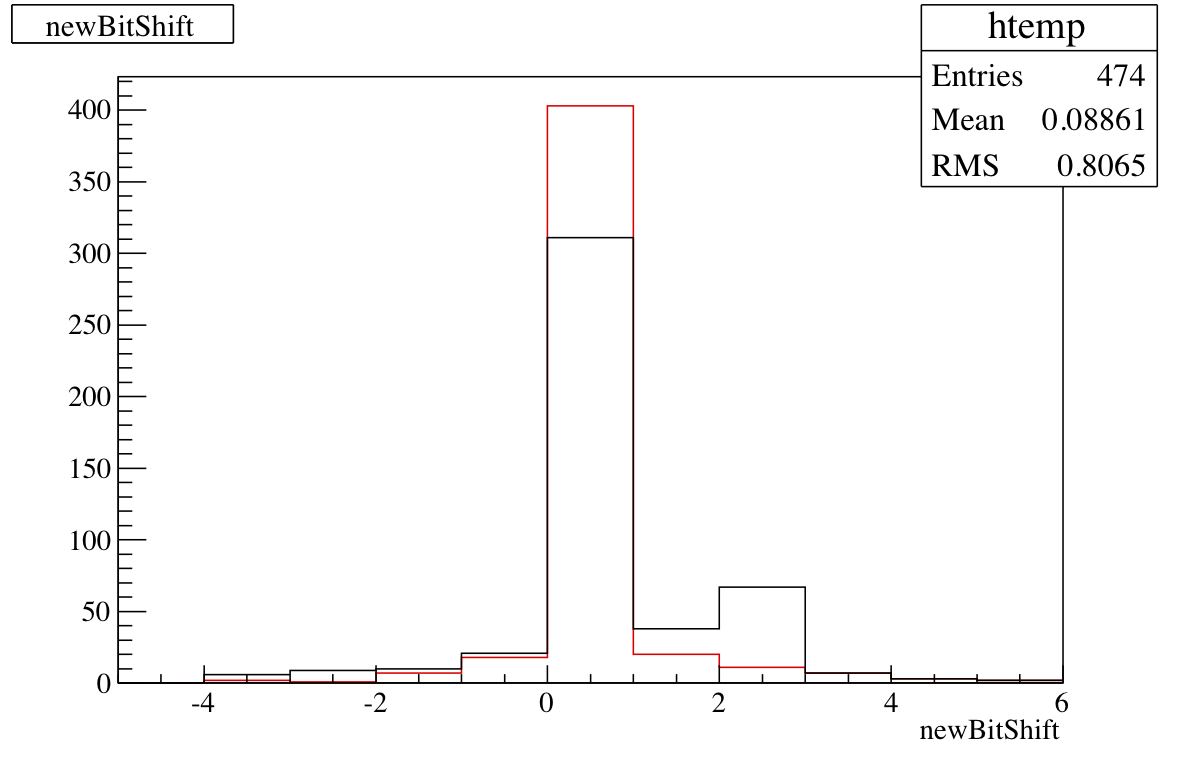
Figure 1: Small cell bit-shifts with new (red) and old (black) algorithm.

Similarly, figure 2 shows the bit-shifts for large cells. Again, there is an increase in the number of cells with zero bit-shift and a reduction of those at larger values. As there is no lower limit imposed on the large cell voltages there are none with negative bit-shift. Figure 3 shows the voltage distributions. The voltages look more sharply peaked with the new algorithm, at slightly larger values, though I'm not clear if there is a particular reason for the big jump in the red distribution around 1400 V.

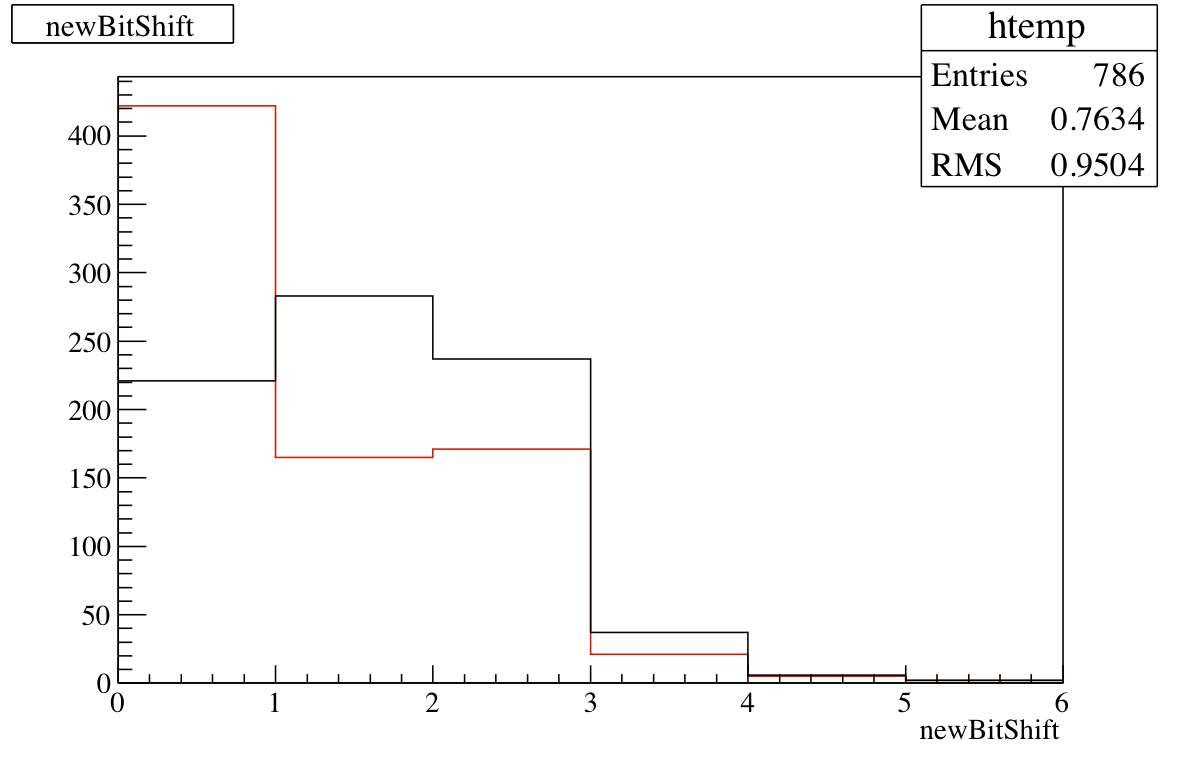
Figure 2: Large cell bit-shifts.

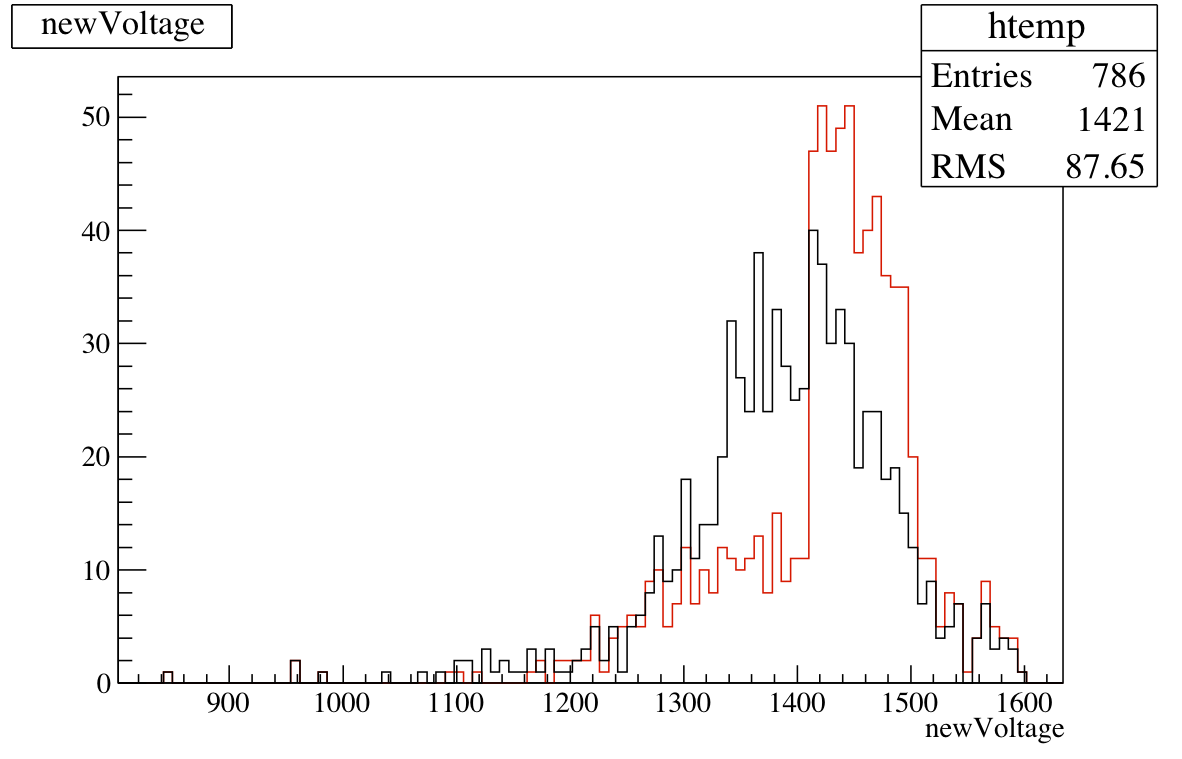
Figure 3: Large cell voltages.

There are still cases where we end up with large bit-shifts, if the requested gain factor is sufficently large. However I think that this approach will serve us better if we want to minimise the number of cells with large bit shifts. We already have an analysis of data taken with iteration 14 (by Steve Heppelmann, dated 13th Feb), therefore this new procedure shall be in effect from iteration 15 onwards.